Numerical study of hydrodynamic behavior and conversion efficiency of a two-buoy wave energy converter ＊

Cen Yang (楊岑), Yong-liang Zhang (張永良)

State Key Laboratory of Hydro-Science and Engineering, Tsinghua University, Beijing 100084, China

Introduction

The oscillating-buoy becomes a main kind of wave energy converters (WECs) to convert the wave energy into other useful energies, due to its advantages of smaller size, lower cost, simpler construction and mooring systems, compared with other kinds of WECs. An excellent review of the oscillating-buoy system for the wave energy conversion was made by Falcao[1]. Numerous theoretical and experimental studies were carried out to analyze the hydrodynamic and operating characteristics of oscillating-buoy WECs[2-8].

The studies however, mostly focused on the hydrodynamic characteristics of either a single-buoy system with or without a power take-off (PTO) system or a two-buoy system without a PTO system based on the linear wave theory. The hydrodynamic results for a semi-submerged cylindrical buoy WEC[9]show that with the increase of the wave frequency, the scattering cross-section, the heave radiation damping coefficient and the heaving response all increase firstly and then decrease after reaching a peak value, and the vertical wave force and the heave added mass are decreased.The maximum heaving responses increase with the increase of the water depth. It is also shown that with the increase of the buoy diameter, the vertical force,the heave added mass and the radiation damping coefficient are increased. When the buoy draught increases, the heave added mass increases, and the scattering cross-section, the vertical wave force and the heave radiation damping coefficient decrease. The effect of a caisson on the hydrodynamics of a semi submerged cylindrical buoy WEC was explored[10,11].It is found that the added mass, the radiation damping coefficient and the exciting wave force increase with the increase of the diameter and the thickness of the caisson. For a single-buoy WEC with a linear PTO system, the maximum wave energy conversion efficiency could be reached when its geometric and physical parameters and external loads are optimal and its natural frequency is close to the wave frequency[12,13].

By the 1990s, the studies of a single-buoy WEC were extended to a two-buoy WEC, consisting of a heaving semi-submerged buoy and a heaving submerged buoy. The hydrodynamic characteristics of a two concentric cylindrical buoy WEC with the same radius were studied[14]. It is shown that the heave added mass and the radiation damping coefficient of the semi submerged buoy decrease with the increase of the vertical distance between the double buoys. With the increase of the radii of the two buoys, the vertical force decreases, and the heave added mass and the radiation damping coefficient increase. Later, the effect of the submerged buoy radius on the hydrodynamics of a two-coaxial circular cylinder WEC was studied when the radius of the submerged buoy is larger than or equal to that of the semi-submerged one[15,16]. It is shown that the influence of the submerged buoy radius on the hydrodynamics of the semi-submerged buoy and the effect of the vertical distance between the two buoys on the heaving response of the semi-submerged buoy become significant mainly at a low wave frequency (with the wave number times the semi-submerged buoy radius less than 1.5). With the increase of the submerged buoy radius, the maximum values of the vertical exciting force on the semi-submerged buoy, the heave added mass, the radiation damping coefficient and the heaving amplitude of the semi-submerged buoy all increase. The maximum heaving amplitude of the semi-submerged buoy decreases with the increase of the vertical distance between the double buoys.

A two-buoy WEC with a linear PTO system was not well studied, even though in practical applications,the relative motion between two heaving buoys was often used to extract the wave energy. The operating characteristics of a two-heaving concentric cylinder WEC with the same radius were investigated[17]. It is found that the strategies of the displacement amplitude restrictions have no effect on the optimal damping and the spring coefficients, but could reduce the output power and the wave energy capture width of the system. Later, a study was carried out on the operating performance of a two-heaving concentric cylindrical buoy WEC with different radii[18,19]. With the increase of the submerged buoy diameter, the peak value of the wave energy conversion efficiency corresponding to the optimal load damping coefficient increases firstly and then decreases after reaching a peak value. And with the increase of the vertical distance between the double buoys, the peak value of the wave energy conversion efficiency corresponding to the optimal load damping coefficient increases whereas the wave frequency corresponding to the peak conversion efficiency decreases.

All these studies focused on the characteristics of a two-heaving buoy system in which the relative motion between two heaving buoys is used to extract the wave energy, and it is shown that the presence of a submerged heaving-buoy does not improve the wave energy conversion probably due to a smaller phase shift between the two heaving buoys. In this paper a fixed submerged buoy is considered and used hopefully to improve the wave energy conversion efficiency of a heaving semi-submerged buoy instead of directly being used to capture the wave energy.This paper presents a hydrodynamic analysis of a two-concentric cylindrical buoy WEC consisting of a heaving semi-submerged cylindrical buoy, a fixed submerged-cylindrical buoy and a PTO system (see Fig.1), focusing on the hydrodynamic behavior and the wave energy conversion efficiency over a wide range of the vertical distance between the double buoys, the diameter ratio of the fixed submerged-buoy to the heaving semi-submerged one and the water depth.

1. Mathematical model

Consider a two-buoy WEC composed of a heaving semi-submerged cylindrical buoy, a fixed submerged-cylindrical buoy and a linear PTO system,as shown in Fig.1. The semi-submerged buoy of diameterDf, thicknessHfand draughtDdfon the sea with water depthHwcan only move up and down along the standing guide bar under the action of incoming regular waves of periodT(frequency ω and wave numberk) and amplitudeA. The submerged-buoy of diameterDc, thicknessHcand submerged depthDdcis fixed onto the guide bar, and a linear PTO system which extracts the wave energy by utilizing the heaving response of the semi submerged buoy and the external load is modelled by a damping term proportional to the heaving displacement and the external load damping coefficient is given byCd.

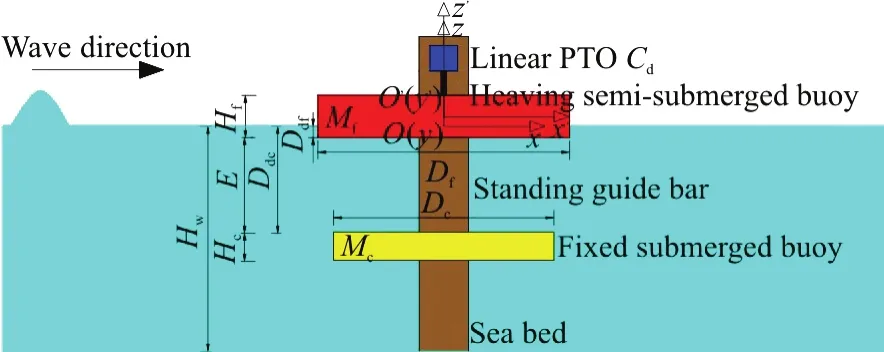
Fig.1 (Color online) Schematic diagram ofwave energy co

Based on the assumption that the fluid is incompressible and inviscid, and the wave amplitude and the heaving amplitude of the semi-submerged buoy are small relative to the wave length λ, the nonlinearity influence is weak, and then the motions of the fluid and the two-buoy WEC could be governed by the classical linear theory and the principle of the linear superposition and the frequency-domain analysis model can be used. We use two right-handed Cartesian coordinate systems, in which the global coordinate systemOxyzis defined with the originOin the undisturbed free surface andz-axis measured positive upwards, and the local coordinate systemO′x′y′z′ is attached to the semi-submerged buoy with originO′at the mass center of the buoy and the axes are all parallel the global ones. The propagation of the incident wave is alongx-axis.

1.1 Equation of fluid

Based on the linearized wave theory, the spatial velocity potential of the fluid φ can be decomposed into the incident velocity potentialiφ, the diffracted velocity potentialdφ and the radiated velocity potentialrφ, which all satisfy the Laplace equation and the related boundary conditions:

Laplace equation

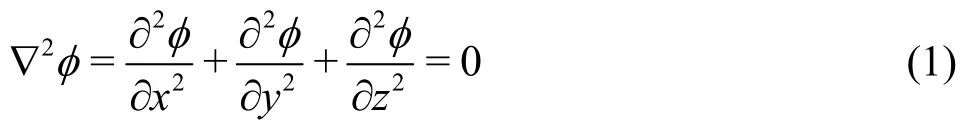
Surface and bottom boundary conditions

Interface conditions

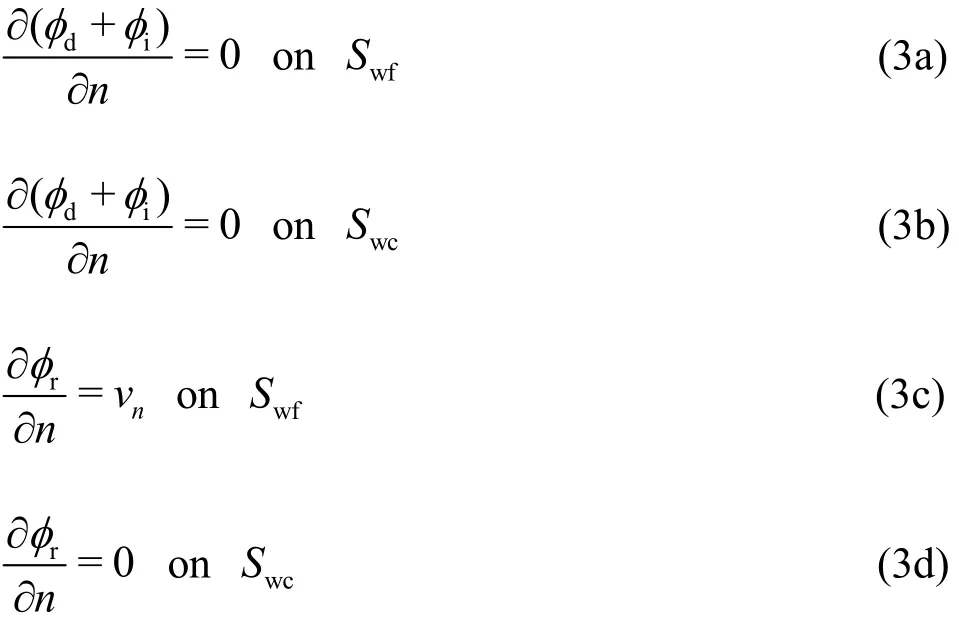
Sommerfeld radiation condition

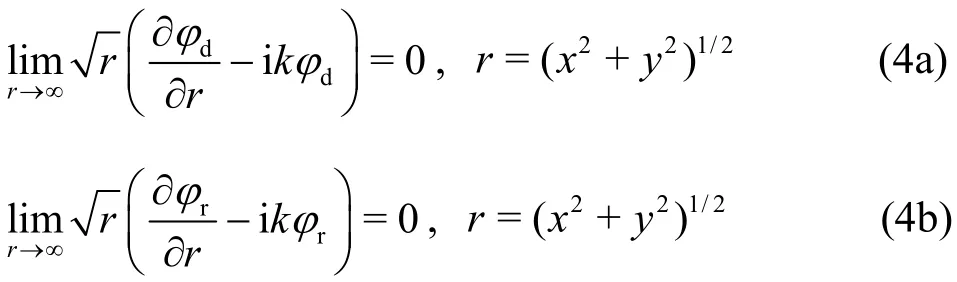
wheregis the acceleration of gravity,SwfandSwcare the average wetted surfaces of the semi submerged buoy and the submerged buoy, respectively,nis the normal direction of the wetted surface,vnis the velocity of the semi-submerged buoy normal to the wetted surface of two buoys, φdand φrare the two-dimensional diffracted and radiated velocity potentials, different from φdand φr, which are defined by φd=φd(x,y)Z(z) and φr=φr(x,y)Z(z), respectively. And the complex velocity potential could be written as Φ (x,y,z,t)=φ(x,y,z) e-iωt.

According to the linearized form of the Bernoulli equation, the vertical wave forces on the semi submerged buoy can be calculated as follows:

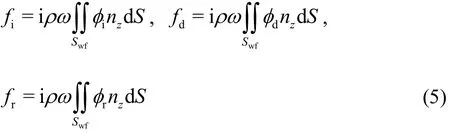
wherefi,fdandfrdenote the incident, diffracted and radiated wave forces on the semi-submerged buoy, respectively,nzdenotes the normal direction of thez-axis. The exciting wave force can be given byfe=fi+fdand the radiated wave force can be expressed by the hydrodynamic coefficients in terms of the added massMaand the radiation damping coefficientCa, which can be written asfr=, in whichanddenote the heaving velocity and acceleration of the semi-submerged buoy inO′x′y′z′, respectively.

The oscillating amplitude at (x,y) in the fluid domain under the diffracted wave could be calculated as follows

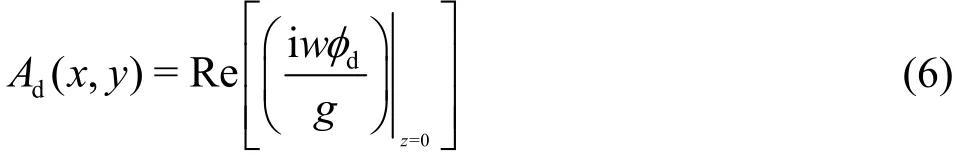
1.2 Equation of structure

The kinematic equation governing the heaving motion of the semi-submerged buoy can be expressed inO′x′y′z′ as

whereMfis the mass of the semi-submerged buoy,Awpis the water plane area of the semi-submerged buoy, the exciting wave force is given byfe=Fe-i(ωt+θ), in whichFand θ are defined as theeeamplitude and the phase of the exciting force,respectively,floadis the external load by the PTO system on the semi-submerged buoy and can be expressed asanddenote the displacement, the velocity and the acceleration of the semi-submerged buoy in the heave motion,respectively, and can be given byz′=Ame-i(ωt+δ),, in whichAmand δ denote the heaving amplitude and the phase of the semi-submerged buoy, respectively.

The kinematic equation of the semi-submerged buoy in the frequency domain can be written as

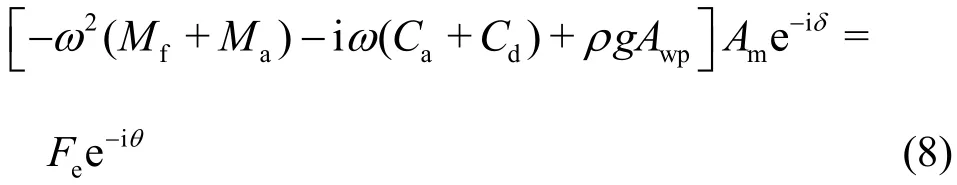
The average output power of the two-buoy WEC per wave period can be calculated as

The input power of the incident wave can be written as

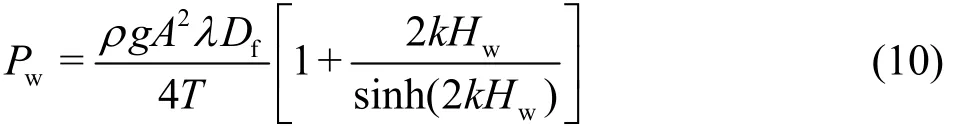
The conversion efficiency of the two-buoy WEC can be calculated by

1.3 Fluid-structure coupled boundary conditions

The pressure and the velocity at the interface between the fluid and the two-buoy WEC satisfy the continuity condition to couple the motions of the fluid and the two buoys:

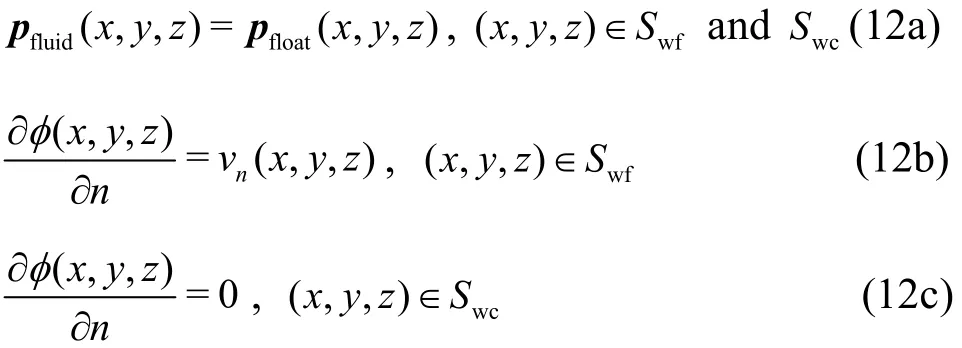
wherepfluid(x,y,z)is the dynamic pressure at(x,y,z) in the fluid,pfloat(x,y,z) is the pressure imposed by the fluid at (x,y,z) on the wetted surface of the two-buoy WEC.

1.4 Non-dimensionalisation

For generality, all variables used in the governing equations are non-dimensionlized as follows:

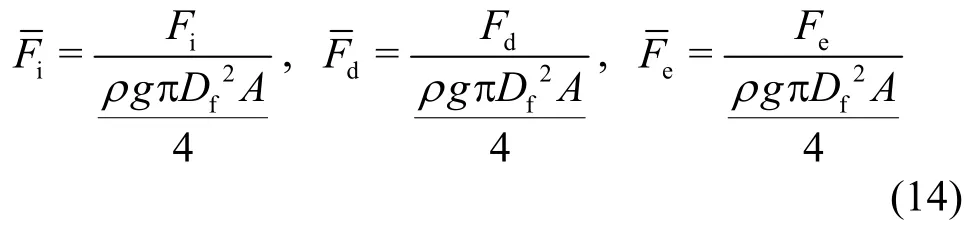
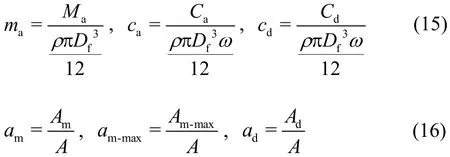
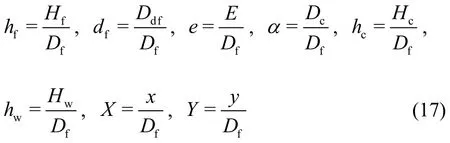
where?is the dimensionless wave frequency,,andare the dimensionless incident, diffracted and exciting wave force amplitudes on the semi-submerged buoy, respectively,maandcaare the dimensionless added mass and the radiation damping coefficient of the semi-submerged buoy,respectively,cdis the dimensionless damping coefficient of the external load,amis the dimensionless heaving amplitude of the semi-submerged buoy,am-maxis the dimensionless maximum heaving amplitude of the semi-submerged buoy corresponding to the optimal wave frequency,adis the dimensionless diffracted wave amplitude,hfanddfare the dimensionless thickness and draught of the semi submerged buoy, respectively,eis the dimensionless vertical distance between the semi-submerged buoy and the submerged one , α is the diameter ratio of the submerged buoy to the semi-submerged one,hcis the dimensionless thickness of the submerged buoy,hwis the dimensionless water depth,XandYare the dimensionlessx-axis andyaxis coordinates, respectively.

2. Numerical results and discussions

The governing equations for the fluid and the two-buoy WEC together with the boundary conditions given in Section 1 are solved by using a commercial code, based on the three-dimensional source distribution method. We present the results from the numerical solutions of the coupling equations governing the motion of the wave and a two-buoy WEC over a wide range of system parameters.

2.1 Convergence analysis and model validation

A convergence analysis of the spatial step of the numerical discrete method is performed, and the dimensionless heaving amplitude of the semi-submerged buoy against the dimensionless wave frequency,for different element numbers,N,is obtained. It is shown that the maximum heaving amplitude for anyNoccurs at Ω= 2.66, and that we have the largest difference in the heaving amplitude among differentNwhen Ω= 2.66. And the maximum heaving amplitude almost remains unchanged forN≥ 3520.Hence all subsequent calculations are therefore carried out by using 3520 elements.

Fig.2 Comparison of dimensionless added mass, dimensionless radiation damping coefficient and dimensionless exciting wave force amplitude between those obtained by using the present model and by Berggren (1992) or Zheng et al.[14]

In order to validate the present model, a comparison of the dimensionless added mass, the radiation damping coefficient and the exciting wave force amplitude in the heave is made between those obtained by using the present model and those obtained by Berggren (1992) and Zheng et al.[14], as shown in Fig.2. It can be seen that the hydrodynamic parameters of the semi-submerged buoy for the two-buoy WEC by using the present model agree well with those obtained by using the analytical model[14].

2.2 Influence of a fixed submerged buoy

In order to see the influence of the fixed submerged buoy on the hydrodynamic characteristics of the semi-submerged buoy and the wave energy conversion efficiency of the converter, a comparison of the characteristics between a single semi-submerged buoy WEC and a two-buoy WEC is made and the results are shown in Figs. 3-5. The geometric parameters of the semi-submerged buoy for a two-buoy WEC are the same as those of the single-buoy WEC which are given ashf=0.2,df=0.1, and the geometric parameters of the submerged buoy for the two-buoy WEC areα=1.00,hc=0.1,e=0.15, and the water depth is constant andhw=5.0.

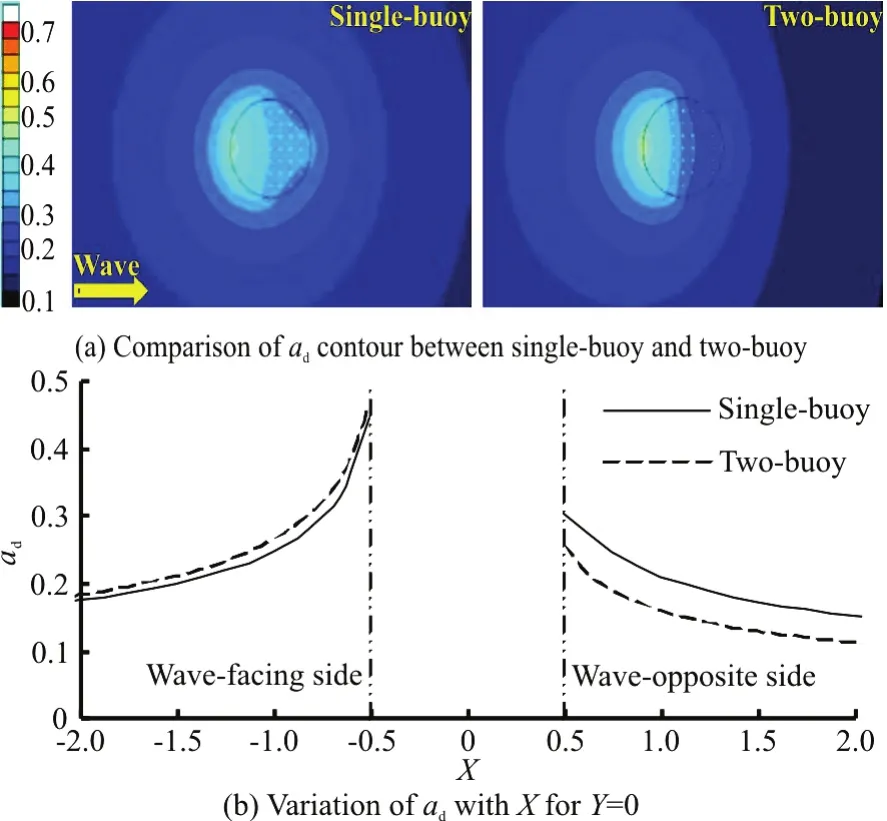
Fig.3 (Color online) Effect of a fixed submerged buoy for Ω=1.30

Figure 3 shows the difference of the dimensionless diffracted wave amplitude between the singlebuoy WEC and the two-buoy WEC for Ω= 1.30. It can be seen from Fig.3(a) that the presence of a fixed submerged buoy in a single semi-submerged buoy WEC generally increases the diffracted wave amplitude on the wave-facing side of the semi-submerged buoy and decreases the diffracted wave amplitudes on the opposite side of the semi-submerged buoy. Figure 3(b) clearly shows that the presence of a fixed submerged buoy in a single semi-submerged buoy WEC has a more significant effect on the diffracted wave amplitude on the wave-opposite side of the semi-submerged buoy than on its wave-facing side.

Figure 4 shows the comparison of the dimensionless diffracted and exciting wave forces on the semi-submerged buoy, and the dimensionless added mass and the radiation damping coefficient of the semi-submerged buoy between a single-buoy WEC and a two-buoy WEC. It can be seen that the presence of a fixed submerged buoy in a single semi-submerged buoy WEC decreases the maximum diffracted wave force, and increases the wave frequency corresponding to the maximum diffracted wave force, and then increases the exciting wave force on the semi subemerged buoy. It also shows that the presence of a fixed submerged buoy in a single semi-submerged buoy WEC increases the added mass and the radiation damping coefficient of the semi-submerged buoy.

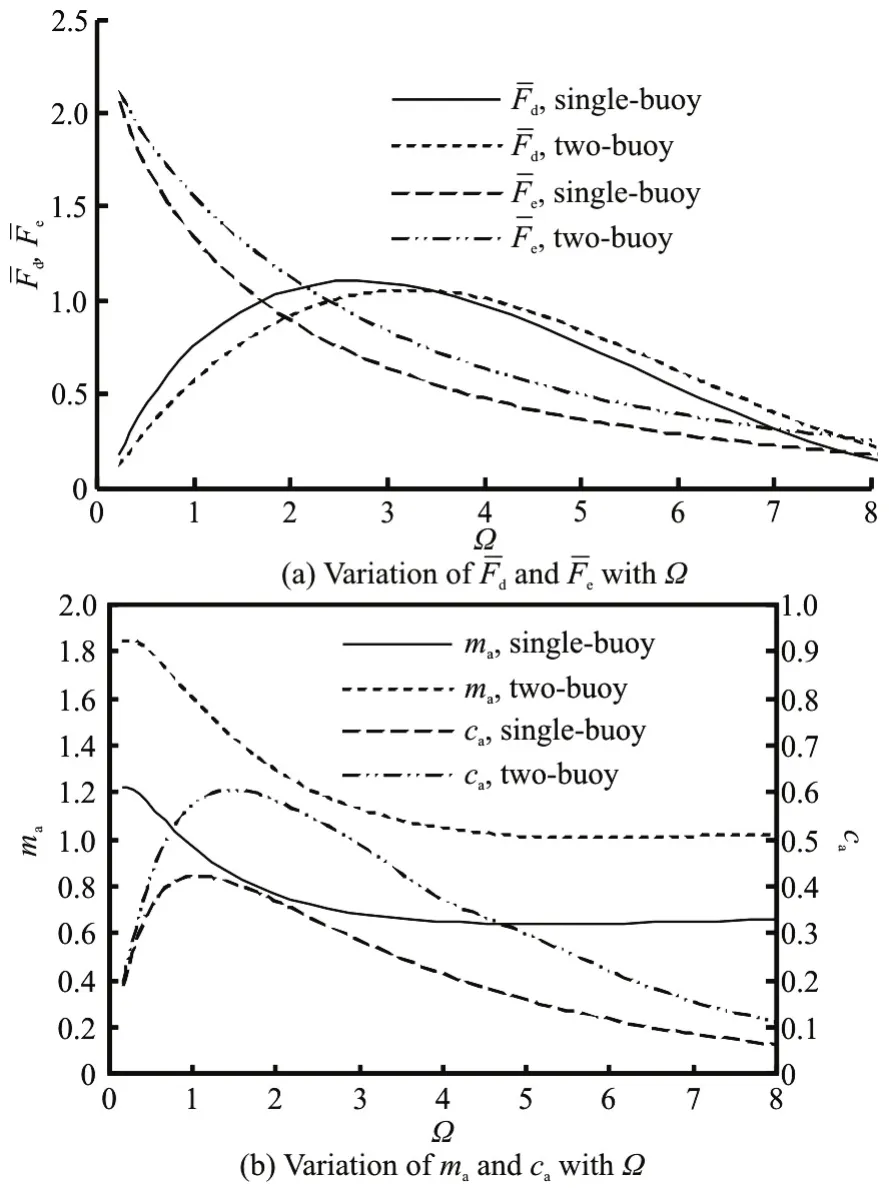
Fig.4 Comparison of dimensionless diffracted wave force amplitude, dimensionless exciting wave force amplitude,dimensionless added mass and dimensionless radiation damping coefficient between single-buoy WEC and two buoy WEC

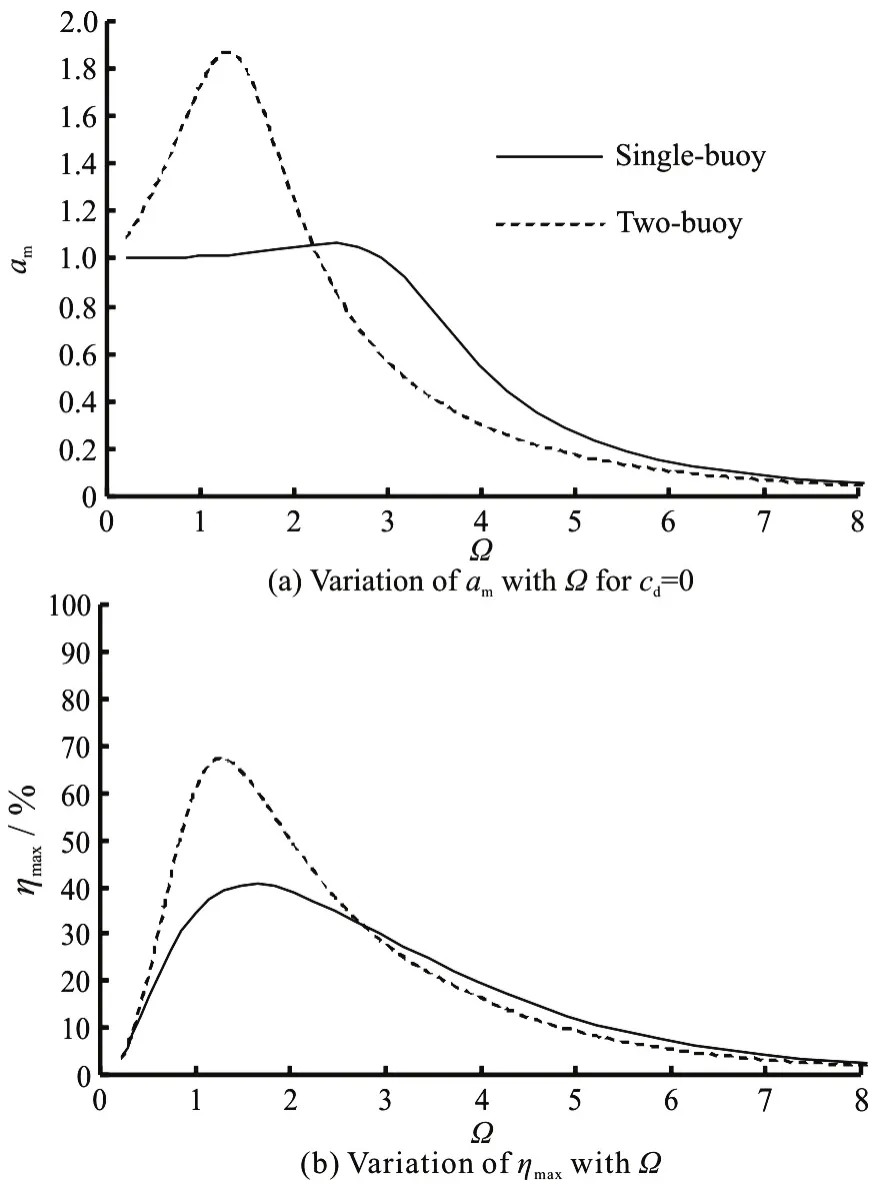
Fig.5 Comparison of dimensionless heaving amplitude of semi-submerged buoy,maximum wave energy conversion efficiency of converter corresponding to optimal load damping coefficient between single-buoy WEC and two-buoy WEC

Figure 5 shows the dimensionless heaving amplitude of the semi-submerged buoy, and the wave energy conversion efficiency corresponding to the optimal load damping coefficient (viz.cd=cd,opt),ηmax, against the dimensionless wave frequency for a single-buoy WEC and a two-buoy WEC. It can be seen from Fig.5(a) that the presence of a fixed submerged buoy in a single semi-submerged buoy WEC increases the maximum heaving amplitude and decreases the wave frequency correspinding to the maximum heaving amplitude. This is due to the fact that the presence of a fixed submerged buoy increases the added mass of the semi-subemerged buoy (see Fig.4(b)), leading to a decrease of the converter natural frequency. Figure 5(b) shows that the presence of a fixed submerged buoy in a single semi-submerged buoy WEC increases the peak wave energy conversion efficiency from 40% for the single-buoy WEC to 67%for the two-buoy WEC. If the diameter of a semi-submerged buoy,Df=8m, is considered, the optimal wave period and the load damping coefficient of a single-buoy WEC,Topt=4.4s andCd,opt=1.6× 105kg/s , can be obtained, respectively, and the optimal wave period and the loading damping coefficient of a two-buoy WEC,Topt=5.0s andC=1.3× 105kg/s , can also be obtained respecd,opttively. And the optimal wave periods of these two WECs both fall within the range of the practical wave condition in China seas, which is mainly in the range ofT=4.0s-6.0 s . Therefore, the presence of a fixed submerged buoy is conducive to enhancing the wave energy conversion efficiency of the semi-submerged buoy WEC.

2.3 Influence of distance between semi-submerged buoy and submerged buoy

As is well demonstrated that with the increase of the vertical distance between the two heaving concentric buoys, the peak wave energy conversion efficiency increases whereas the wave frequency corresponding to the peak decreases[19,20], therefore, we may ask whether the vertical distance between the heaving semi-submerged buoy and the fixed submerged-one plays a similar role in the hydrodynamics of a two concentric buoy WEC. The effect of the dimensionless vertical distance between the heaving semi-submerged buoy and the fixed submerged one, on the two-buoy WEC are examined forhf=0.2,df=0.1, α=1.00,hc=0.1,hw=5.0, as shown in Figs. 6-10.

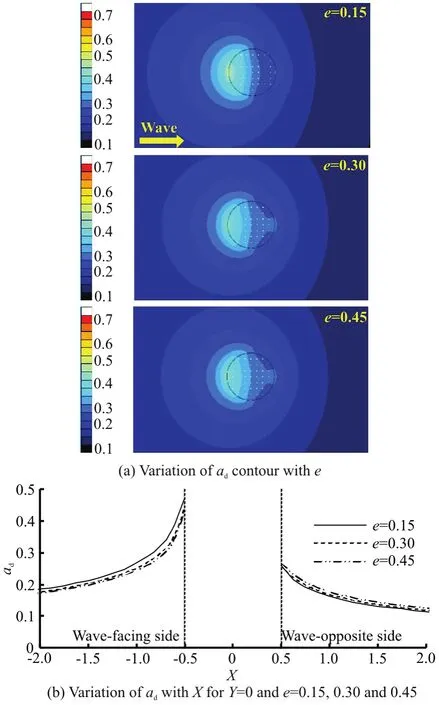
Fig.6 (Color online) Effect of dimensionless distance on dimensionless diffracted wave amplitude for Ω =1.30

Figure 6 shows the dimensionless diffracted wave amplitude against the dimensionless vertical distance between the double buoysfor Ω= 1.30. It can be seen from Fig.6(a) that with the increase ofe,the diffracted wave amplitude on the wave-facing side of the semi-submerged buoy generally decreases whereas that on the opposite side generally increases.Figure 6(b) clearly shows that the vertical distance between the double buoys has a small effect on the amplitude on both the wave-facing and wave-opposite sides of the semi-submerged buoy.

Figure 7 shows the dimensionless diffracted and exciting wave forces on the semi-submerged buoy against the dimensionless vertical distance between the double buoys. It can be seen from Fig.7(a) that with the increase ofe, the maximum diffracted wave force amplitude increases slightly, and the wave frequency corresponding to the maximum decreases.Figure 7(b) shows that the exciting wave force amplitude decreases with the increase ofe. So the maximum diffracted force for the two-buoy WEC with the least distance is the least while the exciting force for that is the largest.

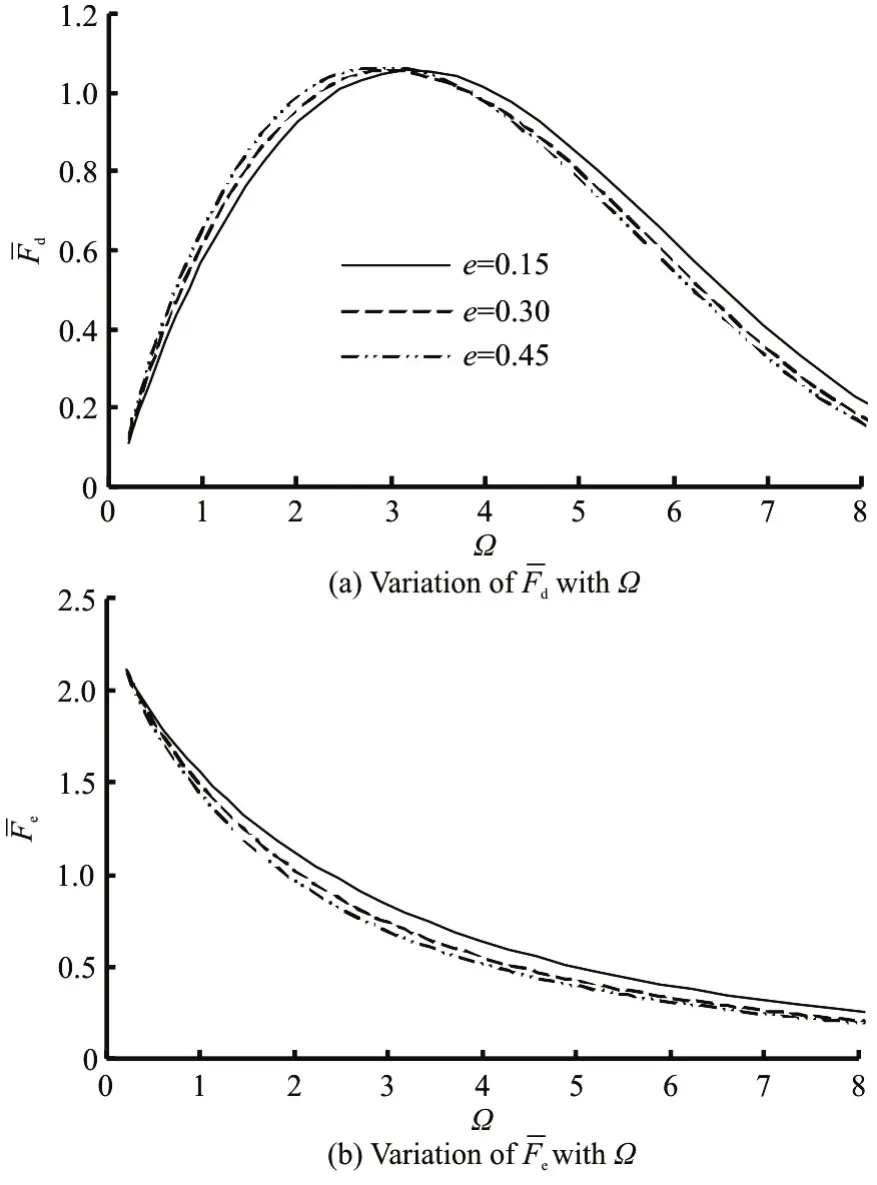
Fig.7 Effect of dimensionless distance on dimensionless diffracted wave force amplitude and dimensionless exciting wave force amplitude

Figure 8 shows the dimensionless added mass and the dimensionless radiation damping coefficient of the semi-submerged buoy against the dimensionless vertical distance between the double buoys. It can be seen thatmaandcaboth decrease with the increase ofe. The radiation damping coefficients for a low frequency (viz. Ω＜1.00) are identical for different distances.

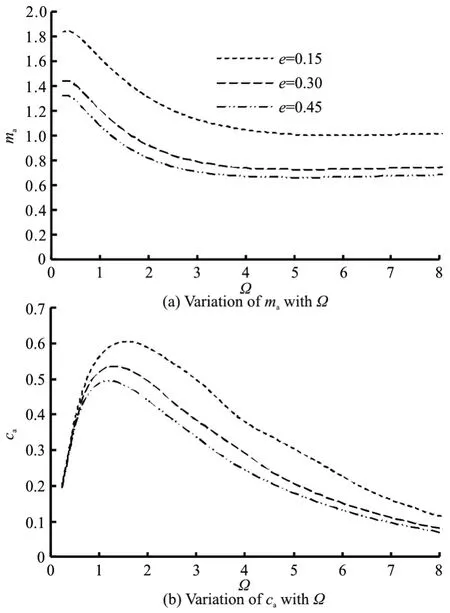
Fig.8 Effect of dimensionless distance on dimensionless added mass and dimensionless radiation damping coefficient

Figure 9 shows the dimensionless heaving amplitude of the semi-submerged buoy against the dimensionless vertical distance between the double buoys. It can be seen from Fig.9(a) that the maximum heaving amplitude of the semi-submerged buoy decreases, and the bandwidth of the heaving amplitude increases with the increase ofeforcd=0.The heaving amplitude against the distanceefor variouscdand Ω= 1.30 is shown in Fig.9(b). The heaving amplitude increases firstly and decreases after reaching a peak value with the increase ofefor various linear damping coefficients, and the peak heaving amplitudes for different damping coefficients all occur whene=0.10.

Fig.9 Effect of dimensionless distance (e) on dimensionless heaving amplitude of semi-submerged buoy (am)

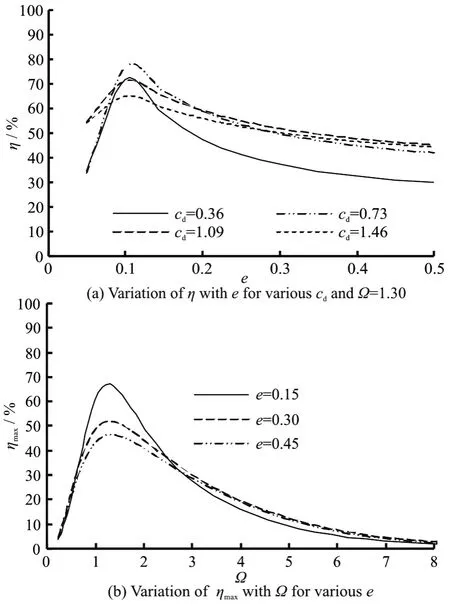
Fig.10 Effect of dimensionless distance on wave energy conversion efficiency

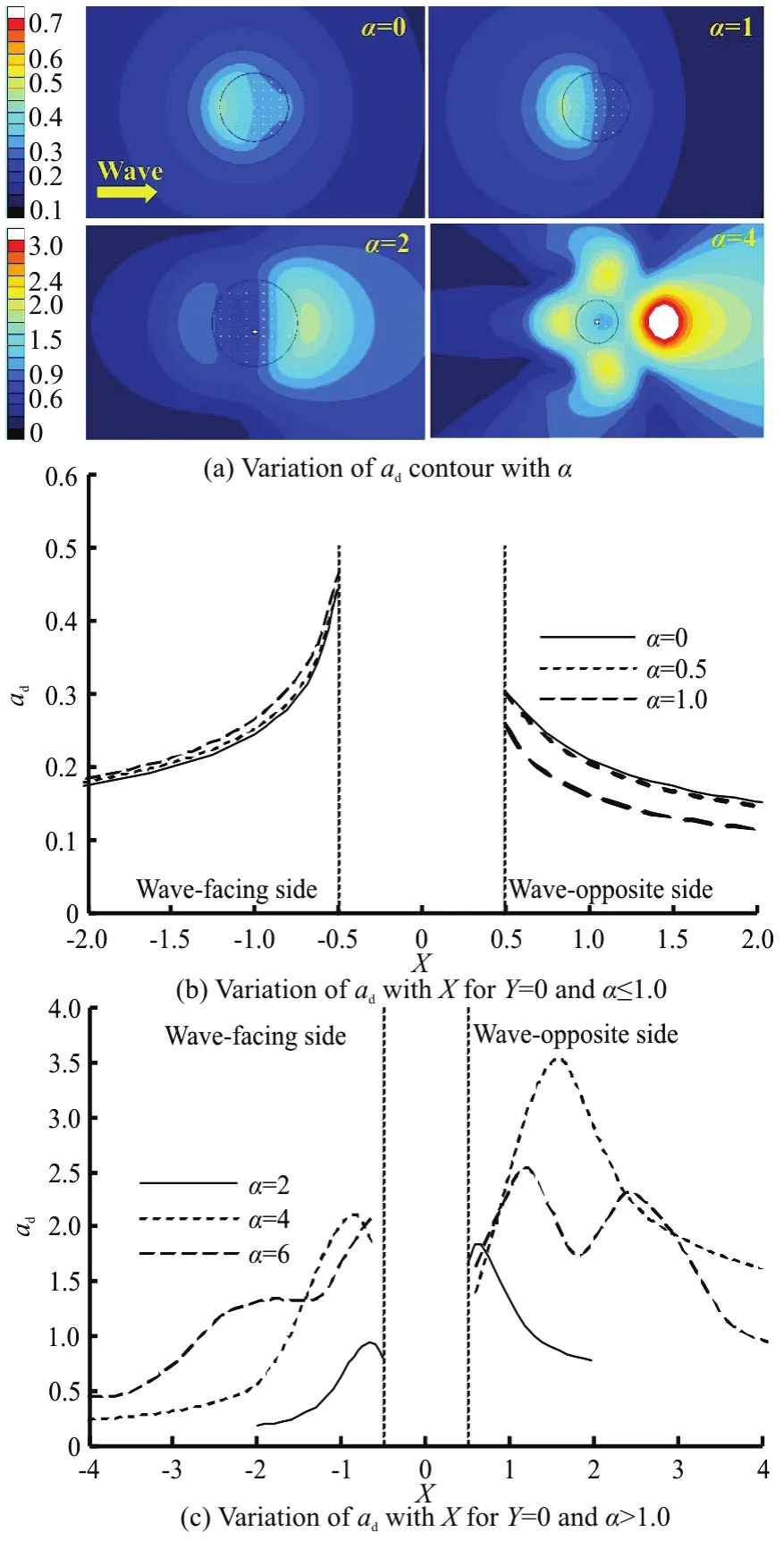
Fig.11 (Color online) Effect of diameter ratio on dimensionless diffracted wave amplitude for Ω=1.30

Figure 10 shows the effect of the dimensionless vertical distance between the double buoys on the wave energy conversion efficiency of the two-buoy WEC. It can be seen from Fig.10(a) that with the increase ofe, ηincreases firstly and decreases after reaching a peak value, and the peak wave energy conversion efficiencies forcd=0.36, 0.73, 1.09 and 1.46 all occur whene=0.10. The wave energy conversion efficiencies corresponding to the optimal load damping coefficient against Ω fore=0.15, 0.30 and 0.45 are shown in Fig.10(b). It can be seen that wheneincreases, the peak value of ηmaxdecreases whereas the curve bandwidth increases slightly, and the wave frequencies corresponding to the peak conversion efficiency are almost the same, viz.Ω= 1.30. This is different from the results for a two-heaving concentric buoy WEC, where the peak increases and the wave frequency corresponding to the peak decreases with the increase ofe.

2.4 Influence of diameter ratio

The effect of the diameter ratio of a heaving submerged-buoy to a heaving semi-submerged buoy on the characteristics of a two-concentric buoy system is significant[18,19]. It is necessary to examine whether the diameter ratio of a fixed submerged-buoy to a heaving semi-submerged one plays a similar role in the hydrodynamics of two concentric cylindrical buoys.

Figure 11 shows the dimensionless diffracted wave amplitude against the diameter ratio of the submerged buoy to the semi-submerged onefor Ω=1.30,hf=0.2,df=0.1,hc=0.1,e=0.15 andhw=5.0. It can be seen that the influence of α when α≤1.00 is different from that when α＞1.00.It can also be seen from Fig.11(a) that with the increase of α, the diffracted wave amplitude when α≤ 1.00 on the wave-facing side of the semi submerged buoy generally increases whereas that on its wave-opposite side generally decreases. The diffracted wave when α＞1.00 does not evenly spread to all around as that when α≤1.00 and with the increase of α, both the diffracted wave amplitude and the disturbance region surrounding to the semi submerged buoy generally increase. Figure 11(b)shows that the increment of αhas a more significant effect onadon the wave-opposite side of the semi submerged buoy than on its wave-facing side when α≤ 1.00, whereas Fig.11(c) shows that αhas a significant effect onadon both the wave-facing and wave-opposite sides of the semi-submerged buoy.

Figure 12 shows the dimensionless diffracted and exciting wave forces on the semi-submerged buoy against the diameter ratio. It can be seen from Fig.12(a) that the maximum diffracted force amplitude on the semi-submerged buoy decreases and its corresponding wave frequency increases with the increase of α when α≤1.00. The exciting wave force amplitude on the semi-submerged buoy increases with the increase of αwhen α≤1.00 as shown in Fig.12(b). The diffracted and exciting forces againstαwhen α＞1.00 are shown in Figs. 12(c), 12(d),respectively, with multiple peaks, not like the single peak curves of-Ωand the monotone curve of-Ωwhen α≤1.00. It can be seen that the influence of αonandis more significant mainly at a lower frequency when α＞1.00,compared with the case when α≤1.00.It can also be seen that when α＞1.00, as αincreases, the maximum peak values of the diffracted and exciting wave forces both increase, and the wave frequencies corresponding to the maximum peak values and the curve bandwidth decrease.

Figure 13 shows the dimensionless added mass and the dimensionless radiation damping coefficient against Ω for various diameter ratios. The variations ofmaandcawith Ωwhen α=0, 0.50, 0.75 and 1.00 are shown in Figs. 13(a), 13(b), respectively.

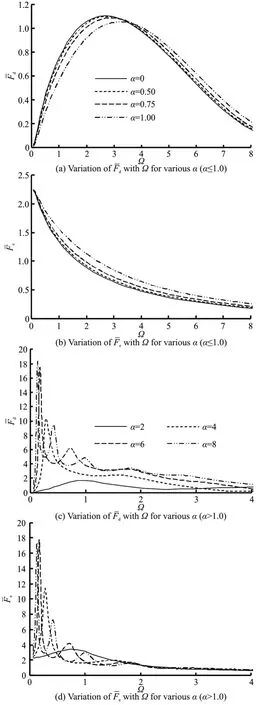
Fig.12 Effect of diameter ratio on dimensionless diffracted wave force amplitude and dimensionless exciting wave force amplitude

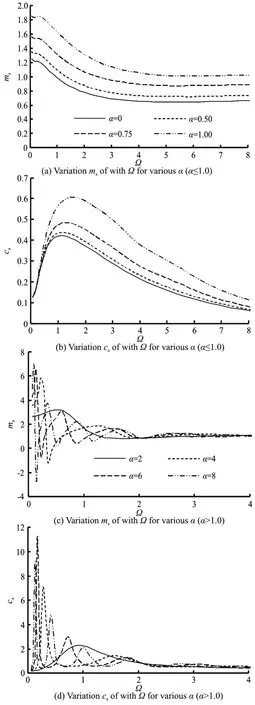
Fig.13 Effect of diameter ratio on dimensionless added mass and dimensionless radiation damping coefficient

It can be seen thatmaandcaboth increase with the increase of α,and that the radiation damping coefficient for various diameter ratios when Ω＜ 0.50 are almost identical. Figures 13(c), 13(d) show the variation ofmaandcawith Ωwhen α=2.00,4.00, 6.00 and 8.00. It is clearly shown that there are multiple peaks when α＞1.00, not like the monotone curve ofma-Ωand a single peak curveca-Ωwhen α≤ 1.00, and the influence of αwhen α＞1.00 is more significant mainly at a lower frequency, viz.,when Ω≤2.00, as compared with the case when α≤ 1.00.ma-Ωandca-Ωcurves fluctuate at a lower frequency and the maximum fluctuation amplitude increases with the increase of α. When α increases, the maximum added mass and the radiation damping coefficient both increase whereas the minimum added mass decreases.

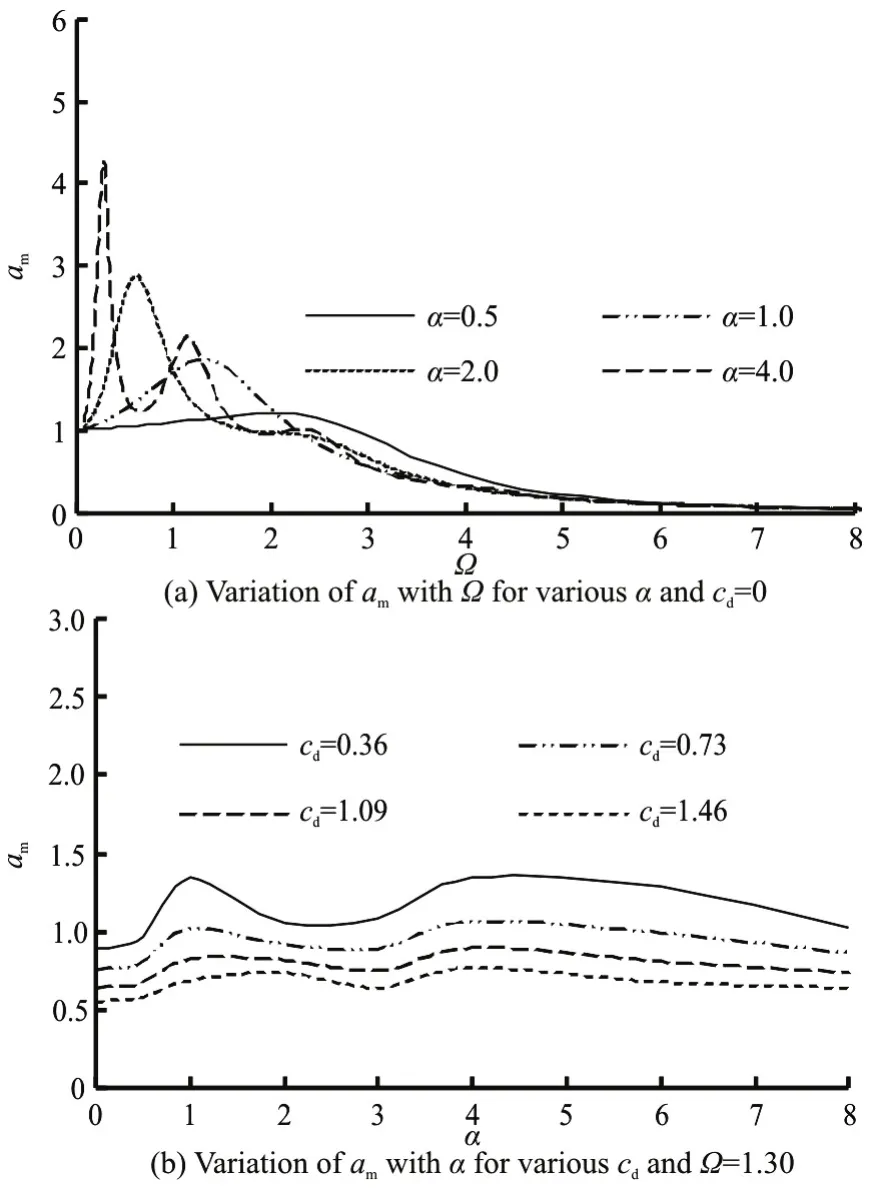
Fig.14 Effect of diameter ratio on dimensionless heaving amplitude of semi-submerged buoy

Figure 14 shows the effect of the diameter ratio on the heaving amplitude of the semi-submerged buoy.It can be seen from Fig.14(a) that with the increase of α, the maximum heaving amplitude of the semi submerged buoy increases whereas the wave frequency correspondingam-maxand the curve bandwidth decreases whencd=0. The variations ofamwith α for Ω= 1.30 andcd=0.36, 0.73, 1.09 and 1.46 are shown in Fig.14(b). It can be seen that the heaving amplitude decreases with the increase of the load damping and the curves ofam-α all have two peaks for variouscdin the examined range. One of the peak heaving amplitudes occurs at α=4.00 for various damping coefficients, and the other peak occurs at α=1.00 for a small damping coefficient,viz. whencd≤1.09, and occurs at α=2.00 for a larger damping coefficient, viz. whencd=1.46.

Figure 15 shows the effect of the diameter ratio on the wave energy conversion efficiency of the two-buoy WEC. Figure 15(a) shows the wave energy conversion efficiency against the diameter ratiofor variouscdand Ω= 1.30. It can be seen that with the increase of α, the wave energy conversion efficiency has two peaks for variouscd, with one at α= 4.00 for various damping coefficients, and the other at α=1.00 for a small damping coefficient,viz. whencd≤1.09, and at α=2.00 for a larger damping coefficient, viz. whencd=1.46. The wave energy conversion efficiencies corresponding to the optimal load damping coefficient against Ω for various α are shown in Fig.15(b). It can be seen that with the increase of α,the peak conversion efficiency increases, and the wave frequency corresponding to the peak and the curve bandwidth decrease.

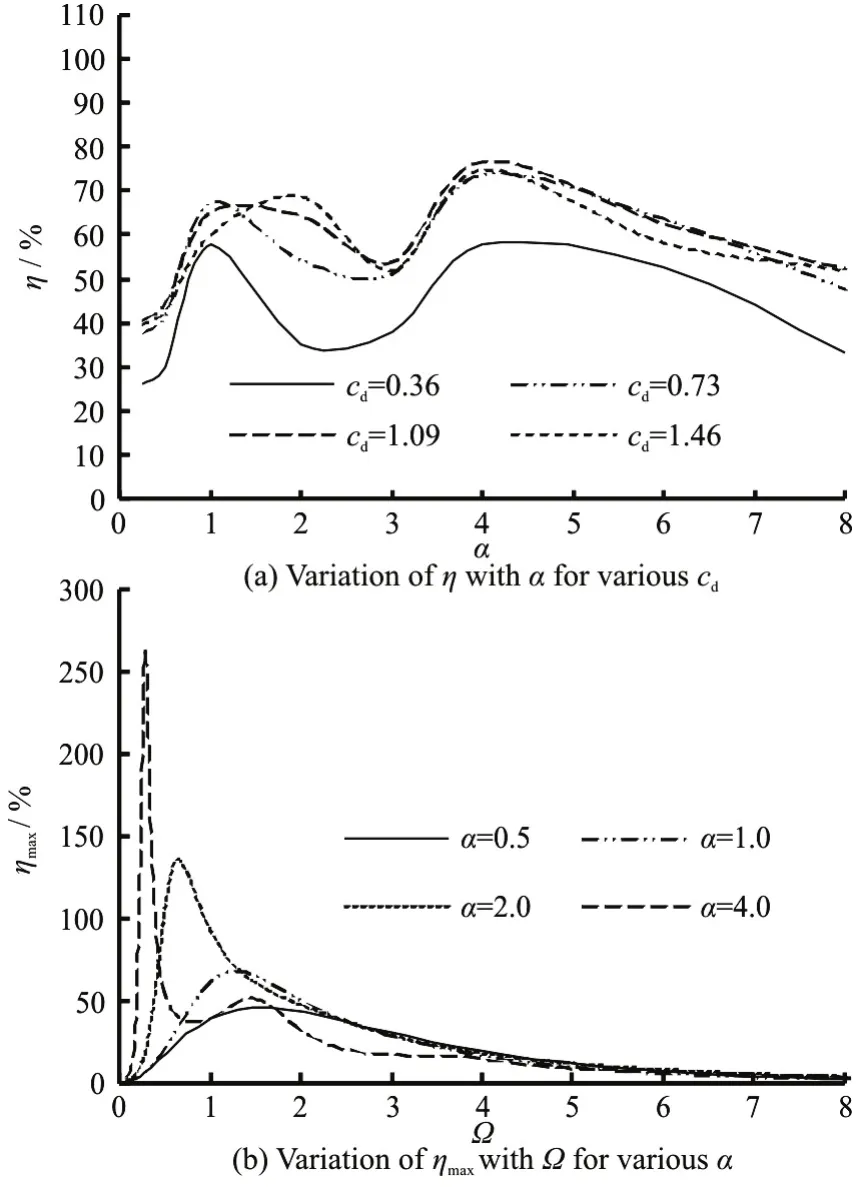
Fig.15 Effect of diameter ratio on wave energy conversion efficiency

2.5 Influence of water depth

The effect of the water depth on the hydrody-namics of the semi-submerged buoy and the wave energy conversion efficiency of the two-buoy WEC is examined forhf=0.2,df=0.1,hc=0.1,e=0.15, α=1.00.

Figure 16 shows the dimensionless diffracted wave amplitude against the dimensionless water depth for Ω= 1.30. It can be seen from Fig.16(a) that with the increase ofhwthe diffracted wave amplitudes surrounding to the semi-submerged buoy generally decrease. Figure 16(b) shows that the water depth has a significant effect on the diffracted wave amplitude on both the wave-facing and wave-opposite sides of the semi-submerged buoy.

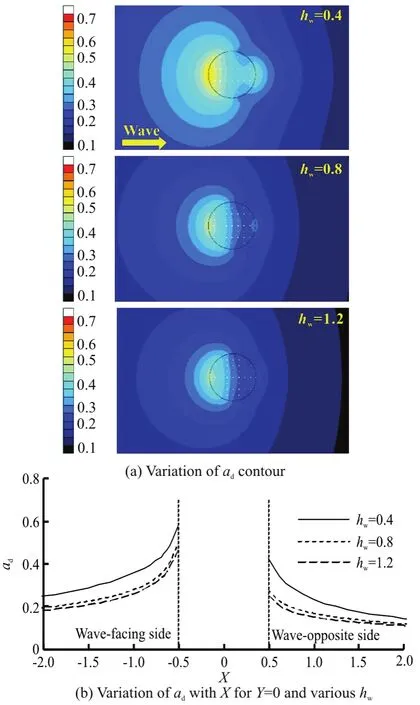
Fig.16 (Color online) Effect of dimensionless water depth on dimensionless diffracted wave amplitude for Ω=1.30

Figure 17 illustrates the dimensionless diffracted and exciting wave forces on the semi-submerged buoy against the dimensionless water depth. It can be seen that the diffracted and exciting wave force amplitudes both decrease with the increase of the water depth.

Figure 18 shows the dimensionless added mass and the dimensionless radiation damping coefficient against the dimensionless wave frequency for various water depths. It can be seen that the water depth has a significant effect on the radiation damping coefficient and the added mass, respectively, for a small Ω,but has less effects for a large Ω. With the increase of the water depth, the added mass decreases when Ω≤ 0.80 and the radiation damping decreases when Ω≤ 2.00, and the radiation damping coefficients at a very low frequency are different when the water depth changes.

Figure 19 shows the effect of the dimensionless water depth on the heaving amplitude of the semi submerged buoy. It can be seen from Fig.19(a) that with the increase ofhwthe maximum heaving amplitude increases, and the wave frequency corresponding to the maximum and the curve bandwidth decrease forcd=0. It can also be seen from Fig.19(b) that with the increase ofhw, the heaving amplitude increases firstly and decreases slightly after reaching a peak value for variouscdand the peak heaving amplitudes for variouscdall occur athw=1.2.

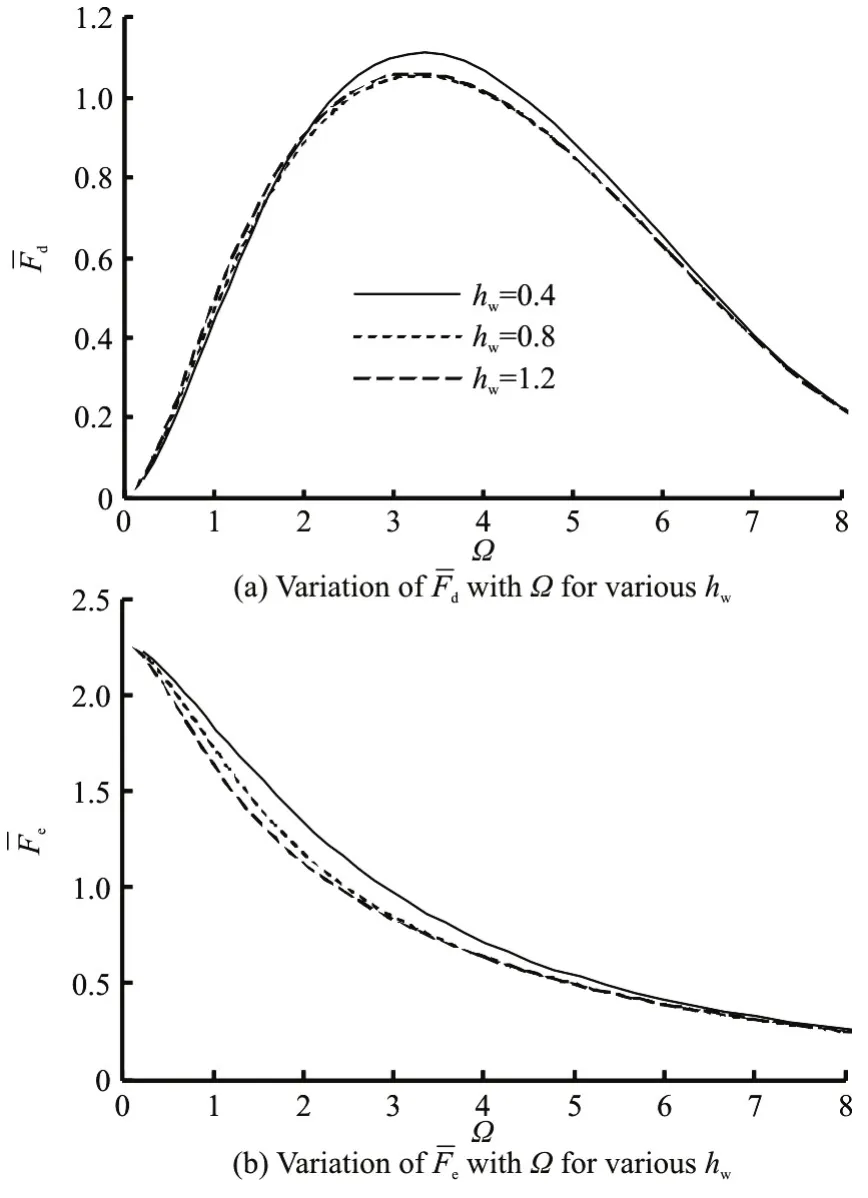
Fig.17 Effect of dimensionless water depth on dimensionless diffracted wave force amplitude and dimensionless exciting wave force amplitude

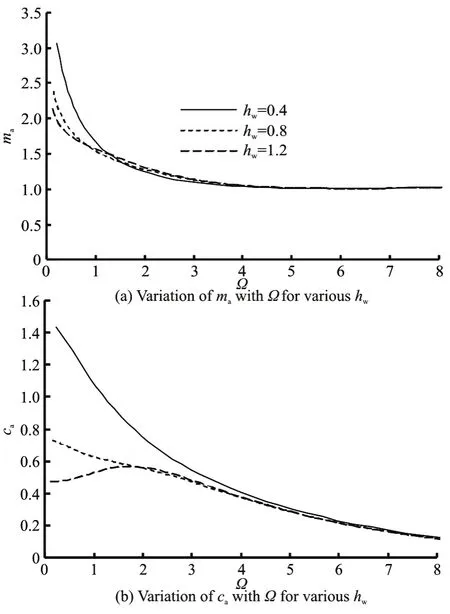
Fig.18 Effect of dimensionless water depth on dimensionless added mass and dimensionless radiation damping coefficient

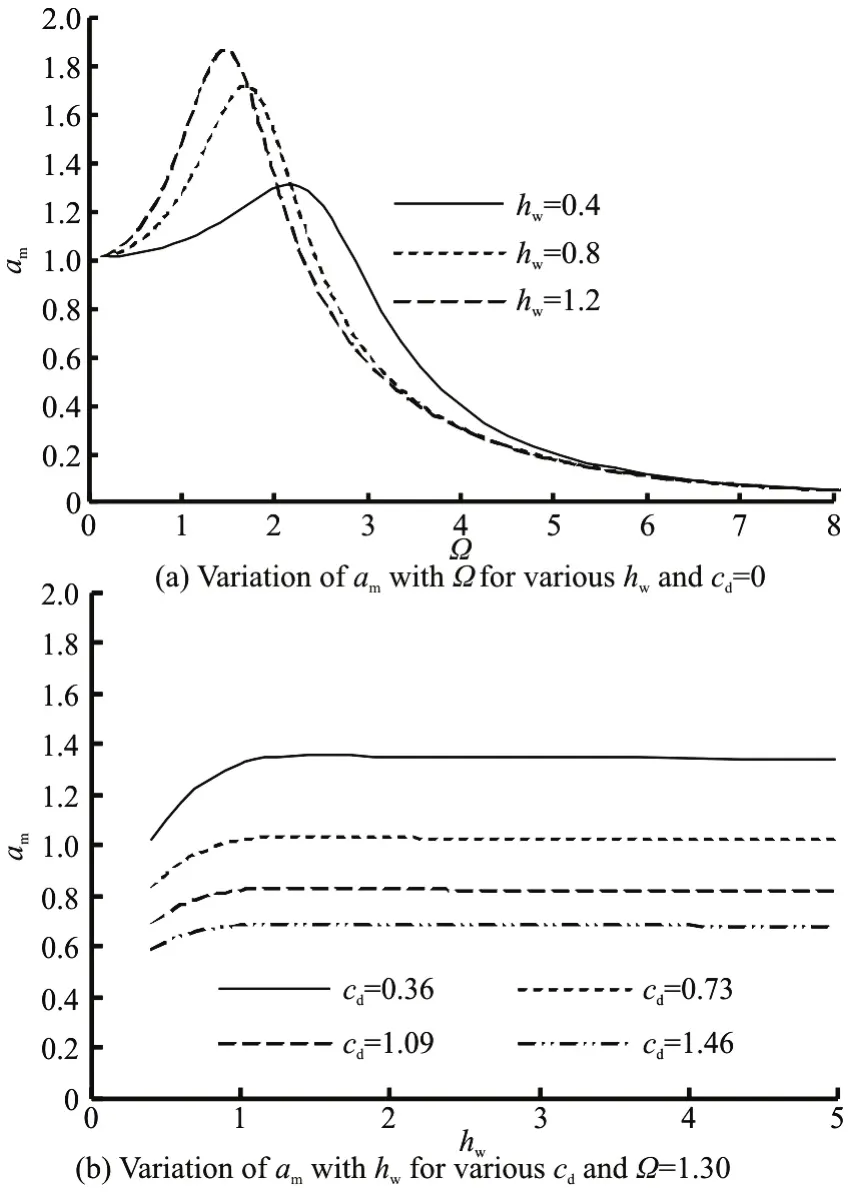
Fig.19 Effect of dimensionless water depth on dimensionless heaving amplitude of semi-submerged buoy

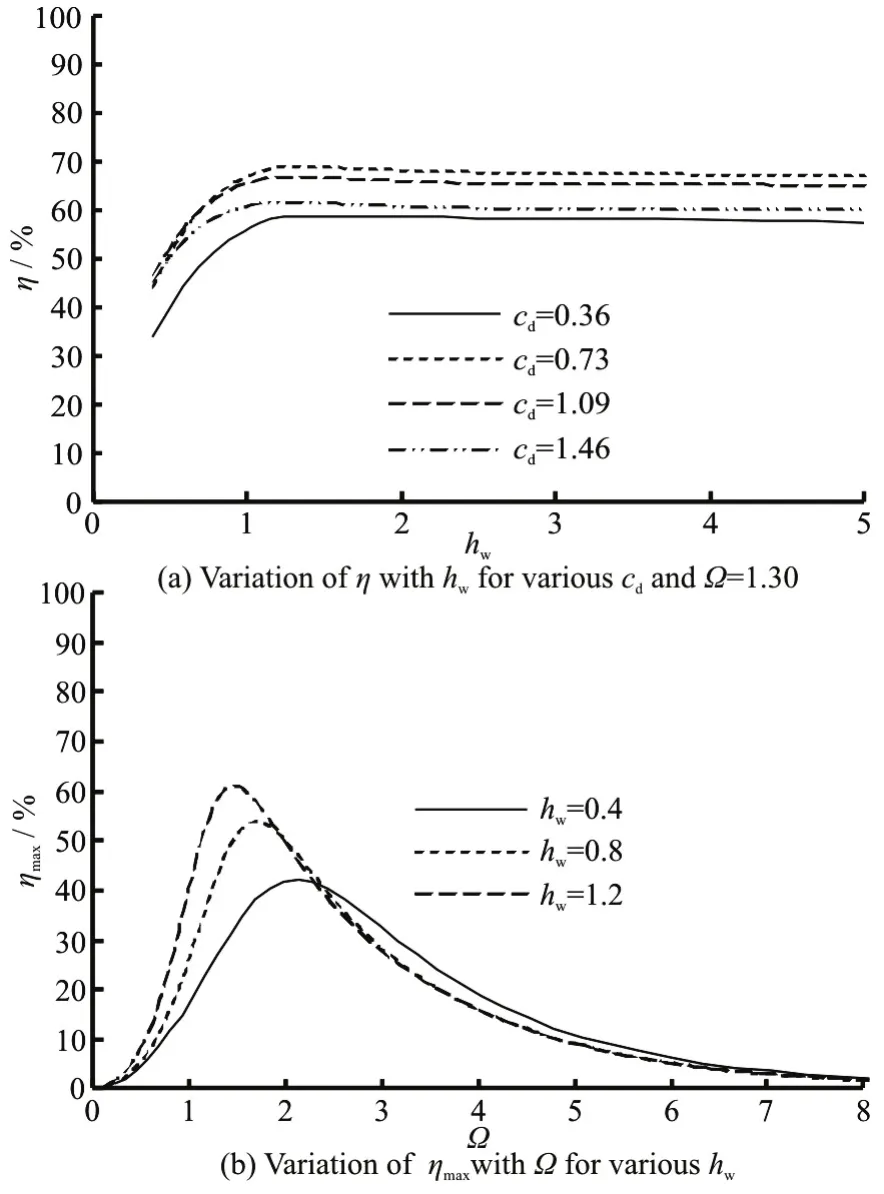
Fig.20 Effect of dimensionless water depth on wave energy conversion efficiency

Figure 20 illustrates the effect of the dimensionless water depth on the wave energy conversion efficiency of the two-buoy WEC. Figure 20(a) illustrates the wave energy conversion efficiency againsthwfor variouscdand Ω= 1.30. It can be seen that with the increase ofhw, the wave energy conversion efficiency increases firstly and decreases slightly after reaching a peak value, and the peak conversion efficiencies all occur athw=1.2 for variouscd.Figure 20(b) shows the wave energy conversion efficiency corresponding to the optimal load damping coefficient against Ω for varioushw. It can be seen that with the increase ofhw, the peak value of the conversion efficiency increases, and the wave frequency corresponding to the peak and the curve bandwidth decrease.

3. Conclusions

This paper presents an investigation of the influence of a fixed submerged buoy on the hydrodynamics of a semi-submerged buoy and the operation characteristics of the two-buoy WEC based on the three-dimensional potential theory. The effects of the distance between two concentric cylindrical buoys, the diameter ratio of the submerged buoy to the semi submerged buoy and the water depth on the hydrodynamics of the WEC are explored. It is concluded that:

(1) Generally, the presence of a fixed submerged buoy in a single semi-submerged buoy WEC increases the diffracted wave amplitude on the wave-facing side of the semi-submerged buoy, the exciting wave force,the added mass and the radiation damping coefficient of the semi-submerged buoy, but decreases the diffracted wave amplitude on its wave-opposite side and the maximum diffracted wave force on the semi submerged buoy.

(2) Compared with a single semi-submerged buoy WEC, the natural frequency of a single semi submerged buoy WEC with the presence of a fixed submerged concentric buoy is lower whereas the dynamic response of the semi-submerged buoy and the wave energy conversion efficiency of such a two buoy WEC are larger. The presence of a fixed submerged buoy in a single semi-submerged buoy WEC increases the peak value of the wave energy conversion efficiency corresponding to the optimal load damping coefficient by 67.5%. Therefore, the presence of a fixed submerged buoy can be a means to enhance the wave energy conversion efficiency of the semi-submerged buoy WEC.

(3) The maximum diffracted wave force on the semi-submerged buoy increases with either increasing the diameter ratio fora＞1.00 and the vertical distance between the double buoys or decreasing the diameter ratio fora≤1.00 and the water depth. The exciting wave force on the semi-submerged buoy increases with the increase of the diameter ratio fora≤8. 00 and with the decrease of the vertical distance fore≤0.50 and the water depth. The added mass and the radiation damping coefficient both increase with either decreasing the vertical distance and the water depth or increasing the diameter ratio.

(4) The peak value of the wave energy conversion efficiency corresponding to the optimal load damping coefficient, increases with the decrease of the vertical distance fore≤0.50 and the peak conversion efficiencies for variouseall occur at Ω= 1.30.This is different from the results for a two-heaving concentric buoy WEC where ηmaxincreases and the wave frequency corresponding to the peak decreases with the increase ofe. When the diameter ratio and the water depth increase, the peak value of the wave energy conversion efficiency corresponding to the optimal load damping coefficient increases.

Acknowledgement

This work was supported by the State Key Laboratory of Hydro-Science and Engineering,Tsinghua University (Grant No. 2013-KY-4).

[1] Falcao A. F. de O. Wave energy utilization: A review of the technologies [J].Renewable and Sustainable Energy Reviews, 2010, 14(3): 899-918.

[2] Vantorre M., Banasiak R., Verhoeven R. Modelling of hydraulic performance and wave energy extraction by a point absorber in heave [J].Applied Ocean Research,2004, 26(1): 61-72.

[3] Agamloh E. B., Wallace A. K., Jouanne A. V. Application of fluid–structure interaction simulation of an ocean wave energy extraction device [J].Renewable Energy, 2008,33(4): 748-757.

[4] Yang C., Zhang Y. L. Experimental study on operation performance of wave-driven pressure pump [J].Journal of Hydraulic Engineering,2013, 44(9): 1107-1111(in Chinese).

[5] Yang C., Zhang Y. L. Experimental study on operation performance of wave pressure pump [C].Proceedings of 1st International Conference on Renewable Energies Offshore, Lisbon, Portugal, 2014.

[6] Zheng S., Zhang Y. Wave radiation from a truncated cylinder in front of a vertical wall [J].Ocean Engineering,2016, 111: 602-614.

[7] Zheng S., Zhang Y. Wave diffraction from a truncated cylinder in front of a vertical wall [J].Ocean Engineering,2015, 104: 329-343.

[8] Chen X. B., Zhan J. M., CHEN Q. Numerical simulations of 2-D floating body driven by regular waves [J].Journal of Hydrodymics, 2016, 28(5): 821-931.

[9] Bhatta D. D., Rahman M. On scattering and radiation problem for a cylinder in water of finite depth [J].International Journal of Engineering Science, 2003, 41(9):931-967.

[10] Wu B. J., Zeng Y. H., YOU Y. G. et al. On diffraction and radiation problem for a cylinder over a caisson in water of finite depth [J].International Journal of Engineering Science, 2004, 42(11-12): 1193-1213.

[11] Hassan G., Bora S. N. Exciting forces for a pair of coaxial hollow cylinder and bottom-mounted cylinder in water of finite depth [J].Ocean Engineering, 2012, 50: 38-43.

[12] Su Y. L., You Y. G., Zheng Y. H. Investigation on the oscillating buoy wave power device [J].China Ocean Engineering, 2002, 16(1): 141-149.

[13] Falcao A. F. de O. Modelling and control of oscillating body wave energy converters with hydraulic power takeoff and gas accumulator [J].Ocean Engineering, 2007,34(14-15): 2021-2032.

[14] Zheng Y. H., Shen Y. M., You Y. G. et al. Hydrodynamic properties of two vertical truncated cylinders in waves [J].Ocean Engineering, 2005, 32(3): 241-271.

[15] Wu B. J., Zheng Y. H., YOU Y. G. et al. On diffraction and radiation problem for two cylinders in water of finite depth [J].Ocean Engineering, 2006, 33(5): 679-704.

[16] Wu B. J., Hu C., Zheng Y. H. et al. Heaving-motion response of two freely floating vertical cylinders [J].Journal of Hydrodynamics,Ser.A, 2006, 21(4): 458-464(in Chinese)

[17] Candido J., Justino P. A. P. Modelling, control and Pontryagin Maximum Principle for a two-body wave energy device [J].Renewable Energy, 2011, 36(5):1545-1557.

[18] Wu B. J., Wang X., Diao X. H. et al. Response and conversion efficiency of a wave energy device consisting of double cylindrical semi-submerged buoys with two degrees of freedom [J].Scientia Sinica Physica, Mechanica and Astronomica, 2013, 43(8): 978-986(in Chinese)

[19] Lin L. Q., Wu C. X., Wu B. J. Study on power conversion features of the two-buoy wave energy device [J].Journal of Shanghai Ocean University, 2014, 23(3): 475-480(in Chinese).