An Iterative Relaxation Approach to the Solution of the Ham ilton-Jacobi-Bellman-Isaacs Equation in Nonlinear Optimal Control

M.D.S.Aliyu,

I.INTRODUCTION

O PTIMAL control problems can be solved using either the minimum principle of Pontryagin[1],[2]or the dynamic programming principle of Bellman,also known as Hamilton-Jacobi theory[1],[2].The latter approach involves the solution of a nonlinear partial-differential equation also known as the Hamilton-Jacobi equation,which was originally derived by Hamilton[3]in 1834 from a mechanics perspective,and later on improved by Jacobi[3]in 1838.The Hamilton-Jacobi equation(HJE)gives necessary and sufficient conditions for the existence of an optimal control for both constrained and unconstrained problems.Lateron,Bellman[1],[2]developed the discrete-time equivalent of the Hamilton-Jacobi equation also known as the dynamic programming principle,and it became known as the Hamilton-Jacobi-Bellman equation.Finally,in 1952,Isaacs[4],[5]further modified it in the context ofN-player non-zero sum differential games,and it became known as the Hamilton-Jacobi-Bellman-Isaacs equation(HJBIE).

Unfortunately,a bottle-neck in the practical application of nonlinear optimal control theory is the difficulty in solving the HJBIE[6]?[17]There are no closed-form solutions for it,and no proven established systematic numerical approaches for solving it.

Several attempts have however been made to find computationally sound methods for solving the HJBIE,and there is a vast literature on the subject.The reader can refer to[18],[19]for an excellent literature review of past approaches.In Glad[14],Lukes[15],Isidori[20],[21],and Huang[22],Taylor series approximations are presented.While in[16]?[19],[23]Gallerkin and other basis functions expansions are used.More recently,in[24],[25]policy iterations are used to deriveiterative solutions in closed-form.This method is also similar in spirit with the ones presented in[18],[19].However,the validity of the method has only been demonstrated with scalar systems.A similar recursive approach is utilized in[7].

In addition,attempts to find exact and analytical approaches for solving the HJBIE have also been made in[5],[8]?[10],[26].The approaches attempt to convert the HJBIEs to algebraic equations,the solution of which can yield the gradient of the desired scalar function.In fact,these were some of the first attempts to derive closed-form solutions to the HJBIEs.However,the success of the approaches in[8],[9]is significantly undermined by the difficulty of solving the resulting discriminant equations.Alternatively,in[26]an attempt is made to find the algebraic gradient from the maximal involutive ideal that contains the Hamiltonian function of the corresponding Hamiltonian system.This approach is mainly useful for Hamiltonians in polynomial form.

On the other hand,in[12],[22]neural network or basis functions and Taylor series approximations respectively,are utilized to obtain recursive solutions to the discrete-time problem.These methods share a lot of spirit with the one originally developed in[23],and are so far some of the most tangible approaches to the discrete-time problem.

The problems with most of the methods so far presented are two fold:1)they are computationally expensive,requiring the solution of a system ofNnonlinear equations,forNbasis functions;2)they do not approximate the scalar function directly,but instead,approximate its gradient.This can lead to undesirable solutions.Consequently,more efficient approaches are still required and desirable.

Thus,in this paper,we present yet a new iterative approach to the solution of the HJBIEs.We apply fixed-point iterations[27],[28]in Banach spaces with a relaxation parameter,to successively approximate the scalar value-function directly,as opposed to its gradient,and we establish convergence of the approach under fairly mild assumptions.The approach is computationally efficient and can easily be automated using symbolic algebra packages such as MAPLE,MATHEMATICA,and MATLAB.It is hoped that the results presented in this paper and subsequent papers will represent the first attempts for establishing a systematic computationally efficient approach for solving the HJBIE which hitherto has been lacking.

The rest of the paper is organized as follows.In Section II,we begin with preliminaries and problem definition.Then in Section III,we develop the iterative relaxation method for the HJBIE in deterministic nonlinear optimal control.Convergence results for the method are established and some examples are presented.Then in Section IV,we extend the results of Section III to Lyapunov equations,and an example is also worked-out.Finally,conclusions and suggestions for future work are presented in Section V.

II.PRELIMINARIES

We consider the time-invariant or stationary HJBIEs associated with the infinite-horizon optimal control of the following smooth affine nonlinear state-space system Σdefined over a subsetX?Rnin coordinates(x1,...,xn):

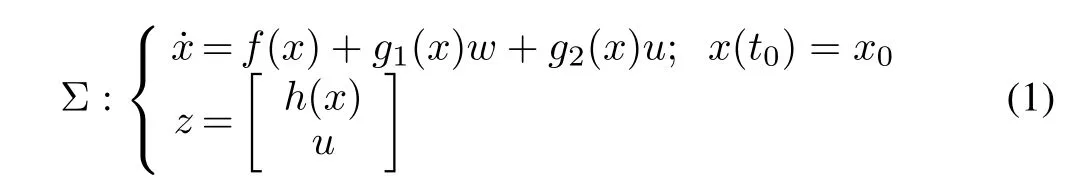
wherex=(x1,...,xn)T∈Xis the state vector;w∈W?Rsis the disturbance into the system which belongs to the setWof admissible disturbances;u∈Uis the control input,which belongs to the setU?Rpof admissible controls;andz∈Rris an objective or error function.Whereas1:X→Rn×s,andg2:X→Rn×p,h:X→Rm.We also assume that foru∈U,and anyx(t0)∈X,there exist smooth solutions to the system Σ[29].In addition,x0=0 is an equilibrium point of the system such that forw=0,u=0,f(x0)=0.

The time-invariant HJBIE associated with the above system either for theH2optimal control[2],[4],[18]or for theH∞optimal control[5],[21],can generally be represented by

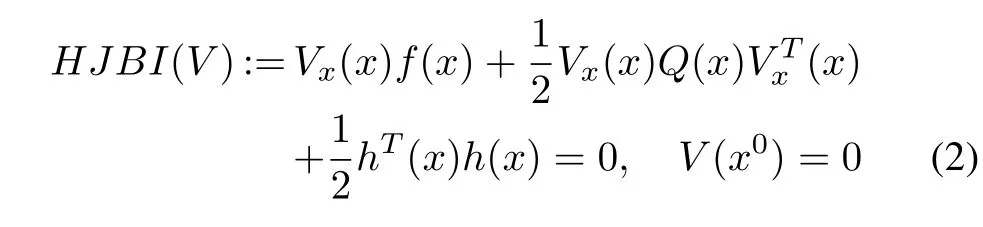
for some smooth functionwhereVxrepresents the row vector of partial derivatives ofVwith respect tox,a smooth matrix functionQ:X→M n×n(X),whereM n×nis the ring ofn×nmatrices overX,and for some smooth output functionh:X→Rm.For instance,in the case of the state-feedback nonlinearH∞control problem[5],the matrix functionwhile for theH2problem[14],[18],[19]

Our aim in this paper is to find iteratively an approximate solution of the HJBIE(2)associated with the optimal control of system(1)in a region ??X.We consider the Banach space of bounded real continuous functions from ? to R with the supremum norm,BC((?,R),sup|.|),which for brevity we shall simply denote byBC(?).However,we shall focus particular attention to a subset of this set containing functions that are also smooth,i.e.,V(?):=C∞∩BC(?).

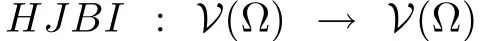
III.RELAXATION METHOD FOR THE HJBIE

Our aim in this section is to develop a gradient-free iterative or successive approximation method for solving HJBIE arising in optimal control problems for affine nonlinear systems.Notice that,sinceVdoes not appear explicitly in(2),a gradient based method such as the steepest-descent or New ton’s method[11],[27],[28],their variants will not be suitable to use at this point.However,the relaxation method becomes very handy in this respect.Accordingly,define the following iterative inverse map by

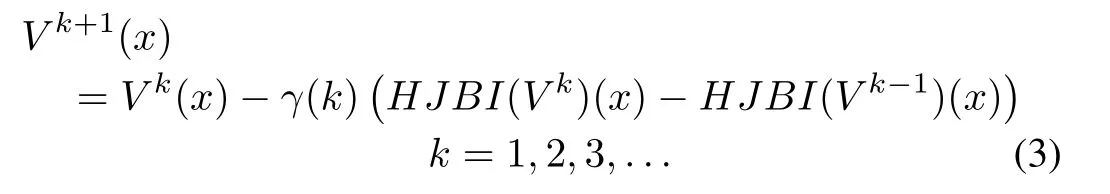
where 0＜γ(k)＜1 is the relaxation parameter which is chosen carefully to improve convergence.

Based on the iterative formula(3),we proceed to establish convergence results for the approximation error|Vk+1(x)?V?(x)|,and forVk,k=0,1,...to a smooth solution of the HJBIE(2).The following assumption on the system(1)will be essential.

Assumption 1:For the nonlinear system Σ(1),the following hold:

1)there exists a solutionV?∈V(?)to the HJBIE(2)for the system,i.e.,V?∈C∞(?)and sup?|V?(x)|＜∞;

2)(real constants)such that

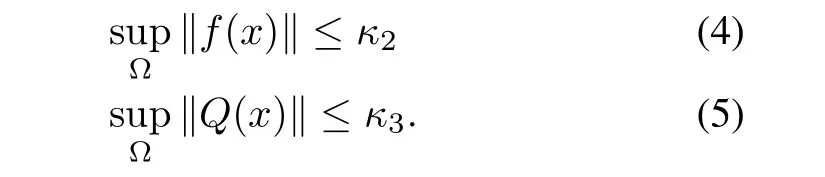
Proposition 1:Consider the HJBIE(2)and let Assumption 1 be satisfied by the system.Suppose in addition,the solutionV?to the HJBIE(2)is such that

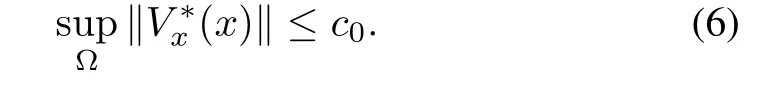
Then,starting with an approximationV0∈V(?),the approximation error at every iteration of the formula(3)remains point-wise bounded for all(rsmall).

Proof:From(3)and noting thatH JB I(V?)=0,we have

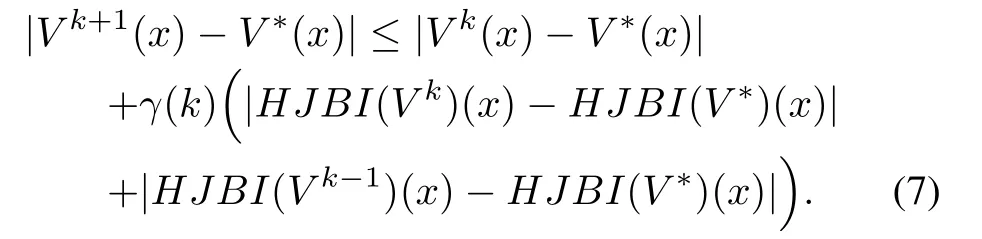
Now from(2),

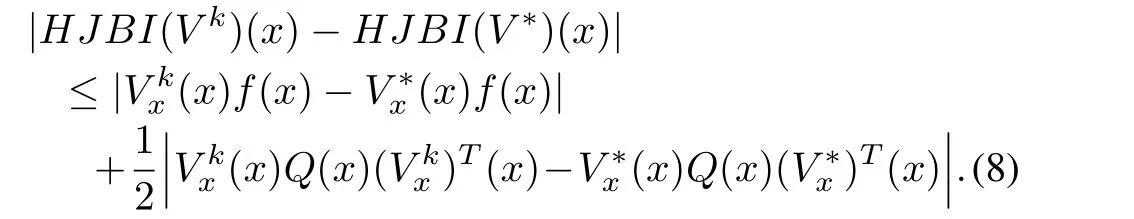
Observe also that

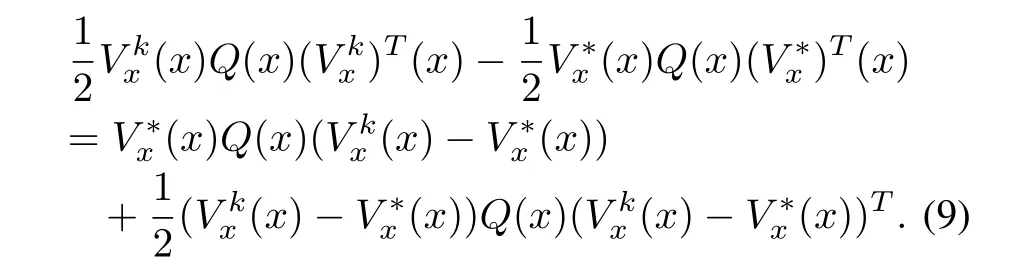
Therefore,using(9),(8)in(7),we have

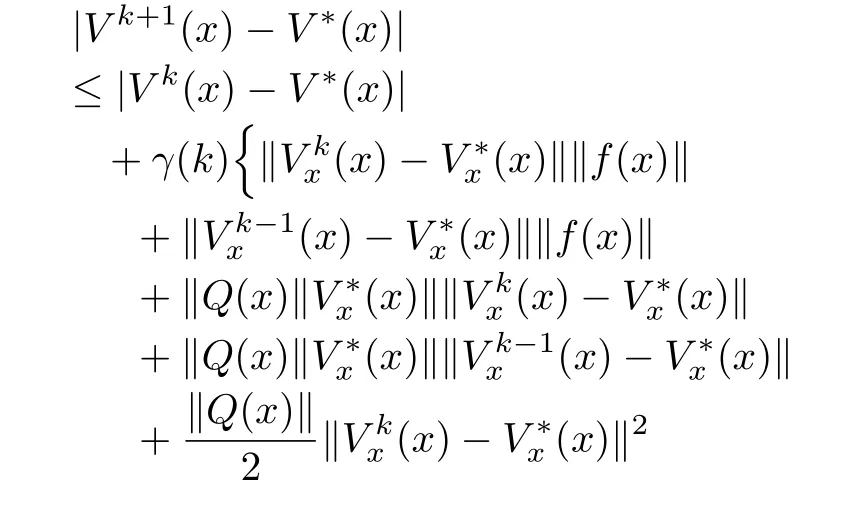
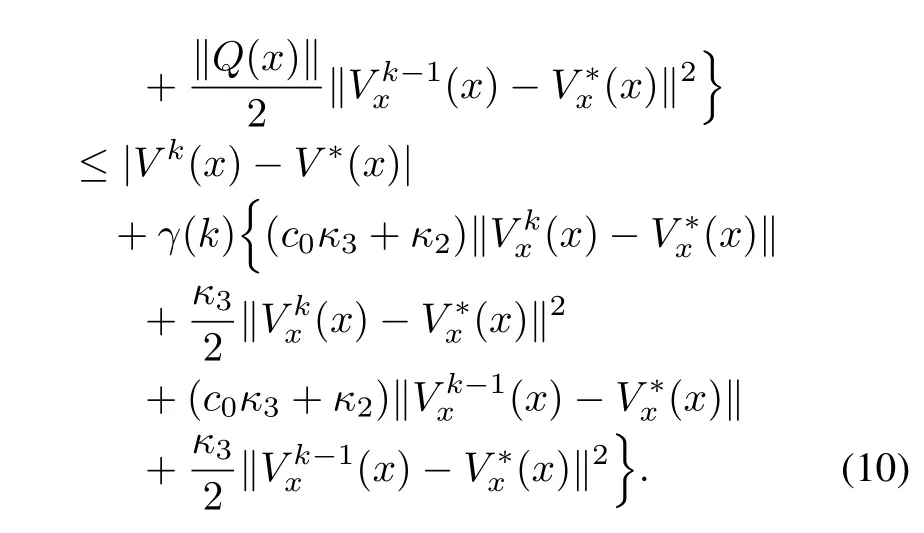
It is desired to compute smooth successive approximationsVk,k=1,...to the solutionV?of(2)in the neighborhood ?r.Thus,the differencecan be estimated as

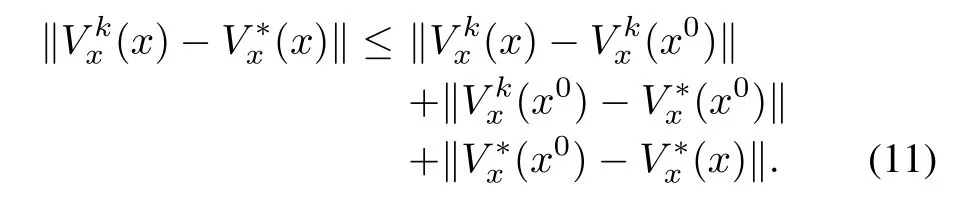
IfV0(x)is smooth,then the iterative formula(3)generates smooth(except possibly at isolated points)successive approximationsVkto the solutionV?of(2).Thus,for‖x?x0‖＜r,?ε1＞0,ε2＞0 such that

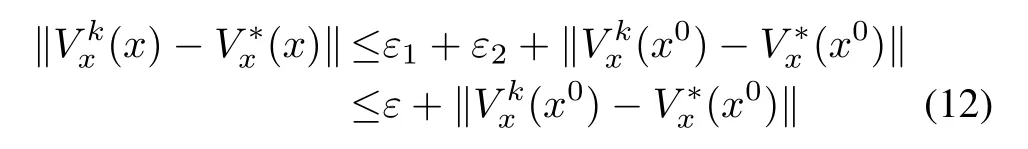
whereε=ε1+ε2.The last term in(10)can be estimated from a first-order Taylor approximation of the differenceVk?V?aroundx0,as

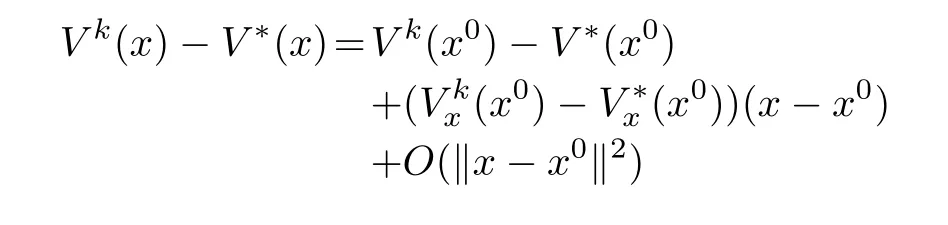
for allxin the neighborhood ?r.Therefore,by the triangle in equality

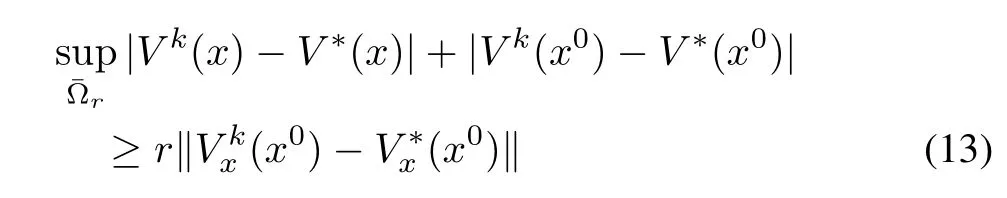
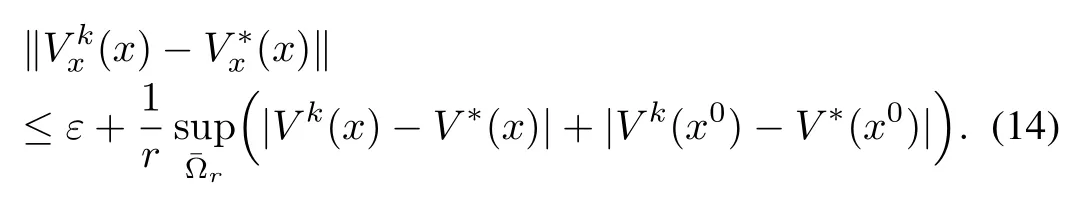
Consequently,using(13)in(12),we have

Finally,using(14)in(10),we get

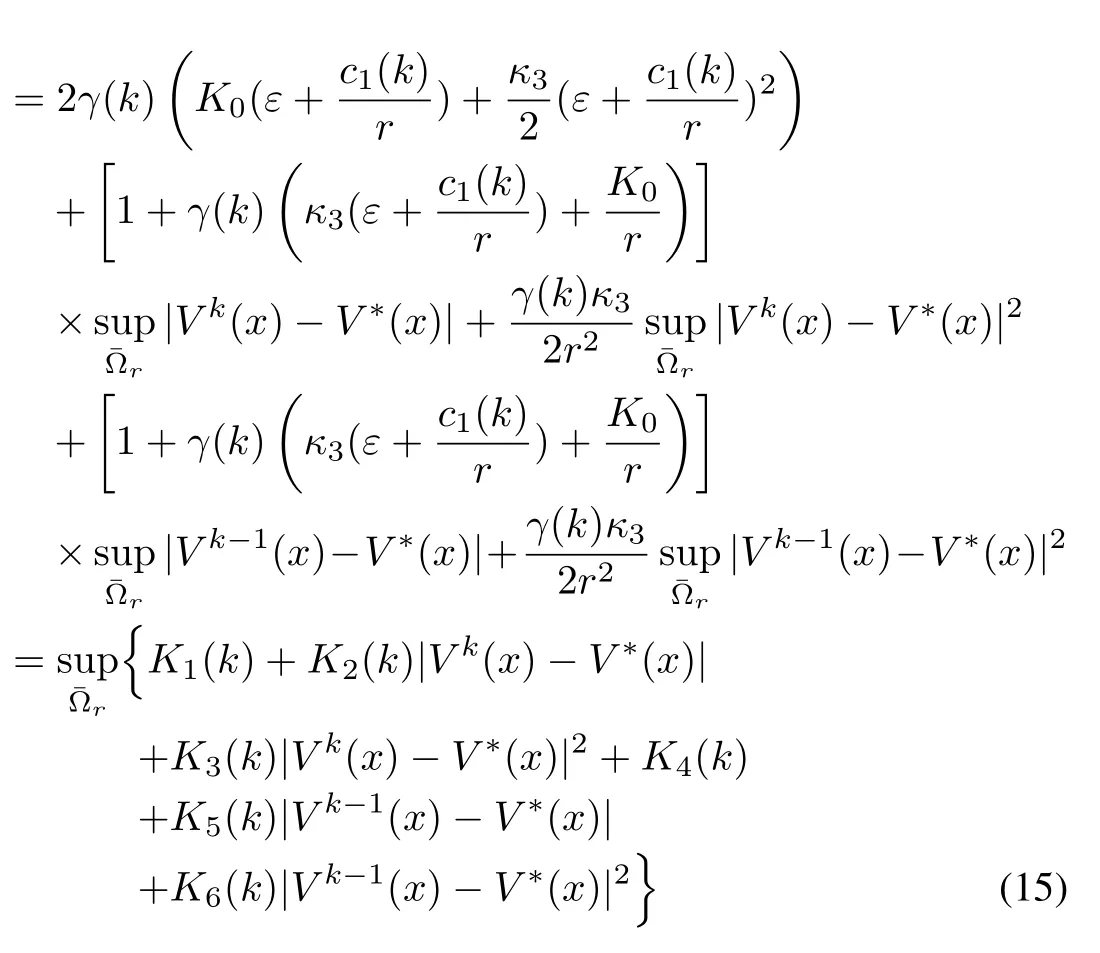
where

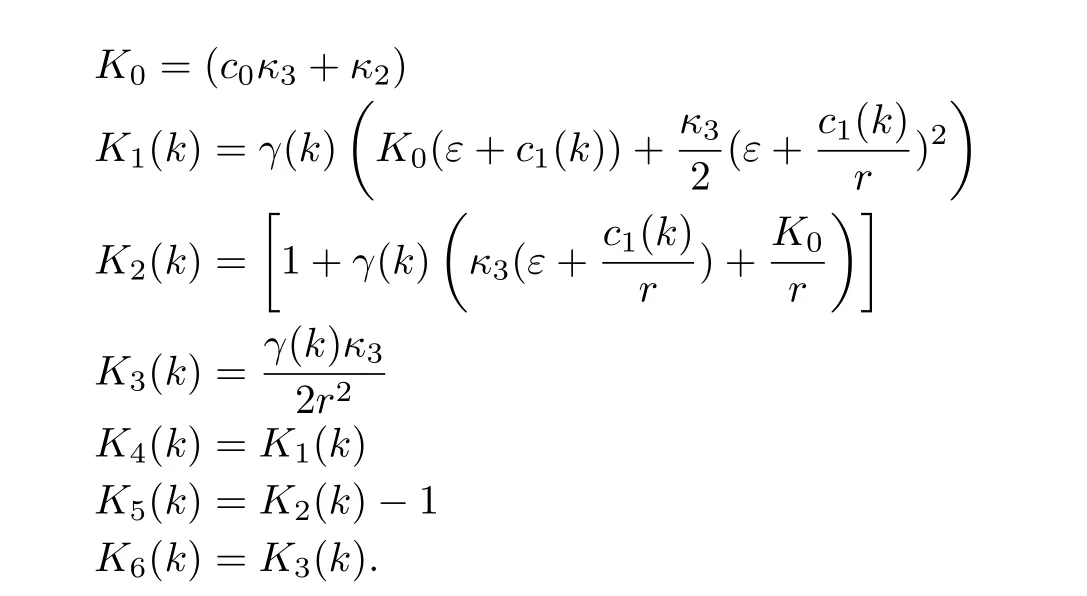
This shows that the iteration error is bounded;for if we start withk=1,we see that the error|V2(x)?V?(x)|is point-wise bounded by|V1(x)?V?(x)|and|V0(x)?V?(x)|.Similarly,the error|V2(x)?V?(x)|is point-wise bounded by|V1(x)?V?(x)|,and so on.Note also that,the above result holds for ?=r+∈,∈small,and thus forˉ?r.

We summarize next the main convergence result of the method.

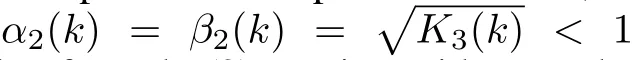
Proof:From the proof of Proposition 1,inequality(15)can without any loss of generality be represented as

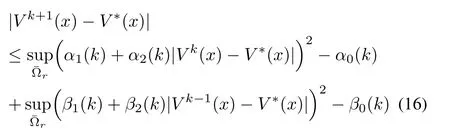
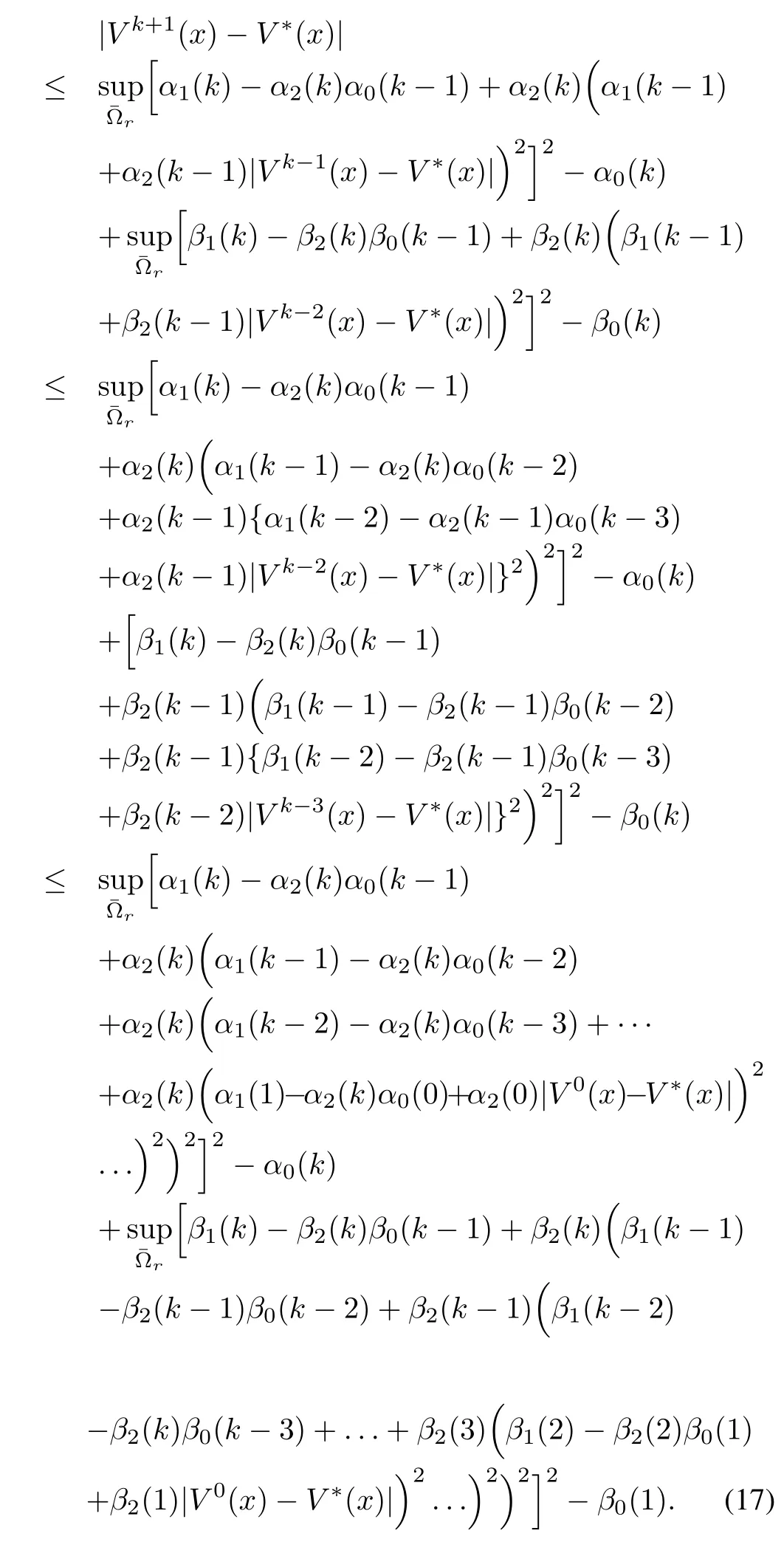
Taking the limit asin the above inequality(17)and sinceα2(k)=β2(k)＜1,all terms of|V0(x)?V?(x)|go to 0 and we have

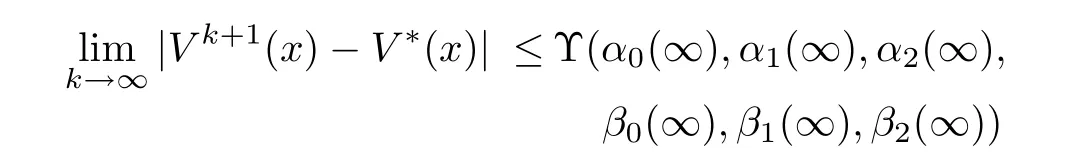
a constant.This implies uniform convergence of the approximationsV kto the solutionV?,which may differ from it by a constant.However,application of the boundary condition in(2)guarantees that this constant is zero.Finally,by(3),V k(x)is smooth on??rand therefore.Moreover,sinceis a Banach space,thenV kconverges to a smooth solution

Remark 1:We notice also from inequality(15)that,if we letr→∞,then the iteration error satisfies

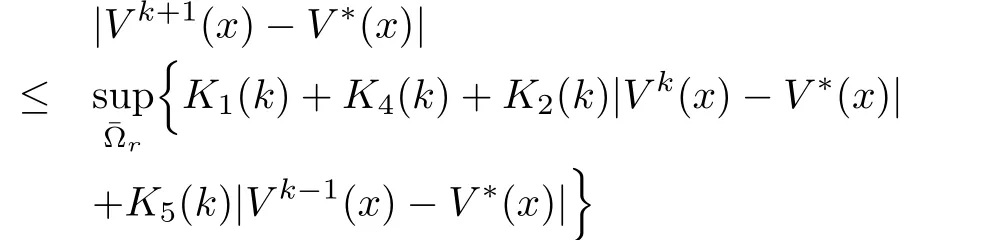
with

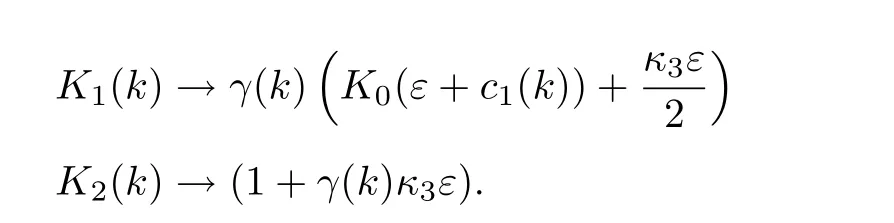
However,sinceK2(k)＞1,it means that the algorithm does not converge.

Remark 2:The relaxation parameterγ(k)is chosen to improve the convergence.Usually,0＜γ(k)＜2.If 0＜γ(k)＜1 we have under-relaxation,and this makes a non-convergent system converges.Alternatively,if 1＜γ(k)＜2 we have over-relaxation,and this used to speed up the convergence of algorithm.

Remark 3:The iterative formula(2)requires one function evaluation,i.e.,H JB IE(Vk)in each iteration.This requires the evaluation of one quadratic-form(see 2)together with two vector scalar-products and polynomial addition operations.Hence,the computational time of the algorithm is of the order ofO(n2).

We specialize the above results to linear systems and the corresponding Riccati equation.Consider the following linear system:

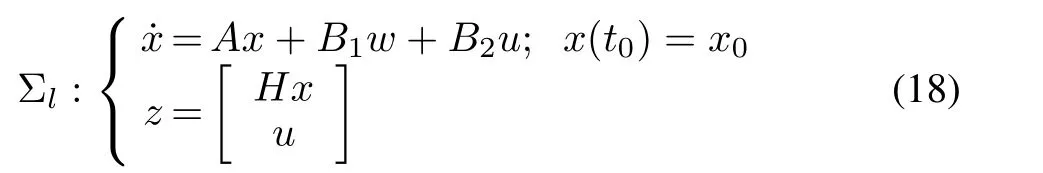
whereA∈Rn×n,B1∈Rn×s,B2∈Rn×p,H∈Rr×n,and the corresponding Riccati equation arising in the quadratic optimal control of the system[1],[2],[30],[31]

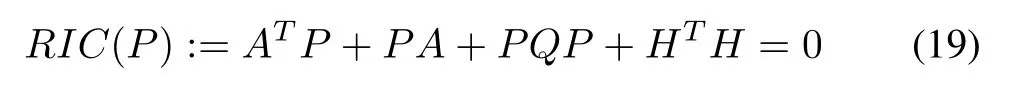
whereLet nowP:={n×nreal symmetric matrices}.Then,application of the formula(3)withV k(x)=xT Pk x/2,leads to the following recursive inverse mapP→Pfor(19):

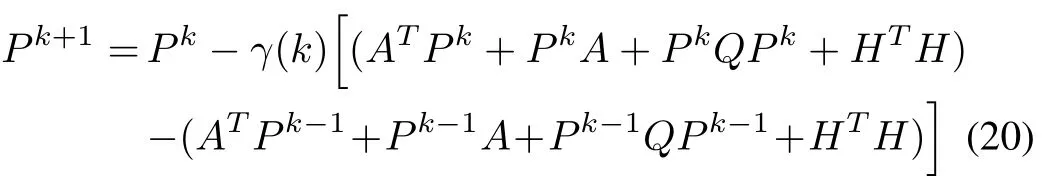
It then follows that,ifP?∈Pis a solution of(19),then

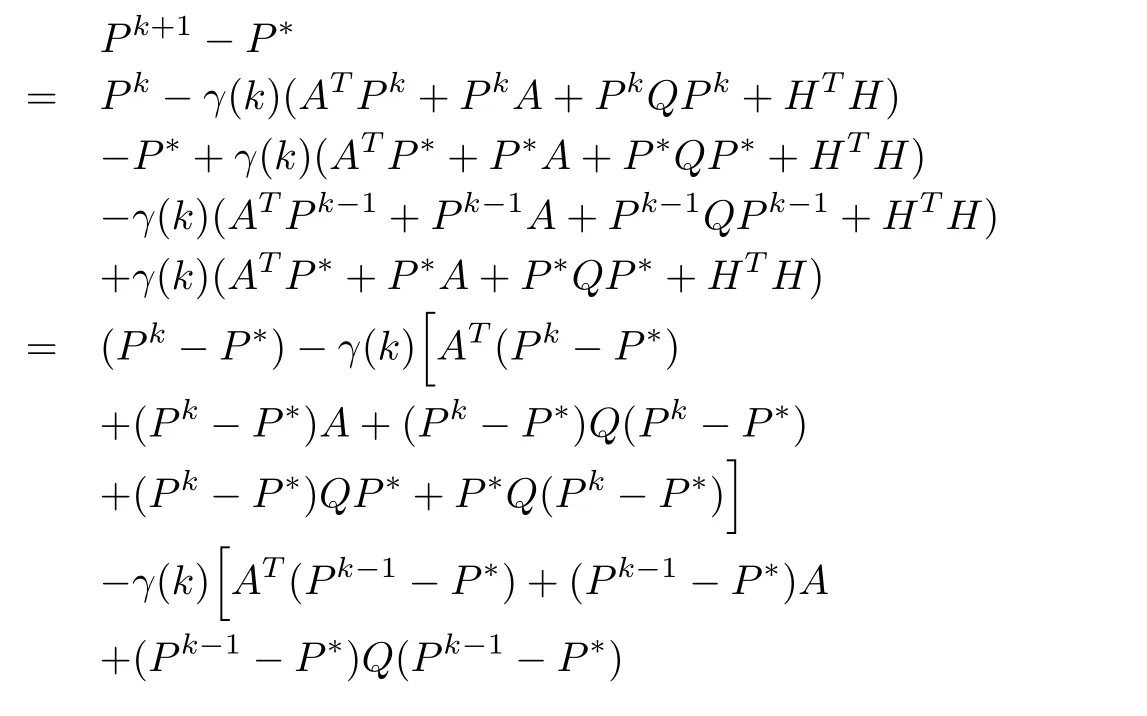
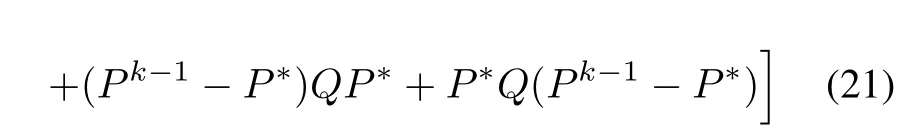
Therefore,

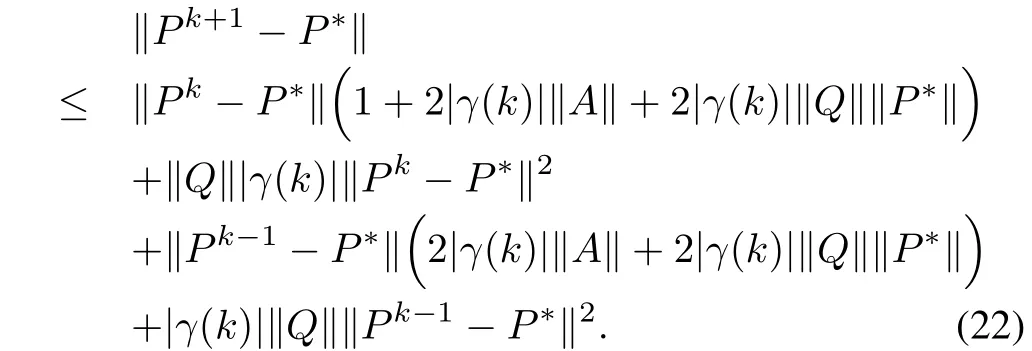
The above inequality(22),can further be represented as

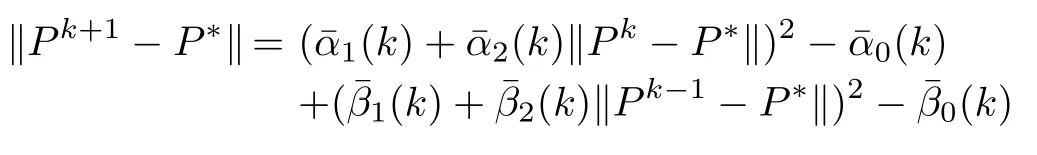
where

Thus,inequality(23)is the linear equivalent of(17),and if,then convergence of the approximations{Pk}toP?can be established from the result of Theorem 1.This result is now summarized in the following corollary to the Theorem.

Corollary 1:Consider the Riccati equation(19),and suppose there exists a symmetric solutionP?to it.In addition,suppose for the systemcan be chosen so thatThen,starting with an initial approximationP0∈P,the iterative formula(20)converges quadratically to a solutionP?∈Pof the Riccati equation(19).

Remark 4:The above recursive formula(20)and algorithm is similar in spirit to the ones proposed in[32]?[34].

IV.EXTENSION TO LYAPUNOV EQUATIONS

It is well-known that Lyapunov equations are special cases of HJBIEs[1],[2],[35].In this section,we discuss how the basic relaxation algorithm(3)can be extended to solve Lyapunov equations that arise in certain factorization problems for nonlinear systems[36].For the nonlinear system(1),we consider the Lyapunov equation[36]:

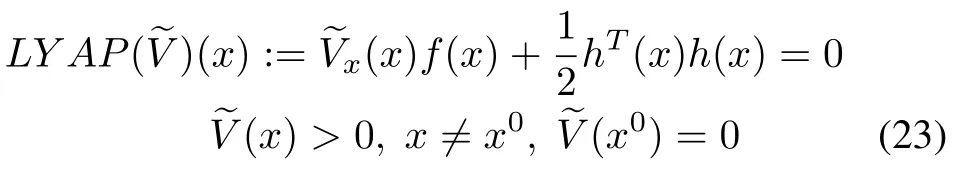
Adapting the iterative formula(3)to the above Lyapunov equation(23),we have the following recursion

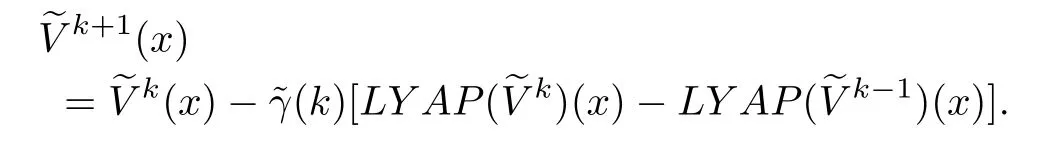
Consequently,we have the following result on the convergence of this iterative procedure.

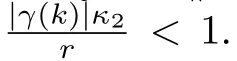
Proof:From(24),we have

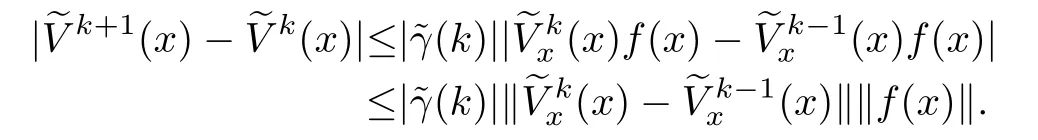
By inequality(14),for any two successive approximations

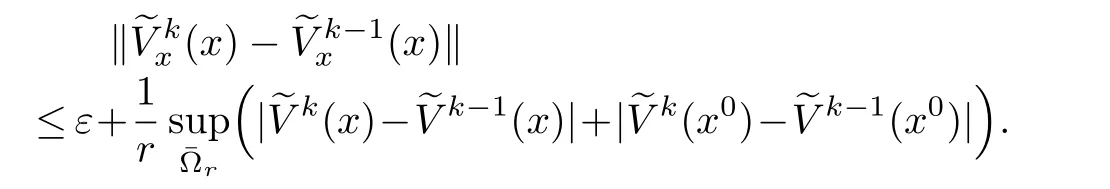
Therefore,

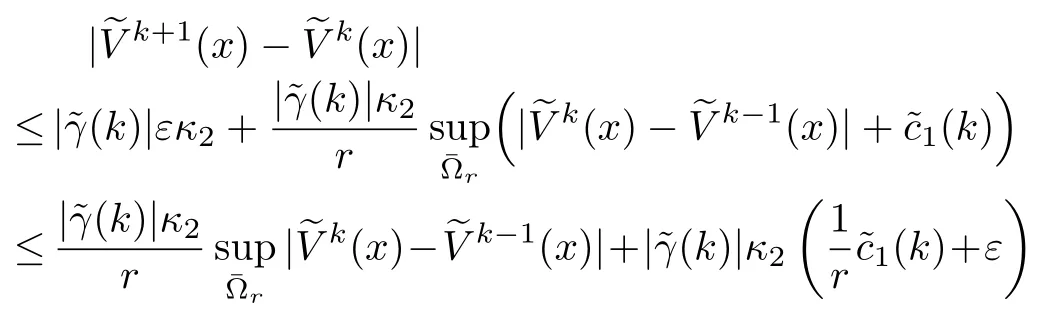
V.COMPUTATIONAL EXAMPLES AND SIMULATIONS

In this section,we present some simple examples and simulation results to demonstrate the effectiveness of the methods developed.

Example 1:Consider the following system and the example:

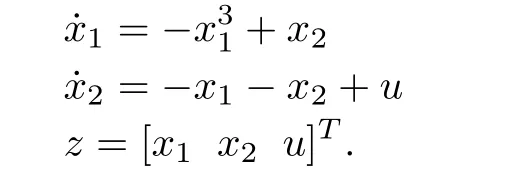
The resulting HJBIE for theH2problem is

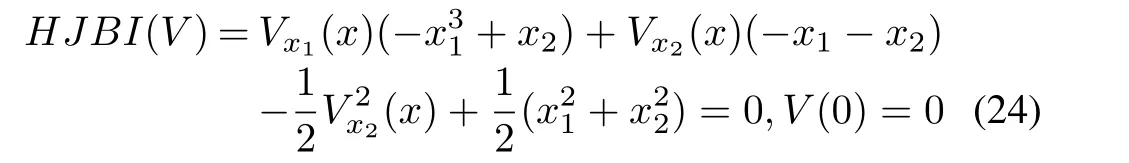
where

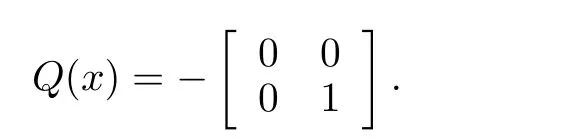
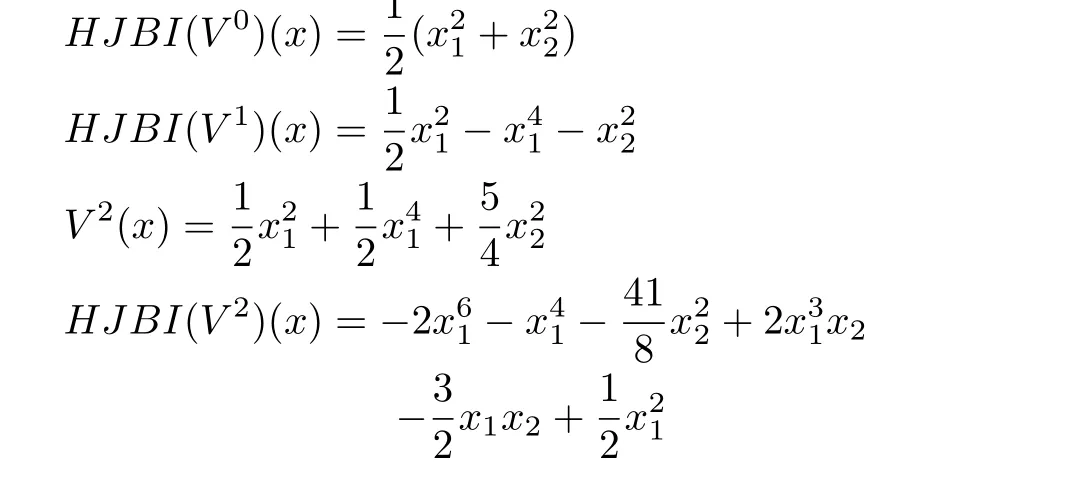
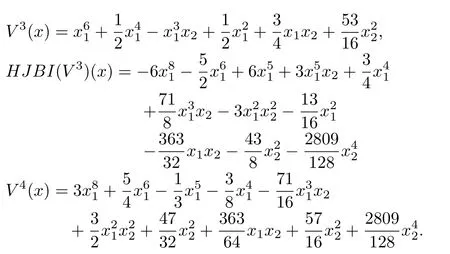
Remark 5:What we see in the above example is that,all the approximationsV2,V3,V4,are locally positive-definite.Thus,starting with a positive-definite initial approximationsV0,V1,the algorithm has the tendency to maintain the sign definiteness of the successive approximations.Whereas,the values of the functionH JB I(Vk),k=1,2,3 are increasingly negative-semidefinite.That is,the successive approximationsVk,k=2,3,4,try to satisfyH JB I(V)≤0 or the inequality form of the HJBIE.It is well-known that a solution for the latter is also a solution for the former[5].

The corresponding control laws for the above approximationsV2,V3,V4are given by

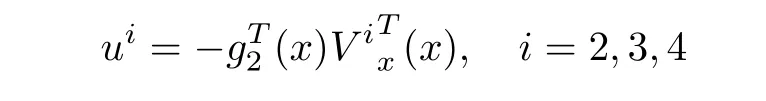
The system was simulated with the above control laws and the results of the simulation are shown respectively on Figs.1?3.The result of the simulation shows that the new iterative method can indeed find stabilizing solutions of the HJBIE.

We consider the following example to solve the Lyapunov equation.

Example 2:Reconsider the system of Example1 above.The corresponding Lyapunov equation(23)for the system is

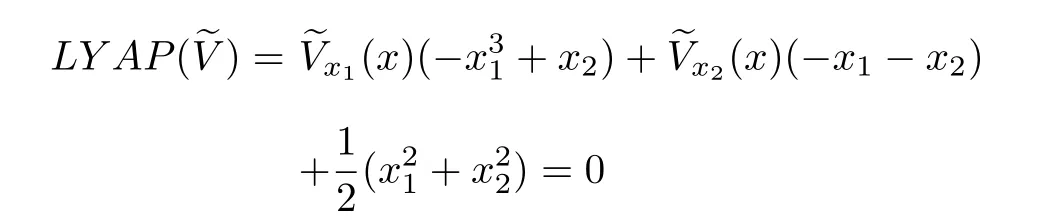
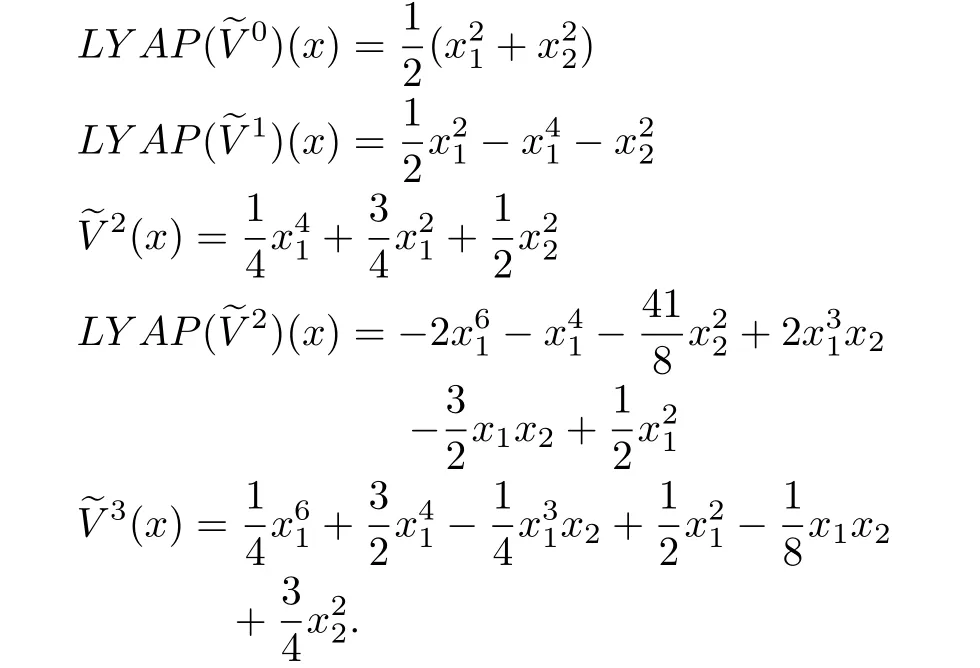
Remark 6:Notice in the above example,the approximationsare locally positive-definite.

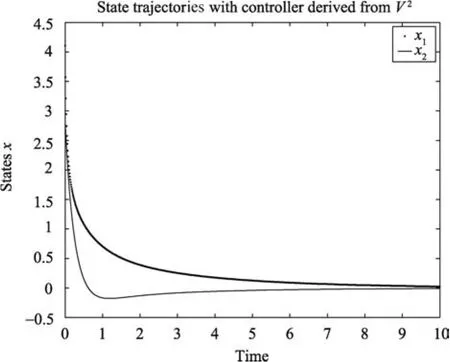
Fig.1.Closed-loop state trajectories with control law u2.

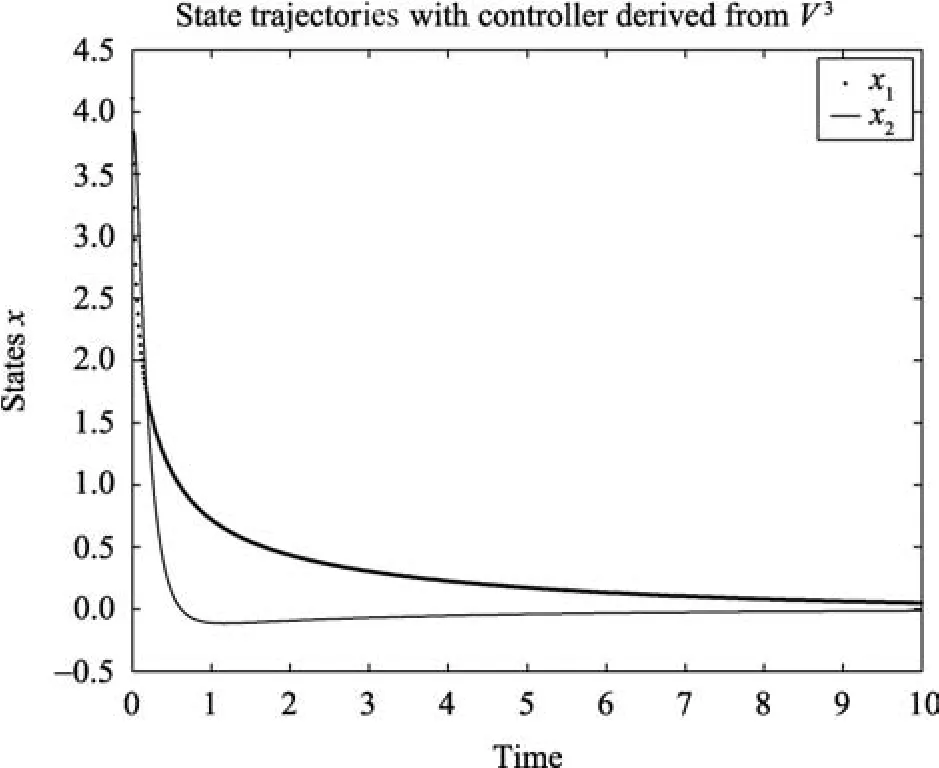
Fig.2.Closed-loop state trajectories with control law u3.

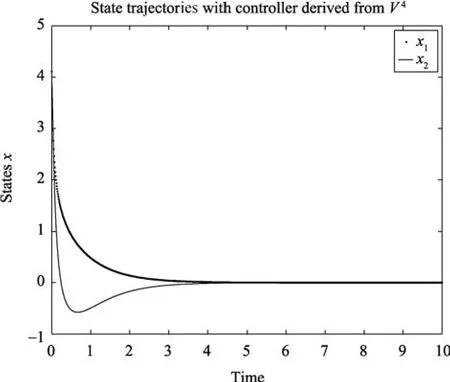
Fig.3.Closed-loop state trajectories with control law u4.

VI.CONCLUSION

In this paper,we have presented a new iterative approach for solving the HJBIE arising in the optimal control of affine nonlinear systems.Fixed-point iterations in Banach spaces and a relaxation method are combined to successively approximate the scalar value-function directly,and convergence results for the approach have been established under fairly mild conditions.Some examples have also been worked-out to demonstrate the effectiveness of the approach.In addition,the approach can easily be automated using symbolic algebra packages.Applications or extensions to Lyapunov equations have also been discussed.

However,the results presented are really preliminary,and it will require many experimentation to establish conclusively it’s usefulness and computational efficiency.It is sufficient here to observe that from the few examples that have been solved,the approach will be suited for affine nonlinear systems with polynomial nonlinearities.As such,future efforts will go into computational experimentations with the method on practical nonlinear systems such as the nonlinear bench-mark problem[16],as well as seeking improvements and refinements of the algorithm.It will also be worth-while to see if convergence of the algorithm can be established under much weaker and more general assumptions.

[1]M.Athans and P.L.Falb,Optimal Control:An Introduction to the Theory and its Applications.New York:Dover Publishers,2006.

[2]D.E.Kirk,Optimal Control Theory.Englewood Cliffs:Prentice Hall,1970.

[3]R.Abraham and J.E.Marsden,Foundations of Mechanics.Reading,MA,USA:Addison Wesley,1978.

[4]T.Basar and P.Bernhard,H∞Optimal Control and Related Minimax Design,Boston:Birkhauser,1991.

[5]M.D.S.Aliyu,Nonlinear H∞Control,Hamiltonian Systems and Hamilton-Jacobi Equations.Boca Raton,FL.USA:CRC Press,Taylor and Francis,2011.

[6]V.Barbu and G.Da Prata,Hamilton-Jacobi Equations in Hilbert Spaces.London:Pitman Advanced Publishing Program,1983.

[7]Y.Feng,B.D.O.Anderson,and M.Rotkow itz,“A game theoretic algorithm to compute local stabilizing solutions of HJBI equations in nonlinearH∞control,”Automatica,vol.45,no.4,pp.881?888,Apr.2009.

[8]M.D.S.A liyu,“An Approach for solving the Hamilton-Jacobi-Isaacs equation(HJIE)in nonlinearH∞control,”Automatica,vol.39,no.5,pp.877?884,May 2003.

[9]M.D.S.Aliyu,“A transformation approach for solving the hamiltonjacobi-bellman equation inH2deterministic and stochastic optimal control of affine nonlinear Systems,”Automatica,vol.39,no.7,pp.1243?1249,Jul.2003.

[10]M.D.S.A liyu and L.Smolinsky,“Aparametrizationapproach for solving the Hamilton-Jacobi equation and application to theA2Toda lattice,”Nonlinear Dyn.Syst.Theory,vol.5,no.4,pp.323?344.2005.

[11]M.D.S.Aliyu,“Adaptive solution of Hamilton-Jacobi-Isaacs equation and PracticalH∞stabilization of nonlinear systems,”inProc.IEEE Int.Conf.Control Applications,Anchorage,A laska,USA,2000,pp.343?348.

[12]A.A l-Tam im i,F.L.Lew is,and M.Abu-Khalaf,“Discrete-time nonlinear HJB solution using approximate dynamic programming:Convergence proof,”IEEE Trans.Syst.,Man Cybern.,vol.38,no.4,pp.943?949,Aug.2008.

[13]S.H.Jr.Benton,The Hamilton-Jacobi Equation:A Global Approach.New York:Academic Press,1977.

[14]S.T.Glad, “Robustness of nonlinear state feedback-a survey,”Automatica,vol.23,no.4,pp.425?435,Jul.1987.

[15]D.L.Lukes,“Optimal regulation of nonlinear dynamical systems,”SIAM J.Control,vol.7,no.1,pp.75?100,Feb.1969.

[16]P.Tsiotras,M.Corless,and M.A.Rotea,“AnL2disturbance attenuation solution to the nonlinear benchmark problem,”Int.J.Robust Nonlinear Control,vol.8,no.4?5,pp.311?330,Dec.1998.

[17]M.J.Yazdanpanah,K.Khorasani,and R.V.Patel,“Uncertainty compensation for a flexible-link manipulator using nonlinearH∞control,”Int.J.Control,vol.69,no.6,pp.753?771,Apr.1998.

[18]R.W.Beard,G.N.Saridis,and J.T.Wen,“Galerkin approximations of the generalized Hamilton-Jacobi-Bellman equation,”Automatica,vol.33,No.12,pp.2159?2177,Dec.1997.

[19]R.W.Beard and T.W.Mclain,“Successive Galerkin approximation algorithms for nonlinear optimal and robust control,”Int.J.Control,vol.71,no.5,pp.717?743,Nov.1998.

[20]A.Isidori and W.Kang,“H∞control via measurement feedback for general nonlinear systems,”IEEE Trans.Automat.Control,vol.40,no.3,pp.466?472,Mar.1995.

[21]A.Isidori and W.Lin,“GlobalL2-Gain design for a class of nonlinear systems,”Syst.Control Lett.,vol.34,no.5,pp.295?302,Jul.1998.

[22]J.Huang,“An algorithm to solve the discrete HJI equation arising in theL2gain optimization problem,”Int.J.Control,vol.72,No.1,pp.49?57,Jan.1999.

[23]H.Guillard,S.Monaco,and D.Normand-Cyrot,“Approximated solutions to nonlinear discrete-timeH∞Control,”IEEE Trans.Automat.Control,vol.40,no.12,pp.2143?2148,Dec.1995.

[24]M.Abu-Khalaf,F.L.Lew is,and L.Huang,“Policy iterations on the Hamilton-Jacobi-Isaacs equation forH∞state feedback control with input saturation,”IEEE Trans.Automat.Control,vol.51,no.12,pp.1989?1993,Dec.2006

[25]M.Abu-Khalaf and F.L.Lew is,“Nearly optimal control laws for nonlinear systems with saturating actuators using a neural network HJB approach,”Automatica,vol.41,no.5,pp.779?791,May 2005.

[26]T.Ohtsuka,“Solutions to the Hamilton-Jacobi equation with algebraic gradients,”IEEE Trans.Automat.Control,vol.56,no.8,pp.1874?1885,Aug.2011.

[27]E.Zeidler,Nonlinear Functional Analysis and Its Applications:I:Fixed-Point Theorems.New York:Springer-Verlag,1986.

[28]J.M.Ortega and W.C.Rheinboldt,Iterative Solution of Nonlinear Equations in Several Variables.London:Academic Press,1970.

[29]H.K.Khalil,Nonlinear Systems,3 rd Edition,Prentice Hall,Upper Saddle River,NJ,USA,2002.

[30]S.Bittanti,A.J.Laub,and J.Willems,The Riccati Equation.Germany:Springer-Verlag,1991.

[31]K.M.Zhou,J.C.Doyle,and K.Glover,Robust and Optimal Control.New Jersey:Prentice Hall,1996.

[32]G.G.L.Meyer and H.J.Payne,“An iterative method of solution of the algebraic Riccati equation,”IEEE Trans.Automat.Control,vol.17,no.4,pp.550?551,Aug.1972.

[33]D.L.K leinman,“On an Iterative technique for Riccati equation Computations,”IEEE Trans.Automat.Control,vol.13,no.1,pp.114?115,Feb.1968.

[34]K.Vit,“Iterative solution of the Riccati equation,”IEEE Trans.Automat.Control,vol.17,no.2,pp.258?259,Apr.1972.

[35]J.M.Saniuk and I.B.Rhodes,“A matrix inequality associated with bounds on Solutions of algebraic Riccati and Lyapunov equations,”IEEE Trans.Automat.Control,vol.32,no.8,pp.739?740,Aug.1987.

[36]J.M.A.Scherpen and A.J.Van der Schaft,“Normalized coprime factorizations and balancing for unstable nonlinear systems,”Int.J.Control,vol.60,no.6,pp.1193?1222,1994.