Robust Formation Maneuvers Through Sliding Mode for Multi-agent SystemsWith Uncertainties
Dianwei Qian,Chengdong Li,SukGyu Lee,and Chao Ma
I.INTRODUCTION
WITH the development of artificial intelligence,multiagent systems have been hailed as a novel paradigm for conceptualizing,designing,and implementing intelligent systems[1]?[3].A multi-agent system is a coupled network of some agents,where the agents can interact to achieve some goals that are beyond the individual capacities or knowledge of each agent[4],[5].The advantages of the multi-agent system include but are not limited to efficiency,extensibility and reliability.On the other hand,many increasing applications in reality require the agents that have to work together[6].To enable these applications,requirement of coordination of the agents has substantially increased.
As one of coordination task,the consensus problem is emerging because it integrates both graph theory and control theory[7].The consensus problem covers some typical control tasks,i.e.,formation control,rendezvous,attitude alignment,flocking and foraging[8].Among the tasks,the formation control concentrates on forming up a multi-agent system as well as making the agents move in given geometrical shapes.The task is rooted in the real applications.For example,the agents have to maintain some formations when they move at disaster sites,warehouses and hazardous areas[9].See[10]for a complete review of recent philosophies in this field.
One scheme of multi-agent formations is called“l(fā)eader follower”[11].As the name suggests,one agent in a multiagent system is named as leader and other agents are successively designated as followers.The sole leader takes charge of tracking a predefined trajectory.The followers keep on tracking the leader to form up a desired formation while the multi-agent system moves.The scheme has been successfully applied to the analysis and design of multi-agent formations.
Inherently,the leader-follower scheme is centralized and heavily depends on the leader and it suffers from the problem of“single point of failure”[12].Besides,the scheme has been paid increasing attention because its dynamics are not only experimentally modelled,but the internal formation stability can be theoretically guaranteed[13].Adopting the scheme,various control methods have been developed for multi-agent formations,that is,neural network-based adaptive design[1],robust control[14],adaptive output feedback method[15],nonlinear predictive mechanism[16],and iterative learning technique[17],to name but a few.
The methodology of sliding mode control(SMC)is popular due to its invariance property[18].Some SMC-based methods have been addressed to solve the formation-control problem of multi-agent systems,that is,fuzzy SMC[19],[20],first-order SMC[21],terminal SMC[22],backstepping SMC[23],[24],etc.Previous contributions have verified the feasibility of the SMC methodology for multi-agent formations.
In a multi-agent system,uncertainties exist everywhere.Each agent may contain uncertainties,i.e.,external disturbances,unmodelled dynamics and parameter perturbations.Originated from the uncertainties of the agents,formation dynamics of the multi-agent system become uncertain.In previous works about the SMC-based multi-agent formations,uncertainties are considered because they adversely affect the formation stability.However,two solutions can be summarized from the aforementioned works.One solution is to discuss the formation stability by means of graph theory[19],[24].The other is to analyze the formation stability in light of Lyapunov’s theorem[20]?[23].To guarantee the formation stability,the uncertainties are usually assumed to be bounded by a known boundary.Unfortunately,the assumption is not mild because the uncertainties are rather hard to exactly measure or to know in advance.The lack of such a boundary may result in severe problems,i.e.,decrease of the formation robustness,deterioration of the formation performance as well as deficiency of the formation stability.In order to obtain the important information,it is desired to adaptively approximate the formation uncertainties.
The technique of nonlinear disturbance observer(NDO)has been proven to be effective in handling uncertainties and improving robustness[25].The applications of NDO have been investigated by some actual cases[26],[27].This technique can be considered as an alternative to attack the issue of uncertainties for multi-agent formations.So far,the academic problem of how to eliminate the adverse effects of uncertainties in multi-agent formations via NDO still remains unsolved.
This paper touches the academic problem and investigates a robust control design for formation maneuvers of a multiagent system.The multi-agent system under consideration is leader-follower-based,and the communication topology is considered in order to strengthen the adaptability,reliability and practicability of the leader-follower scheme.Since the multi-agent system is subjected to uncertainties,the robust control design contains two parts.One is to develop an SMC-based controller and the other is to present an NDO-based observer.The controller and observer work together to realize formation maneuvers of the multi-agent system in the presence of uncertainties.The main contributions of this paper can be summarized as follows:1)a formation control design that integrates SMC and NDO is proposed for each follower agent;2)the presented design with guaranteed stability is extended to the multi-agent system under a given communication topology;3)some comparisons are drawn to illustrate the feasibility and validity of the presented design.
The remainder of this paper is organized as follows.The modelling of one single agent and the communication topology of the agents are given in Section II.Formation design is presented in Section III.Simulation results are illustrated in Section IV.Finally,conclusions are drawn in Section V.
II.SYSTEM MODELLING
A.Modelling One Agent
The multi-agent system under consideration consists ofNmobile robots.The robots are identical and each robot can be treated as an agent.Fig.1 displays a robot in the multi-agent system.The robot is round with differential wheels having radiusR,and its movement is actuated by two separately driven wheels placed on either side of its body.Indexiis used to represent the robot.The Cartesian coordinate system in Fig.1 specifies(xLi,yLi)as the center of the left wheel,(xRi,yRi)as the center of the right wheel,(xci,yci)as the center of the robot’s body and(xhi,yhi)as the robot’s head.In Fig.1,xhi=xci+hcosθi,xLi=xci?lsinθi,xRi=xci+lsinθi,yhi=yci+hsinθi,yLi=yci?lcosθiandyRi=yci+lcosθi,whereris the radius of wheels,lis the distance between the center of robot and the wheel,his the distance between the center and the head position andθiis the rotation angle.Let us specify aqi=[xhi yhiθi]Tto describe the robot’s posture.
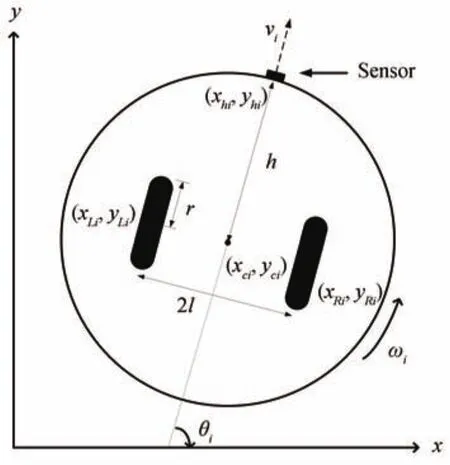
Fig.1.Schematic diagram of one agent.
The Lagrangian equations of motion to describe the agent can have the form of(1)with respect to the vectorqi.

whereLi=K i?Pi(K iandPidenote the kinetic energy and the potential energy of the agent,respectively.),τi=[τLiτRi]Tis the torque vector applied to the wheels andB(qi)is a time-varying matrix.
Concerning the agent,its motion is restricted to horizontal plane,its potential energy is kept unchanged andPican be defined as 0.Therefore,Lican be written by
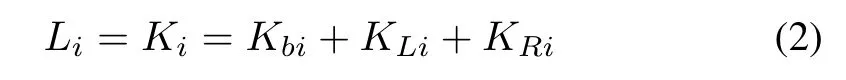
whereK bi,K LiandKRiare the kinetic energies of the agent’s body,left wheel and right wheel,respectively.The kineticenergies can be formulated byandwherembandIbare the mass and the moment of inertia of the agent’s body,respectively;mwandIware the mass and the moment of inertia of the agent’s wheel,respectively.
LetandBy the Lagrangian method,the dynamic model of the agent can be formulated by
where the matricesandin order are determined by
From Fig.1,two symbols of the agent are kept unexplained,that is,the linear velocityviand the rotation angular velocityωi.Differentiatingqiwith respect to timetyields

Substituting(4)into(3)gives
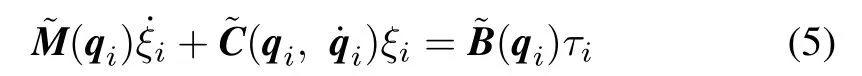
In(3),det[M(qi)]=0 if and only ifConsequently,it is justified to assume thatis invertible in(5).Taking the assumption into consideration,the equations of motion describing the behavior of the agent can be written as
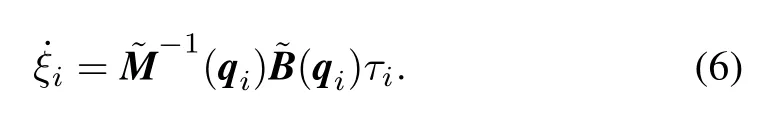
Recall(4)such that the equations of motion of the agent at its head has a form of
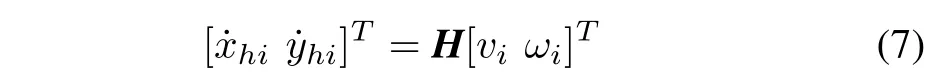
Differentiating(7)with respect to timetyields
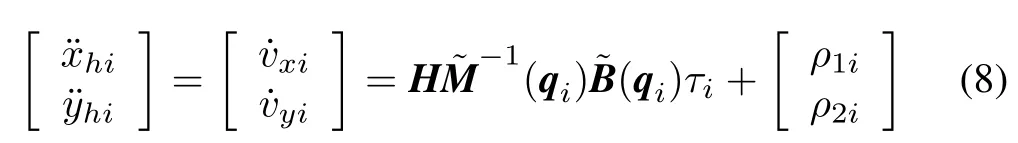
whereandsinθi.
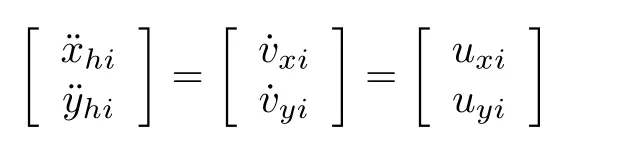
Considering the agent’s uncertainties,the equations of motion of the agent can be described by
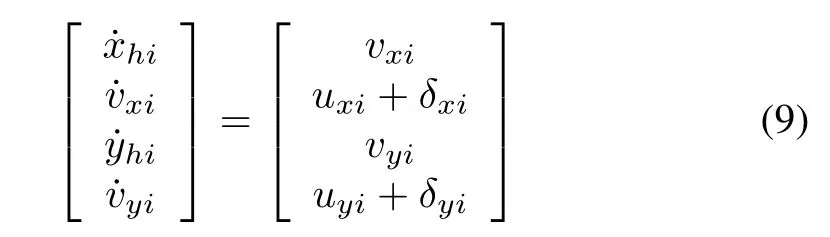
whereδxiandδyidenote the uncertain terms.
This paper deals with formation maneuvers of multi-agent systems in the presence of uncertainties.It is justified to assume that the uncertainties are bounded by an unknown constant,that is,andwhereandare constant but unknown.In order to implement the technique of nonlinear disturbance observer,the designed observer should evaluate or calculateδxiandδyimuch faster than the changing rates ofδxiandδyi.In this sense,bothδxiandδyiare assumed to be slow ly time-varying,that is,and
B.Modelling Communication Topology
Recall the multi-agent system.Its formation maneuvers are leader-follower-based.In the leader-follower scheme,the sole leader agent takes the responsibility of tracking a pre-defined trajectory while other follower agents keep on tracking the leader.Such a scheme indicates that the sole leader does not need to receive any information from the followers.On the other hand,the followers need to receive some information by communication link in order to form up a desired formation.Here some ideal conditions are considered,such as no communication delay or no packet loss.
The communication topology of the multi-agent system can be modelled via the theory of algebraic graph.Define a directed graphG=(V,E)composed of a vertex setVand an edge setE,wherethe nodeνidenotes theith agent andi=1,2,...,N.This paper investigates the directed graphGin the multi agent system.Assuming thatGof the multi-agent system has a spanning tree,the zero eigenvalue ofLis simple.Consider theith agent whose collection of neighbors is defined asN i={νj∈V: (νi,νj)∈E}.The ordered pair(νi,νj)∈Emeans that thejth agent can send information to theith agent,but the information cannot be sent vice versa.
The weighted adjacency matrixAofGhas a form of
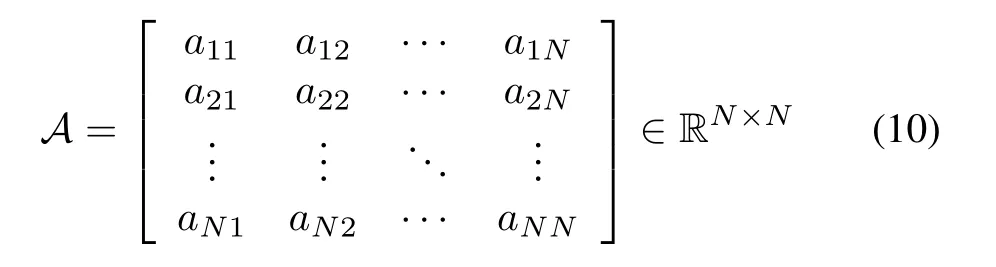
whereaijindicates the weight of the pair(νi,νj);andaii=0.
The degree matrix ofGis a diagonal matrix,determined byD=diag{d1,d2,...,dN}∈RN×N.In the diagonal matrix,diis the in-degree ofνi,formulated by(i=1,2,...,N).Accordingly,the Laplacian matrix ofGcan be defined byL=D?A∈RN×N.As proven in[4],Lhas at least one zero eigenvalue as well as all other eigenvalues are located at the open right-half plane ifGis connected.
ConcerningL,its zero eigenvalue is simple.For the zero eigenvalue,an eigenvector ofLis1N,that is,L1N=0Nholds true,where1N=[1,1,...,1]T∈RN×1and0N=[0,0,...,0]T∈RN×1.Further,rank(L)=N?1 for the simple zero eigenvalue[4].
Without loss of generality,theNth agent in the multi-agent system is named leader and otherN?1 agents are followers,that is,aNi=0(i=1,2,...,N)and the Laplacian matrixLofGcan be written as
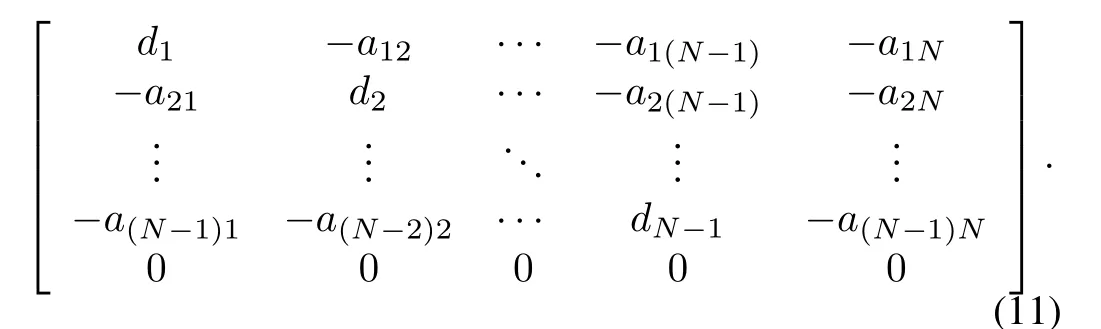
Further,the communication topology among all the followers can be described by a directed graphApparently,is a subgraph ofG.The weighted adjacency matrixA∈R(N?1)×(N?1)ofis defined by
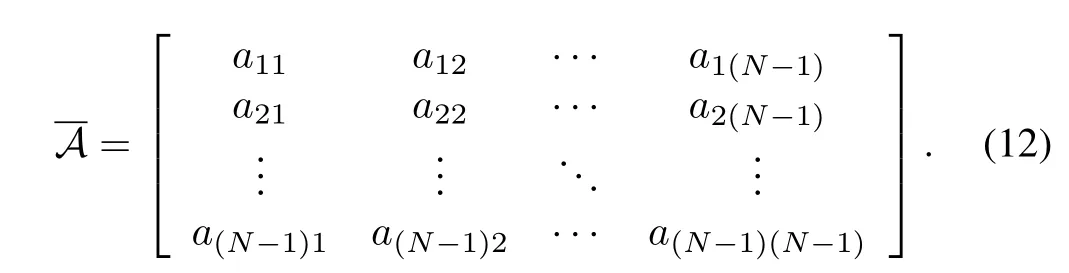
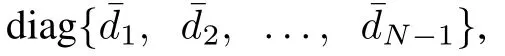
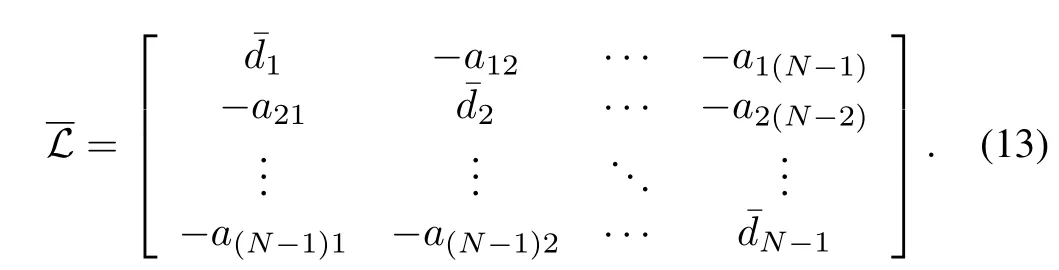
Similarly,assuming that the subgraphGis itself a directed graph,can be drawn.Here1N?1= [1,1,...,1]T∈R(N?1)×1and0N?1=[0,0,...,0]T∈R(N?1)×1.Moreover,define a matrixwhere1,2,...,N?1).Apparently,it holds rank(L+B)=rank(L)=N?1.
III.FORMATION DESIGN
The formation maneuvers in this paper are leader-follower based.Concerning the leader’s duty,its control problem is the tracking-control problem of a single robot,which can be well controlled by a developed technology[9].In the multi-agent system,theNth agent has been named as leader that can be treated as a nominal one in the formation-control problem,that is,δxN=δyN=0.Accordingly,the otherN?1 agents act as followers and they are equipped with the designed formation controllers to achieve the formation maneuvers of the multiagent system.
In order to concentrate on the formation-control design of theith follower(i=1,2,...,N?1),recall its equations of motion(9).The equations in(9)are decoupled in thexaxis andy-axis.Consequently,its formation-control design can be divided into the design of thex-axis subsystem and the design of they-axis subsystem.Here the design of thex-axis subsystem is taken into account at first.From(9),thex-axis subsystem with uncertainties can be written by
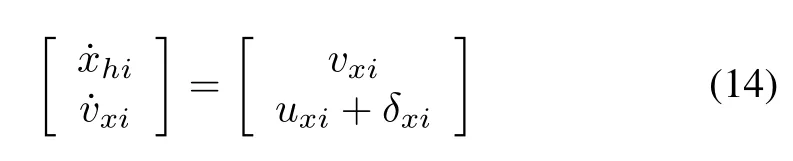
which can be re-written by the following state-space representation.
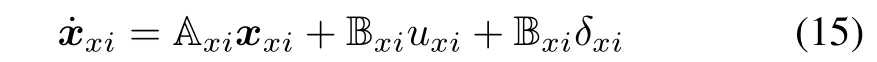
A.Design of NDO-based Observer
Consider thex-axis subsystem(15)and design its NDO-based observer(16)[25].
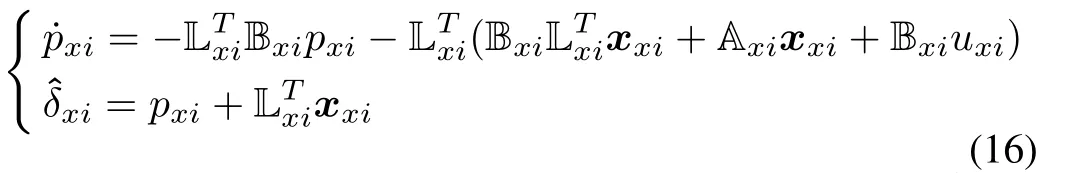
wherepxiis the internal state variable of the observer,is the approximation ofδxiand the gain vector Lxi∈R2×1is designed such that the constantis positive.
Define an estimation-error variableHere an assumption of the estimation-error variable iswhereis constant but unknown.Differentiate the error variable with respect to timetand substitute(16)into the derivative ofexid.Subsequently,(17)can be obtained.
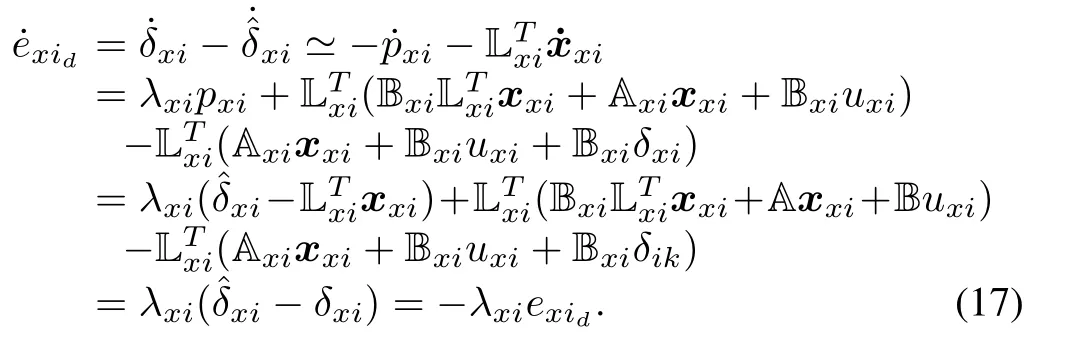
The solution of(17)iswhereexid(0)is the initial condition att=0.Owing toλxi>0,this fact indicates that the estimation-error variableexidis exponentially convergent to 0 as
B.Design of SMC-based Controller
The formation maneuvers of the multi-robot system need to achieve a designated formation pattern with velocity consensus,where the agents have to transmit information among local neighbors according to a designated communication topology.Therefore,the error function is defined as
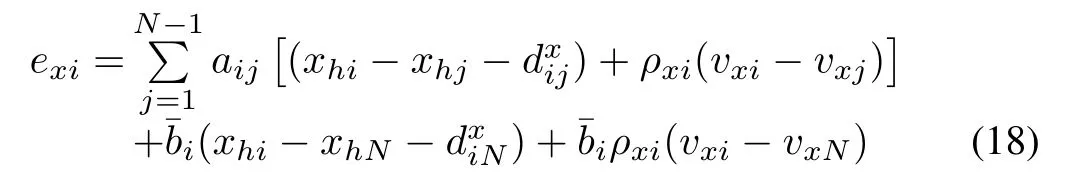
whereρxi>0 is a pre-defined constant,is the pre-defined relative position between theith follower and thejth follower andis the pre-defined relative position between theith follower and the leader.
Differentiatingexiin(18)with respect to timetand substituting thex-axis subsystem(14)into the derivative ofexiyields
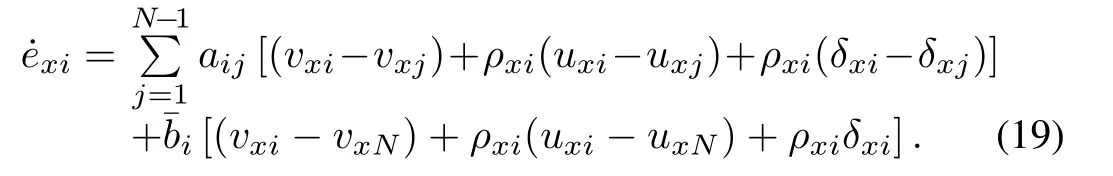
Successively,differentiatingin(19)with respect to timetand substituting thex-axis subsystem(14)into the second derivative ofexiyields
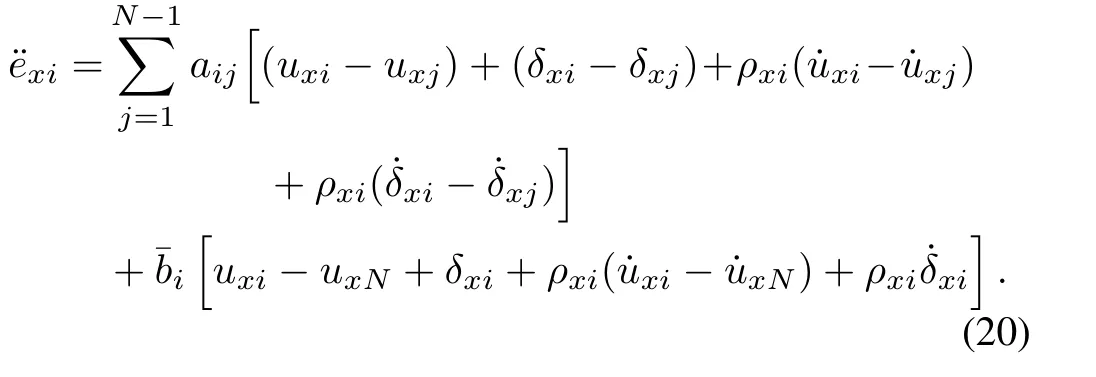
With regard to thex-axis subsystem(14),a sliding surface with the output of the NDO-based observer(16)is defined as
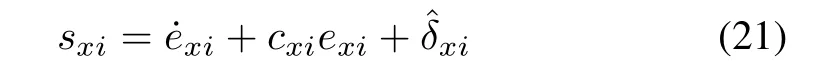
wherecxi>0 is constant.
Differentiating the sliding-surface variable with respect to timetgives
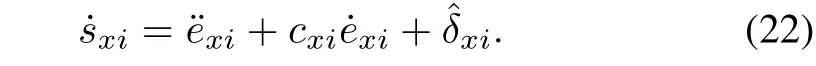
Substituting(18),(19)and(20)into(22)yields
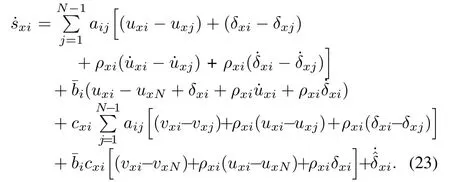
Design the following formation-control law for thex-axis subsystem of theith follower.
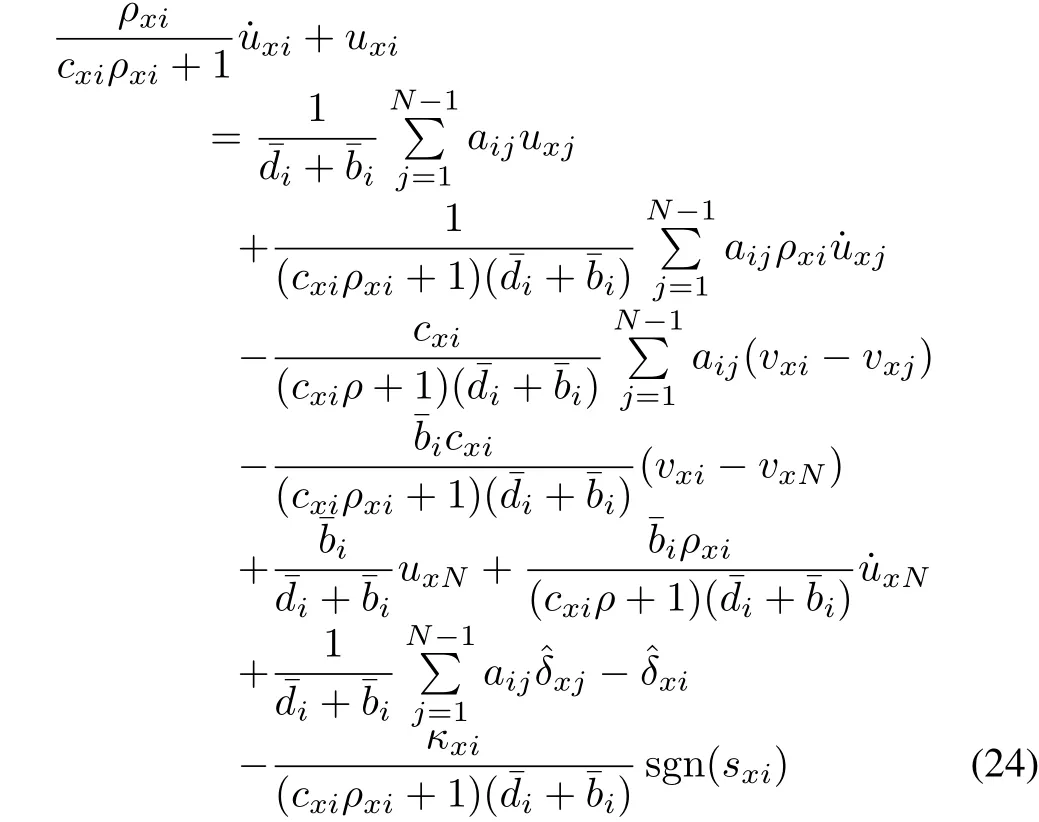
whereκxi>0 is a predefined parameter and sgn(·)is the sign function.In(24),the control signaluxiis determined by a first-order differential equation with the zero initial condition.Further,the control signals of other agents also contribute touxi,which can be obtained by the given communication topology.
Substituting(24)into(23)and re-arranging˙sxiin(23)gives
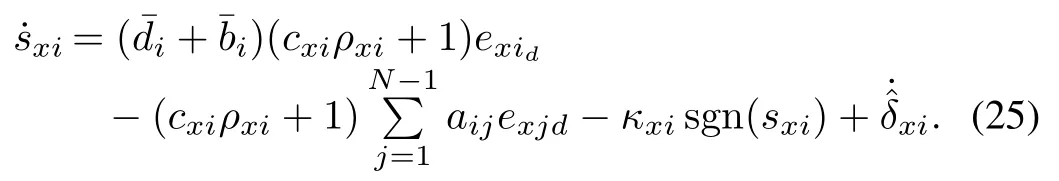
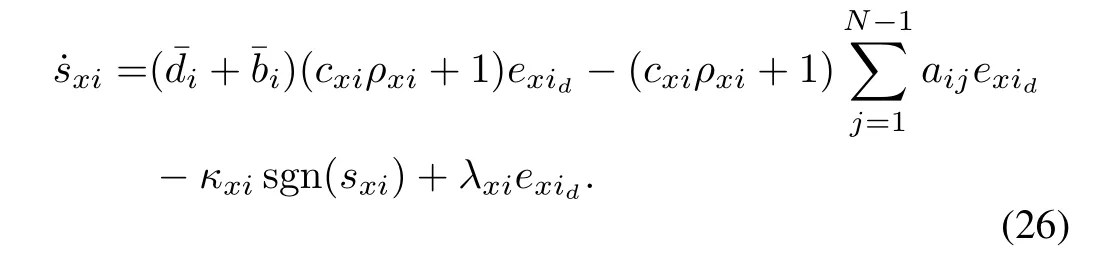
C.Stability Analysis
Theorem 1:For theith follower agent,consider itsxaxis subsystem(14),design the NDO-based observer(16),define the sliding-mode surface(21)and utilize the SMC-based control law(24).The closed-loop control system of thex-axis subsystem is asymptotically stable ifκxi>[(cxiρxi
Proof:Pick up a Lyapunov candidate function

DifferentiateVwith respect to timetin(27).The derivative ofVcan be written byReplacewith(26).The derivative ofVhas the form of
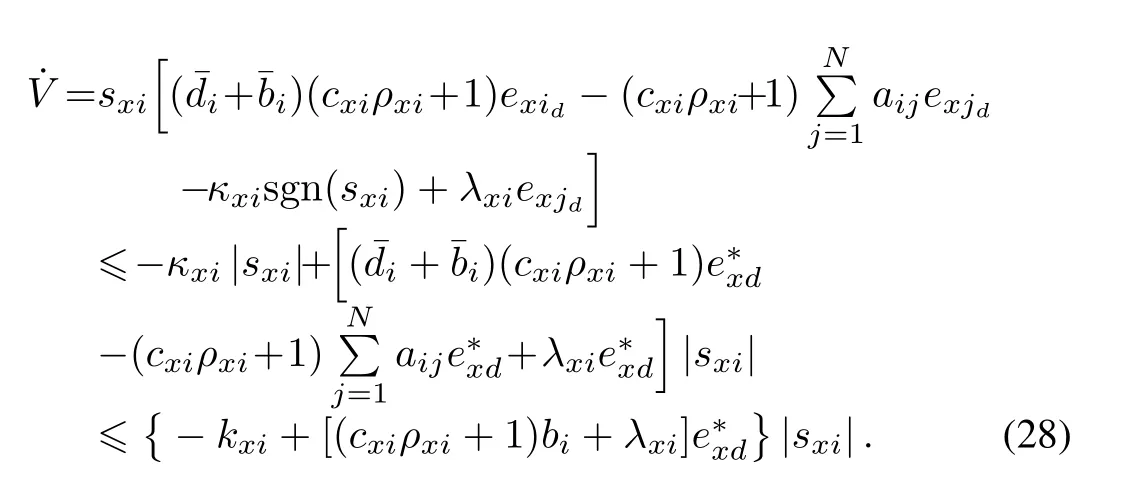
Selectsuch thatexists.ConcerningV≥0,the closed-loop control system of thex-axis subsystem is asymptotically stable in the sense of Lyapunov.
D.Extension to the Multi-agent System
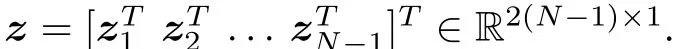
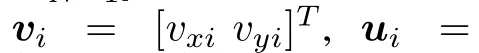
For theNth leader agent,the following augmented vectors can be defined,that is,zN=[xhN yhN]T,uN=[uxN uyN]TandvN=[vxN vyN]T.HerezN,uNandvN∈R2×1.
Further,define the following diagonal matrices
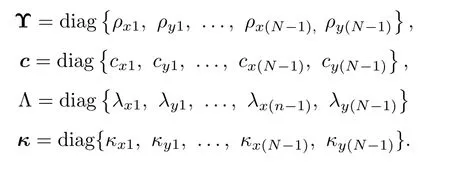
whereΥ,c,Λandκ∈R2(N?1)×2(N?1).
The augmented tracking-error vectorecan be written by
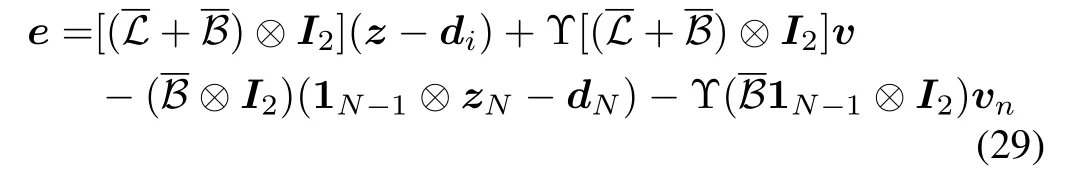
whereI2is a 2×2 identity matrix and?means the Kronecker product.
Differentiatingein(29)with respect to timetgives
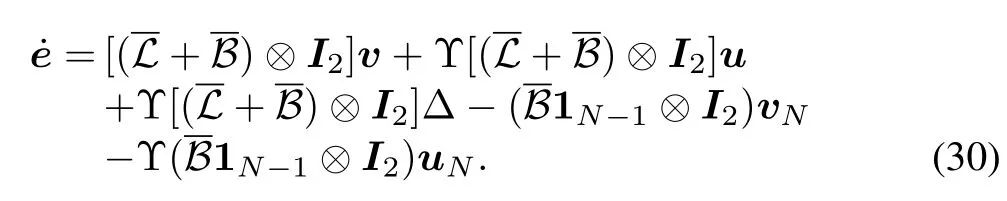
Considering the properties of uncertainties in(9),we haveHereis a zero vector.Further,the second derivative ofewith respect to timethas the form of
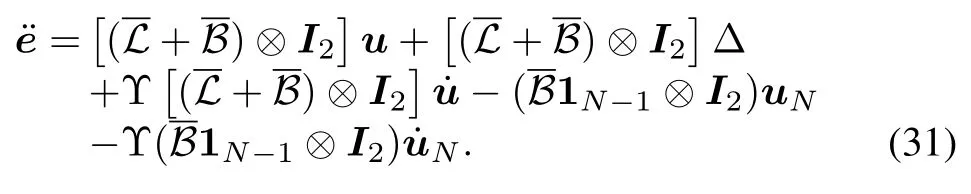
The augmented sliding-surface vector is formulated by
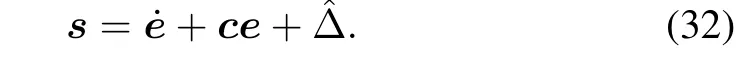
Differentiatingswith respect to timetyields
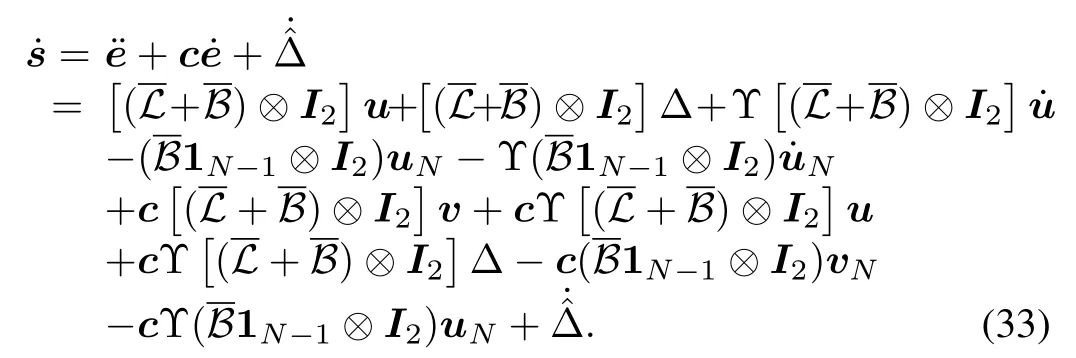
Design the following control law(34).
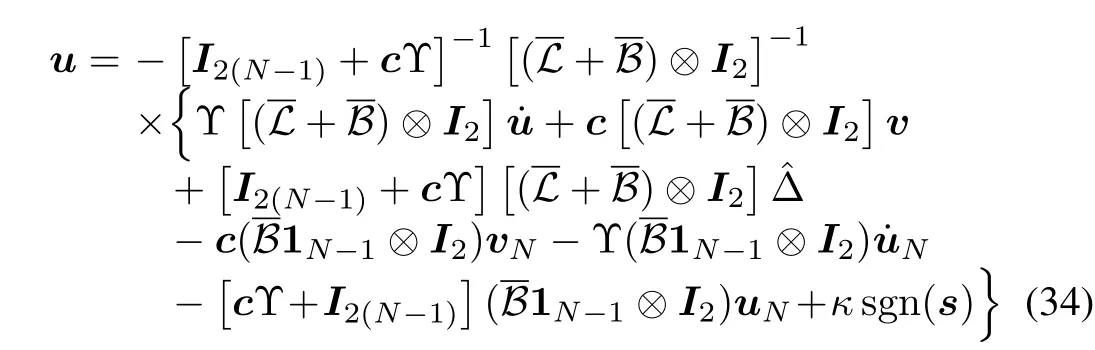
Substituting(34)into(33)gives
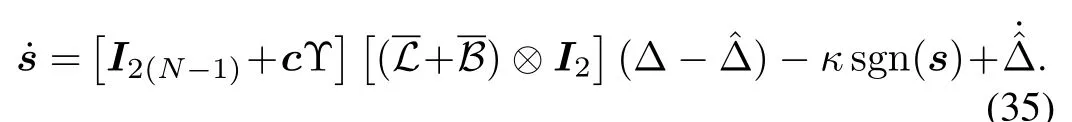
Theorem 2:Take the multi-agent system into consideration,suppose that its communication graph has a directed spanning tree.The stability of the leader-follower-based formation control is guaranteed if the controller parameters of each follower agent are designed by Theorem 1.
Proof:Define a Lyapunov candidate function

where‖·‖2means 2-norm.
DifferentiateV′(t)with respect to timetin(36).The derivative ofV′can be written by
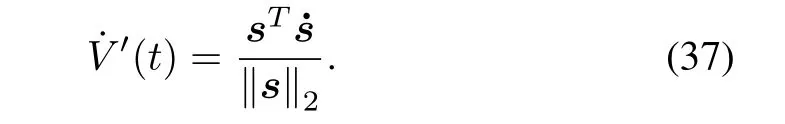
Replacing˙sin(37)with(35)yields
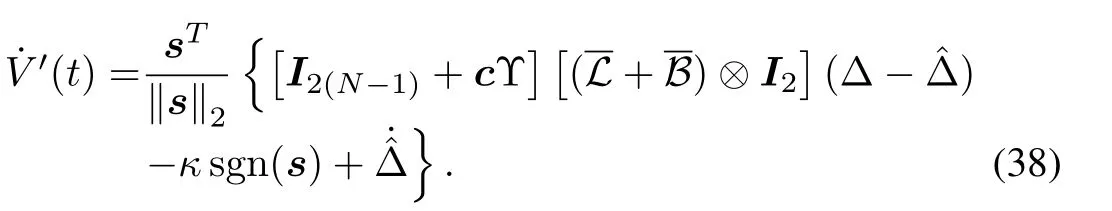
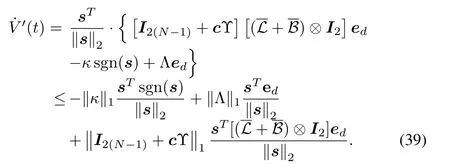
Note thataii=0(i=1,...,N?1)in(12)such thatLetSubsequently,(39)can be re-arranged by
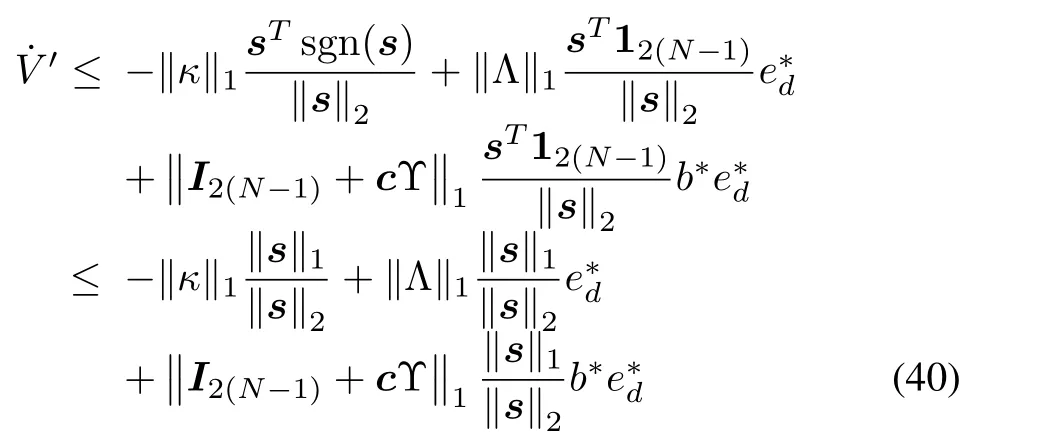
wherewheremeans∞-norm.
If the controller parameters of each follower agent are selected by Theorem 1,˙V′<0 can be deduced from(40).ConsideringV′≥0,the formation control of the multi-agent system is asymptotically stable in the sense of Lyapunov.
From Theorem 1 and Theorem 2,the formation stability is concerned to the tracking-error variablethat is constant but unknown as well,indicating that it is hard to determineκikin Theorem 1 as well asκin Theorem 2.To guarantee the formation stability,a conservative value ofshould be designated.From this aspect,there seem no benefits earned from such a robust control method.However,exidoriginated from the presented method is exponentially convergent as proven,meaning that a small value ofcould be chosen.According to Theorem 1,the kind of formation-control design could contribute to the decrease of chattering phenomenon as well as the improvement of the formation performance.
IV.SIMULATION RESULTS
This section implements some simulations on a multi-agent platform and discusses the results.The platform consists of four mobile robots.These robots are structured by the leader follower scheme.One robot is designated as leader and the other three as followers.The follower agents are numbered as indexes1,2 and 3,respectively.The sole leader is identified by index 4.Some physical parameters of these agents are picked up from[24],listed asl=0.0265m,h=0.04m,r=0.02m,m b=0.018 kg,mw=0.007 kg,Ib=1.44×10?4kg·m2andIw=1.44×10?6kg·m2.The communication topology of this multi-agent system under consideration is illustrated in Fig.2.
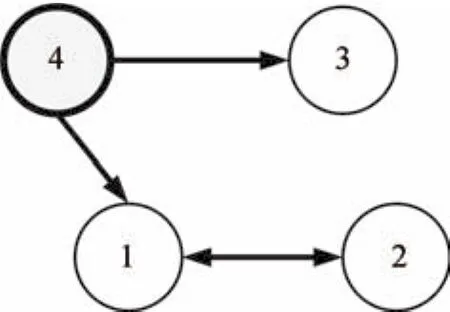
Fig.2.Communication topology of the multi-agent platform.
According to this communication topology,the communication graphGin Fig.2 becomes a standard spanning tree,where the adjacency and Laplacian matrices are determined by
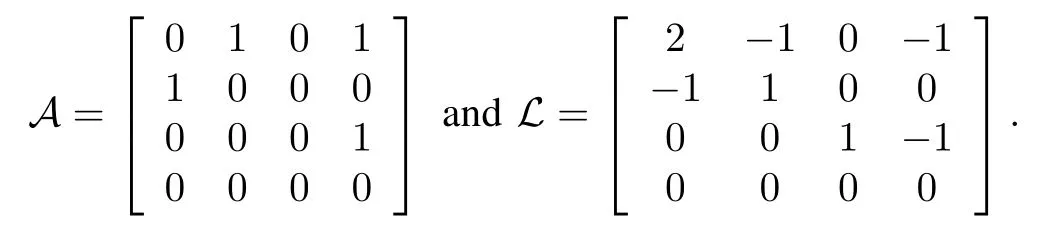
Further,the communication subgraphis derived fromG,whose adjacency and Laplacian matrices are formulated by
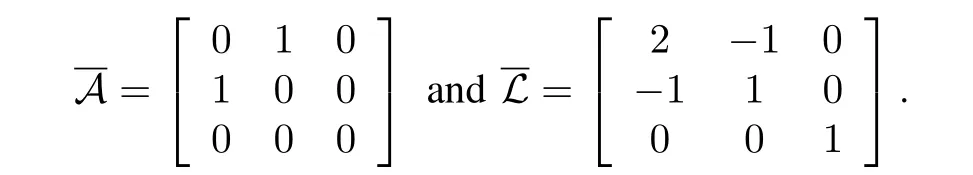
Apparently,the subgraphGis itself a directed graph.
For theith follower agent(i=1,2,3),the presented robust control design of itsx-axis subsystem can be implemented.The uncertain term of thex-axis subsystem is designed byδxi=0.02×rand(),where rand()is a uniformly distributed random number in the closed interval[?1 1].Some parameters of the SMC-based controller are predefined ascxi=9 andκxi=0.4.The gain vector of the NDO-based observer is chosen as L=[0 6]Tby trial and error such thatλxi=LTB=6 and the constantρxiin(18)is set as 1.0.Successively,the SMC-based controller and the NDO-based observer of theyaxis subsystem are kept unchanged from those corresponding parameters of thex-axis subsystem.Considering the motor load of the follower agents,bothuxianduyiare limited touxi≤0.5 anduyi≤0.5.
In order to achieve formation maneuvers of the multi-agent system,a given formation task is taken into consideration.In the formation task,the leader agent 4 moves along a straight line and the other follower agents keep tracking the leader and form up into a diamond-shaped formation.
The straight trajectory of the leader is presented as follows.In a Cartesian coordinate system,the initial head position of the leader is located at(0m,0.6m).Correspondingly,its velocities in thex-direction andy-direction are setby 0.2m/s and 0.1m/s,respectively.In order to form up into the desired diamond in this coordinate system,the initial head positions of follower agent 1,follower agent 2 and follower agent 3 in order are placed at(0m,1.1m),(0m,0.8m)and(0m,0.3m),respectively.Their relative coordinations in order are designated as(?0.2m,0.2m),(?0.4m,0m)and(?0.2m,?0.2m)with respect to the leader agent 4.
Fig.3 displays the simulation results of the presented robust control method by the multi-agent system.In Fig.3(a),the four agents form up into the diamond-shaped formation from a string while moving in straight lines,whereas filled triangles denote the initial positions of the agents and filled circles indicate the agents’positions in the dynamic process.In order to demonstrate the formation maneuver,the dashed lines bond the agents together at the same moment.
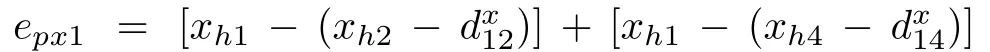
These results in Figs.4 and 5 are adopted for performance comparisons and our motivation is to highlight the superiority of the presented control scheme.Fig.4 illustrates the simulation results of the sole sliding-mode control approach by the same multi-agent system.In this formation-control system,the parameter of the sliding-surfacecxiis kept unchanged from the presented control method and the parameter ofκxiis selected as 1.1,where the value ofκxiis conservative to guarantee the formation stability.Compared with the results in Figs.4(f)?(g),the presented robust control method in Figs.3(f)?(g)can apparently decrease the chattering phenomenon because its formation stability is concerned with the exponentially-convergent tracking errorwhich is also the benefit we can earn from the presented robust control method.
As another comparison,the simulation results of the adaptive fuzzy sliding-mode control approach[24]is displayed in Fig.5 by the same multi-agent system.From Fig.5(a),the approach in[24]can also realize the same formation maneuver as the formation in Fig.4(a).However,the presented robust control method has better control performance in Figs.4(f)?(g)via the comparisons in Figs.5(f)?(g)because it can apparently decrease the magnitude of control action.On the other hand,the presented method in the paper and the approach in[24]focus on dealing with formation maneuvers in spite of uncertainties.In[24],a fuzzy inference system(FIS)is designed to resist the uncertainties such that the control performance is subject to the number of fuzzy logic rules.The FIS with the limited number of fuzzy rules is hard to keep better performance against the variations of uncertainties.The uncertainties in this paper are formulated by 0.02×rand(),compared with the expression of 0.005×rand()in[24].
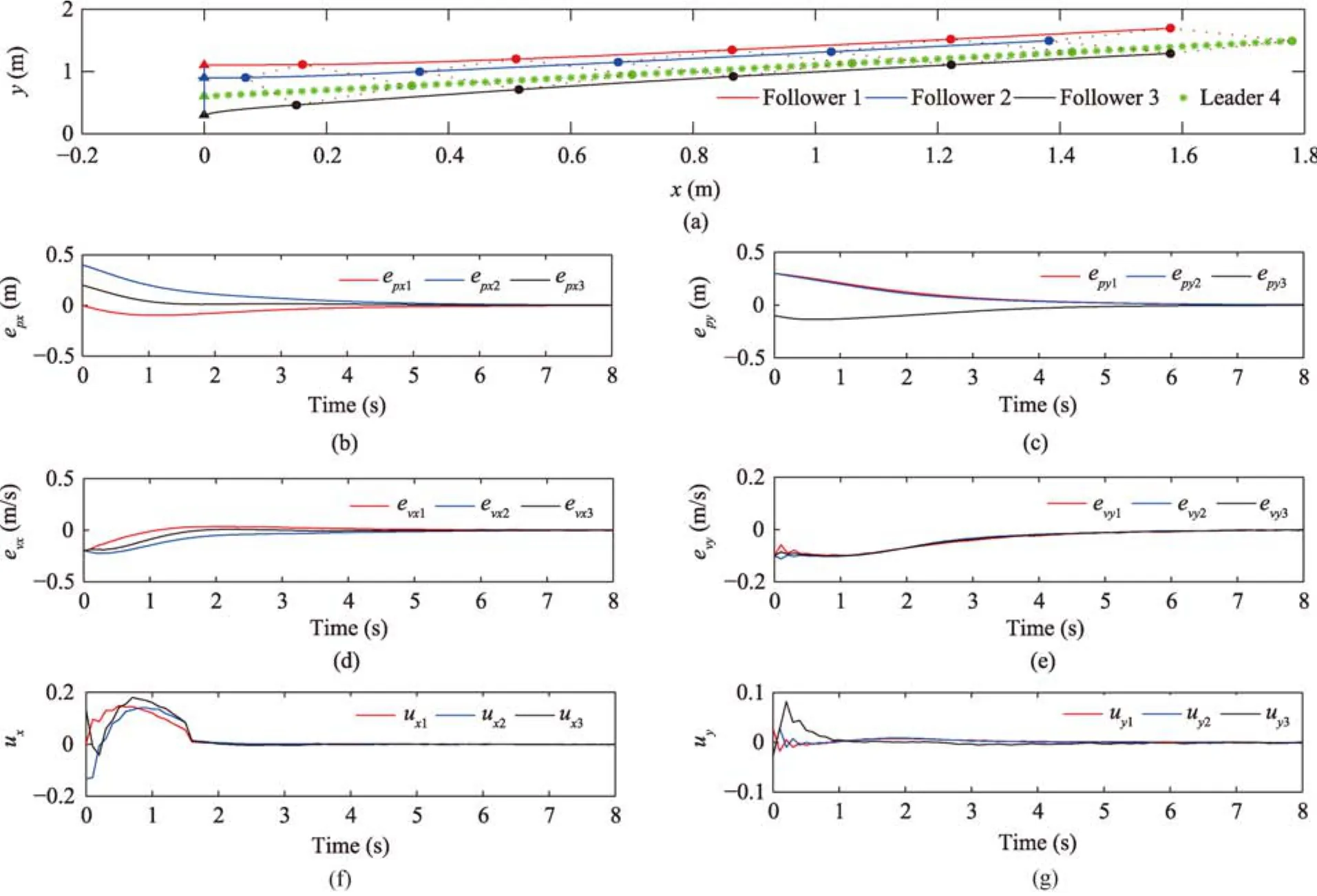
Fig.3.Simulation results of the presented robust control method.(a)Formation maneuvers in the Cartesian coordinate system.(b)Curves of epxi.(c)Curves of epyi.(d)Curves of evxi.(e)Curves of evyi.(f)Curves of uxi.(g)Curves of uyi(i=1,2,3).
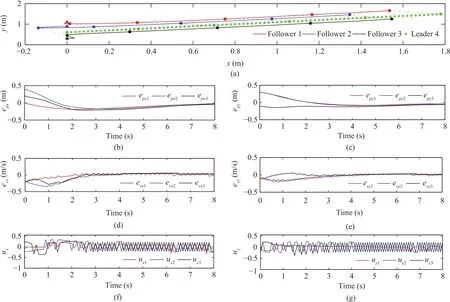
Fig.4.Simulation results of the sole sliding-mode control approach without an NDO-based observer.(a)Formation maneuvers in the Cartesian coordinate system.(b)Curves of epxi.(c)Curves of epyi.(d)Curves of evxi.(e)Curves of evyi.(f)Curves of uxi.(g)Curves of uyi(i=1,2,3).
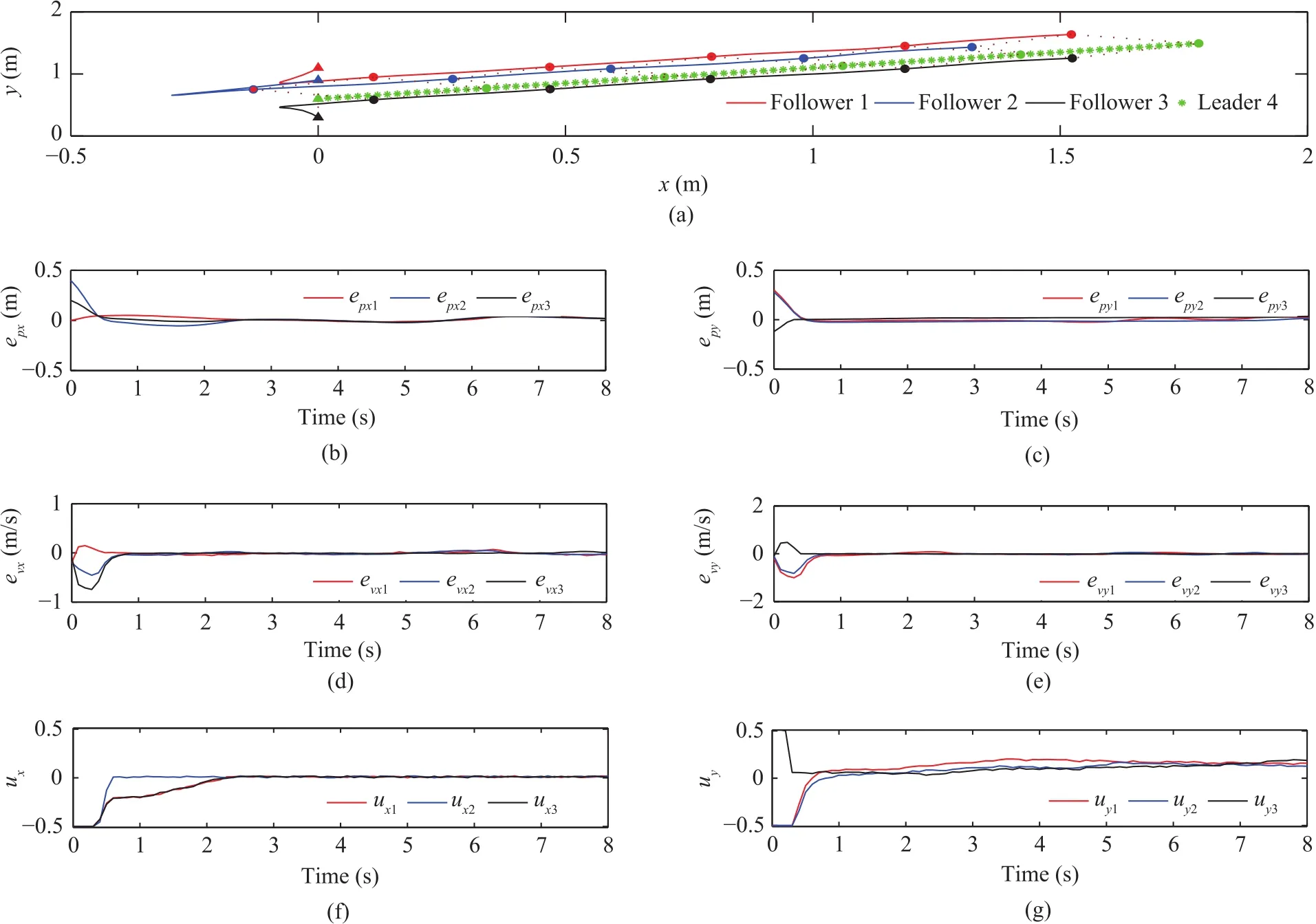
Fig.5.Simulation results of the adaptive sliding mode control approach[24].(a)Formation maneuvers in the Cartesian coordinate system.(b)Curves of epxi.(c)Curves of epyi.(d)Curves of evxi.(e)Curves of evyi.(f)Curves of uxi.(g)Curves of uyi(i=1,2,3).
V.CONCLUSIONS
This paper has investigated the formation-control problem of multiple agents.The agents under consideration are wheeled mobile robots.The formation mechanism is leader-follower based.The uncertainties originated from each individual agent result in the formation uncertainties.It is conveniently assumed that the formation uncertainties are bounded by an unknown boundary.In order to resist the formation uncertainties when forming up the agents,a robust control method that integrates the technique of NDO-based observer and the method of SMC-based controller is addressed.According to a given communication topology,the theoretical analysis has proven that the formation control of multiple agents in the presence of uncertainties is asymptotically stable.The control scheme has achieved the formation maneuvers by amulti-robot platform.The simulation results have demonstrated the effectiveness of the control scheme through some performance comparisons.In order to focus on the motivation of control design,some difficulties in reality,such as communication delays and collisions between agents,are not considered during the control design.The no-communication-delay and no-collision conditions are mild enough for small-scale formations but they are rather idealized for large-scale formations.In order to take the presented robust control method into practical account,this field is of our continuous interest and some contributions are still in progress.
[1]L.Cheng,Z.G.Hou,M.Tan,Y.Z.Lin,and W.J.Zhang,“Neural network-based adaptive leader-following control for multiagent systems with uncertainties,”IEEE Trans.Neural Netw.,vol.21,no.8,pp.1351?1358,Aug.2010.
[2]L.Cheng,Y.P.Wang,W.Ren,Z.G.Hou,and M.Tan,“On convergence rate of leader-following consensus of linear multi-agent systems with communication noises,”IEEE Trans.Autom.Control,vol.61,no.11,pp.3586?3592,Nov.2016.
[3]L.Cheng,Y.P.Wang,W.Ren,Z.G.Hou,and M.Tan,“Containmennt control of multiagent systems with dynamic leaders based on aP I-type approach,”IEEE Trans.Cybern.,vol.46,no.12,pp.3004?3017,Dec.2016.
[4]W.Ren and R.W.Beard,Distributed Consensus in Multi-Vehicle Cooperative Control.London,UK:Springer,2008.
[5]C.L.P.Chen,G.X.Wen,Y.J.Liu,and F.Y.Wang,“Adaptive consensus control for a class of nonlinear multiagent time-delay systems using neural networks,”IEEE Trans.Neural Netw.Learn.Syst.,vol.25,no.6,pp.1217?1226,Jun.2014.
[6]H.G.Zhang,T.Feng,G.H.Yang,and H.J.Liang,“Distributed cooperative optimal control for multiagent systems on directed graphs:An inverse optimal approach,”IEEE Trans.Cybern.,vol.45,no.7,pp.1315?1326,Jul.2015.
[7]H.Zhang,R.H.Yang,H.C.Yan,and F.W.Yang,“H∞consensus of event-based multi-agent systems with switching topology,”Inf.Sci.,vol.370?371,pp.623?635,Nov.2016.
[8]H.Rezaee and F.Abdollahi,“Average consensus over high-order multiagent systems,”IEEE Trans.Autom.Control,vol.60,no.11,pp.3047?3052,Nov.2015.
[9]M.Biglarbegian,“A novel robust leader-following control design for mobile robots,”J.Intell.Robot.Syst.,vol.71,no.3?4,pp.391?402,Sep.2013.
[10]J.Y.C.Chen and M.J.Barnes,“Human-agent team ing for multirobot control:A review of human factors issues,”IEEE Trans.Hum.Mach.Syst.,vol.44,no.1,pp.13?29,Feb.2014.
[11]C.C.Hua,X.You,and X.P.Guan,“Leader-following consensus for a class of high-order nonlinear multi-agent systems,”Automatica,vol.73,pp.138?144,Nov.2016.
[12]D.W.Qian,S.W.Tong,J.R.Guo,and S.Lee,“Leader-follower-based formation control of nonholonomic mobile robots with mismatched uncertainties via integral sliding mode,”Proc.Inst.Mech.Eng.IJ.Syst.Control Eng.,vol.229,no.6,pp.559?569,Jul.2015.
[13]D.W.Qian,S.W.Tong,and C.D.Li,“Leader-following formation control of multiple robots with uncertainties through sliding mode and nonlinear disturbance observer,”ETRIJ.,vol.38,no.5,pp.1008?1018,Oct.2016.
[14]J.Dasdemir and A.Loría,“Robust formation tracking control of mobile robots via one-to-one time-varying communication,”Int.J.Control,vol.87,no.9,pp.1822?1832,Mar.2014.
[15]S.J.Yoo,“Formation tracker design of multiple mobile robots with wheel perturbations:Adaptive output-feedback approach,”Int.J.Syst.Sci.,vol.47,no.15,pp.3619?3630,Dec.2016.
[16]T.P.Nascimento,A.G.S.Conceic?a?,and A.P.Moreira,“Multi-robot nonlinear model predictive formation control:The obstacle avoidance problem,”Robotica,vol.34,no.3,pp.549?567,Mar.2016.
[17]Y.Liu and Y.M.Jia,“Robust formation control of discrete-time multiagent systems by iterative learning approach,”Int.J.Syst.Sci.,vol.46,no.4,pp.625?633,Apr.2015.
[18]V.I.Utkin,Sliding Modes in Control and Optimization.Berlin Heidelberg,Germany:Springer,1992.
[19]Y.H.Chang,C.W.Chang,C.L.Chen,and C.W.Tao,“Fuzzy sliding-mode formation control for multirobot systems:Design and implementation,”IEEE Trans.Syst.Man Cybern.B Cybern.,vol.42,no.2,pp.444?457,Apr.2012.
[20]Y.Y.Dai,Y.Kim,S.Wee,D.Lee,and S.Lee,“Symmetric caging formation for convex polygonal object transportation by multiple mobile robots based on fuzzy sliding mode control,”ISA Trans.,vol.60,pp.321?332,Jan.2016.
[21]L.J.Dong,S.C.Chai,B.H.Zhang,and S.K.Nguang,“Sliding mode control for multi-agent systems under a time-varying topology,”Int.J.Syst.Sci.,2016,vol.47,no.9,pp.2193?2200,Sep.2016.
[22]A.M.Zou,K.D.Kumar,and Z.G.Hou,“Distributed consensus control for multi-agent systems using terminal sliding mode and Chebyshev neural networks,”Int.J.Robust Nonlinear Control,vol.23,no.3,pp.334?357,Feb.2013.
[23]D.Zhao,T.Zou,S.Li,and Q.Zhu,“Adaptive backstepping sliding mode control for leader-follower multi-agent systems,”IET Control Theory Appl.,vol.6,no.8,pp.1109?1117,May2012.
[24]Y.H.Chang,C.Y.Yang,W.S.Chan,H.W.Lin,and C.W.Chang,“Adaptive fuzzy sliding-mode formation controller design for multirobot dynamic systems,”Int.J.Fuzzy Syst.,vol.16,no.1,pp.121?131,Mar.2014.
[25]W.H.Chen,J.Yang,L.Guo,and S.H.Li,“Disturbance-observer based control and related methods-an overview,”IEEE Trans.Industr.Electron.,vol.63,no.2,pp.1083?1095,Feb.2016.
[26]B.Xiao,S.Yin,and O.Kaynak,“Tracking control of robotic manipulators with uncertain kinematics and dynamics,”IEEE Trans.Industr.Electron.,vol.63,no.10,pp.6439?6449,Oct.2016.
[27]T.Du,L.Guo,and J.Yang,“A fast initial alignment for SINS based on disturbance observer and Kalman filter,”Trans.Inst.Meas.Control,vol.38,no.10,pp.1261?1269,Oct.2016.
 IEEE/CAA Journal of Automatica Sinica2018年1期
IEEE/CAA Journal of Automatica Sinica2018年1期
- IEEE/CAA Journal of Automatica Sinica的其它文章
- IoT-based Smart and Complex Systems:A Guest Editorial Report
- New Chief,New Journey,New Excellence
- Bionic Quadruped Robot Dynamic Gait Control Strategy Based on Twenty Degrees of Freedom
- Robust Adaptive Gain Higher Order Sliding Mode Observer Based Control-constrained Nonlinear Model Predictive Control for Spacecraft Formation Flying
- An Iterative Relaxation Approach to the Solution of the Ham ilton-Jacobi-Bellman-Isaacs Equation in Nonlinear Optimal Control
- Suboptimal Robust Stabilization of Discrete-time Mismatched Nonlinear System
