QUASISYMMETRICALLY PACKING-MINIMAL MORAN SETS
LI Yan-zhe,HE Qi-han
(Colledge of Mathematics and Information Science,Guangxi University,Nanning 530004,China)
QUASISYMMETRICALLY PACKING-MINIMAL MORAN SETS
LI Yan-zhe,HE Qi-han
(Colledge of Mathematics and Information Science,Guangxi University,Nanning 530004,China)
In this paper,we study the problem of packing-minimality of 1-dimensional Moran sets.By using the principle of mass distribution,we obtain that a large class of Moran sets on the line with packing dimension 1 is quasisymmetrically packing-minimal,which extends a known result of quasisymmetrically packing-minimality.
quasisymmetric mapping;packing dimension;Moran set
1 Introduction
A homeomorphism mappingf:X→Y,whereXandYare two metric spaces,is said to be quasisymmetric if there is a homeomorphismη:[0,∞)→[0,∞)such that

for all triplesa,b,xof distinct points inX.Here we follow the notation in Heinonen[1]by using|x?y|to denote the distance between the two pointsxandyin every metric space.In particular,we also say thatfis ann-dimensional quasisymmetric mapping whenX=Y=Rn.
De finition 1We call a setE?Rnquasisymmetrically packing-minimal,if dimPf(E)≥dimPEfor anyn-dimensional quasisymmetric mappingf.
In this paper,we will show that a large class of Moran sets in R1of packing dimension 1 have quasisymmetric packing-minimality.
Similarly,we call a setE?Rnis quasisymmetrically Hausdor ff-minimal,if dimHf(E)≥dimHEfor anyn-dimensional quasisymmetric mappingf.Recall some results on the Hausdor ffdimensions of quasisymmetric images.First,n-dimensional quasisymmetric mappings are locally H?lder continuous[2],so if dimHE=0,then dimHf(E)=0 andEis quasisymmetrically Hausdor ff-minimal.In Euclidean space Rnwithn≥2,Gehring[3,4]obtainedthat for any subsetE?Rnof Hausdor ffdimensionn,its quasisymmetric image also has Hausdor ffdimensionn,soEis quasisymmetrically Hausdor ff-minimal.If 0<dimHE<1,there are 1-dimensional quasisymmetric mappingsfεandFεsuch that dimHfε(E)< ε(see[5])and dimHFε(E)>1?ε(see[6]),that is anyE?R1satisfies 0<dimHE<1 is not quasisymmetrically Hausdor ff-minimal.
For R1,Tukia[7]found an interesting fact,quite different from Gehring’s result for Rnwithn≥2,that there existsE?R1such that dimHE=1 and dimHf(E)<1 for some 1-dimensional quasisymmetric mappingf,soEis not quasisymmetrically Hausdor ff-minimal.
There is a question:what kinds of sets in R1are quasisymmetrically Hausdor ff-minimal?
For R1,many works were devoted to the quasisymmetrically Hausdor ff-minimal set,i.e.,the subsetE?R1satisfying dimHf(E)≥dimHEfor any 1-dimensional quasisymmetric mappingf.
Kovalev[5]showed that any quasisymmetrically Hausdor ff-minimal set in R1with dimHE>0 has full Hausdor ffdimension 1.Hakobyan[8]proved that middle interval Cantor sets of Hausdor ffdimension 1 are all quasisymmetrically Hausdor ff-minimal.Hu and Wen[9]obtained that some uniform Cantor sets of Hausdor ffdimension 1 are quasisymmetrically Hausdor ff-minimal.Dai,Wen,Xi and Xiong[10]found a large class of Moran sets of Hausdor ffdimension 1 which are quasisymmetrically Hausdor ff-minimal.
Compared with quasisymmetric Hausdor ff-minimality,there are few results on quasisymmetric packing-minimality.
Kovalev[5]showed that any quasisymmetrically packing-minimal set in R1with dimpE>0 has packing dimension 1.Li,Wu and Xi[11] find two classes of Moran sets of packing dimension 1 which are quasisymmetrically packing-minimal.Wang and Wen[12]obtained that the uniform Cantor sets of packing dimension 1 are quasisymmetrically packing-minimal.
In this paper,we will show that aresult of[11]is not accidents.In fact,a larger class of Moran sets on the line with packing dimension 1 is quasisymmetrically packing-minimal(Theorem 1).
This paper is organized as follows.In Section 2,we state our main results and give the introduction to the Moran sets.Some preliminaries are given in Section 3,including quasisymmetric mappings,Moran sets and certain probability measure supported on the quasisymmetric image.The key of this paper is to get the estimate in Lemma 1 for the above measure.Section 4 is the proof of Theorem 1.
2 De finition and Main Results
2.1 De finition of Moran Sets
Before the statement of theorems,we introduce the notion of Moran setsin R1.Letandbe sequences satisfyingnk≥2 andfor anyk≥1,setand ?0={?}with empty word?.Writeand(σ1···σk)? σk+1=σ1···σkσk+1.LetI?R1be a closed interval.Denote by|A|the diameter ofA?Rn.We say thatF={Iσ:σ∈?},which is a collection of closed intervals,has Moran structure(I,{nk},{ck,j}),ifI?=Iand for anyσ ∈?k?1,Iσ?1,···,Iσ?nk,whose interiors are pairwise disjoint,are subintervals ofIσsuch that

Then a Moran set determined byFis de fined by

where anyIσinFis called a basic interval of rankkifσ ∈?k.Denote byM(I,{nk},{ck,j})the class of all Moran sets associated withI,{nk}and{ck,j}.
For the classM(I,{nk},{ck,j}),we write

and

whereskis de fined by the equation

Ifσ ∈?k?1,k≥1,letbe the most left(or the most right)one ofIσ?1,···,Iσ?nk.Write
Some probability of quasisymmetric mappings and Moran sets can be seen in[13]and[14].
2.2 Main Results
The main result of paper are stated as follows.
Theorem 1SupposeE∈M(I,{nk},{ck,j}),r?>0 and supknk<∞,and there exist a costantl>1 such thatfor anyσ ∈?k?1andk≥2.If dimPE=1,then dimPf(E)=1 for any 1-dimensional quasisymmetric mappingsf.
Remark 1Without loss of generality,supposeandforσ ∈?k,k≥1,the conditions of Theorem 1 impliesck,1andck,nkis neither too“l(fā)arge”nor too“small”,and for 2≤i≤nk?1,ck,imay be very“small”,evenc?=0,butis not too“small”.
Remark 2Notice that the condition“and there exist a costantl>1 such thatfor anyσ ∈?k?1andk≥2”impliesnk≥3 for allk≥1.Notice that IfE∈M(I,{nk},{ck,j}),thenE∈M(I,{Nk},{Ck,q}),whereNk=n2k?1·n2k≥3 andCk,(i?1)n2k?1+j=c2k?1,i·c2k,jfor 1≤i≤n2k?1,1≤j≤n2k,so without loss of generality,we always assume thatnk≥3 for allk≥1 in this paper.
Example 1LetE∈M(I,{nk},{ck,j})withc?>0.Ifnk≥3 for allk≥1,thenr?≥c?>0,supknk< ∞andfor anyσ ∈?k?1andk≥2;if infknk=2,thenE∈M(I,{Nk},{Ck,q}),whereNkandCk,qare de fined the same as the above remark(Nk≥3),it is easy to obtain thatE∈M(I,{Nk},{Ck,q})satisfies the conditions of Theorem 1.Then by Theorem 1,if dimPE=1,we have dimPf(E)=1 for any 1-dimensional quasisymmetric mappingf.
Therefore Theorem 1 extends the results of Theorem 2 in[11].
Example 2LetEbe an uniform Cantor set(see[12])withc?>0.Ifnk≥3,thenr?=c?>0,supknk< ∞andfor anyσ ∈?k?1andk≥2;if infknk=2,thenE∈M(I,{Nk},{Ck,q}),whereNkandCk,qare de fined the same as the above remark(Nk≥3),it is easy to obtain thatE∈M(I,{Nk},{Ck,q})satisfies the conditions of Theorem 1.Then by Theorem 1,if dimPE=1,we have dimPf(E)=1 for any 1-dimensional quasisymmetric mappingf.
Therefore Theorem 1 extends the results of Theorem 1.2 in[12]whenc?>0.
3 Preliminaries
Before the proofs of the two theorems,we give some preliminaries.
The following fact on packing dimension can be found in Proposition 2.3 of[15].
Lemma 1LetE?Rnbe a Borel set,andμa probability measure supported onE.If there existsE′?Ewithμ(E′)>0 and a constantc>0 such that

then dimPE≥s.
We need some properties on quasisymmetry.For closed intervalI,setρIbe a closed interval with a length ofρ|I|and with the same center withI.
From[16],it is easy to check the following lemma.
Lemma 2Supposef:R1→R1is quasisymmetric,there exist constantsλ,Kρ>0,q≥1 andp∈(0,1]such that

and

whenever closed intervalI,I′satisfyingI?I′
The following lemma comes from[17].
Lemma 3SupposeEis a Moran set satisfying the following conditions
Then we have dimPE=s?.
It is easy to verify that if for a Moran setE∈M(I,{nk},{ck,j}),the conditions of Theorem 1 hold,thenEsatisfiesby Lemma 3,dimPE=s?.
The length ofσ ∈?kwill be denoted by|σ|(=k).
Fix a 1-dimensional quasisymmetric mappingf:R1→R1.Given a Moran setEand its basic intervalIσofEwith rankk,we also callf(Iσ)a basic interval off(E)with rankkfor convenience.LetJσ=f(Iσ).
3.1 The MeasureμdSupported on f(E)
Fixd∈(0,1).We will de fine a probability measureμdonf(E)as follows.
Without loss of generality,we setI=[0,1]the initial interval ofE.
Letμd(f([0,1]))=1,for everyk≥1,and for every basic intervalJσof rankk?1,we de fine

for 1≤j′≤nk.
3.2 Estimate ofμd(Jσ)
The next proposition can be found in[11].
Proposition 1SupposeEis the Moran set satisfyingand

for some constantα ∈(0,1).If s?=1,then there exists a subsequence{kt}tand a constantc>0 such that

for any basic intervalJσoff(E)with|σ|∈{kt}t.
By Proposition 1,we have the corollary below.
Corollary 1SupposeEis the Moran satisfies the conditions of Theorem 1.If dimPE=1,then there exists a subsequence{kt}tand a constantc>0 such that

for any basic intervalJσoff(E)with|σ|∈{kt}t.

ProofSincenk≥2,r?>0,we haveDk≤1?r?<1.Takeα=1?r?,we have notice that dimpE=s?by Lemma 3 and Proposition 1,the corollary follows.
4 Proof of Theorem 1
Let{kt}tbe the subsequence in Proposition 1.Let

Lemma 4Suppose thatnk≥3 andc?>0.Then there exists a constant∈>0 such that

for allσwith|σ|=k?1 and 1≤j1,j2≤nk.
ProofWith out loss of generality,we letJLσ=Jσ?1,JRσ=Jσ?nk,sincenk≥3.Takei0(1≤i0≤nk)as follows
Case 1Ifpicki0such thatthen 2≤i0≤nk?1,we have
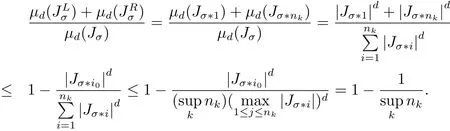

Case 2Ifpicki0such thatwe have

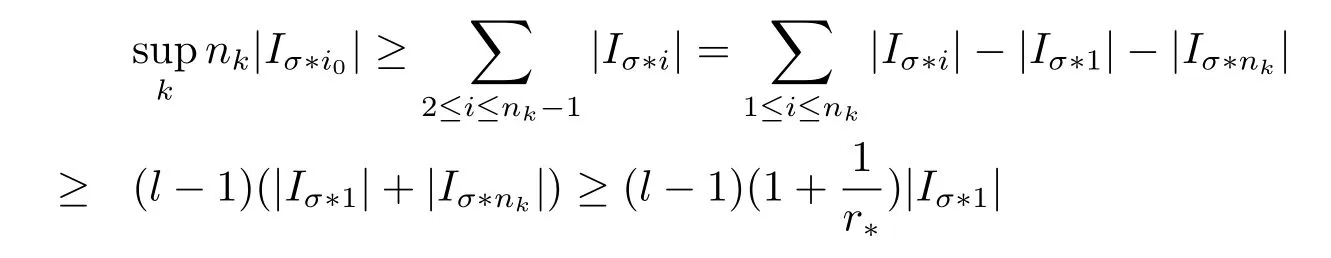
By Lemma 2,we have

which imply

Therefore

where
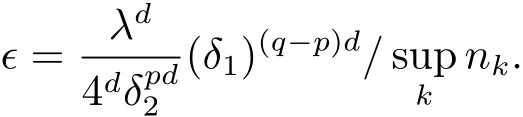
Proposition 2μd(B)=0 ford∈(0,1).
ProofIt suffices to provefor anys.
Let


For anyσ,letJLσ=f(ILσ),JRσ=f(IRσ).Therefore,fort≥s,

By Lemma 4,we have

it follows from(4.1)and(4.2)that

which implies

Next we finish the proof of Theorem 1.
From the proposition above,we haveμd(f(E)B)=1>0.Fixx∈(f(E)B),then we can picktn↑∞satisfieswith some

notice thatrn→0 whenn→∞.

which impliesB(x,rn)?Jσ.
LetJσ?j1,Jσ?j2,···,Jσ?jl′(1≤l′≤nktn)be the basic intervals of rankktnmeetingB(x,rn).Then
Using the conclusion of Corollary 2,we get

Sincer? >0,for anyi,there exists a constantδ≥1,

hence|Iσ?ji|?(3δ)f?1(B(x,rn)),whereδ≥1.By Lemma 2,we have

whereK3δ >0 is a constant.This together with(4.4)gives

Letn→∞,then for anyx∈f(E)B,there exists a constantC′>0,such that
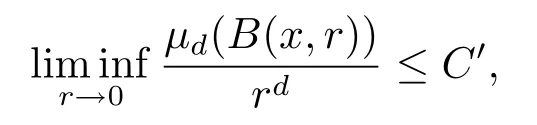
it follows fromμd(f(E)B)>0 and Lemma 1 that dimpf(E)≥d.Letd→1,we have

[1]Heinonen J.Lectures on analysis on metric spaces[M].New York:Springer-Verlag,2001.
[2]Ahlfors L V.Lectures on quasiconformal mappings(2nd ed.)[M].Unversity Lecture Series,Vol.38,Maryland:American Mathematical Society,2006.
[3]Gehring F W.TheLp-integrability of the partial derivatives of a quasiconformal mapping[J].Acta Math.,1973,130:265–277.
[4]Gehring F W,V?is?l? J.Hausdor ffdimension and quasiconformal mappings[J].J.London Math.Soc.,1973,6(2):504–512.
[5]Kovalev L V.Conformal dimension does not assume values between zero and one[J].Duke Math.J.,134(1):1–13,2006.
[6]Bishop C J.Quasiconformal mappings which increase dimension[J].Ann.Acad.Sci.Fenn.Math.,1999,24(2):397–407.
[7]Tukia P.Hausdor ffdimension and quasisymmetric mappings[J].Math.Scand.,1989,65(1):152–160.
[8]Hakobyan H.Cantor sets that are minimal for quasisymmetric mappings[J].J.Contemp.Math.Anal.,2006,41(2):13–21.
[9]Hu Meidan,Wen Shengyou.Quasisymmetrically minimal uniform Cantor sets[J].Topology.Appl.,2008,155(6):515–521.
[10]Dai Yuxia,Wen Zhixiong,Xi Lifeng,Xiong Ying.Quasisymmetrically minimal Moran sets and Hausdor ffdimension[J].Ann.Acad.Sci.Fenn.Math.,2011,36:139–151.
[11]Li Yanzhe,Wu Min,Xi Lifeng.Quasisymmetric minimality on packing dimension for Moran sets[J].J.Math.Anal.Appl.,2013,408:324–334.
[12]Wang Wen,Wen Shengyou.Quasisymmetric minimality of Cantor sets[J].Topology Appl.,2014,178:300–314.
[13]Lou Manli.Gap sequence and quasisymmetric mapping[J].J.Math.,2015,35:705–708.
[14]Liu Xiaoli,Liu Weibin.The Hausdor ffdimension of a class of Moran sets[J].J.Math.,2016,36:100–104.
[15]Falconer K.Techniques in fractal geometry[M].Chichester:John Wiley Sons Ltd,1997.
[16]Wu J M.Null sets for doubling and dyadic doubling measures[J].Ann.Acad.Sci.Fenn.Ser.A.Math.,1993,18(1):77–91.
[17]Hua Su,Rao Hui,Wen Zhiying,Wu Jun.On the structures and dimensions of Moran sets[J].Sci.China Ser.A.,2000,43(8):836–852.
擬對稱packing極小Moran集
李彥哲,何其涵
(廣西大學數(shù)學與信息科學學院,廣西南寧 530004)
本文研究了一維Moran集的擬對稱packing極小性的問題.利用質(zhì)量分布原理的方法,獲得了直線上一類packing維數(shù)為1的Moran集為擬對稱packing極小集的結(jié)果,推廣了參考文獻中關(guān)于擬對稱packing極小性的已知結(jié)果.
擬對稱映射;packing維數(shù);Moran集
O174.12
28A75;28A78;28A80
A
0255-7797(2017)06-1125-09
date:2016-08-15Accepted date:2016-11-09
Supported by NSFC(11626069);Guangxi Natural Science Foundation(2016GXNSFAA380003);Science Foundation of Guangxi University(XJZ150827).
Biography:Li Yanzhe(1986–),male,born at Guilin,Guangxi,lecturer,major in fractal geometry.
He Qihan.

