A high-fidelity memory scheme for quantum data buses?
Bo-Yang Liu(劉博陽(yáng)),Wei Cui(崔巍),Hong-Yi Dai(戴宏毅),Xi Chen(陳希),and Ming Zhang(張明),?
1 College of Mechatronics and Automation,National University of Defense Technology,Changsha 410073,China
2 School of Automation Science and Engineering,South China University of Technology,Guangzhou 510641,China
3 College of Science,National University of Defense Technology,Changsha 410073,China
A high-fidelity memory scheme for quantum data buses?
Bo-Yang Liu(劉博陽(yáng))1,Wei Cui(崔巍)2,Hong-Yi Dai(戴宏毅)3,Xi Chen(陳希)1,and Ming Zhang(張明)1,?
1 College of Mechatronics and Automation,National University of Defense Technology,Changsha 410073,China
2 School of Automation Science and Engineering,South China University of Technology,Guangzhou 510641,China
3 College of Science,National University of Defense Technology,Changsha 410073,China
A novel quantum memory scheme is proposed for quantum data buses in scalable quantum computers by using adjustable interaction.Our investigation focuses on a hybrid quantum system including coupled flux qubits and a nitrogen–vacancy center ensemble.In our scheme,the transmission and storage(retrieval)of quantum state are performed in two separated steps,which can be controlled by adjusting the coupling strength between the computing unit and the quantum memory.The scheme can be used not only to reduce the time of quantum state transmission,but also to increase the robustness of the system with respect to detuning caused by magnetic noises.In comparison with the previous memory scheme,about 80%of the transmission time is saved.Moreover,it is exemplified that in our scheme the fidelity could achieve 0.99 even when there exists detuning,while the one in the previous scheme is 0.75.
quantum memory,hybrid quantum system,quantum data bus
1.Introduction
To extend the processing ability of quantum computers, transmitting[1,2]and correlating[3,4]quantum information by coupling computing units is regarded as an effective way.[5–8]In classical computer systems,caches,registers,and memories play the role in sharing information between processing units.Correspondingly,quantum data buses based on processors and memory units have also been proposed for constructing quantum information processing systems.[9–11]Sending and receiving quantum states can be conducted asynchronously with the help of memory units,which make sit possible to realize complex quantum algorithms that require many computing units and long processing times.[12,13]There are various quantum memory schemes proposed based on different physical effects,[14–16]storage materials,[17–19]and system structures.[20–23]By employing different memory schemes, sharing quantum information has been widely studied in theory and experiment.[24–28]It suggests a full potential for the application of quantum memories in quantum state buses.
The information transmission in quantum memory systems is generally directly performed by keeping the computing units interacting with the memory units for a specific period of time.At present,such memory schemes have been studied in a variety of coupling models,including direct electromagnetic interaction,[29,30]transmission line resonator,[31–33]LC resonator,[34–37]and ancillary qubits coupling.[38,39]In theory and experiment,the feasibility of direct memory schemes have been shown.Nevertheless,in practicable quantum data buses,the application of these schemes still faces challenges in processing efficiency and system robustness.When the computing unit interacts with a memory unit,the processing time would be occupied for the whole quantum state transmission process.As a result,the processing efficiency of performing other quantum operations will be limited.Moreover,quantum transmission systems are sensitive to magnetic fields.[35,40]In order to protect the coherence of the quantum state transmitted,the robustness of the system remains to be improved in the presence of environmental noises.
Aiming at the aforementioned challenges,we propose a novel quantum memory scheme for quantum data buses in scalable quantum computers.In most of the previous quantum memory schemes,state storage(retrieval)is done in one single step by finding and implementing some specific unitary evolution.Although the analyses of complicated systems are simplified,parts of the degrees of freedom of the system are lost.In contrast,degrees of freedom,including coupling strength and the state of qubit,are utilized in our scheme. State transmission and storage(retrieval)are achieved in two steps by adjusting the interaction between the computing and the memory units.A hybrid superconducting(SC)memory system combining flux qubits with a nitrogen–vacancy centers(NV)ensemble is considered conducting our two-step scheme.The NV ensemble has been regarded as a promising candidate for storage units because of its long coherence time at room temperature,narrow optical line widths,and flexible scalability.[41–45]In SC circuits,NV ensembles couple flux qubits through magnetic interactions.[29,46,47]Spins in NV ensemble are usually considered to have a low excitation rate and homogeneous energy splitting,hence the NV ensemblecan be approximated as a bosonic mode.[48,49]As an intermediate state,the entangled state of SC qubit and NV ensemble is utilized to temporarily keep the quantum information,with which the state transmission process could be finished in advance.By tuning the coupling strength between SC qubits, we are able to further trade off time costs of two steps and to reduce the influence of frequency detuning caused by environmental noises.The simulation reflects that both the transmission speed and the robustness with respect to detuning could be effectively enhanced in our scheme.
2.Model and Hamiltonian
We briefly introduce the model and the Hamiltonian of our memory system for quantum data buses in scalable quantum computers.The system comprises SC flux qubits and a NV ensemble.[29,47,48]The schematic architecture of our model is depicted in Fig.1,which consists of three parts:a computing unit,a quantum memory unit,and a transmission unit.Here a computing flux qubit(CQ)is utilized as the computing unit.The quantum memory unit is made up of a memory qubit(MQ)and a NV ensemble.An ancillary qubit (AQ)is introduced as the transmission unit,which couples the distant computing unit and the quantum memory together.By modifying voltage,current,and magnetic induction,energy levels and transition frequencies of SC qubits can be accurately controlled.[50–55]Additionally,the coupling strength between the computing unit and the memory can be adjusted by changing the energy level of AQ.By controlling the coupling strength between the memory and the computing units,one can store the quantum state of a computing unit in the memory and retrieve it at another computing unit.Here,the memory plays the role of a quantum state buffer.Benefiting from the memory unit,the quantum state could be shared in a longer time period,and the controllability and scalability of the system would be improved.
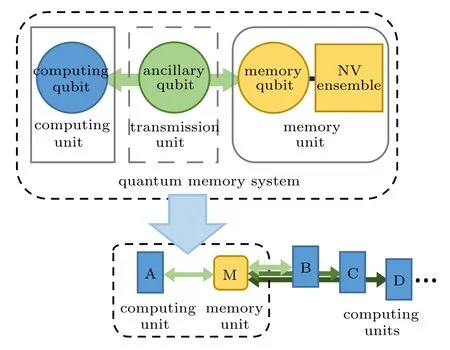
Fig.1.(color online)The architecture of our hybrid SC circuit memory system.The whole quantum memory system consists of three flux qubits and an NV ensemble.The computing qubit(CQ)is employed as the computing unit.Memory qubit(MQ)together with the NV ensemble compose the memory unit.The ancillary qubit(AQ)plays the role in data transmission between the computing unit and the memory.Coupling spatially separated computing units A,B,C,D,...,and the memory unit M respectively,a series of memory systems are composed.By storing and retrieving the quantum information,they can act as a quantum data bus.
Under the rotating wave approximation,the Hamiltonian of the memory unit[29,40]is
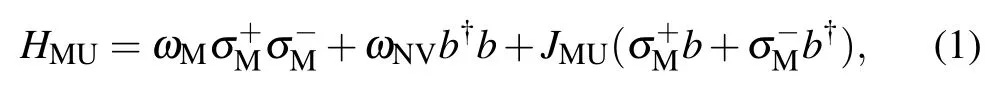
where the reduced Planck constantˉh=1.The NV ensemble is considered as an effective bosonic mode.[48,49]The straininduced fine-structure splitting of NV centers are ignored and the spins of the NV centers are assumed to have the homogeneous energy splitting.The increasing and decreasing operators of the excited NV centers are denoted by b+and b, respectively.They are derived from the raising and lowering operators of the the NV center and are approximately bosonic commutation operators.In addition,andare raising and lowering operators of MQ.Parameter JMUis the coupling strength between the NV ensemble and MQ,and ωMand ωNVare the frequencies of MQ and NV ensemble.
In superconducting circuits,the ancillary qubit could be a flux qubit,whose frequency is much larger than the frequencies of CQ and MQ.In this dispersive interaction case,AQ evolves faster than any other unit of the system,and operators corresponding to the ancillary qubit can be adiabatically eliminated.[56]Under the rotation wave approximation,the interaction Hamiltonian between MQ and CQ[57]is
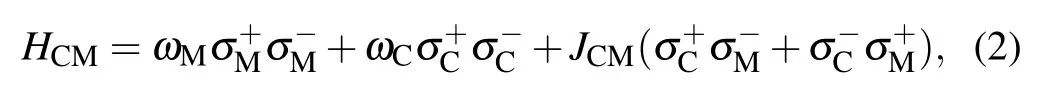
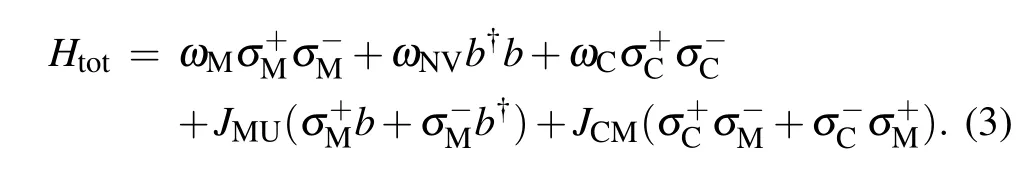
We can describe the evolution of the whole system with a Schr?dinger equationHere the initial state of the system is|ψ(0)〉=|ψC(0)〉?|ψM(0)〉?|ψNV(0)〉. |ψC(t)〉,|ψM(t)〉,|ψNV(t)〉,and|ψ(t)〉represent the states of CQ,MQ,NV ensemble,and the whole memory system,respectively.
In the following,the evolution of the memory system is discussed in the interaction picture.Under the resonate condition,ωC=ωM=ωNV,the interaction Hamiltonian of our memory system is
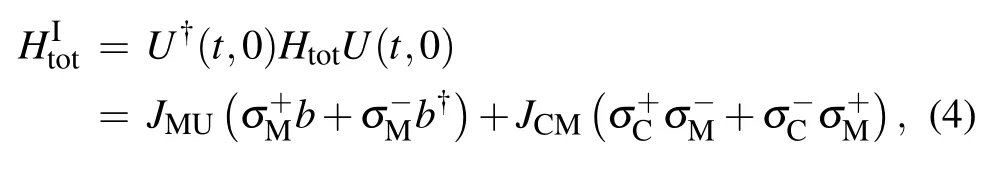
where
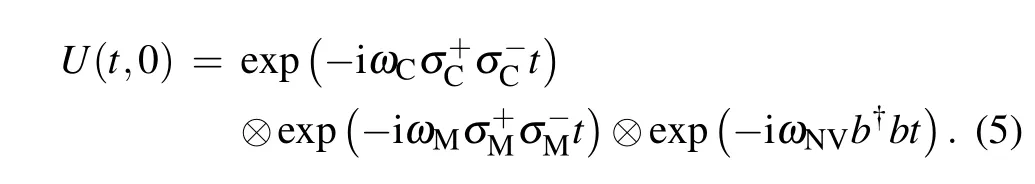
H√ereand b?|n〉=State vectors|g〉and|e〉are the ground state and the excited state of the flux qubits respectively,and|n〉denotes the state of n NV centers excited in the NV ensemble.
In the quantum memory system employed in our scheme, the coupling between CQ and MQ can be controlled by adjusting the ancillary qubit via adapting the external magneticfield.Through setting the coupling strength JCM=Jt≥JMUand JCM=0 respectively,we can achieve the quantum state storage and retrieval in two steps.
3.Two-step scheme for quantum state storage and retrieval
In this section,we consider the two-step scheme for quantum state storage and retrieval.We assume that the computing qubit,the memory qubit,and the NV ensemble have been set off-resonance.Additionally,the states of the memory |ψM〉?|ψNV〉and the computing unit|ψC〉are assumed to be ground states before conducting the storage and the retrieval process.
To store the state of the computing unit into the NV ensemble,quantum information is firstly transmitted from CQ to the memory unit.The entangled state of MQ and NV ensemble is utilized to keep the quantum information temporarily. We can adjust magnetic fields on MQ and the NV ensemble to make the whole memory system resonate,ωC=ωM=ωNV, and modify the magnetic flux through the ancillary qubit AQ to couple MQ and CQ with the strength JCM=Jt≥JMU.
For initial states|ψC(0)〉=cg|g〉+ce|e〉,|ψM(0)〉=|g〉, and|ψNV(0)〉=|0〉,the state of the whole quantum memory system at time t can be expressed with parametersandas
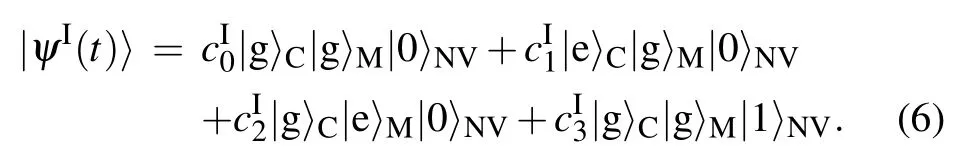
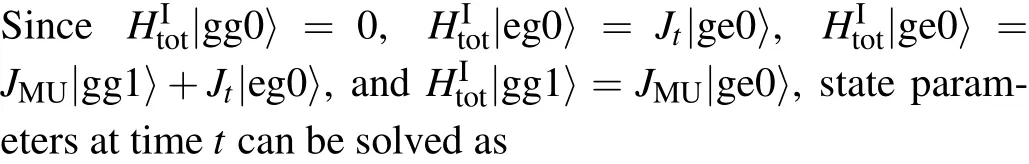

As a result,at some specific moments
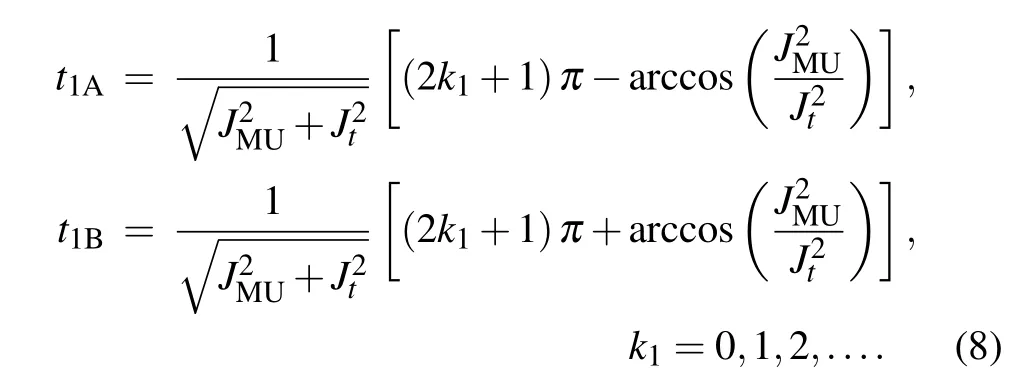
In the second step,the quantum information transmitted to the quantum memory unit is stored in the NV ensemble. We cut off the interaction between the computing unit and the memory by setting JCM=0.Thus the Hamiltonian of the system will beFor an initial statethe state of the quantum memory system at time t>t1can also be expressed as the form of|ψI(t)〉with
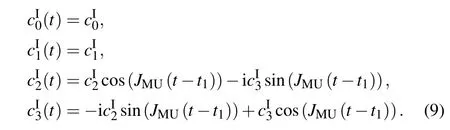
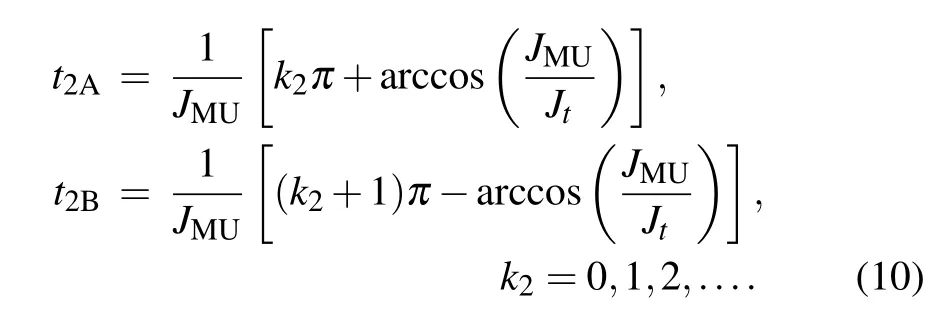
which correspond to two different cases with evolution times t1=t1Aand t1=t1Bin the first step,respectively.At the moments t1+t2=t1A+t2Aor t1+t2=t1B+t2B,the initial quantum state would be completely stored in the NV ensemble,and the interaction between the memory flux qubit and the NV ensemble could then be cut off by tuning the external magnetic field.The NV ensemble will preserve the quantum information for a certain period before retrieving it.
Corresponding to our storage process,the two-step state retrieval scheme is introduced in the following.To retrieve the stored quantum information,the NV ensemble firstly interacts with the flux qubit MQ for a time period t3=?t2+2k3π/JMU, with k3=1,2,...and t3≥0.Then the quantum information will be coded by an entangled state of the memory unit.In the second step,we couple the memory unit to the computing unit with the coupling strength JCM=Jt≥JMU. Through their interaction,the quantum state is transmitted back to the computing unit.Corresponding to two cases in the retrieval step,transmission time of the second step iswith k4=1,2,...and t4≥0.After the evolution for the time period t4,the initial state would be finally retrieved at the desired computing qubit.
In the following,we make a discussion on how transmission time can be adjusted by modifying the coupling strength. According to our discussion in the previous section,the total time cost for a complete state storage and retrieval process is
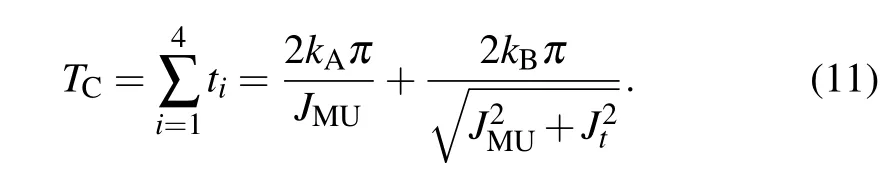
The total time costs are functions of the cycle numbers,kA, kB≥1,and the coupling strength parameters,JCMand JMU. To ensure the resonance of the memory unit,JMUshould be kept at a specific value.[29,58]On the other hand,the coupling strength between the computing unit and the memory unit, JCM=Jt,could be modified by controlling the flux threading the loop of the ancillary qubit,[56,57]and our scheme can thus be adjusted.As a special case,when JCM=JMUand k1=k2=0,k3=k4=1,we find t2A=0,which means that the state storage process can be finished in one step.By setting parameters of the system to be a specific set of values, our scheme degenerates to a direct storage scheme.Moreover,when JCM=JMUand k1=0,k2=k3=k4=1,we have t3B=0,which means that the state retrieval process degenerates to a direct retrieval scheme.
By strengthening the coupling JCM,the time cost TCcould be reduced and the performance of the system would be more efficient.Because the memory processes in case A and case B have inverse time costs,we just focus on case A in the following study and take tl=tlAfor l=1,2,3,4.To simplify the scheme and reduce the total transmission time,we take k1=0 and k2=k3=k4=1,which leads to

According to Eq.(12)the relationship between the coupling strength Jtand the time costs is shown in Fig.2.It indicates that the transmission times t1and t4would be reduced when increasing the coupling strength Jt.Considering the coupling strength limitation of the rotating wave approximation,[59–61]we propose that the optimal value of the coupling strength Jtis around 8JMU–10JMU,with which 80%of the transmission time will be saved.
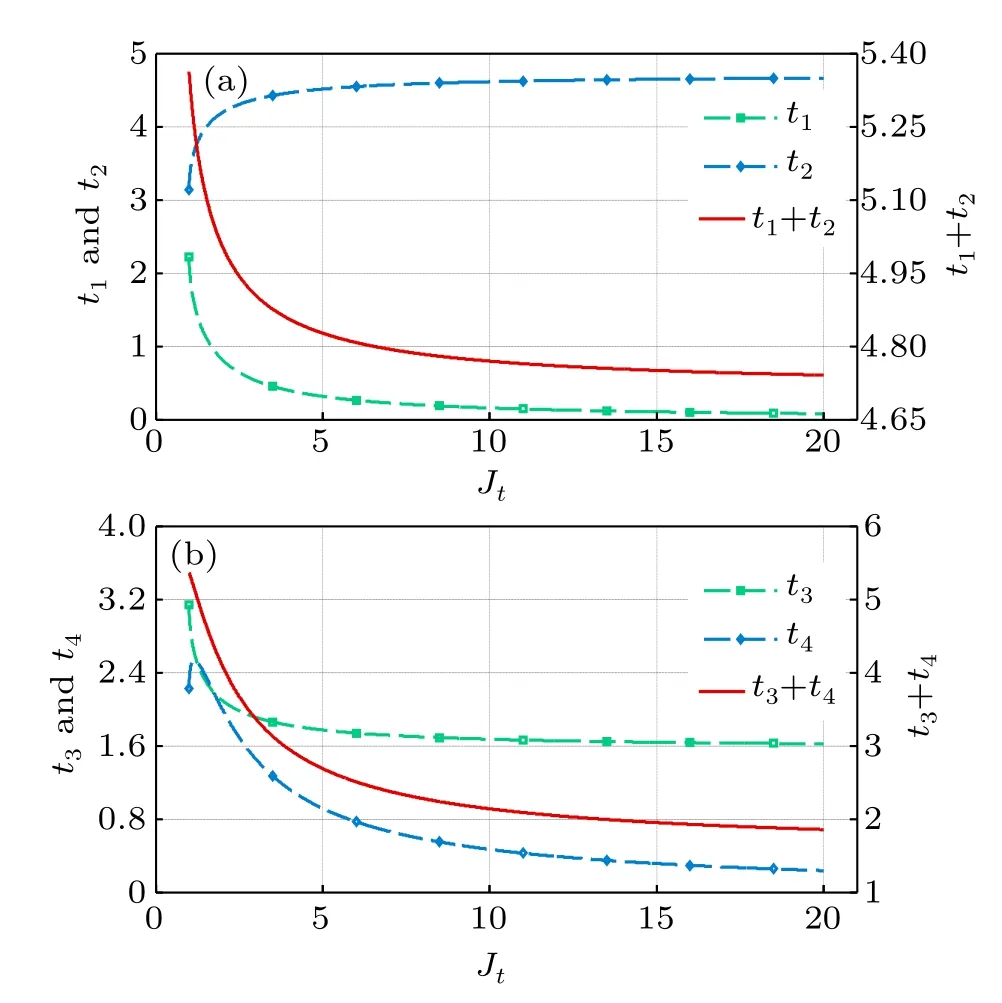
Fig.2.(color online)The relationship between time costs of quantum memory processes and the coupling strength parameter Jt.Time costs of quantum state storage(a)and retrieval(b)are influenced by Jt.Here the relative value Jt/J MU is employed to judge Jt.We take tl=tlA and k1=0,k2=k3=k4=1.
4.The robustness of the memory scheme against detuning
In this section,we discuss the robustness of our control method under quantum detuning caused by magnetic noises. Currents of SC qubits nearby and acts of conducting classical or quantum operations on computing qubits may cause interruptions to the control magnetic fields of flux qubits.[38]With regard to resonant coupling qubits,frequency detuning is one of the main influences caused by such kind of interruptions, since the frequency of flux qubits are sensitive to the magnetic flux threading their loops.[52,57]Focusing on frequency detuning,we study the evolution of our memory system and show the robustness of our memory scheme in the following.
With δ1=ωC?ωMdenoting the detuning between CQ and MQ,and δ2=ωM?ωNVdenoting the detuning between MQ and the NVensemble,the Hamiltonian of the whole memory system can be expressed in the interaction picture as
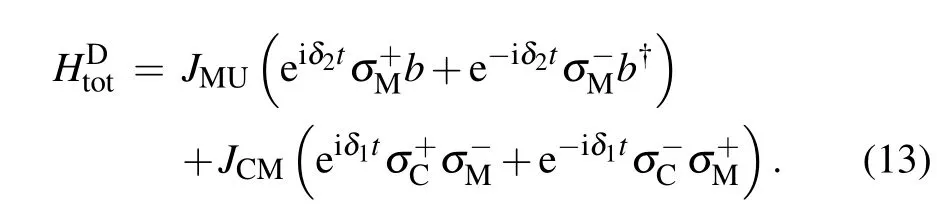
We take time periods of quantum state storage and retrieval processes as those given in Eq.(12)and focus on the quan-tum state storage process in the following,since the state retrieval is just its inverse process.Under the initial condition |ψC(0)〉=cg|g〉+ce|e〉,|ψM(0)〉=|g〉,and|ψNV(0)〉=|0〉, the state of the whole quantum memory system at time t can generally be written as
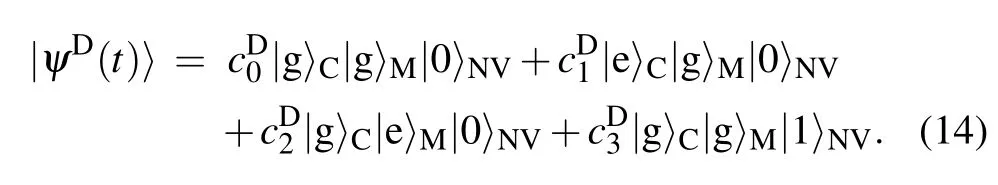
Since detuning is considered to be much smaller than the coupling strength,the second and higher level items of detuning are omitted in our model.According to our derivation shown in Appendix A,when δ1t1,δ2t1?1,state parameters for 0≤t≤t1can be approximately expressed as
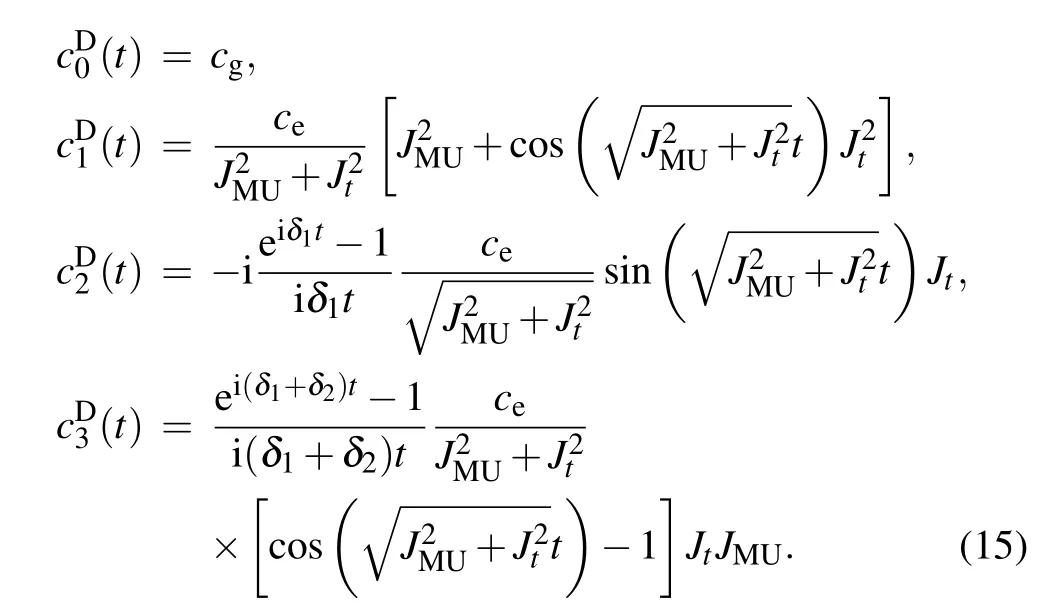
Additionally,we have t1≤t≤t1+t2in the second step.When δ1t2,δ2t2?1,state parameters in Eq.(14)are approximately expressed as
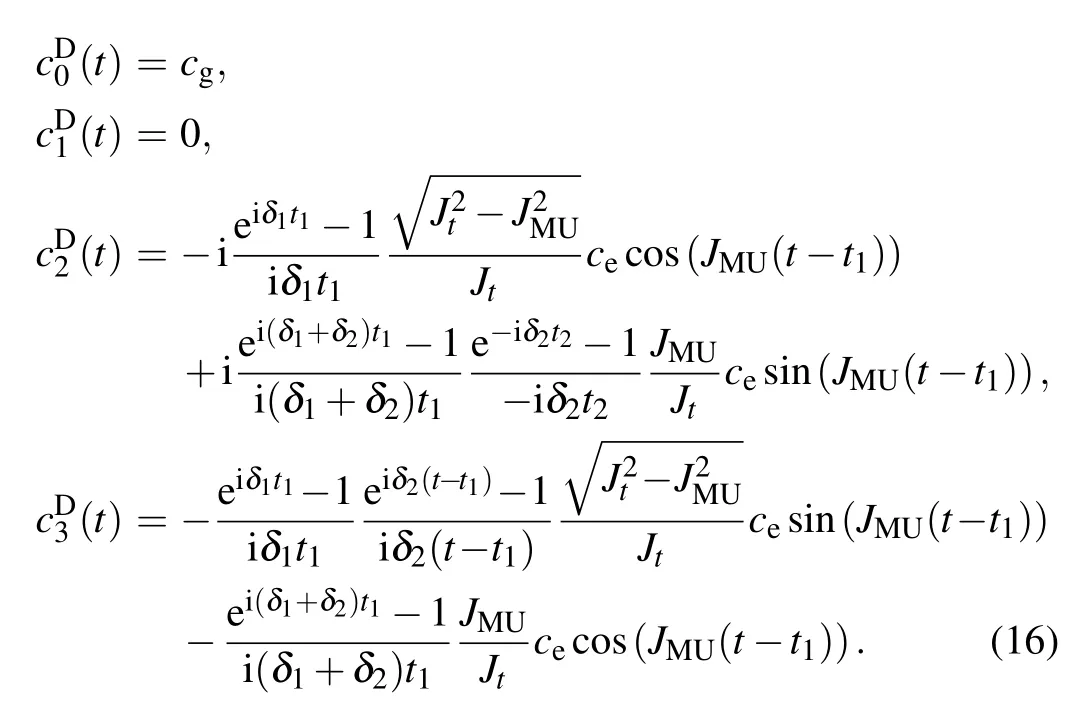
We firstly study how detuning influences the transmission time in our scheme.Comparing Eq.(15)with Eq.(7),we find that,which suggests that there is little variance caused by detuning in the transmission time.Here we consider only the influence of lower level items of detuning,since the second and higher level items of the perturbation are much smaller and they can be omitted consequently.As the estimated state parameter,the quantum state transmission will still be completed at t1even under the detuning condition.The time cost of the state transmission process in our scheme is robust with respect to detuning.
Detuning may also cause errors in the states transmitted. According to the expressions ofandin Eq.(15), state errors in the intermediate state〉can be described by two factors, which are
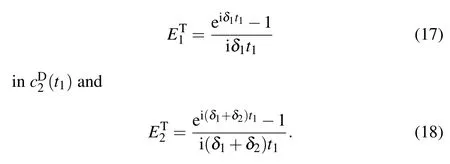
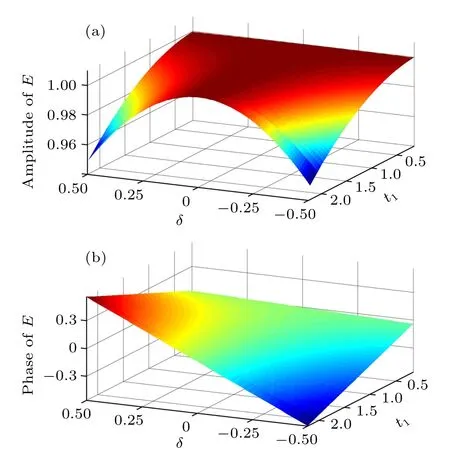
Fig.3.(color online)The relationship between phase error E,transmission time t1,and detuning δ,which are depicted with the relative values t1/J MU∈(0~2.5)and δ/J MU∈(?0.5~0.5).The amplitude and phase of the error factor E are plotted,respectively.
To investigate the error in the final state,the fidelity of quantum storage versus δ1and δ2is plotted in Fig.4 with t1=2,1.5,1,and 0.5.It is shown that the influence of detuning can be depressed through reducing the state transmission time t1.By tuning the coupling strength JCM,we can cut down the time cost of state storage and get a higher fidelity under the specific detuning condition.
According to the aforementioned discussion,although detuning influences the transmission time and the transmitted state in different ways,both kinds of influence can be depressed in our scheme.The transmission time is immune to detuning when the second and higher level items of the perturbation are omitted.By reducing the transmission time,the error in the intermediate state could be depressed and thefidelity of the state stored would be improved.These facts indicate that our control method can be used to improve the system robustness under the influence of quantum detuning.
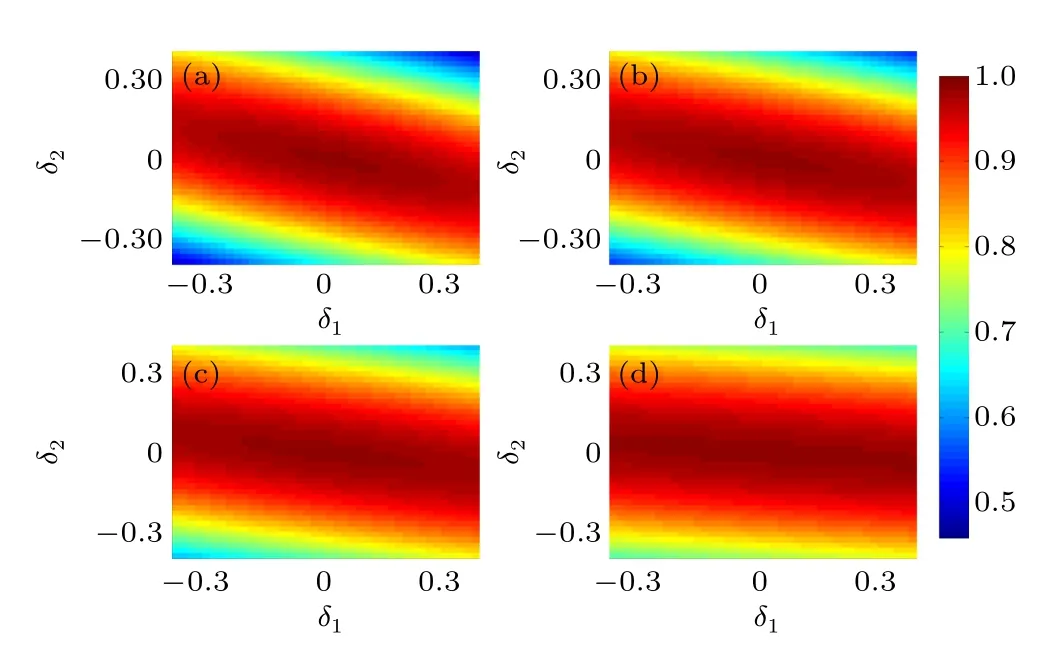
Fig.4.(color online)The fidelity of the stored state F versus detuning δ1=ωC?ωM and δ2=ωM?ωNV under different state transmission times t1=2(a),1.5(b),1(c),and 0.5(d),where δ1/J MU,δ2/J MU∈(?0.4~0.4). The value of F is indicated by the colorbar on the right.Here,we consider that the initial state to be stored isthe state stored in the NV ensemble is|ψNV〉,and F=〈ψT|ψNV〉.
5.A comparison with the direct memory scheme
In this section,we make a comparison between the storing processes of our scheme and the previous direct memory schemes.We note that the direct memory scheme[38]can be regarded as a special case of our two-step scheme.According to Eqs.(8)and(10),by taking k1=k2=0,our scheme will degenerate to the direct memory scheme when JCM=JMU.To simplify the comparison,we take times of two steps to be
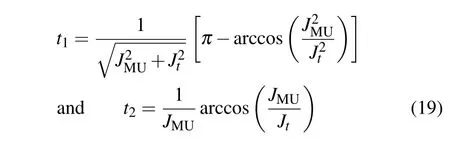
in the following discussion.
The efficiency of our memory scheme is judged by the evolution of fidelityHereis the state of the NV ensemble with the additional phase omitted.The initial state of the flux qubit is assumed to be |ψC(0)〉=α|g〉+β|e〉and the target state of the NV ensemble is accordingly denoted by|ψT〉=α|0〉+β|1〉.In addition,thefidelityis employed to indicate the transmission process,where|g〉is the ground state of the flux qubit. Since CQ decays to the ground state|g〉in the transmission process,FT(t)=1 means that the quantum state transmission from CQ to the memory unit is completed.
Currently,the coupling strength between a flux qubit and a NV ensemble,JMU,has been achieved with dozens of MHz.[30,38,62]Via the mediating of the ancillary qubit,the interaction strength between CQ and MQ can be adjusted within 0~2π×300 MHz.[57,59]The energy splitting of the NV ensemble ωNVcan be adjusted around the zero-field splitting D=2.88 GHz.[14,63,64]Correspondingly,the typical energy gap of SC qubits is about a few GHz.[65,66]SC flux qubits can be tuned resonate with the NV ensemble by modifying external magnetic fields.[50–54]Considering the available values of parameters in current experiment condition,we take JMU=?, and the frequenciesωC,ωM,andωNVaroundω=100? in our discussion.Moreover,to ensure the rotating wave approximation in Eq.(2)is valid,[60,61]the range of the coupling strength Jtis taken to be ?~10?.
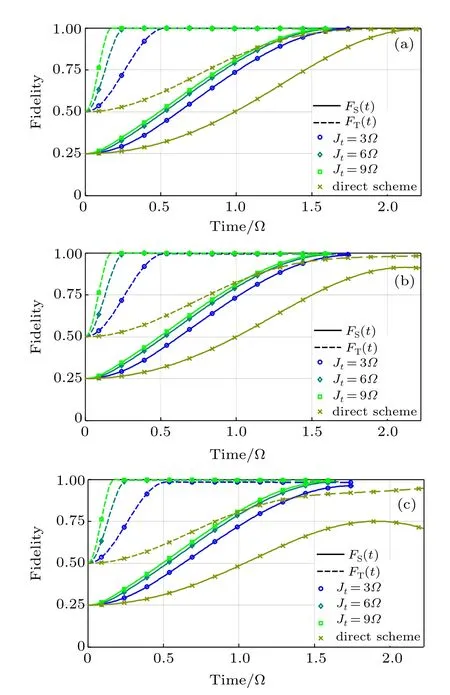
Fig.5.(color online)Fidelity evolutions of the quantum storage process under different detuning conditions.We set the computing unit initially at the state(|0〉+|1〉)/.Under detuning conditions δ1/?=0(a), 0.5(b),and 1(c),we compare the evolution of F T(t)and F S(t)of our two-step memory scheme with the direct memory scheme.
6.Conclusion
The state storage and retrieval of quantum memories is studied based on the application of quantum data buses in a scalable quantum computer system.A novel two-step quantum memory scheme is proposed for the hybrid SC memory system.Taking advantage of the adjustable coupling parameter of the ancillary qubit and utilizing the entangled state of MQ and NV ensemble,our scheme divides the state transmission and storage(retrieval)into two separately performed steps.Through adjusting the value of coupling strength JCM, our scheme can trade off the time costs of the transmission and the storage(retrieval),and includes one step direct memory scheme as a special case.The quantum state transmission could be performed much faster and the performance of the quantum data bus will be improved with a stronger coupling. During the transmission procedure,quantum states are vulnerable to the variance of environmental magnetic fields,which may lead to detuning of the system.By studying the evolution of our memory system under the detuning condition,it is found that both the time cost and the final state are robust with respect to detuning.We further make a comparison between our scheme and the previous direct memory scheme based on an available experimental condition.The results indicate the feasibility of our scheme,and suggest its robustness and effi ciency over another scheme[38]for the quantum data bus in scalable quantum computers.
Appendix A
To get the state parameters in Eqs.(15)and(16),we derive the state evolution under a detuning condition.Detuning between CQ and MQ δ1=ωC?ωMand the one between MQ and NV center δ2=ωM?ωNVare considered.It is assumed that both δ1and δ2are small in comparison to the coupling strength between units of our system,hence their higher level items are omitted in our derivation.
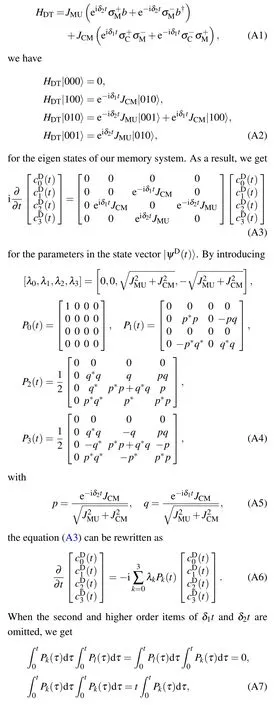
With the Hamiltonian for any k,l=0,1,2,3,and kl.Thus we have

The state parameters at any time t could be finally gotten by simply substituting initial state parameters into Eq.(A8)and extending it.
[1]Shi Z G,Chen X W,Zhu X X and Song K H 2009 Chin.Phys.B 18 910
[2]Wang D M,Qian Y,Xu J B and Yu Y H 2015 Chin.Phys.B 24 110304
[3]Wu C,Fang M F,Xiao X,Li Y L and Cao S 2011 Chin.Phys.B 20 020305
[4]Hua M,Tao M J and Deng F G 2016 Sci.Rep.6 22037
[5]Shahriar M S,Kumar P and Hemmer P R 2012 J.Phys.B-At.Mol.Opt. Phys.45 124018
[6]Garcia-Escartin J C and Chamorro-Posada P 2006 Phys.Rev.Lett.97 110502
[7]Majer J,Chow J M,Gambetta J M,Koch J,Johnson B R,Schreier J A, Frunzio L,Schuster D I,Houck A A,Wallraff A,Blais A,Devoret M H,Girvin S M and Schoelkopf R J 2007 Nature 449 443
[8]Reiserer A and Rempe G 2015 Rev.Mod.Phys.87 1379
[9]Li T,Yang G J and Deng F G 2014 Opt.Express 22 23987
[10]Yu L B,Feng J S,Dong P,Li D C and Cao Z L 2015 Quantum Inf. Process.14 3303
[11]Mariantoni M,Wang H,Yamamoto T,Neeley M,Bialczak R C,Chen Y,Lenander M,Lucero E,O’Connell A D,Sank D,Weides M,Wenner J,Yin Y,Zhao J,Korotkov A N,Cleland A N and Martinis J M 2011 Science 334 61
[12]Yang C P,Su Q P,Zheng S B and Han S 2015 Phys.Rev.B 92 054509
[13]Kurizki G,Bertet P,Kubo Y,Molmer K,Petrosyan D,Rabl P and Schmiedmayer J 2015 P.Natl.Acad.Sci.USA 112 3866
[14]Matsuzaki Y,Zhu X,Kakuyanagi K,Toida H,Shimooka T,Mizuochi N,Nemoto K,Semba K,Munro W J,Yamaguchi H and Saito S 2015 Phys.Rev.A 91 042329
[15]Averin D V,Xu K,Zhong Y P,Song C,Wang H and Han S 2016 Phys. Rev.Lett.116 010501
[16]Douce T,Stern M,Zagury N,Bertet P and Milman P 2015 Phys.Rev. A 92 052335
[17]Ginossar E and Grosfeld E 2014 Nat.Commun.5 4772
[18]Zhang X,Zou C L,Zhu N,Marquardt F,Jiang L and Tang H X 2015 Nat.Commun.6 8914
[19]Wolfowicz G,Maier-Flaig H,Marino R,Ferrier A,Vezin H,Morton J J L and Goldner P 2015 Phys.Rev.Lett.114 170503
[20]Bensky G,Amsuss R,Majer J,Petrosyan D,Schmiedmayer J and Kurizki G 2011 Quantum Inf.Process.10 1037
[21]Wu Q Q,Xu L,Tan Q S and Yan L L 2012 Int.J.Theor.Phys 51 1482
[22]Cohen G Z and Ventra M 2013 Phys.Rev.B 87 014513
[23]Liu T,Cao X Z,Su Q P,Xiong S J and Yang C P 2016 Sci.Rep.6 21562
[24]Li P B,Gao S Y and Li F L 2011 Phys.Rev.A 83 054306
[25]Blais A,Huang R S,Wallraff A,Girvin S M,and Schoelkopf R J 2004 Phys.Rev.A 69 062320
[26]Wallquist M,Hammerer K,Rabl P,Lukin M and Zoller P 2009 Phys. Scripta T137 014001
[27]Duan L M and Monroe C 2010 Rev.Mod.Phys.82 1209
[28]Sillanpaeae M A,Park J I and Simmonds R W 2007 Nature 449 438
[29]Marcos D,Wubs M,Taylor J M,Aguado R,Lukin M D and Sorensen A S 2010 Phys.Rev.Lett.105 210501
[30]Zhu X,Saito S,Kemp A,Kakuyanagi K,Karimoto S,Nakano H, MunroWJ,Tokura Y,Everitt M S,Nemoto K,Kasu M,Mizuochi N and Semba K 2011 Nature 478 221
[31]Zhao Y J,Fang X M,Zhou F and Song K H 2012 Phys.Rev.A 86 052325
[32]Wang Z L,Zhong Y P,He L J,Wang H,Martinis J M,Cleland A N and Xie Q W 2013 Appl.Phys.Lett.102 163503
[33]Kyaw T H,Felicetti S,Romero G,Solano E and Kwek L C 2015 Sci. Rep.5 8621
[34]Qian Y,Zhang Y Q and Xu J B 2012 Chin.Sci.Bull.57 1637
[35]Zhang F Y,Chen X Y,Li C and Song H S 2015 Sci.Rep.5 17025
[36]McKay D C,Naik R,Reinhold P,Bishop L S and Schuster D I 2015 Phys.Rev.Lett.114 080501
[37]Feng Z B,Wang H L and Yan R Y 2016 Quantum Inf.Process.15 3151
[38]Lu X Y,Xiang Z L,Cui W,You J Q and Nori F 2013 Phys.Rev.A 88 012329
[39]Blum S,O’Brien C,Lauk N,Bushev P,Fleischhauer M,and Morigi G 2015 Phys.Rev.A 91 033834
[40]Xiang Z L,Lu X Y,Li T F,You J Q and Nori F 2013 Phys.Rev.B 87 144516
[41]Togan E,Chu Y,Trifonov A S,Jiang L,Maze J,Childress L,Dutt M V G,Sorensen A S,Hemmer P R,Zibrov A S and Lukin M D 2010 Nature 466 730
[42]Shi F,Rong X,Xu N,Wang Y,Wu J,Chong B,Peng X,Kniepert J, Schoenfeld R S,Harneit W,Feng M and Du J 2010 Phys.Rev.Lett. 105 040504
[43]Neumann P,Kolesov R,Naydenov B,Beck J,Rempp F,Steiner M, Jacques V,Balasubramanian G,Markham M L,Twitchen D J,Pezzagna S,Meijer J,Twamley J,Jelezko F and Wrachtrup J 2010 Nat.Phys. 6 249
[44]Zhao N,Hu J L,Ho S W,Wan J T K and Liu R B 2011 Nat.Nanotech. 6 242
[45]Liu G Q,Jiang Q Q,Chang Y C,Liu D Q,Li W X,Gu C Z,Po H C, Zhang W X,Zhao N and Pan X Y 2014 Nanoscale 6 10134
[46]Li P B,Liu Y C,Gao S Y,Xiang Z L,Rabl P,Xiao Y F and Li F L 2015 Phys.Rev.Applied 4 044003
[47]Grezes C,Julsgaard B,Kubo Y,MaWL,Stern M,Bienfait A,Nakamura K,Isoya J,Onoda S,Ohshima T,Jacques V,Vion D,Esteve D, Liu R B,Molmer K and Bertet P 2015 Phys.Rev.A 92 020301
[48]Twamley J and Barrett S D 2010 Phys.Rev.B 81 241202
[49]Huemmer T,Reuther G M,Haenggi P and Zueco D 2012 Phys.Rev.A 85 052320
[50]van der Ploeg S H W,Izmalkov A,van den Brink A M,Huebner U, Grajcar M,Il’ichev E,Meyer H G and Zagoskin A M 2007 Phys.Rev. Lett.98 057004
[51]Liu Y X,Wei L F,Tsai J S and Nori F 2006 Phys.Rev.Lett.96 067003
[52]Niskanen A O,Harrabi K,Yoshihara F,Nakamura Y,Lloyd S and Tsai J S 2007 Science 316 723
[53]Neumann P,Kolesov R,Jacques V,Beck J,Tisler J,Batalov A,Rogers L,Manson N B,Balasubramanian G,Jelezko F and Wrachtrup J 2009 New J.Phys.11 013017
[54]Forrester D M and Kusmartsev F V 2016 Sci.Rep.6 25084
[55]Qiu Y,Xiong W,He X L,Li T F and You J Q 2016 Sci.Rep.6 28622
[56]Ashhab S,Niskanen A O,Harrabi K,Nakamura Y,Picot T,de Groot P C,Harmans C J P M,Mooij J E and Nori F 2008 Phys.Rev.B 77 014510
[57]Niskanen A O,Nakamura Y and Tsai J S 2006 Phys.Rev.B 73 094506
[58]Bertet P,Chiorescu I,Burkard G,Semba K,Harmans C,DiVincenzo D P and Mooij J E 2005 Phys.Rev.Lett.95 257002
[59]Xiang Z L,Ashhab S,You J Q and Nori F 2013 Rev.Mod.Phys.85 623
[60]Casanova J,Romero G,Lizuain I,Garcia-Ripoll J J and Solano E 2010 Phys.Rev.Lett.105 263603
[61]Fedorov A,Feofanov A K,Macha P,Forn-Diaz P,Harmans C J P M and Mooij J E 2010 Phys.Rev.Lett.105 060503
[62]Song W L,Yin Z Q,Yang W L,Zhu X B,Zhou F and Feng M 2015 Sci.Rep.5 7755
[63]Jin L,Pfender M,Aslam N,Neumann P,Yang S,Wrachtrup J and Liu R B 2015 Nat.Commun.6 8251
[64]Kubo Y,Grezes C,Dewes A,Umeda T,Isoya J,Sumiya H,Morishita N,Abe H,Onoda S,Ohshima T,Jacques V,Dreau A,Roch J F,Diniz I,Auffeves A,Vion D,Esteve D and Bertet P 2011 Phys.Rev.Lett.107 220501
[65]Liu Y,You J and Hou Q 2016 Sci.Rep.6 21775
[66]van der Wal C H,ter Haar A C,Wilhelm F K,Schouten R N,Harmans C J,Orlando T P,Lloyd S and Mooij J E 2000 Science 290 773
7 March 2017;revised manuscript
16 May 2017;published online 31 July 2017)
10.1088/1674-1056/26/9/090303
?Project supported by the National Natural Science Foundation of China(Grant Nos.61673389,61273202,61134008,and 11404113).
?Corresponding author.E-mail:zhangming@nudt.edu.cn
?2017 Chinese Physical Society and IOP Publishing Ltd http://iopscience.iop.org/cpb http://cpb.iphy.ac.cn
- Chinese Physics B的其它文章
- Relationship measurement between ac-Stark shift of 40Ca+clock transition and laser polarization direction?
- Air breakdown induced by the microwave with two mutually orthogonal and heterophase electric field components?
- Collective motion of active particles in environmental noise?
- Temperature dependence of heat conduction coefficient in nanotube/nanowire networks?
- Analysis of dynamic features in intersecting pedestrian flows?
- Heat transfer enhancement in MOSFET mounted on different FR4 substrates by thermal transient measurement?

