Geometry and thermodynamics of smeared Reissner–Nordstr?m black holes in d-dimensional AdS spacetime
Bo-Bing Ye(葉伯兵),Ju-Hua Chen(陳菊華),and Yong-Jiu Wang(王永久)
College of Physics and Information Science,Hunan Normal University,Changsha 410081,China
Geometry and thermodynamics of smeared Reissner–Nordstr?m black holes in d-dimensional AdS spacetime
Bo-Bing Ye(葉伯兵),Ju-Hua Chen(陳菊華)?,and Yong-Jiu Wang(王永久)
College of Physics and Information Science,Hunan Normal University,Changsha 410081,China
We construct a family of d-dimensional Reissner–Nordstr?m-AdS black holes inspired by noncommutative geometry.The density distribution of the gravitational source is determined by the dimension of space,the minimum length of spacetimel,and other parameters(e.g.,n relating to the central matter density).The curvature of the center and some thermodynamic properties of these black holes are investigated.We find that the center of the source is nonsingular for n≥0(under certain conditions it is also nonsingular for?2≤n<0),and the properties at the event horizon,including the Hawking temperature,entropy,and heat capacity,are regular for n>?2.Due to the presence of l,there is an exponentially small correction to the usual entropy.
noncommutative geometry,physics of black holes,thermodynamics
1.Introduction
The noncommutativity of spacetime was originally studied by Snyder.[1]It is currently encoded in the commutator [xμ,xν]=i?μν,where ?μνis an anti-symmetric matrix which determines the fundamental cell discretization of spacetime much in the same way as the Planck constant discretizes the phase space.In recent years,the noncommutative geometry inspired black hole,based on the coordinate coherent state formalism,[2,3]has been studied intensively.In such a framework,Nicolini et al.[4]pointed out that it is not necessary to change the Einstein tensor part of the field equations,and the noncommutative effects can be implemented acting only on the matter source.[4]Furthermore,the noncommutativity eliminates point-like structures in favor of smeared objects in flat spacetime.The effect of smearing is obtained by replacing the point-like gravitational source with a Gaussian distribution of minimal widthFor instance,the density of mass M becomes
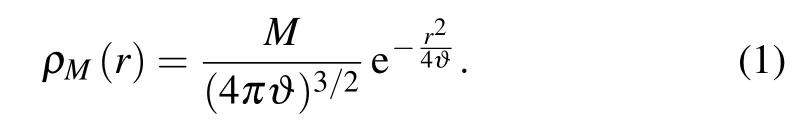
In this framework,Nicolini et al.first found a noncommutative-inspired Schwarzschild black hole in four dimensions.[4]Then the black hole was extended to the cases including electric charge,[5]cosmological constant,[6]and extra-spatial dimensions.[7,8]More generally,the charged rotating noncommutative black holes were also derived.[9]Furthermore,many authors have studied the effects of noncom-mutativity on some properties of a black hole(see Ref.[10]), such as thermodynamics,[11–13]Hawking radiation,[14]and geodesic structure.[15]In the study of the noncommutative Schwarzschild black hole,Nicolini et al.[4]pointed out that the usual problems of the terminal phase of black hole evaporation no longer exist due to the noncommutativity.Nozari and Mehdipour investigated the Hawking radiation from a non-commutative Schwarzschild black hole.[14]Larra?aga investigated the geodesic structure and the precession of the perihelion in noncommutative Schwarzschild-AdS spacetime.[15]For the noncommutative Reissner–Nordstr?m(RN)black hole,Mehdipour and Nozari et al.investigated the tunneling process of charged massive particles;[16,17]Mehdipour and Keshavarz investigated the entropic force;[18]Bhar et al.investigated geodesics,the motion of the test particle,and the scattering of scalar waves.[19]In addition,some authors have also studied the 3-dimensional noncommutative AdS spacetime with charge,angular momentum or not.[20–23]
Park pointed out that the Gaussianity is not always required,and showed that three-dimensional analog of de Sitter black holes does exist when non-Gaussian(ring-type)smearings of point matter hairs are considered.[24]He gave the matter density as
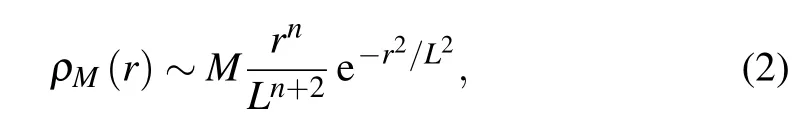
where L is a characteristic length scale of the matter distribution and n=0,1,2 correspond to the Gaussian distribution,Rayleigh distribution,and Maxwell–Boltzmann distribution,respectively.The Rayleigh distribution was first introduced by Myung et al.[25]In addition,Liang et al.investigated thermodynamics of noncommutative 3-dimensional black holes based on the Maxwell–Boltzmann smeared mass distribution.[26]Miao and Xu investigated thermodynamics of noncommutative high-dimensional Schwarzschild–Tangherlini-AdS black holes with this kind of general distribution.[27]
The organization of this paper is as follows.In the next section,the wave packet distribution(2)will be extended and a metric solution of the gravitational source with this more general distribution will be given.In Section 3,we study the properties of this metric solution,including the formation of event horizons,curvature of the center,Hawking temperature, entropy,and heat capacity.Finally,a brief conclusion is given.
2.Generalized wave packet distribution and its gravitational field
In this paper,we consider a more general distribution which is an extension of the wave packet distribution(2).Note that for Re(k)>0,Re(d+n)>0,and Re(1/alk)>0 in d space,
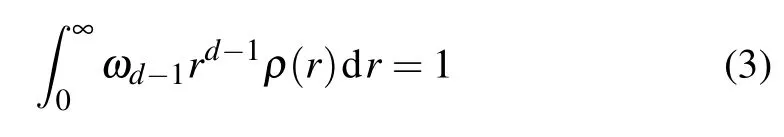
with
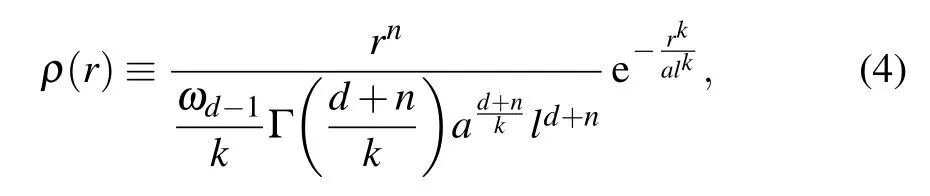
where ωd?1=2πd/2/Γ(d/2)is the area of a unit sphere in (d?1)space.Based on Eq.(3),the densities of total mass M and charge Q can be written as
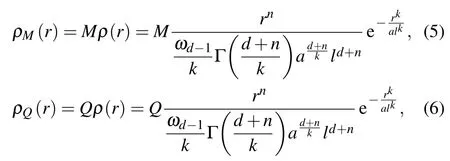
where n,k,a,andlare all positive,andlis related to the standard deviation or the width of the distribution.For n>0,the density at the center is zero,so the object is hollow.For n=0, the object is solid and regular,and there is an infinite center density for n<0.
The density distribution(5)can be understood from two aspects.One is the noncommutative geometry.If we take d=3,k=2,a=1,andequation(5)will reduce to Eq.(1);and similarly if we take d=2,k=2,a=1,and l=L,equation(5)will reduce to Eq.(2).The other is from quantum mechanics.If there is an object described by wave function ψ(r)with|ψ(r)|2=ρ(r),e.g.,a bound particle or a Gaussian wave packet,then ρ(r)can be considered as the probability density of the object to be found.An observer will see or think that the mass distribution of the object has a form described by Eq.(5).More specifically,giving M(r)a measured value at point(r,θ,?),M(r)is then proportional to the probability of finding the object in the region of radius r,i.e.,
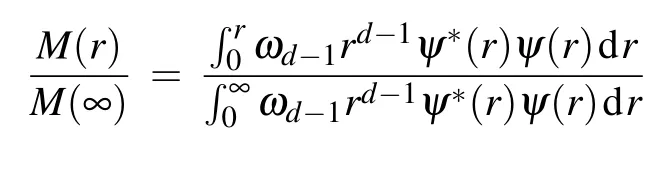
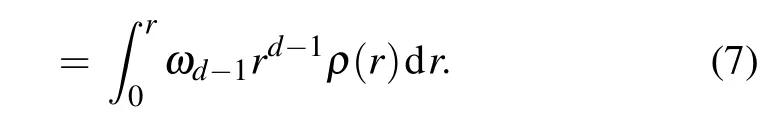
Since M(∞)=M,equation(7)becomes

Mρ(r)is therefore equal to ρM(r),which is just Eq.(5).In quantum mechanics,l is related to the standard deviation of position,and l0 determined by the uncertainty principle.
The line element describing the spacetime of a static, spherically symmetric distribution of a gravitational field source in(d+1)dimensions has the following form:

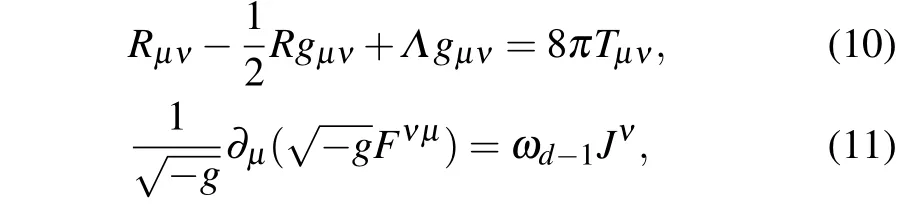
with
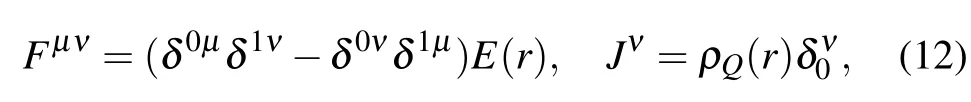
where Fμνand Jνare the electromagnetic tensor and the current density,respectively,and the Greek indicesμ,ν,...vary over 0,1,2,...,d.
We take the distribution of the source to be anisotropic and therefore choose the energy–momentum tensorin the form

where ρ,pr,p⊥,and Tμν|elrepresent the energy density(apart from the electromagnetic field),the radial pressure,the tangential pressure,and the electromagnetic energy–momentum tensor,respectively.uμis the velocity of the fluid,and χμ=is an unit vector along the radial direction.Thus,we have

We do not know the contribution of the charge Q to the energy density ρ,so we take the following form:
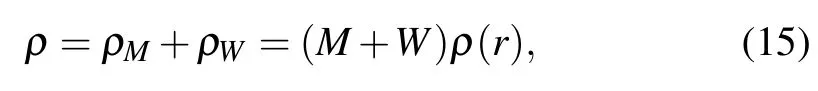
where W is to be determined.
With the charge density(6),one can solve Eq.(11)to yield
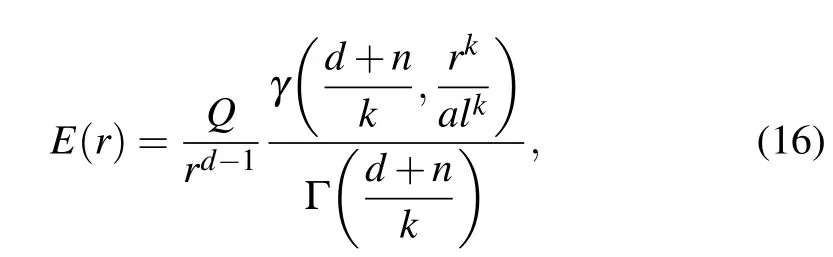
where γ(s,x)is the lower incomplete gamma function
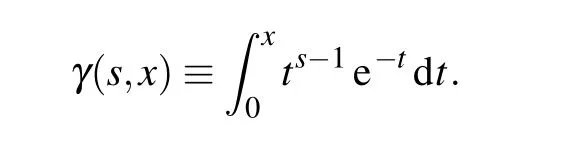
To preserve the property of RN-AdS metric aswe take pr=?ρ.Using the conservation conditionwe can obtain the tangential pressure as
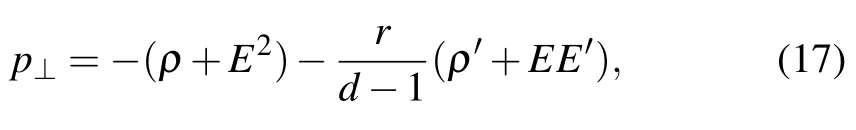
where the prime represents the derivative with respect to r.For an asymptotic observer,
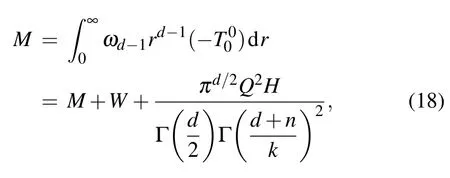
so this requires
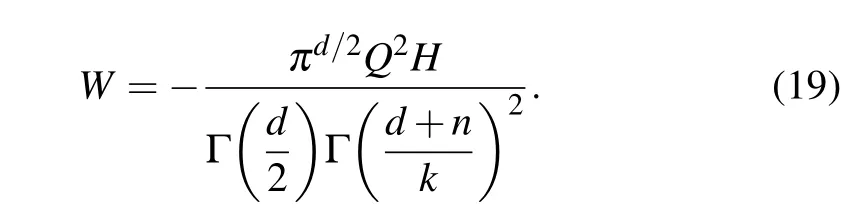
Then the Einstein–Maxwell field equations lead to the following solution(d>2):

with

and H=?H(∞),e.g.,

When l→0,m(r)→1,and q(r)→1 for n≤0,equation(21)reduces to the usual RN-(A)dS metric.[29]For n>0, in order to be reduced to the RN-(A)dS metric,the limit must be taken as l→ε with small ε.If we take l→0 for n>0,both ρM(r)and ρQ(r)in Eqs.(5)and(6)will be zero,i.e.,there will be no gravitational source.
Far away from the center,we can see that the(anti-)de Sitter spacetime is shown in Eq.(21).At the neighborhood of the center,we have

By substituting Eq.(26)into Eq.(21)and retaining only the leading order terms,f(r)becomes

with

which shows the(anti-)de Sitter type or just flat for n≥0,depending on the relative values of the parameters Λ,M,Q,l,n, d,a,and k.
3.Properties of the smeared RN-(A)dS black holes
3.1.Formation of event horizons
The horizon radius rhcan be found from the equation g00(rh)=0.In our case we cannot solve analytically rh,so we solve M in terms of rh,Q,and Λ as
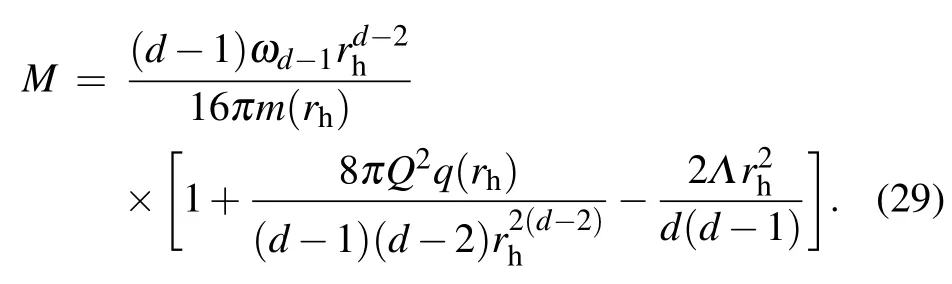
By expanding Eq.(29)near infinity and the center,we can see that
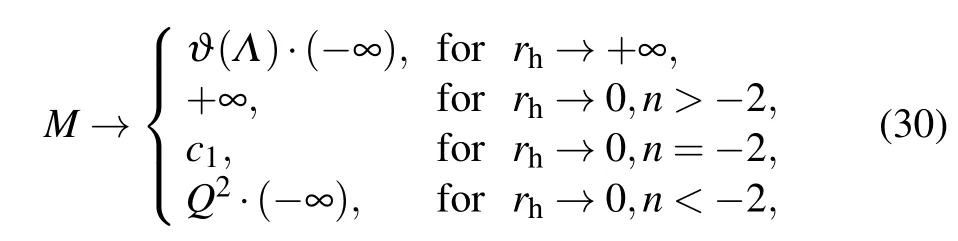
with
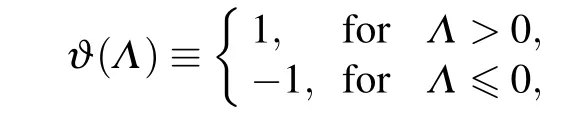
where c1is finite and larger than zero.
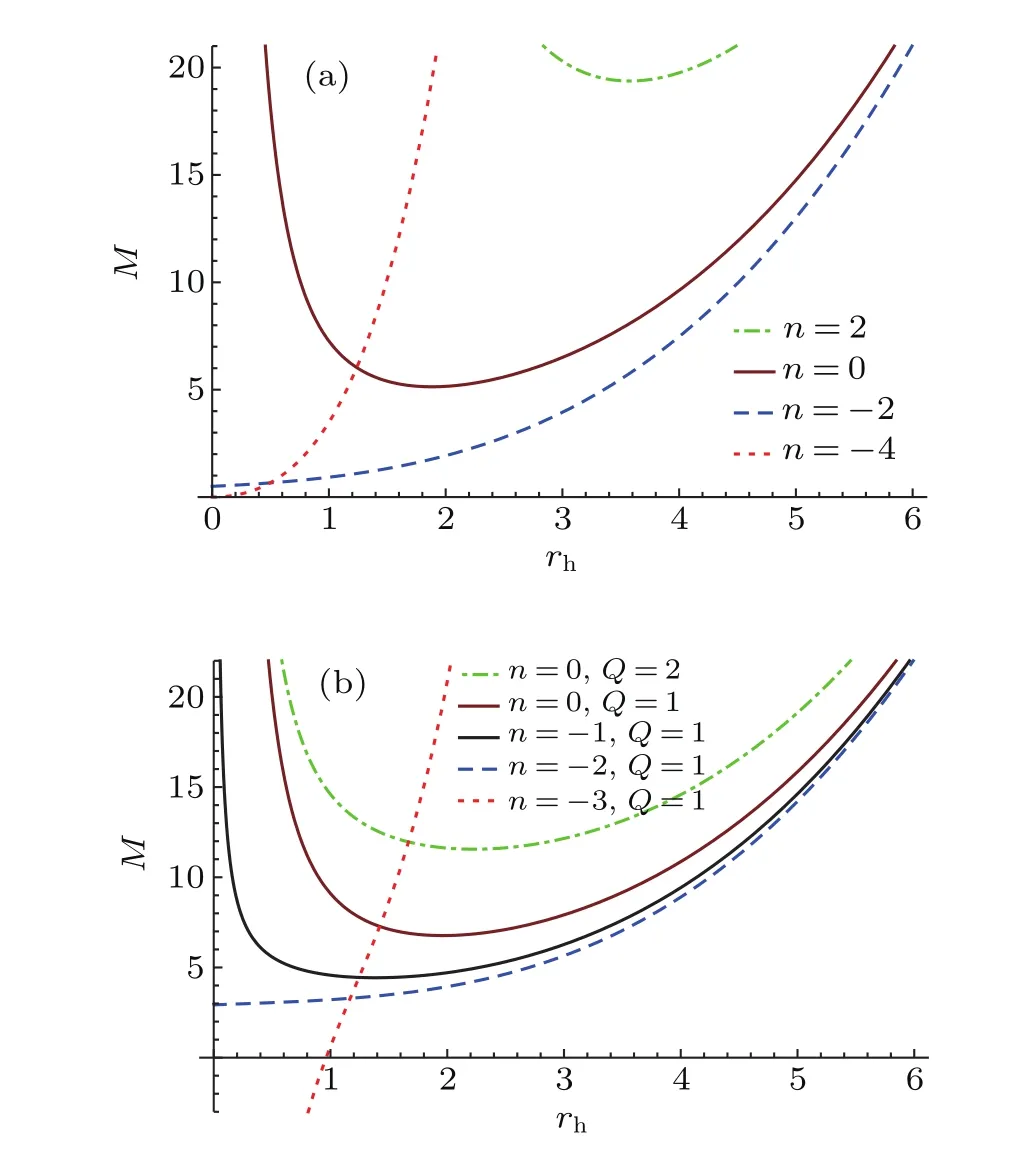
Fig.1.(color online)Plots of M versus r h:(a)Q=0,Λ=?0.5,and k=a=l=1;d=3 for n≥?2 and d=5 for n<?2;(b)Λ=?0.5 and a=l=1;d=3,k=1 for n≥?2 and d=5,k=2 for n<?2.
The behavior of M(rh)is shown in Fig.1.We can see that when n>?2,there are the inner and outer horizons and M(rh) has a minimum M0at r0where the two horizons are merged. For example,M02.57land r0?3.38lfor Q=Λ=n=0, k=a=1,and d=3.That means there is an extremal black hole,and no black hole exists with mass less than M0.In the case of n≤?2,there is no extremal black hole.From Fig.1, we can also find that both M0and r0increase with the increase of Q and n.More generally,the effects of different parameters on M0and r0are summarized in Table 1.Table 1 shows that the parameters Q2,d,n,a,andlhave similar effects on M0and r0,while the k parameter is the opposite.

Table 1.The effects of different parameters on M0 and r0,e.g.,M0 decreases and r0 increases with the increase of Λ.
3.2.Curvature of the center
For the Schwarzschild black hole or RN black hole,we know that there is a gravitational singularity at the center, where the gravitational field becomes infinite in a way that does not depend on the coordinate system.Due to the presence of l,it should be expected that the situation will be different.Curvature invariants of spacetime,e.g.,the Kretschmann scalar K(K≡RμνστRμνστ),can be used to measure the gravitational field strength and verify the existence of the singularity.Such quantities become infinite within the singularity but finite outside the location,e.g.,for the RN black hole,K is infinite for r=0 and finite for r>0.
The curvature scalar R for the smeared RN-(A)dS metric is found as
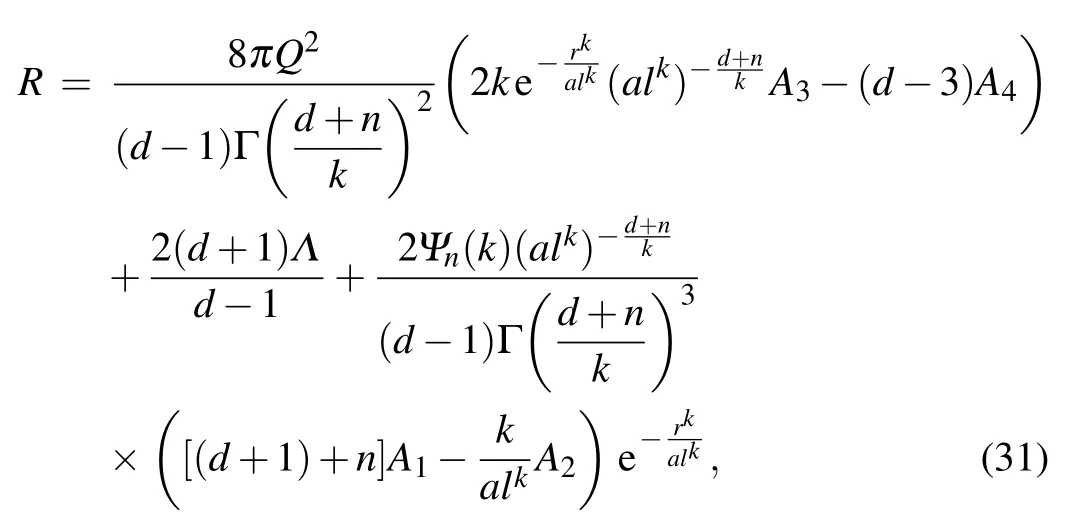

In addition,the Kretschmann scalar K is given by


where

At the neighborhood of the center,we obtain
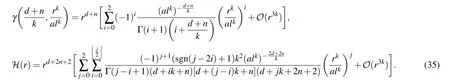
For n>0,with R(0)≡limr→0R and K(0)≡limr→0K, one can obtain from Eqs.(31),(33),and(35)that

Furthermore,

Equations(36)and(37)show that there is a simple relationship between K and R at r=0 for the smeared RN-(A)dS black hole,but not for the usual black hole.For n<0,we will see that R and K are still limited under conditions of Eqs.(38)and (39),even though the central matter density is divergent.For instance,in the case of?1≤n<0,in order to avoid the divergent term r2n(or the term A5)in K,the coefficient of r2nmust be zero,i.e.,Ψn(k)=0.More generally,we have
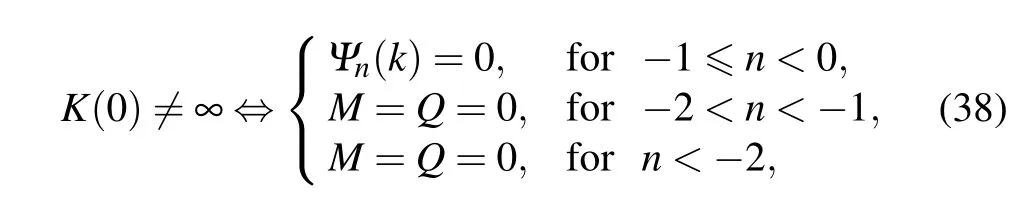
and

It is interesting to note that in the case of n=?2 and k=1, the massive object only in(3+1)dimensions is nonsingular. From the above equations,we can see that in the case of n<0, the conditions are required to make the curvature limited,but it is not for the case of n≥0,which shows that the wave packet with n≥0 is always regular.
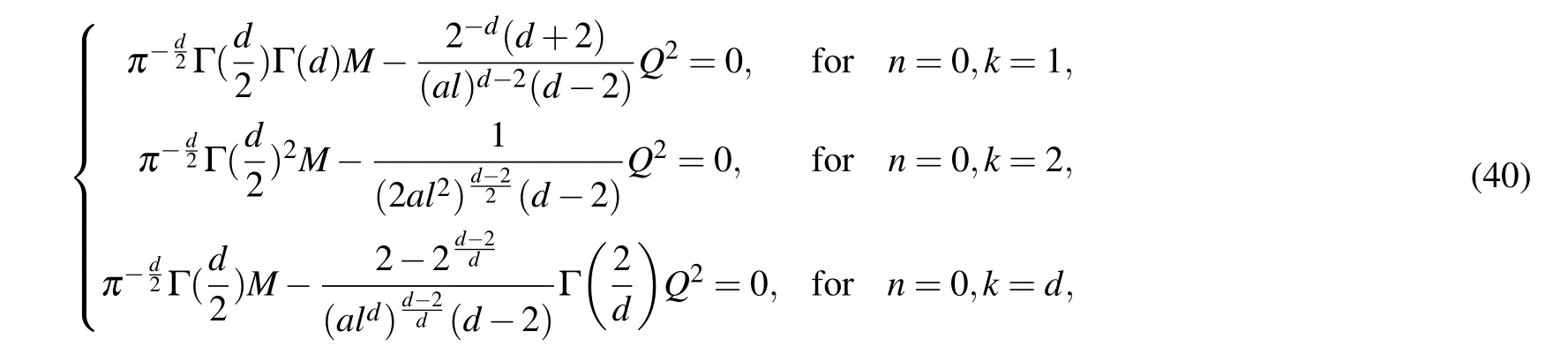
For a special class of objects with Ψn(k)=0(or ρ=0, M=?W),e.g., the energy–momentum tensor is equivalent to purely electrical that can be written as

with ?=?rE E′/(d?1),and for n≥?1 the center is nonsingular.Moreover,K(0)=8(d+1)Λ2/d(d?1)2for n>?1, which shows that the center is the(anti-)de Sitter type or just flat.
3.3.Hawking temperature and entropy
The Hawking temperature can be calculated as follows:

By simplifying the above equation for the metric(21),we obtain


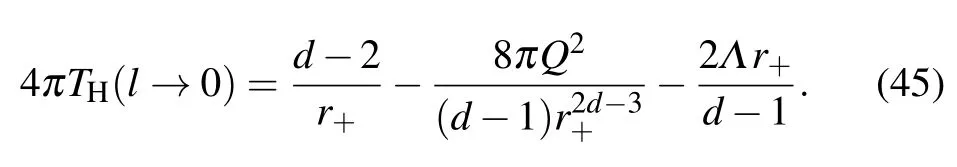
Near infinity or the center,one can find from Eq.(43)that
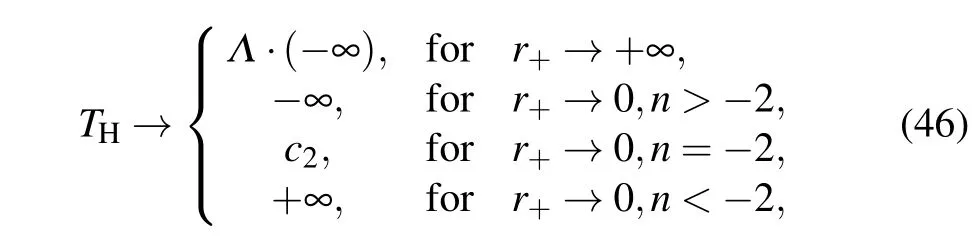
where c2is finite and c2≥0.
The Hawking temperature variation is plotted against the black hole radius r+in Fig.2.(i)When n<?2,figure 2(a) shows that TH(0)is divergent,just like the Schwarzschild black hole or RN black hole.(ii)When n=?2,THis positive and finite as r+tends to zero.(iii)When n>?2,we can see that the temperature is negative where r+<r0(see also Fig.5),which is not physical;for r+=r0(corresponding to the radius of the extremal black hole),TH=0 which means a frozen extremal black hole;for r+>r0,there is a(local)maximum Tmax(where we call rmax)to replace the divergence,e.g.,Tmax0.01/l and rmax6.54lfor Q=Λ=n=0, k=a=1,and d=3.Moreover,forΛ=0,THapproaches zero as r+→∞.We can also see from Fig.2(b)that there is a local minimum Tmin(where we call rmin)when Λ is larger than a critical value and less than zero.
On the other hand,we can find from Fig.2(a)that,both rmaxand r0(see also Fig.1 or Table 1)increase but Tmaxdecreases with the increase of n.More generally,the effects of different parameters on Tmax,rmax,Tmin,and rminare shown in Table 2.From Table 2 we can see that the parameters Q2,n,a, andlhave similar effects on Tmax,rmax,Tmin,and rmin,and the k parameter is the opposite.Furthermore,for each parameter,Tmaxand Tminare affected in the same direction,and from Fig.2(b)we know that there will be no local maximum and minimum temperature if Λ is too small.
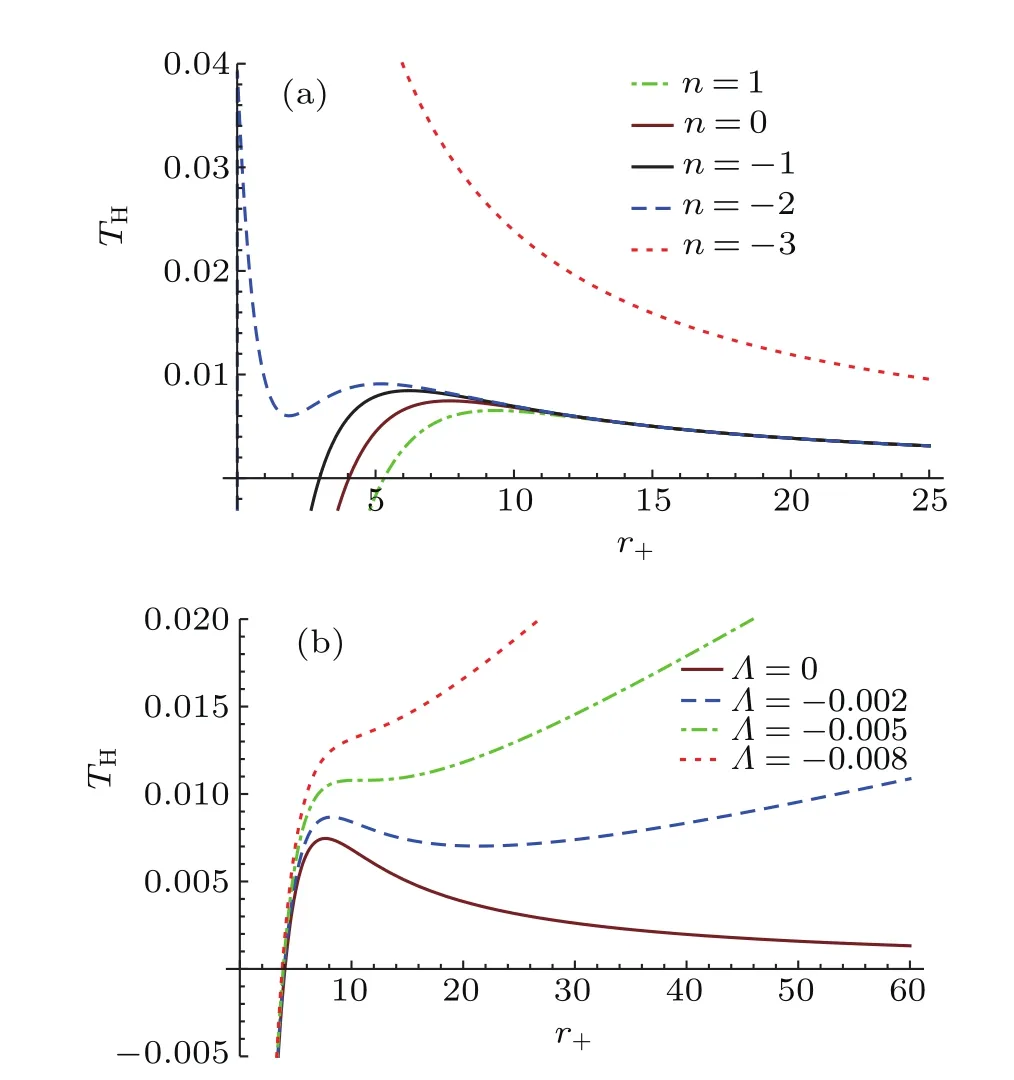
Fig.2.(color online)Plots of T H versus r+:(a)Λ=0,Q=1,and a=l=1; d=3,k=1 for n≥?2 and d=5,k=2 for n<?2;(b)Q=1,d=3, n=0,and k=a=l=1.

Table 2.The effects of different parameters on T max,r max,T min,and r min,e.g.,T max decreases and r max increases with the increase of Q2. There is a local minimum T min only when Λ is larger than a critical value and less than zero.
For the case of charged black hole,the first law of thermodynamics is described by
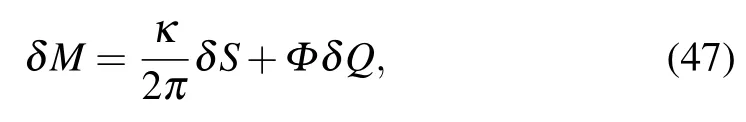
where κ,S,and Φ are the surface gravity,entropy,and electric potential on the exterior horizon,respectively.Substituting Eq.(42)into Eq.(47)for fixed electric charge Q,one can derive

Using Eq.(21),we can obtain
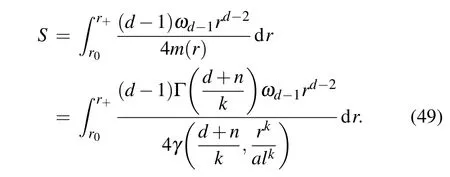
It is worth noting that the lower limit r0of the integral is not equal to zero,and for different parameter values(such as the charge Q),the value of r0is different.The behavior of the entropy S with respect to r+is shown in Fig.3.We can see that d,n,and k affect not only the size of r0,but also the ratio of S to r+.

Fig.3.(color online)Plots of the entropy S versus r+for Λ=?0.5 and Q=a=l=1.
By expanding Eq.(49),we can obtain
where Γ(s,x)is the upper incomplete gamma function
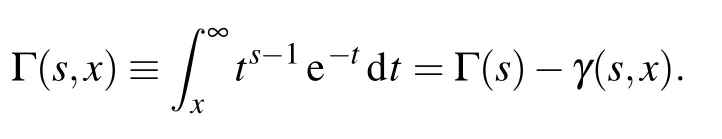
From Eq.(50),we can see that the first term is the usual semi-classical Bekenstein–Hawking area law,and the other is the correction to the area law.Expanding S(r)for smalllor large r to the leading order,we have
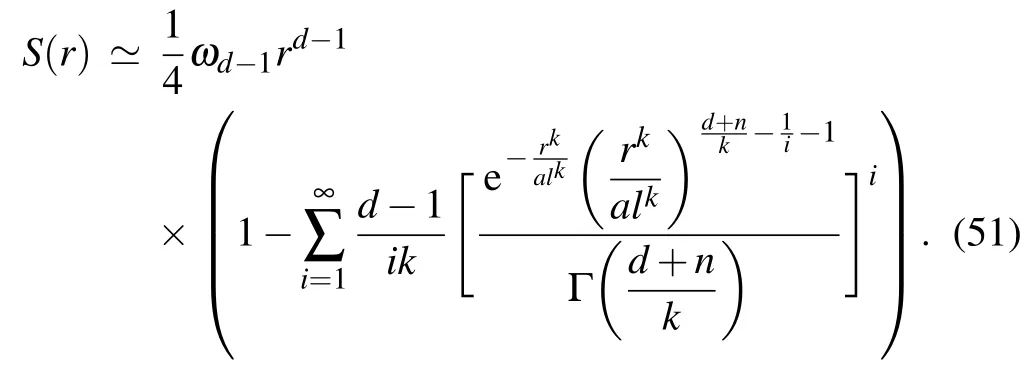
Hence,one can find that it is an exponentially small correction to the usual entropy due to the fundamental minimum length l.
The heat capacity at a constant charge is given by
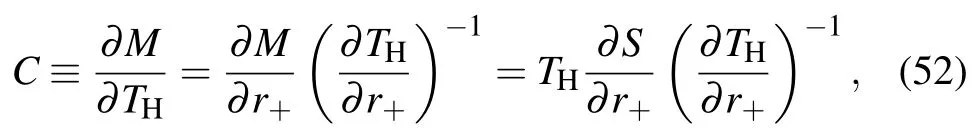
which determines the thermodynamic stability of the black holes.We can see from Fig.1 and Eq.(30)that?M/?r+is generally positive(?M/?r+=0 at r+=r0)for Λ≤0,so the sign of C is the same as that of?TH/?r+.Therefore,the black hole is unstable when?TH/?r+<0.
Using Eqs.(43)and(49),we obtain

The behavior of C is shown in Fig.4.Figure 4(a)shows the case of Λ=0.(i)When n<?2,C<0(for all r+),so this black hole is unstable,just like the usual Schwarzschild black hole or RN black hole.(ii)When n=?2,the middle black hole is stable and the two sides are unstable.(iii)When n>?2,the black hole is stable if r0≤r+<rmax.When n>?2, we see from Fig.4(b)that Λ has a significant influence on C.Λ=Λcritis a critical case where Tmax=Tmin.(i)When Λcrit<Λ<0,the black hole is stable for r0≤r+<rmaxor r+>rmin(see Fig.5).C is divergent at rmaxor rminfor Λcrit≤Λ<0,where a phase transition occurs.(ii)When Λ≤Λcrit,the black hole is stable for all r+.

Fig.4.(color online)Plots of C versus r+:(a)Λ=0,Q=1,and a=l=1; d=3,k=1 for n≥?2 and d=5,k=2 for n<?2;(b)Q=1,d=3,n=0, and k=a=l=1.
Figure 5 shows the behavior of M,TH,S,and C for a smeared and regular RN-AdS black hole as a whole. We can see that for a black hole with suitable parameters Q,Λ,d,n,k,a,and l,there is an extremal black hole with r+=r?=r0.The extremal black hole has the minimum total mass,and both its temperature and entropy are equal to zero. In addition,the extremal black hole is also stable.From Table 1 and Table 2,we can find that the parameters Q2,n,a,andlhave similar effects on M(and TH),while the k parameter is the opposite to the previous parameters.We can also find that for a higher dimension d,both M and THwill increase forfixed r+,and the radius of the extremal black hole r0will also be greater.

Fig.5.(color online)Plots of M,T H,S,and C as a whole in the case of Q=1,Λ=?0.003,d=3,n=0,and k=a=l=1.
4.Conclusion
We have constructed a general Reissner–Nordstr?m-(A)dS black hole inspired by noncommutative geometry for which the gravitational source is described by the density distribution(5)and(6),and the characteristics of the spacetime are affected by the following parameters:the total mass M, electric charge Q,cosmological constant Λ,and several parameters affecting the density distribution,including d(the dimension of space),n(relating to the central matter density),l (the minimum length),and so on.This black hole spacetime is asymptotically flat or(A)dS at large distance,and it is flat or the(A)dS type near the center of the gravitational source for n≥0,which depends on the relative values of the above parameters.
By analyzing the central curvature K,the formation of event horizons rh,Hawking temperature TH,entropy S,and heat capacity C,we found that the center of the source is nonsingular for n≥0,and under certain conditions(describing by Eqs.(38)and(39))it is also nonsingular for?2≤n<0.We also found that the Hawking temperature THhas no usual divergence problem for n>?2.These results show that about nonsingularity,the critical point of n for the central curvature and thermodynamic properties is different.We have also found that the parameters Q2,n,a,and l have similar effects on both M and TH,while the k parameter is the opposite to the previous parameters.If Λ is too small,there will be no local maximum and minimum temperature.Λ also has an important effect on C.Due to the fundamental minimum length l, there is a correction to the usual semi-classical area law and the correction of entropy decreases exponentially.
[1]Snyder H S 1947 Phys.Rev.71 38
[2]Smailagic A and Spallucci E 2003 J.Phys.A 36 L467
[3]Smailagic A and Spallucci E 2003 J.Phys.A 36 L517
[4]Nicolini P,Smailagic A and Spallucci E 2006 Phys.Lett.B 632 547
[5]Ansoldi S,Nicolini P,Smailagic A and Spallucci E 2007 Phys.Lett.B 645 261
[6]Nicolini P and Torrieri G 2011 J.High Energy Phys.08 097
[7]Spallucci E,Smailagic A and Nicolini P 2009 Phys.Lett.B 670 449
[8]Nozari K and Mehdipour S H 2010 Commun.Theor.Phys.53 503
[9]Modesto L and Nicolini P 2010 Phys.Rev.D 82 104035
[10]Nicolini P 2009 Int.J.Mod.Phys.A 24 1229
[11]Myung Y S,Kim Y W and Park Y J 2007 J.High Energy Phys.02 012
[12]Banerjee R,Majhi B R and Samanta S 2008 Phys.Rev.D 77 124035
[13]Kim W,Son E J and Yoon M 2008 J.High Energy Phys.04 042
[14]Nozari K and Mehdipour S H 2008 Classical and Quantum Gravity 25 175015
[15]Larra?aga A 2013 Rom.J.Phys.58 50
[16]Mehdipour S H 2010 Int.J.Mod.Phys.A 25 5543
[17]Nozari K and Islamzadeh S 2013 Astrophys.Space Sci.347 299
[18]Mehdipour S H and Keshavarz A 2012 Europhys.Lett.98 10002
[19]Bhar P,Rahaman F,Biswas R and Mondal U 2015 Commun.Theor. Phys.64 1
[20]Tejeiro J M and Larra?aga A 2011 The Abraham Zelmanov Journal 4 28
[21]Rahaman F,Bhar P,Sharma R and Tiwari R K 2015 Eur.Phys.J.C 75 107
[22]Tejeiro J M and Larra?aga A 2012 Pramana J.Phys.78 155
[23]Rahaman F,Kuhfittig P K F,Bhui B C,Rahaman M,Ray S and Mondal U F 2013 Phys.Rev.D 87 084014
[24]Park M I 2009 Phys.Rev.D 80 084026
[25]Myung Y S and Yoon M 2009 Eur.Phys.J.C 62 405
[26]Liang J,Liu Y C and Zhu Q 2014 Chin.Phys.C 38 025101
[27]Miao Y G and Xu Z M 2016 Eur.Phys.J.C 76 217
[28]Tangherlini F R 1963 Nuovo Cimento 27 636
[29]Daghigh R G,Kunstatter G,Ostapchuk D and Bagnulo V 2006 Classical and Quantum Gravity 23 5101
14 March 2017;revised manuscript
15 May 2017;published online 18 July 2017)
10.1088/1674-1056/26/9/090202
?Corresponding author.E-mail:jhchen@hunnu.edu.cn
?2017 Chinese Physical Society and IOP Publishing Ltd http://iopscience.iop.org/cpb http://cpb.iphy.ac.cn
- Chinese Physics B的其它文章
- Relationship measurement between ac-Stark shift of 40Ca+clock transition and laser polarization direction?
- Air breakdown induced by the microwave with two mutually orthogonal and heterophase electric field components?
- Collective motion of active particles in environmental noise?
- Temperature dependence of heat conduction coefficient in nanotube/nanowire networks?
- Analysis of dynamic features in intersecting pedestrian flows?
- Heat transfer enhancement in MOSFET mounted on different FR4 substrates by thermal transient measurement?

