活躍于競賽與高考中的取整函數(shù)*

甘肅臨澤一中(734200) 魏正清

活躍于競賽與高考中的取整函數(shù)*

甘肅臨澤一中(734200) 魏正清

取整函數(shù)在各類競賽及近幾年的高考中頻頻出現(xiàn),本文擬通過一些實例來解析處理相關問題的方法.

1.換元法

例1 計算___.(這里[x]表示不超過實數(shù)x的最大整數(shù)).

2.以退為進

例2 [log21]+[log22]+···+[log22012]=___([x]表示不超過實數(shù)x的最大整數(shù)).

3.配湊法

例3的個位數(shù)字是____([x]表示不超過實數(shù)x的最大整數(shù)).

4.周期性

例4 某校課外活動小組,在坐標紙上某沙漠設計植樹方案如下：第k棵樹種植在點Pk(xk,yk)處,其中x1=1,y1=1.當k≥2時,

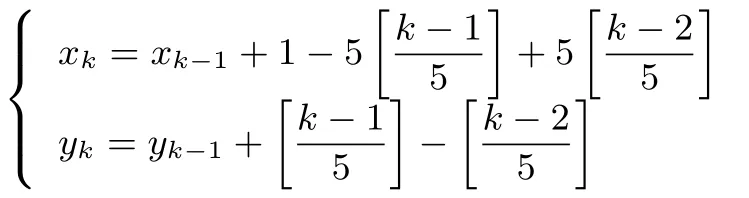
其中[x]表示不超過實數(shù)x的最大整數(shù).按此方案,第2008棵樹種植點的坐標為____.

5.構造函數(shù)

例5證明方程[x3]+x2=x3+[x2]有非整數(shù)解([x]表示不超過實數(shù)x的最大整數(shù)).

6.估算法

例6計算的值(其中2008共出現(xiàn)了2008次,[x]表示不超過實數(shù)x的最大整數(shù)).

7.用定義

例7 方程在區(qū)間[0,2π]內的所有實根之和為___([x]表示不超過實數(shù)x的最大整數(shù)).

8.構不等式

例8=____([x]表示不超過實數(shù)x的最大整數(shù)).

分析注意到取整函數(shù)中含有三角函數(shù),可構建不等式脫去三角函數(shù),從而找到解題思路.

9.構等式

例9被63除的余數(shù)為____([x]表示不超過實數(shù)x的最大整數(shù)).

10.分類討論

例10 計算___([x]表示不超過實數(shù)x的最大整數(shù)).

分析注意到取整函數(shù)的結構特征,可對整數(shù)n進行分類討論處理.

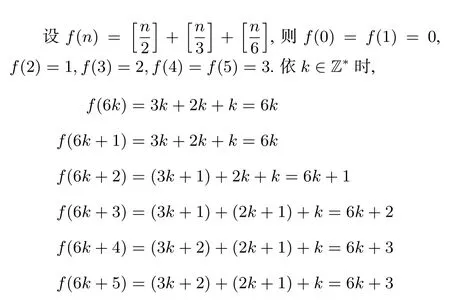
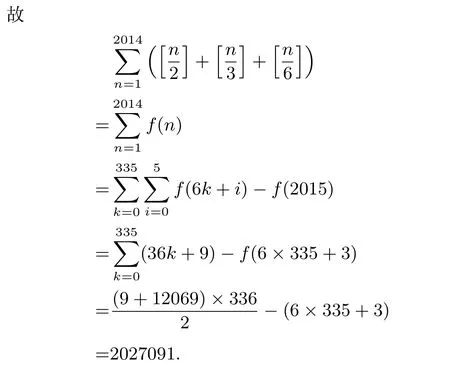
11.利用性質

例11 記[x]表示不超過實數(shù) x的最大整數(shù),且[x1],[x2],···,[xn]為1,2,···,n的一個排列,其中n≥2為給定整數(shù).求的最大值和最小值.

分析利用取整函數(shù)的性質xn-1＜[xn]≤xn,是解決此類問題的重要途徑.

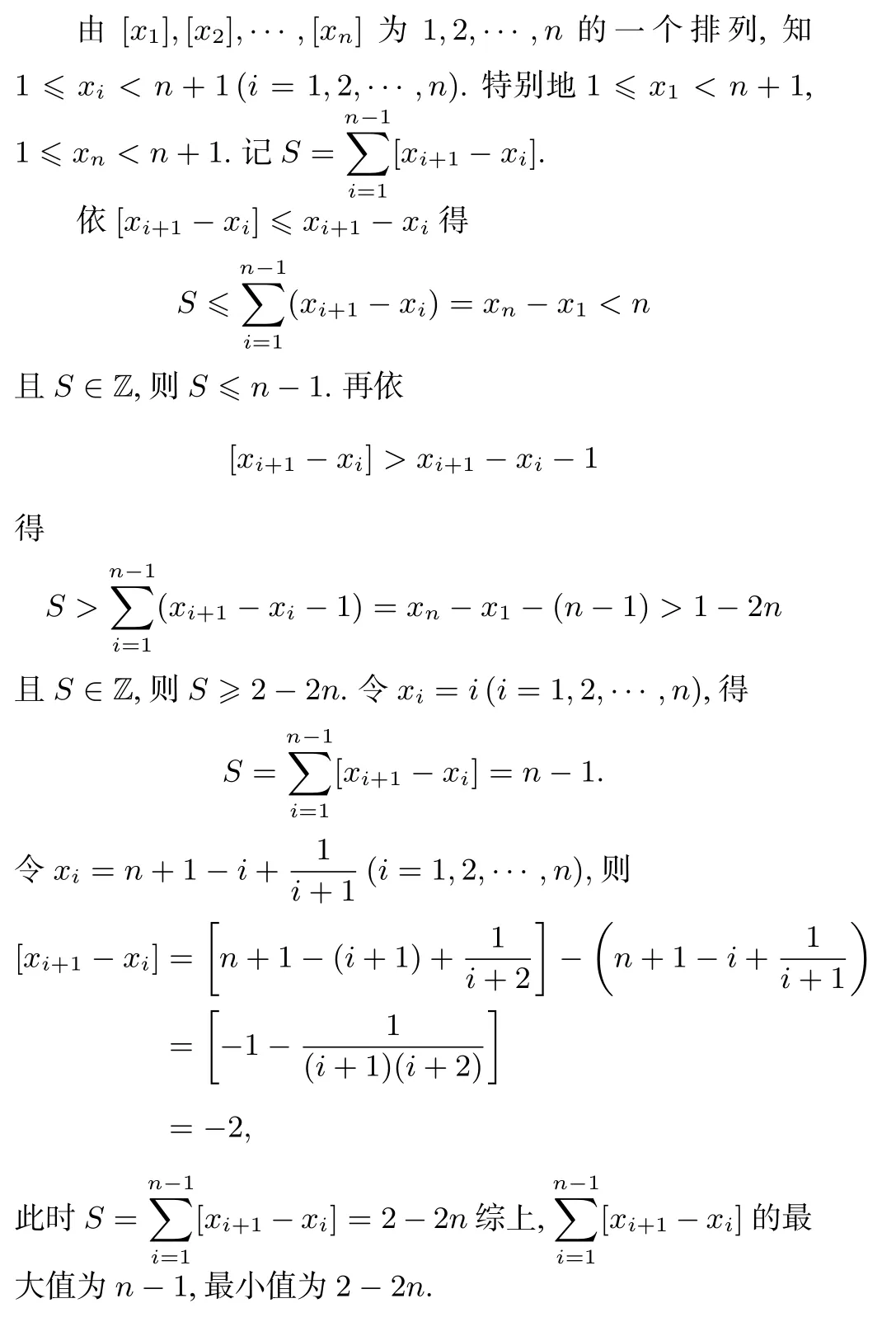
*本文是甘肅省十二五規(guī)劃課題“新課程背景下數(shù)學課堂教學情景中師生關系重建研究”成果.