Robust H∞Consensus Control for High-order Discrete-time Multi-agent Systems With Parameter Uncertainties and External Disturbances

Jun Xu Guoliang Zhang Jing Zeng Boyang Du Xiao Jia

1 Introduction

In recent years,distributed coordination of multi-agent systems(MASs)has received great attention from many researchers due to its broad applications on MASs in many areas including formation control[1],[2], fl ocking[3],[4],distributed fi ltering[5],[6],synchronization of coupled chaotic oscillators[7]?[9].Consensus is an essential problem of distributed coordination of MASs,which is to make each agent agree on some common values of interest through feedback of local information from neighboring agents.

The theoretical framework for posing and solving the consensus problem for MASs was fi rst introduced in[10]?[12]. Their work mostly focused on the fi rst-order and second-order consensus in MASs.Furthermore,the consensus problem of MASs has obtained a tremendous surge of interest and extensive development.These works can be generally divided into two categories depending on whether the agent models are continuous-time or discrete-time.The union of interaction topologies must contain a spanning tree if MASs are expected to achieve consensus asymptotically[13].A framework of high-dimensional state space for the consensus problems of MASs was studied in[14],and then the consensus problems of high order or more general linear MASs models were discussed in[15]?[17].The consensus problem of discrete-time MASs(D-MASs)based on general linear models was investigated in[18],[19].The leaderfollowing consensus problem of D-MASs based on general linear models was studied in[20].The robust guaranteed cost consensus problem of general linear D-MASs models with parameter uncertainties and time-varying delays was investigated in[21].

With the development of the research,theH∞consensus control problem of MASs subject to external disturbances was considered in[22]?[24].RobustH∞consensus control problems of fi rst-order MASs with external disturbances and model uncertainties are discussed in[22].The secondorder robustH∞consensus control problem of MASs with measurement noises and asymmetric delays is studied in[23].DistributedH2andH∞consensus control problems are investigated in[24]for MASs with linear dynamics subject to external disturbances.The robustH∞consensus control problem of high-order linear MASs with parameter uncertainties and external disturbances was studied in[25],which also considered the time-delay and switching topology simultaneously.Speci fi cally,the aforementioned works were based on continuous-time models,while the study of discrete-time model cases is more widely applied in practice.In[26],H∞synchronization and state estimation problems were considered for an array of coupled discrete time-varying stochastic complex networks over a fi nite horizon.The robustH∞consensus control problem of high-order linear time-varying D-MASs with uncertainties/disturbances and missing measurements was investigated in[27].The event-basedH∞consensus control problem for high-order linear time-varying D-MASs over a fi nite horizon was studied in[28].Nevertheless,although the robustH∞control consensus problem of high-order D-MASs with parameter uncertainties and external disturbances was addressed in[26]?[28],the fi nal convergence value was not provided in these studies.

Motivated by the above,in this paper,the robustH∞control consensus problem of high-order D-MASs with parameter uncertainties and external disturbances is investigated by state space decomposition approach.We consider the leaderless consensus of the uncertain high-order D-MASs with fi xed topologies.In this problem,if an appropriate consensus protocol is applied,the D-MASs should converge to a common value.Comparing with the existing works,the contribution of this paper is two-fold.On one hand,by state space decomposition approach,a sufficient linear matrix inequality(LMI)condition is given to guarantee that,high-order D-MASs subject to parameter uncertainties and external disturbances achieve robust consensus with aH∞performance indexγ.On the other hand,withωx(k)≡0 orωx(k)interpreted as deterministicl2signal,fi nal consensus values of high-order D-MASs with parameter uncertainties and external disturbances,which are fi rst provided in this paper for the fi rst time.

The rest of the paper is organized as follows.The problem formulation is presented in Section 2.In Section 3,the robustH∞consensus control problem of MASs(1)is transformed to a robustH∞control problem of a set of independent uncertain systems,and a sufficient LMI condition insuring the robust consensus,and a fi nal consensus value of MASs(1)with protocol(4)are given.A numerical example is provided in Section 4 to verify the theoretical analysis.Some conclusions are fi nally drawn in Section 5 which concludes the paper and proposes some possible future directions.The notions of graph theory and Kronecker product that will be used in this paper are summarized in Appendix A and Appendix B,respectively.

Notations:A matrix or a vector is said to be positive(respectively,non-negative)if all of its entries are positive(respectively,non-negative).A square matrix is called Schur stable if all of its eigenvalues lie in the open unit disk.Let diag{a11,a22,...,ann}be the diagonal matrix with diagonal entriesa11,a22,...,ann.The symbol?represents the Kronecker product.MTdenotes the transpose conjugate of matrixM.Iis an appropriate dimensions identity matrix.1N=[1,...,1]Tdenotes an N-dimensional vector with all of its elements being 1.

2 Problem Formulation

A high-order MAS can be described as a linear system,which has been presented in[15],and thus,consider a highorder identical D-MAS consisting ofNagents indexed by 1,2,...,N,distributed on an undirected communication graphG,in which the dynamics of agentiis described by a linear discrete-time system as follows

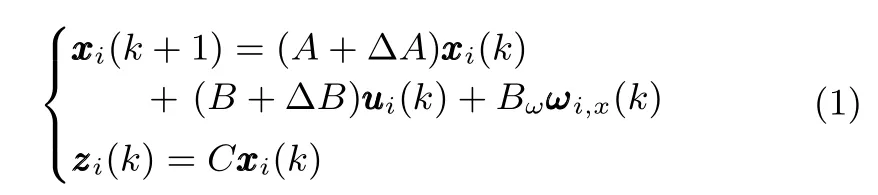
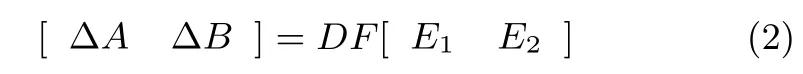
whereDis a real constant matrix,andFis an unknown matrix function satisfying

The parameter uncertainties?Aand?Bare said to be admissible if both(2)and(3)hold.For the leaderless consensus problem of uncertain D-MASs(1),the following local consensus protocol is applied to each agenti

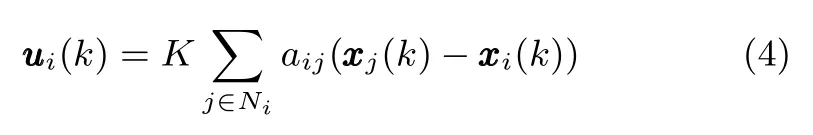
whereKis a constant gain matrix with appropriate dimensions,andaijbeing the graph edge weights.This protocol is distributed in nature as it only depends on the immediate neighborsNiof agent(node)i.This is known as a local voting protocol because the control input of each agent depends on the difference between its state and all its neighbors.Then,the de fi nition of consensus for highorder D-MASs(1)with consensus protocol(4)is given as follows.

De fi nition 1:For a given gain matrixK,system(1)is said to achieve consensus if for any given bounded initial condition,there exists a vector-valuedc(k)which is dependent on the initial condition such that limk→∞(x(k)?1N?c(k))=0,wherec(k)is called a fi nal consensus value.

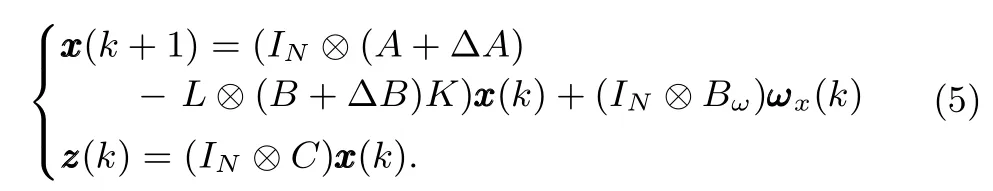
The suboptimal robustH∞consensus control problem of system(5)is stated to fi nd a distributed protocol(4)such that

1)withωx(k)=0,the closed-loop system(5)is asymptotically stable for all admissible uncertain matricesF.

2)withωx(k)interpreted as deterministicl2signal,the closed-loop transfer function fromωx(k)toof system(5),which is denoted byTωz,satis fi es‖Tωz‖∞＜γfor all admissible uncertain matricesFand a given allowable scalarγ＞0,where‖Tωz‖∞is theH∞norm ofTωz,de fi ned by.

In order to analyze the robustH∞consensus control problem of closed-loop D-MASs(6),we assume hereafter that the communication graphGis connected and give the following lemma about the graph theory.

Lemma 1[29]:LetLbe the Laplacian matrix of an undirected graphG,then zero is an eigenvalue ofL.If,in addition,Gis connected,the zero eigenvalue ofLis simple,and all the other eigenvalues ofLare positive and real.

Moreover,letλi(i=1,2,...,N)be eigenvalues of the Laplacian matrixL∈RNfor an undirected topologyG,whereλ1=0 with the associated eigenvector,andλ1≤λ2≤···≤λN.There exists an orthogonal matrix

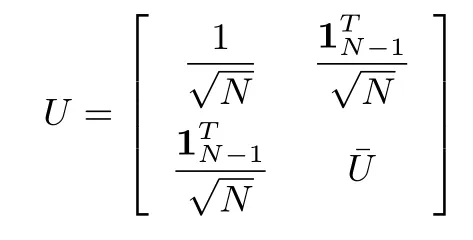
such thatUTLU=diag{λ1,λ2,...,λN}.

Theorem 1:For a givenγ＞0,system(5)is asymptotically stable and‖Tωz‖∞＜γ,if and only if the followingNsystems are simultaneously asymptotically stable and theH∞norms of their transfer function matrices are all less thanγ:

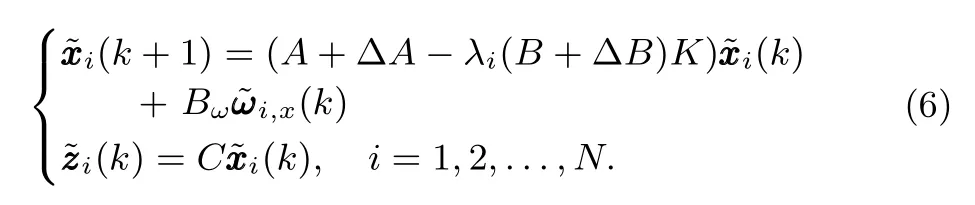
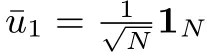
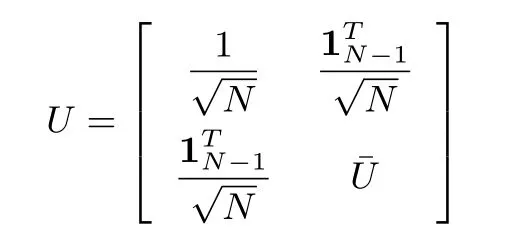
such thatUTLU=diag{λ1,λ2,...,λN}= Λ.Let

Then,system(5)can be rewritten in terms ofas

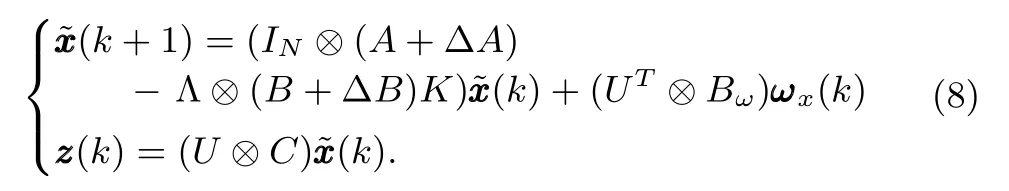
Moreover,reformulate the disturbance variableωx(k)and the performance variablevia

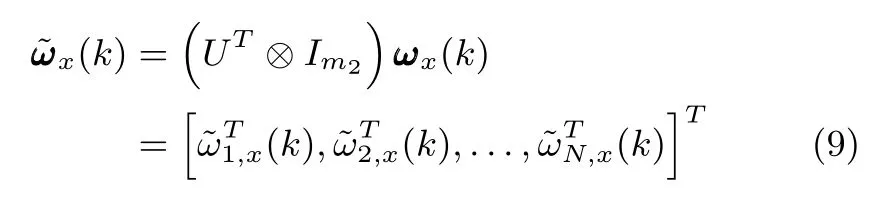
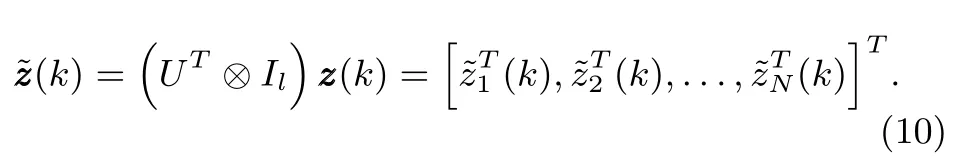
Subsequently,substituting(9)and(10)into(8)gives

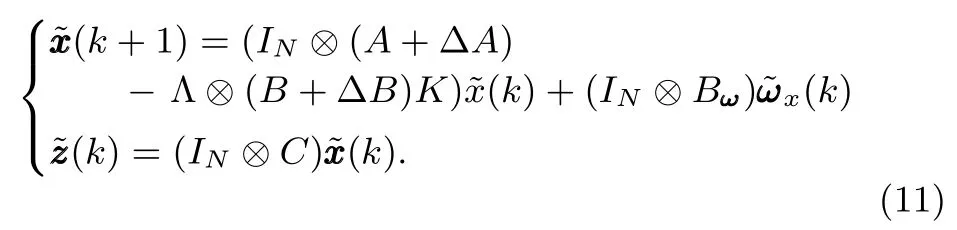
Note that(11)is composed ofNindividual systems of(6).Denote bythe transfer function matrices of systems(11)and(5),respectively.Then,it follows from(5),(9),(10)and(11)that

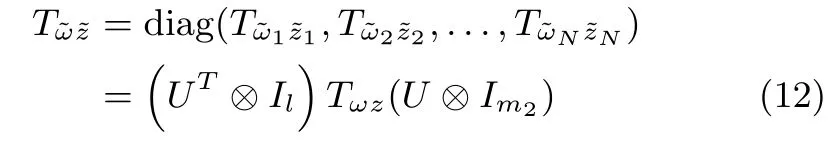
which implies that

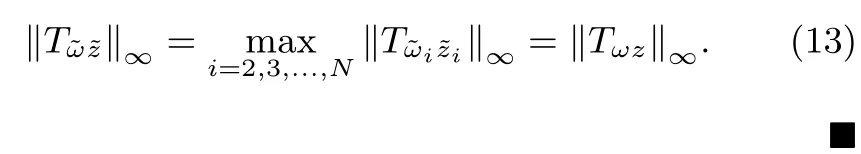
In addition,it is worth mentioning that,

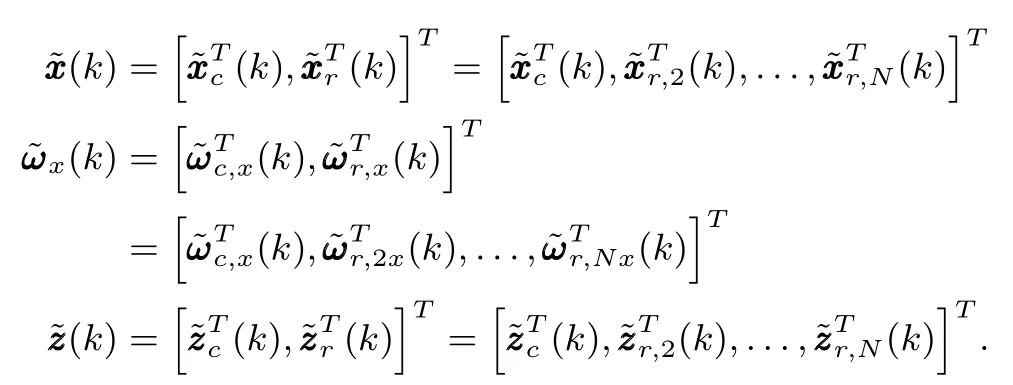
By Lemma 1,the discrete-time system(11)also can be rewritten as the followingNsubsystems

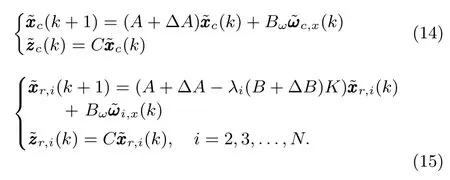
Obviously,if subsystems(15)are asymptotically stable,then D-MASs(5)reach consensus.Subsystem(14)determines the fi nal consensus value of D-MASs(5),and the details of it will be discussed below.

Remark 1:The robustH∞leaderless consensus problem of uncertain D-MASs(1)is to design distributed consensus protocols,?i∈Nisuch that the consensus is reached and‖Tωz‖∞＜γ,simultaneously.Theorem 1 converts the robustH∞consensus control problem of D-MASs(5)into the robustH∞control problems ofNsubsystems(6),which is a set of independent systems having the same dimensions as a single agent in(1),thereby reducing the computational complexity signi fi cantly.The key tools leading to this result rely on the state space decomposition approach,as used in[15].

3 Main Results

Lemma 2:Given the pair(K,γ＞0),if the matrix inequality

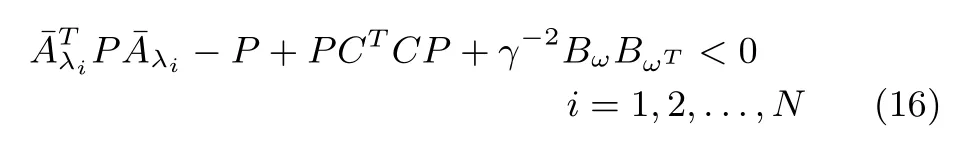
admits a symmetric positive de fi nite solutionP∈Rd×d,whereˉAλi=A+?A?λi(B+?B)K=Aλi+DFEλi,Aλi=A?λiBK,Eλi=E1?λiE2K.Then,D-MASs(1)are said to achieve robust consensus with aH∞performance indexγ.

Proof:GivenK,γ＞0,assume thatP=PT＞0 satisfi es the matrix inequality(16).In this case(dropping the quadratic semide fi nite positive term inP)it follows

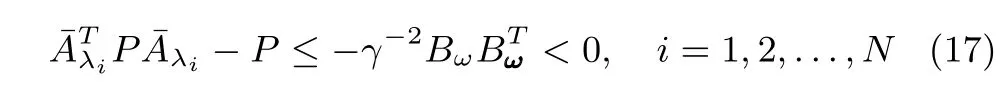
(complying with the previous assumptions)thatis asymptotically stable.To prove theH∞-norm.Inequality,we proceed as follows.For each system(6),consider the closed-loop transfer function fromgiven by

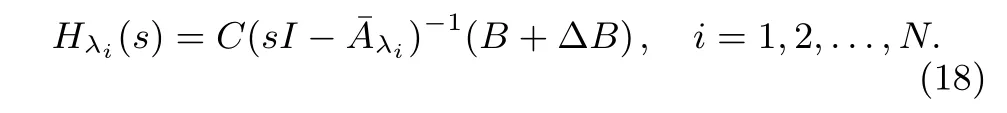
De fi nings=ejω,ω∈[?π,π]and the auxiliary transfer functionafter simple but tedious algebraic manipulations,inequality(17)can be factorized as

which,after completing squares,becomes

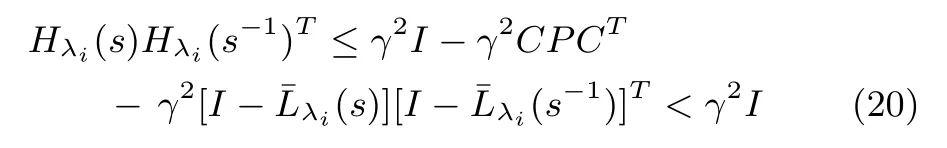
meaning that‖Hλi‖∞＜γ,which proves the lemma proposed.

Remark 2:In Lemma 2,a sufficient condition is given to guarantee D-MASs(5)achieving robust consensus with aH∞performance indexγ.Nevertheless,it is not difficult to fi nd that(16)is a nonlinear matrix inequality(NMI)and therein lies parameter uncertainties.

To cope with the uncertain matricesFand the nonlinear terms of(16),the following two lemmas are given.

Lemma 4[30]:Given matricesY,DandEof appropriate dimensions and withYsymmetric,then for allFsatisfyingFTF≤I,if and only if there exists a scalarε＞0 such that

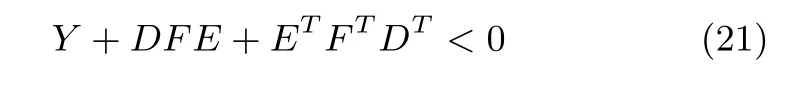
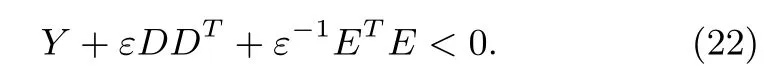
Lemma 5(Schur complement)[31]:The linear matrix inequality

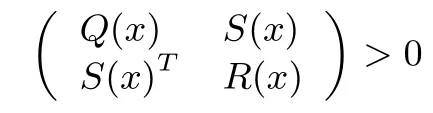
whereQ(x)=Q(x)T,R(x)=R(x)T,andS(x),depends affinely onx,is equivalent to one of the following conditions

1)Q(x)＞0,R(x)?S(x)TQ(x)?1S(x)＞0;

2)R(x)＞0,Q(x)?S(x)R(x)?1S(x)T＞0.

Theorem 2:Consider D-MASs(1)with a fi xed,undirected and connected communication topologyG.The distributed consensus protocol(4)globally asymptotically solves the robust consensus problem of D-MASs(1)withH∞-norm consensus performance boundγif there exist a scalarε＞0,a matrixWwith appropriate dimensions and a positive de fi nite matrixXsuch that

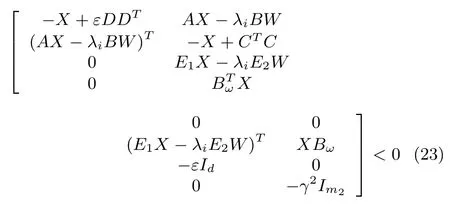
wherei=1,2,...,N.Furthermore,if LMI(23)has a feasible solutionε,W,X,then the feedback gain matrixKof protocol(4)can be calculated byK=WX?1.

Proof:By Lemma 5,matrix inequality(16)is equivalent to

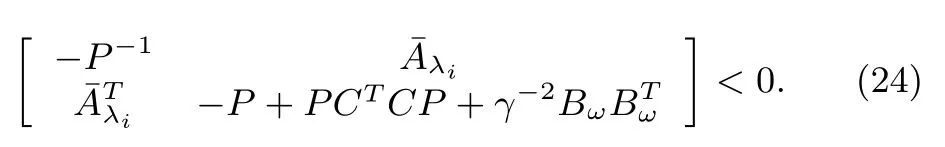
Moreover,the above inequality can be rewritten as

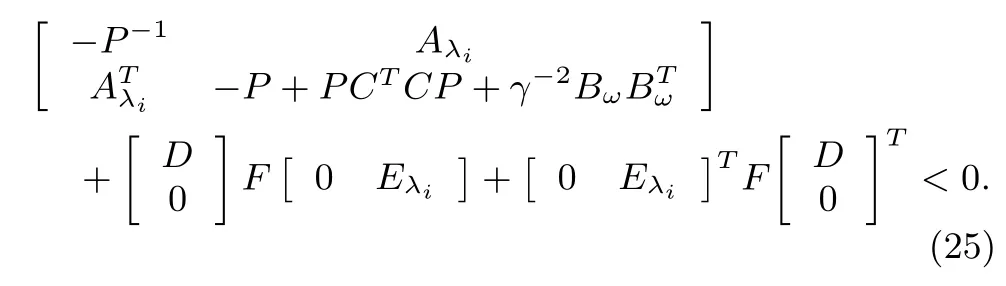
It follows from the Lemma 4 that(25)can be expressed as

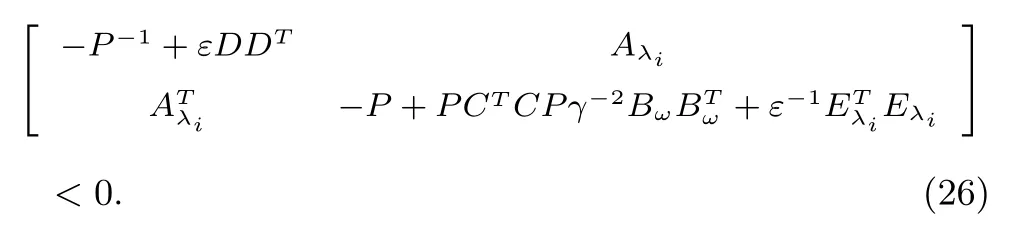
Through Lemma 5 again,matrix inequality(26)is equivalent to

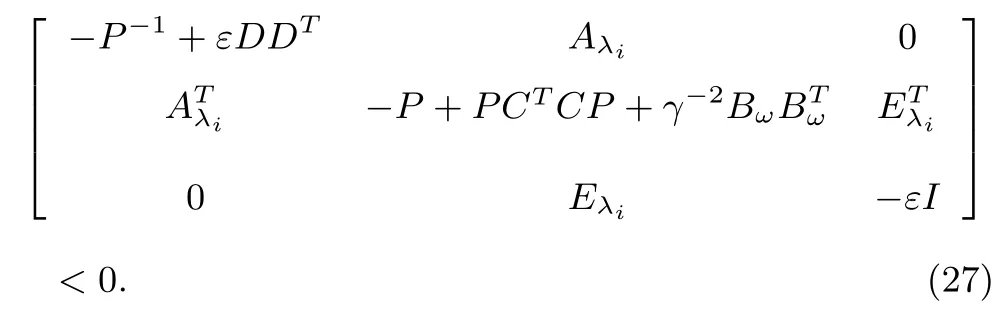
Pre-and post-multiplying both sides of(27)by

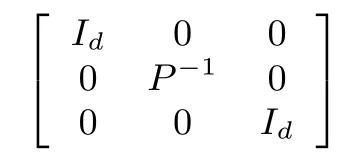
lettingX=P?1,W=KP?1,and applying Lemma 5 again yield LMI(23),wherei=1,2,...,N.

Remark 3:In Theorem 2,it can be noted that the NMI(16)is transformed to a LMI condition(23).Subsequently,high-order D-MASs(1)with the distributed consensus protocol(4)achieve robust consensus with aH∞performance indexγ.Thereby the neighboring feedback matrixKalso can be obtained.Then,the local consensus protocol(4)can be implemented by each agent in a fully distributed fashion requiring no global information of the communication topology.

Remark 4:From Theorem 2,we can also get that,the communication disturbances have effects on the performance of the control object,such as switching interaction topologies.In[32],[33],the time-varying formation tracking problems for second-order MASs with switching interaction topologies were studied.Switching topologies include two cases.One is that every interaction topology of MASs has a spanning tree;another is joint-contained spanning tree topologies.It should be mentioned that,this approach can be easily extended to the fi rst case,and more details can be seen in our work[34].There have been some difficulties to the joint-contained spanning tree case.We will consider it in the future.

Theorem 3:Withωx(k)interpreted as deterministicl2signal,when D-MASs(5)achieve robust consensus,the final consensus valuec(k)satis fi es

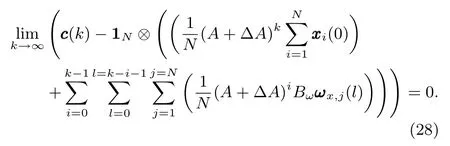
Proof:Letand,then by(7),xxx(k)can be uniquely decomposed as.As discussed above,we can know that if the system(5)achieves robust guaranteed cost consensus,the subsystem(15)should be Schur stable,which means that the response of system(15)due toshould satisfy.Hence the final consensus valuec(k)is determined solely upon.Since,we have,and because,then we can obtain,that is to say

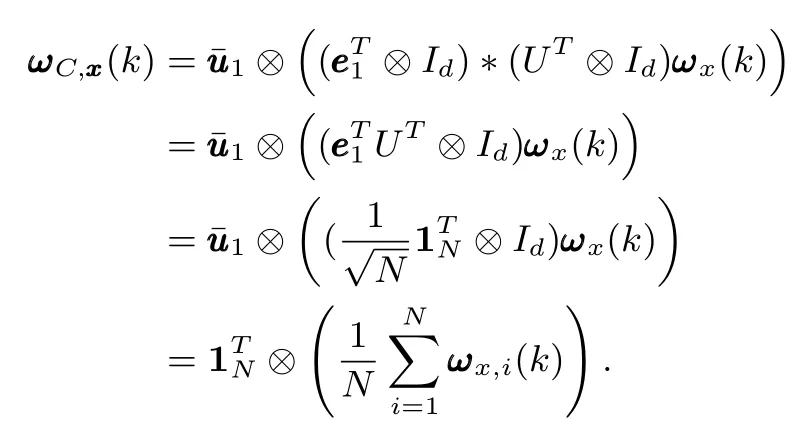
Hence,we have

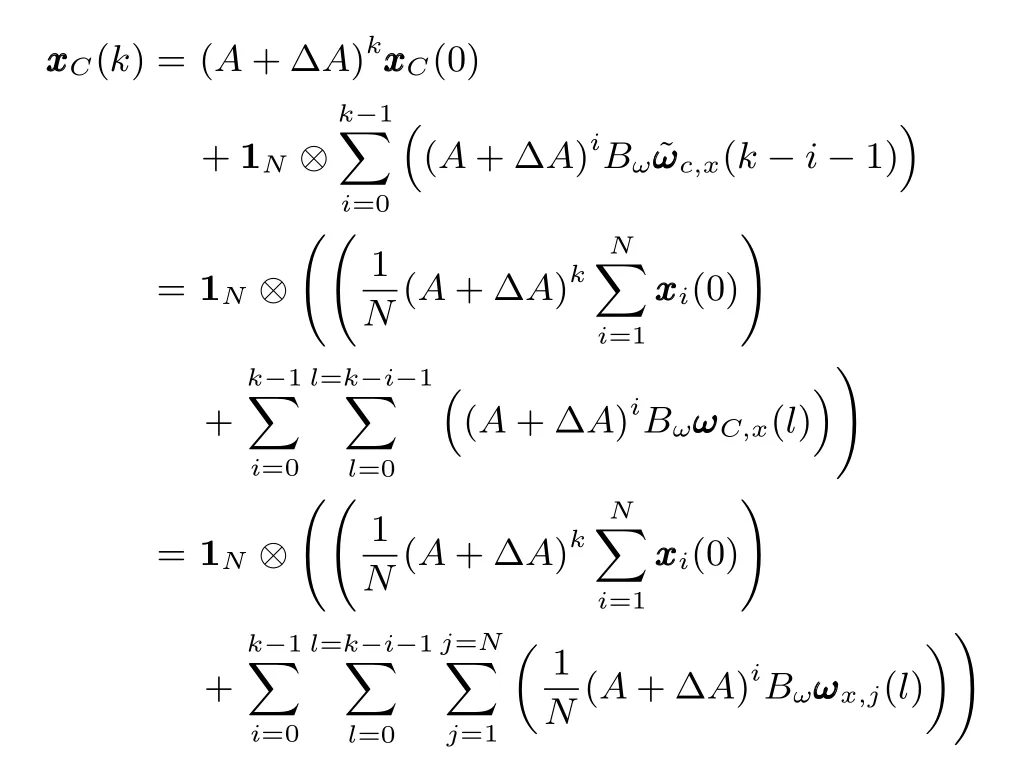
then the fi nal consensus valuesatis fi es

Corollary 1:Withωx(k)≡0,when multi-agent system(5)achieves robust consensus,the fi nal consensus valuesatis fi es

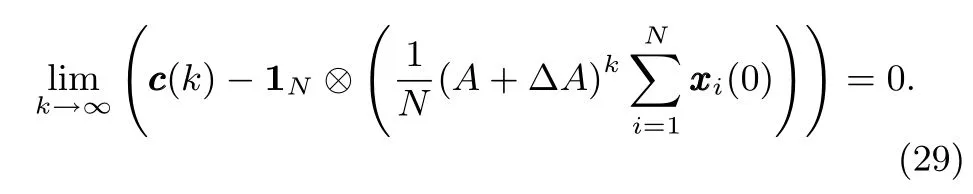
Proof:This proof can be easily obtained from the proof of Theorem 3.

Remark 5:Withωx(k)interpreted as deterministicl2signal,the fi nal consensus valueof system(5)is given by Theorem 3.The fi nal consensus valuecan be divided into two parts,one is,which is related to the system matrixA+?Aand initial statex(0),the other is,which is related to the external disturbanceωx(k).This implies that the external disturbanceωx(k)has an effect on the fi nal consensus value,and which is also related to the system matrixA+?A,and initial state.This condition is different from that of highorder D-MASs without parameter uncertainties and external disturbances,which is discussed in[34].Withωx(k)≡0,the fi nal consensus valueof system(5)is given by Corollary 1.That is,in this case,the fi nal consensus value is only related to the system matrixA+?A,and initial state.

Remark 6:It should be pointed out that,in[26]?[28],by recursive linear matrix inequalities(RLMIs)techniques,the robustH∞consensus control problem of high-order D-MASs(1)with uncertainties/disturbances was investigated over a fi nite horizon.They were concerned about the boundedness of the consensus error but did not actually guarantee its convergence.Different from[26]?[28],we consider the in fi nite time horizon case,which took care of the consensusability of D-MASs rather than consensus errors.In Theorems 1 and 2,a sufficient LMI condition is given to guarantee that high-order D-MASs(1)with parameter uncertainties and external disturbances achieve robust consensus with a performance levelγ.Comparing to related works[25]?[28],this approach has a favorable decoupling feature.Speci fi cally,note that theH∞performance levelγminof network(6),consisting ofNagents in D-MASs(1)under consensus protocols(4),is actually equal to the minimalH∞norm of a single agent(1)by means of a state feedback controller of the form,independent of the communication topologyGas long as it is connected.In addition, fi nal consensus values of highorder D-MASs(1)with parameter uncertainties and external disturbances are fi rst given in this paper.In addition,practical consensus problems for general high-order linear time-invariant swarm systems with interaction uncertainties and time-varying external disturbances on directed graphs were investigated in[35].The authors paid attention to the output consensus of continuous-time highorder linear time-invariant swarm systems.However,the state consensus problem of discrete-time multi-agent systems is addressed in this paper.Moreover,the external disturbance was solved by the Lyapunov-Krasovskii functional approach and the linear matrix inequality technique in the literature,but we use theH∞control method to deal with it.

4 Simulations

In this section,a numerical example is given to illustrate the effectiveness of the proposed theoretical results.We apply the above proposed consensus protocol(4)to achieve state alignment among 8 agents.The dynamics of them are described by(1),where

andr1,r2andr3are uncertain parameters which satisfy?1≤r1≤1,?1≤r2≤1 and?1≤r3≤1.Then,D-MASs(1)can be rewritten as

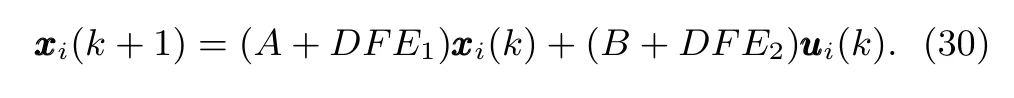
We apply the consensus protocol(4)to achieve consensus among the above those 8 agents under a fi xed topologyG,which is shown in Fig.1.

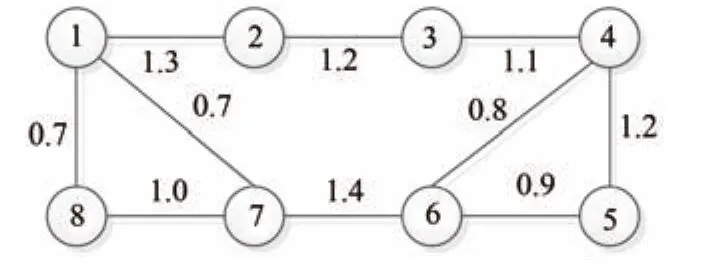
Fig.1. The interaction topology G of 8 agents.

Assume that the initial state values of the all agents 1,...,8 are randomly produced withx1(0)=[1,5,?2]T,x2(0)=[2,4,3]T,x3(0)=[1,1,2]T,x4(0)=[3,2,1]T,x5(0)=[5,6,?2]T,x6(0)=[?3,3,4]T,x7(0)=[?2,?4,?3]T,x8(0)=[?5,?2,?1]T,and letr1=0.15,r2=0.25,r3=0.15 andτmax=3.Each agent uses protocol(4).Letγ=1 and suppose that the exogenous disturbance inputs are selected asωi,x(k)=0.1ie?0.5ksin(k).By Theorem 2,we can get that

In Figs.2?4,the simulation results are given.The state trajectories of uncertain D-MASs(1)with and without external disturbances are shown in Figs.2?4(b)and(a),respectively.Final consensus valuesc(k)andc?(k),which are produced by Corollary 1 and Theorem 3,are marked by the red asterisk and blue circle,respectively.

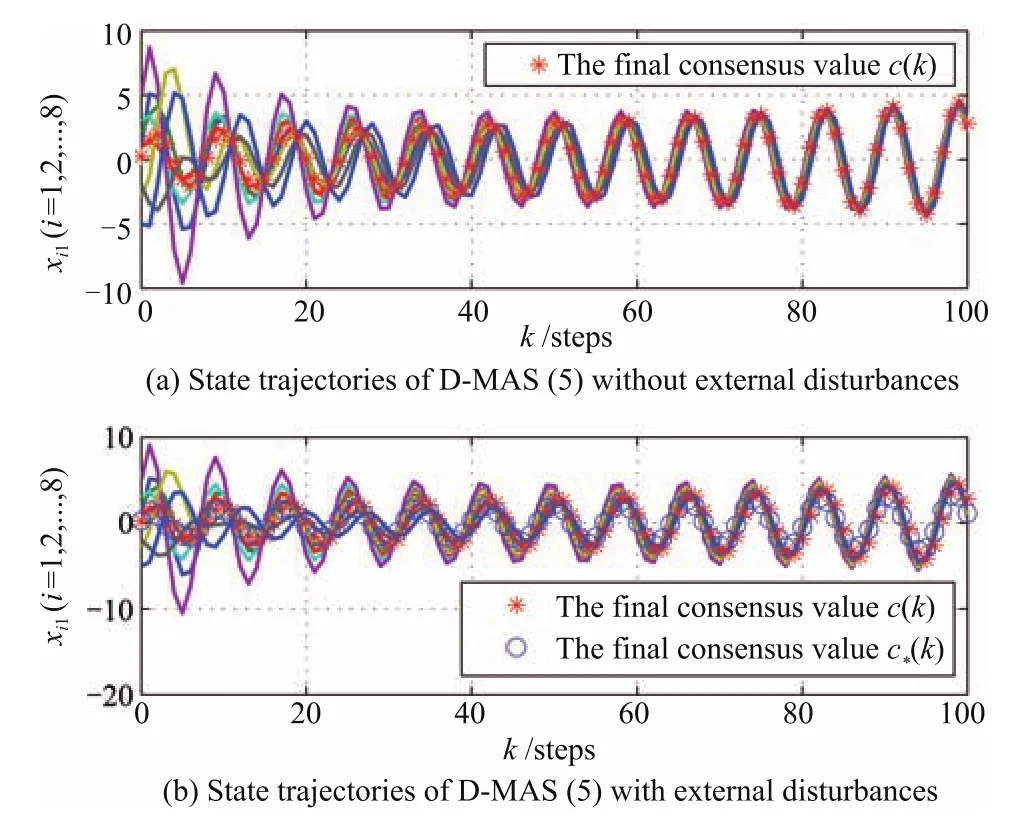
Fig.2. The state 1 trajectories of D-MASs(1).

From Figs.2?4(a),it can be seen that the state trajectories of D-MASs(1)withωx(k)≡0 asymptotically converge to the common value,which is related torj(j=1,2,3).The fi nal consensus value of D-MASs(1)with parameter uncertainties is.This is in accord with Corollary 1.Nevertheless,in Figs.2?4(b),we can know that the common value of D-MASs(1)is related toωx(k),and ifωx(k)/=0,c(k)is altered and asymptotically converges to

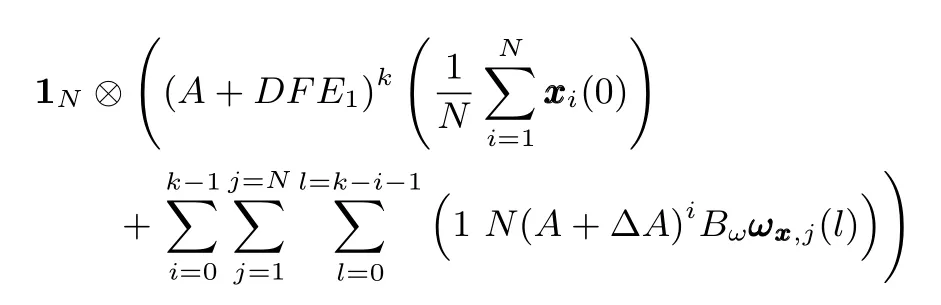
which is in accordance with Theorem 3.By De fi nition 1,it is clear that D-MASs(1)achieves robust consensus with protocol(4).Therefore,the correctness and validity of proposed protocols and theorems are demonstrated.

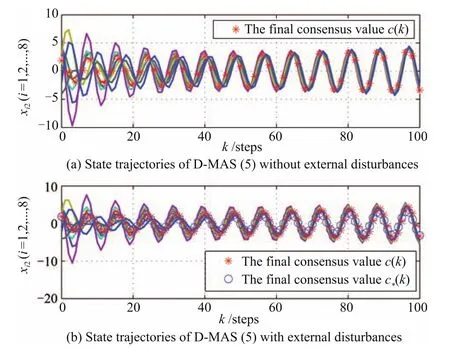
Fig.3. The state 2 trajectories of D-MASs(1).

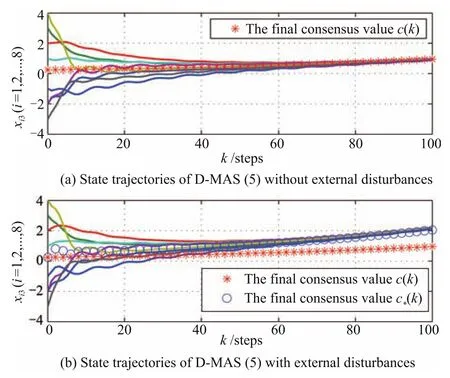
Fig.4. The state 3 trajectories of D-MASs(1).

5 Conclusions

The robustH∞consensus control problem of high-order D-MASs with parameter uncertainties and external disturbances is investigated in this paper.A sufficient LMI condition is obtained to guarantee that D-MASs(1)achieve robust consensus with protocol(4).Meanwhile,the convergence result is given as a fi nal consensus value.Finally,an illustrative example is given to demonstrate the correctness and effectiveness of the theoretical results.Further research will be conducted on the consensus problem of DMASs with switching topologies and time-delays.

Appendix A Graph

Let a weighted digraph(or directed graph)G=(V,E,A)of orderNrepresents an interaction topology of a network of agents,with the set of nodesV={v1,...,vN},set of edgesE?V×V,and a weighted adjacency matrixA=[aij]with nonnegative adjacency elementsaij.

The node indexes belong to a fi nite index setI={1,2,...,N}.An edge ofGis denoted byeij=(vi,vj),whereviandvjare called the initial and terminal nodes.It implies that nodevjcan receive information from nodevi,but not necessarily vice versa.The adjacency elements associated with the edges of the graph are positive ifeij∈Ewhileaij=0 ifeij/∈E.Furthermore,we assumeaii=0 for alli∈I.The set of neighbors of nodeviis denoted byNi={vj∈V:(vi,vj)∈E}.A cluster is any subsetJ?Vof the nodes of the graph.The set of neighbors of a clusterNJis de fi ned byNJ=∪vi∈JNi={vj∈V:vi∈J,(vi,vj)∈E}.The in-degree and out-degree of nodeviare de fi ned asand,respectively,The degree matrix of the digraphGis a diagonal matrix ? =[?ij],where

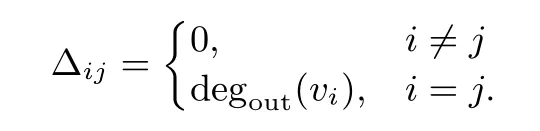
The graph Laplacian matrix associated with the digraphGis de fi ned asL(G)=L=??A.

Appendix B Kronecker Product

Given matricesP=(pij)n×n∈Rm×nandQ=(qij)n×n∈Rp×q,their Kronecker product is de fi ned as

P?Q=[pijQ]∈Rmp×nq

in[36].For matricesA,B,CandD,with appropriate dimensions,we have the following conditions.

1)(γA)?B=A?(γB),whereγis a constant;

2)(A+B)?C=A?C+B?C;

3)(A?B)(C?D)=(AC)?(BD);

4)(A?B)T=AT?BT;

5)Suppose thatAandBare invertible,then(A?B)?1=A?1?B?1;

6)IfAandBare symmetric,so is(A?B);

7)IfAandBare symmetric positive de fi nite(respectively,positive semide fi nite),so is(A?B);

8)Suppose thatAhas the eigenvaluesβiwith associated eigenvectorsfi∈Rp,i=1,...,p,andBhas the eigenvaluesρiwith associated eigenvectorsgj∈Rp,j=1,...,q.Then thepqeigenvalues of(A?B)areβiρjwith associated eigenvectorsfi?gj,i=1,...,p,j=1,...,q.

1 A.Sinha and D.Ghose,“Generalization of linear cyclic pursuit with application to rendezvous of multiple autonomous agents,”IEEE Trans.Automat.Control,vol.51,no.11,pp.1819?1824,Nov.2006.

2 M.Cao,C.B.Yu,and B.D.O.Anderson,“Formation control using range-only measurements,”Automatica,vol.47,no.4,pp.776?781,Apr.2011.

3 R.Olfati-Saber,“Flocking for multi-agent dynamic systems:Algorithms and theory,”IEEE Trans.Automat.Control,vol.51,no.3,pp.401?420,Mar.2006.

4 H.T.Zhang,C.Zhai,and Z.Y.Chen,“A general alignment repulsion algorithm for fl ocking of multi-agent systems,”IEEE Trans.Automat.Control,vol.56,no.2,pp.430?435,Feb.2011.

5 R.Olfati-Saber,“Distributed Kalman fi lter with embedded consensus fi lters,”Proc.44th IEEE Conference on Decision and Control,and the European Control Conference,Seville,Spain,2005,pp.8179?8184.

6 B.A?cskme?se,M.Mandi′c,and J.L.Speyer, “Decentralized observers with consensus fi lters for distributed discrete-time linear systems,”Automatica,vol.50,no.4,pp.1037?1052,Apr.2014.

7 M.Barahona and L.M.Pecora,Synchronization in smallworld systems,”Phys.Rev.Lett.,vol.89,no.5,Article ID:054101,Jul.2002.

8 K.Hengster-Movric,K.Y.You,F.L.Lewis,and L.H.Xie,“Synchronization of discrete-time multi-agent systems on graphs using Riccati design,”Automatica,vol.49,no.2,pp.414?423,Feb.2013.

9 Z.H.Wang,J.J.Xu,and H.S.Zhang,“Consensusability of multi-agent systems with time-varying communication delay,”Syst.Control Lett.,vol.65,pp.37?42,Mar.2014.

10 R.O.Saber and R.M.Murray,“Consensus protocols for networks of dynamic agents,”inProc.2003 American Control Conference,Denver,CO,USA,2003,pp.951?956.

11 R.Olfati-Saber and R.M.Murray,“Consensus problems in networks of agents with switching topology and timedelays,”IEEE Trans.Automat.Control,vol.49,no.9,pp.1520?1533,Sep.2004.

12 R.Olfati-Saber,J.A.Fax,and R.M.Murray,Consensus and cooperation in networked multi-agent systems,”Proc.IEEE,vol.95,no.1,pp.215?233,Jan.2007.

13 W.Ren and R.W.Beard,“Consensus seeking in multiagent systems under dynamically changing interaction topologies,”IEEE Trans.Automat.Control,vol.50,no.5,pp.655?661,May2005.

14 F.Xiao and L.Wang,“Consensus problems for highdimensional multi-agent systems,”IET Control Theory Appl.,vol.1,no.3,pp.830?837,May2007.

15 J.X.Xi,N.Cai,and Y.S.Zhong,“Consensus problems for high-order linear time-invariant swarm systems,”Phys.A,vol.389,no.24,pp.5619?5627,Dec.2010.

16 J.X.Xi,Z.Y.Shi,and Y.S.Zhong,“Consensus and consensualization of high-order swarm systems with time delays and external disturbances,”J.Dyn.Syst.Meas.Control,vol.134,no.4,Article ID:041011,May2012.

17 J.X.Xi,Z.Y.Shi,and Y.S.Zhong,“Consensus analysis and design for high-order linear swarm systems with time-varying delays,”Phys.A:Statist.Mech.Appl.,vol.390,no.23?24,pp.4114?4123,Nov.2011.

18 K.Y.You and L.H.Xie,“Network topology and communication data rate for consensusability of discrete-time multiagent systems,”IEEE Trans.Automat.Control,vol.56,no.10,pp.2262?2275,Oct.2011.

19 G.X.Gu,L.Marinovici,and F.L.Lewis,“Consensusability of discrete-time dynamic multiagent systems,”IEEE Trans.Automat.Control,vol.57,no.8,pp.2085?2089,Aug.2012.

20 Y.F.Su and J.Huang,“Two consensus problems for discrete-time multi-agent systems with switching network topology,”Automatica,vol.48,no.9,pp.1988?1997,Sep.2012.

21 J.Xu,G.L.Zhang,J.Zeng,J.X.Xi,and B.Y.Du,“Robust guaranteed cost consensus for high-order discrete-time multi-agent systems with parameter uncertainties and timevarying delays,”IET Control Theory Appl.,vol.11,no.5,pp.647?667,Mar.2017.

22 P.Lin,Y.M.Jia,and L.Li,“Distributed robustH∞consensus control in directed networks of agents with time-delay,”Syst.Control Lett.,vol.57,no.8,pp.643?653,Aug.2008.

23 Y.G.Sun and L.Wang,“H∞consensus of second-order multi-agent systems with asymmetric delays,”Syst.Control Lett.,vol.61,no.8,pp.857?862,Aug.2012.

24 Z.K.Li,Z.S.Duan,and G.R.Chen,“OnH∞andH2performance regions of multi-agent systems,”Automatica,vol.47,no.4,pp.797?803,Apr.2011.

25 Y.Liu and Y.M.Jia,“RobustH∞consensus control of uncertain multi-agent systems with time delays,”Int.J.Control,Automat.Syst.,vol.9,no.6,pp.1086?1094,Dec.2011.

26 B.Shen,Z.D.Wang,and X.H.Liu,“BoundedH∞synchronization and state estimation for discrete time-varying stochastic complex networks over a fi nite horizon,”IEEE Trans.Neural Network,vol.22,no.1,pp.145?157,Jan.2011.

27 Z.D.Wang,D.R.Ding,H.L.Dong,and H.S.Shu,“H∞consensus control for multi-agent systems with missing measurements:The fi nite-horizon case,”Syst.Control Lett.,vol.62,no.10,pp.827?836,Oct.2013.

28 Q.Y.Liu,Z.D.Wang,X.He,and D.H.Zhou,“Event-BasedH∞consensus control of multi-agent systems with relative output feedback:The fi nite-horizon case,”IEEE Trans.Automat.Control,vol.60,no.9,pp.2553?2558,Sep.2015.

29 J.A.Fax and R.M.Murray,“Information fl ow and cooperative control of vehicle formations,”IEEE Trans.Automat.Control,vol.49,no.9,pp.1465?1476,Sep.2004.

30 Y.Y.Wang,L.H.Xie,and C.E.de Souza,“Robust control of a class of uncertain nonlinear systems,”Syst.Control Lett.,vol.19,no.2,pp.139?149,Aug.1992.

31 S.Boyd,L.El Ghaoui,E.Feron,and V.Balakrishnan,Linear Matrix Inequalities in System and Control Theory.Philadelphia,USA:Society for Industrial and Applied Mathematics,1994.

32 X.W.Dong,Y.Zhou,Z.Ren,and Y.S.Zhong,“Timevarying formation control for unmanned aerial vehicles with switching interaction topologies,”Control Eng.Pract.,vol.46,pp.26?36,Jan.2016.

33 X.W.Dong,Y.Zhou,Z.Ren,and Y.S.Zhong,“Timevarying formation tracking for second-order multi-agent systems subjected to switching topologies with application to quadrotor formation fl ying,”IEEE Trans.Ind.Electron.,Jul.2016,doi:10.1109/TIE.2016.2593656.

34 G.L.Zhang,J.Xu,J.Zeng,J.X.Xi,and W.J.Tang,“Consensus of high-order discrete-time linear networked multi-agent systems with switching topology and time delays,”Trans.Inst.Measur.Control,Feb.2016,doi:10.1177/0142331216629197.

35 X.W.Dong,J.X.Xi,Z.Y.Shi,and Y.S.Zhong,“Practical consensus for high-order linear time-invariant swarm systems with interaction uncertainties,time-varying delays and external disturbances,”Int.J.Syst.Sci.,vol.44,no.10,pp.1843?1856,Oct.2013.

36 R.A.Horn and C.R.Johnson,Matrix Analysis.Cambridge,USA:Cambridge University Press,1999.