Numerical simulation of viscous flow past an oscillating square cylinder using a CIP-based model*
Ying-nan Fu (付英男), Xi-zeng Zhao (趙西增), Fei-feng Cao (曹飛鳳), Da-ke Zhang (張大可), Du Cheng (程都), Li Li (李莉),3
1.Ocean College, Zhejiang University, Hangzhou 310058, China
2.Shanghai Merchant Ship Design and Research Institute, Shanghai 201203, China, E-mail: fyn_zju@163.com
3.State Key Laboratory of Satellite Ocean Environment Dynamics, Second Institute of Oceanography, Hangzhou 310012, China
4.Institute of Harbor-Channel and Coastal Engineering, Department of Civil Engineering, Zhejiang University of Technology, Hangzhou 310014, China
(Received February 11, 2015, Revised December 11, 2016)
Numerical simulation of viscous flow past an oscillating square cylinder using a CIP-based model*
Ying-nan Fu (付英男)1,2, Xi-zeng Zhao (趙西增)1,2, Fei-feng Cao (曹飛鳳)4, Da-ke Zhang (張大可)1, Du Cheng (程都)1, Li Li (李莉)1,3
1.Ocean College, Zhejiang University, Hangzhou 310058, China
2.Shanghai Merchant Ship Design and Research Institute, Shanghai 201203, China, E-mail: fyn_zju@163.com
3.State Key Laboratory of Satellite Ocean Environment Dynamics, Second Institute of Oceanography, Hangzhou 310012, China
4.Institute of Harbor-Channel and Coastal Engineering, Department of Civil Engineering, Zhejiang University of Technology, Hangzhou 310014, China
(Received February 11, 2015, Revised December 11, 2016)
The flow past an in-line forced oscillating square cylinder at Reynolds number of 200 is studied using an in-house code, named constrained interpolation profile method developed in Zhejiang University (CIP-ZJU). The model is established in the Cartesian coordinate system using the CIP method to discretise the Navier-Stokes equations. The fluid-structure interaction is treated as a multiphase flow of the liquid and solid phases to be solved simultaneously. An immersed boundary method is used to deal with the boundary of the solid body. The CFD model is first applied to the computation of the flow past a fixed square cylinder for its validation. Computations are then performed for the flow past a square cylinder oscillating in the streamwise direction. Considerable attention is paid to the symmetric and anti-symmetric modes of the vortex shedding in the oscillating square cylinder wake. Various oscillation amplitudes and frequencies are simulated and their effects on the vortex shedding modes are analyzed via Lissajous patterns of the unsteady lift coefficient. The relationship among the lift coefficient, the drag coefficient and the lock-on range is also investigated quantitatively.
Flow past cylinder, oscillating square cylinder, lock-on, CIP method, immersed boundary method
Introduction
A flow past bluff or slender bodies can lead to vortex shedding from the tail and induce a considerable dynamic load on the bodies, resulting in the vibration of the structures[1,2]. The vortex shedding from bluff bodies involves an unsteady flow with a wide range of practical engineering applications. The flow past an in-line oscillating cylinder is one of the classic topics in this field. This study is a first step to investigate thecapability of coupled fluid-structure interactions with an in-house code which can be used later on for the vortex induced vibration of pipelines, like those in offshore engineering.
Extensive experimental and numerical studies were reported about the flow past an in-line oscillating circular cylinder, focusing mainly on the appearance of the vortex shedding synchronization (lock-on). It is demonstrated that the lock-on occurs in a range nearfd/f0≈2(fdis the forcing frequency,f0is the frequency of the vortex shedding from a stationary cylinder, as is shown by an FFT analysis ofFl). Ongoren and Rockwell[3]concentrated on the modes of the vortex shedding by experimental studies, and five modes were identified: the symmetric S mode, the anti-symmetric A-I mode, the A-II mode, the A-III mode and the A-IV mode. Al-Mdallal et al.[4]analyzed the modes of the lock-on numerically through Lissajous patterns of the unsteady lift coefficient. Bai[5]employed the LES and the detached eddy simulation (DES) to study fixed and forced moving circular cylinders in turbulent flows, and the influences of oscillation amplitudes, frequencies and free stream velocities were discussed. Yokoi and Hirao[6]investigated the modes of the vortex shedding at the Reynolds number of 620 by laboratory experiments and numerical simulations. They found that the flow near the cylinder in the S mode is two-dimensional, but the vortex shedding along the cylinder is out of phase. Al-Mdallal[7]presented a computational study of the two-dimensional flow of a viscous fluid past a circular cylinder subject to a circular motion. The numerical simulations revealed the occurrence of multiple lock-in regions.
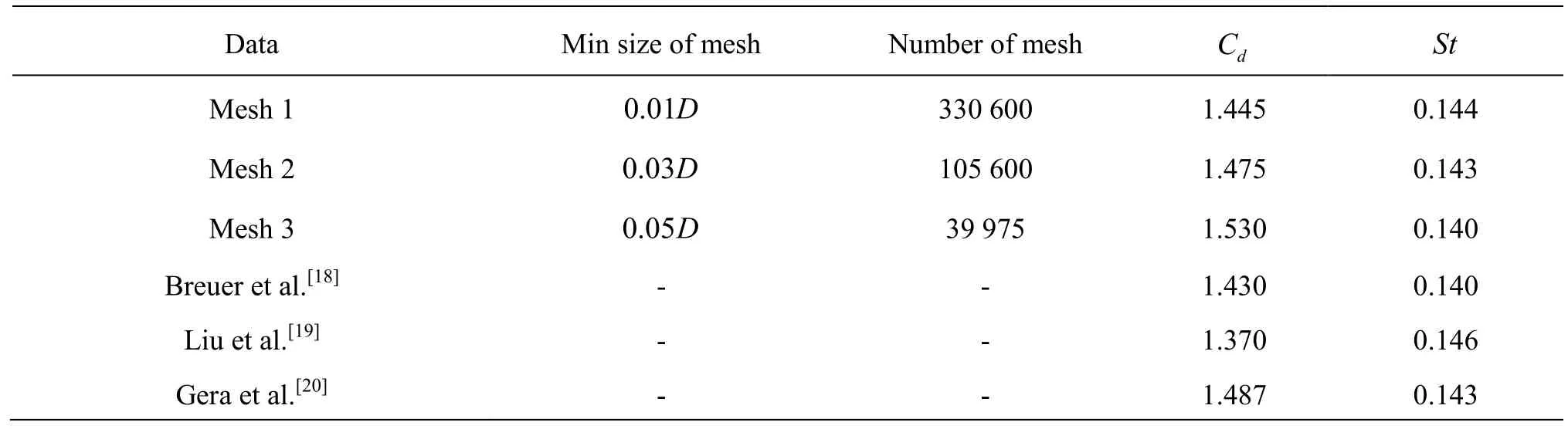
Table 1 Comparison of mean drag coefficient (Cd)and Strouhal number (St)with those of other authors
Most researches were focused on the oscillating circular cylinder, while the oscillating square cylinder was paid relatively less attention. Steggel and Rockliff[8]simulated the oscillatory flow past a rectangular-section cylinder at low Reynolds numbers using a discrete vortex method. It is shown that the aspect ratio has a great impact on the modes of the vortex shedding in the lock-on region. A strong regime of the symmetric vortex shedding is found atL/D=2.0 (whereLis the length along stream,Dis the width) when the forcing frequency is over twice of the natural shedding frequency. Chung and Kang[9]simulated the vortex shedding behind a square cylinder in an oscillatory incoming flow and obtained the relationship between the Reynolds shear stress and the phase difference between the flow velocity and the mean drag coefficient. Srikanth et al.[10]computed the flow past in-line oscillating rectangular cylinders of various aspect ratios and observed the competition between various modes by changing the aspect ratio of the rectangular section. Tudballsmith et al.[11]carried out experiments to investigate the response and the trends of the modes of streamwise oscillating cylinders, suggesting that the physical mechanism is similar regardless of the details of the body. In most of the studies listed above, the stationary cylinders with oscillatory flow were usually used. However, laboratory tests involve high costs and the technical limitation of experimental facilities. As a result, there is an increasing interest in numerically simulating such fluid-structure interactions.
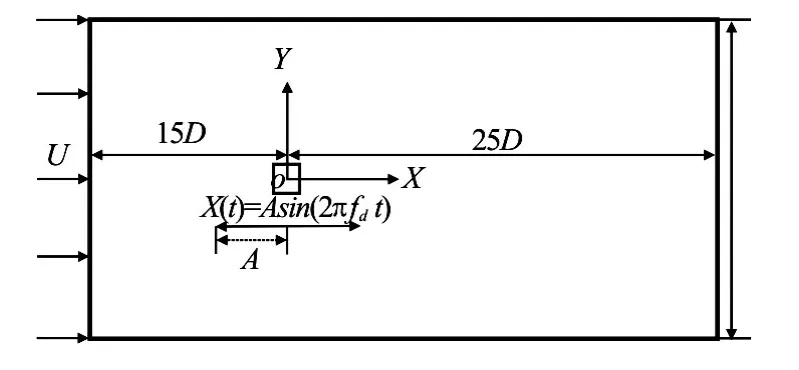
Fig.1 Sketch of computational domain for flow past an in-line oscillating square cylinder
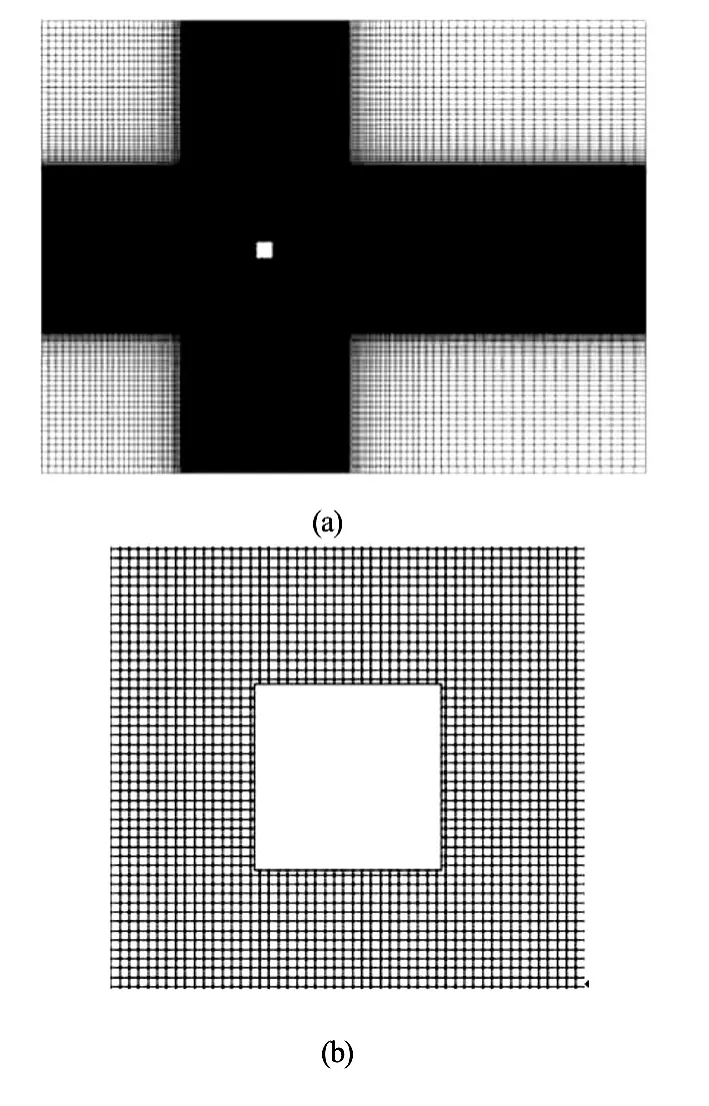
Fig.2 The computational mesh for flow past an in-line oscillating square cylinder
One of the greatest challenges in the simulation of the fluid-structure interaction is to deal with the moving solid boundaries in complex geometries, especially for large amplitude body motions. The traditio-nal boundary-fitted, unstructured finite-element method is usually adopted to treat movable structure boundaries. However, the grid generation and the remeshing calculation are required and they are timeconsuming. In this paper, a computational fluid dynamics (CFD) model is proposed under the Cartesian grid system to avoid the grid updating. In the model, an immersed boundary method[12]is adopted to treat the movable structure boundaries. Meanwhile, the fluidstructure interaction is treated as a multi-phase problem. To do so, the constraint interpolation profile/ CIP combined, unified procedure (CIP/CCUP)[13]is combined with the Cartesian grid system where the multi-phase problem is solved in one set of equations. The CIP method has been applied for water-body intraction problems of free surface flow[14,15]. In the present study, the CIP method is used for the study of the flow over oscillating square cylinders without free surface.
The objective of the present study is to extend the CIP-based method for investigating the vortex shedding and the lock-on phenomenon in the near-wake region of an oscillating square cylinder, characterized by a wide range of oscillation frequencies and large oscillation amplitudes.
1. Mathematical modeling
1.1Governing equations
The basic equations governing the incompressible fluid flow are the mass conservation equation and the Navier-Stokes momentum equations as
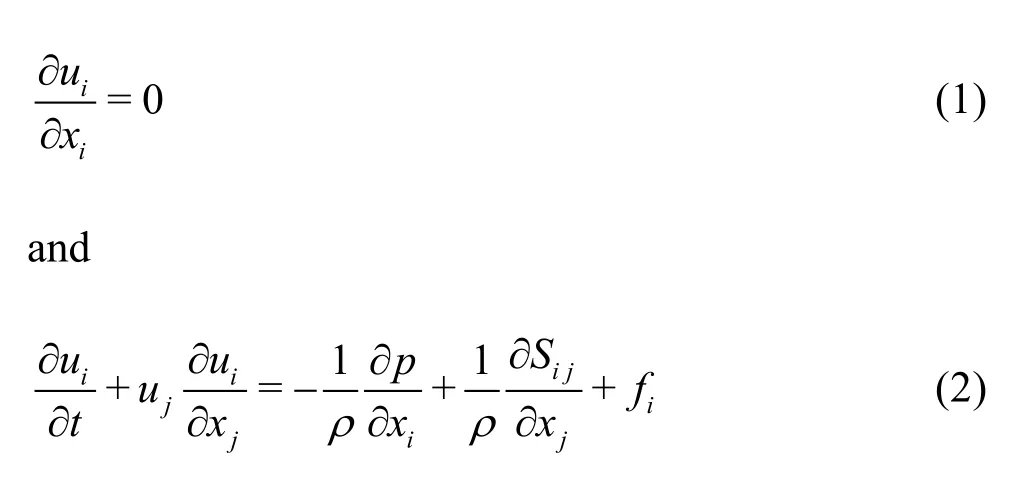
where the Cartesian tensor notation is used,(i=1,2),t,uj,pandxjare the time, the velocities, the hydrodynamic pressure and the spatial coordinates, respectively,firepresents the momentum forcing components, andSijis the viscous term given by

whereρandμare the density and the viscosity, respectively, appropriate for the phase that occupies the particular spatial location at a given instant.
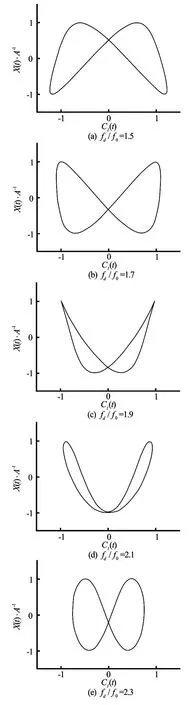
Fig.3 Lissajous patterns inside lock-on range atA/D=0.1
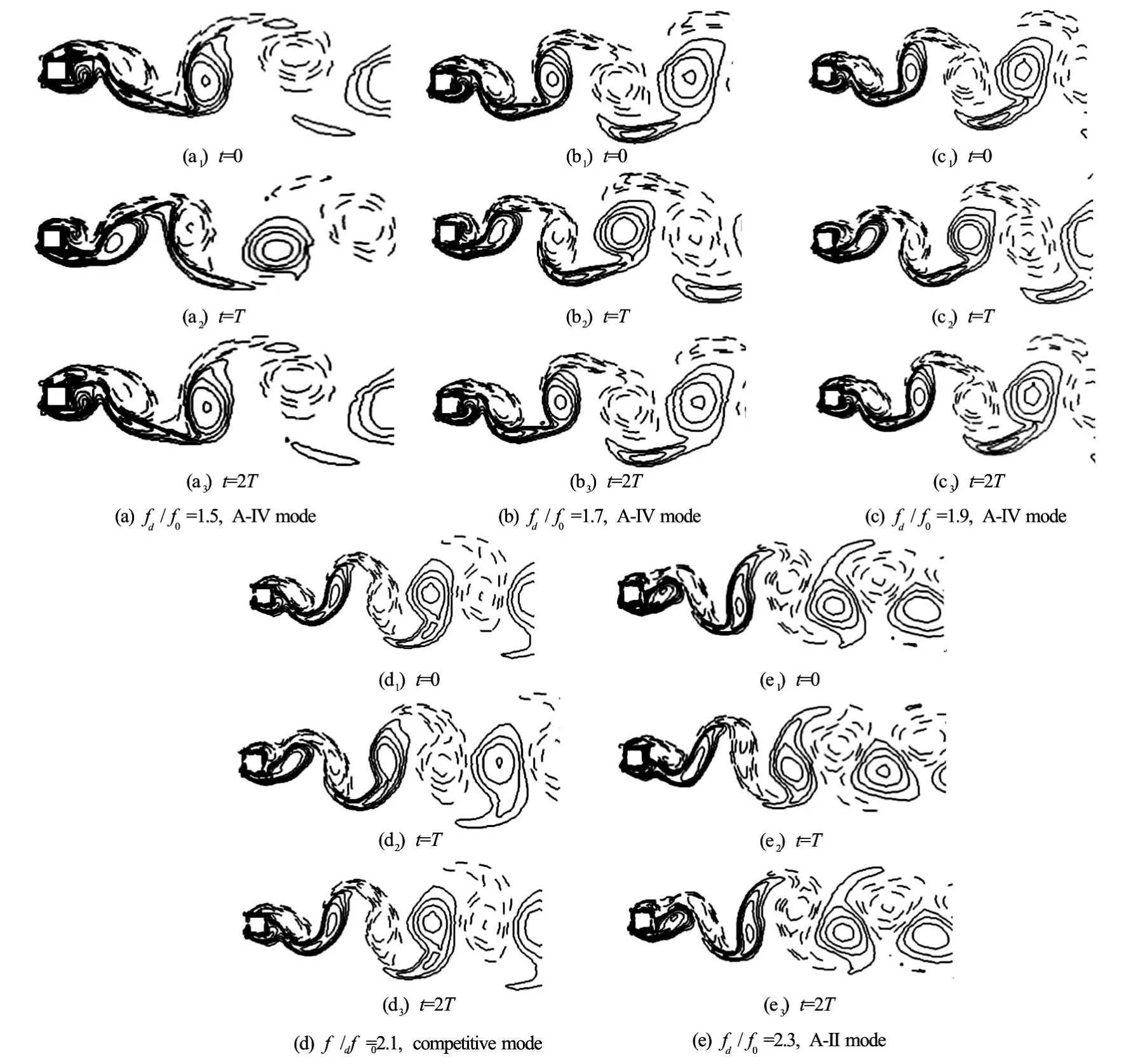
Fig.4 Vorticity contours in lock-on range over two periods of oscillation,2TatA/D=0.1,Re=200and different oscillation frequencies
In the numerical model, the fluid-body interaction is considered as a multi-phase problem including the fluid and the structure. A fixed Cartesian grid that covers the whole computation domain is used. A volume function (or the color function)φm(m=1 and 2 indicate the water and the solid, respectively) is defined to represent and track the interface. The total volume function for the water and the body is solved by using the following advection equation

Hereφ12=φ1+φ2. The density and the viscosity of the solid phase are assumed to be the same as those of a liquid phase to ensure stability. The volume function for the solid bodyφ2is determined by a Lagrangian method in which a rigid body is assumed. The volume function for the fluidφ1is then determined byφ1= 1.0?φ2. After all volume functions have been calculated, the physical propertyλ, such as the density and the viscosity, is calculated by the following formula.

More details can be found in the Refs.[15-17].
1.2Numerical methods
Following Zhao and Hu[16], the governing equations are discretized using a high-order finite difference method on a Cartesian grid system. A staggered grid configuration is used to discretize the dependent variables. The governing Eqs.(1) and (2) are solved using a fractional step scheme.
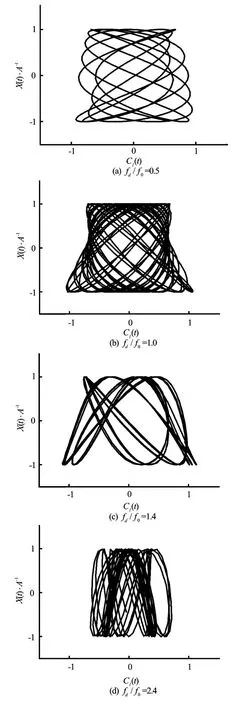
Fig.5 Lissajous patterns outside lock-on range atA/D=0.1 forfd/f0=0.5, 1.0, 1.4 and 2.4

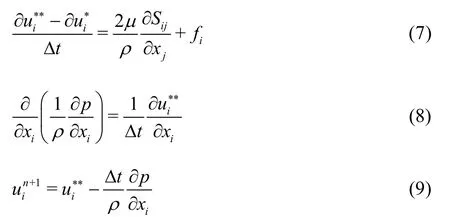
In the advection phase, the spatial derivatives of the velocities are needed in the CIP method[13]for this phase. In the first non-advection phase, the terms of diffusion and external forces are solved by the explicit method and the intermediate velocities are updated. In the final phase, the velocities are updated coupling with the pressure field.
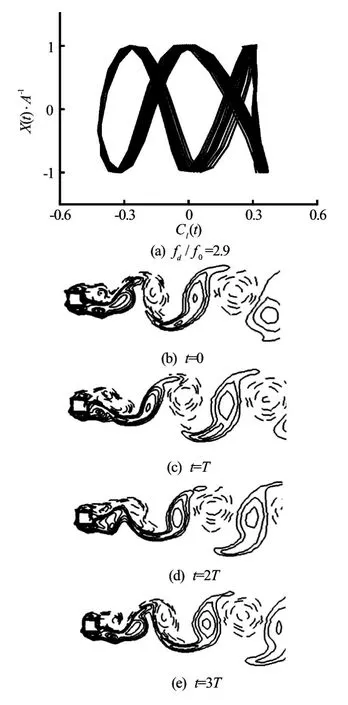
Fig.6 Lissajous patterns and vorticity contours in 3 periods atfd/f0=2.9 andA/D=0.1
To model the body motions, the fluid-structure interaction is coupled by using the fractional area volume obstacle representation (FAVOR) method. The FAVOR was shown to be one of the most efficient methods to treat the immersed solid bodies[17]. Theeffect of a moving solid body on the flow is included by imposing the velocity field of the solid body in the flow at the solid edge. The following equation is introduced to update the local information of the fluid domain covered by the body.

HereUbis the local velocity of the solid body andudenotes the flow velocity obtained from the fluid flow solver.Ub, the local velocity of the solid body, is tracked by a Lagrange method. By integrating the pressure on the body surface, the hydrodynamic forces on the body are first calculated. With the Newton’s law, the body accelerations and velocities are calculated. More details can be found in previous references[15-17].
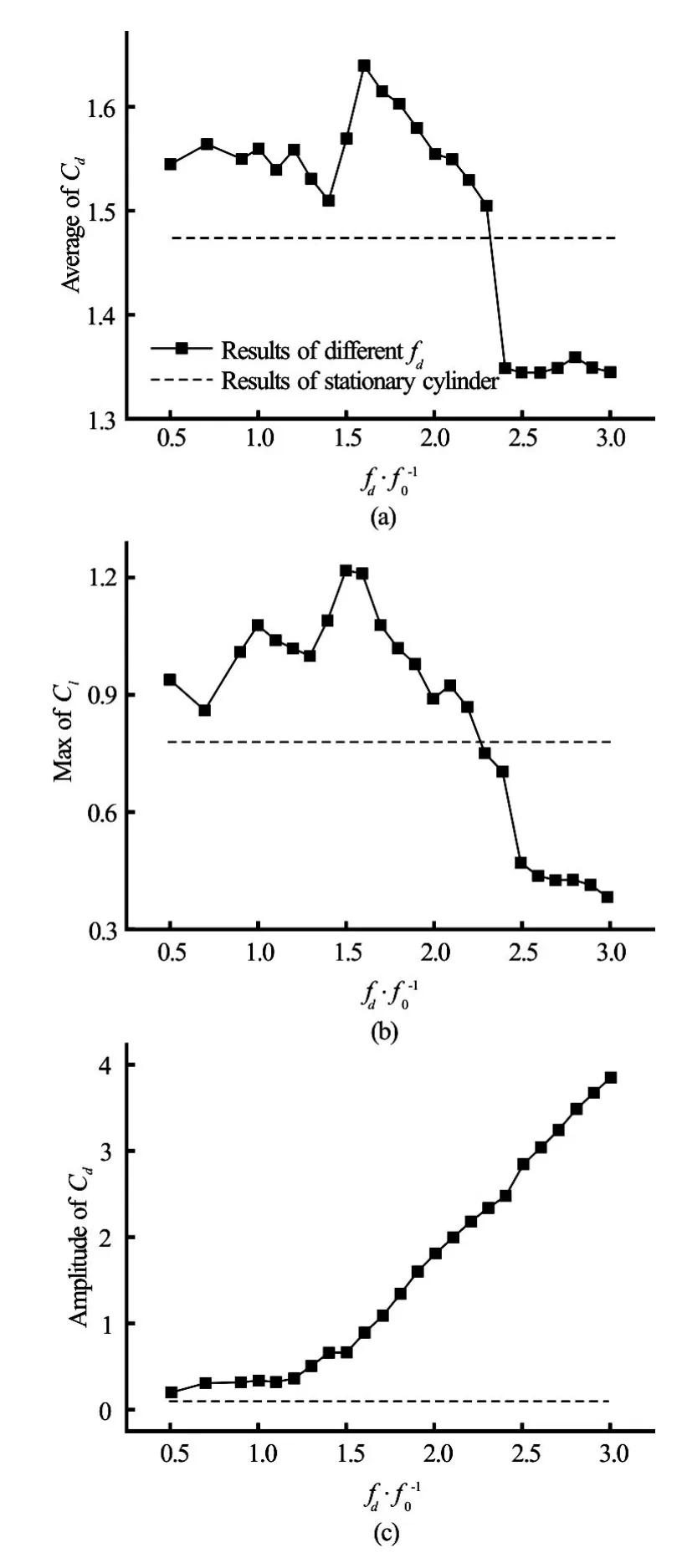
Fig.7 Mean values ofCd, maximum values ofCland the amplitudes ofCdversusfd/f0atA/D=0.1
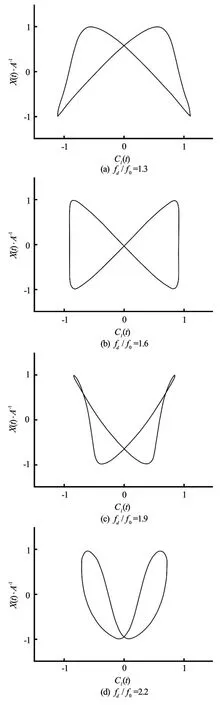
Fig.8 Lissajous patterns inside lock-on range atA/D=0.2 forfd/f0=1.3, 1.6, 1.9 and 2.2
1.3Definition of the parameters
The Reynolds number is defined asRe=ρUD/μ, whereρis the density of the liquid,Uis theinflow velocity,Dis the side length of the square cylinder andμis the dynamic viscosity coefficient.
The drag coefficient is defined asCd=2Fd/ρU2D, whereFdis the force on the cylinder along the inflow velocity.
The lift coefficient is defined asCl=2Fl/ρU2D, whereFlis the force on the cylinder perpendicular to the inflow velocity.
The Strouhal number is defined asSt=f0D/U.
2. Numerical results
2.1Flow past a fixed square cylinder
The convergence study is first performed for the flow past a stationary square cylinder at a low Reynolds number (Re=200)as a reference for further investigation. Three different non-uniform meshes are used with a minimum grid size ofΔx=Δy= 0.01D,0.03Dand 0.05D, respectively. Numerical results of the mean value of the drag coefficient(Cd) and the Strouhal number (St)are shown in Table 1 and compared with previous experimental and numerical results. It can be seen that the computation results converge fast and the results of Mesh 1 and Mesh 2 are in excellent agreements with both the experimental and numerical data in the existing literature. Thus mesh 2 is adopted in the following calculations.
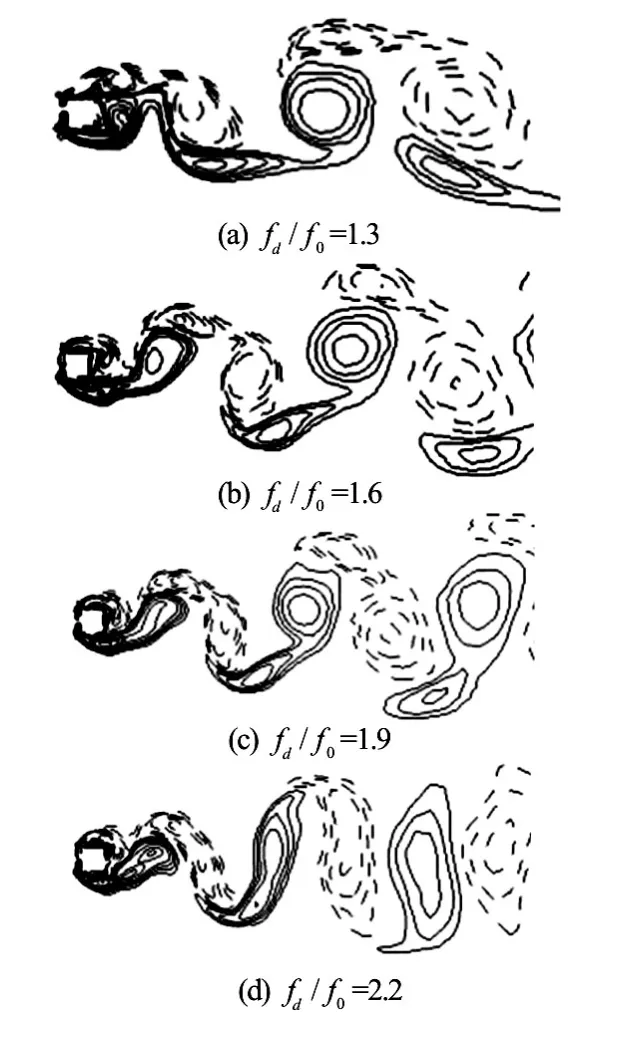
Fig.9 Vorticity contours atA/D=0.2forfd/f0=1.3, 1.6, 1.9 and 2.2
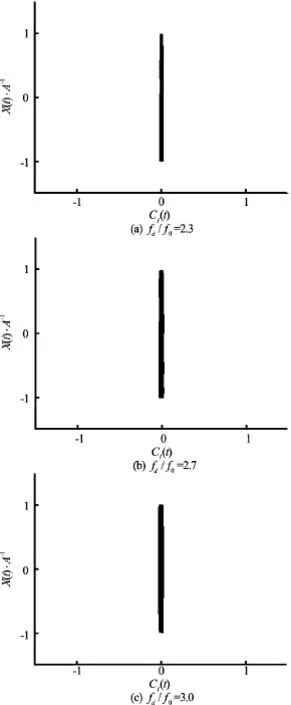
Fig.10 Lissajous patterns inside S mode atA/D=0.2forfd/f0=2.3, 2.7 and 3.0
2.2Flow past an oscillating square cylinder
In this section, the flow past an oscillating square cylinder is computed atRe=200. A computational domain of30D×40Dis employed, as shown in Fig.1 and the corresponding arrangement of the mesh is plotted in Fig.2. The inlet boundary is located15Dupstream the center of the square cylinder and the outlet boundary is25Ddownstream. The upper and lower boundaries are located15Daway from the horizontal centerline of the computational domain. On the inlet, the streamwise velocity is set to makeRe=200for the fixed squa re cylinder and the transverse velocity is equaltozero.On the outlet, a zero gradient boundarycondition is specified. The horizontal motion of the square cylinder is set asX(t)=Asin(2πfdt). Various oscillation amplitudes,A/D=0.1, 0.2, 0.3 and a wide range of oscillation frequencies,0.5≤fd/f0≤3.0 are used in the following computations.
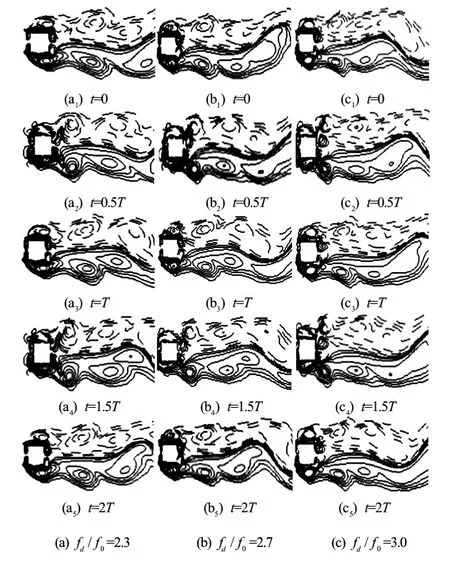
Fig.11 Vorticity contours of S mode atA/D=0.2forfd/f0=2.3, 2.7 and 3.0
2.2.1 AmplitudeA/D=0.1
The case for a small oscillation amplitudeA/D= 0.1 is firstly considered with different oscillation frequencies. The Lissajous patterns (X(t)/AversusCl(t)) are shown in Fig.3 for 1.5≤fd/f0≤2.3. It is clear that these curves show the phase-locked pattern over two cycles of the cylinder oscillation,2T(Tis the period of the oscillation, equal to 1/fd), which suggests that the near wake is in the lock-on in the range offd/f0=1.5-2.3. Figure 4 displays the corresponding vorticity contours forfd/f0=1.5, 1.7, 1.9, 2.1 and 2.3 in two periods of the cylinder oscillation. Positive contours are plotted in solid lines and negative contours in dashed lines. It can be seen that the contours at 0Tand 2Tin these cases are almost identical. The vortex shedding from the cylinder in the nearwake region is locked-on over two periods. From Figs.4(a)-4(c), it is observed that a strong and a weak vortex shed from each side of the cylinder. Consequently, it is locked to the anti-symmetric A-IV mode per 2Tfor 0.5≤fd/f0≤1.9. The second weaker vortex soon decays downward owing to the lower power. In Fig.4(d), two vortexes from each side of the cylinder of nearly the same size are formed atfd/f0=2.1and soon coalesced with each other to form the A-II mode. And it is the A-II mode completely in Fig.4(e). It is observed that the primary wavelength is decreasing, while the width of the vortex street increases firstly and then decreases. They are both influenced by the second weaker vortex during the mode transition.
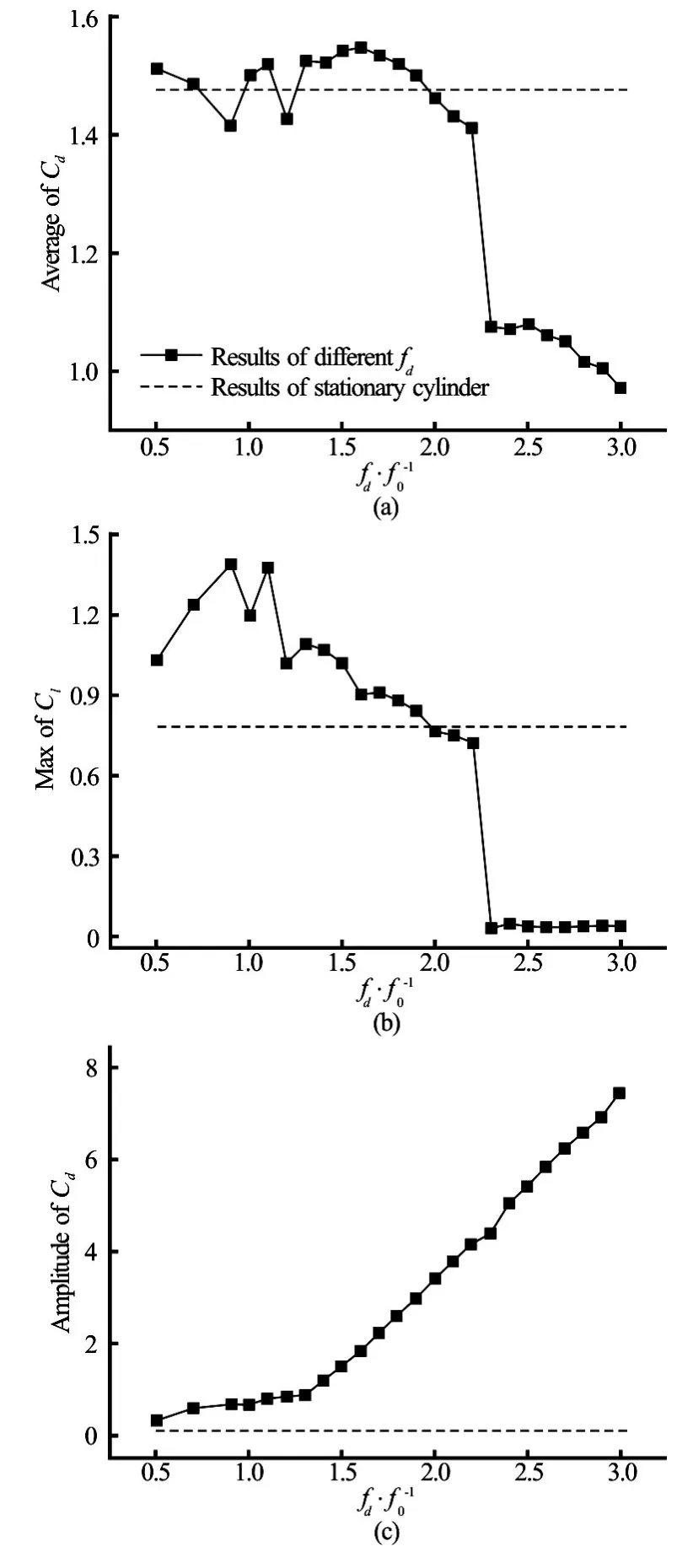
Fig.12 Mean values ofCd, maximum values ofCland amplitudes ofCdversusfd/f0atA/D=0.2
Figure 5 shows the Lissajous patterns atfd/f0=0.5 , 1.0, 1. 4, 2.4 outside the lock-on region. None of these curves shows a phase-locked form. Figure 6displays the Lissajous pattern and the corresponding vorticity contours forfd/f0=2.9in three oscillation periods. The motion of the cylinder andCl(t)are phase-locked again. The vorticity contours at 0Tand 3Tare nearly identical in the near-wake region. One vortex sheds from the upper side of the cylinder and simultaneously two shed from the lower side. This mode is referred as the anti-symmetricP+Smode every three oscillating periods,3T. It should be noted that this pattern is not observed for any other oscillating frequency. The effects of the oscillation frequency,fd/f0on the mean value of the drag coefficientCd, the maximum value of the lift coefficientCland the amplitude of the drag coefficientCdare plotted in Fig.7. The mean value of the drag coefficientCd, and the maximum value of the lift coefficientClshow a clear peak within the lock-on range, and decrease rapidly outside the synchronization region. The amplitude ofCddisplays a monotonic increase asfd/f0increases.

Fig.13 Lissajous patterns inside lock-on range atA/D=0.3 forfd/f0=1.2, 1.5, 1.8 and 2.1
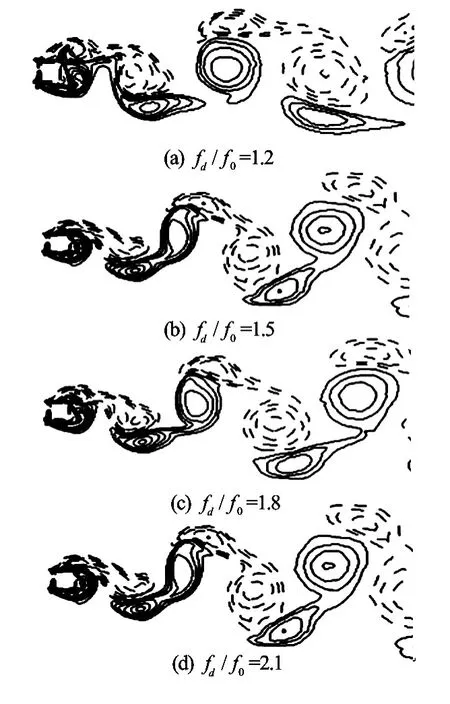
Fig.14 Vorticity contours atA/D=0.3forfd/f0=1.2, 1.5, 1.8 and 2.1
2.2.2 AmplitudeA/D=0.2
This section shows the results ofA/D=0.2andRe=200. The lock-on phenomenon appears atfd/f0=1.3, earlier than that whenA/D=0.1. Symmetric S mode does not appear untilfd/f0=2.3, which is not found for the case ofA/D=0.1. The Lissajous patterns within the lock-on range are plotted in Fig.8. A good phase-locked pattern is found in the range of 1.3≤fd/f0≤2.2. Figure 9 shows the vorticity contours forfd/f0=1.3, 1.6, 1.9, and 2.2 atT. It can be noticed that the A-IV mode of the vortex sheddingis observed atfd/f0=1.3, 1.6 and 1.9. However, the A-II mode is observed atfd/f0=2.2. The smaller vortex decays in the progression and coalesces with the larger vortex. Figure 10 displays the Lissajous patterns in the S mode at a larger oscillation frequency,fd/f0=2.3, 2.7 and 3.0. These figures reveal thatClis close to zero due to the symmetric S vortex shedding mode. The vorticity contours of the S mode atfd/f0=2.3, 2.7 and 3.0 are displayed in Fig.11. It can be seen that the vortex shedding is not alternative but simultaneous from each side of the cylinder with an opposite rotation. Take the flow velocity around the cylinder and the oscillating motion into account, ifRe≤50, the vortex will not shed from the cylinder but shed with the oscillation of the cylinder, just like the vortex shedding from a cylinder oscillating in the still fluid. It is also noted that the near-wake structures show an identical pattern per oscillation period,Tand the vortex street is very narrow again. Figure 12 shows the main force coefficients versusfd/f0. A significant reduction of the mean value ofCdand the maximum value ofClis observed in the S mode. However, the amplitude ofCdis not affected. It steadily increases asfd/f0increases.
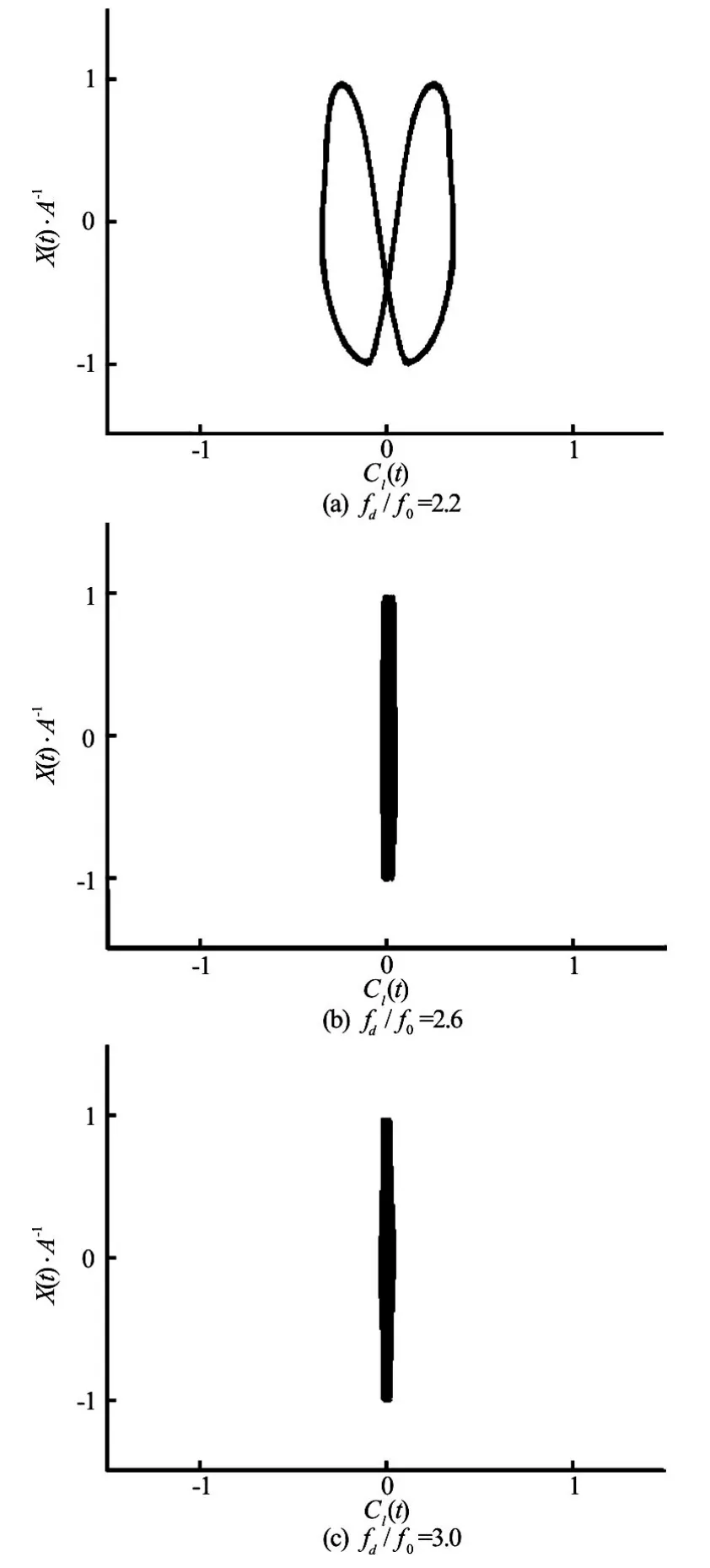
Fig.15 Lissajous patterns inside S modes atA/D=0.3forfd/f0=2.2, 2.6 and 3.0
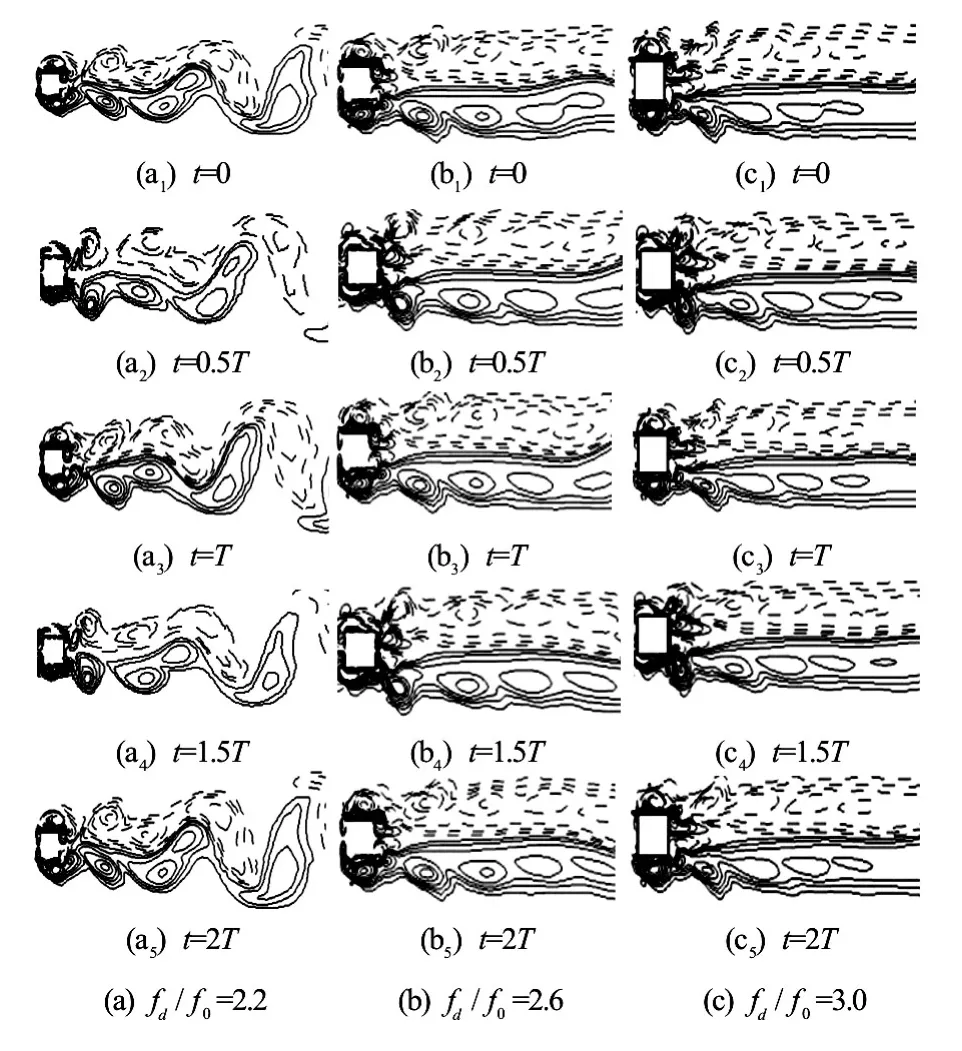
Fig.16 Vorticity contours atA/D=0.3forfd/f0=2.2, 2.6 and 3.0
2.2.3 AmplitudeA/D=0.3
The case of a larger oscillation amplitudeA/D= 0.3 is computed finally atRe=200. Numerical results show that the lock-on phenomenon appears atfd/f0=1.2, and the vortex shedding is transformed to the S mode atfd/f0=2.2. The Lissajous patterns are plotted in Fig.13 and the phase-locked status is clearly shown. Figure 14 displays the corresponding vorticity contours atTforfd/f0=1.2, 1.5, 1.8, and 2.1, respectively. It is observed that the second weaker vortex becomes larger and stronger with the increase of the frequencyfd/f0, and the lock-on anti-symmetric A-IV mode is observed. Figure 15 shows the Lissajous patterns in the S mode atfd/f0=2.2, 2.6 and 3.0, the corresponding vorticity contours are shown in Fig.16. The S mode begins to appear atfd/f0=2.2, as shown in Fig.16(a). One sees almost no difference at 0Tand 2T. However, the near-wake structures are already locked atT. Figs.16(b) and 16(c) show the stabilized symmetric S mode atfd/f0=2.6 and 3.0. It can be observed that a pair of vortices is shed from each side of the cylinder. Each of the strong vortices is established by a weak counterrotating secondary vortex on the centerline of the rear side, and the secondary vortex decays quickly downward after its formation. It is defined as the S-III mode by Srikanth et al.[10]. The formations of the primary vortex and the secondary weaker vortex have different mechanisms. The fluid near the cylinder is accelerated by the primary vortex, which leads to the formation of the boundary layer. With enough area available at the lee side of the cylinder, the vortices of opposite sign are generated. Figure 17 shows the results from the dynamic forces acting on the cylinder as a function of the oscillating frequencyfd/f0. The mean value ofCdand the maximum ofClappear to decrease atfd/f0≈2.0when the vortex shedding begins to be transformed from the A-IV mode to the A-II mode. The small vortex mergers with the primary vortex, and then decays rapidly as a result of the appearance of the symmetric S mode. The amplitude ofCdincreases monotonically asfd/f0increases.
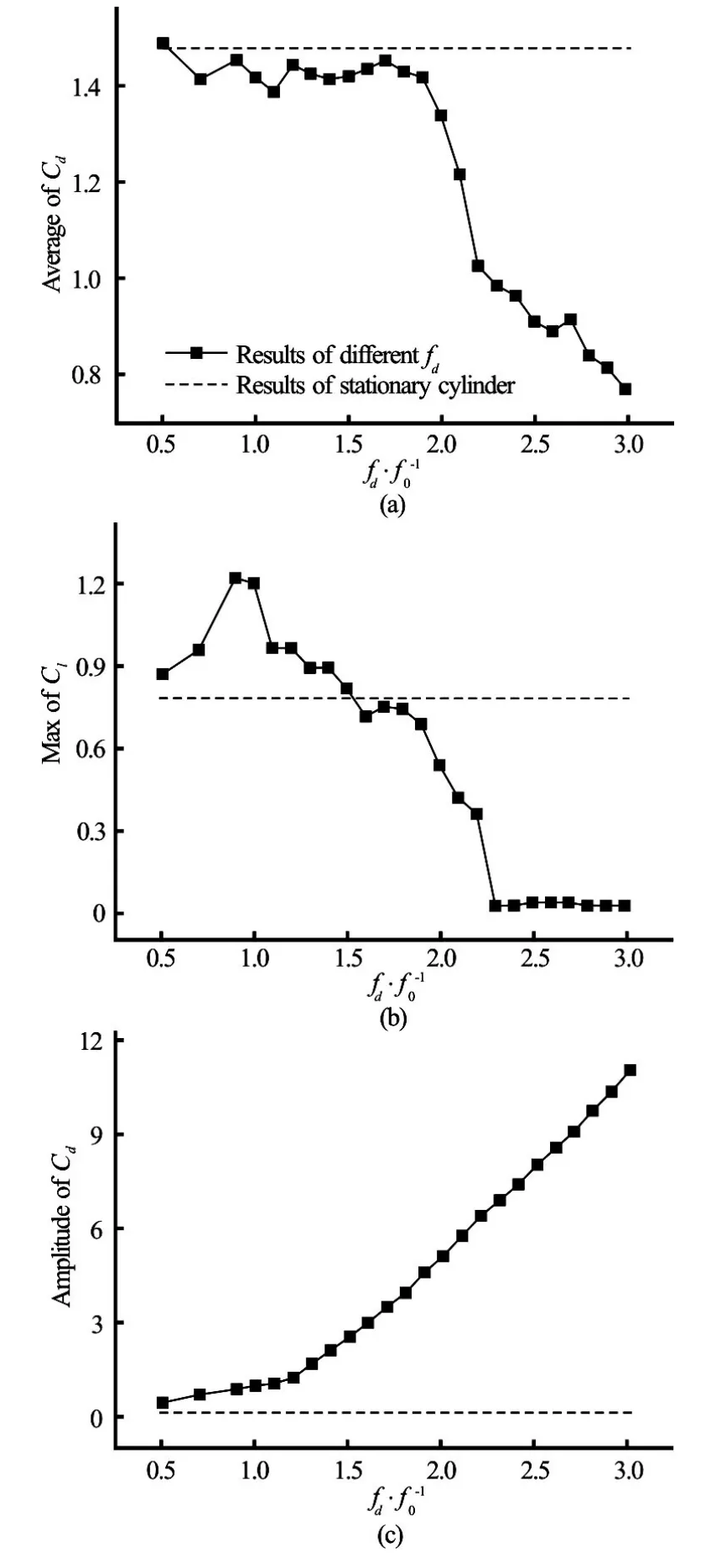
Fig.17 Mean values ofCd, maximum values ofCland amplitudes ofCdversusfd/f0atA/D=0.3
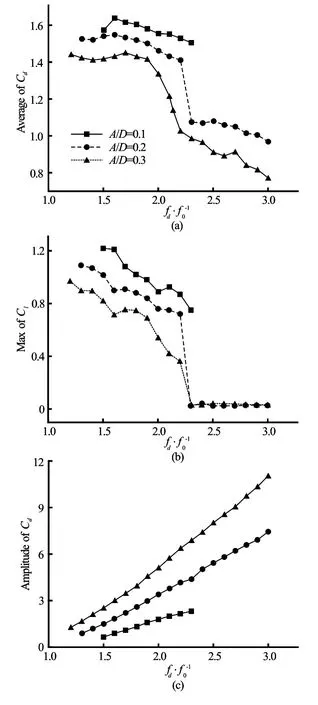
Fig.18 Mean values ofCd, maximum values ofCland the amplitudes ofCdversusfd/f0inside lock-on range
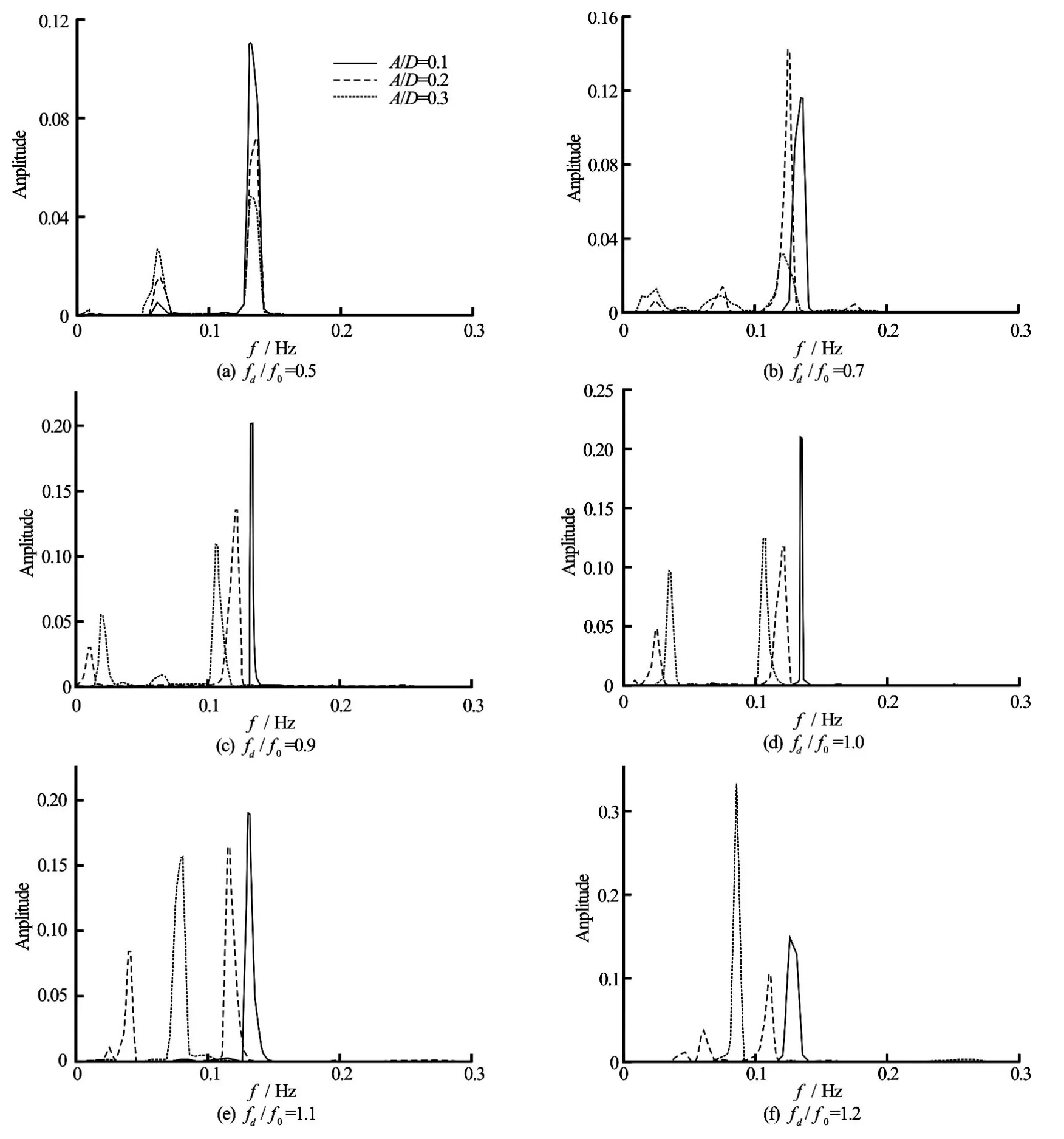
Fig.19 Comparison of primaries frequencies of lift coefficient outside lock-on range
2.2.4 Comparison of results atA/D=0.1, 0.2 and 0.3
Figure 18 displays the comparison of the mean value ofCd, the maximum value ofCland the amplitude ofCdat different oscillation amplitudes inside the lock-on range. It can be noticed that the force coefficients decrease with the increase of the oscillation amplitudes. Because of the existence of the S mode, the maximum value ofCldecreases to a value close to zero atA/D=0.2 and 0.3 at the back of the lock-on range. While the amplitude ofCdincreases monotonically independent of the lock-on range and the S mode. Figure 19 shows the comparison of the primary frequencies of the lift coefficient outside the lock-on range. Atfd/f0=0.5, the primary frequency is close to the natural frequency of the vortex shedding from a stationary cylinderf0and plays a dominant role, while for other oscillation frequencies, the primary frequencies differ from each other at various oscillation amplitudes and the difference increases with the increase of the oscillation frequency. The primary frequency is observed to decrease as the oscillation amplitude increases. The amplitude of the primary frequency is observed to show a significant increase atA/D=0.3, while atA/D=0.1 and 0.2, the variation of the amplitude of the primary frequency is not as distinct as that ofA/D=0.3.
3. Conclusion
A CIP-ZJU model is utilized in this paper, which is established in the Cartesian coordinate system, using the CIP method as the base flow solver to discretise the N-S equations. The fluid-structure interaction is treated as a multiphase flow with the fluid and solid phases solved simultaneously. An immersed boundary method is used to deal with the boundary of the solid body. The flow past a stationary square cylinder atRe=200is computed firstly to validate the method. Good agreements are obtained comparing with existing data in literature. Then a two-dimensional flow around an in-line oscillating square is numerically computed atRe=200, and different oscillation amplitudesA/D=0.1, 0.2, 0.3 and in a wide oscillation frequency range of0.5≤fd/f0≤3.0. Symmetric and anti-symmetric modes are obtained clearly. The P+S mode is observed atA/D=0.1forfd/f0=2.9, which cannot be obtained under any other conditions. The S-III mode is observed atA/D=0.3for highfd. The proposed CIP-based model can effectively and accurately resolve the nonlinear fluid-structure interactions. Progress in this direction will be reported later on.
[1] Wanderley J. B. V., Soares L. F. N. Vortex-induced vibration on a two-dimensional circular cylinder with low Reynolds number and low mass-damping parameter [J].Ocean Engineering, 2015, 97: 156-164.
[2] Zhao M., Cheng L. Vortex-induced vibration of a circular cylinder of finite length [J].Physics of Fluids, 2014, 26(1): 015111.
[3] Ongoren A., Rockwell D. Flow structure from an oscillating cylinder Part 2. Mode competition in the near wake [J].Journal of Fluid Mechanics, 1988, 191: 225-245.
[4] Al-Mdallal Q. M., Lawrence K. P., Kocabiyik S. Forced streamwise oscillations of a circular cylinder: Locked-on modes and resulting fluid forces [J].Journal of Fluids and Structures, 2007, 23(5): 681-701.
[5] Bai W. Numerical simulation of turbulent flow around a forced moving circular cylinder on cut cells[J].Journal of Hydrodynamics, 2013, 25(6): 829-838.
[6] Yokoi Y., Hirao K. The appearance of two lock-in states in the vortex flow around an in-line forced oscillating circular cylinder[C].EPJ Web of Conferences, 2014, 67(4): 02131.
[7] AL-MDALLAL Q. M. Numerical simulation of viscous flow past a circular cylinder subject to a circular motion [J].European Journal of Mechanics B/Fluids, 2014, 49: 121-136.
[8] Steggel N., Rockliff N. Simulation of the effects of body shape on lock-in characteristics in pulsating flow by the discrete vortex method [J].Journal of Wind Engineering, 1997, 69-71(5): 317-329.
[9] Chung Y. J., Kang S. H. A study on the vortex shedding and lock-on behind a square cylinder in an oscillatory incoming flow [J].JSME International Journal, 2003, 46(2): 250-261.
[10] Srikanth T., Dixit H. N., Rao T. et al. Vortex shedding patterns, their competition, and chaos in flow past inline oscillating rectangular cylinders [J].Physics of Fluids, 2011, 23(5): 1-9.
[11] Tudballsmith D., Leontini J. S., Sheridan J. et al. Streamwise forced oscillations of circular and square cylinders [J].Physics of Fluids, 2012, 24(20): 111703.
[12] Peskin C. S. Flow patterns around heart valves [J].Journal of Computational Physics, 1972, 10(2): 252-271.
[13] Yabe T., Xiao F., Utsumi T. The constrained interpolation profile method for multiphase analysis [J].Journal of Computational Physics, 2001, 169(2): 556-593.
[14] Ye Z., Zhao X., Deng Z. Numerical investigation of the gate motion effect on a dam break flow [J].Journal of Marine Science and Technology, 2016, 21(4): 579-591.
[15] Zhao X., Ye Z., Fu Y. Green water loading on a floating structure with degree of freedom effects [J].Journal of Marine Science and Technology, 2014, 19(3): 302-313
[16] Zhao X., Hu C. Numerical and experimental study on a 2-D floating body under extreme wave conditions [J].Applied Ocean Research, 2012, 35(1): 1-13.
[17] Zhao X., Ye Z., Fu Y. et al. A CIP-based numerical simulation of freak wave impact on a floating body [J].Ocean Engineering, 2014, 87: 50-63.
[18] Breuer M., Bernsdorf J., Zeiser T. et al. Accurate computation of the laminar flow past a square cylinder based on two different methods: Lattice-Boltzmann and finite-volume [J].International Journal of Heat and Fluid Flow, 2000, 21(2): 186-196.
[19] Liu T. C., Ge Y. J., Cao F. C. et al. Reynolds number effects on flow around square cylinder based on lattice Boltzmann method [C].Proceedings of the Fluid International Conference on Fluid Mechanics. Shanghai, China, 2007.
[20] Gera B., Pavan K. S., Singh R. K. CFD analysis of 2D unsteady flow around a square cylinder [J].International Journal of Applied Engineering Research, 2010, 1(3): 602-610.
* Project supported by the National Natural Science Foundation of China (Grant Nos. 51209184, 51479175 and 51679212), the Natural Science Foundation of Zhejiang Province (Grant No. LR16E090002).
Biography:Ying-nan Fu (1990-), Male, Master Candidate
Xi-zeng Zhao, E-mail: xizengzhao@zju.edu.cn
- 水動力學(xué)研究與進(jìn)展 B輯的其它文章
- Journal of Hydrodynamics, Vol. 28 Annual Classified Catalog (2016)
- Numerical study of the flow and dilution behaviors of round buoyant jet in counterflow*
- Numerical simulation of flow through circular array of cylinders using porous media approach with non-constant local inertial resistance coefficient*
- Numerical estimation of bank-propeller-hull interaction effect on ship manoeuvring using CFD method*
- Insoluble additives for enhancing a blood-like liquid flow in micro-channels*
- Entropy generation analysis for the peristaltic flow of Cu-water nanofluid in a tube with viscous dissipation*

