Observer-based leader-following tracking control under both fixed and switching topologies

Jinhuan WANG,Pengxiao ZHANG,Zhixin LIU,Xiaoming HU

1.School of Sciences,Hebei University of Technology,Tianjin 300130,China;

2.Key Laboratory of Systems and Control,Academy of Mathematics and Systems Science,Chinese Academy of Sciences,Beijing 100190,China;

3.Optimization and Systems Theory and ACCESS Linnaeus Center,Royal Institute of Technology,Stockholm 100 44,Sweden Received 27 November 2015;revised 17 December 2015;accepted 17 December 2015

Observer-based leader-following tracking control under both fixed and switching topologies

Jinhuan WANG1,Pengxiao ZHANG1,Zhixin LIU2,Xiaoming HU3?

1.School of Sciences,Hebei University of Technology,Tianjin 300130,China;

2.Key Laboratory of Systems and Control,Academy of Mathematics and Systems Science,Chinese Academy of Sciences,Beijing 100190,China;

3.Optimization and Systems Theory and ACCESS Linnaeus Center,Royal Institute of Technology,Stockholm 100 44,Sweden Received 27 November 2015;revised 17 December 2015;accepted 17 December 2015

Thispaperstudiesthetrackingproblemforaclassofleader-followermulti-agentsystemsmovingontheplaneusingobserverbased cooperative control strategies.In our set-up,only a subset of the followers can obtain some relative information on the leader.We assume that the control input of the leader is not known to any of the followers while the system matrix is broadcast to all the followers.To track such a leader,an observer-based decentralized feedback controller is designed for each follower and detailed analysis for the convergence is presented for both fixed and switching interaction topologies between agents with the method of common Lyapunov function.We can also generalize the result to the higher dimension case for fixed topology and some special system matrices of the leader for switching topology.

Multi-agent systems,leader-following,decentralized control,observer

1 Introduction

In recent years,there is a large amount of literature concerningthecoordinationproblemofmulti-agentsystems,such as consensus problem of communication networks[1,2],formation control of mobile robots[3],attitudecontrolofspacevehicles[4],andsoon,inwhich neighbor-based local rules are usually applied to each agent mainly based on the relative information between its own and its neighbors,e.g.,[1,2,5-9],to name a few.

In collective behaviors of multiple agents,the leaderfollower model has been an interesting topic[10-19],since it may have various applications.The leaders are those agents that know the desired trajectory or destination for the whole group,while the other agents(followers)simply follow the leaders using relative information obtained from their neighbors including possibly some of the leaders.In[10],for the sake of reaching consen-sus,the connectivity keeping problem was considered by computing the ratio of the numbers of leaders and followers.In[11],Li et al.considered the distributed tracking control problem of multiagent systems with general linear dynamics and a leader whose control input is bounded and not available to any follower.[12]studied the consensus for a leader-follower system with a varying-velocity leader and delay.Cao et al.considered the distributed containment control problem of a group of mobile autonomous agents with multiple leaders under both fixed and switching directed network topologies[13].

In practice,some state variables of agents(or even their leaders)may not be measured.In this case,decentralized observer design is needed for each agent.some estimation strategies have been proposed for multiagent systems with partial measurements and bounded disturbances.For example,Hong et al.proposed a neighbor-based observer to estimate the unmeasurable state variables of an active leader[14,15].Furthermore,Hu et al.developed a decentralized adaptive tracking control for the same system as in[15]with unknown dynamicsandrelativepositionmeasurements[16].In[17],the distributed observers were designed to estimate the velocity of the active leader and sampled-data controls were introduced in a disturbance environment.The robust consensus problem for second-order multi-agent systems with matched disturbances was studied in[20],in which a finite-time control technique was adopted to ensure that the virtual velocity can estimate the real velocity for each agent.In addition,some adaptive control protocols have been designed for multiagent systems subject to unknown disturbances.Some related literature can refer to[21-23],to name a few.

In this paper,we consider the tracking problem for a class of leader-follower multi-agent systems moving on the plane.Different from the existing results,in this paper,the control inputul=Alxl+blof the leader is unknown to any of the followers andAlcan be of any form,which allows the two state variables of the leader coupled.With a differentAlthat is known to the followers,the leader moves along a different trajectory.To track such a leader,we first estimate the control inputul,based on which a decentralized feedback controller is designed for each follower.Both the observer and the controller are based on local information only.We proved that the tracking problem can be solved if the adjacent graph of the system is switching and connected at any time interval.Moreover,this result can be generalized to the higher dimensional case for fixed topologyandsomespecialsystemmatricesoftheleader for switching topology.

We want to point out that our approach is partly motivated by applications from for example mobile robotics.A typical problem could be navigation in formation.It is reasonable to assume that in such a multi-agent system,only a few mobile robots are equipped with expensive sensors that can do both localization and path planning,while the rest of the robots only have on-board range sensors.With our approach what we aim to achieve is that once the parameters of the desired trajectory(for example,“we will move in a circle”)is broadcast to the followers,the trajectory will be tracked by all the follower robots using those onboard range sensors.

The rest of the paper is organized as follows.Section2 is our problem formulation.Sections3 and 4 are the main results.We deals with the tracking problem by constructing neighbor-based controller and observer under the fixed and switching interaction topology,respectively.In Section5,an illustrative example is given.Section6 is the conclusion.

2 Preliminaries and problem formulation

In this paper,we consider a system withNfollowers and one leader.The topology relationship of theNfollowers and the leader is described by a graphˉG.Assume the information transfer between followers is undirected(denoted by an undirected graph G),while the followers are connected to the leader by directed edges.The graphˉG is said to be connected if at least one agent in each component of graph G is connected to the leader by a directed edge[14].Note that graphˉG is connected does not mean graph G is also connected.The adjacency matrix of graph G is denoted by A=[αij] ∈ RN×N,where αii=0 and αij= αji≥ 0.αij＞ 0 if and only if there is an edge between agentiandjand the two agents are called adjacent(or they are mutual neighbors).The set of neighbors of agentiis denoted by Ni={j∈V:(i,j)∈,j≠i}.Define Δ =diag{α1,...,αN}as the leader adjacency matrix,where αi＞ 0 if the leader is a neighbor of agenti(that is,there is a directed edge from agentito the leader)and otherwise αi=0.

Define the LaplacianLwith respect to graph G as

where the diagonal matrixD=diag{d1,...,dN}∈ RN×Nis called degree matrix with the diagonal elementsdi=

By the definition,for an undirected graph,Lis symmetric and every row sum of it is zero.0 is an eigenvalue ofLand1Nis the associated eigenvector,that is,L1N=0,where1N=[1 1 ···1]T∈ RN.If G is connected,then 0 is the algebraically simple eigenvalue ofLand all the other eigenvalues are positive.

The following lemma,reported in[24],is very helpful to check the positive definiteness of a matrix.

Lemma 1(Schur complement)Suppose that a symmetric matrix is partitioned as

whereAandCare square.This matrix is positive definite if and only if bothAandC-ETA-1Eis positive definite.

In this paper,the dynamics of each follower is

wherexi∈R2is the state andui∈R2is the control input of thei-th follower.

The dynamics of the leader is

wherexl=[x1lx2l]T,ul∈R2are the state and the control of the leader,respectively.For simplicity,we choose

whereAl∈ R2×2,bl=[b1lb2l]Tcan be any matrix such that the leader can move along different trajectories.

To track the leader,uiis designed only by the relative information between itself and its neighbors.In our problem,ulis unknown to each follower.Therefore,it cannot be used in the control design.Instead,we have to estimateulin the evolution.The estimated value ofulby agentiis denoted by.

Remark1Insomesense,Alandbldenotetheshape and the translation of the leader’s trajectory,respectively.We assume thatAlandblare known to each agent,which means each follower may know the shape of the leader’s trajectory,but not the initial value.In fact,it is necessary to know the shape of the target’s trajectory in the tracking problem,according to the Internal Model Principle.

3 Tracking control under fi xed interaction topology

In this section,we consider the case when the adjacent topology is fixed.

Foreachfollower,weproposethefollowingneighborbased control law:

and the decentralized observer

whereK,Kl∈R2×2need to be determined,is the estimate ofxlby agenti,i=1,...,N.

Letthen associate with(2)and(3),we have the error closed-loop system

The control aim is to findK,Klsuch that all the followers can track the leader asymptotically and at the same time allconverge toul,that is,

Denotebyeandelthestacksofandrespectively.We have

where?denotes the Kronecker product,H:=L+Δ,Lis the Laplacian of graph G and Δ =diag{α1,...,αN}is the leader adjacency matrix of graphdefined in Section2.

Lemma 2[14]If graphis connected,then the symmetric matrixHassociated withis positive definite.

SinceHis symmetric,there is an orthogonal matrixTsuch that

is diagonal,where λi,i=1,...,Nare the eigenvalues ofH.By Lemma 2,if graphˉG is connected,all λi＞0.

Denote λmin=min{λi,i=1,...,N}the smallest eigenvalue ofH.Similar to Theorem 2 in[25],for the fixed adjacent graph case,we give the following result.

Theorem 1Consider the leader-follower multiagentsystem(2)and(3).Assumetheadjacentgraphis connected.ChooseKl=wherePis any symmetric positive definite matrix whose smallest eigenvalue δ is larger than the largest eigenvalue ρ of,then for anyAlandbl,all the followers can track the leader asymptotically via the decentralized feedback control(5)and the observer(6)and simultaneouslyconverge toulastgoes to infinity fori=1,2,...,N.

ProofBy the above analysis,we need to provewhich is equivalent to prove→0 and→0 since(11)is an orthogonal transformation.

Consider system(12)(or(13)).Construct the candidate Lyapunov function

Then the time derivative ofVialong the trajectory of each subsystem(13)is

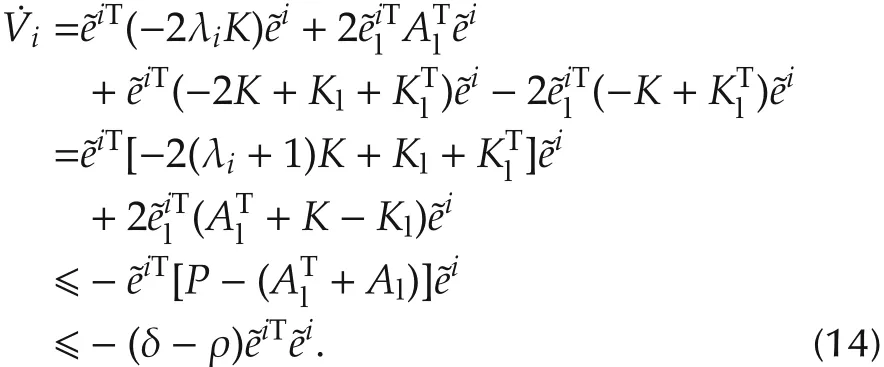
By the LaSalle’s invariance principle,the solution to system(12)converge to the largest invariant set contained in the setFrom=0 we have=0.Associated with system(12),we obtain the largest invariant set of the setis,which implies the conclusion. □

Remark 2From the proof of Theorem 1,the result of Theorem 1 is also true for any dimension ofAl∈ Rn×nandbl∈Rn.

4 Tracking control under switching interaction topology

Next,we consider the case when the topology structureoftheadjacentgraphistime-varyingandconnected.

In time-varying topology case,we define the switching signal σ(t):[0,+∞) → P={1,2,...,m}which is a piecewise constant right continuous function.A switched system is said to have a non-vanishing dwell time,if there is a positive time period τ＞0,such that the switching moments 0＜t1＜...＜tk＜...,satisfy

De fi nition 1For a switched linear system

where the switching signal σ(t)is defined above.If there exists a quadratic functionV(x)=xTPxwith positive definite matrixP＞0 and satifying the following property

thenV(x)(or briefly,P)is called a common quadratic Lyapunov function(CQLF)of system(15).

In this paper,we assume that

A1)Admissibleswitchingsignals haveapositive dwell time τ＞0.

A2)The adjacent graph is switching and connected at any time.

Then the control law(5)and the observer(6)are changed into

where the neighbor set Ni(t)of agentiis time-varying.For simplicity,we assume the weights of all the interaction links are time-invariant.That is,when agentj∈ Ni(t),the weight αij(t)= αij＞ 0 is a constant.Similarly,αi(t)= αi＞ 0 is also a constant once agentiis connected to the leader.

Similar to last section,still letand denoteeandelthe stacks ofrespectively.Then the error system becomes

whereHσ(t)=Lσ(t)+ Δσ(t),Lσ(t)is the Laplacian of the graph Gσ(t)and Δσ(t)is its leader adjacency matrix.

Now for each subsystem of(19)by the orthogonal transformation

fori=1,...,N,p∈P,whereTpis an orthogonal matrix such thatdiagonal,andare the eigenvalues ofHp.

Note that system(21)is a switched system.The common Lyapunov function method is a useful tool for stability analysis of switched systems.But it is difficult to construct a common Lyapunov-like function for system(21).Moreover,the control aim is to findKandKlsuch thatas timet→ +∞.From the analysis of last section,we can see that system(21)(and system(9)for the fixed topology case)is not stabilized unless the matrixAlis nonsingular.

Next,we will analyze the tracking problem for different structure ofAl.Since all possible cases of matrixAlwill be considered,by the similarity transformation we transformAlinto the Jordan canonical form,whereSis nonsingular matrix.

Notethatthecoordinatetransformationkeepsthestability unchanged.Hereafter,without loss of generality,we assume that the matrixAlis already in the Jordan canonical form.

According to the eigenvalues ofAl,we will discuss the following six cases.

Case 1A trivial case:Al=0 ∈ R2×2,thenul=bl.The leader moves with the constant velocitybl,which is the same as in[1],[6]and[7],etc.In this case,we do not need to estimateuland just choose the control

Infact,choosethecommonLyapunovfunctionV(t)=eT(t)e(t),then the derivative ofValong the trajectory of system(25)is

for any positive definite matrixK＞0.

Case 2Alhas two positive(real part)eigenvalues.

SinceAlhas two positive(real part)eigenvalues(called anti-stable),there is a unique positive definite matrixP1∈ R2×2satisfying the Lyapunov equation

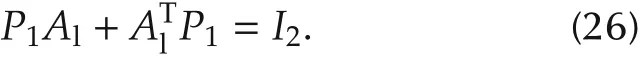
For any connected graph Gp,define

Proposition 1Consider system(2)and(3).Assume Assumptions A1 and A2 hold and the system matrixAlhas two positive(real part)eigenvalues.ChooseK=kAlandKl=γkAl,wherek,γ∈R satisfy

whereP1is the solution to the Lyapunov equation(26)and ‖·‖2denotes the matrix 2-norm.Then system(22)is asymptotically stable.Hence all the followers can track the leader asymptotically via the decentralized feedback control(17)and the observer(18)and simultaneouslyconverge toulfori=1,2,...,N.

ProofSetK=kAlandKl= γkAlwithk＞ 0,γ ＞ 0.Then the system matrix of(22)becomes

where

due to(26).

By Lemma 1,is positive definite if and only if bothanyp∈P.Then by virtue of(28),is positive definite,which shows thatVis a common Lyapunov function.The conclusion is true. □

Corollary 1ForAlwith both negative(real part)eigenvalues case,the conclusion of Proposition 1 is also true,if γ andksatisfy

whereP1∈ R2×2is the unique positive definite matrix solution to the Lyapunov equation

Infact,wechoosethesamePasintheproofofProposition 1,butP1satisfies(30)sinceAlis stale.

Remark 3The method in Case 2 is independent of thedimensionofAl.Therefore,theresultsofProposition 1 and Corollary 1 can be generalized to any dimension ofAl∈ Rn×nandbl∈ Rn.

Case 3Alhas one positive and one negative eigenvalues.

Under the Jordan canonical form,σ1＜ 0＜ σ2.In this case,we chooseK=diag{k1,k2}andKl=diag{γk1,μk2}.Then the error system(22)becomes

fori=1,...,N,?p∈P,which can be further rewritten to two separate systems

Denote the system matrix of system(32)by=For system(32),choose the common

quadraticLyapunovfunctionasP=then

is positive definite if and only if both γk1＞ 0 and0 for anyp∈ P.

Note that σ1＜ 0,then we can get 0 ＜ γ ＜ 1 andHence system(32)is asymptotically stable.Similarly,for system(33),we can choose the common quadratic Lyapunov function asPwith μ ＞ 0.A similar calculation gets that system(33)is asymptotically stable if μ＞1

Now,we summarize the above analysis as follows.

Proposition 2Assume Assumptions A1 and A2 hold and under the Jordan canonical form,with σ1＜ 0 ＜ σ2.ChooseK=diag{k1,k2}andKl=diag{γk1,μk2},wherek1,k2,γ,μ ∈ R satisfy

Then system(22)is asymptotically stable,that is,all the followers can track the leader asymptotically via the decentralized feedback control(17)and the observer(18)and simultaneouslyconverge toulfori=1,2,...,N.

Case 4Alhas one zero and one positive(negative)eigenvalues.

whereHσ(t)=Lσ(t)+ Δσ(t).

Then we have

Proposition3Assume Assumptions A1 and A2 hold and0.Under the control law(17)and the observer(36)withK=kI2satisfying

Then system(37)is asymptotically stable.

ProofThe stability ofe1is obvious under the Assumptions A1 and A2.We only need to consider the last two equations of(37),that is,

Under Assumption A2,is positive definite if and only if γkHp＞ 0 andanyp∈ P.One can see thatγ＞1 assure＞0.Hence system(37)is asymptotically stable. □

Corollary 2If σ ＜0,the conclusion of Proposition3 is also true,if choose

Case 5Alhas two zero eigenvalues.

In this case,the Jordan canonical form ofAlisTherefore,we just need to estimatex2l.Choose the control law the same as in(17)withK=kI2and the reduced-order decentralized observer

where γ ＞0,k＞0,is the estimate ofx2lby agenti.Using the same notations as in Case 4,the error system is

If system(42)is asymptotically stable,we are done.

Proposition 4Assume Assumptions A1 and A2 hold andUnder the control law(17)and the observer(41)withK=kI2satisfying

Then system(42)is asymptotically stable.

ProofThe stability ofe2is obvious under the Assumptions A1 and A2.We only need to consider the first and the last equations of(42),that is,γ＞0,then

Case 6Alhas a pair of pure imaginary eigenvalues.

Proposition 5AssumeAssumptions A1 and A2 hold and the system matrixChoosewhere γ,k∈ R satisfy

Then,system(21)is asymptotically stable,that is,all the followers can track the leader asymptotically via the decentralized feedback control(17)and the observer(18)and simultaneouslyconverge toulfori=1,2,...,N.

ProofSince,the system matrix of(21)is denoted by

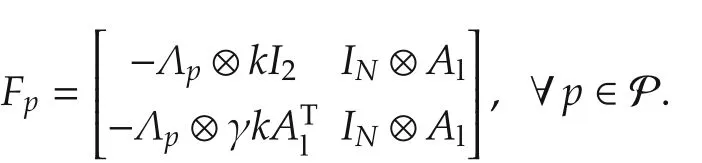
ConstructtheCQLFofsystem (21)asP=Sinceby Lemma 1,it is not difficult to see thatPis positive definite for any

Note that=0,then

By Lemma 1,Qpis positive definite if and only if bothfor anyp∈P.Under AssumptionsA1andA2,Q＞0isobviousif0By a straightforward computation,

To summarize,we have the following result:

Theorem 2Consider the leader-follower multiagent system(2)and(3).Under Assumptions A1 and A2,for any matricesAlandbl,there existKandKlsuch that all the followers can track the leader asymptotically via the decentralized feedback control(17)and the observer(18)and,simultaneously,the observed valueconverge toulastgoes to infinity fori=1,2,...,N.Specifically,

1)forAl=0,the controller is degenerated to(24)with any positive definite matrixK＞0;

2)if the eigenvalues ofAlare both positive(real part),chooseK=kAl,Kl= γkAlwithkand γ satisfying(28)(or(29)for the negative case);

Remark 4For the switching topology case,we assumeAl∈ R2×2and construct the common Lyapunov function case by case.This method is difficult for highdimensional systems.Hence we do not generalize the results to higher dimension case except Case 2.

5 Illustrative example

Finally,we give an example to validate the theoretical results.

Example 1Consider a leader-follower multi-agent system with 4 followers satisfying system(2)and(3)with

Assume the interaction topology between agents is time-varying.Three possible adjacent graphs denoted by(with a leader labeled 0)are given in Fig.1.For simplicity,assume the switching signal σ(t)is periodic and the period is 1 second.The interconnection graphs are switched according to

Fig.1 Possible interaction topologies between agents.(a).

The Laplacian of graphs G1,G2,G3(without leader)are

and the leader adjacency matrices are

The smallest eigenvalue ofHp=Lp+Δp,p=1,2,3 is λmin=0.1206.

TakeK=where γ,ksatisfy(45).Chooseandk=12,then by the observer-based feedback control(17)and(18),the tracking problem is solved.Refer to Fig.2 for the simulation result with the initial values

All four trajectories converge to a common circle which is the trajectory of the leader.Fig.3 shows that all the followers can track the leader eventually.Fig.4 shows that the estimated valueby agentiwill converge toxl. □

Fig.2 The trajectories of four followers and one leader.

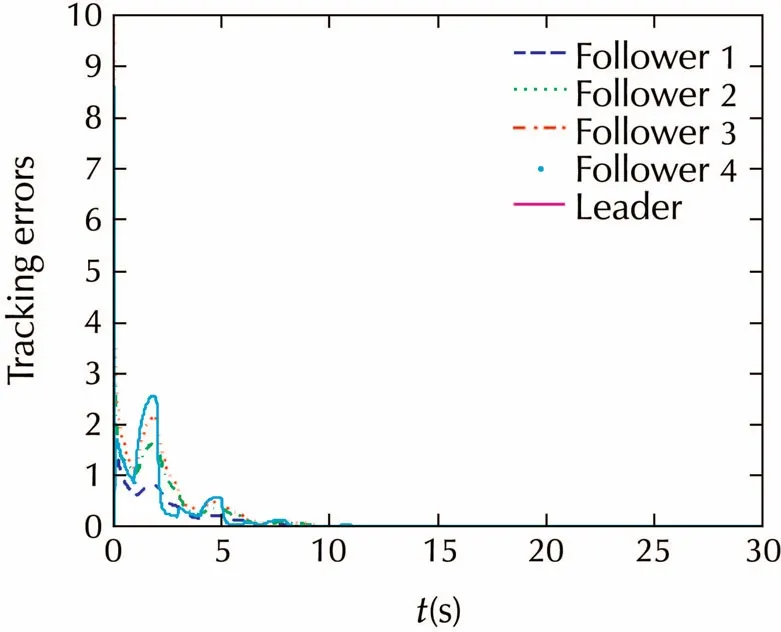
Fig.3 The tracking errors of four followers.

Fig.4 The estimate errors:,i=1,2,3,4.

6 Conclusions

In this paper,the tracking problem for leader-follower multi-agent systems was considered.We allow the two state variables of the leader to be coupled,which is different from many existing results.The control inputulof the leader is further to be assumed unknown to the followers even if they are connected to the leader.To track such a leader,we first constructed a neighbor-based observer to estimate the controlul,based on which a local feedback controller was designed for each follower.We proved that the tracking problem can be solved if the adjacent graph of the system is switching and connected at any time interval.

This paper just considered the case that all the agents will track the leader asymptotically,regardless of the collision problem.Further research will focus on the true platooning problem.By designing appropriate controller,all the agents move along the same trajectories but keep certain distance to avoid collision.

[1]A.Jadbabaie,J.Lin,A.S.Morse.Coordination of groups of mobile autonomous agents using nearest neighbor rules.IEEE Transactions on Automatic Control,2003,48(6):998-1001.

[2]R.Olfati-Saber,R.Murray.Consensus problems in networks of agentswithswitchingtopologyandtime-delays.IEEETransactions on Automatic Control,2004,49(9):1520-1533.

[3]M.Guo,M.Zavlanos,D.Dimarogonas.Controllingthe relative agent motion in multi-agent formation stabilization.IEEE Transactions on Automatic Control,2014,59(3):820-826.

[4]S.Weng,D.Yue,T.Yang.Coordinated attitude motion control of multiple rigid bodies on manifold SO(3).IET Control Theory and Applications,2013,7(16):1984-1991.

[5]W.Ren.On consensusalgorithmsfordouble-integrator dynamics.IEEE Transactions on Automatic Control,2008,53(6):1503-1509.

[6]Y.Hong,L.Gao,D.Cheng,et al.Coordination of multiagent systems with varying interconnection topology using common Lyapunovfunction.IEEETransactionsonAutomaticControl,2007,52(5):943-948.

[7]D.Cheng,J.Wang,X.Hu.An extension of LaSalle’s invariance principle and its application to multi-agent consensus.IEEE Transactions on Automatic Control,2008,53(7):1765-1770.

[8]H.Shi,L.Wang,T.Chu.Flocking of multi-agent systems with a dynamic virtual leader.International Journal of Control,2009,82(1):43-58.

[9]G.Shi,K.Johansson,Y.Hong.Reaching an optimal consensus:dynamical systems that compute intersections of convex sets.IEEE Transactions on Automatic Control,2013,58(3):610-622.

[10]T.Gustavi,D.Dimarogonas,M.Egerstedt,et al.Sufficient conditions for connectivity maintenance and rendezvous in leader-follower networks.Automatica,2010,46(1):133-139.

[11]Z.Li,X.Liu,W.Ren,et al.Distributed tracking control for linear multiagent systems with a leader of bounded unknown input.IEEE Transactions on Automatic Control,2013,58(2):518-523.

[12]K.Peng,Y.Yanga.Leader-following consensus problem with a varying-velocity leader and time-varying delays.Physica A,2009,388(2/3):193-208.

[13]Y.Cao,W.Ren,M.Egerstedt.Distributed containment control with multiple stationary or dynamic leaders in directed networks.Automatica,2012,48(8):1586-1597.

[14]Y.Hong,J.Hu,L.Gao.Trackingcontrolformulti-agentconsensus with an active leader and variable topology.Automatica,2006,42(7):1177-1182.

[15]Y.Hong,G.Chen,L.Bushnell.Distributed observers design for leader-following control of multi-agent networks.Automatica,2008,44(3):846-850.

[16]J.Hu,W.Zheng.Adaptive tracking control of leader-follower systems with unknown dynamics and partial measurements.Automatica,2014,50(5):1416-1423.

[17]Y.Cheng,D.Xie.Distributed observer design for bounded tracking control of leader-follower multi-agent systems in a sampled-data setting.International Journal of Control,2014,87(1):41-51.

[18]W.Ni,D.Cheng.Leader-following consensus of multi-agent systems under fixed and switching topologies.Systems&Control Letters,2010,59(3/4):209-217.

[19]X.Lu,R.Lu,S.Chen,et al.Finite-time distributed tracking control for multi-agent systems with a virtual leader.IEEE Transactions on Circuits and Systems-I:Regular Papers,2013,60(2):352-362.

[20]H.Du,S.Li,P.Shi.Robust consensus algorithm for second-order multiagent systems with external disturbances.International Journal of Control,2012,85(12):1913-1928.

[21]H.Yu,X.Xia.Adaptive consensus of multi-agents in networks withjointlyconnectedtopologies.Automatica,2012,48(8):1783-1790.

[22]H.Bai,M.Arcak,J.Wen.Adaptive design for reference velocity recoveryinmotioncoordination.Systems&ControlLetters,2008,57(8):602-610.

[23]A.Das,F.Lewis.Distributed adaptive control for synchronization of unknown nonlinear networked systems.Automatica,2010,46(12):2014-2021.

[24]R.Horn,C.Johnson.Matrix Analysis.New York:Cambbridge University Press,1985.

[25]L.Wang,J.Markdahl,X.Hu,et al.High level decentralized tracking algorithm for three manipulators subject to motion constraints.Proceedings of the 10th World Congress on Inteligent Control and Automation,Beijing:IEEE,2012:1920-1924.

DOI10.1007/s11768-016-5121-y

?Corresponding author.

E-mail:hu@kth.se.

This work was supported by the National Natural Science Foundation of China(Nos.61203142,61304161),the Natural Science Foundation of Hebei Province(Nos.F2014202206,F2015202231).

Jinhuan WANGwas born in 1980 in Shandong Province,China.She received the B.Sc.and M.Sc.degrees from School of Mathematical Sciences,Shandong Normal University,in 2002 and 2005,respectively,and the Ph.D.degree from Academy of Mathematics and Systems Science,Chinese Academy of Sciences in 2008.She is currently an associate professor of School of Sciences,Hebei University of Technology.Her research interests include complex systems control and switched systems.E-mail:jinhuan@hebut.edu.cn.

Pengxiao ZHANGwas born in 1992 in Hebei Province,China.She received the B.Sc.degree in Mathematics from Tianjin Normal University in 2014.She is currently a postgraduate student in Hebei University of Technology.Her research interest is multi-agent systems.E-mail:821319896@qq.com.

the B.Sc.degree in Mathematics from Shandong University,in 2002,and the Ph.D.degree in Control Theory from Academy of Mathematics and Systems Science(AMSS),Chinese Academy of Sciences(CAS)in 2007.She is currently an associate professor of AMSS,CAS.From February 2009 to April 2009,she was with Royal Institute of Technology,Sweden,as a visiting researcher.Her current research interests are complex systems and multi-agent systems.E-mail:lzx@amss.ac.cn.

Xiaoming HUwas born in Chengdu,China,in 1961.He received the B.Sc.degree from University of Science and Technology of China in 1983.He received the M.Sc.and Ph.D.degrees from Arizona State University,in 1986 and 1989,respectively.He served as a research assistant at the Institute of Automation,the Chinese Academy of Sciences,from 1983 to 1984.From 1989 to 1990 he was a Gustafsson Postdoctoral Fellow at the Royal Institute ofTechnology,Stockholm,whereheiscurrentlyafullprofessorofOptimization and Systems Theory,and a vice director of the Center for Autonomous Systems.He is leading or participating in many research projects sponsored by EU,the Swedish Research Council,the Swedish Strategic Research Foundation,and the Swedish Defense Institute.His mainresearchinterests areinnonlinearcontrolsystems,nonlinearobserver design,sensing and active perception,motion planning,control of multi-agent systems,and mobile manipulation.E-mail:hu@kth.se.