GLOBAL FINITE ENERGY WEAK SOLUTION TO THE VISCOUS QUANTUM NAVIERSTOKES-LANDAU-LIFSHITZ-MAXWELL MODEL IN 2-DIMENSION?
Boling Guo(Institute of Applied Physics and Computational Math.,China Academy of Engineering Physics,Beijing 100088,PR China)Guangwu Wang(Graduate School of China Academy of Engineering Physics,Beijing 100088,PR China)
GLOBAL FINITE ENERGY WEAK SOLUTION TO THE VISCOUS QUANTUM NAVIERSTOKES-LANDAU-LIFSHITZ-MAXWELL MODEL IN 2-DIMENSION?
Boling Guo
(Institute of Applied Physics and Computational Math.,China Academy of Engineering Physics,Beijing 100088,PR China)
Guangwu Wang?
(Graduate School of China Academy of Engineering Physics,Beijing 100088,PR China)
In this paper,we prove the global existence of the weak solution to the viscous quantum Navier-Stokes-Landau-Lifshitz-Maxwell equations in two-dimension for large data.The main techniques are the Faedo-Galerkin approximation and weak compactness theory.
global finite energy weak solution;viscous quantum Navier-Stokes-Landau-Lifshitz-Maxwell system;Faedo-Galerkin method
2000 Mathematics Subject Classification35A01;35D30;35M31; 35Q40;35Q61
1 Introduction
In studying the dispersive theory of magnetization of ferromagnets,we also consider the viscous quantum of a fluid on motion under the Maxwell electric-magnetic field,that is,the macroscopic motion of a fluid and the quantum effects and the interactions between electrons in microscopic will be considered similarly.
In this paper we study the viscous quantum Navier-Stokes-Landau-Lifshitz-Maxwell system (QNSLLM) in (0,T) ×?:

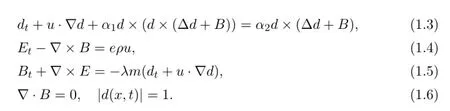
Roughly speaking,system (1.1) - (1.6) is a coupling between the viscous isentropic quantum Navier-Stokes equations and Landau-Lifshitz-Maxwell equations.This model can be used to describe the dispersive theory of magnetization of ferromagnets with the electromagnetic field.
For system (1.1) - (1.6) ,we impose the following initial conditions

which satisfy that

Furthermore,we always assume thatare 2D-periodic.
Firstly setting E=B=0,d is a constant vector,and using a effective velocity transformation[18]system (1.1) - (1.6) becomes the isentropic compressible quantum Navier-Stokes equation (IQCNS) .Setμ=0,we get the isentropic compressibleNavier-Stokes equation (ICNS) .For the Navier-Stokes equations with constant viscosity,the existence of global weak solution to ICNS with large initial data in Rnwas first obtained by P.L.Lions[22],whereFeireisl et al.[6,7]extended Lions’s work to the caseFor solutions with spherical symmetry,Jiang and Zhang[15]relaxed the restriction on γ in[22]to the case γ>1,and got the global existence of the weak solutions for N=2 or 3.Luo, Xin and Yang[24]proved the existence and regularity of weak solutions with density connecting to vacuum continuously in 1D.
If ν=E=B=0,d is a constant vector,system (1.1) - (1.6) is called quantum hydrodynamic model (QHD) .In[24]J¨ungel and Li proved the existence of local-intime solutions and global-in-time solutions to (1.1) - (1.6) for the one-dimensional case with Dirichlet and Neumann boundary conditions for the particle density ρ.In[16], the authors gave the local-in-time existence of the solutions to equations (1.1) - (1.6) in the multi-dimensional torus for the irrotational velocity,and they also proved that local-in-time solutions exit globally in time and exponentially converge toward the corresponding steady-state under a“subsonic”type stability condition.In[14], the authors proved the local-in-time and global-in-time existence of the solutions to equations (1.1) - (1.6) in Rnfor rotational fluid.
If E=B=0,d is a constant vector,then system (1.1) - (1.6) becomes the viscous quantum hydrodynamic model (vQHD) (see[10,17]for the derivation) .In[18], J¨ungel proved the existence of the global finite energy weak solution to the vQHD.
If u=E=B=0 and ρ is a constant,then system (1.1) - (1.6) is Landau-Lifshitz model (LL) .In 1981,a group headed by Zhou and Guo proved the existence of the global weak solutions to the initial value problems and initial boundary value problems for Landau-Lifshitz equations from one dimension to multi-dimensions[27]. Alouges and Soyeur[1]proved similar results by penalty method in 1992.In 1993, Guo and Hong began the studies on two-dimensional Landau-Lifshitz equations,they established in[12]the relations between two-dimensional Landau-Lifshitz equations and harmonic maps and applied the approaches studying harmonic maps to get the global existence and uniqueness of partially regular weak solution.In this aspect, in 2004,Liu[23]proved that the“stationary”weak solutions to higher dimensional Landau-Lifshitz equations are partially regular.
If d is a constant vector,system (1.1) - (1.6) is the viscous quantum Navier-Stokes-Maxwell model (QNSM) .Furthermore ifμ=ν=0,it becomes the Navier-Stokes-Maxwell model (NSM) .In[13],Hong et al.got the existence and uniqueness of global spherically symmetric classical solution to the initial boundary value problem to the system of NSM.Germain,Ibrahim and Masmoudi[9]proved the local and global well-posedness of incompressible NSM.
If u=0 and ρ is constant,it obtains the Landau-Lifshitz-Maxwell model (LLM) . In[5],Ding,Guo,Li and Zeng obtained the existence of the global weak solution for the LLM for 3-dimensional case.The global existence of the unique smooth solution to the LLM of the ferromagnetic spin chain without disspation in one or two dimensions were established in[26].Ding and Guo[4]proved the existence of partial regular weak solution to LLM.
In this paper,we are interested in the global existence of finite energy solutions to the initial problem of (1.1) - (1.6) in two-dimensional case.Besides difficulties pointed in[18],the main difficulty is the coupling of velocity,electric field,magnetic field and magnetization field.Therefore,the key in our analysis is to deal with convection term,the quantum term,the electric-magnetic term and the last two terms about the magnetization field in the momentum equation.Inspired by[18],we choose the test function of the form ρ? for the momentum equation,the magnetization field equation and the magnetic field equation.
Next we state our main results.
Theorem 1.1 (Global existence) Let T>0,P (ρ) =Aργ(γ≥1) . (1.8) holds. And ρ0,u0,d0,E0,B0are 2D-periodic functions.Furthermore E (ρ0,u0,d0,E0,B0) (see (4.2) for the definition of E (ρ,u,d,E,B) ) is finite.There exists a weak solution (ρ,u,d,E,B) to (1.1) - (1.6) with the regularity

satisfying (1.1) pointwise and for all smooth test functions satisfying ? (·,T) =0,


The product A:B means summation over both indices of matrices A and B.
It is easy to see that (1.1) - (1.6) lacks compactness which we need to get the estimate of L2or H1-norm for u.To overcome this difficult,we first add the right hand of (1.2) a viscosity term δ?u+δu:

Then we want to send the viscosity constant δ to 0.Finally,we obtain the desired weak solution to the original problem (1.1) - (1.6) .
This paper is organized as follows.In Section 2,we give some preliminaries which will be used in the following section.We show the local existence of (1.1) - (1.6) in Section 3.In Section 4,we firstly prove the a-priori estimates and the existence of global weak solution to the viscosity system (1.20) - (1.25) ,then show the limit of δ→0.The global-in-time existence weak solutions can be achieved according to the Faedo-Galerkin method and weak compactness techniques.
2 Preliminaries
In this section we first give some notation.In this paper we denote C the constant dependent of N and δ.Lp([0,T];Lq(?) ) (p,q≥1) is a space whose element is the p-integrable respect to time variable and q-integrable respect to space variable function.Wk,pand Hsare the Sobolev spaces. (Hs)?is the dual space of Hs.
Lemma 2.1 (Gagliardo-Nirenberg inequality) Let ??Rd(d≥1) be a bounded open set with??∈C0,1,m ∈N,1≤p,q,r≤∞.Then there exists a constant C>0 such that for all u∈Wm,p(?) ∩Lq(?) ,

Next we give a weak compactness lemma which will be used in the following section.
Lemma 2.2 (Aubin-Lions Lemma) Assume X?Y?Z are Banach spaces andThen the following immbedding are compact:

3 Local Existence of Solutions
In this section we will show the local existence of solutions to the viscosity system (1.20) - (1.25) by Faedo-Galerkin method.Let T>0,and {ωj} be an orthonormal basis of L2(?) which is also an orthogonal basis of H1(?) .Introduce the finite-dimensional space XN=span {ω1,···,ωN} ,n∈N.Denote the approximate solutions to problem (1.21) - (1.25) byin the following form

where βj(t) ,γj(t) ,δj(t) ,ηj(t) ,ζj(t) (j=1,···,N,N=1,2,···) are 2-dimensional vector-valued functions.For some functions λi(t) ,and the norm of v in C0([0,T];XN) can be formulated as

As a consequence,v can be bounded in C0([0,T];Ck(?) ) for any k∈N,and there exists a constant C>0 depending on k such that
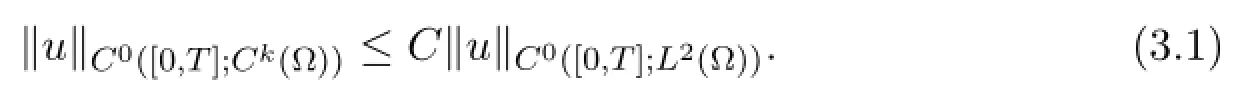
The approximate system is defined as follows.Let ρ∈C1([0,T];C3(?) ) be the classical solution to

The maximum principle provides the lower and upper bounds ([15],Chapter 7.3)
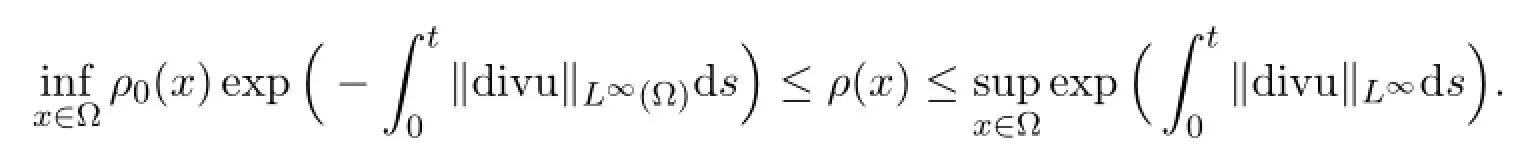


Next we wish to solve (1.20) - (1.25) on the space XN.To this end,for given,we are looking for functionssuch that
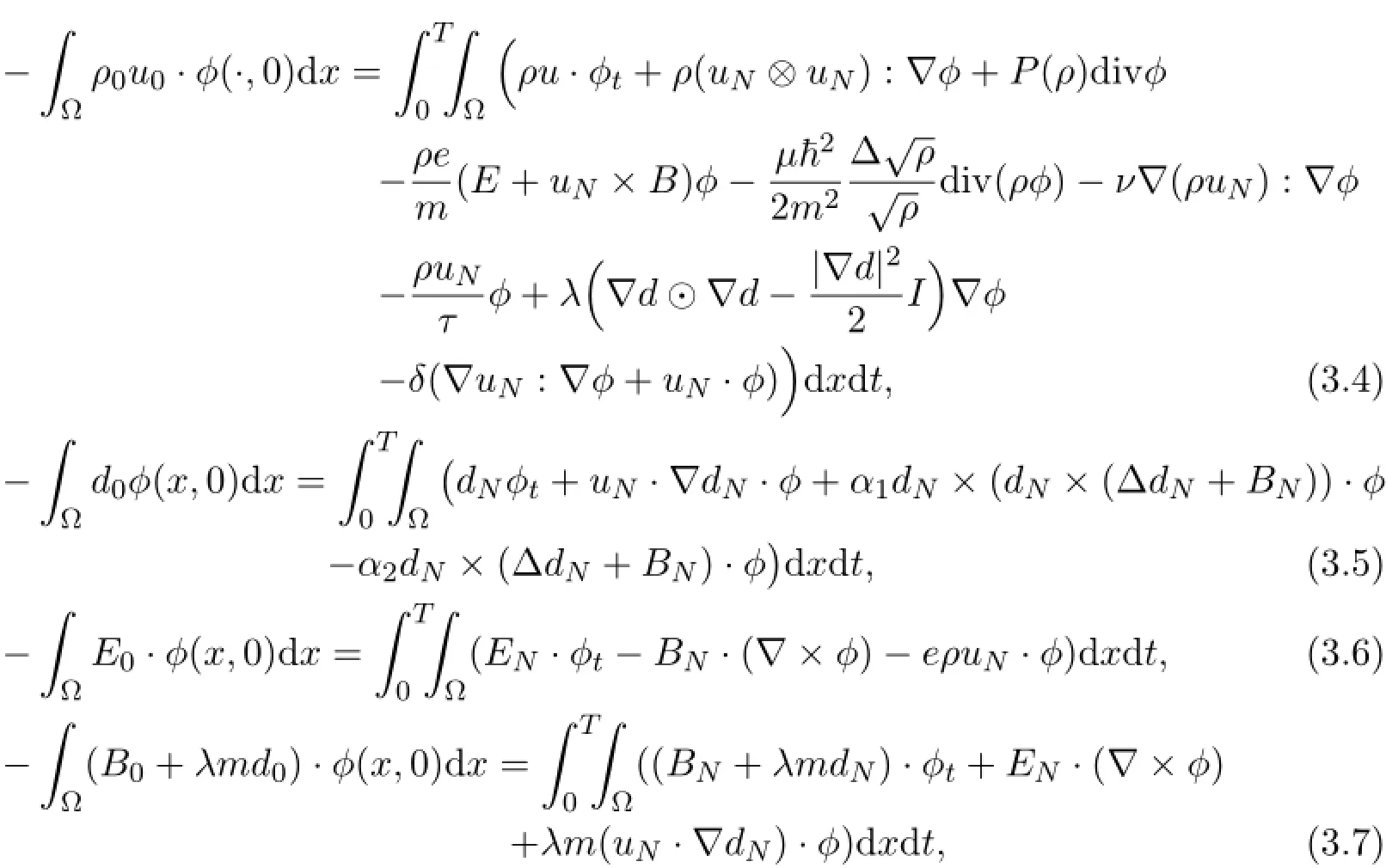
To solve (3.4) - (3.7) ,we follow ([15],Chapter 7.3.3) and introduce the following family of operators,given a function

These operators are symmetric and positive definite with the smallest eigenvalue

Hence,since XNis finite-dimensional,the operators are invertible with


for all ?1,?2∈L1(?) such that
Now the integral equation (3.4) can be rephrased as an ordinary differential equation on the finite-dimensional space XN,

when ρ=S1(u)


Integrating (3.9) over (0,t) yields the following nonlinear equation:Since the operators S1and M are Lipschitz type, (3.10) can be solved by evoking the fixed point theorem of Banach on a short time interval[0,T′],where T′≤T, in the space C0([0,T];XN) .In fact,we have evenThen we can solve system (3.5) - (3.7) .Thus,there exists a unique local-in-time solution
4 A Priori Estimates and Global Existence
In this section,we will give some a-priori estimates.Using these estimates, we can show that the local-in-time solutionwhich are proved in Section 2 can be extended globally.In the case of not confusing,we omit the subscript N and superscript δ in this section.
Theorem 4.1 Set the conditions in Theorem 1.1 to be hold.Then we have the following energy inequality:



Then multiplying (1.21) by u,and integrating both sides of it by parts respectively in ?,we have

Indeed we have the following fact:

Multiplying (1.22) by?d+B,and integrating both sides of it by parts respectively in ?,we get

here we use the following computation:



We can easily have

Combining (4.3) - (4.7) ,we can get

The proof is completed.
From Theorem 4.1,by Gronwall inequality,we can easily get the following estimates:
Corollary 4.1 Set Theorem 4.1 to hold,then we have

The energy inequality (4.1) and Corollary 4.1 allow us to conclude some estimates.
Lemma 4.1 The following uniform estimate holds for some constant C>0,

Proof The lemma follows form the energy estimate in Theorem 4.1.The inequality

with κ2,was shown in[18],and the inequality

was proved in[18],the proof is completed.
We able to deduce more regularity from the H2bound for
Lemma 4.2 (space regularity for ρ and ρu) The following uniform estimates hold for some constant C>0 not depending on N and δ:

where p<2.
Proof Since the space H2(?) embeds continuously into L∞(?) ,showing thatis bounded in L2([0,T];L∞(?) ) .Thus,in view of (4.11) , (4.12) ,is uniformly bounded in L2([0,T];L2(?) ) .By (4.9) and (4.18) ,is bounded inis bounded in L∞([0,T];L6(?) ) .This,together with (4.9) , implies that

is uniformly bounded in L2([0,T];L3/2(?) ) ,which proves the first claim.
For the second claim,we observe first that,by the Gagliardo-Nirenberg inequality in Lemma 2.1,with p=2γ/ (γ+1) and θ=1/2,


is bounded in L2([0,T];Lp(?) ) which proves the second claim.
Finally,the Gagliardo-Nirenberg inequality,with θ=3/ (4γ+3) and q=2 (4γ+ 3) /3

shows that ρ is bounded in Lq/2([0,T];Lq/2(?) ) .This finishes the proof.
From (4.16) we can get the estimate about
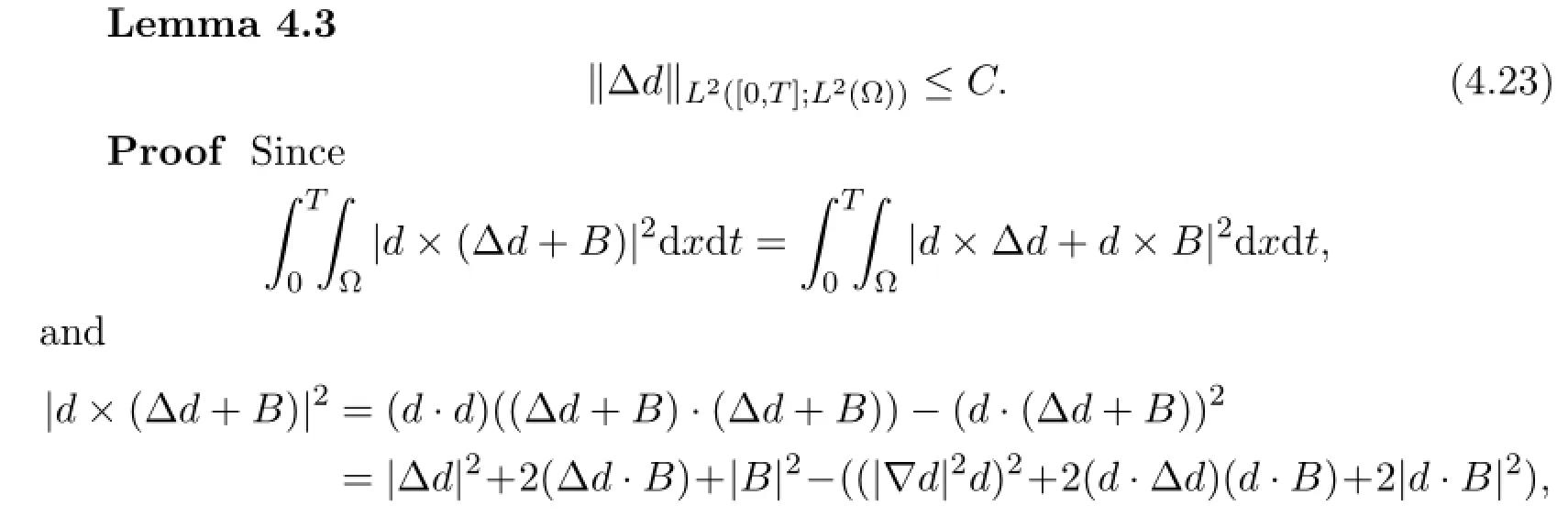

Lemma 4.4 (Time regularity for ρ and ρu) The following uniform estimates hold for s>2,

Proof By (4.20) , (4.21) ,we find that?tρ=?div (ρu) ?ν?ρ is uniformly bounded in L2([0,T];L3/2(?) ) ,which proves the first claim.
The sequence ρu?u is bounded in L∞([0,T];L1(?) ) ;hence,div (ρu?u) is bounded in L∞([0,T]; (W1,∞(?) )?) ,because of the continuous embedding of Hs(?) into W1,∞(?) for s>2,and also in L∞([0,T]; (Hs(?) )?) .The estimate
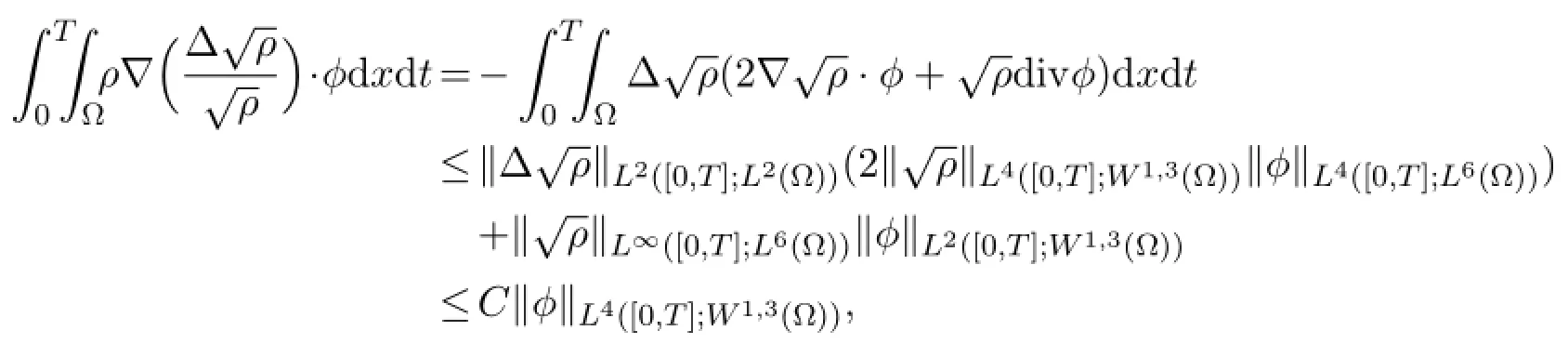
for all ?∈L4([0,T];W1,3(?) ) proves thatis uniformly bounded inIn view of (4.22) ,ργis bounded inFurthermore,by (4.20) ,? (ρu) is uniformly bounded in L2([0,T]; (W1,3(?) )?) ,and by (4.17) ,δ?u is bounded in L2([0,T]; (H1(?) )?) .Therefore,using Corollary 4.1 and Lemma 4.3,we get that
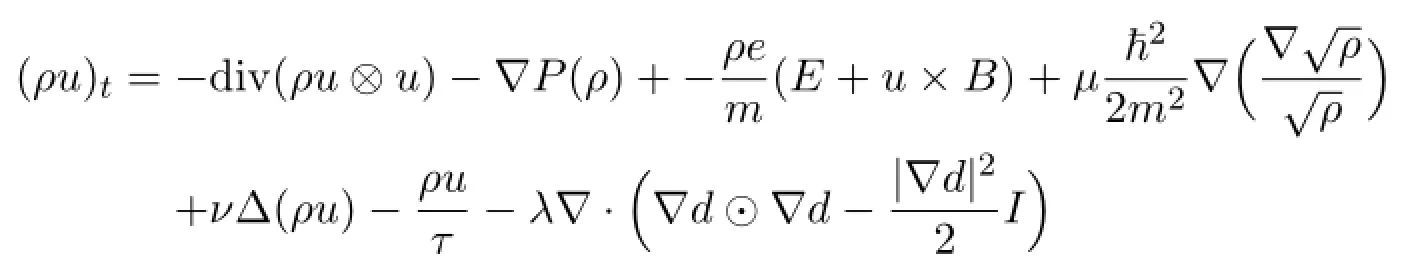
is uniformly bounded in L4/3([0,T]; (Hs(?) )?) .The proof is completed.
The L4([0,T];W1,4(?) ) bound (4.18) onprovides a uniform estimate for
Lemma 4.5 (Time regularity forThe following estimate holds:

Proof Dividing the mass equation (1.1) bygives

The first term on the right-hand side is bounded in L2([0,T]; (H1(?) )?) by (4.11) and (4.12) .The remaining terms are uniformly bounded in L2([0,T];L2(?) ) ;see (4.11) , (4.12) , (4.17) .The proof is completed.
Lemma 4.6 There is

Proof Multiplying (1.3) by dt,and integrating by parts respect to x in ?,we have

Here C1,C2,C3,C4are constants independent of N.Then integrating by parts respect to t in[0,T],using the Corollary 4.1 and Lemma 4.3 we get (4.27) .Thus we complete the proof of this lemma.
Next we will show the limit of the Fadeo-Galerkin approximated solution.We perform first the limit N→∞,with δ>0 being fixed.The limit δ→0 is carriedout in the last part of this section.We consider both limits separately since the weak formulation (1.16) - (1.19) for the viscous quantum NSLLM equations is different from its approximation (3.1) and (3.4) - (3.7) .
We conclude from the Aubin-Lions lemma,taking into account the regularity (4.21) and (4.24) for ρN,the regularity (4.18) and (4.26) forand the regularity (4.20) and (4.25) for ρNuN,that there exist subsequences of ρN,and ρNuN, which are not related,such that,for some function ρ and J,as N→∞,

Here we have used that the embeddingare compact.The estimate (4.17) on uNprovides further the existence of a subsequence (not relabeled) such that,as N→∞,

Then,since ρnuNconverges weakly to ρu in L1([0,T];L6(?) ) ,we infer that J=ρu.
We are now in the position to let N→∞in the approximate system (3.1) and (3.4) - (3.7) with ρ=ρN,u=uN,d=dN,E=ENand B=BN.Clearly,the limit N→∞shows immediately that n solves

Next we consider the weak formulation (3.4) term by term.The strong convergence of ρNuNin L2([0,T];L2(?) ) and the weak convergence of ρNin L2([0,T];L6(?) ) leads to

Furthermore,in view of (4.21) (up to a subsequence) ,

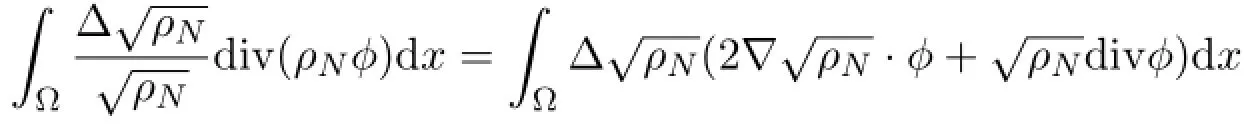
equals,for sufficiently smooth test functions,




Similarly,using the a-priori estimates we can show that as N →∞,the limit of (dN,EN,BN) satisfies

Finally,we will show the limit asbe a solution to (3.2) , (3.4) - (3.7) with the regularity proved in the previous.By employing the test function ρδ? in (3.4) (which is possible as long as the integrals are well defined) ,we obtain,according to

The Aubin-Lions lemma and the regularity results from the previous allow us to extract subsequences (not relabeled) such that as δ→0,for some functions ρ and j,

Estimate (4.11) , (4.12) and Fatou lemma yield

This implies that J=0 in ρ=0.Then,when we define the limit velocity u:=J/ρBy (4.11) , (4.12) ,there exists a subsequence (not relabeled) such that

for some function g.Hence,sinceconverges strongly towe infer thatconverges weakly to
Now we are able to pass to the limit δ→0 in the weak formulation (4.32) term by term.The strong convergences (4.33) and (4.34) imply that

The strong convergence of ρδuδimmediately gives

Furthermore,we have
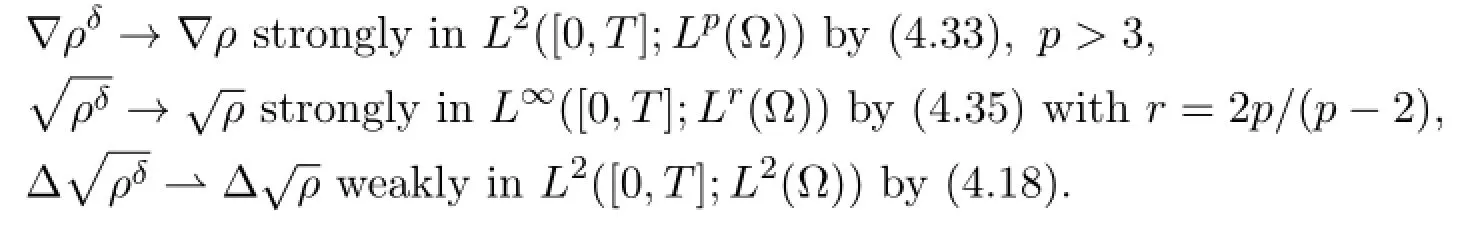
It holds that r<6 since we have p>3.This implies that


The almost everywhere convergence of ρδand thebound on ρδ(see (4.22) ) ,together with the fact that 4γ/3+1>γ+1,proves that

Using the estimate (4.17) forwe obtain further,for smooth test functions,

It remains to show the convergence of (ρδ)2div (uδ) uδ.To this end,we proceed similarly as in[11]and introduce the functionssatisfyingThen we estimate the low-density part of (ρδ)2div (uδδ) uδby

where C>0 is independent of δ and α.We write

As δ→0,the first term on the right-hand side converges strongly to div (Gα(ρ) ρu) in L1([0,T]; (H1(?) )?) since Gα(ρδ) converges strongly to Gα(ρ) in Lp([0,T];Lp(?) ) for any p<∞and ρδuδconverges strongly to ρu in L2([0,T];Lq(?) ) for any q<3. In view of (4.35) and (4.36) ,we infer the weak?convergenceThus,because of (4.33) ,



Moreover,in view of the strong convergence of ρδuδto ρu in L2([0,T];Lq(?) ) for all q<3,we infer that


For fixed α>0,the first integral converges to zero as δ→0.Furthermore,the last integral can be estimated byuniformly in δ ( (4.37) ) .For the second integral,we recall thatFurthermore, by the Gagliardo-Nirenberg inequality,the bounds of ρu in L2([0,T];W1,3/2(?) ) andThus,since

As a consequence,the second integral converges to 0 as δ→0.Thus,in the limit δ→0, (4.39) can be made arbitrarily small,and hence,

Here we will omit the rest term convergence about d,E,B,you can refer to[11].
We have proved that (ρ,u,d,E,B) solves (1.20) - (1.25) for smooth initial data.Let (ρ0,u0,d0,E0,B0) be some finite-energy initial data,that is ρ0≥0 andbe smooth approximations satisfyingstrongly in H1(?) andstrongly in L3/2(?) .By the above proof,there exists a weak solutionwith initial datasatisfying all the above bounds.In particular,converges strongly in some spaces toand there exist uniform bounds forand forThus,up to subsequences,as δ→0,
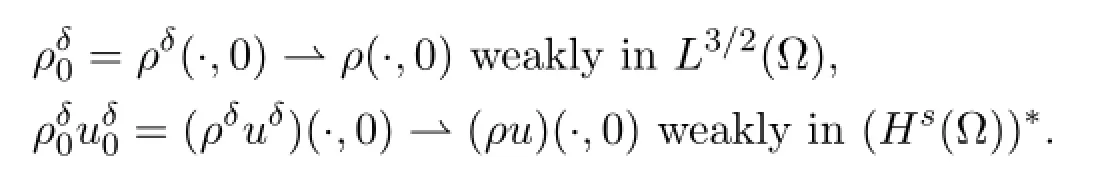
Note that a priori estimates in Section 4 are independent of D.By using the diagonal method and letting D→∞,we can obtain the global existence of weak solution to the Cauchy problem of system (1.1) - (1.6) and (1.7) .For simplicity,we do not state the theorem here.
In the following work we will show the partial regularity of these weak solution to NSLLM.We will show that if the solution to (1.1) - (1.6) is smooth except finitely many singular point.
References
[1]F.Alouges and A.Soyeur,On global weak solutions for Landau-Lifshitz equations: Existence and nonuniqueness,Nonlinear Anal.TMA,18 (1992) ,1071-1084.
[2]D.Bresch,B.Desjardins and C.K.Lin,On some compressible fluid models:Korteweg,lubrication and shallow water systems,Comm.Partial Differential Equations, 28 (2003) ,1009-1037.
[3]S.Brull and F.M′ehats,Derivation of viscous correction terms for the isothermal quantum Euler model,Z.Angew.Math.Mech.,90 (2010) ,219-230.
[4]S.J.Ding and B.L.Guo,Existence of partial regularity weak solutions to Landau-Lifshitz-Maxwell equations,Journal of Differential Equations,244:10 (2008) ,2448-2472.
[5]S.J.Ding,B.L.Guo,J.Y.Lin and M.Zeng,Global existence of weak solution for Landau-Lifshitz-Maxwell equtions,Discrete and Continuous Dynamical Systems-Series A,17:4 (2007) ,867-890.
[6]E.Feireisl,Dynamics of Viscous Compressible Fluids,Oxford University Press,Oxford, 2004.
[7]E.Feireisl,A.Novotn′y and H.Petzeltov′a,On the existence of globally defined weak solutions to the Navier-Stokes equations,J.Math.Fluid Mech.,3 (2001) ,358-392.
[8]C.Gardner,Numerical simulation of a steady-state electron shock wave in a submicron semiconductor device,ⅠEEE Trans.El.Dev.,38 (1991) ,392-398.
[9]P.Germain,S.Ibrahim and N.Masmoudi,Well-posedness of the Navier-Stokes-Maxwell equations,Proceedings of the Royal Society of Edinburgh,144:1 (2014) ,71-86.
[10]M.P.Gualdani and A.J¨ungel,Analysis of the viscous quantum hydrodynamic equations for semiconductors,Eur.J.Appl.Math.,15 (2004) ,577-595.
[11]B.L.Guo and S.J.Ding,Landau-Lifshitz Equations,Word Science:Singapore,2008.
[12]B.L.Guo and M.C.Hong,The Landau-Lifshitz equations of the ferromagnetic spin chain and harmonic maps,Calc.Var.,1 (1993) ,311-334.
[13]G.Y.Hong,X.F.Hou,H.Y.Peng and C.J.Zhu,Global spherically symmetric classical solution to the Navier-Stokes-Mawell system with large initial data and vacuum, Science China Mathematics,57:12 (2014) ,2463-2484.
[14]F.M.Huang,H.L.Li,A.Matsumura and S.Odanaka,Well-posedness and stability of multi-dimensional quantum hydrodynamics for semiconductors in R3,Series in Contemporary Applied Mathematics CAM 15,High Education Press,Beijing,2010.
[15]S.Jiang and P.Zhang,Global sphereically symmetric solutions of the compressible isentropic Navier-Stokes equations,Comm.Math.Phys.,215 (2001) ,559-581.
[16]H.L.Li and P.Marcati,Existence and asymptotic behavior of multi-dimensional quantum hydrodynamic model for semiconductors,Comm.Math.Phys.,245 (2004) ,215-247.
[17]A.J¨ungel,A Steady-state quantum Euler-Poisson system for potential flows,Commun. Math.Phys.,194 (1998) ,463-479.
[18]A.J¨ungel,Global weak solutions to cmpressible Navier-Stokes equations for quantum fluids,SⅠAM J.Appl.Math.,42:3 (2010) ,1025-1045.
[19]A.J¨ungel,Quasi-hydrodynamic Semiconductor Equations,Birkh¨ause,Basel,2001.
[20]L.D.Landau and E.M.Lifshitz,On the theory of the dispersion of magnetic permeability in ferromagnetic bodies,Phys.Z.Sovietunion.,8 (1935) ,153-169.
[21]Z.Lei,D.Li and X.Y.Zhang,Remarks of global wellposedness of liquid crystal flows and heat flow of harmonic maps in two dimensions,Proceedings of American Mathemathical Society,142:11 (2012) ,3801-3810.
[22]P.L.Lions,Mathematical Topic in Fluid Mechanics,Vol.2 Compressible models,in; Oxford Lectures Series in Mathematics and its Applications,Vol.10,Oxford Science Publications,The Clarendon Press,Oxford University Press,New York,1998.
[23]X.Liu,Partial regularity for Landau-Lifshitz system of ferromagnetic spin chain,Calc. Var.,20 (2004) ,153-173.
[24]T.Luo,Z.P.Xin and T.Yang,Interface behavior of compressible Navier-Stokes equtions with vacuum,SⅠAM J.Math.Anal.,31 (2000) ,1175-1191.
[25]P.M.Markowich,C.Ringhoffer,and C.Schmeiser,Semiconductor Equations,Wien, Springer,1990.
[26]F.Q.Su and B.L.Guo,The global smooth solution for Landau-Lifshitz-Maxwell equation without dissipaton,Journal of Partial Differential Equations,3 (1998) ,193-208.
[27]Y.L.Zhou,H.S.Sun,and B.L.Guo,Existence of weak solution for boundary problems of systems of ferromagnetic chain,Science in China A,27 (1981) ,779-811.
(edited by Liangwei Huang)
?Manuscript March 3,2016
?.E-mail:yunxianwgw@163.com
 Annals of Applied Mathematics2016年1期
Annals of Applied Mathematics2016年1期
- Annals of Applied Mathematics的其它文章
- INFORMATION FOR AUTHORS
- EXACT SOLUTIONS OF(2+1)-DIMENSIONAL NONLINEAR SCHR¨ODINGER EQUATION BASED ON MODIFIED EXTENDED TANH METHOD?
- EVANS FUNCTIONS AND INSTABILITY OF A STANDING PULSE SOLUTION OF A NONLINEAR SYSTEM OF REACTION DIFFUSION EQUATIONS??
- CYCLES EMBEDDING ON FOLDED HYPERCUBES WITH FAULTY NODES??
- A NEW CLASS OF SOLUTIONS OF VACUUM EINSTEIN’S FIELD EQUATIONS WITH COSMOLOGICAL CONSTANT??
- EXISTENCE OF PERIODIC SOLUTIONS OF A CLASS OF SECOND-ORDER NON-AUTONOMOUS SYSTEMS??
