Modal parameter identification for a roof overflow powerhouse under ambient excitation
Yn Zhng,Ji-jin Lin*,Fng Liu
aState Key Laboratory of Hydraulic Engineering Simulation and Safety,Tianjin University,Tianjin 300072,ChinabState Key Laboratory of Simulation and Regulation of Water Cycle in River Basin,China Institute of Water Resources and Hydropower Research, Beijing 100038,China
?
Modal parameter identification for a roof overflow powerhouse under ambient excitation
Yan Zhanga,b,Ji-jian Liana,*,Fang Liua
aState Key Laboratory of Hydraulic Engineering Simulation and Safety,Tianjin University,Tianjin 300072,China
bState Key Laboratory of Simulation and Regulation of Water Cycle in River Basin,China Institute of Water Resources and Hydropower Research, Beijing 100038,China
Available online 24 December 2015
Abstract
Modal parameter identification is a core issue in health monitoring and damage detection for hydraulic structures.For a roof overflow hydropower station with a bulb tubular unit under ambient excitation,a complex unit-powerhouse-dam coupling vibration system increases the difficulties of modal parameter identification.In this study,in view of the difficulties of modal order determination and the noise jamming caused by ambient excitation,along with false mode identification and elimination problems,the ensemble empirical mode decomposition(EEMD) method was used to decrease noise,the singular entropy increment spectrum was used to determine system order,and multiple criteria were used to eliminate false modes.The eigensystem realization algorithm(ERA)and stochastic subspace identification(SSI)method were then used to identify modal parameters.The results show that the relative errors of frequencies in the first four modes were within 10%for the ERA method, while those of SSI were over 10%in the second and third modes.Therefore,the ERA method is more appropriate for identifying the structural modal parameters for this particular powerhouse layout.
?2016 Hohai University.Production and hosting by Elsevier B.V.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).
Hydraulic structure;Order determination;Ensemble empirical mode decomposition;Singular entropy;Eigensystem realization algorithm; Bulb tubular unit
1.Introduction
In general,the reduction of hydraulic structural strength and stiffness results from the effects of design loads,working conditions,and unexpected external factors such as earthquakes.Hence,structural damage will occur during the structure's service life,affecting the safety and stability of its operation.Therefore,this type of damage must be considered instructural health monitoring.Recently,the topic of vibration-based structural health monitoring has attracted considerable interest.This type of monitoring offers the possibility of obtaining more accurate and objective information with respect to the deterioration and damage of instrumented structures.With damage,the structural dynamic properties will change.This can be reflected in the modal parameters. Therefore,obtaining modal parameters with accurate techniques is a key prerequisite for monitoring the structural operation conditions(Darbre et al.,2000).
Traditionally,modal parameter identification is carried out through the frequency domain-or time domain-based methods (Ibrahim and Pappa,1982;James et al.,1996;Brinker et al., 2001;Schoukens et al.,1998).The latter can avoid errors caused by data conversion and increase the identification accuracy,because it deals directly with measured response signals,without going through the Fourier transform(FT)process(Kim,1998).Thus,it has been widely used in modal parameter identification of hydraulic structures,large-scale machines,and aerospace structures.Zhang et al.(2007)extracted the components of free-decay response of a powerhouse from its vibration signals after its dynamic loads were suddenly released with the random decrement technique and identified the modal parameters of the powerhouse in China's Lijiaxia Hydropower Station.Li and Lian(2009)used the genetic algorithm to identify the modal parameters of the powerhouse in China's Qingtongxia Hydropower Station.Lian et al.(2009) used the eigensystem realization algorithm(ERA)to identify dynamic characteristics and damage scenarios of China's Yingxiuwan Hydropower Station sluice after strong seismic shocks with flood discharge excitation,as well as the operational modal parameters of the Three Gorges left guide wall during the flood season.D¨ohler and Mevel(2013)obtained modal parameters of the Z24 Bridge with a multi-setup subspace identification algorithm and determined the first ten mode shapes by estimating the covariances of modal parameters.
In the time domain-based methods,the ERA(Juang and Pappa,1985;Juang,1994)and the stochastic subspace identification(SSI)method(Peeters and Roeck,2001;Han et al.,2010)are mostly used for structural modal parameter identification(Fu,1990;Hong et al.,2001;D¨ohler et al., 2013;Cheng and Zheng,2014).The system order necessary to obtain the correct modal properties with comparable efficiency and accuracy varies depending on the system identification method.As a result,it is important to understand the advantages and disadvantages of each method and determine the most appropriate method to implement in different applications.Lew et al.(1993)compared four methods:the ERA(Juang and Pappa,1985),the ERA using data correlation(ERA/DC)(Juang et al.,1988),the Q-Markov cover theory(Anderson and Skelton,1988),and an algorithm proposed by Moonen et al.(1989).It was concluded that the ERA/DC is the best identification method of the four for input-output data.Petsounis and Fassois(2001)compared the identified modal parameters using four stochastic methods,including the prediction error method(PEM),the two-stage least squares(2SLS)method,the linear multi stage (LMS)method,and the instrumental variable(IV)method, based on the autoregressive moving average(ARMA). However,the necessity of input and output data for the ERA decreases its practical applicability in system identification for some existing structures,for which stochastic methods are preferred.Peeters et al.(1998)assessed the SSI methods, including the peak picking and poly-reference least-square complex exponential methods.The results show that the quality of the identified mode shapes from SSI is better than that of other methods.When excited only by environmental loads(such as flow-fluctuating loads and turbine-operating loads),the ERA method usually runs into several problems. The first,because of the mixed response data(including structural free vibration,forced vibration,flow fluctuation and white noise information,to name a few data types) caused by ambient excitation(Lee et al.,2002),is extraction of system-practicable free-decaying responses from one or more structural vibration responses.Second,due to noise jamming under ambient excitation,the accuracy of modal parameters derived directly from response data is poor.Thus, the response data should be pre-processed to decrease noise jamming(Li et al.,2011).The third is determination of order. With ambient excitation the system is unknown,and,therefore,its order is uncertain,leading to necessity of determining the order and which modals are true or false,so as to eliminate false ones.The SSI method can directly use the excitation response data and is less affected by noise.However,this method also requires determining order and has very strict requirements for the arrangement of measuring points.
A roof overflow powerhouse with bulb tubular units,which is a new form of hydraulic structure,has remarkable advantages over other forms under conditions of large discharges and low heads because of its high efficiency,small size,large flow capacity,and minimal engineering requirements,and it has wide application prospects.For this structure,the powerhouse is not only the support body of the bulb tubular unit but also the carrier of flow-induced vibration.A more complex vibration source is produced by the unit-powerhouse-dam coupling system with flood discharge from the surface outlet or sand-flash outlet,resulting in more excitation sources, excitation spectrums that are not smooth,and significant noise jamming.It is consequently more difficult to identify modal parameters(Lian et al.,2013).De-noising is the key to accurate modal parameter identification.In recent years,many de-noising methods have been proposed,including the wavelet technique(Chang et al.,2000),the singular value decomposition(SVD)method(Brincker et al.,2000),blind source separation(Jing and Meng,2009),the empirical mode decomposition(EMD)method(Huang et al.,1998),and the ensemble EMD(EEMD)method(Wu and Huang,2009).The noise reduction effect of wavelets is poor for non-stationary signals(Chang et al.,2000).Lian et al.(2009)de-noised the vibration signals of a dam using SVD.However,the noise reduction effect is unsatisfactory when the energy of noise is less than 10%or is almost equal to the energy of the useful signal(Qian et al.,2011).Therefore,this method is no longer applicable when the interference factors of the structures increase,as they do where there is a roof overflow powerhouse. The EMD method is versatile,and used in a broad range of applications for signals with nonlinear components,singular points,and irregular transient parts.However,it produces mode mixing,end effects,and stopping criterion problems, which cause a loss in useful signal(Rato et al.,2008;Sweeney et al.,2013).EEMD can not only self-adaptively decompose both nonlinear and non-stationary data,but also effectively solve the mode mixing,end effects,and termination condition problems of EMD.
In this study,two identification methods,ERA and SSI, were used to identify modal parameters of a roof overflow powerhouse under ambient excitation.In order to overcome the difficulties of practical application due to noise,system order,and false modes,we used the EEMD method todecrease noise,the random decrement technique(RDT)to extract free-decaying response data after de-noising,the singular entropy increment spectrum to determine system order, and multiple criteria to eliminate false modes.A finite element method was used to calculate the dynamic properties of a coupled bedrock-structure-water model.The simulated results and experimental results are compared.Finally,some conclusions are drawn.
2.Theoretical aspects
2.1.Random decrement technique
RDT is a data processing method that can be used to obtain the free vibration response of a system from one or more stationary random responses(Lee et al.,2002).
For a powerhouse under any excitation function,the forced vibration response of a measuring point y(t)can be expressed as
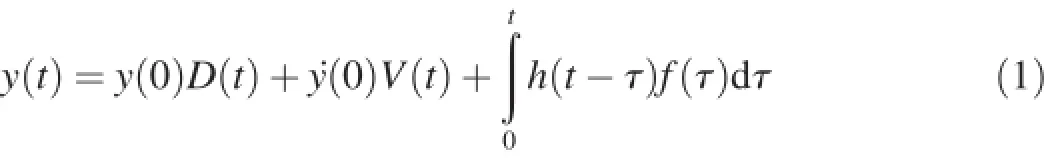
where t is time,D(t)is a free vibration response with an initial displacement of 1 and initial velocity of 0,V(t)is a free vibration response with an initial displacement of 0 and initial velocity of 1,y(0)and.y(0)are the initial displacement and initial velocity of system vibration,respectively,h(t)is the unit impulse response function of a system,and f(t)is external excitation(the dynamic loads under the powerhouse operating conditions).
Selecting an appropriate constant A,there are a series of intersection points with time ti(i=1,2,…,N)between y=A and y(t).The response y(t-ti)with a starting time of tican be regarded as a linear superposition of three parts:a free vibration response caused by the initial displacement,a free vibration response caused by the initial velocity,and a forced vibration response caused by random excitation f(t),i.e.,
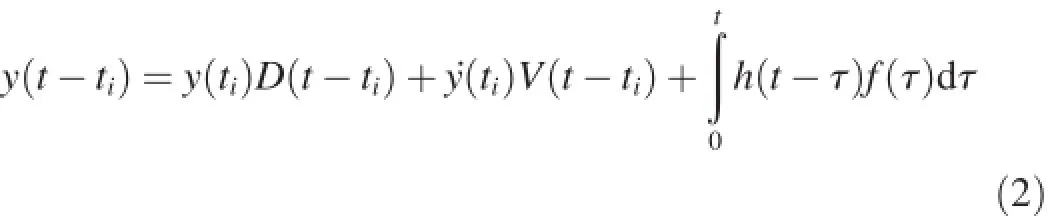
where.y(ti)is the acceleration of system vibration at time ti. Because f(t)is stationary random vibration,the starting time does not affect random characteristics.Thus,the starting time tiof y(t-ti)can be moved to the coordinate origin,allowing us to obtain a series of sub-sample functions xi(t)of a random process of response y(t-ti).xi(t)can be expressed as
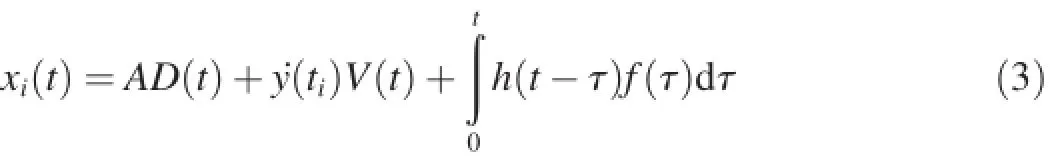
The statistical average value of xi(t)can be expressed as
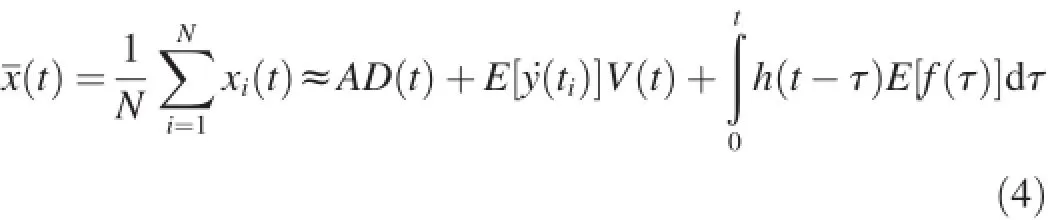
where E is the mathematical expectation.Because f(t)and.y(t)are stationary random vibration and the mean value of each of them is 0,that is,E[y(t)]=0 and E[.y(t)]=0,we have

Thus,a free vibration response with an initial displacement of A and initial velocity of 0 can be obtained.
2.2.Eigensystem realization algorithm
The ERA is a multi-input multi-output(MIMO)modal parameter identification algorithm in the time domain.The algorithm consists of two major parts:the basic formulation of the minimum-order realization and the modal parameter identification.It uses the Hankel matrix and the singular value decomposition technique to analyze the impulse response test data and free response test data,and generates an input and output linear model to match the dynamic system.The linear model is then transformed into modal space for modal parameter identification.
An n-dimensional discrete-time,linear dynamic system with m inputs and p outputs has the following state-space equations:
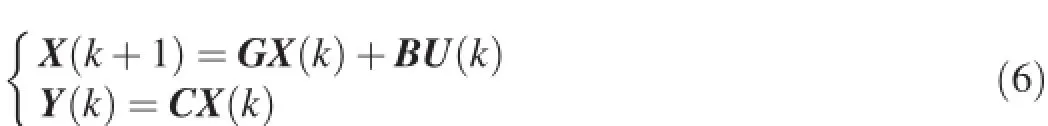
where X is an n-dimensional state vector;U is an m-dimensional control input vector;Y is a p-dimensional output or measurement vector;k is the sample indicator,where k=0,1, 2,…;and G,B,and C are the system matrix with n rows and n columns,control matrix with n rows and m columns,and observation matrix with p rows and n columns,respectively. Based on Eq.(6),Y can be expressed as

In the case of initial state response,whererepresents the ith initial state vector.ERA can use multiple initial condition response data to identify the closely spaced and repeated modes.
The algorithm begins by forming a Hankel matrix H:
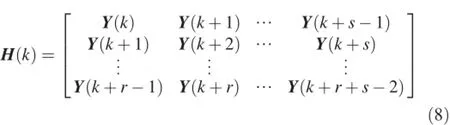
A singular value decomposition of H(0)is

where P is the left singular vector matrix with rp rows and n columns;V is the right singular vector matrix with s rows and n columns(the column vectors of P and V are orthonormal); and D is a diagonal matrix,where D=diag(d1,d2,…,dn).
The matrices G,B,and C can be obtained from following formulas:

where Emis an s×m matrix,and=[ImOm…Om], with Imbeing a unit matrix with an order of m and Ombeing a null matrix with an order of m;and Epis a p×rp matrix,where=[IpOp…Op],with Ipbeing a unit matrix with an order of p and Opbeing a null matrix with an order of p.
The last step is the eigenvalue decomposition of the matrix G and the obtaining of system modal parameters.
2.3.Stochastic subspace identification
The SSI algorithm is based on the discrete-time state-space equation of a linear system,which is suitable for the process of steady excitation.It is an output-only time domain method that directly uses time data.The state model is

where wkis the process noise vector,and vkis the measurement noise vector.They have a mean of zero and are not related.We define

The autocovariance matrix Riof Y(k)is defined as


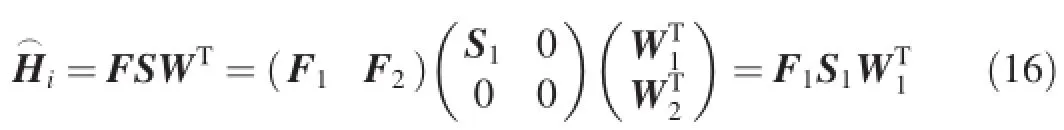
The Toeplize matrix can also be decomposed as follows:

where Qiis an observability matrix,with;and Ziis a reversed random controllable matrix,withwhere A=E[X(k+1)YT(k)].
The matrix pair[G,C]is assumed to be observable,which implies that all the dynamic modes of the system can be observed in the output.
The matrices G and C can be obtained from Eqs.(16)and (17):

After the system matrix G and the observation matrix C are determined,the modal parameters can be identified through eigenvalue decomposition of the system matrix G:

where Λ=diag(λ1,λ2,…,λN),λiis the ith discrete eigenvalue,and ψ is the eigenvector of the system.
3.De-noising,system order determination,and false mode elimination
3.1.De-noising based on EEMD
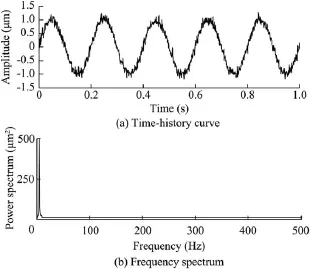
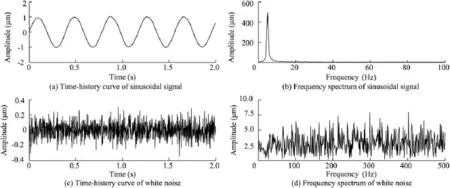
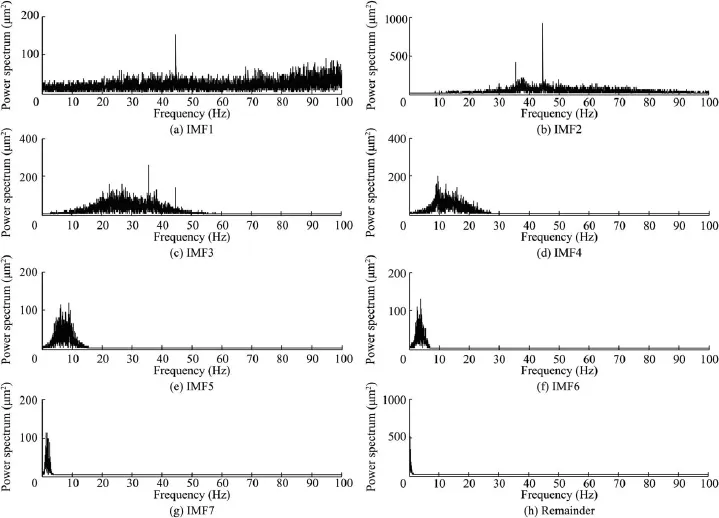
The vibration of the powerhouse experiencing ambient excitation is characterized by multiple vibration sources, broadband,and complex vibration modes.The vibration signal is a superposition of the signals excited by different excitation sources,and has instantaneous nonlinear and non-stationary characteristics,which cause significant difficulties for denoising.Fig.1 is the time-history curve and frequency spectrum of the displacement signal of a typical powerhouse at a measuring point.As can be seen,the different peak values in the frequency spectrum show free vibration frequencies of the structure,noise frequencies(yellow box),flow fluctuation frequencies(red box),and frequencies of excitation source vibration(green box).This study used the EEMD technique to conduct preprocessing of structural vibration response.
3.1.1.Ensemble empirical mode decomposition
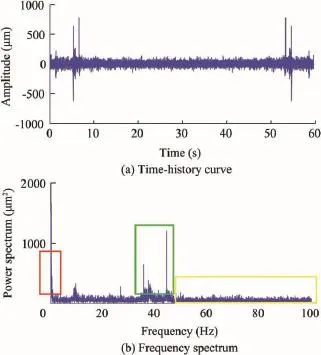
Fig.1.Time-history curve and frequency spectrum of displacement signal of typical powerhouse at measuring point.
The core task of EMD is decomposing data into a small number of independent and nearly periodic intrinsic modes based on the local characteristic time scale of the data,and representing each intrinsic mode as an intrinsic mode function (IMF).However,when using EMD,mode mixing,which is defined as a single IMF consisting either of signals of widely disparate scales,or of a signal of a similar scale residing in different IMF components,frequently occurs.In order to overcome the mode mixing problem,Wu and Huang(2009) proposed the EEMD method.The basic idea of EEMD is that observed data are amalgamations of the true time series and noise.Thus,even if data are collected through separate observations with different noise levels,the ensemble mean is close to the true time series.
In EEMD,low-level random noise is added to the input signal,and then the signal is decomposed through EMD.The process of adding noise to the signal and decomposing the signal through EMD is one trial.This procedure is repeated Q times to obtain the final IMF.The algorithm of EEMD is, therefore,organized into the following steps:
(1)The ensemble size Q is initialized,and the number of trials q is set to 1.
(2)The qth trial for the signal with the added white noise is implemented,a step that involves the following tasks:(a)A white noise series n′(t)with amplitude Aqis added to the input signal x(t)to generate a modified signal:

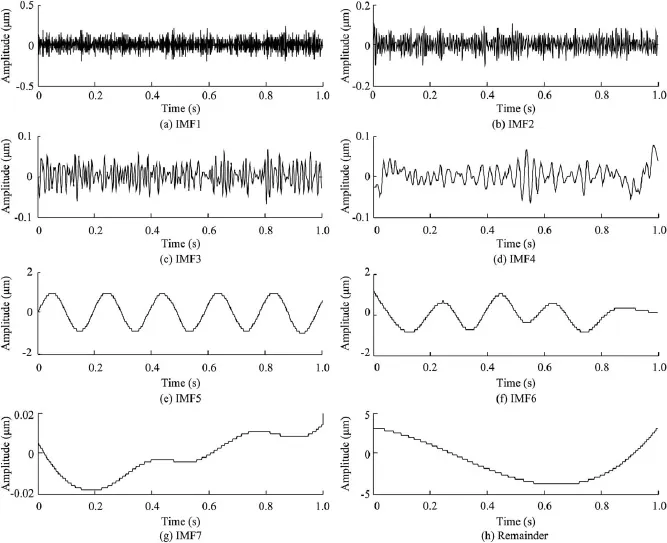
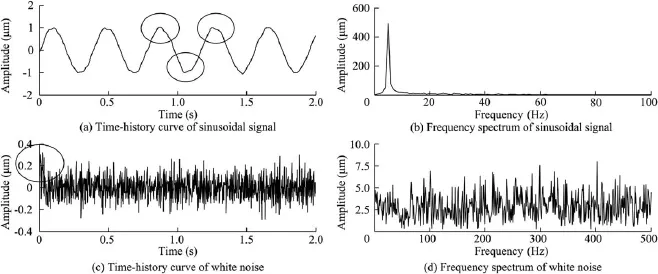
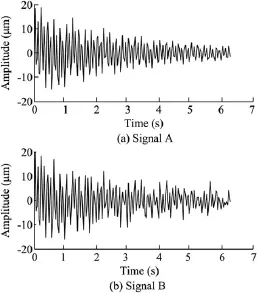
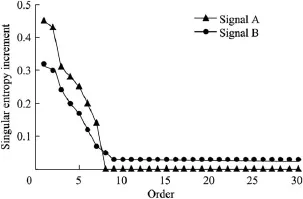
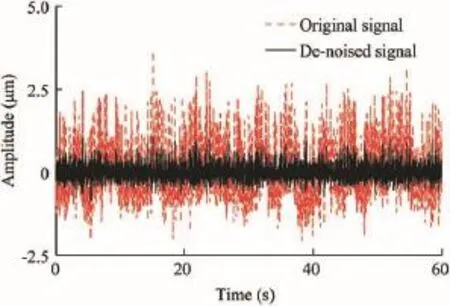
where xq(t)is the noise-added signal of the qth trial.(b)The signal xq(t)is decomposed into M IMFs and a remainder with the EMD:

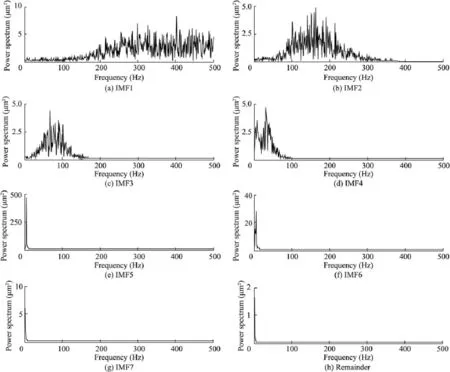
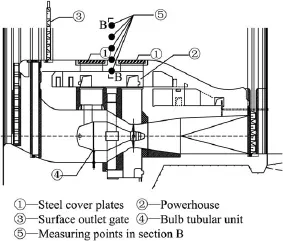
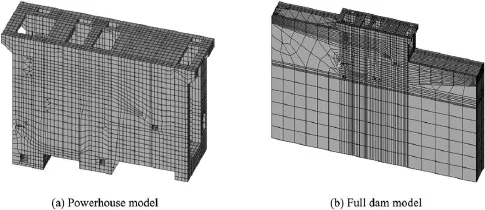
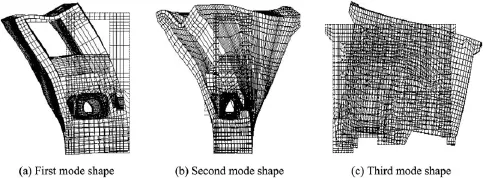
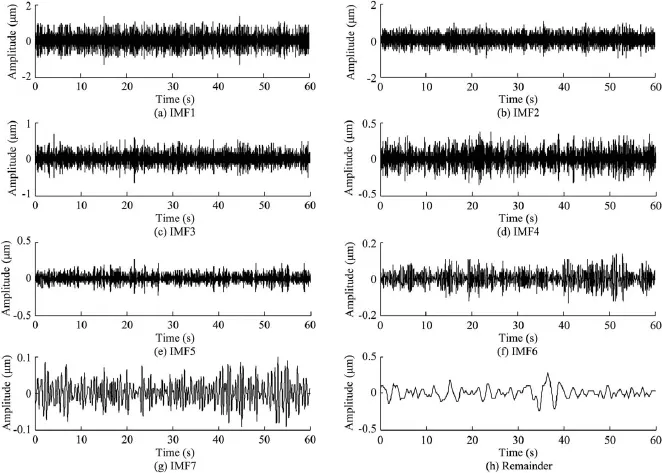
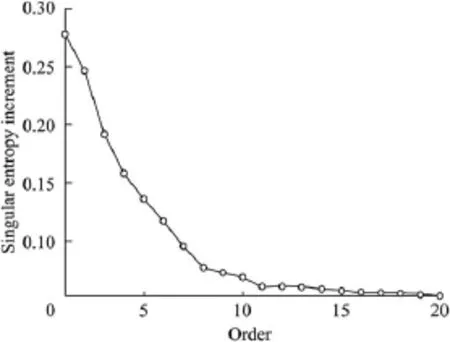
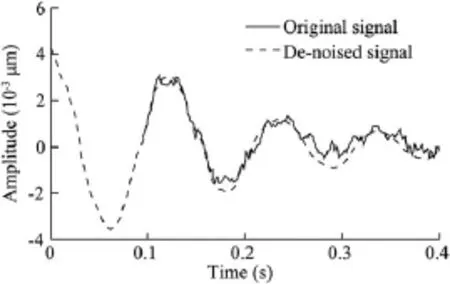
where ciq(t)is the ith IMF of the qth trial,and rNq(t)is the remainder after removing M IMFs for the qth trial.(c)If q (3)The ensemble mean of the Q trials for the ith IMF,Ci(t), is calculated: (4)Ci(t)(i=1,2,…,M)is considered the final ith IMF. Therefore,the goal of de-noising through EEMD is decomposition of the signal into a series of IMF components whose characteristic time scales vary from small to large(or whose frequencies vary from high to low).For a signal mixed with random noise,the high-frequency IMF components are usually the noise.Then,these IMF components are removed, the signal is reconstructed with the rest of the IMF components,and the noise can be reduced. 3.1.2.Application of EEMD to de-noising A simulated signal C was composed of a sinusoidal component with a frequency of 5 Hz and normally distributed white noise with a mean of 0 and a standard deviation of 0.1, as shown in Fig.2. The decomposition results of the signal with the EEMD are shown in Figs.3 and 4.The signal was decomposed into seven IMF components and a remainder.According to the time history curves and frequency spectrum distribution,IMF5, IMF6,and IMF7,with dominant frequencies of 5 Hz,were selected to reconstruct the signal.The reconstructed sinusoidal signal and noise signal from EEMD decomposition results are shown in Fig.5.Fig.6 shows the reconstructed sinusoidal signal and noise signal from EMD decomposition results,with obvious disturbance components(circle regions).This was due to the mode mixing of EMD. Fig.2.Timer-history curve and frequency spectrum of simulated signal C. Fig.3.Time-history curves of components with EEMD method. The signal-to-noise ratio(SNR)of the original signal was 16.831.After de-noising through the EMD and EEMD methods,the SNRs of the signal were 21.463 and 25.012, respectively.The EEMD method obtains a higher SNR.This proves that the EEMD method is feasible and more effective. 3.2.System order determination based on singular entropy The system order is one of the most important parameters for modal identification in the time domain.For the ERA,it is necessary to construct a Hankel matrix and to determine the orders of the Hankel matrix and system matrix.Because the system is unknown when it is experiencing ambient excitation, and its order is unknown in advance,a tentative system order must be provided before modal parameter identification.Here we introduce the concept of entropy to overcome the difficulty of system order determination. 3.2.1.Singular entropy Considering the structural dynamic response signal x,the original signal x(t)=[x(t)x(t+τ)x(t+2τ)…]is mapped into the phase space with a size of m×n by means of a time-lapse technique(τ is the time lapse),and the reconstructed attractor orbit matrix L can be formed like a Hankel matrix as follows: Through singular value deposition of the matrix L,the singular spectrum σican be obtained based on the main diagonal element fi(i=1,2,…,l)of the diagonal matrix and can be described as follows(Yang and Peter,2003): The singular spectrum indicates energy proportions of the various state variables throughout the system.In order to investigate the changes of signal information with the singular spectrum order,the concept of the singular entropy increment is introduced.Its formula is where ΔEiis a increment of singular entropy on the order of i. Fig.4.Frequency spectra of components with EEMD method. In view of this,we can use the singular entropy increment spectrum to determine system order.When the singular entropy increment tends toward stabilization,the corresponding order can be considered an approximated system order,or, based on the required accuracy for projects,when ΔEi≤ξ,the smallest integer i can be considered the system order,where ξis a parameter.After the eigenvalue elimination of the nonmode items(non-conjugate roots)and the conjugate items (repetitive modes)of the system,the order of the system is i/2 (Lian et al.,2009). Fig.5.Reconstructed sinusoidal signal and noise signal from EEMD decomposition results. Fig.6.Reconstructed sinusoidal signal and noise signal from EMD decomposition results. 3.2.2.Application of singular entropy to system order determination A comparison study was made with two simulated signals: signal A was an impulse signal composed of three impulse functions,and signal B was a mixing signal composed of the impulse signal and normally distributed white noise with a mean of 0 and a standard deviation of 1.The time period was 0-6.28 s,and the time interval was 0.01 s.The time-history curves of signals A and B are shown in Fig.7. Fig.7.Time-history curves of two signals. Fig.8 shows the calculated singular entropy increment of the two simulated signals.It is obvious that,for an impulse response signal not affected by noise,a greater singular entropy increment value is correlated with a lower order.In addition,in the transition region between lower and higher orders,a smaller SNR value of the impulse response signal is correlated with a smaller decrease in the singular entropy. Thus,for the same signal,as the singular entropy increment begins to decrease toward the asymptotic value,the available characteristic information of the signal tends to become saturated(and approximately full).No matter how serious the interference in the signal,the order corresponding to the singular spectrum that extracts completely effective characteristic information is definite.The singular entropy increment corresponding to orders greater than the determined order is caused by noise with a wide frequency band and should be ignored.Thus,the order of this simulated signal A can be determined to be 7,and after the eigenvalue decomposition of matrix G and eigenvalue elimination of the nonmode items(non-conjugate roots)and the conjugate items (repetitive items),the effective order of the impulse response function is 3. 3.3.False mode elimination The tentative order should include as much structure vibration information as possible in order to avoid losing modes, leading to the occurrence of false modes.Therefore,three criteria are proposed to eliminate false modes: Fig.8.Relationship between order and singular entropy increment of simulated signals. (1)The obvious non-structural natural frequency from identification results(such as the unit vibration frequency and flow fluctuation-induced vibration frequency)can be removed. (2)The identified modes with a structural damping ratio beyond the range of 0.01-0.1 are false and should be eliminated. (3)After determination of the system order using the singular entropy increment spectrum,a modal parameter stabilization diagram is obtained by increasing the number of row spatial data of the Hankel matrix from iminto imax(imaxis a relatively larger value that satisfies the size requirement of j/imax).When the differences in the frequency and damping ratio between two adjacent points in the modal parameter stabilization diagram are within the limit of tolerance,the modes corresponding to both points are temporarily considered to be real modes.After investigation of all points,the stable and most frequent modes are considered the real modes. 4.1.Powerhouse layout The powerhouse layout of a roof overflow hydropower station with bulb tubular units uses a combination of a spillway and powerhouse.The spillway overlaps all or part of the powerhouse in the plane projection.Both share the water retaining wall(Xie and Huang,1981). The Bingling Hydropower Project consists of a powerhouse in a river channel,roof overflow surface outlets,discharge bottom orifices,sand-flash outlets,and left and right assisting dams.The dam crest elevation is 1751.0 m.There are five bulb tubular units in the main channel.Each unit's capacity is 48 MW,with a rated speed of 107.1 r/min,rated flow of 335 m3/s,and rated water head of 16.1 m.There is a sand-flash outlet on the left side of the 1st,2nd,and 4th units.Five surface outlets with a width the same as the channel width are arranged on the units.Under the conditions of unit operation,surface outlet discharge,and surface outlet discharge in conjunction with unit operation,prototype observation was made for the 4th powerhouse dam section and unit,respectively.The 4th powerhouse dam section and unit are shown in Fig.9. Fig.9.Sketch of 4th powerhouse dam section and unit. 4.2.Establishment of finite element model In this study,the commercial finite element software (ANSYS)(Ji et al.,2006)was used to simulate the structure and calculate the main modal parameters.Based on the layout of the powerhouse,a three-dimensional model was established,and the flow passage of the turbine,a surface outlet floor,sand-flash outlets,and channels with a size larger than 1.0 m×1.0 m×1.0 m were simulated.The frame structure on the powerhouse was not included in the model.Accessory equipment such as cranes,treated as added mass,was exerted on corresponding nodes.The boundary conditions were set, including multiple constraints on the bottom of foundation, normal chain constraints at the four sides,and a free boundary all around the concrete structure.The meshes of the powerhouse model and the full dam model are shown in Fig.10.The natural frequencies of the 1st through 10th modes of the whole powerhouse were 3.239,5.069,5.884,8.472,9.184,9.467, 9.532,9.919,10.627,and 10.987 Hz,respectively.Fig.11 shows the first three mode shapes of the powerhouse. Fig.10.Meshes of powerhouse and full dam models. Fig.11.First three mode shapes of powerhouse. Various dynamic loads were used as the sources of environmental excitations.The response signals of the powerhouse were collected from a DP low-frequency vibration transducer with a sampling rate of 400 Hz.ERA was used to obtain the modal information from response data of the measuring point in section B with an elevation of 1732.0 m(⑤in Fig.9).SSI was used to obtain the dynamic displacement response from nine measuring points in section B,including a measuring point with an elevation of 1732.0 m,two measuring points on the ground of the left and right guide walls,and six measuring points 1.0 m,2.5 m,and 5.0 m away from the ground of the left and right guide walls.The data collection was completed under discharge in conjunction with unit operation conditions. 5.1.De-noising and order determination Taking a measurement point in section B as an example, response data(Fig.12)were decomposed using the EEMD method.This process obtained seven IMF components and a remainder,as shown in Figs.13 and 14.The time-domain waves of IMF1 and IMF2 show the characteristics of white noise,and the remainder is the harmonic component.IMF1, IMF2,and the remainder should be removed.The de-noised signal can be obtained by reconstructing the rest of IMF components.A comparison between the original signal and the de-noised signal is shown in Fig.15. The change of the singular entropy increment after denoising is shown in Fig.16.The singular entropy increment decreases slowly and tends to stabilize when the order is larger than 8.This means that the available characteristic information of the signal tends to become saturated(and approximately full).The singular entropy increment corresponding to orders larger than 8 can be neglected and considered the results of broadband noise.According to the complex mode theory, eliminating the non-mode items(non-conjugate roots)and the conjugate items(repetitive items)of the system,the modal order of the structure is 4. 5.2.Identification results of ERA The damped-free vibration signals of the original and denoised systems were extracted from the output signal through RDT(Fig.17).After identification of modal parameters with ERA,according to the determined system order and false mode elimination principles,the frequencies of the unit vibration and flow fluctuation were clearly seen to be nonstructural natural frequencies,including the frequency of flow fluctuation induced by discharge(≤2 Hz),the lowfrequency vortex core(band)vibration frequency (0.297-0.595 Hz),the vibration frequency of the runner blade, the frequency of vibration due to incorrect connection relationships and its doublefrequency(8.925Hzand 17.850 Hz),and the Karman vortex-induced vibration frequency(80-100 Hz)(Cao et al.,2007).The modes corresponding to these frequencies and the modes with damping ratios beyond the range of 0.01-0.1 were eliminated.The modal identification results are shown in Table 1. It can be observed from Table 1 that,when ERA is used for the original signal,there are fairly large differences between simulated frequency values and identified results for the first three modes,and the damping ratios are also significantly larger.After the fifth mode,all of the frequencies are noise frequency,and the structural modal information is covered.Although the frequency value of the fourth mode is close to the simulated one,the validity cannot be determined due to the unknown order of the excitation system.In contrast,the de-noised identified results for the first four modes are very close to the simulated values,therelative errors of frequencies are within 10%,and the identified damping ratio is within the range from 0.01 to 0.1.Even though the order number of operational modes of the powerhouse is determined to be 4,the relative error between the identification results of high-order(5th to 10th)natural frequencies obtained from ERA and the simulated values are less than 15%,and the identified damping ratios are within the range from 0.01 to 0.1.Generally,the inherent dynamic characteristics of a hydraulic structure are mainly reflected in the first few modes.Therefore,these results meet engineering precision requirements. Fig.12.Time-history curve and frequency spectrum of response signal. Fig.13.Time-history curves of all components with EEMD method. Fig.14.Frequency spectra of all components with EEMD method. Fig.15.Comparison between original signal and de-noised signal. Fig.16.Change of singular entropy increment with order. Fig.17.Damped-free vibration signals extracted through RDT. Fig.18.Frequency stabilization diagrams of original and de-noised signals. 5.3.Identification results of SSI The first task was analysis of the original and de-noised displacement response data from nine measurement points through the SSI method.Then,as in the ERA identification process described above,the frequencies of false modes were eliminated.The frequency stabilization diagram is shown in Fig.18.After averaging all the frequencies and damping ratios of real modes,stable identification results were obtained.The identified results are shown in Table 2. Table 1 Modal identification results of ERA. Table 2 Modal identification results of SSI. It can be seen from Table 2 that,for the original signal,SSI can identify the first-order modal parameters,the frequency and damping ratio for the second and third modes are too large because of noise,and the modal information is completely covered by noise after the fourth mode.Meanwhile,the denoised identification results for the first mode are very close to the simulated results.However,the relative errors of frequency for the rest of the modes are over 10%.Compared with ERA,the precision of identification results of SSI is poor, probably due to incomplete arrangement of measurement points or because SSI is unsuitable for identifying modal parameters of a roof overflow powerhouse. A modal parameter identification technique was developed for determination of modal parameters of the powerhouse of a roof overflow hydropower station with bulb tubular units under ambient excitation.The EEMD method was used to decrease noise,RDT was used to extract free-decaying responses,the singular entropy was used to determine the modal order, multiple criteria were used to eliminate false modes,and the ERA and SSI were used to identify modal parameters.The following conclusions can be obtained: (1)The EEMD,singular entropy,and multiple criteria, combined with ERA,can precisely identify the low-order modal parameters of the structure under study.For highorder modal parameters,the identification precision decreases,but is still within the acceptable error limits. (2)Although the SSI method is convenient,compared with ERA,the precision of identification results is poor for this structure,probably due to incomplete arrangement of measurement points or because the SSI method is unsuitable for identifying modal parameters of a roof overflow powerhouse. Specific conclusions require further prototype observation for authentication. (3)The EEMD possesses attractive properties,such as a strong noise reduction ability,recovery of the entire useful vibration signal,and a high calculation efficiency.The singular entropy can determine the order of operational modes of structures when the order of the vibrated structure is unknown and the structure is experiencing unknown input excitation,and multiple criteria can help eliminate the false modes effectively. (4)The relative errors of frequencies in the first four modes were within 10%for the ERA method,and the method has demonstrated its robustness and reliability when applied to identification of the modal parameters and real-time monitoring of hydraulic structures with strong noise with complex ambient excitation. References Anderson,B.D.O.,Skelton,R.E.,1988.The generation of all q-Markov covers.IEEE Trans.Circuits Syst.Video Technol.35(4),375-384. Brincker,R.,Zhang,L.,Andersen,P.,2000.Modal identification from ambient responses using frequency domain decomposition.In:Proceedings of SPIE: The International Society for Optical Engineering.Society of Photo-optical Instrumentation Engineers,Bellingham,pp.625-630. Brinker,R.,Zhang,L.,Andersen,P.,2001.Modal identification of output-only systems using frequency domain decomposition.Smart Mater.Struct. 10(3),441-445.http://dx.doi.org/10.1088/0964-1726/10/3/303. Cao,W.,Zhang,Y.L.,Ma,Z.Y.,Chen,J.,2007.Vibration analysis of roof overflow powerhouse.J.Hydraulic Eng.38(9),1090-1095(in Chinese). Chang,S.G.,Yu,B.,Vetterli,M.,2000.Adaptive wavelet thresholding for image denoising and compression.IEEE Trans.Image Process.9(9), 1532-1546. Cheng,L.,Zheng,D.J.,2014.The identification of a dam's modal parameters under random support excitation based on the Hankel matrix joint approximate diagonalization technique.Mech.Syst.Signal Process. 42(1-2),42-57.http://dx.doi.org/10.1016/j.ymssp.2013.07.015. Darbre,G.R.,De Smet,C.A.M.,Kraemer,C.,2000.Natural frequencies measured from ambient vibration response of the arch dam of Mauvoisin. Earthq.Eng.Struct.Dyn.29(5),577-586.http://dx.doi.org/10.1002/ (SICI)1096-9845(200005)29:5<577::AID-EQE924>3.0.CO;2-P. D¨ohler,M.,Lam,X.B.,Mevel,L.,2013.Uncertainty quantification for modal parameters from stochastic subspace identification on multi-setup measurements.Mech.Syst.Signal Process.36(2),562-581.http://dx.doi.org/ 10.1016/j.ymssp.2012.11.011. D¨ohler,M.,Mevel,L.,2013.Efficient multi-order uncertainty computation for stochastic subspace identification.Mech.Syst.Signal Process.38(2), 346-366.http://dx.doi.org/10.1016/j.ymssp.2013.01.012. Fu,Z.F.,1990.Vibrational Modal Analysis and Parameter Identification. Machinery Industry Press,Beijing(in Chinese). Han,J.P.,Li,D.W.,Wang,F.X.,2010.Modal parameter identification based on Hilbert-Huang transform and stochastic subspace identification.J.Earthq. Eng.Eng.Vib.30(1),53-59(in Chinese). Hong,V.M.,Masato,A.,Yozo,F.,Kiyoyuk,K.,2001.The eigensystem realization algorithm for ambient vibration measurement using laser Doppler vibrometers.In:Proceedings of the American Control Conference.IEEE,Arlington,pp.435-440. Huang,N.E.,Shen,Z.,Long,S.R.,Wu,M.C.,Shih,H.H.,Zheng,Q.N., Yen,N.C.,Tung,C.C.,Liu,H.H.,1998.The empirical mode decomposition method and the Hilbert spectrum for nonlinear and non-stationary time series analysis.Proc.R.Soc.A Math.Phys.Eng.Sci.454, 903-995.http://dx.doi.org/10.1098/rspa.1998.0193. Ibrahim,S.R.,Pappa,R.S.,1982.Large modal survey testing using the Ibrahim time domain identification technique.J.Spacecr.Rockets 19(5), 459-465.http://dx.doi.org/10.2514/3.62285. James,J.H.,Carne,T.G.,Lauffer,J.P.,1996.The natural excitation technique (NExT)for modal parameter extraction from operating structures.Int.J. Anal.Exp.Modal Analysis 10(4),260-277. Ji,X.D.,Qian,J.R.,Xu,L.H.,2006.Experimental study of modal parameter identification in a simulated ambient-excited structure.J.Tsinghua Univ. (Sci.Technol.)46(6),769-772. Jing,J.,Meng,G.,2009.A novel method for multi-fault diagnosis of rotor system.Mech.Mach.Theory 44(4),697-709.http://dx.doi.org/10.1016/ j.mechmachtheory.2008.05.002. Juang,J.N.,Pappa,R.,1985.An eigensystem realization algorithm for modal parameter identification and model reduction.J.Guid.Control Dyn.8(5), 620-627.http://dx.doi.org/10.2514/3.20031. Juang,J.N.,Cooper,J.E.,Wright,J.R.,1988.An eigensystem realization algorithm using data correlations(ERA/DC)for modal parameter identification.Control Theory Adv.Technol.4(1),5-14. Juang,J.N.,1994.Applied System Identification.Prentice Hall,Englewood Cliffs. Kim,T.,1998.Frequency-domain Karhunen-Loeve method and its application to linear dynamic systems.AIAA J.36(11),2117-2123.http://dx.doi.org/ 10.2514/2.315. Lee,J.W.,Kim,J.D.,Yun,C.B.,Yi,J.H.,Shim,J.M.,2002.Health-monitoring method for bridges under ordinary traffic loadings.J.Sound Vib.257(2), 247-264.http://dx.doi.org/10.1006/jsvi.2002.5056. Lew,J.S.,Juang,J.N.,Longman,R.W.,1993.Comparison of several system identification methods for flexible structures.J.Sound Vib.167(3),461-480. Li,P.,Wang,S.Q.,Li,H.J.,2011.Noise handling of the eigensystem realization algorithm.Periodical Ocean Univ.China 41(7-8),176-182(in Chinese). Li,S.H.,Lian,J.J.,2009.Genetic algorithm for hydraulic power house modal parameters identification.J.Tianjin Univ.42(1),11-16(in Chinese). Lian,J.J.,Li,H.K.,Zhang,J.W.,2009.ERA modal identification method for hydraulic structures based on order determination and noise reduction of singular entropy.Sci.China Ser.E:Technol.Sci.52(2),400-412.http:// dx.doi.org/10.1007/s11431-008-0200-z. Lian,J.J.,Zhang,Y.,Liu,F.,Yu,X.H.,2013.Vibration source characteristics of roof overflow hydropower station.J.Vib.Shock 32(18),8-14(in Chinese). Moonen,M.,De Moor,B.,Vandenberghe,L.,Vandewalle,J.,1989.On-and off-line identification of linear state-space models.Int.J.Control Autom. Syst.49(1),219-232.http://dx.doi.org/10.1080/00207178908559631. Peeters,B.,Roeck,G.D.,Hermans,L.,Wauters,T.,Krmer,C.,De Smet,C., 1998.Comparison of system identification methods using operational data of a bridge test.In:Proceedings of ISMA 23,The International Conference on Noise and Vibration Engineering.ISMA,Leuven,pp.923-930. Peeters,B.,Roeck,G.D.,2001.Stochastic system identification for operational modal analysis:A review.J.Dyn.Syst.Meas.Control 123(4),659-667. http://dx.doi.org/10.1115/1.1410370. Petsounis,K.A.,Fassois,S.D.,2001.Parametric time-domain methods for the identification of vibrating structures:A critical comparison and assessment.Mech.Syst.Signal Process.15(6),1031-1060.http://dx.doi.org/ 10.1006/mssp.2001.1424. Qian,Z.W.,Cheng,L.,Li,Y.H.,2011.Noise reduction method based on singular value decomposition.J.Vib.Meas.Diagn.31(4),459-463,534 (in Chinese). Rato,R.T.,Ortigueira,M.D.,Batista,A.G.,2008.On the HHT,its problems, and some solutions.Mech.Syst.Signal Process.22(6),1374-1394.http:// dx.doi.org/10.1016/j.ymssp.2007.11.028. Schoukens,J.,Dobrowiecki,T.,Pintelon,R.,1998.Parametric and nonparametric identification of linear systems in the presence of nonlinear distortions:A frequency domain approach.Autom.Control 43(2),176-190. http://dx.doi.org/10.1109/9.661066. Sweeney,K.T.,McLoone,S.F.,Ward,T.E.,2013.The use of ensemble empirical mode decomposition with canonical correlation analysis as a novel artifact removal technique.IEEE Trans.Biomed.Eng.60(1), 97-105.http://dx.doi.org/10.1109/TBME.2012.2225427. Wu,Z.H.,Huang,N.E.,2009.Ensemble empirical mode decomposition:A noise-assisted data analysis method.Adv.Adapt.Data Anal.1(1),1-41. http://dx.doi.org/10.1142/S1793536909000047. Xie,Z.X.,Huang,Z.W.,1981.Development of roof overflow hydropower station.Water Power 17,24-32(in Chinese). Yang,W.X.,Peter,W.T.,2003.Development of an advanced noise reduction method for vibration analysis based on singular value decomposition. NDT E Int.36(6),419-432.http://dx.doi.org/10.1016/S0963-8695(03) 00044-6. Zhang,H.D.,Zhou,Y.,Lian,J.J.,2007.A method based on ARMA model for modal parameter identification of a power house.J.Vib.Shock 26(5), 115-118,159(in Chinese). 1 November 2014;accepted 30 August 2015 This work was supported by the Foundation for Innovative Research Groups of the National Natural Science Foundation of China(Grant No. 51321065)and the National Natural Science Foundation of China(Grants No. 51379140,51209158,and 51379177). *Corresponding author. E-mail address:fj_np@126.com(Ji-jian Lian). Peer review under responsibility of Hohai University. http://dx.doi.org/10.1016/j.wse.2015.12.004 1674-2370/?2016 Hohai University.Production and hosting by Elsevier B.V.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).
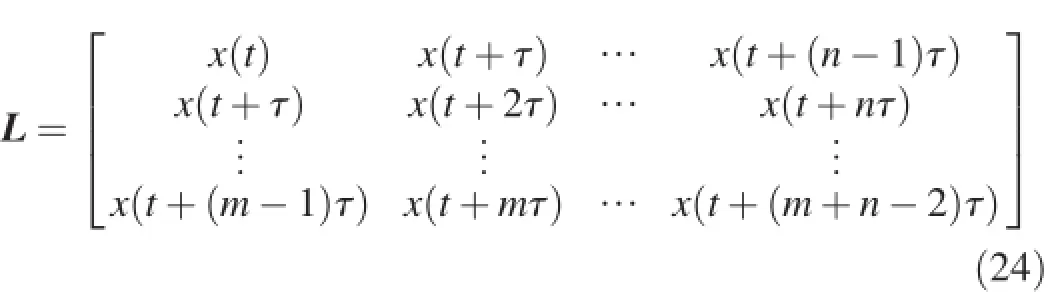


4.Powerhouse layout and finite element model
5.Modal identification

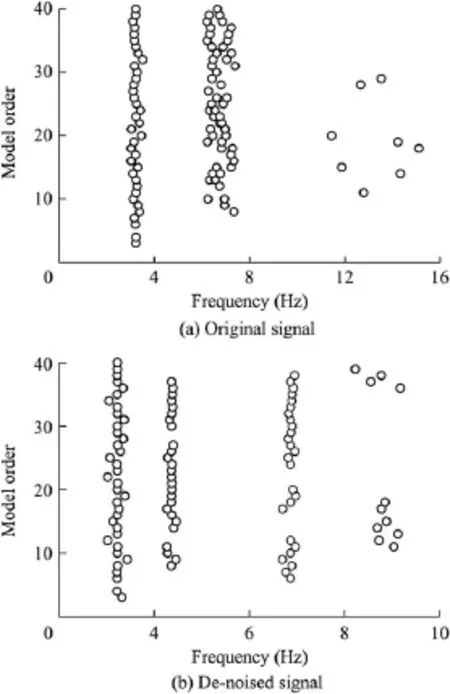
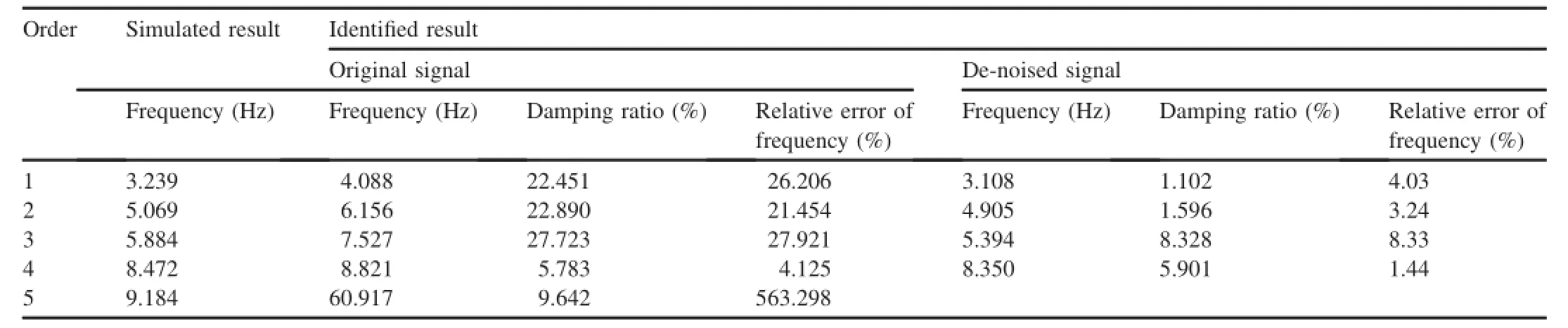

6.Conclusions
 Water Science and Engineering2016年1期
Water Science and Engineering2016年1期
- Water Science and Engineering的其它文章
- Information for Authors
- An experimental study on embankment failure induced by prolonged immersion in floodwater
- Improvement of wind field hindcasts for tropical cyclones
- Optimization of multi-model ensemble forecasting of typhoon waves
- Performance of a data-driven technique applied to changes in wave height and its effect on beach response
- Application of SWAN+ADCIRC to tide-surge and wave simulation inGulf of Maine during Patriot's Day storm
