Statistical mechanics and artificial intelligence to model the thermodynamic properties of pure and mixture of ionic liquids☆
Fakhri Youse fi*,Zeynab Amoozandeh
Department of Chemistry,Yasouj University,Yasouj 75914-353,Iran
1.Introduction
The research community has considered ionic liquids(ILs)as interesting compounds since 2005.These compounds have lots of advantages when compared to other solvents.Phosphonium-based ILs are a readily accessible family of ILs.They have greater properties as compared with nitrogen cation-based ILs in some applications.The ILs are used as extraction and synthesis solvents,electrolytes in batteries and super capacitors,and in corrosion protection[1].Pyridinium-based ILs can also be used as extractants to remove aromatic sulfur compounds in extractive desulfurization.They can effectively extract the sulfur content from the oil phase[2].On the other hand,pyridinium-based ILs are applied in the synthesis of organic compounds.For example,they increase the reaction rate and product yields of Diels–Alder reactions[3].
Binary mixtures of ILs with extra fluids have been employed for electrochemical applications(solarcells)[4].Besides,the mixtures of ILs can improve the thermodynamic and transport properties of working fluids as well as the efficiency of the chemical equipments such as batteries,photo electrical cells,and other electro chemical equipment.Moreover,the IL mixtures with supplementary compounds such as alcohols permit the modification and control of the properties of the mixtures to suit a given situation[4].
It should be stated that although there are a lot of experimental data for volumetric properties of ILs,prediction of these properties is still a vital task because these compounds have been in focus as substances offering many highly talented applications[5–8].It is needed to decide whether the use of these fluids could be extended from the laboratory level to large-scale industrial applications,therefore the prediction of volumetric properties of these fluids is a key task.
In recent times,several models have been proposed to predict the densities of ILs.For example,a group contribution equation of state based on electrolyte perturbation theory is used to calculate the densities of ILs by Wang et al.[9].They separated ILs to several groups counting cations,anions,and alkyl substituent groups.The performance of the model was examined by describing the densities of a large number of imidazolium-based ILs over a broad range of temperatures(293.15–414.15 K)and pressures(0.1–70.43 MPa).The model was found to estimate the densities of ILs with an overall average relative deviation(ARD)of 0.41%for correlation and an ARD of 0.63%for prediction.
Shenet al.[10]calculated the densities of ILs using the Patel–Teja equation of state together using the modified Lydersen–Joback–Reid group contribution method.The correlation accuracy in terms of overall average absolute relative deviation(AARD)is 4.4%for 918 data points of density at ambient temperature and atmospheric pressure.The temperature dependence of Sanchez–Lacombe EOS is modified to find accounts that hydrogen bonding and ionic interactions existed in ILs by Machida et al.[11].They used a simple function in the form of the Langmuir equation that reduced to the original SL EOS at high temperature.The ε*-modified SL EOS could represent volumetric data for ionic liquids to within an absolute average deviation(AAD)of 0.054%,whereas,the original Sanchez–Lacombe EOS gave AAD value of 0.21%.
In addition,Abildskovet al.[12,13]clarified a technique to correlate the densities of pure ILs based on a corresponding state form for the direct correlation function integrals.The results show excellent agreement with the experimental data for nearly all substances over all ranges of conditions.The obtained AADs of these models from experimental data for 7 and 46 set of ILs are 0.051%and 0.034%,respectively.
Moreover,this method is improved to predict the phase behavior of mixtures ofILs and organic solvents[14].The results show that the average absolute deviations of this method from literature for ionic liquid mixture at high and low pressure are 0.17%and 0.21%,respectively.
It should be stated that for predicting the densities of ILs some computational methods have been recommended.For example,the specific density and molar liquid volume of 40 imidazolium-based ionic liquids were predicted using the COSMO-RS method,a thermodynamic model based on quantum chemistry calculations by Palomaret al.[15].Consequently,the calculated and experimental density values of ILs(and also other common solvents)were fitted by linear regressions with coefficient of determinationR2>0.99 and standard deviations SD<20 kg·m-3..As well,Trohalakiet al.[16]reported QSPR method for predicting the densities of ILs.Ostwald solubility coefficients and partition coefficients of organic solutes in eight different ionic liquids are correlated by molecular descriptors calculated solely from their structures.Two to four-parameter best multilinear regression models were obtained with coefficients of determination ranging from 0.913 to 0.992.
Besides,the different thermodynamic properties of ILs are modeled using several SAFT equations of state.For example,Rahmati-Rostamiet al.[17]added an additional polar contribution to the Helmholtz free energy to both PC-SAFT and SAFTVR equations of state for calculating of the solubility of H2S in ILs.They enhanced the accuracy of the proposed model,but,this came at the expense of increasing the number of model parameters.For pure components,the average relative deviation between the calculated and experimental densities is less than 2.42%in the PC-SAFT model and 5.44%in the SAFT-VR approach and for binary mixture of ILs and H2S,the average deviation of less than 5%in the calculation of the mole fraction of H2S in the ionic liquids.Also,Hunget al.[18]used an extended Riedel(ER)model and an artificial neural network(ANN)model for density prediction of mixtures of ILs and molecular solvents.Average absolute relative deviations of the ER model and the ANN model are 0.92%and 0.37%,respectively,which indicates that both developed models can achieve a universal and accurate density prediction of IL mixtures.
Some simple and accurate van der Waals(vdW)-family equations of state are recognized to predict the volumetric properties of molecular and ILs using Papariet al.[19].The average absolute deviation of the calculated densities of studied ILs from vdW–CS–β,compared with those obtained from the experiment and the AAD for 997 data point is 1.42%.Yousefiet al.[20,21]extended the TM EOS[22](based on statistical–mechanical perturbation theory)to pure and binary mixtures of ILs.The overall average absolute deviation of calculated densities from experimental data for 1633 data points for nine pure ILs is 2.05%.Besides,this model predicts the densities of mixture of ILs for 428 data points with a mean AAD of 1.69%.
However,these models have some limitations due to the use of many adjustable parameters or combining rules.Therefore,they sometimes need a sufficient amount of data for calibration and justification purposes that makes them computationally incompetent.In such cases,an artificial neural network(ANN)can be an appropriate option for modeling the different thermodynamic properties.The relationship between the physical and thermodynamic properties is extremely nonlinear,and the ANN approach is a particularly capable algorithm to approximate a certain property such as density using learning the relations between the input and output data[23].Consequently,thermodynamic properties can be modeled by the ANN method as an alternative tool[24,25].Recently,the ANNs have been intensively applied to different fields.The major reason for this fast development and varied applications of neural networks is their capability to virtually approximate any function in a stable and efficient way.
Formerly,Tao–Mason equation of state(TM EOS)[22]has been successfully improved to fluid and their mixtures[26–28].Besides,the applications of equation of state and artificial neural networks approaches[23,29]were studied to predict the properties of pure polymers.This research concentrates on the potential of both new versions of TM EOS and ANN with principle component analysis(PCA)to estimate of thermodynamic properties of ILs and their mixtures in broad range of temperatures,pressures and mole fractions.As a final point,the efficiency of these methods is evaluated with experimental data and other equations of state.
2.Theory
2.1.Tao-Mason equation of state
The common equations of state are rooted in the van der Waals family of cubic equations or equations based on the results of statistical mechanics and computer simulations[30–32].The TM EOS belongs to the second category.Tao and Mason added a perturbation correction term(which affects the attractive forces)to Ihm–Song–Mason(ISM)equation of state[33]to present an advanced equation of state(TM EOS)[22].The TM EOS for pure system is as follow:where ω,λ and ρ are the Pitzer acentric factor,adjustable parameter and the numberdensity,respectively.TC,B2,αand b are the critical temperature,the second virial coefficient,the scaling parameter,the effective van der Waals co-volume,respectively.
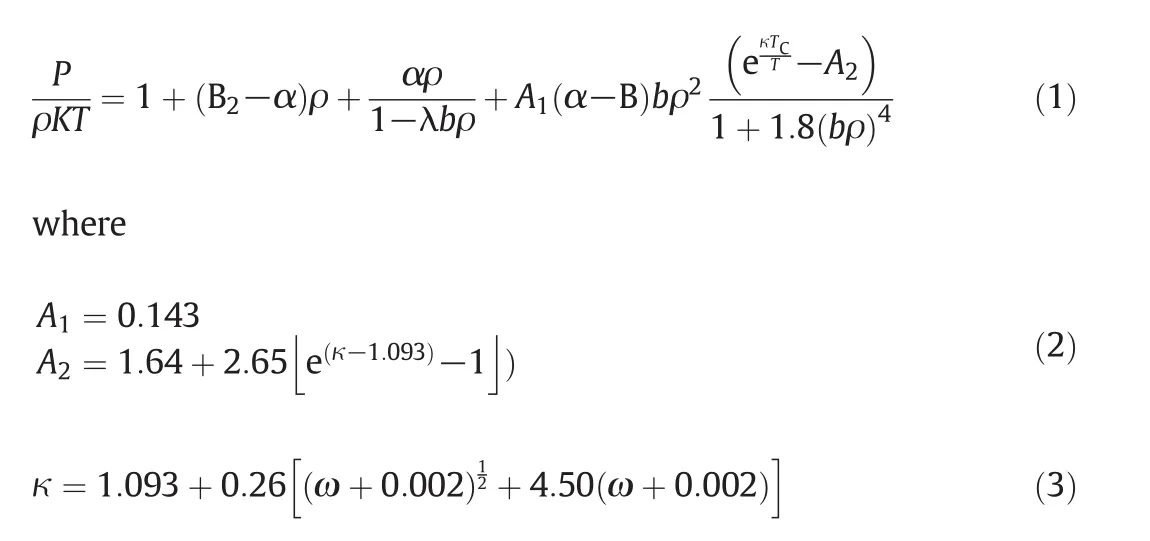
The second virial coefficient together with the parameters α,andbrequires the usage of the TM EOS.It should be mentioned that if the intermolecular potential is not accessible,the information of experimental second virial coefficient data is sufficient to calculate the values of α andb[22].In this case,there are numerous functions,usually based on the corresponding state principal that lead to the computation of the second virial coefficient.
In the main text,α and b are formulated based on the Boyle temperature(TB)and volume(VB)[22].

where the constanta1,a2,c1,andc2are-0.0648,1.8067,2.6038,and 0.9726,respectively.
The Tsonopoulos correlation can be calculated second virial coefficient in the lack of adequate experimental data[34].

In this project,a new corresponding state correlation was tested in order to assess whether TM EOS can be applied to predict the densities of pure ILs and their mixtures.B2is correlated by means of one new scaling parameter(molar density at 298.15 K)that has been developed and presented as follow:
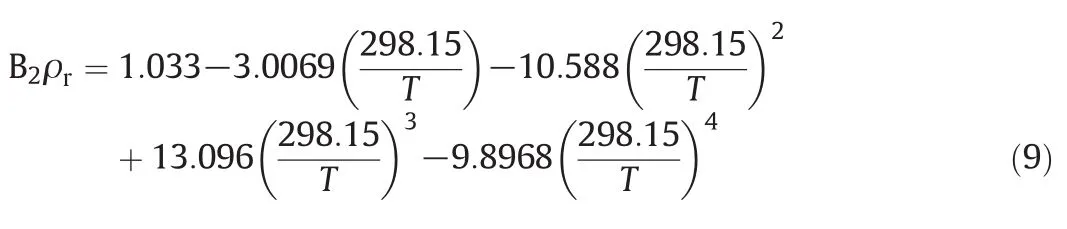
where ρris density at room temperature.
In Tao and Mason examination,the dimensionless quantities α/VBandb/VBare universal functions of the reduced temperature(T/TB).They can be calculated from the exponential for mulae based on a LJ(12-6)model potential[22].At this point,the scale factorsTBandVBare the Boyle temperature and volume,and can be stated based on the room temperature parameters.The empirical equations given in Ref.[22]for α/VBandb/VBas a function of T/TBcan be rescaled by 298.15 K and ρr(density at 298.15 K)in place ofTBandVBas pointed out by Eslami[35].
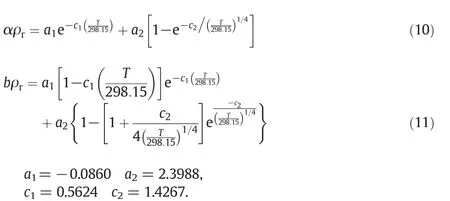
Thus,the temperature-dependent parameters of the equation of state can be determined using density value at room temperature.
Before,the TM EOS was extended to the refrigerant mixtures as follow[26]:
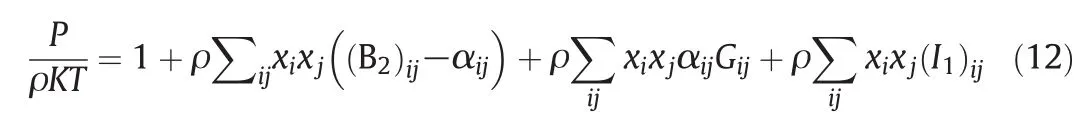
whereGijis a pair distribution function calculated by Ihmet al.[33]:

where η is the packing fraction of the mixture:
For a pure system,I1=(α -B2) ζ(T) Φ(bρ)which Φ(bρ)and ζ(T)are temperature dependence and density dependence parameters.
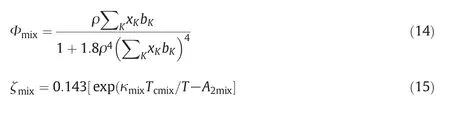
that

whereTcmixis the traditional pseudocritical temperature.
In the present study,the second virial coefficient and two temperature-dependent parameter assessments can be extended to mixtures via simple geometric mean of liquid density at the room temperature:
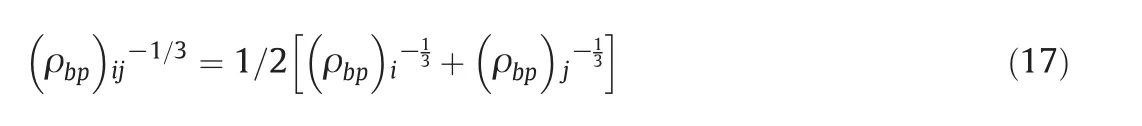
The λ parameter is obtained from some experimentalP-V-Tdata at high density and permits the whole procedure self-correcting.
2.2.ANN modeling
The artificial neural network(ANN)is the non-linear mathematical techniques which get huge attention because of its simplicity,flexibility,and accessibility to different training algorithms as well as its large modeling ability[36–38].An ANN is derived based on the activity process of the human brain and has been applied to model of many scientific disciplines up to now[37–40].Several applications and good explanations of the ANN were presented in earlier publications[41,42].
The structure of an ANN forms the input layer(independent variables),the output layer(dependent variables)and one or more neuron layers called hidden layers can be placed between them(Fig.1).The number of net layers,the number of neurons in each layer,the nature of learning algorithms and neurons transfer functions define the construction of an the ANN.
2.3.Principles component analysis(PCA)
PCA is a statistical technique that modifies an orthogonal transformation to change a set of observations of maybe correlated variables to a set of values of linearly uncorrelated variables named principal components.It is a method of recognizing patterns in data,and stating the data in such a way as to highlight their similarities and dissimilarities.The PCA is a great tool for analyzing data,while patterns in data can be hard to find in data of high dimension.The other key advantage of the PCA is that you compress the data by reducing the number of dimensions,without much loss of information.
If the data set is jointly normally distributed,the PCA is guaranteed to be independent.The PCA is sensitive to the relation of the original variables[43].
As a final point,the PCA was used to make a classifier system more effective and it is based on the assumption that most information about classes is contained in the directions along which the variations are the largest.The details of the PCA are clarified in Ref.[44,45].
2.4.Network training and selection of the best network architecture
Multilayer perceptron(MLP)is the most regular neural network technique in solving problems.The MLP learns the data pattern by means of algorithms known as “training”,these algorithms adjust the weights of the neurons that are consistent with the error between the values of actual and target output where they provide non-linear regression between inputs and output variables and are very precious in identifying designs in complex data.One of the most important training algorithms is the back-propagation algorithm that extensively used to training of the ANN in numerous applications.
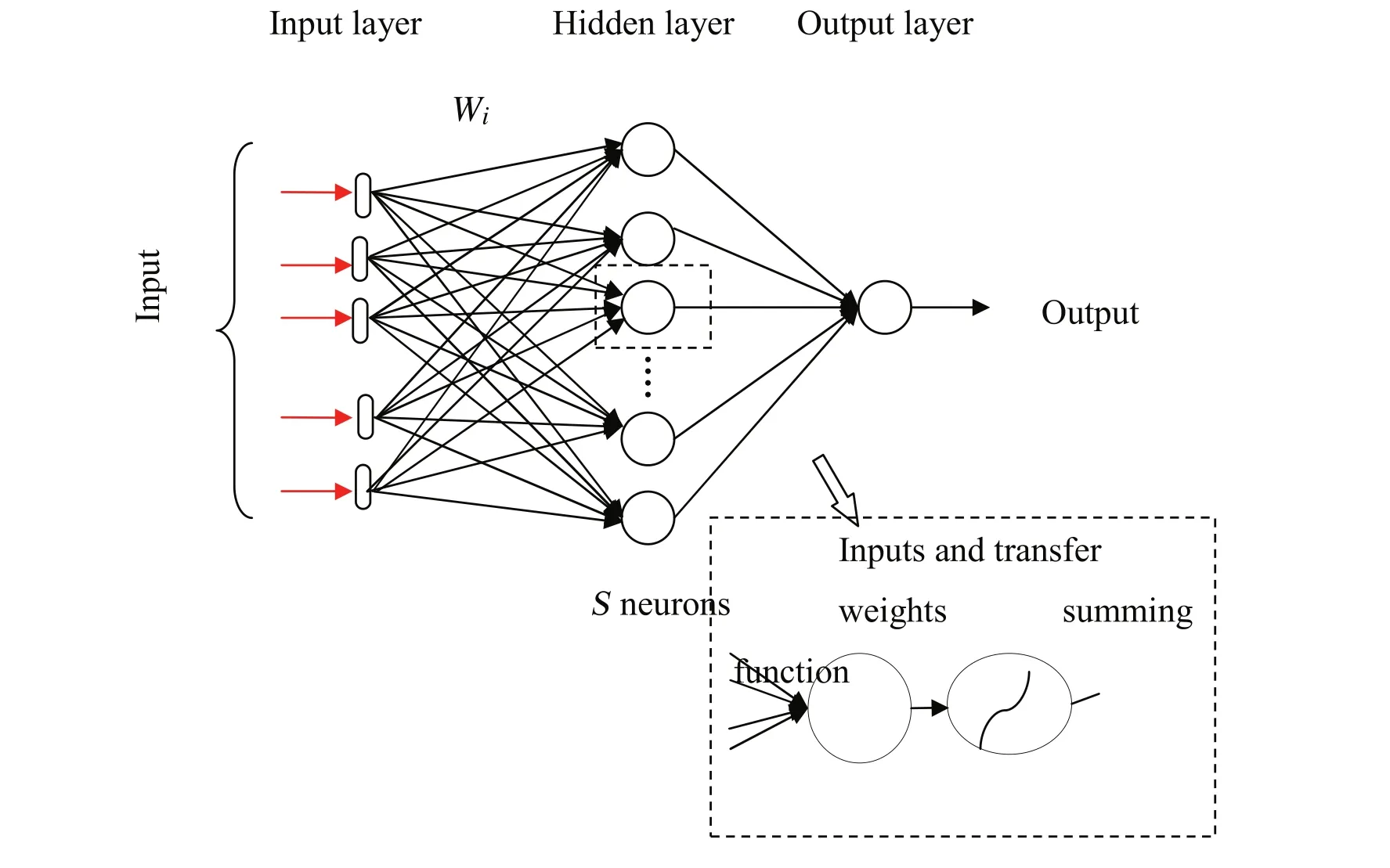
Fig.1.Topology of conventional P-S-1 MLP.
Two transfer functions that is used in the hidden layer and output layer are Hyperbolic tangent sigmoid transfer function “Tansig”and Linear transfer function “Purelin”,respectively.Also,the back propagation algorithm of Levenberg–Marquardt(trainlm),was used to determine the best network structure.The trial and error method is the most basic method of training a net.The number of hidden layers is to be chosen depending on the difficulty of the problem,but generally one hidden layer is suitable to model most of the problems.In this technique,the number of hidden layers is initially considered one and varied one by one to attain the desire objective function outputs using the trial and error approach.This leaning is continued to achieve the number of neurons which leads to the lowest error for the testing subset and presented as the best number of neurons in the hidden layer.
The average absolute deviation(AAD)and coefficient of determination(R2)values(mathematical definition of the errors criteria)are defined as follow:

3.Result and Discussion
The volumetric properties of pure ILs and some mixtures were approximated from the improved TM EOS.Then,the ANN with PCA was trained over the whole range of temperatures,pressures and mole fractions.
Some modifications are required to the extent of TM EOS for pure and mixtures of ILs.1)Tcin Eq.(1)is changed to 298.15 K.2)The second virial coefficient was developed by means of the density and 298.15 K that simply can be computed in contrast to the critical parameters.Consequently,the numbers of input parameters in the Tsonopoulos' correlation[34]are reduced to just one parameter(ρr)using Eslami correlation[35].3)kin Eq.(2)is a weak function of the acentric factor so thatkis estimated to 1.093 andA2was changed to 1.64.4)α andbparameters were formulated using Eqs.(10)and(11),respectively.The input parameters in both equations are the molar density at 298.15 K and more accessible than the Boyle temperature and volume.Overall,using these revisions,the number of input parameters reduced from five(critical temperature,critical pressure,acentric factor,Boyle temperature,and Boyle volume)to one(molar density at 298.15 K).5)In this work,the λ parameter for pure ILs that was adjusted by nonlinear regression method is as follows:

The required parameters for calculation ofλare listed in Table 1.The abbreviation and physical properties of all pure ILs are shown in Table 2.
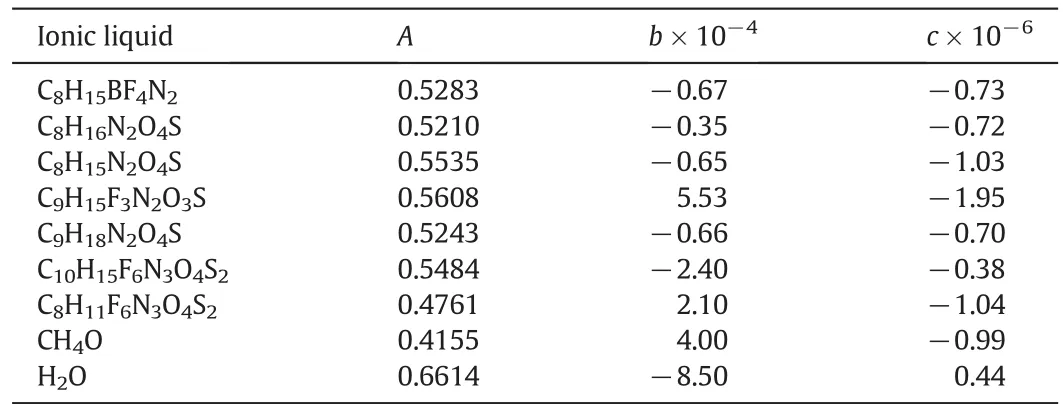
Table 1Coefficients in Eq.(20)
The calculations of molar volume of pure ILs were performed by modified TM EOS with minimum input data and the outcomes of the computed results have been collected sequentially in Table 3.It can be seen that the agreement between the calculated molar density and the experimental data[46–48]is quite appropriate.Generally,theobtained average of the deviations of all pure ILs for 1662 data points and in broad range of temperatures(283.15 K–473.15 K)and pressures(0.1–60 MPa)was found in order of 0.25%.

Table 2Abbreviation and physical properties of pure ionic liquids

Table 3Result of density prediction for all mentioned pure systems
In this work,the obtained deviations from the experimental data for pure ILs are compared with those obtained using Yousefi and Karimi[20].The overall average absolute deviation fromliterature that was calculated by Yousefi and Karimi[20]for 1633 data points is 2.05%.
Alavianmehret al.[49]applied an ion contribution equation of state based on the electrolyte perturbation theory for 29 ILs.They tested this model for estimating densities of 4353 data points over a wide range of temperatures(272 K–472 K)and pressures(0.1 MPa–204 MPa).The average absolute deviation(AAD)of the calculated densities from the experiment is about 0.64%.
In addition,the obtained densities of pure ILs from modified TMEOS were compared with Hosseiniet al.[50]who developed a cubic equation of state(CEOS)to model the volumetric properties of different ILs.The predicted densities of pure ILs were compared with the experimental data over a broad range of pressures(1 to 100 MPa).The AADs of the calculated densities of 948 data points from literature are 1.82%using the critical property and 0.96%using the surface tension and liquid density as scaling parameters.
Furthermore,the densities of binary mixture of ILs based on modified TM EOS in various conditions were computed and compared with experimental data(Table 2)[51,56].
In this study,to predict the densities of ILs mixtures,the temperature(T),mole fraction,molecular weight and total molecular weight are used as input variables and the densities of IL mixtures are used as target.The ranges of input–output variables for each system are given in Table 4.
The MLP is trained,validated,and tested with random 70%(398 data points),15%(85 data points),and 15%(85 data points),respectively.
In the beginning,a set of observations are changed to a set of data of linearly uncorrelated variables with a statistical method namely PCA method.The number of principal component variables in this plan is like to the original variables but the variable values are linearly uncorrelated.
Because of the difference in dimension and magnitude of the original experimental data,the training and testing data should be normalized before they are fed to the ANN.All data points that made from PCA were balanced to the range of[0.1,1]as follow:
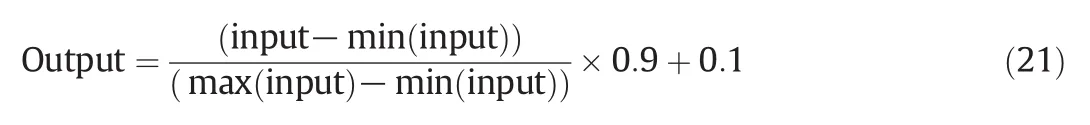
Over-training is a problem in the ANN and can be overcome by appropriate choice of the number of neurons in hidden layer.The performance of the network in training step should increase with increasing the neuron number;at the same time the performance of the network in testing data phase leads to the best value at an optimal number of hidden neurons(see Fig.2).This trained network is generalized and has the greatest prediction on testing data.Thus,the use of more or less than the optimal number of hidden neurons was discouraged.In this work,the mean square error(MSE)was selected as a measure of the performance of the net.The net with one hidden layer(28 neurons)with a mean square error of 1.0141×10-5shows to the greatest prediction in Fig.2.Fig.3 shows the progress of training,validation,and test errors as a function of the number of training epochs(based on early stopping approach).
Based on testing data,the bestneural network model was employed to predict the density of ionic liquid mixtures.Fig.4 shows the comparison between predicted values and experimental values and demonstrates good harmony between them with absolute average deviation,AAD=0.37%and high coefficient of determination,R2=0.9999.Fig.5 shows the error analysis of trained net over temperature variation.
In conclusion,the PCA–ANN and modified TM EOS were compared with literature values[51–56]for all mixtures of ILs.
The calculated densities of 1-butyl-3-methylimidazolium tetrafluoro borate+methanol from modified TM EOS and PCA–ANN at different temperatures and mole fractions are compared from experimental data[51]and the deviation plot of this systemversusmole fraction at 293.15 K is shown in Fig.6.

Table 4Summary of the input–output dataset characterization

Fig.2.Effect of the number of hidden layer neurons on AAD.
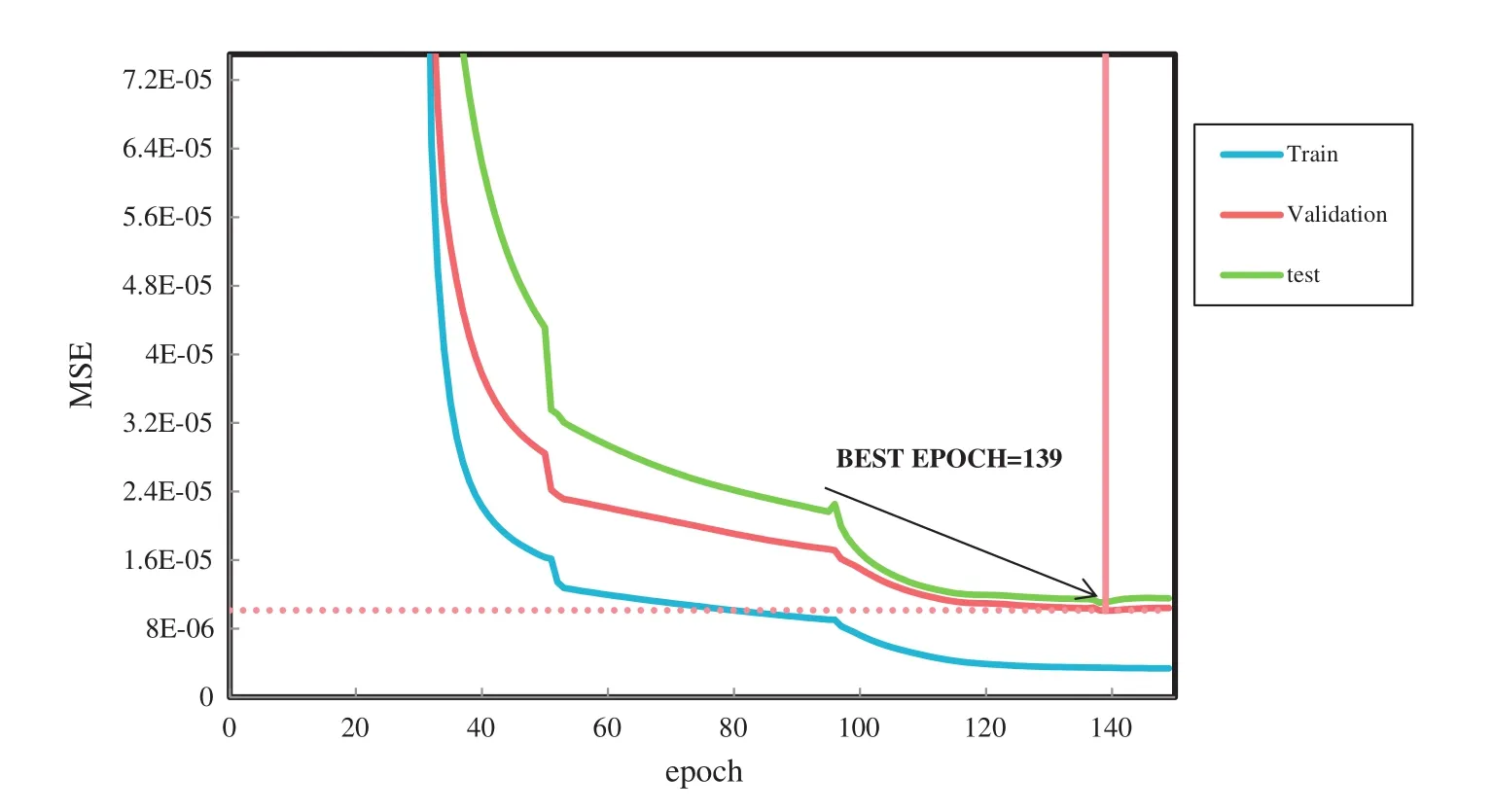
Fig.3.Evolution of training,validation,and test errors as a function of the number of training epochs during ANN training.
The absolute average deviation from experimental data[52]for the predicted densities of the 1-ethyl-3-methylimidazolium ethyl sulfate+H2O is calculated from new modified EOS and PCA–ANN and these deviations for 303.15 K are presented in Fig.7.It should be stated that the ANN model has good harmony with experimental data and is better than improved TM EOS.

Fig.4.Modeling ability of the optimized ANN to predict the effective densities of all mixtures of ionic liquids:(R2=0.999,AAD=0.48%).
The TM EOS and the PCA–ANN were performed to calculate the binary mixture densities of 1-ethyl-3-methylimidazolium ethyl sulfate,1-butyl-3-methylimidazolium tetra fluoroborate,1-butyl-3-methylimidazolium trifluoromethanesulfonate in water and deviation plot of these mixtures from experiment[53–55]versusmole fraction at 303.15 K are presented in Figs.8–10.In all figures the PCA–ANN is better than the modified TM equation of state.
Besides,the densities of 1-butyl-3-methylimidazolium methylsulfate+1-butyl-3-methylimidazolium tetra fluoroborate are calculated from the new equation of state and PCA–ANN at various mole fraction and temperatures and AAD%plot of binary mixture at 298.015 K is presented in Fig.11.
Table 5 contains the AAD%of the calculated molardensity of all binary mixtures of ILs using the modified TM EOS and ANNat different temperatures,pressures and volume fractions.Also,three equations of state[55–57]for all data points that are tested in the present work are studied and the results are reported in Table 5.As it is clear from Table 5,the accuracy of the calculated densities of IL mixtures using the ANN is better than other EOS,but all of them have an agreement with literature.The AADs of new EOS,Hosseini et al.EOS[56],Fadaei et al.EOS[56],Alavianmehr et al.EOS[58]and ANN for 568 data points are 1.03%,0.79%,1.07%,0.97%and 0.68%,respectively.
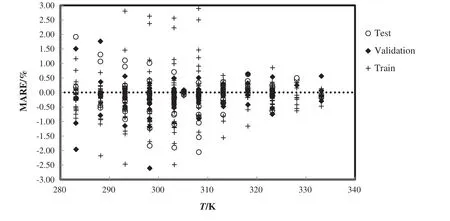
Fig.5.Mean absolute relative error for the train,test and validation of densities of all ionic liquids mixtures with the experimental data[51–56].
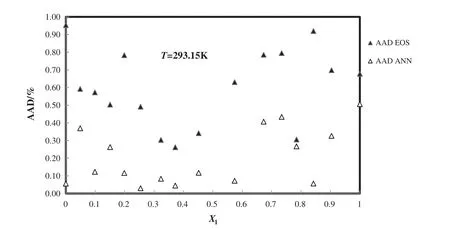
Fig.6.Deviation plot for the calculated density of 1-butyl-3-methylimidazolium tetra fluoroborate+methanol from modified TM EOS and the ANN at different mole fractions and 298 K,compared with the experiment[51].
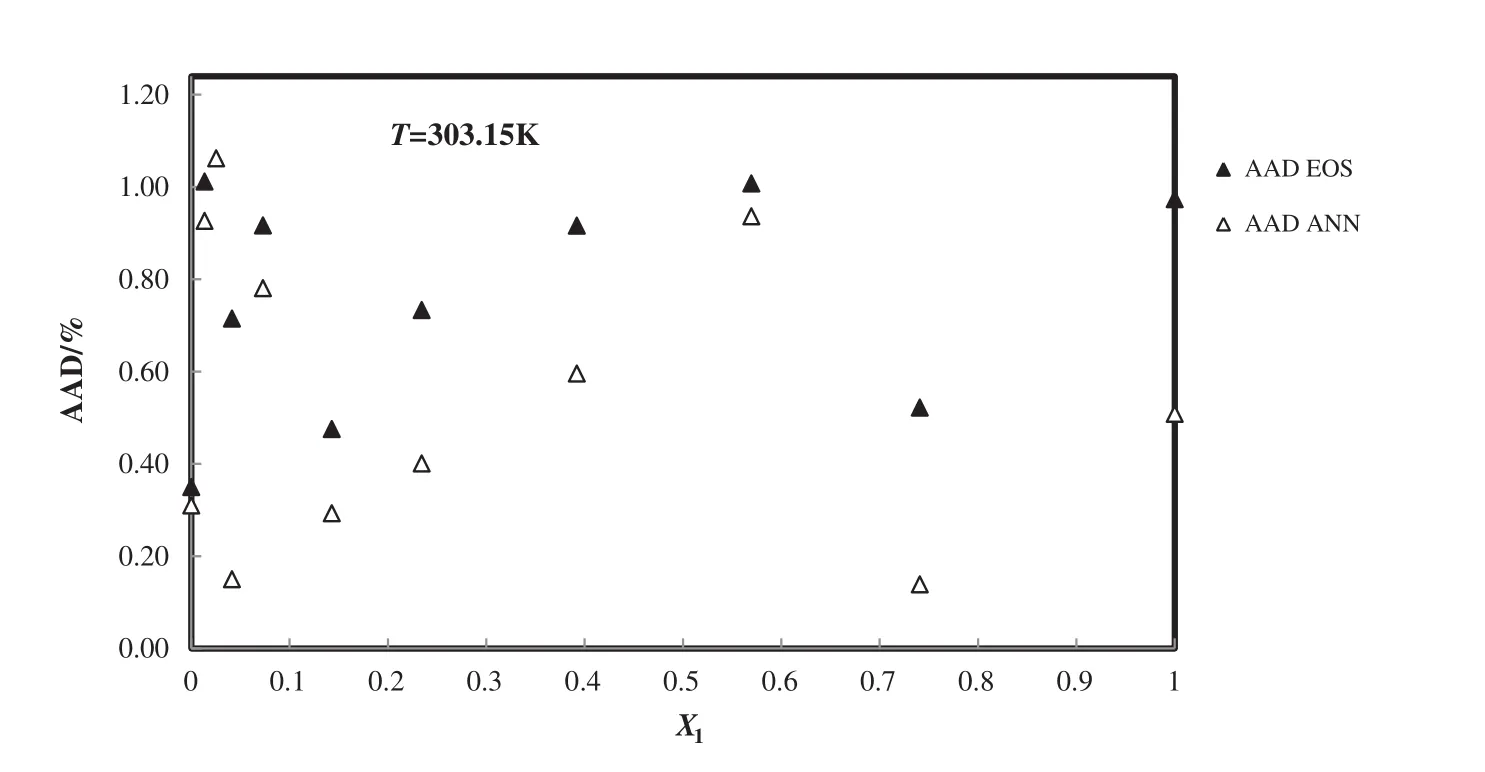
Fig.7.Deviation plot for the calculated density of1-ethyl-3-methylimidazolium ethyl sulfate+H2Ofrommodified TMEOSand the ANNat different mole fractions and 303.15 K,compared with the experiment[52].

Fig.8.Deviation plot for the calculated density of 1-ethyl-3-methylimidazolium ethyl sulfate+H2O from modified TM EOS and the ANN at different mole fractions and 303.15 K,compared with the experiment[53].
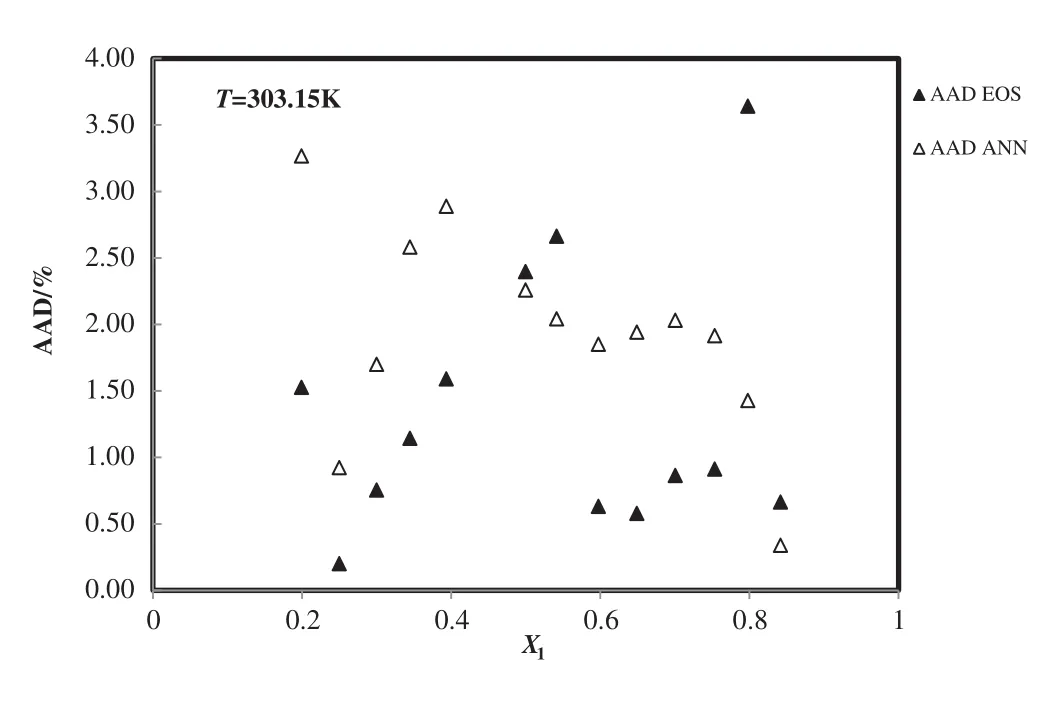
Fig.9.Deviation plot for the calculated density of 1-butyl-3-methylimidazolium tetra fluoroborate+H2O from modified TM EOS and the ANN at different mole fractions and 303.15 K,compared with the experiment[54].
In this research,the excess molar volume of binary mixtures of ILs is predicted using the following equations:

The deviation plot of the calculated excess molar volume of ANN for C8H15BF4N2+CH4O at different temperatures and mole fractions,is evaluated with the experiment[51]in Fig.12.It is shown thatt he calculated excess molar volume has good harmony with literature(AAD=1.30%).
Also,the plot of deviations of the excess molar volume of the modified TM EOS for C8H15N2O4S+H2O in different temperatures and mole fractions is presented in Fig.13 and the absolute average deviation from the experiment[53]is 1.44%.
The excess molar of all systems are calculated from TMEOS and ANN and the results are collected in Table 6.This table shows the AAD of TM EOS and ANN that is 1.65%and 1.17%,respectively.
Besides,the densities of pure ILs are compared with other models[49,50,57–65]and the outcomes of the calculations are collected in Table 7.Since the values of AAD can be characterized by the fact that the calculated values are more or less close to the experimental data,it can be claimed that our model can predict the experimental density of pure ILs with a good accuracy.
Finally,Table 8 illustrates the average absolute deviations of densities of ionic liquid mixtures from other equation of states[9,50,56–58,60–62,66,67].It is observed that,our results are supporting the favorite of the modified TM EOS.But,sometimes,the present work has great error in contrast to other models but,it must be stated that the present EOS needs just one input parameter to predict of PVT properties of ILs.
4.Conclusions

Fig.10.Deviation plot for the calculated density of 1-butyl-3-methylimidazoliumtrifluoro methane sulfonate+H2O from modified TM EOS and the ANN at different mole fractions and 303.15 K,compared with the experiment[55].
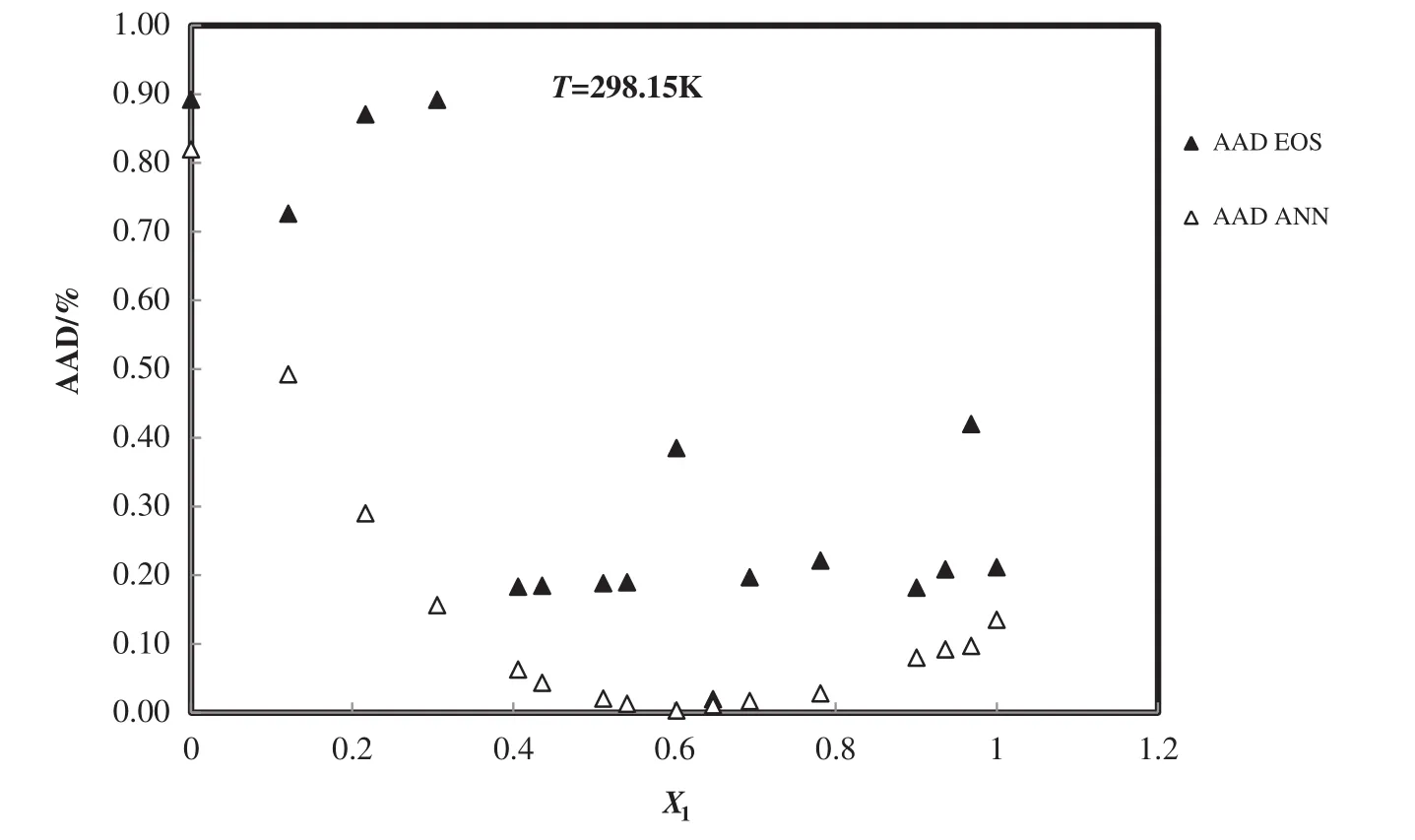
Fig.11.Deviation plot for the calculated density of 1-butyl-3-methylimidazolium methylsulfate+1-butyl-3-methylimidazolium tetra fluoroborate from modified TMEOS and the ANNat different mole fractions and 298.15 K,compared with the experiment[56].
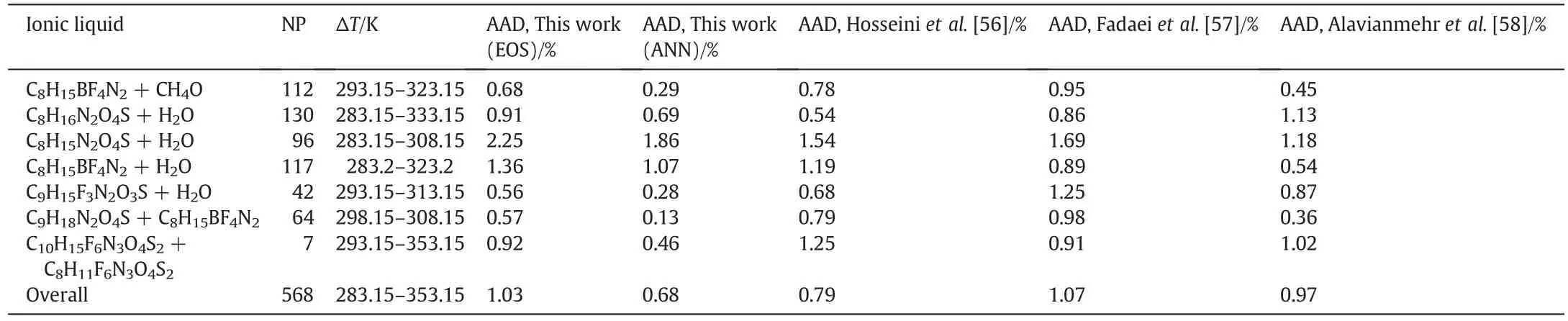
Table 5Result of density prediction for all mentioned mixtures
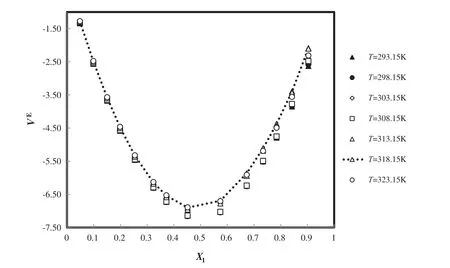
Fig.12.The deviation plot of the calculated excess molar volume of ANN for C8H15BF4N2+CH4O at different temperatures and mole fractions,compared with the experiment[51].
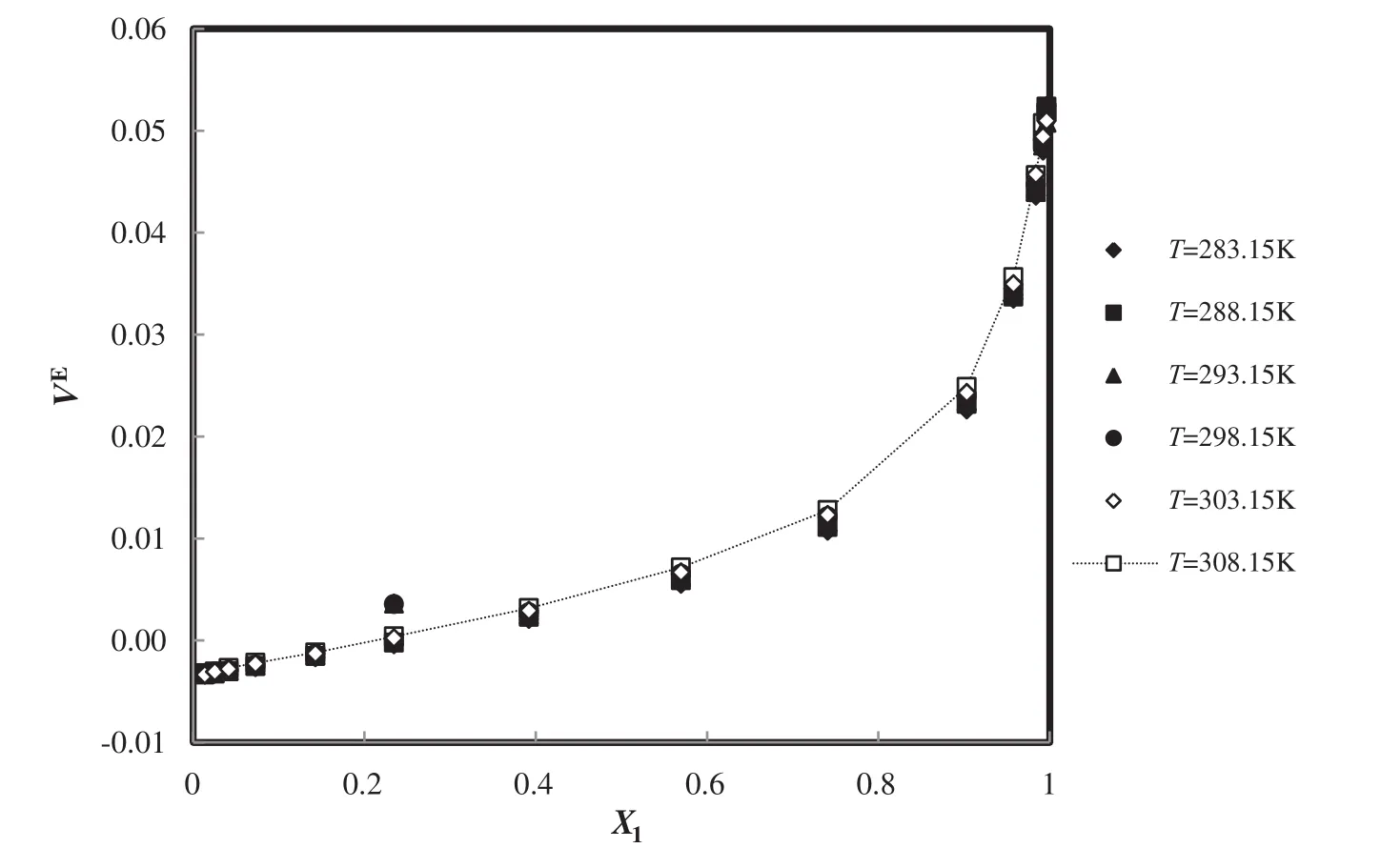
Fig.13.The deviation plot of the calculated excess molar volume of TM EOS for C8H15N2O4S+H2O at different temperatures and mole fractions,compared with the experiment[53].
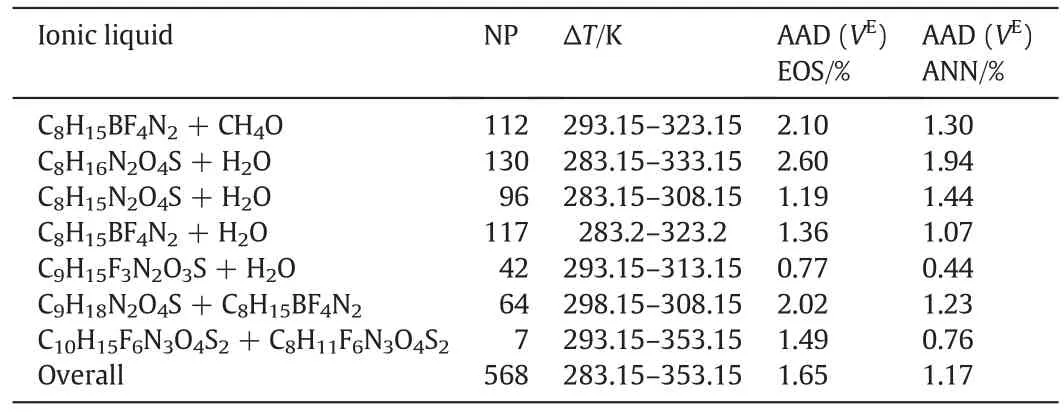
Table 6Result of excess volume prediction for all mentioned mixtures
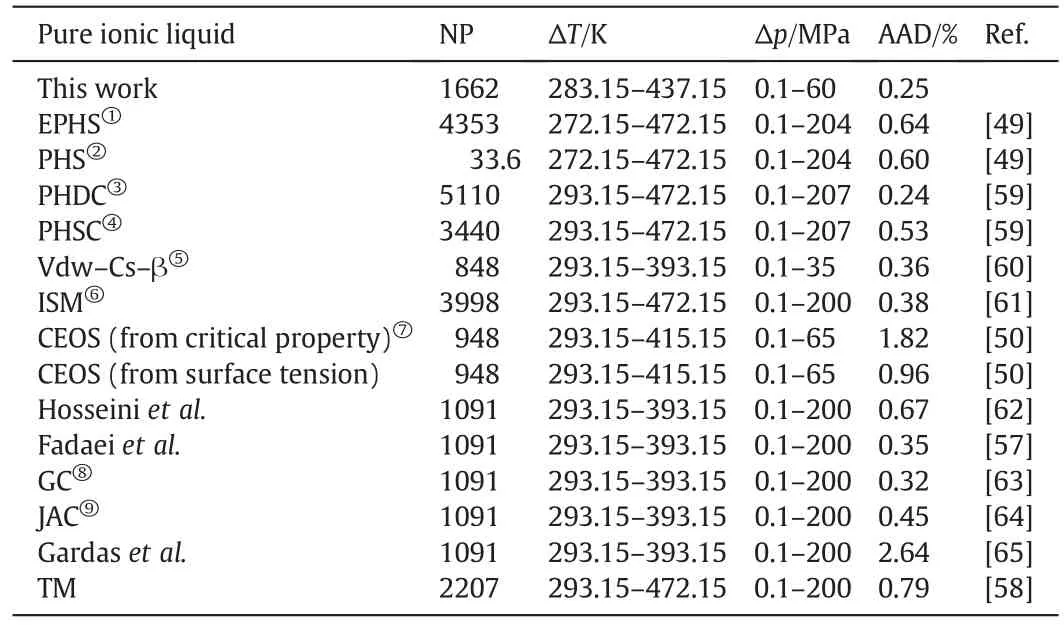
Table 7AADs of the calculated densities of pure ILs using the presented two models from the literature data

Table 8AADs of the calculated densities of ILs mixtures using the presented two models from literature data
In the present work,the modified TM EOS was applied to estimate the volumetric and thermodynamic properties of pure ILs and their mixtures in broad range of temperatures,pressures and mole fractions.The obtained mean of the deviations for density of all pure ILs for 1662 data points was 0.25%.Besides,the performance of the PCA–ANN based on back propagation training with 28 neurons in hidden layer for predicting the behavior of binary mixtures of ILs was examined.The AADs of the calculated molar density of all binary systems for 568 data points using the EOS and the ANN in different temperatures and mole fractions are 1.03%and 0.68%,respectively.As well,the excess molar volume of all binary mixtures is predicted by means of obtained densities of the modified TM EOS and PCA–ANN and the results show that these properties have good agreement with literature.The AADs of the calculated excess molar volume of all binary systems using the EOS and the ANN at various temperatures and mole fractions are 1.65%and 1.17%,respectively.
[1]K.J.Fraser,D.R.MacFarlane,Phosphonium-based ionic liquids:An overview,Aust.J.Chem.62(2009)309–321.
[2]D.Zhao,Y.Wang,E.Duan,Oxidative desulfurization of fuel oil by pyridinium-based ionic liquids,Molecules14(2009)4351–4357.
[3]Y.Xiaoa,S.V.Malhotra,Diels–Alder reactions in pyridinium based ionic liquids,Tetrahedron Lett.45(2004)8339–8342.
[4]I.M.Abdulagtov,A.Tekin,J.Safarov,A.Shahverdiyev,E.Hassel,High-pressure densities and derived volumetric properties(excess and partial molar volumes,vapor pressures)of binary methanol+ethanol mixtures,J.Chem.Thermodyn.40(2008)1386–1401.
[5]B.Garcia,S.Lavallee,G.Perron,C.Michot,M.Armand,Room temperature molten salts as lithium battery electrolyte,Electrochim.Acta49(2004)4583–4588.
[6]T.Sato,G.Masuda,K.Takagi,Electrochemical properties of novel ionic liquids for electric double layer capacitor applications,Electrochim.Acta49(2004)3603–3611.
[7]M.J.Earle,K.R.Seddon,Ionic liquids:Green solvents for the future,Pure Appl.Chem.72(2000)1391–1398.
[8]N.V.Plechkova,K.R.Seddon,Applications of ionic liquids in the chemical industry,Chem.Soc.Rev.37(2008)123–150.
[9]J.Wang,Z.Li,C.Li,Z.Wang,Density prediction of ionic liquids at different temperatures and pressures using a group contribution equation of state based on electrolyte perturbation theory,Ind.Eng.Chem.Res.49(2010)4420–4425.
[10]C.Shen,C.Li,X.Li,Y.Lu,Y.Muhammad,Estimation of densities of ionic liquids using Patel–Teja equation of state and critical properties determined from group contribution method,Chem.Eng.Sci.66(2011)2690–2698.
[11]H.Machida,Y.Sato,R.L.Smith Jr.,Simple modification of the temperature dependence of the Sanchez–Lacombe equation of state more collapse,Fluid Phase Equilib.297(2010)205–209.
[12]J.Abildskov,M.D.Ellegaard,J.P.O'Connell,Correlation of phase equilibria and liquid densities for gases with ionic liquids,Fluid Phase Equilib.286(2009)95–106.
[13]J.Abildskov,M.D.Ellegaard,J.P.O'Connell,Densities and isothermal compressibilities of ionic liquids-modeling and application,Fluid Phase Equilib.295(2010)215–229.
[14]J.Abildskov,M.D.Ellegaard,J.P.O'Connell,Phase behavior of mixtures of ionic liquids and organic solvents,J.Supercrit.Fluids55(2010)833–845.
[15]J.Palomar,V.R.Ferro,J.S.Torrecilla,F.Rodriguez,Density and molar volume predictions using COSMO-RS for ionic liquids.An approach to solvent design,Ind.Eng.Chem.Res.46(2007)6041–6048.
[16]S.Trohalaki,R.Pachter,G.Drake,T.Hawkins,Quantitative structure–property relationships for melting points and densities of ionic liquids,Energy Fuel19(2005)279–287.
[17]M.Rahmati-Rostami,B.Behzadi,C.Ghotbi,Thermodynamic modeling of hydrogen sulfide solubility in ionic liquids using modified SAFT-VR and PC-SAFT equations of state,Fluid Phase Equilib.309(2011)179–189.
[18]Y.Huang,Y.Zhao,S.Zeng,X.Zhang,S.Zhang,Density prediction of mixtures of ionic liquids and molecular solvents using two new generalized models,Ind.Eng.Chem.Res.53(2014)15270–15277.
[19]M.M.Papari,J.Moghadasi,S.M.Hosseini,F.Akbari,Modification of van der Waals family equations of state,J.Mol.Liq.158(2011)57–60.
[20]F.Yousefi,H.Karimi,Modification of Tao–Mason equation of state to ionic liquids,Ionics18(2012)135–142.
[21]F.Yousefi,Correlation of volumetric properties of binary mixtures of some ionic liquids with alcohols using equation of state,Ionics18(2012)769–775.
[22]F.M.Tao,E.A.Mason,Statistical–mechanical equation of state for nonpolar fluids:Prediction of phase boundaries,J.Chem.Phys.100(1994)9075–9084.
[23]F.Yousefi,H.Karimi,Application of equation of state and artificial neural network to prediction of volumetric properties of polymer melts,J.Ind.Eng.Chem.19(2013)498–507.
[24]J.A.Lazzus,ρ-T-Pprediction for ionic liquids using neural networks,Inst.Chem.Eng.40(2009)213–232.
[25]H.Karimi,F.Yousefi,Equation of state and artificial neural network to predict the thermodynamic properties of pure and mixture of liquid alkali metals,Fluid Phase Equilib.336(2012)79–83.
[26]F.Yousefi,J.Moghadasi,M.M.Papari,A.Campo,Extension of Tao–Mason equation of state to mixtures:results for PVTx properties of refrigerants fluid mixtures,Ind.Eng.Chem.Res.48(2009)5079–5084.
[27]H.Karimi,F.Yousefi,M.M.Papari,Extension of Tao–Mason equation of state to mixtures:Results for PVTx properties of refrigerants fluid mixtures,J.Chem.Eng.Jpn.44(2011)295–303.
[28]H.Karimi,F.Yousefi,M.M.Papari,Prediction of volumetric properties(p-v-T)of natural gas mixtures using extended Tao–Mason equation of state,Chin.J.Chem.Eng.19(2011)496–503.
[29]F.Yousefi,H.Karimi,P-V-Tproperties of polymer melts based on equation of state and neural network,Eur.Polym.J.48(2012)1135–1143.
[30]J.M.H.Levelt Sengers,U.K.Deiters,U.Klask,P.Swidersky,G.M.Schneider,Application of the Taylor dispersion method in supercritical fluids,Int.J.Thermophys.14(1993)893–922.
[31]S.I.Sandler,Chemical and engineering thermophysics,Wiley,New York,1989.
[32]J.M.Prauznitz,R.N.Lichtentaler,E.G.Azevedo,Molecular thermodynamics of fluid phase equilibria,Prentice-Hall,Englewood Cliffs,NJ,1999.
[33]G.Ihm,Y.Song,E.A.Mason,Strong principle of corresponding states:Reduction of ap-v-Tsurface to a line,Fluid Phase Equilib.75(1992)117–125.
[34]C.Tsonopoulos,Second virial coefficient of water pollution,AIChE J.24(1978)1112–1115.
[35]H.Eslami,Equation of state for nonpolar fluids:Prediction from boiling point constants,Int.J.Thermophys.21(2000)1123–1137.
[36]S.Haykin,Neural networks:A comprehensive foundation,second ed.Prentice-Hall,New York,1999.
[37]P.Xu,S.Xu,H.Yin,Application of self-organizing competitive neural network in fault diagnosis of suck rod pumping system,J.Pet.Sci.Eng.58(2007)43–48.
[38]B.Vaferi,Y.Rahnam,P.Darvishi,A.R.Toorani,M.Lashkarbolooki,Phase equilibria modeling of binary systems containing ethanol using optimal feed forward neural network,J.Supercrit.Fluids84(2013)80–88.
[39]B.Vaferi,M.Karimi,M.Azizi,H.Esmaeili,Comparison between the artificial neural network,SAFT and PRSV approach in obtaining the solubility of solid aromatic compounds in supercritical carbon dioxide,J.Supercrit.Fluids77(2013)45–51.
[40]B.Vafaei,R.Eslamloueyan,S.Ayatollahi,Simulation of steam distillation process using neural networks,Chem.Eng.Res.Des.87(2009)997–1002.
[41]C.Bishop,Neural networks for pattern recognition,Oxford Clarendon,Oxford,1996.
[42]B.Ripley,Pattern recognition and neural networks,Cambridge University Press,Cambridge,1996.
[43]http://en.wikipedia.org/wiki/Principal_component_analysis.
[44]X.Wang,K.K.Paliwal,Feature extraction and dimensionality reduction algorithms and their applications in vowel recognition,J.Pattern Recognit.Soc.36(2003)2429–2439.
[45]I.S.Lindsa,A tutorial on principal components analysis,http://kybele.psych.cornell.edu/~edelman/Psych-465Spring-2003/PCA-tutorial2002.
[46]D.Matkowska,T.Hofman,High-pressure volumetric properties of ionic liquids:1-Butyl-3-methylimidazolium tetra fluoroborate,[C4mim][BF4],1-butyl-3-methylimidazolium methylsulfate[C4mim][MeSO4]and 1-ethyl-3-methylimidazolium ethylsulfate,[C2mim][EtSO4],J.Mol.Liq.165(2012)161–167.
[47]R.L.Gardas,M.G.Freire,P.J.Carvalho,I.M.Marrucho,I.M.A.Fonseca,A.G.M.Ferreira,J.A.P.Coutinho,PVT property measurements for some aliphatic esters from(298 to 393)K and up to 35 MPa,J.Chem.Eng.Datas52(2007)1881–1888.
[48]C.A.de Castro,E.Nieto,A.L.Langa,M.L.M.Morais,M.J.V.Lopes,F.J.V.Lourenco,M.S.Santos,J.N.C.Santos,H.M.Lopes,M.Veiga,J.M.S.S.Macatrao,C.S.Esperanca,L.P.N.Marques,C.A.Rebelo,M.Afonso,Studies on the density,heat capacity,surface tension and infinite dilution diffusion with the ionic liquids[C4mim][NTf2],[C4mim][dca],[C2mim][EtOSO3]and[Aliquat][dca],Fluid Phase Equilib.294(2010)157–179.
[49]M.M.Alavianmehr,S.M.Hosseini,J.Moghadasi,Volumetric properties of ionic liquids and their binary mixtures from improved Tao–Mason equation of state,J.Mol.Liq.197(2014)287–294.
[50]S.M.Hosseini,M.M.Alavianmehr,D.Mohammad-Aghaie,F.Fadaei-Nobandegani,J.Moghadasi,Volumetric properties of ionic liquids from cubic equation of state:Application to pure and mixtures,J.Ind.Eng.Chem.19(2013)769–775.
[51]M.A.Iglesias-Otero,J.Troncoso,E.Carballo,Solution thermodynamics near the liquid–liquid critical point:I.First-order excess derivatives,J.Solut.Chem.36(2007)1219–1230.
[52]X.M.Lu,W.G.Xu,J.S.Gui,H.W.Li,J.Z.Yang,Volumetric properties of room temperature ionic liquid 2:The concentrated aqueous solutions of{1-methyl-3-ethylimidazolium ethyl sulfate+water}in a temperature range of 278.2 K to 338.2 K,J.Chem.Thermodyn.37(2005)1250–1255.
[53]J.Lehmann,M.H.Rausch,A.Leipertz,A.P.Froba,Densities and excess molar volumes for binary mixtures of ionic liquid 1-ethyl-3-methylimidazolium ethylsulfate with solvents,J.Chem.Eng.Datas55(2010)4068–4074.
[54]Q.G.Zhang,F.Xue,J.Tong,W.Guan,B.Wang,Studies on volumetric properties of concentrated aqueous solutions of the ionic liquid[bmim][BF4],J.Solut.Chem.35(2006)297–309.
[55]G.Garcia-Miaja,J.Troncoso,L.Romani,Excess enthalpy,density,and heat capacity for binary systems of alkylimidazolium-based ionic liquids+water,J.Chem.Thermodyn.41(2009)161–166.
[56]S.M.Hosseini,M.M.Papari,F.Fadaei-Nobandegani,J.Moghadasi,A simple equation for predicting the volumetric properties of mixtures involving ionic liquids,J.Solut.Chem.42(2013)1854–1862.
[57]F.Fadaei-Nobandegani,S.M.Hosseini,M.M.Papari,J.Moghadasi,Volumetric properties of mixtures involving ionic liquids from improved equation of state,Thermochim.Acta546(2012)94–101.
[58]M.M.Alavianmehr,S.M.Hosseini,S.Amighi,Volumetric properties of ionic liquids and their binary mixtures from improved Tao–Mason equation of state,J.Mol.Liq.191(2014)166–171.
[59]S.M.Hosseini,M.M.Alavianmehr,Density and isothermal compressibility of ionic liquids from perturbed hard-dimer-chain equation of state,Fluid Phase Equilib.356(2013)185–192.
[60]M.Kiani,M.M.Alavianmehr,F.Rezaei,M.R.Noorbala,Development of a modified van der Waals-type equation of state for pure and mixture of ionic liquids,J.Mol.Liq.198(2014)101–106.
[61]M.M.Papari,S.M.Hosseini,F.Fadaei-Nobandegani,J.Moghadasi,Modeling of P–rho–T properties of ionic liquids using ISM equation of state:Application to pure component and binary mixtures,Korean J.Chem.Eng.29(2012)1628–1637.
[62]S.M.Hosseini,J.Moghadasi,M.M.Papari,F.Fadaei Nobandegani,Modeling the volumetric properties of ionic liquids using modified perturbed hard-sphere equation of state:Application to pure and binary mixtures,Ind.Eng.Chem.Res.51(2012)758–766.
[63]R.L.Gardas,J.A.P.Coutinho,Extension of the ye and Shreeve group contribution method for density estimation of ionic liquids in a wide range of temperatures and pressures,Fluid Phase Equilib.263(2008)26–32.
[64]J.Jacquemin,P.Nancarrow,D.W.Rooney,M.F.Costa Gomes,P.Husson,V.Majer,A.A.H.Padua,C.Hardacre,Prediction of ionic liquid properties.II.Volumetric properties as a function of temperature and pressure,J.Chem.Eng.Datas53(2008)2133–2143.
[65]R.L.Gardas,M.G.Freire,P.J.Carvalho,I.M.Marrucho,I.M.A.Fonseca,A.G.M.Ferreira,J.A.P.Coutinho,P–rho–Tmeasurements of imidazolium-based ionic liquids,J.Chem.Eng.Datas52(2007)1881–1888.
[66]S.M.Hosseini,J.Moghadasi,M.M.Papari,F.Fadaei-Nobandegani,Modeling the volumetric properties of mixtures involving ionic liquids using perturbed hard-sphere equation of state,J.Mol.Liq.160(2011)67–71.
[67]M.Sheikhi-Kouhsar,H.Bagheri,S.Raeissi,Modeling of ionic liquid+polar solvent mixture molar volumes using a generalized volume translation on the Peng–Robinson equation of state,Fluid Phase Equilib.395(2015)51–57.
 Chinese Journal of Chemical Engineering2016年12期
Chinese Journal of Chemical Engineering2016年12期
- Chinese Journal of Chemical Engineering的其它文章
- Hemicellulose in corn straw:Extracted fromalkali solution and produced 5-hydroxymethyl furfural in HCOOH/HCOONa buffer solution☆
- Molar volume of eutectic solvents as a function of molar composition and temperature☆
- Investigation on molar heat capacity,standard molar enthalpy of combustion for guaiacol and acetyl guaiacol ester
- A comprehensive fractal char combustion model☆
- Development of a bifurcation analysis approach based on gPROMS platform☆
- Catalytic kinetics of dimethyl ether one-step synthesis over CeO2–CaO–Pd/HZSM-5 catalyst in sulfur-containing syngas process☆
