三個(gè)5-階圖與圈聯(lián)圖的交叉數(shù)

岳為君, 黃元秋, 唐 玲

?

岳為君1, 黃元秋*1, 唐 玲2

(1. 湖南師范大學(xué) 數(shù)學(xué)與計(jì)算機(jī)科學(xué)學(xué)院, 湖南 長(zhǎng)沙, 410081; 2. 中南林業(yè)科技大學(xué) 理學(xué)院, 湖南 長(zhǎng)沙, 410004 )

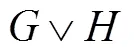
畫法; 交叉數(shù); 聯(lián)圖; 圈

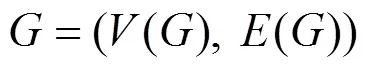
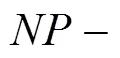
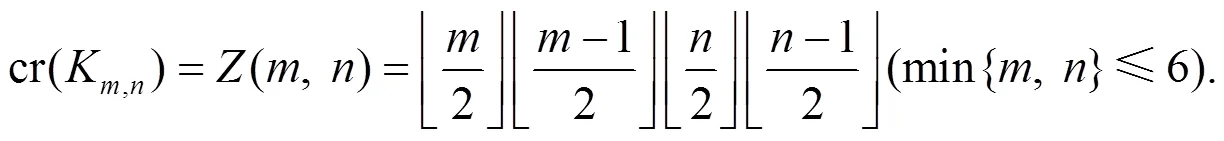
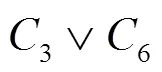
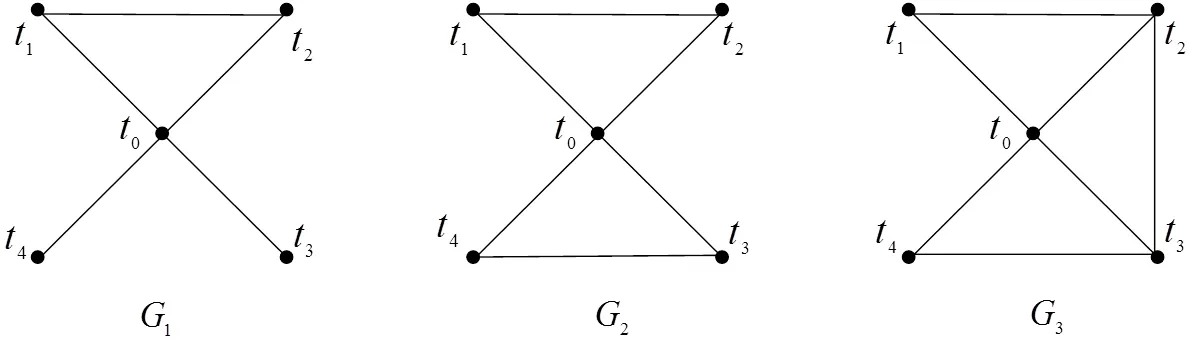
圖1 圖

1 基本性質(zhì)和引理

在證明本文的主要結(jié)果之前, 先給出一些基本性質(zhì)和引理.

首先, 由交叉數(shù)的定義, 易有如下性質(zhì):

2 定理的證明

定理1(1)的證明

定理1(2)的證明

定理1(3)的證明

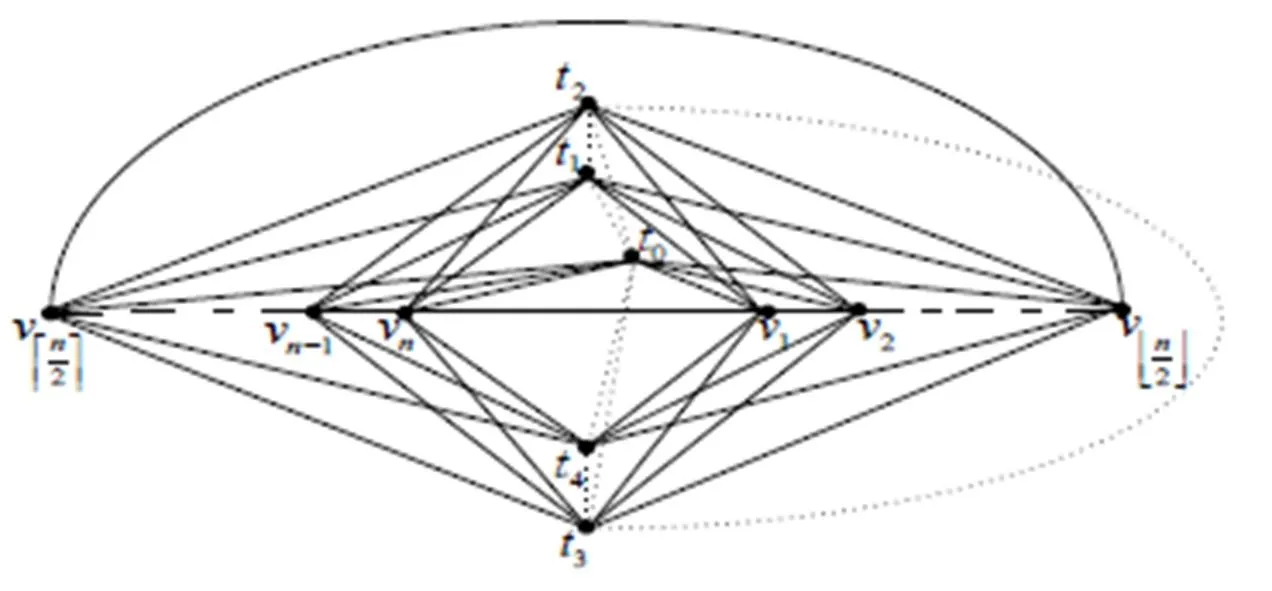
圖3 的一個(gè)好畫法

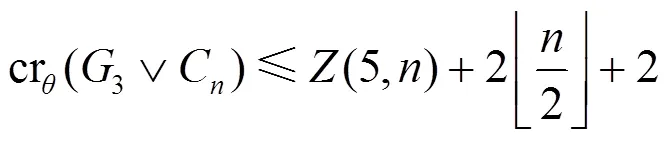
以下證明總能得到一個(gè)與(1)式相矛盾的結(jié)論, 從而完成定理1(3)的證明.

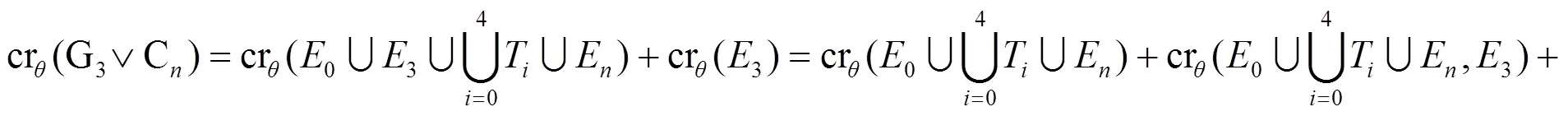
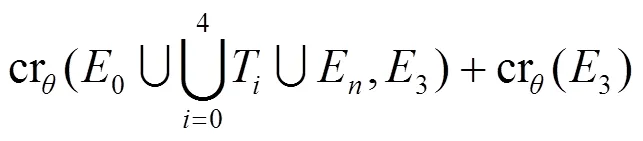
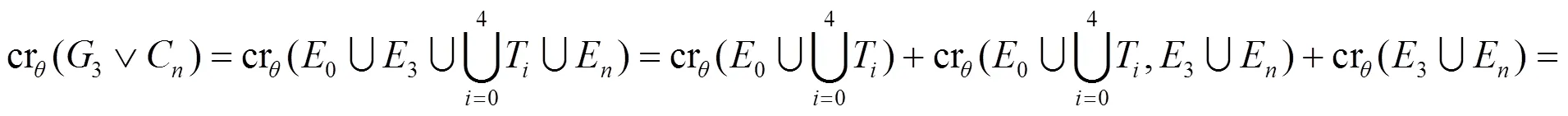
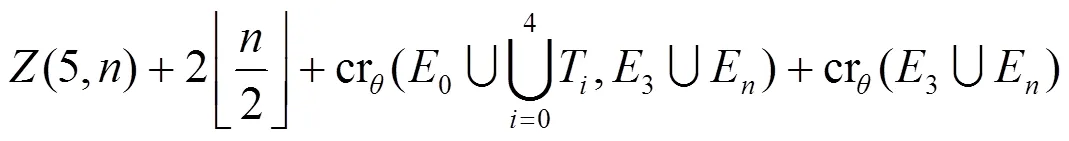
根據(jù)性質(zhì)1和斷言1可得:

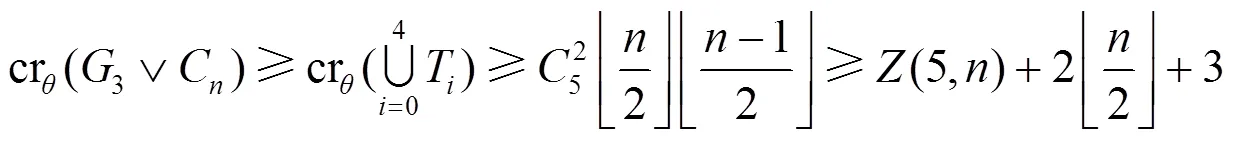
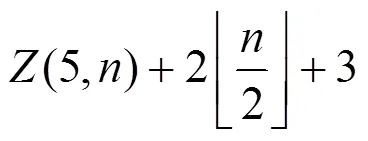
圖4 情形2

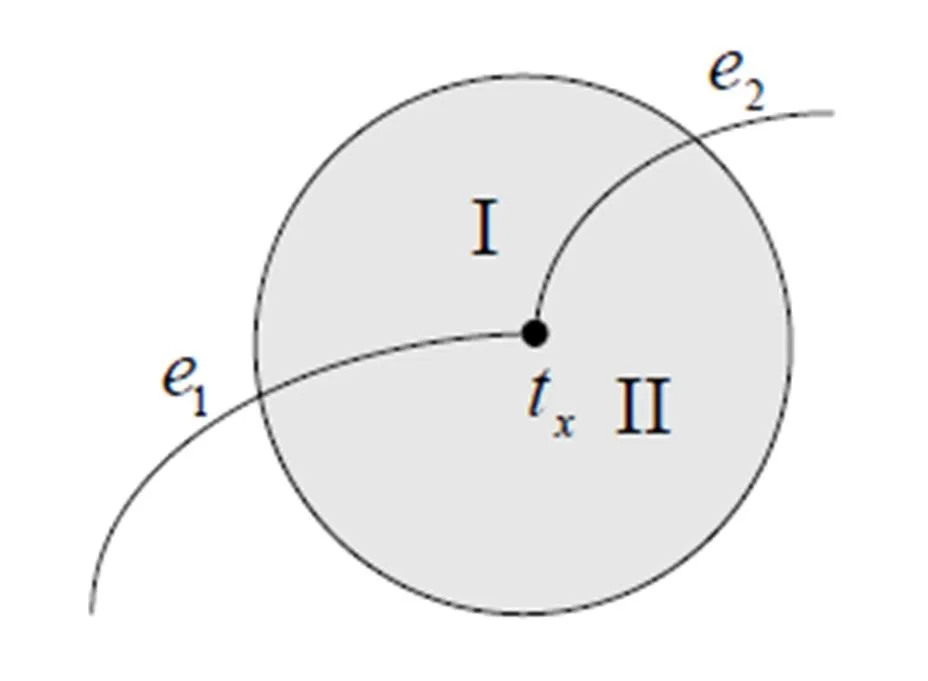
圖5 子情形3.1

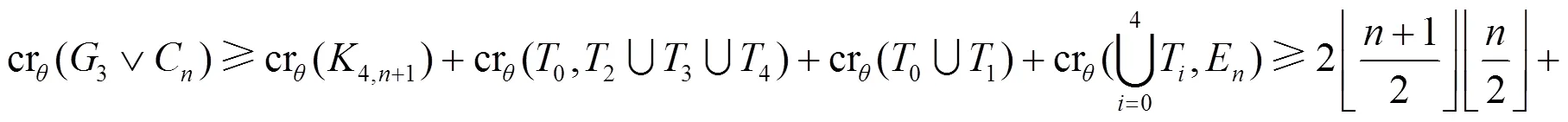
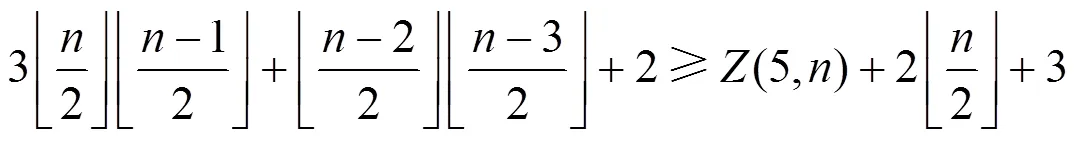
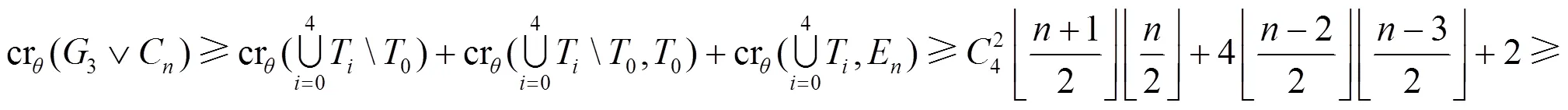
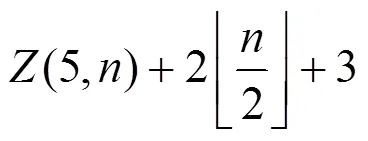
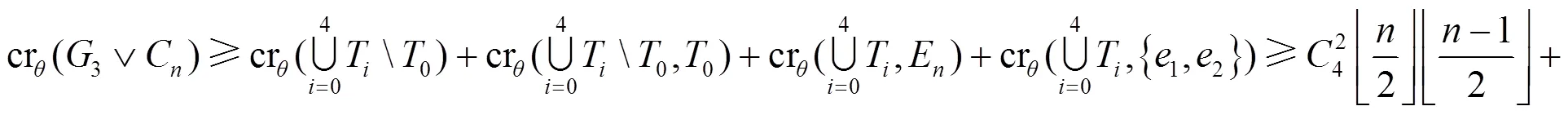
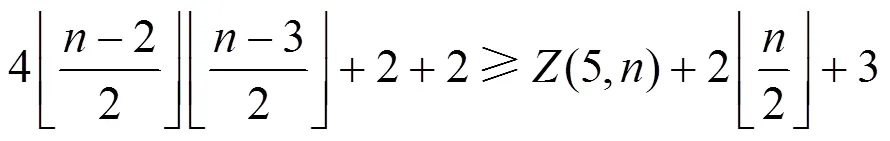
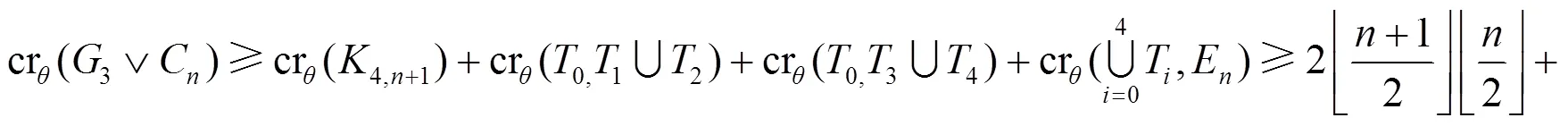
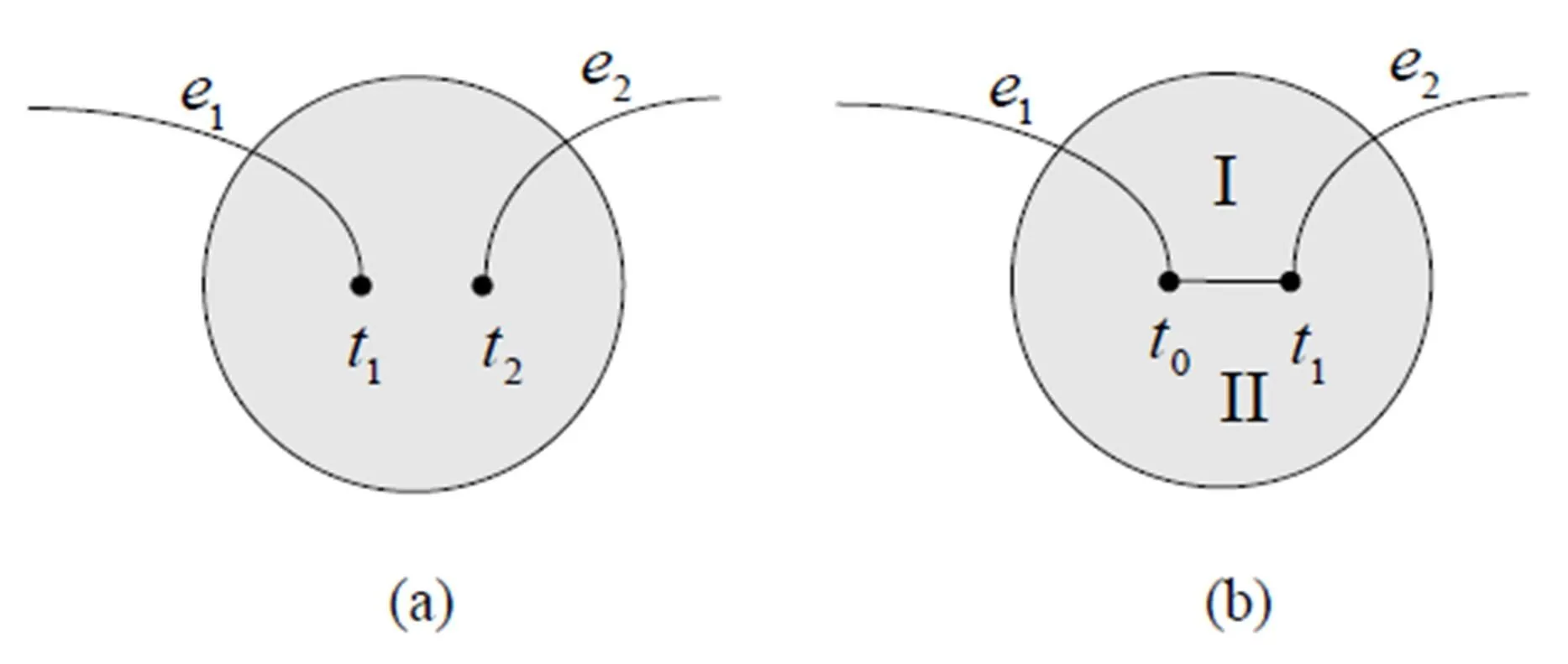
圖6 子情形3.2

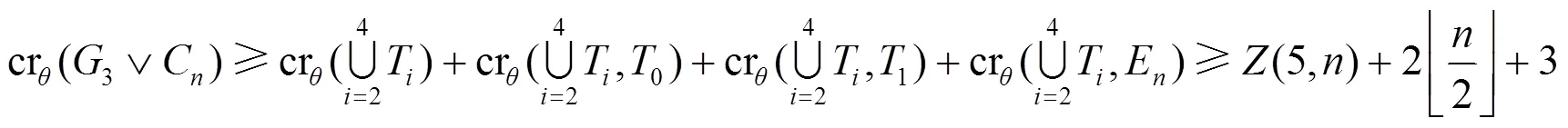
[1] Bondy J A, Murty U S R. Graph Theory With Applications[M]. London: Macmilan, 1976.

[2] Garey M R, Johnson D S. Crossing number is NP-complete[J]. Slam J Algebric Discrete Methods, 1993, 4: 312—316.

[4] Ho P T. On the crossing number of some complete multipartite graphs[J]. Utilitas Mathematica, 2009, 79: 143—154.

[7] Klesc M. On the crossing number of Cartesian products of stars and paths or cycles[J]. Math Slovaca, 1991, 41: 113—120.

[8] Beineke L W, Ringeisen R D. On the crossing number of products of cycles and graphs of order four[J]. Graph Theory, 1980, 4: 145—155.

[10] Zarankiewicz K. On a Problem of P Turan Concerning Graphs[J]. Fund Math, 1954, 41: 137—145.

[11] Oporowski B, Zhao D. Coloring graphs with crossing[J]. Discrete Mathematics, 2009, 309: 2948—2951.

[13] Klesc M. The join of the graphs and crossing numbers[J]. Discrete Math, 2007, 28: 349—350.

YUE Wei-jun1, HUANG Yuan-qiu1, TANG Ling2

(1. Department of Mathematics, Hunan Normal University, Changsha 410081, China; 2. Department of Mathematics, Central South University of Forestry and Technology, Changsha 410004, China)

drawing; crossing number; join graph; cycle

10.3969/j.issn.1672-6146.2013.04.001

O 157.5

1672-6146(2013)04-0001-07

email: hyqq@hunnu.edu.cn.

email: yueweijun121@163.com.

2013-08-11

國(guó)家自然科學(xué)基金資助項(xiàng)目(11371133)

(責(zé)任編校:劉曉霞)