偽補MS-代數(shù)的濾子同余關(guān)系

趙秀蘭,馬紅娟

(黃河科技學(xué)院數(shù)理部,河南鄭州450063)

偽補MS-代數(shù)的濾子同余關(guān)系

趙秀蘭,馬紅娟

(黃河科技學(xué)院數(shù)理部,河南鄭州450063)

在偽補MS-代數(shù)上引入余核濾子和完全濾子的概念,研究偽補MS-代數(shù)的余核濾子和完全濾子的性質(zhì),獲得了余核濾子和完全濾子生成的同余關(guān)系的表達式,證明了具有余核濾子的最小同余關(guān)系有同余一致性.

偽補代數(shù);MS-代數(shù);余核濾子;完全濾子;同余關(guān)系

1 引言及預(yù)備知識

一個偽補代數(shù)(簡稱p-代數(shù))是一個代數(shù)(L;∨,∧,?,0),它具有一個最小元0及一個映射?:L→L使得

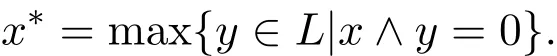
有關(guān)p-代數(shù)的基本性質(zhì)請參看文獻[1-3].文獻[4]在de Morgan代數(shù)和Stone代數(shù)的基礎(chǔ)上引入一類重要的代數(shù)MS-代數(shù),所謂MS-代數(shù)是指一個有界分配格被賦予一個一元運算x→x?使得

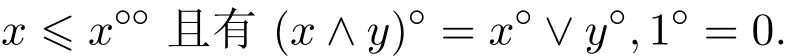
文獻[5]從p-代數(shù)與MS-代數(shù)中抽象出一類新的代數(shù),稱為偽補MS-代數(shù)(簡稱pMS-代數(shù)).所謂pMS-代數(shù)(L;∨,∧,?,?,0,1),是指一個有界分配格,其上賦予兩個一元運算?和?,其中(L;?)是p-代數(shù),(L;?)是MS-代數(shù),且一元運算?和?滿足條件(?x∈L)x??=x??.文獻[5]主要研究了pMS-代數(shù)的運算屬性,同余關(guān)系及其次直不可約代數(shù).文獻[6-7]分別討論了偽補分配格的同余理想與同余關(guān)系以及MS-代數(shù)的理想和同余關(guān)系.文獻[8]刻畫了擬補Ockham代數(shù)上的理想與濾子.2007年,文獻[9]進一步刻畫了平衡擬補Ockham代數(shù)的理想格.對于平衡半擬補Ockham代數(shù)的濾子格,文獻[10]研究了這類代數(shù)的余核濾子和稠密濾子的特征,并刻畫這些濾子的某些同余一致與同余凝聚性質(zhì).2012年文獻[11]就雙重偽補代數(shù)的假值理想和假值同余給出了特征表示.文獻[12]研究了雙重偽補Ockham代數(shù)上的理想與濾子的性質(zhì),證明了雙重偽補Ockham代數(shù)的核理想格與其余核濾子格同構(gòu).在此研究工作的基礎(chǔ)上,在這篇文章中,主要討論pMS-代數(shù)的余核濾子和完全濾子的性質(zhì)與特征,并刻畫余核濾子和完全濾子所生成的同余關(guān)系的特征,以及濾子的同余一致性質(zhì).

便于闡述,沿用文獻[1-5]中的術(shù)語.假定L是pMS-代數(shù),F是L的子集.如果對a∈F,則x≥a蘊涵x∈F,稱F是L的濾子.設(shè)θ是L的一個格同余,且對任意的a,b∈L, (a,b)∈θ蘊涵(a?,b?)∈θ及(a?,b?)∈θ,則稱θ是L的一個pMS-同余.對于L的濾子F,若存在L的一個同余關(guān)系φ使得

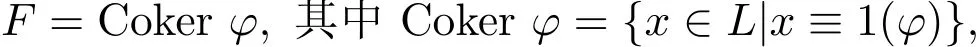
稱濾子F為L的余核濾子.

設(shè)a,b是L中的元素,又F是L的一個子集.用符號θ(a,b)和θlat(a,b)分別表示包含a,b的最小同余與最小格同余(即由a,b所生成的主同余和格主同余);用θ(F)和θlat(F)分別表示包含F(xiàn)的最小同余與最小格同余(即由F所生成的主同余和格主同余);用Con L表示L的所有同余所組成的同余格.

2 余核濾子的同余性質(zhì)

現(xiàn)給出pMS-代數(shù)余核濾子的判別定理.

定理2.1設(shè)(L;∨,∧,?,?,0,1)是一個pMS-代數(shù),F是L的濾子,則F是L的余核濾子當(dāng)且僅當(dāng)(?a∈L)a∈F=?a??∈F.

證明設(shè)F是L的一個余核濾子,則存在φ∈Con L,使得F=Coker φ.對于a∈F,有a≡1(φ),所以a??≡1(φ),于是由余核濾子的定義知a??∈F.

?:設(shè)任意的a∈L,a∈F蘊涵a??∈F.定義L上的一個等價關(guān)系RF如下:

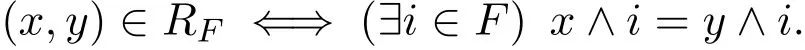
易見,RF是一個格同余.

下證RF∈Con L.設(shè)(x,y)∈RF,則存在i∈F使得x∧i=y∧i.從而有x?∨i?=y?∨i?,于是得

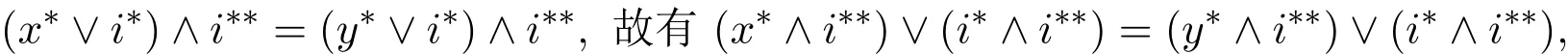
由文獻[2]知,i?∧i??=0,故x?∧i??=y?∧i??.又因為i??≥i∈F,所以i??∈F.因此(x?,y?)∈RF.另一方面,有x∧i=y∧i可得x?∨i?=y?∨i?.從而有

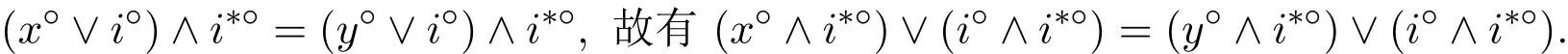
又由文獻[5]知i?=i???,所以

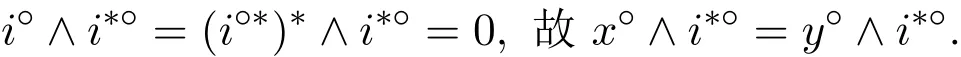
又由題設(shè)知i??∈F,因此(x?,y?)∈RF.所以RF∈Con L.

現(xiàn)證Coker RF=F.若x∈Coker RF,則存在i∈F使得x∧i=i,所以x≥i,故x∈F.所以Coker RF?F.另外,設(shè)i∈F,由i∧i=1∧i=i得(i,1)∈RF,故i∈Coker RF,所以F?Coker RF.從而得到F=Coker RF.

沿用定理2.1中的符號RF,現(xiàn)證明下面的結(jié)果.

推論2.1RF是具有余核濾子F的最小同余關(guān)系.

證明由定理2.1的證明知,RF是一個具有余核濾子F的同余關(guān)系.現(xiàn)設(shè)φ∈Con L且具有余核濾子F,即F=Coker φ.對于任意的i∈F有i≡1(φ).若(x,y)∈RF,則存在i∈F,使得x∧i=y∧i.于是x≡x∧i(φ),y≡y∧i(φ),從而(x,y)∈φ,所以RF≤φ.

設(shè)(L;∨,∧,?,?,0,1)是一個pMS-代數(shù),記F(L),CF(L)分別為L的所有濾子與所有余核濾子所構(gòu)成的集合,它們有下面的關(guān)系定理.

定理2.2設(shè)(L;∨,∧,?,?,0,1)是一個pMS-代數(shù),則CF(L)是F(L)的一個子格.

證明設(shè)F1,F2∈CF(L),由文獻[3]及定理2.1易得F1∧F2∈CF(L).

下證F1∨F2∈CF(L).令x∈F1∨F2,由文獻[3]知則存在i∈F1和j∈F2使得x≥i∧j,從而由文獻[5]得x??≥i??∧j??和x??≥i??∧j??.又由F1,F2∈CF(L),根據(jù)定理2.1知i??∈F1,j??,j??∈F2,所以x??∈F1∨F2,故由定理2.1得F1∨F2∈CF(L).因而CF(L)是F(L)的子格.

定理2.3設(shè)(L;∨,∧,?,?,0,1)是一個pMS-代數(shù).令

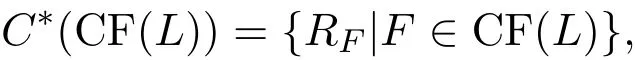
其中RF如定理2.1中所定義,則C?(CF(L))是Con L的子格.

證明易得R{1}=ω(相等關(guān)系)及RL=ι(泛同余關(guān)系).

先證對任意的F1,F2∈CF(L),有由定理2.2知F1∧F2∈CF(L).設(shè)(x,y)∈RF1∧RF2,由文獻[3]知且因此存在i∈F1,j∈F2使得

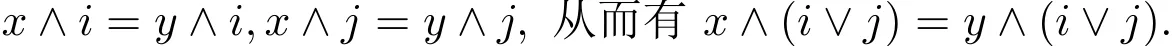
則存在i1,i2,………,it∈F1及j1,j2,………,js∈F2使得

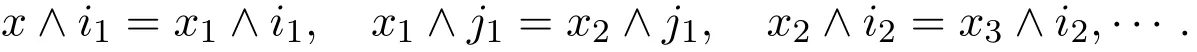
令i=i1∧i2∧………∧it∧j1∧j2∧………∧js,顯然有i∈F1∨F2.因此x∧i=x1∧i=………=y∧i,即有所以故定理得證.

現(xiàn)設(shè)F是L的余核濾子,定義Fo={x∈L|(?a∈F)x≤a?}.顯然,Fo是L的理想,有如下的結(jié)論:

定理2.4設(shè)(L;∨,∧,?,?,0,1)是一個pMS-代數(shù),又設(shè)F是L的余核濾子,則

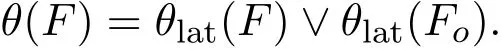
證明設(shè)a,b∈F且a≤b,顯然a?,b?∈Fo.由文獻[5]知a?=a???,b?=b???,又由定理2.1知a??,b??∈F,從而有a?∈Fo,b?∈Fo,所以得θlat(a,b)≤θlat(F),θlat(b?,a?)≤θlat(Fo), θlat(b?,a?)≤θlat(Fo).由文獻[5]知若L∈pMS,a,b∈L且a≤b,有

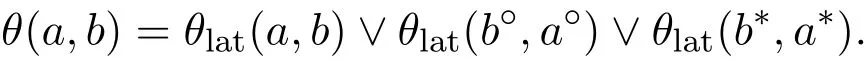
所以,θ(a,b)≤θlat(F)∨θlat(Fo).又由文獻[3]知,θ(F)=∨{θ(a,b)|a,b∈F},于是可推知θ(F)≤θlat(F)∨θlat(Fo).

另一方面,假設(shè)a,b∈Fo,a≤b,由Fo的定義知,存在c∈F使得a≤b≤c?.由于(c,1)∈θ(F),因此(c?,0)∈θ(F∨).又因(a,a),(b,b)∈θ(F),故(a,0),(b,0)∈θ(F),從而得(a,b)∈θ(F).結(jié)合事實θ(Fo)={θ(a,b)|a,b∈Fo},因此有

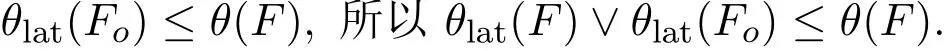
命題得證.

進一步地,用另一種形式刻劃θ(F).

定理2.5設(shè)(L;∨,∧,?,?,0,1)是一個pMS-代數(shù),又設(shè)F是L的余核濾子,則

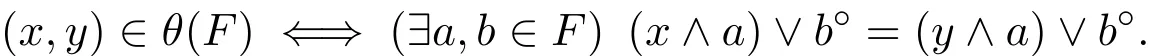
證明在L上定義一個等價關(guān)系φ如下:

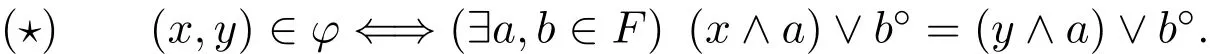
易見,φ是一個格同余.

先證φ∈Con L.設(shè)(x,y)∈φ,則存在a,b∈F使得

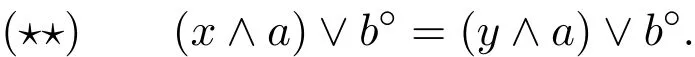
這樣可得(x?∨a?)∧b??=(y?∨a?)∧b??,于是有

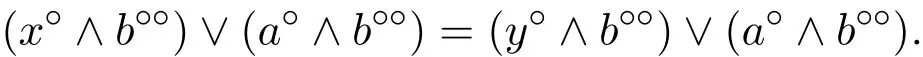
因為a?∧b??≤a?,故得(x?∧b??)∨a?=(y?∧b??)∨a?.由文獻[5]知a?=a???=(a??)?,故(x?∧b??)∨(a??)?=(y?∧b??)∨(a??)?,而且有a??≥a∈F,b??≥b∈F.因此a??,b??∈F,所以(x?,y?)∈φ.

另一方面,由(??)得

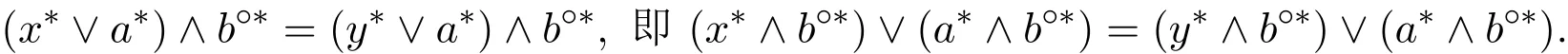
由定理2.1知,b??∈F且結(jié)合文獻[5]有a?=a???,于是得到

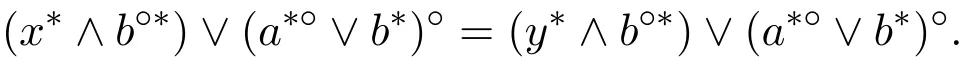
注意到a??∨b?≥a??∈F,則a??∨b?∈F.再結(jié)合φ的定義可得(x?,y?)∈φ,所以φ∈Con L.

現(xiàn)證φ=θ(F).為此設(shè)(x,y)∈φ,則存在a,b∈F使得(x∧a)∨b?=(y∧a)∨b?.因為(a,1)∈θlat(F),(b?,0)∈θlat(Fo),所以

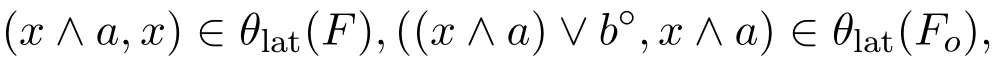
所以

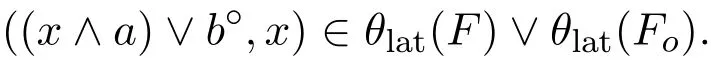
同理可得,((y∧a)∨b?,y)∈θlat(F)∨θlat(Fo).

所以可得,(x,y)∈θlat(F)∨θlat(Fo),即φ≤θlat(F)∨θlat(Fo).結(jié)合定理2.4有φ≤θ(F).另一方面,設(shè)(x,y)∈θ(F)=θlat(F)∨θlat(Fo),則存在x=x0,x1,………,xn?1=y且

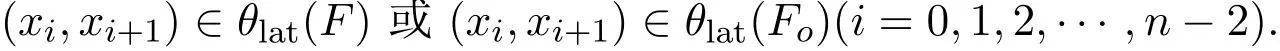
不失一般性,設(shè)

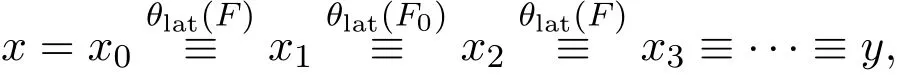
則存在i1,i2,………,it∈F和j1,j2,………,js∈F,使得

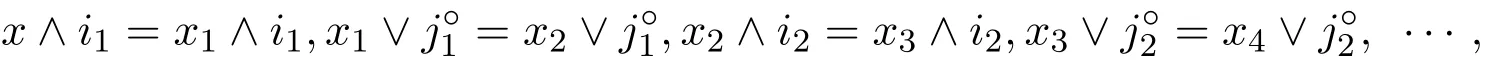
因此,(x,y)∈φ.故θ(F)≤φ.

綜上可得θ(F)=φ.定理得證.

定理2.6設(shè)(L;∨,∧,?,?,0,1)是一個pMS-代數(shù),φ∈Con L,則Coker φ是L的余核濾子且

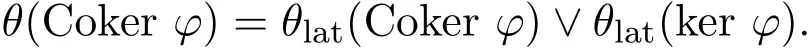
證明設(shè)x∈Coker φ,即x≡1(φ).對于任意的y≥x,有y≡y(φ),故y∨x≡y∨1(φ),于是有y≡1(φ),故y∈Coker φ,所以Coker φ為L的濾子.又因若x≡1(φ),則有x??≡1(φ),所以x??∈Coker φ.由定理2.1知Coker φ為L的余核濾子.

欲證θ(Coker φ)=θlat(Coker φ)∨θlat(ker φ),由定理2.4知只需證(Coker φ)o=ker φ.

設(shè)x∈(Coker φ)o,則存在a∈Coker φ,使得x≤a?.由于a≡1(φ),則a?≡0(φ),因而x=x∧a?≡x∧0=0(φ),于是得x∈ker φ,所以(Coker φ)o≤ker φ.

另一方面,設(shè)x∈ker φ,則x?∈Coker φ.由文獻[4]MS代數(shù)運算特征知x≤x??=(x?)?,從而得x∈(Coker φ)o,故ker φ≤(Coker φ)o.定理得證.

已知,關(guān)系Φ是pMS-代數(shù)的一個基本同余關(guān)系[5].它由所給出,可得如下性質(zhì).

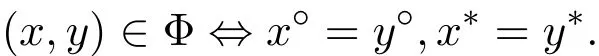
推論2.2θ(Coker Φ)=θlat(Coker Φ).

證明由定理2.4和定理2.6得只需證(Coker φ)o=ker φ=0.

設(shè)x∈(Coker φ)o,則存在a∈Coker φ使得x≤a?.又因(a,1)∈Φ,即a?=0,故有x=0.即證.

3 完全濾子

設(shè)L是一個pMS-代數(shù),F是L的任一余核濾子.對于任意的x∈F,有

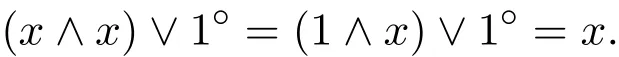
由定理2.5得x∈Coker θ(F),即F?Coker θ(F).但是下面舉例說明.

設(shè)(L;∨,∧,?,?)∈pMS,如下圖所示:

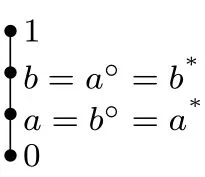
令F={a,b,1},由定理2.1知F是L的余核濾子,并且θ(F)=θ(a,b)∨θ(a,1)∨θ(b,1),易見a,b∈Coker θ(F).再由定理2.5知,0∈Coker θ(F).故Coker θ(F)=L/=F.

若Coker θ(F)=F,給出如下定義.

定義3.1設(shè)(L;∨,∧,?,?,0,1)是一個pMS-代數(shù),F是L的余核濾子,若F=Coker θ(F),則稱F是L的完全濾子.

下面給出完全濾子的判別定理.

定理3.1設(shè)(L;∨,∧,?,?,0,1)是一個pMS-代數(shù),F是L的余核濾子,若F是L的完全濾子當(dāng)且僅當(dāng)

證明?:設(shè)x∈F,因為F=Coker θ(F),則有(x,1)∈θ(F).由定理2.5知存在a,b∈F使得(x∧a)∨b?=(1∧a)∨b?,于是可得(x∨b?)∧(a∨b?)=a∨b?.又因a∨b?≥a∈F,所以a∨b?∈F.命題得證.

?:若x∈F?(?a,b∈F)(x∨b?)∧a=a,下證F=Coker θ(F).因為(a,1)∈θ(F), (b?,1)∈θ(F),(x,x)∈θ(F),所以(x∨b?,x)∈θ(F),而(x∨b?)∧a=a,故(a,x)∈θ(F),從而(x,1)∈θ(F),即x∈Coker θ(F).另一方面,設(shè)x∈Coker θ(F),即(x,1)∈θ(F).由定理2.5知存在a,b∈F,使得又因a∨b?∈F,所以x∈F.定理得證.

定理3.2設(shè)(L;∨,∧,?,?,0,1)是一個pMS-代數(shù),F1,F2是L的完全濾子,則F1?F2當(dāng)且僅當(dāng)θ(F1)?θ(F2).

證明?:由題設(shè)知至少存在一個元素a∈L且a∈F2F1,于是(a,1)∈θ(F2),則必有(a,1)/∈θ(F1).否則有a∈Coker θ(F1),相應(yīng)地a∈F1,此與a/∈F1相矛盾,因此θ(F1)/=θ(F2).又由F1?F2,易得θ(F1)?θ(F2).所以有θ(F1)?θ(F2).

?:對于任意的a∈F1,都有(a,1)∈θ(F1).因為θ(F1)?θ(F2),所以(a,1)∈θ(F2),于是a∈Coker θ(F2),即a∈F2,從而F1?F2.若F1=F2,則θ(F1)=θ(F2),這與θ(F1)?θ(F2)相矛盾,故F1?F2.定理得證.

4 同余一致性質(zhì)

設(shè)θ是pMS-代數(shù)的一個同余,若對任意的a,b∈L,有

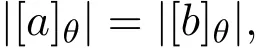
其中[a]θ|={x∈L|(x,a)∈θ},|[a]θ|表示[a]θ的基數(shù),則稱θ是同余一致的.下面文中的RF均是由定理2.1證明中所定義的同余,其中F是L的余核濾子.由推論2.1知,RF是包含F(xiàn)的最小同余.有下面的結(jié)果.

定理4.1設(shè)(L;∨,∧,?,?,0,1)是一個pMS-代數(shù),F是L的余核濾子,則RF是同余一致的,且對任意的a∈L有|[a]RF|=|F|.

證明設(shè)F是L的余核濾子,a,b∈L,不失一般性,不妨假設(shè)a≥b.現(xiàn)證為此設(shè)

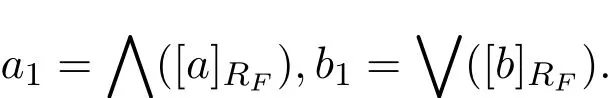
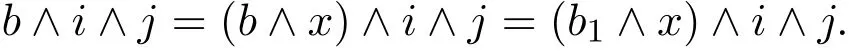
易知fa是格同態(tài).現(xiàn)證fa也是滿格同態(tài).為此設(shè)則存在i1∈F,使得b∧i1=s∧i1.又因故存在j1∈F,使得s∧j1=b1∧j1.令x=s∨(a∧j1),有

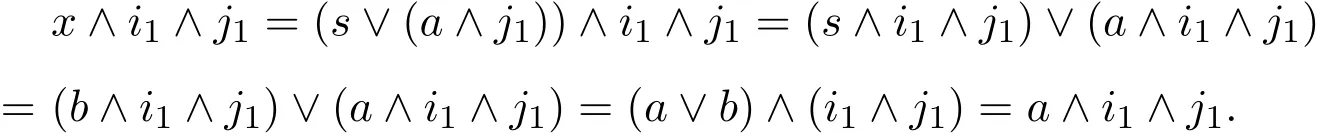
由于i1∧j1∈F,故又因s≤b1,故

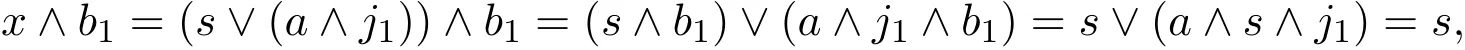
即fa(x)=s.所以fa是滿射.于是有

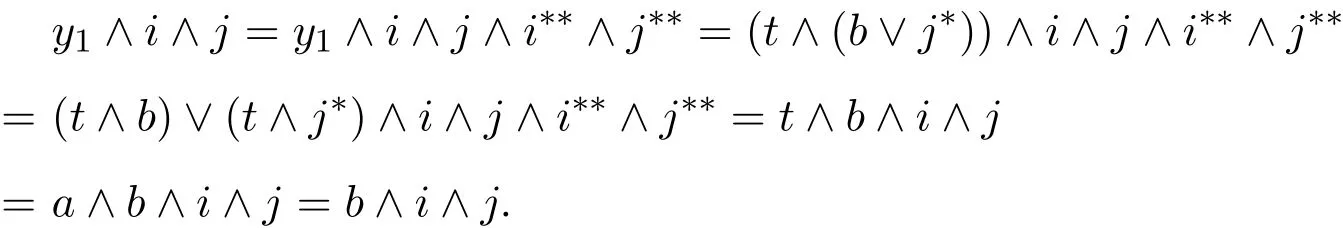
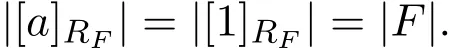
[1]Blyth T S,Varlet J C.Ockham Algebras[M].Oxford:Oxford University Press,1994.

[2]Blyth T S,Fang Jie,Varlet J C.Ockham algebras with pseudocomplementation[J].Communications in Algebra,1997,25:3605-3615.

[3]Gr¨atzer G.Lattice Theory[M].New York:W.H.Freeman and Company,1971.

[4]Blyth T S,Varlet J C.On a common abstraction of de Morgan algebras and Stone algebras[J].Proc.Roy. Soc.Edinburgh,1983,94A:301-308.

[5]Fang Jie.Pseudocomplementde MS-algebras[J].Algebra Colloq.,1996,3(1):59-65.

[6]王尊全.偽補分配格的同余理想與同余關(guān)系[J].純粹數(shù)學(xué)與應(yīng)用數(shù)學(xué),2001,17(4):363-367.

[7]王尊全.MS-代數(shù)的理想和同余關(guān)系[J].純粹數(shù)學(xué)與應(yīng)用數(shù)學(xué),2004,20(4):389-392.

[8]方捷,吳麗云.擬補Ockham代數(shù)的理想與濾子[J].數(shù)學(xué)學(xué)報,2004,47(4):647-652.

[9]趙秀蘭,方捷.平衡擬補Ockham代數(shù)的理想格[J].華南師范大學(xué)學(xué)報,2007,2:42-47.

[10]方捷,沈嚇妹.平衡半擬補Ockham代數(shù)的濾子[J].模糊系統(tǒng)與數(shù)學(xué),2010,24(3):38-45.

[11]王雷波,方捷.雙重偽補代數(shù)的假值理想的一點注記[J].純粹數(shù)學(xué)與應(yīng)用數(shù)學(xué),2012,28(1):119-122.

[12]趙秀蘭,孫中舉.雙重偽補Ockham代數(shù)的理想與濾子[J].模糊系統(tǒng)與數(shù)學(xué),2012,26(3):70-76.

Filters congruences of pseudocomplemented MS-algebras

Zhao Xiulan,Ma Hongjuan
(Department of Mathematics and Physics,Huang He Science and Technology College, Zhengzhou450063,China)

The concepts of cokernel filter and full filter on a pseudocomplemented MS-algebra are introduced. By discussing the properties of the cokernel fi lters and full fi lters,the expressions of the cokernel filter congruences and full fi lters congruences on a pseudocomplemented MS-algebra are got.We prove that the smallest congruence with the cokernel filter has the congruence uniformity.

pseudocomplemented Ockham algebra,MS-algebra,cokernel filter,full filter,congruence

O153

A

1008-5513(2014)03-0255-09

10.3969/j.issn.1008-5513.2014.03.006

2014-02-05.

河南省教育廳科學(xué)技術(shù)研究重點項目（12B110017).

趙秀蘭(1982-),碩士,講師,研究方向:格論與有序代數(shù).

2010 MSC:06D15