Capillary effect on the sloshing of a fluid in a rectangular tank submitted to sinusoidal vertical dynamical excitation*
MEZIANI Bachir, OURRAD Ouerdia
Laboratoire de Physique Théorique, Université A. Mira de Bejaia, Campus de targua Ouzemour, Bejaia 06000, Algeria, E-mail: bachirdidih@yahoo.fr
Capillary effect on the sloshing of a fluid in a rectangular tank submitted to sinusoidal vertical dynamical excitation*
MEZIANI Bachir, OURRAD Ouerdia
Laboratoire de Physique Théorique, Université A. Mira de Bejaia, Campus de targua Ouzemour, Bejaia 06000, Algeria, E-mail: bachirdidih@yahoo.fr
(Received March 30, 2013, Revised February 17, 2014)
Surface tension effects on fluid sloshing in a tank subjected to external excitation has been less studied. This work aims at understanding this phenomenon in order to derive practical solutions to problems faced in several engineering. A tank containing a fluid with a free surface is submitted to gravity and capillary forces and subject to external dynamic excitation. Introduction of vertical sinusoidal dynamical excitation leads to a problem of paramtric oscillations governed by the Mathieu equation. Analysis of the Mathieu equation shows the existence of stable and unstable regions in the stability diagram. Some results induced by harmonic excitations on the fluid sloshing are presented. When the external dynamical excitation amplitude ε is small, periodic solutions appear in stable regions and when ε increases, the fluid behavior is not perfectly periodic and the amplitudes are not regular. Nonlinear effects make the behavior of the fluid complicated and render it almost unpredictable. In stable regions, the solution remains bounded at any time. When changing the perturbation parameter ε, the phase difference increases and also with the increase of the surface tension.
parametric sloshing, capillary effects, stability
Introduction
A vibrating tank partially or completely filled with fluid having a free surface is involved with free surface movement, and by reaction the tank is affected by the movement. In particular, we are interested in the free surface movement called sloshing. It is caused by external excitation acting on the tank partially filled with one or more fluids. Depending on the type of excitation and the geometry of the tank, the free surface of fluid undergoes different types of motions. Thus, the liquid-liquid interface or liquid-air interface oscillates around its equilibrium stable state due to the forces induced by external excitation, gravity and surface tension. This movement can be visualized as a sum of vibration modes of the fluid. There are, in principle, an infinite number of modes representing the free surface deformation. However, in many applications, a finite number of modes appear. Knowledge of these modes and their corresponding eigenfrequencies plays an important role in industrial processes where control frequencies are set to avoid the risk of damage.
This is a difficult mathematical problem to solve analytically because the boundary conditions at the free surface are not linear and the position of the latter is a priori unknown. Moreover, the, external excitations acting on the free surface make the problem more complicated. In fact, analytical solutions are limited to the regular geometric shapes such as cylindrical tank and rectangular tank. This is why analytical techniques to predict large-amplitude sloshing are not yet fully developed. The sloshing of fluids in stationary or mobile tanks garnered many preoccupations to physicists, mathematicians, aerospace, civil and nuclear engineers. Civil engineers and seismologists have studied the liquid sloshing effects on large dams and oil tanks subjected to seismic excitations.
Motivation of the present work is to explore capillary effects of sloshing liquids in a tank vertically excited. The historical review of fluid sloshing was given in Ref.[1] with detailed analysis of the linear theory. Reference [2] summarized the work carried out on the external excitation effects on the discrete orcontinuous vibratory systems. Second order perturbation method was used by Ref.[3] to solve the sloshing problem of an inviscid fluid in tank with an arbitrary bed shape.
Simulation of the sloshing in fixed and vertically excited tank without surface tension was explored in Refs.[4] and [5]. Standing waves of different fundamental wavelengths was simulated and nonlinear effects of increasing wave steepness were examined. Free surface wave resonated by periodic oscillation along an axis aligned with the wave number vector was investigated using the weakly-nonlinear analysis[6]. Weak viscosity, general water depth, and transient wave evolution effects were simultaneously considered. Sloshing waves under horizontal and vertical random excitations were simulated in Ref.[7]. To simulate the sloshing phenomenon inside a liquid tank subjected to horizontal harmonic oscillations, earthquake excitations, tanks isolation under long-period ground motions, nonlinear lateral forced tank and motion cargo effects on the sloshing, numerical and experimental study have been conducted. Among the most important results in Ref.[8], the authors confirmed that the base shear force of a liquid tank calculated from the hydrostatic pressure is valid only when the forced frequency is in the neighborhood of the first fundamental tank frequency and the linear wave theory may substantially under- or over-estimate the base shear force for large-displacement excitations. The study conducted in Ref.[9] has confirmed that the dynamic response of tanks during seismic ground motions might be considerably reduced in the liquid tank with base-isolation system. The work in Ref.[10] identified four classes regimes in the movement of the free surface after a full scanning of the parametric regime and tank sloshing with ship motion coupling effects have been investigated in Ref.[11]. The impulse-response function method was employed to determine the ship motion. This study concluded that when the frequency is in the resonance range significant reduction of the role motion occure due to the bigger moment phase difference between the wave excitation and sloshing induced moments.
In engineering, dampers and screen are used to remove liquid vibrations induced by wind in buildings, and to limit the damage of the resonance in tanks used for liquid storage in seismic zones. Liquid sloshing motion inside a tank of a tuned liquid damper undergoing arbitrary interface deformation was numerically analyzed in Ref.[12]. This study showed that the external excitation amplitude has a strong effect on the sloshing behavior of the liquid in the tank.
The sloshing in a rectangular tank with a vertical slat-type screen in its middle and horizontally excited in a frequency range covering the two lowest natural sloshing frequencies has been analytically modeled[13]and showed that the screen involves a damping mechanism for low and intermediate solidity ratios. Other applications in the aerospace industry were described in Ref.[14]. To provide maximum forces due to fluids responses to the excitation, it is essential to model the steep waves correctly, especially when nonlinear effects become significant. The surface tension effect on the sloshing was considered in several works. Numerical approach to solve the three-dimensional linear sloshing problem of an incompressible inviscid liquid proposed in Ref.[15] used the vectorial parameterization of the free surface deformation to derive an expression of the capillary and contact angle stiffness operators. The tank wall curvature is taken into account through an additional stiffness on the free surface and its influence on the sloshing eigenfrequencies might be strong and even create instabilities if its effect on the stiffness is negative.
The goal of this paper is to analyze the surface tension effects on sloshing in a rigid rectangular tank of uniform depth filled with free surface inviscid fluid and submitted to external dynamical excitation. Indeed, after introduction we give the dimensional equations governing the problem. Taking into account some assumptions with the choice of reference variables, we derive the equations governing the linear dimensionless problem. Solutions to the problem are discussed in the second section; we begin with the non-excited problem. The introduction of a dynamical excitation gives a parametric problem governed by the Mathieu equation[16]. The analysis of the Mathieu equation shows the existence of stable and unstable regions[17]. We present the explicit solution in the excited case. Results are given in the third section. Firstly, we study the effect of capillarity on the sloshing eigenfrequencies and eigenmodes in the non-excited case. A stability diagram is given in the parameters of the problem for the exited case. The analysis of sloshing in stable regions shows nonlinear effects. These effects are linked both to the external excitation amplitude and frequency, and also to the surface tension. Free surface elevation, phase space diagram and power spectrum are showed to explain the nonlinear effects.

Fig.1 Scheme of the problem
1. Formulation of problem
We consider A rectangular tank of width L and hight H partially or totally filled by inviscid fluid with density ρ and capillary coefficient σ with free surface denoted by η. The tank is subjected to vertical periodic excitation Z=acos(γt) applied at the free surface (see Fig.1). We introduce the two-dimensional cartesian coordinates with x and z corresponding to the horizontal and vertical directions respectively. The origin of the vertical axis is set at the average of the free surface of the fluid. The movement of the fluid is assumed to be irrotational. The tank is periodically excited with an acceleration, Z˙˙= -aγ2cos(γt ), where t is time and γ is the angular frequency of the vertical movement.
The basic equations governing the motion of a fluid in a tank are the equations of conservation of mass and momentum. These equations are written for a non-viscous incompressible fluid as follows

where φ=φ(x, z, t) is the velocity potential. The velocity potential must satisfy the kinematic and dynamical conditions at the free surface and the no slipping conditions on the flat bottom and vertical walls, which are expressed respectively by

where L is the width of the tank.
The kinematic condition on the free surface is given by

where g is the gravity acceleration, σ is the surface tension coefficient and C is the mean curvature of the free surface C=1/R1+1/R2with R1and R2being the principal radii of curvature. In the 2-D case, the expression of C is given by C=1/R1+1/R2= ηxx.
In order to form a dimensionless system we scale lengths with the width L, time with the gravitational time scaleand velocity potentials with LLg.
We obtain (x, z, h, H,η)=(x~, z~, h~, H~,η~)L , φ= L,t=. The Eqs.(1)-(5) can be rewritten as
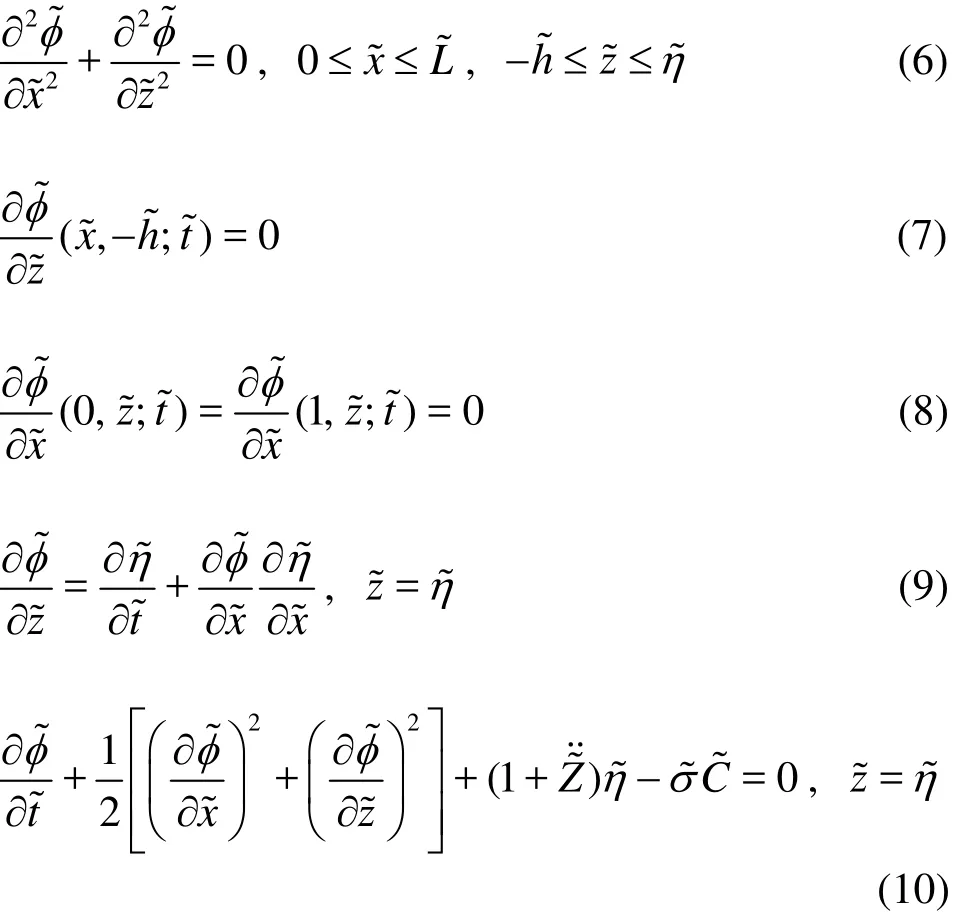
where σ~=σ/ ρgL2is the Weber number expressing the effect of free surface tension.
We will, in the following, omit the tildes in the equations.
We consider the motion of small amplitude. In this case, we can neglect the nonlinear terms in the free surface conditions and these conditions are taken at the average of free surface z=0. The linearized equations system is given by
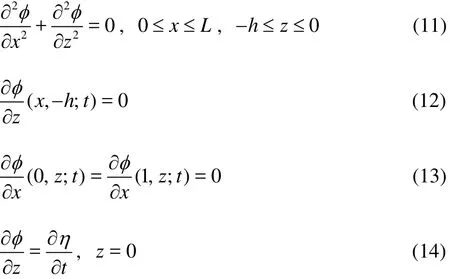

A combination of kinematic and dynamical conditions at the free surface gives
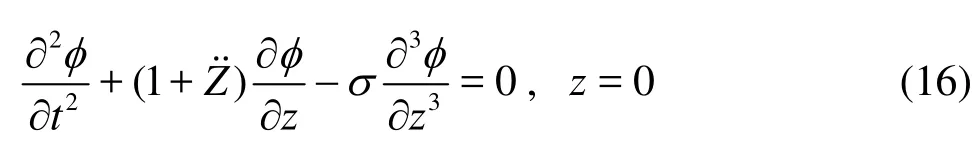
Obviously, this assumption simplifies the solution of these equations. Indeed, with this linearity condition, we will solve analytically these equations in the case of the considered geometry. Knowing that the linear approximate solutions is obtained only for a regular shaped tank with all walls straight and vertical.
After linearizing the system of equations governing the sloshing in rectangular tank, we propose in the following to solve these equations and determine the eigenfrequencies and eigenmodes that give the deformation of the free surface relative to the equilibrium position. We will start by solving the problem in the non-excited and determine the eigenfrequencies and free surface eigenmodes.
The capillary effects are highlighted in this case. We will thereafter give the solution in the case of a vertically excited tank.
2. Solution
2.1 Solution without external excitation
To solve the Laplace equation with the boundaries conditions, the simplest method is clearly the separation of variables method. We determine the eigenfrequencies and eigenmodes numerically and showing clearly the influence of surface tension on the eigenfrequencies and eigenmodes obtained for spatial, temporal and spatio-temporal representation.
The velocity potential φ satisfying the boundary conditions at the tank bottom z=-h and at the two vertical sides x=0 and x=1 is given by

which is the wave number of the nth potential mode.
Substituting Eq.(17) into Eq.(16) without external excitation, we obtain:

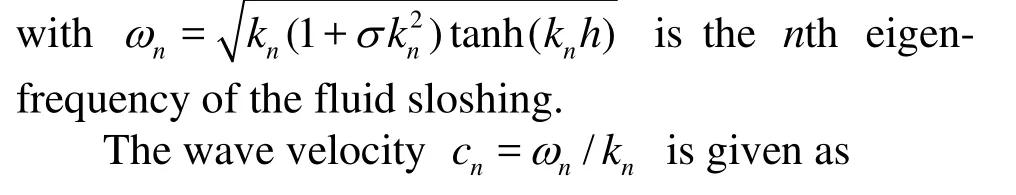

Assuming initially the fluid is at rest with an initial perturbation of the free surface

The elevation of the free surface, η(x, t), deduced from the kinematic condition at the free surface, can be written as

where anis the initial wave amplitude.
Finally, the general solution of the problem of two-dimensional linear sloshing in rectangular tank is given by
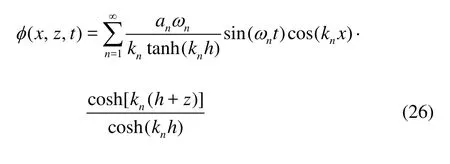

2.2 Solution with external excitation
The introduction of a vertical dynamical excitation of sinusoidal type gives a problem of parametric oscillations governed by the Mathieu equation. The analysis of the Mathieu equation shows the existence of stable and unstable areas. A stability diagram is given as function of the problem parameters. The analysis of sloshing in stable regions shows nonlinear effects. These effects depend on the frequency and the amplitude of the external excitation. The time evolution of the free surface, phase space diagrams and power traces are shown to explain the nonlinear effects.
We consider a liquid in a rectangular tank subject to vertical excitation. The change is done on the dynamic condition at the free surface. The tank is periodically excited with the vertical acceleration, Z˙˙= -εcos(γt), where γ is angular frequency of the excitation. In the vertically excited tank the parameter ε=aγ2/g is an important measure of vertically excited movement.
The problem is governed by the system of Eqs.(11)-(16). By substituting Z˙˙ by its formula, the kinematic and dynamic conditions at the free surface are given by
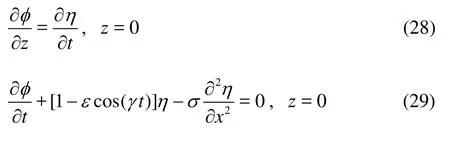
The velocity potential and the free surface elevation are

Assume that initially the fluid is at rest with an initial disturbance of the free surface

Inserting the velocity potential and the free surface elevation expressions into the kinematic and dynamic conditions at the free surface leads to
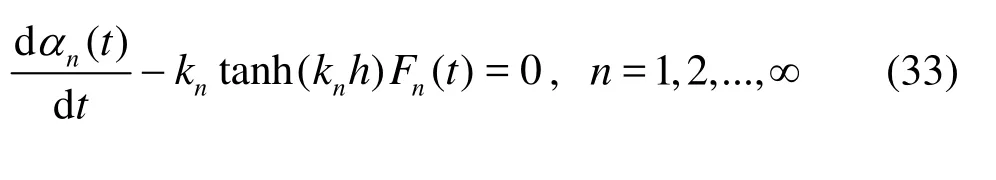


The Mathieu equation is encountered in many areas of physics such as fluid mechanics, the study of waves and vibrations and there are several methods for solving the Mathieu equation which are adapted to each individual case[18,19].
There are several methods used to solve the Mathieu equation[20]. The most widely-used one is the Floquet theory[21]. When the parameter ε is small, we can use the perturbation method to solve the equation and obtain solutions in stable regions. We put the solution of the Eq.(37) in the form
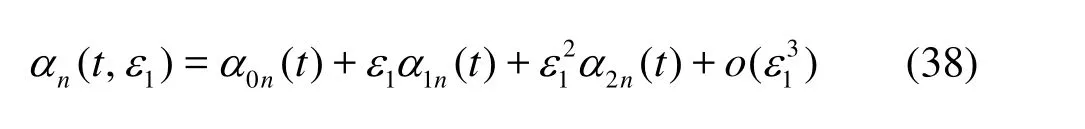
Substituting Eq.(38) into Eq.(37), we obtain an ordinary differential equation for each ε order. Their solutions allow us to reconstruct the final solution in the form:


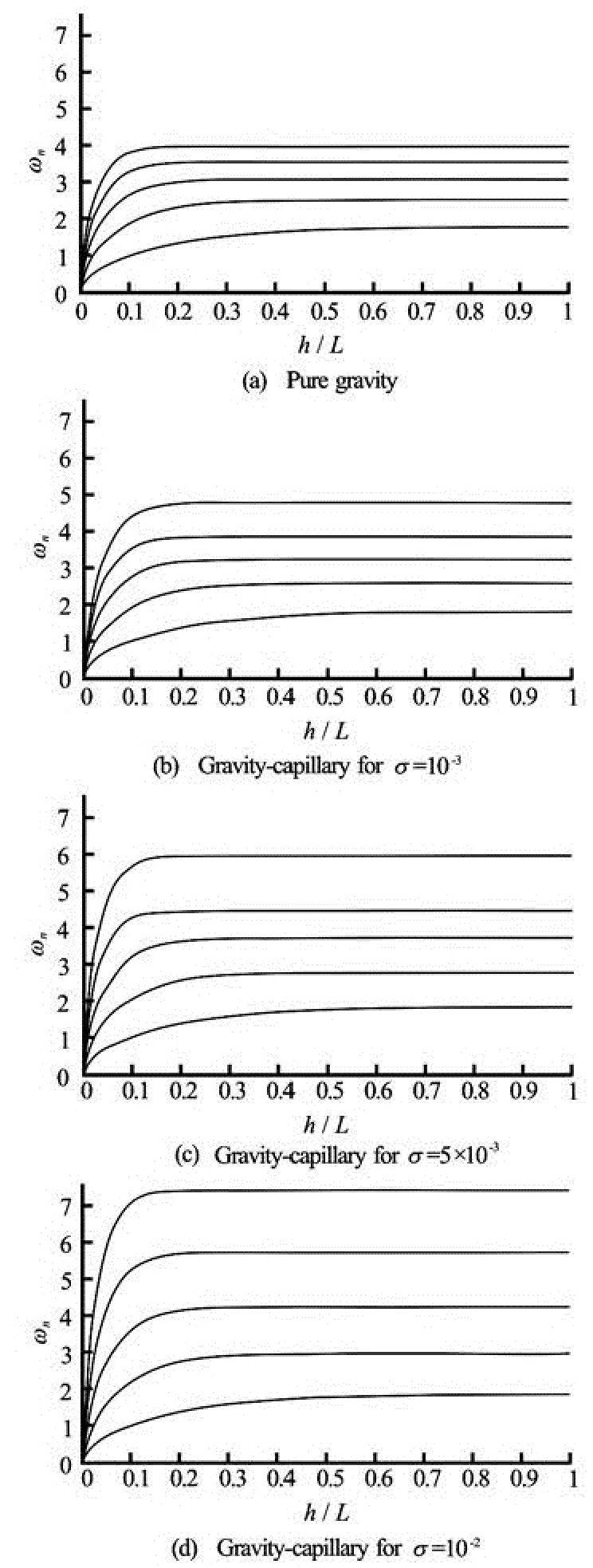
Fig.2 Variation of dimensionless frequency in a rectangular tank versus fluid depth h/ L for N=1,2,…5
3. Analysis and discussion
3.1 Solution without external excitation
The dispersion relation in the case of capillary gravity surface waves indicates the connection between the fluid sloshing eigenfrequencies with the cor-responding wave number. We show in Fig.2 the variations of the fluid sloshing eigenfrequency in a rectangular tank with and without the surface tension as a function of dimensionless depth h/ L.
First, we see that, whatever the frequency, the increase is faster for low loads and they are stabilized with the increase of the latter. This figure also shows that the capillary is shifted up to the values of these frequencies. This shift is more pronounced for higherorder eigenfrequencies. It is noted that the presence of surface tension induces an increase in the eigenfrequencies. In fact, this increase is obvious for large values of the modes number and the surface tension σ~=σ/ ρgL2, that is to say, capillarity effects are important when the fluid is very light or in microgravity hydrodynamic experiments and in the study of sloshing in tanks with a small length scale. Otherwise, these effects are masked by the influence of gravity.
For a given value of x, the free surface of the fluid moves up and down with time as a cosine curve, and such a wave does not propagate. Indeed, the free surface oscillates vertically. In the case of mode vibration of a solid structure, sloshing modes appear as a stationary surface due to the conditions imposed at the vertical walls of the tank. In addition, if the wall is flexible, coupling between sloshing modes and the modes of vibration of the flexible walls may occur, leading to new modes of vibration from the fluid structure coupling. In the following, we fixed the spatial coordinate at x=L/2 and represent the temporal evolution of the free surface in the case of a tank half filled h=0.5.

Fig.3 Temporal elevation of the free surface η with two modes (n=2) by setting x=L/2 and h=0.5
The presence of capillarity, as we mentioned above, increases the frequency of sloshing liquid. With this increase, the elevation of the free surface is affected by these frequencies. Thus, an increase of the phase shift induced by a surface tension will be observed. This is verified in Fig.3, representing the elevation of the free surface in the case of pure gravity and in the case of gravity capillary with a surface tension that takes the values: σ=10–3, σ=5.10–3, σ=10–2. It is also shown that the temporal profile of the free surface depends on the mode number taken into account in the representation of the surface.
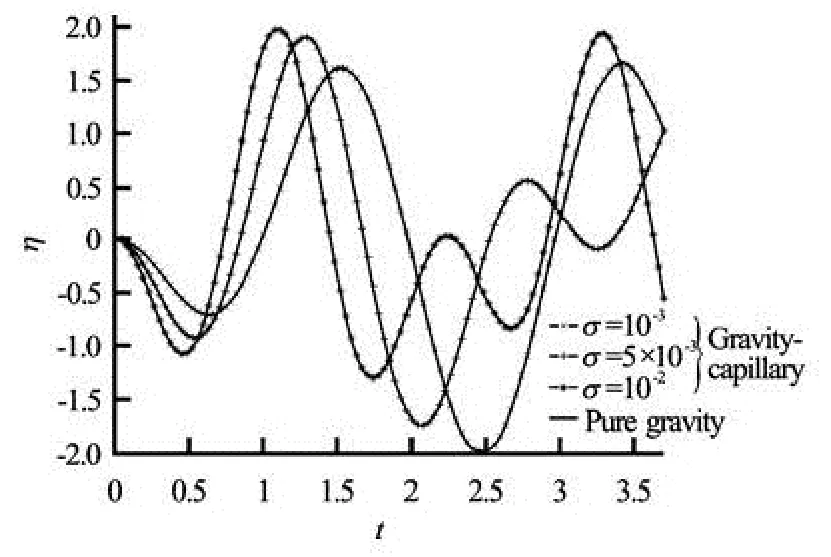
Fig.4 Temporal elevation of the free surface η with five modes (n=5) by setting x=L/2 and h=0.5
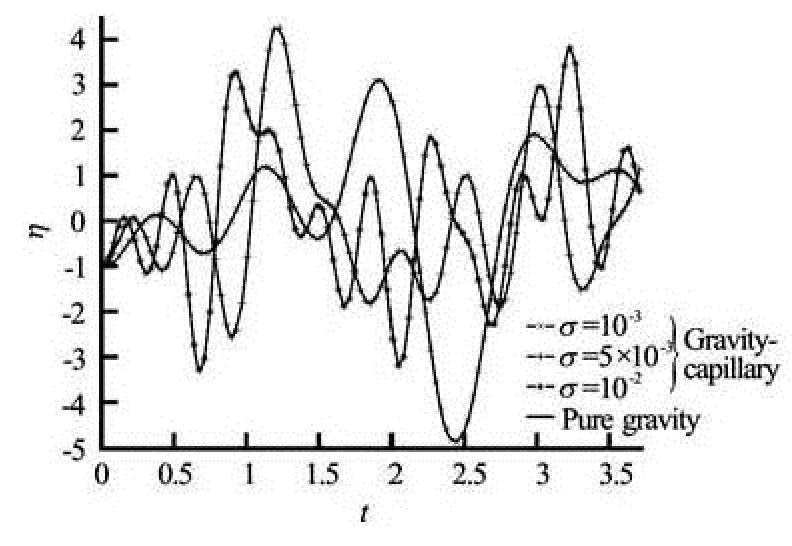
Fig.5 Temporal elevation of the free surface η with ten modes (n=10) by setting x=L/2 and h=0.5
The shape of the free surface appears to be sinusoidal when the number of modes is small (see Fig.3) and when the number of modes increases, the sinusoidal form tends gradually to disappear as shown in Figs.3, 4 and 5 corresponding to 2, 5 and 10 modes respectively. We also notice in these figures that the disappearance of the sinusoidal character is accentuated when the surface tension increases. This is verified by the evolution of the free surface, corresponding to the surface tension σ=10–3, σ=5.10–3, σ=10–2in these figures. The deformation of the free surface for moderate time remains small and the deformation becomes more and more important as time increases. This scenario of the deformation over time is longer in the case of pure gravity than in the case of gravity and capillary becomes smaller when the capillarity increases.
Spatial representation of the evolution of the free surface shows other effects as phenomenon related to peaks and troughs. In Fig.6, we see that when the surface tension increases, the peak becomes higher and steeper and troughs become deeper. When represe-nting the spatial evolution of the free surface with several modes (see Figs.7 and 8), we note that the first peak of the free surface appears more and more away from the origin when the surface tension increases and the phase of the free surface at the origin changing not only with the surface tension but also with the number of modes considered in its representation.
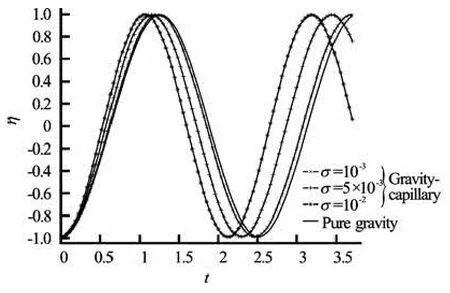
Fig.6 Spatial elevation of the free surface η with two modes (n=2) by setting x=L/2 and h=0.5
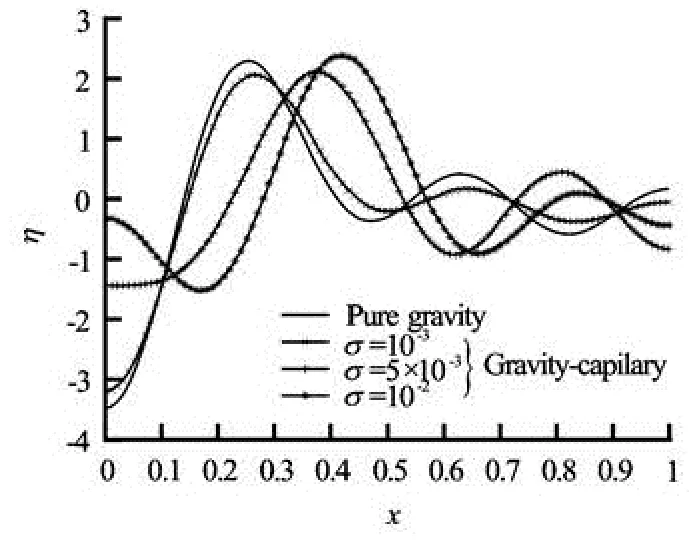
Fig.7 Spatial elevation of the free surface η with five modes (n=5) by setting x=L/2 and h=0.5

Fig.8 Spatial elevation of the free surface η with ten modes (n=10) by setting x=L/2 and h=0.5
The free surface is perturbed more on the left side of the tank than on the right one in the case of pure gravity and gravity capillary with a low surface tension. This large deformation moves towards the center of the tank when the surface tension increases (see the graph corresponding to σ=10–2in Fig.8) and the form of the free surface deformation is anti-symmetrical on both sides of the large deformation.
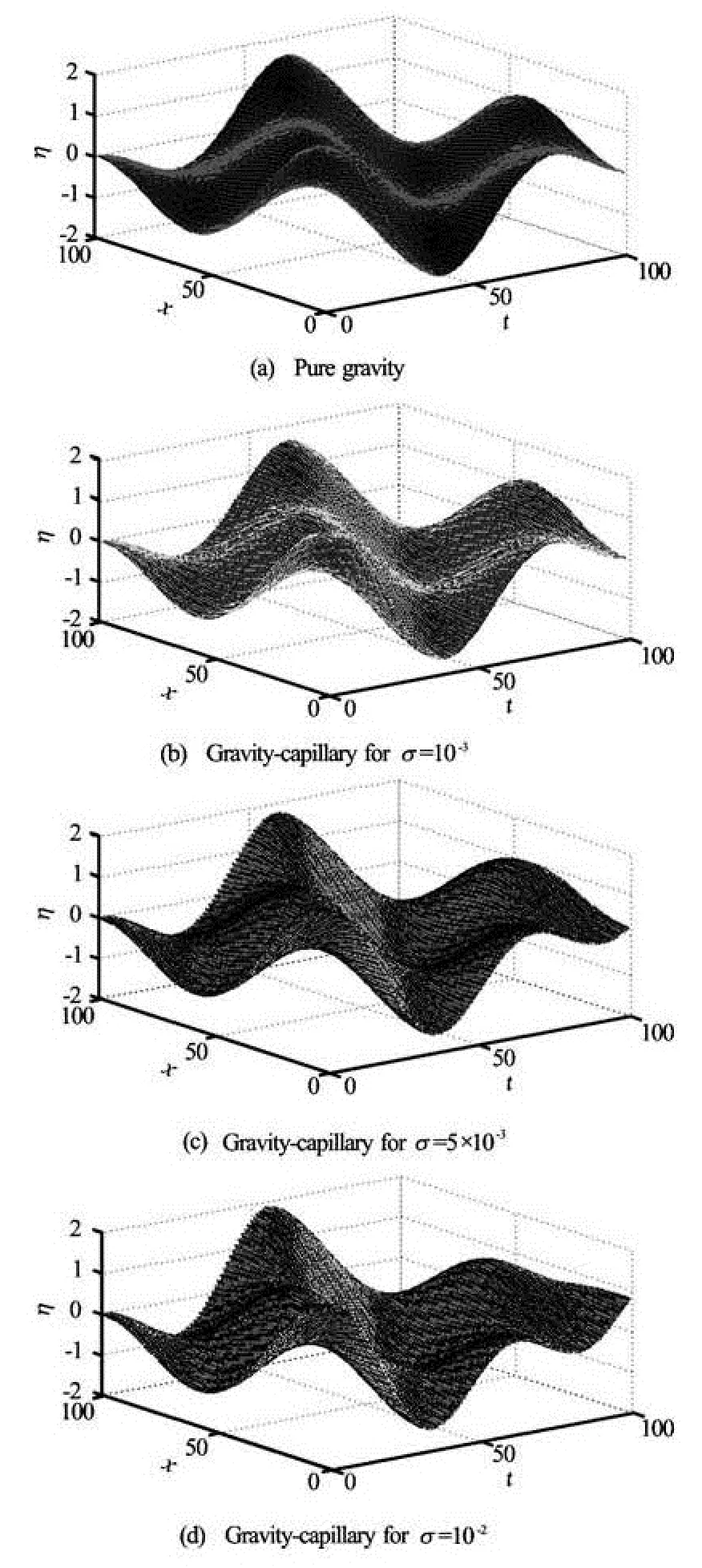
Fig.9 Spatiotemporal elevation of the free surface η with two modes (n=2) by setting x=L/2 and h=0.5
The spatiotemporal evolution of the free surface in the cases of pure gravity and gravity capillary with increasing surface tension and for a different number of mode shows clearly the combined effects of surface tension and the number of modes considered in its representation (shown in Fig.9-Fig.11). In fact, at the free surface, particles exhibit vertical oscillation and harmonics. The phase of the movement of fluid particles for the same modes is the same for all values ofσ but when the mode is changed, the phase decreases.

Fig.10 Spatiotemporal elevation of the free surface η with five modes (n=5) by setting x=L/2 and h=0.5
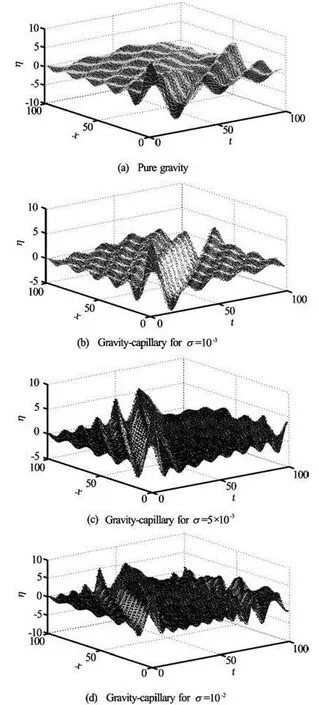
Fig.11 Spatiotemporal elevation of the free surface η with ten modes (n=10) by setting x=L/2 and h=0.5
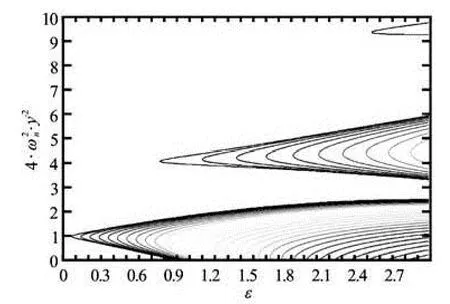
Fig.12 Stability diagram of dynamic vertical excitation with two modes (n=1…10) h=0.5 for pure gravity
The linear theory of liquid sloshing in rigid tanks supposes that the equations can be linearized around a state of static equilibrium, obviously to simplify the problem to be solved. It is based on the estimation of the movement of the free liquid surface. The explicit solutions could be given only for certain special cases. We note that the linearization of the boundary conditions for free surface does not provide good information on the deformation of the free surface. Linearization leads to neglect the nonlinear terms in the equations, but also to replace the boundary conditions onthe moving surface z=η unknown a priori with boundary conditions on a fixed surface z=0. The natural frequencies and the corresponding mode shape are obtained in the framework of this theory. We take into account the surface tension and explained its effect on the natural frequencies and the form of the free surface. Some forms in the case of the geometry studied are presented to illustrate these results.
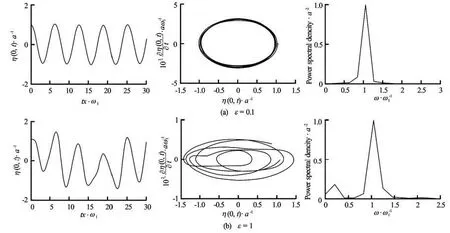
Fig.13 Temporal evolution, phase space diagrams and power spectra of the free surface first mode n=1 for ε=0.1 and ε=1 with h=0.5 in the pure gravity case
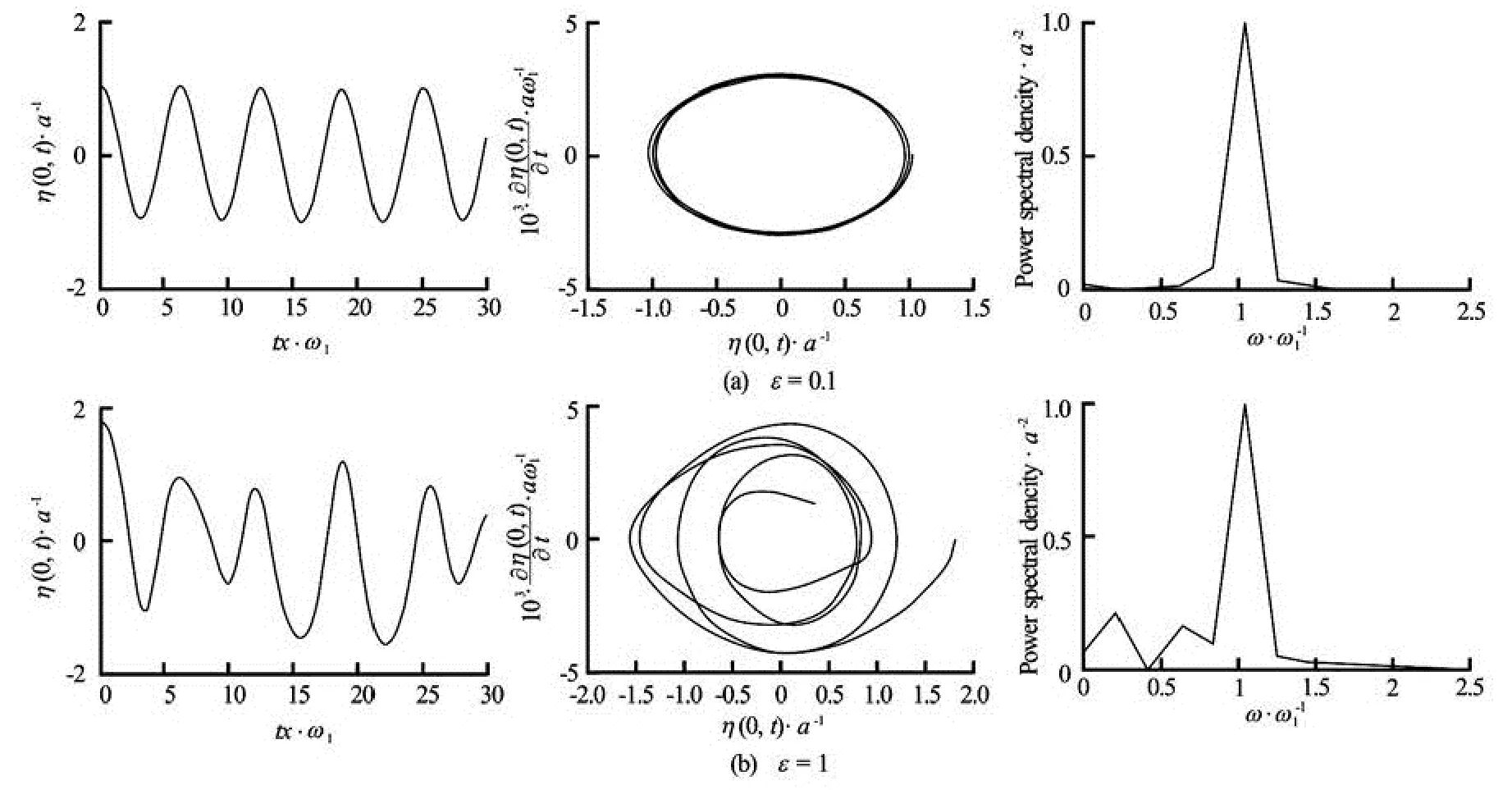
Fig.14 Temporal evolution, phase space diagrams and power spectra of the free surface first mode n=1 for ε=0.1 and ε=1 with h=0.5 in the gravity capillary case
The linear theory is developed based on the assumption of a wave of low amplitude. The deformation of the free surface is expressed as a superposition of the propagating modes. This method is the most classic, because it is relatively simple and provides important information. But unfortunately, it is unable to explain some complex phenomena observed experimentally.
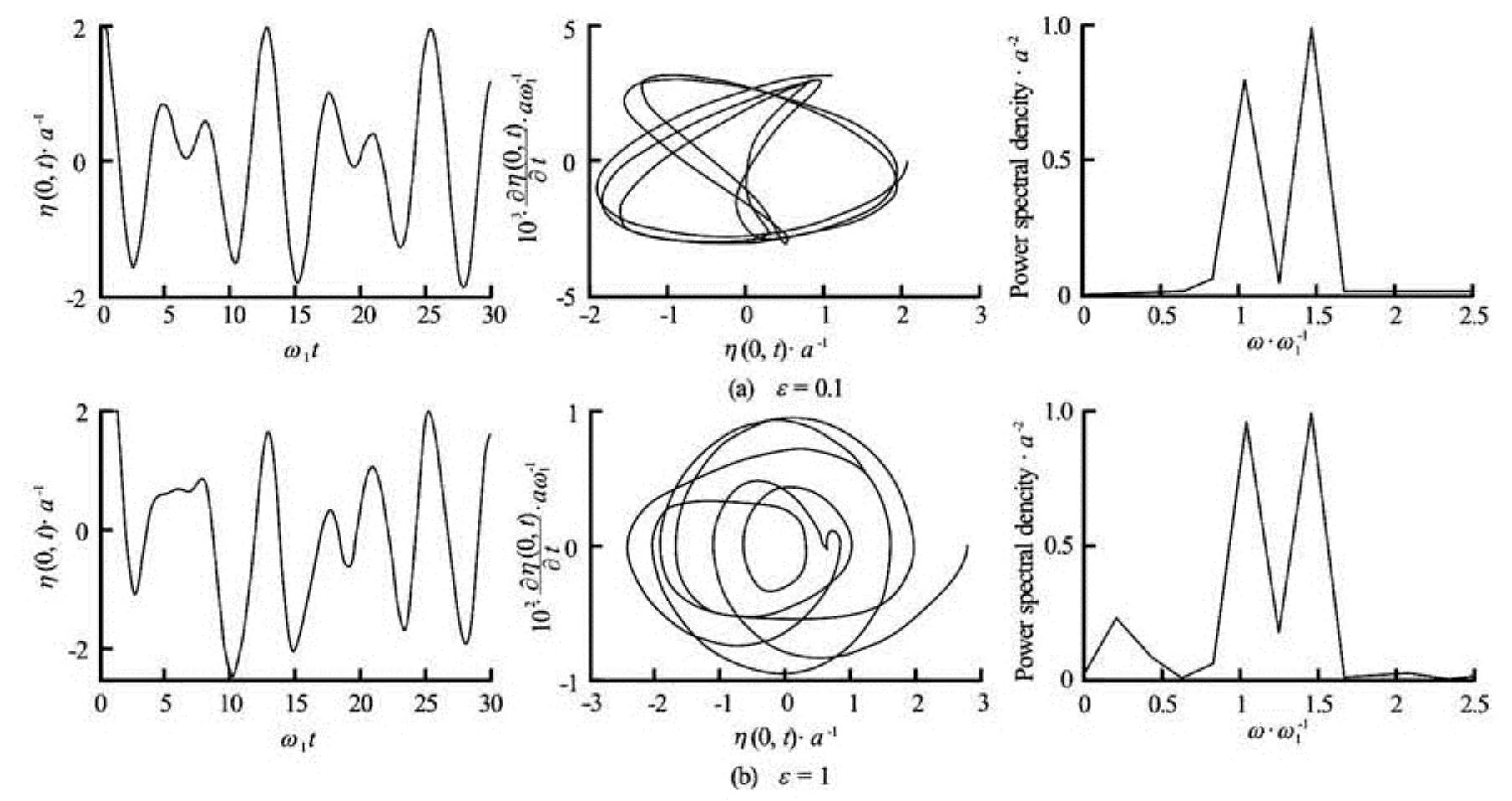
Fig.15 Temporal evolution, phase space diagrams and power spectra of the free surface first mode n=1 and n=2 for ε=0.1 and ε=1 with h=0.5 in the pure gravity case
3.2 Solution with external excitation
3.2.1 Stability diagram analysis
The stability diagram corresponding to the vertical excitation studied is shown in Fig.12, whcih is obtained for an external excitation frequency γ=2 with the amplitude a=0.5. There are three stable regions. For low fluid eigenfrequencies, the first stable region is wide, becomes narrow for intermediate fluid eigenfrequencies and finally narrower for the high eigenfrequencies. The structure of this diagram is similar for low values of the surface tension σ. However, when the capillary increases, three stable regions disappear and are replaced by a single stable region for low and intermediate fluid eigenfrequencies.
3.2.2 Time evolution, phase space and power
To see the effect of external excitation on the evolution of the free surface and understand the surface tension impact, we examine the temporal evolution, the phase space diagrams and the power spectra of the free surface elevation modes for some values of the perturbation parameter ε for different surface tension values σ.
When we take into account only the fundamental mode in the representation of the free surface, we observe for a small amplitude of the external excitation = ε0.1 in the pure gravity case (see Fig.13), and find that the temporal evolution of the free surface still sinusoidal, corresponding to a closed curve in the phase space and we see that the fundamental eigenfrequency is dominant. When the external excitation amplitude increases to ε=1, the free surface time evolution is not periodic and the phase space representation confirms this changes. We also note the increase in the time derivative of the free surface elevation, which leads to an increase in the vertical component of the fluid velocity at the interface. In the corresponding power spectrum, the emergence of a frequency does not owe to the fluid eigenfrequencies spectrum and the latter results from the interaction between the external excitation frequency and fundamental fluid eigenfrequency.
In the case of the presence of surface tension (see Fig.14), we observe the same free surface temporal evolution behavior for small external excitation amplitude. However, when the external excitation amplitude increases, the temporal evolution of free surface is perturbed and the profile changes compared to that obtained without capillarity. The first hallow is deeper when one takes into account of the capillarity. Also, the phase diagram shows that the vertical fluid velocity component is not as important as in the case of pure gravity, this means that capillarity plays an attenuator role. We note the existence of two frequencies which are derived from the interaction between the external excitation frequency and the fluid eigenfrequencies and the second frequency appears closest to the first fluid eigenfrequency.
If we consider the two firsts modes to reconstruct the free surface temporal evolution, we observe from Fig.15 in the absence of surface tension and for small external excitation amplitudes that the free surface profile still periodic, which is corroborated by thephase diagram and the power spectrum which highlyghts the first and the second fluid eigenfrequencies.
When the external excitation amplitude increases, the free surface temporal profile is no longer periodic. We also note the increase in the fluid velocity vertical component as in the case of one mode. Finally, the power spectrum reveals the existence of third frequency less than the two fluid eigenfrequencies.
Figure 15 represent the temporal evolution, phase space diagram and power spectrum of the free surface reconstructed with the two first modes in the presence of capillarity and external excitation amplitudes low and large. For small amplitudes, the temporal evolution is periodic and the preponderance of terms associated to the corresponding fluid eigenfrequencies modes. However, when the amplitude of the external excitation is large, the periodic nature of the temporal profile disappears and we make in evidence three frequencies that are result of the interaction of external excitation with the free surface modes vibrations. Two of these frequencies have an impact similar to fluid eigenfrequencies and the effect of the third remains moderate.
4. Conclusion
Results of liquid sloshing induced by harmonic excitations when the surface tension is considered are presented. The simulations are limited to a tank depth = h0.5. The effect of capillarity on the evolution of the free surface is first analyzed in the case without excitation. Among the effects induced by surface tension, the increase of the sloshing eigenfrequencies is found, which induces wavelengths decrease. The introduction of a dynamic excitation of vertical sinusoidal type gives a problem of parametric oscillations governed by the Mathieu equation. The analysis of the Mathieu equation shows the existence of stable and unstable regions. The analysis of sloshing in stable regions shows nonlinear effects. These effects depend on the frequency and the amplitude of the dynamic excitation. The effects of sloshing in a tank vertically excited in stable regions show the periodic behavior of solutions for low external excitation amplitude ε. When ε increases, the fluid behavior is not perfectly periodic, and the amplitudes are not regular. The temporal evolution of the free surface, phase space diagrams and power spectra are given to explain the nonlinear effects. These effects complicate the behaviour of the fluid and make it almost unpredictable. In stable regions, the solution remains bounded at any time. In these regions, small excitations can cause the growth of small disturbances acting on the tank. We also show some examples when the frequency changes during increasing amplitudes. When changing the perturbation ε, the phase difference increases also with the increase of the surface tension.
[1] IBRAHIM R. A.Liquid sloshing dynamics: theory and applications[M]. Cambridge, UK: Cambridge Uni- versity Press, 2005.
[2] KELLY W. G., PETERSON A. C.The theory of differential equations, classical and qualitative[M]. New York, USA: Springer, 2010.
[3] CHAPMAN G. J., PORTER R. Second order sloshing over an arbitrary bed[J].Journal of Fluid Mechanics,2005, 524: 331-355.
[4] FRANDSEN J. B., BORTHWICK A. G. L. Simulation of sloshing motions in fixed and vertically excited containers using a 2-D inviscid σ transformed finite difference solver[J].Journal of Fluids and Structures,2003, 18(2): 197-214.
[5] FRANDSEN J. B. Sloshing motions in excited tank[J].Journal of Computational Physics,2004, 196(1): 53- 87.
[6] HILL D. F. Transient and steady state amplitudes of forced waves in rectangular basins[J].Physics of Fluids,2003, 15(6): 1576-1587.
[7] SRIRAM V., SANNASIRAJ S. A. and SUNDAR V. Numerical simulation of 2D sloshing waves due to horizontal and vertical random excitation[J].AppliedOcean Research,2006, 28(1): 19-32.
[8] CHEN Y.-H., HWANG W.-S. and KO C.-H. Sloshing behaviours of rectangular and cylindrical liquid tanks subjected to harmonic and seismic excitations[J].Earthquake Engineering Structural Dynamics,2007, 36(12): 1701-1717.
[9] SHEKARI M. R., KHAJI N. and AHMADI M. T. On the seismic behavior of cylindrical base-isolated liquid storage tanks excited by long-period ground motions[J].Soil Dynamics and Earthquake Engineering,2010, 30(10): 968-980.
[10] JI Y. M., SHIN Y. S. and PARK J. S. et al. Experiments on non-resonant sloshing in a rectangular tank with large amplitude lateral oscillation[J].Ocean Enginee-ring,2012, 50: 10-22.
[11] LI Yu-long, ZHU Ren-chuan and MIAO Guo-ping et al. Simulation of tank sloshing based on open foam and coupling with ship motions in time domain[J].Journalof Hydrodynamics,2012, 24(3): 450-457.
[12] SIDDIQUE M. R., HAMED M. S. and El DAMATTY A. A. A nonlinear numerical model for sloshing motion in tuned liquid dampers[J].International Journal for Numerical Methods in Heat and Fluid Flow,2005, 15(3): 306-324.
[13]FALTINSEN O. M., FIROOZKOOHI R. and TIMOKHA A. N. Analytical modeling of liquid sloshing in a twodimensional rectangular tank with a slat screen[J].Journal of Engineering Mathematics,2011, 70(1-3): 93-109.
[14] VELDMAN A. E. P., GERRITS J. and LUPPES R. et al. The numerical simulation of liquid sloshing on board spacecraft[J].Journal of Computational Physics,2007, 224(1): 82-99.
[15] El-KAMALI M., SCHOTTE J. S. and OHAYON R. Three-dimensional modal analysis of sloshing under surface tension[J].International Journal of Numeri-cal Methods in Fluids,2011, 65(1-3): 87-105.
[16] BROUWERS J. J. H. Asymptotic solutions for Mathieu instability under random parametric excitation and nonlinear damping[J].Physica D: Nonlinear Phenomena,2011, 240(12): 990-1000.
[17] LI Y., FAN S. and GUO Z. et al. Mathieu equation with application to analysis of dynamic characteristics of resonant inertial sensors[J].Communications Nonlinear Science Numerical Simulation,2013, 18(2): 401-410.
[18] BALACHANDRAN B., KALMAR-NAGY T. and GILSINN D. E.Delay differential equations, recent advances and new directions[M]. New York, USA: Springer, 2009.
[19] BETOUNES D.Differential equations, theory and applications[M]. Second Edition, New York, USA: Springer, 2010.
[20] JORDAN D. W., SMITH P.Nonlinear ordinary differential equations, an introduction for scientists and engineers[M]. Fourth Edition, New York, USA: Oxford University Press, 2007.
[21] BITTANTI S., COLANERI P.Periodic systems, filtering and control[M]. London, UK: Springer-Verlag, 2009.
10.1016/S1001-6058(14)60036-6
* Biography: MEZIANI Bachir (1969-), Male, Ph. D., Professor
- 水動力學(xué)研究與進展 B輯的其它文章
- The analysis of second-order sloshing resonance in a 3-D tank*
- Comprehensive analysis on the sediment siltation in the upper reach of the deepwater navigation channel in the Yangtze Estuary*
- Two-phase air-water flows: Scale effects in physical modeling*
- Numerical prediction of 3-D periodic flow unsteadiness in a centrifugal pump under part-load condition*
- Effect of compressive stress on the dispersion relation of the flexural–gravity waves in a two-layer fluid with a uniform current*
- Improved conservative level set method for free surface flow simulation*

