Entangled Three Qutrit Coherent States and Localizable Entanglement

Mehrzad Ashrafpour,Mojtaba Jafarpour,and Abbass Sabour

Physics Department,Shahid Chamran University,Ahvaz,Iran

1 Introduction

It is well known that entanglement is of vital importance in the f i eld of quantum computation and quantum information theory.[1?5]Most of the investigations in this f i eld have focused on qubits.[6?8]However,recent investigations have revealed that systems with higher dimensions may improve the eきciency of quantum information protocols,security of quantum cryptography and channel capacities.[9?16]This has inspired some investigations concerning qutrits in the recent years.[17?20]In addition,entangled coherent states also have found applications in several areas,including quantum nonlocality,[21?26]interferometeric studies,[27]and quantum information theory.[28?30]

In this work we consider a three-qutrit system,set up a superposition of the coherent-states of the latter,and study its localizable entanglement,as a function of the parameters involved.We also obtain the conditions at which the system may become maximally entangled or not entangled at all.Entanglement of formation of the superposition of two qubit-and two qutrit-coherent states,have also been studied previously.[31?32]In this work,we use the less studied,but intricate reduction method of projective measurement to study localizable entanglement in the system.The organization of the rest of this paper is as follows.The coherent states,their superposition and the measure of entanglement(I-concurrence)are introduced in Sec.2.Localizable entanglement and its method of evaluation are elaborated on in Sec.3.Our calculations and results are presented in Sec.4.Finally,Sec.5 is devoted to conclusions and discussion.

2 Qutrit Spin Coherent States and Their Superposition

The spin-j coherent state is given by[33]

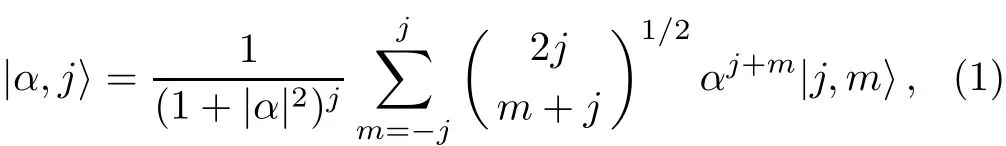
where,|j,m〉are the eigenvectors of the angular momentum operators?J2and?Jzwith eigenvalues equal to j(j+1)and m,respectively.For j=1 we have

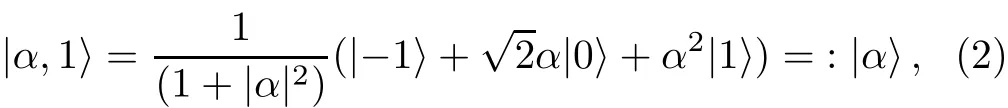
where,we def i ne|1,0〉=:|0〉,|1,1〉=:|1〉,|1,?1〉=:|?1〉for simplicity.

A separable pure state of the three qutrits,each in their respective coherent state,may be given by

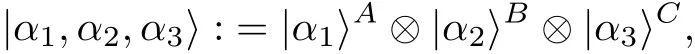
where αiare considered real for computational simplicity.The superscripts enumerate the subsystems.We now construct the following normalized pure state,which is non-separable in the general case

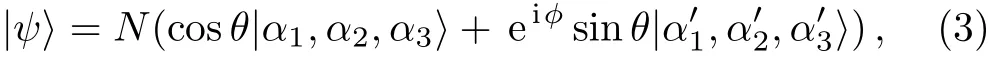
where N is the normalization constant.

We will use I-concurrence,which is an appropriate measure of entanglement for qutrits and higher dimensional systems.It is def i ned by the following relation for a bipartite system composed of subsystems[34]A and B

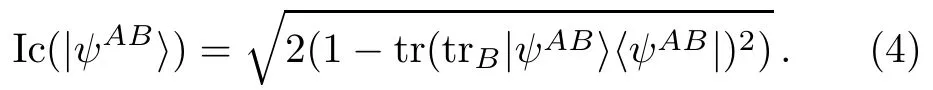
3 LE inN-Partite Systems

We now setup a framework to study localizable entanglement in an N-partite qudit system,which will be applied to our 3-partite qutrit system in the sequence.One may def i ne LE in a collection of qudits as the maximum average of the entanglement one can create between a pair of them,by performing local measurements on the rest. In fact,one needs to choose a measurement method and a measure of bipartite entanglement;then,the required maximization may be achieved by performing the measurements in a suitably selected basis.[35]We choose Projective von Neumann Local Measurement(PM)as our measurement method.[35]Moreover,we use“I-concurrence” as the measure of pairwise entanglement,which is suitable for such systems.A brief introduction of the framework is in order now.

Let us assume that our N-qudit system is in the pure state

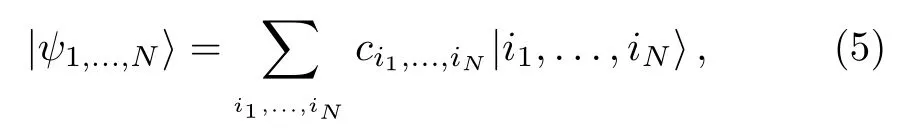
where,the orthonormal states|i1,...,iN〉have been defi ned in the computational basis and i1,...,iNeach assume d quantities for the collection of qudits.Now,excluding any two qudits,for example the fi rst and the last,we perform a speci fi c PM on the N?2 qudits left,to obtain the following reduced state in the computational basis

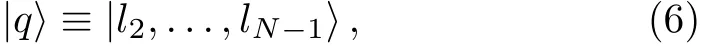
where,l2indicates the post-measurement eigenvalue of the qudit located at the position 2,and so on.The postmeasurement state of the system is then given by

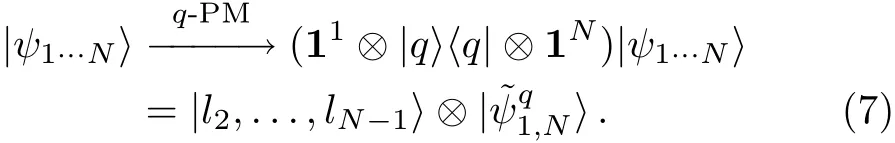
We may write

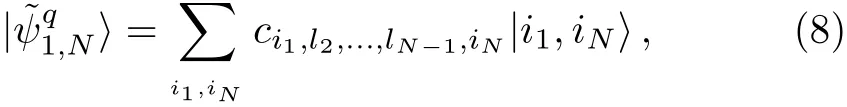
where,the orthogonality relation

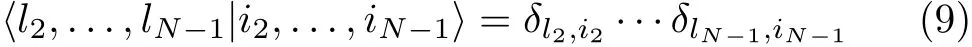
has been used.

The probability of the projective measurement(6)leading to(7)is expressed by

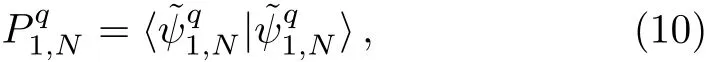
therefore,normalizing|ψq

1,N〉we have

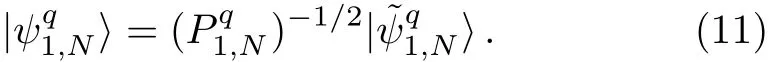
We are to emphasize here that instead of using the orthogonal set{|q〉}that partially projects the state|ψ1···N〉onto the computational basis,one may use a parameterized general orthogonal set like{|Q〉}for maximizing purposes,which will be related to the former by a unitary transformation u as follows

Equivalently,the state|ψ1···N〉may be transformed under the parameterized unitary transformation

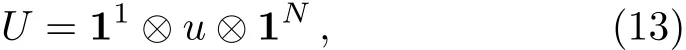
if one keeps working with the set{|q〉}.This is the scheme that we have used in this work.We also note that if the original wave function|ψ1···N〉is transformed under the local unitary transformation U,|ψ1q,N〉and P1q

,Nalso change accordingly and we adhere to the notations

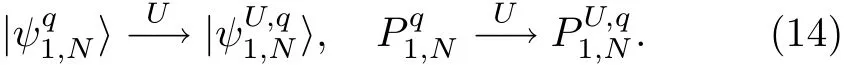
Now,we are all set to write down our f i nal expression for the localizable entanglement between the end qutrits;it is based on the projective measurements and I-concurrence as is expressed by[34]

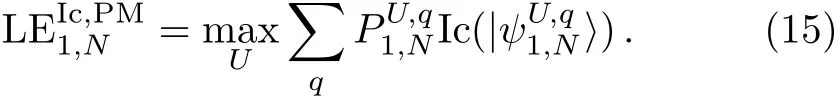
We note here that I-concurrence,similar to the concurrence,is invariant under local unitary transformations;thus,we conclude that we can also choose arbitrary onequdit unitary transformations to act on the fi rst and the fi nal qudit instead of 11and 1Nin Eq.(13),without any physical consequences.

4 Localizable Entanglement in a 3-Qutrit Systems

Now,we focus on a system of three qutrits.Def i ning|q=1〉≡ |l2= ?1〉,|q=2〉≡ |l2=0〉,and|q=3〉≡|l2=1〉;equation(15)may f i nally be cast into

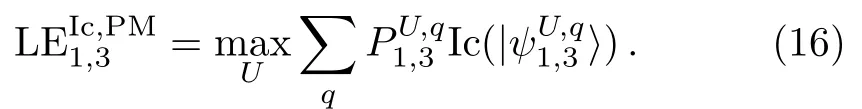
This is the expression we use to evaluate the localizable entanglement between the two qutrits in the 3-qutrit system,based on I-concurrence and von Newman projective local measurements.

We note that Eq.(16)involves an intricate optimization process,which has to be performed numerically.In fact,analytical results for LE are few and far between even in the case of small systems;therefore,one usually resorts to numerical calculations or seeks bounds on the entanglement values.

The f i rst relevant question is:What is the maximum achievable entanglement in the state(3)irrespective of the values assumed by the parameters def i ning the state and the unitary transformation applied.In fact,we have to seek the supremum of LEIc,PM1,3by variation of a total of 17 parameters;the 8 parameters α1, α2, α3, α′1, α′2, α′3,θ,and φ def i ne the state;while,nine more are required to express the most general unitary transformation in the case of 3-dimmensional qutrits,as def i ned in Eq.(13).[17]

It was found that the maximum of the localizable entanglement is equal to unity for several sets of parameters(each set def i ning a state).Of course,no analytic expression or general rule may be given to derive the latter;however,we are able to analyze some special cases in the sequence.

Now,we select

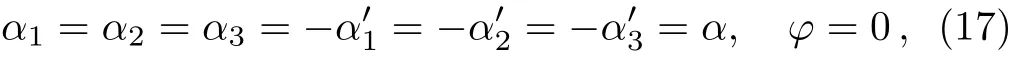
which def i ne an important case,the so called GHZ-type state,which one may expect also to display the maximum of entanglement.Production,manipulation and application of such states have been the focus of several investigations in the recent years.[36?37]We have presented a 3-D plot of LEIc,PM1,3as a function of α and θ in Fig.1 for this GHZ-type state.We note that LE vanishes at θ=nπ/2 for n=1,2,3,4 in the range[0,2π]for any value of α,which is of course expected;in fact state(4)reduces to a separable one for this choices of θ.Moreover,we note that it does yield 1 for the supremum of LE,as we have predicted;it occurs at α = ±1 and θ=+nπ/4 for n=1,3,5,7 in the range[0,2π].It is also inferred that irrespective of the value of θ,one always observes the maximum of entanglement(not necessarily equal to the maximum)at α = ±1,and LE reduces as α,moves away from±1.

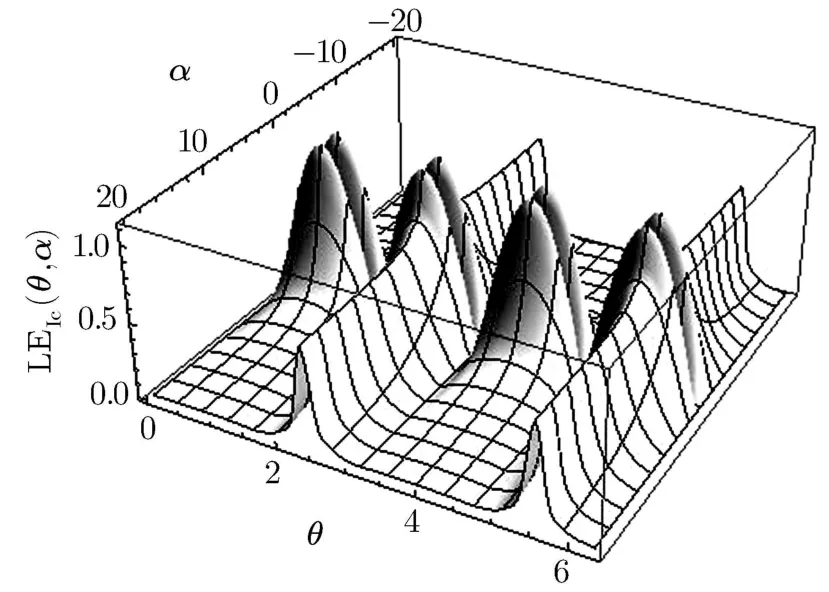
Fig.1 LEIc,PM1,3 as a function of α and θ.

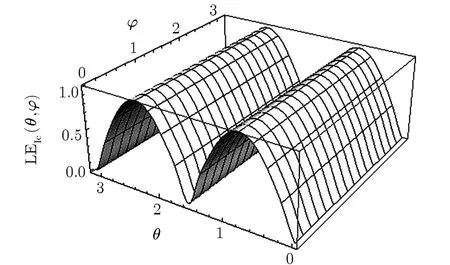
Fig.2 LE as a function of θ and ? for maximizing α =1;It is independent of ?.

We also intend to study the role of the phase ? on the LE properties of the state.First we consider α = ±1,which corresponds to the maximum of entanglement,as explained above.Figure 2 presents a 3-D plot of LE as a function of θ and ? at α =1,which corresponds to the maximum of entanglement,as explained above.An interesting phenomenon is observed here;LE is independent of ? for any θ at this specif i c value of α.This means that one may achieve the maximum of entanglement in the system by choosing α =1 and only adjusting the parameter θ;however,in the general case(arbitrary value of α)LE is a sensitive function of ?.This may be observed in Fig.3 which displays LE as a function of θ and ? for α =5.Figure 4 also displays LE as a function of ? and α;it reveals the independence of LE from ? at α = ±1.

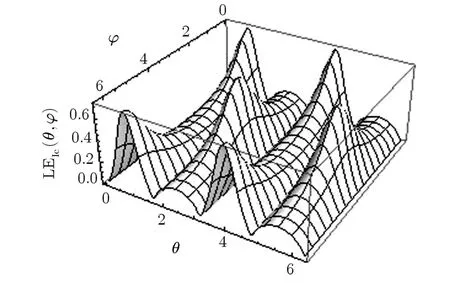
Fig.3 LE as a function of θ and ? for α =5.

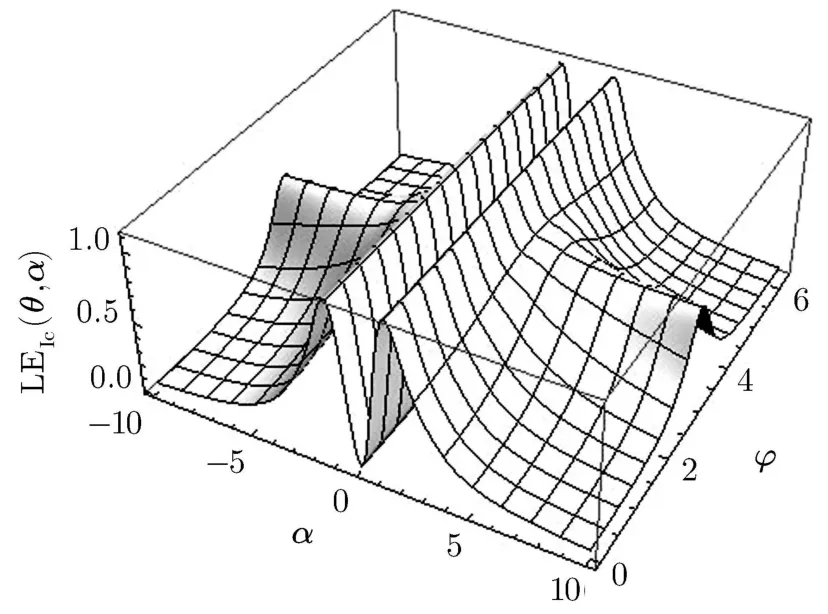
Fig.4 LE as a function of α and ? for θ = π/4.

5 Discussion and Conclusions

We have set up a framework to explore localizable entanglement in a multi-qudit system,based on von Neumann projective measurement and I-concurrence as the measure of entanglement.We have used this framework to study entanglement of the qutrit GHZ-type coherent states.We have observed that depending on the statedef i ning parameters θ, α,and ?,this system may acquire maximum localizable entanglement corresponding to the value 1 or no entanglement at all,corresponding to null for the latter.A summary of the conclusions are as follows.

i)We note that LE vanishes at θ=nπ/2 for any value of α,which corresponds to a separable state.

ii)The supremum of LE which is 1,occurs at α = ±1 and θ=nπ/4.

iii)Irrespective of the value of θ,the maximum of entanglement(not necessarily equal to the maximum)occurs at α = ±1 and it is reduced as α moves away from ±1.

iv)LE is independent of ? for any θ at the maximizing value α = ±1;thus,one may achieve the maximum of entanglement in the system by choosing α=1 and only adjusting the parameter θ.

v)In the general case(arbitrary value of α)LE is a sensitive function of ?.

[1]J.Audretsch,Entangled World: The Fascination of Quantum Information and Computation,WILLY-VCH,Verlag GmbH,Berlin(2006).

[2]C.H.Bennett,G.Brassard,C.Crepeau,R.Jozsa,A.Peres,and W.K.Wootters,Phys.Rev.Lett.70(1993)1895.

[3]A.K.Ekert,Phys.Rev.Lett.67(1991)661.

[4]J.Audretsch,Entangled Systems,WILLY-VCH,Verlag GmbH,Berlin(2007).

[5]G.Jaeger,Quantum Information,Springer,New York(2007).

[6]W.K.Wootters,Phys.Rev.Lett.80(1998)2245.

[7]D.Deutsch,A.K.Ekert,R.Jozsa,C.Macchiavello,S.Popescu,and A.Sanpera,Phys.Rev.Lett.77(1996)2818.

[8]A.Sabour and M.Jafarpour,Chin.Phys.Lett.28(2011)070301.

[9]A.A.Klyachko,B.Oztopand,and A.S.Shumovsky,Laser Phys.17(2007)226.

[10]M.V.Fedorov,P.A.Volkov,and Y.Mikhailova,quantph/1009.2744.

[11]X.G.Yang,Z.X.Wang,X.H.Wang,and S.M.Fei,quantph/0809.1556v1.

[12]Zhen-Biao Yang,Huai-Zhi Wu,and Shi-Biao Zheng,Chin.Phys.B 19(2010)094205.

[13]R.Inoue,T.Yonehara,Y.Miyamoto,M.Koashi,and M.Kozuma,quant-ph/0903.2903v2.

[14]N.J.Cerf,M.Bourennane,A.Karlsson,and N.Gisin,Phys.Rev.Lett.88(2002)127902.

[15]T.Durt,N.J.Cerf,N.Gisin,and M.Zukowski,Phys.Rev.A 67(2003)012311.

[16]D.Brub and C.Macchiavello,Phys.Rev.Lett.88(2002)127901.

[17]A.Sabour,M.Jafarpour,and M.Ashrafpour,Quantum Inf.Process.12(2013)1287.

[18]G.Vallone,E.Pomarico,F.De Martini,P.Mataloni,and M.Barbieri,Phys.Rev.A 76(2007)012319.

[19]B.P.Lanyon,T.J.Weinhold,N.K.Langford,J.L.O.Brien,K.J.Resch,A.Gilchrist,and A.G.White,Phys.Rev.Lett.100(2008)060504.

[20]M.Jafarpour and M.Ashrafpour,Quantum Inf.Process.12(2013)761.

[21]B.C.Sanders,Phys.Rev.A 45(1992)6811.

[22]P.Domotor and M.G.Benedict,Phys.Scr.T.135(2009)014030.

[23]X.Wang,B.C.Sanders,and S.Pan,J.Phys.A:Math.Gen.33(2000)7467.

[24]S.Sivakumar,Int.J.Theor.Phys.48(2009)894.

[25]S.J.Van Enk and O.Hirota,Phys.Rev.A 64(2001)022313.

[26]T.C.Ralph,W.J.Munro,and G.J.Milburn,quantph/0110115.

[27]D.A.Rice,G.Jaeger,and B.C.Sanders,Phys.Rev.A 62(2000)012101.

[28]H.Jeong,M.S.Kim,and J.Lee,Phys.Rev.A 64(2001)052308.

[29]D.Wilson,H.Jeong,and M.S.Kim,quant-ph/0109121.

[30]H.Jeong and M.S.Kim,Quantum Inf.Computation 2(2002)208.

[31]G.Vallone,E.Pomarico,F.de.Martini,and P.Malaloni,Phys.Rev.A 76(2007)012319.

[32]W.J.Munro,G.J.Milburn,and B.C.Sanders,Phys.Rev.A 62(2000)052108.

[33]J.M.Radcliあe,J.Phys.A 4(1971)313.

[34]P.Rungta and C.M.Caves,quant-ph/0208002.

[35]M.Popp,F.Verstraete,M.A.Martin-Delgado,and J.I.Cirac,quant-ph/0411123.

[36]H.M.Li,H.C.Yuan,and H.Y.Fan,Int.J.Theor.Phys.48(2009)2849.

[37]H.Jeong and B.A.Nguyen,Phys.Rev.A 74(2006)022104.