Convex Solutions of an Iterative Functional Equation in Banach Spaces

GONG Xiaobing, LIU Lei

(1. College of Mathematics and Information Science, Neijiang Normal College, Neijiang 641100, Sichuan; 2. School of Mathematics and Information Science, Shangqiu Normal College, Shangqiu 476000, Henan)

LetSbe a nonempty subset of a Banach space andC(S,S) consist of all continuous functionsf:S→S. Theith iteratefioff∈C(S,S) is defined byfi(x)=f(fi-1(x)) andf0(x)=xfor allx∈Srecursively.A functional equation having iteration as its main operation is called an iterative functional equation. As indicated in the books[1-2]and the surveys[3-4], the polynomial-like iterative equation

(1)

whereF:S→Sis a given function,λns (n=1,2,…,m) are real constants, is one of important forms of functional equation since the problem of iterative roots and the problem of invariant curves can be reduced to the kind of equations. ForS?R, while some works (e.g. [5-11]) are contributed to the case of linearF, there are given many results to the case of nonlinearF, for example, [12-13] form=2, [14] for generalm, [15-16] for smoothness, [17] for analyticity. Some efforts were also devoted to equation (1) in high-dimensional spaces such as in [18-19], radially monotonic solutions were discussed in high-dimensional Euclidean spaces by properties of orthogonal group in [19] and the existence of convex solutions was proved by introducing a partial order in Banach space in [18]. One of generalizations for equation (1) is the following equation

(2)

which was investigated in [20-23]. More concretely, in [20], the existence of solutions for functional equation

P(f)°f=F

was proved, then using this result, the existence of Lipschitzian solutions for equation (2) was investigated on a compact interval ofRand a compact convex subset ofRN,N>1. Later, the results in [20] were partially generalized to an arbitrary closed (not necessarily convex) subset of a Banach space and the existence of solutions for iterative functional equations

was proved in [23], whereAnare bounded linear operators on the Banach space. In 2009, as a continuation of [20], the existence and uniqueness of Lipschitz solutions of the equation (2) were investigated with a general boundary restriction on a compact convex subsets ofRN,N>1 in [22]. By constructing another operator, the existence of differentiable solution for equation (2) was proved on a compact convex subsets ofRN,N>1 in [21].

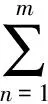
In this paper we study convexity of solutions for equation (2) in Banach spaces. Using the idea of [18], we first discuss increasing (decreasing) solutions for this equation. Then we investigate increasing convex (concave) solutions.

1 Preliminaries

As in [18], in order to discuss convexity of solutions in Banach spaces, we need to introduce a partial order. For convenience, we use the conventions of [18]. As in [28], a nonempty subsetKof a real vector spaceXis called a cone ifx∈Kimplies thatax∈Kfor alla>0. A nonempty and nontrivial (≠{θ}, whereθdenotes the zero element ofX) subsetK?Xis called an order cone inXifKis a convex cone and satisfiesK∩(-K)={θ}. Having chosen such an order coneKinX, we can define a partial orderx≤KyinX, simply called theK-order, ify-x∈K. A real vector spaceXequipped with aK-order is called an ordered vector space, abbreviated by OVS and denoted by (X,K). A real Banach space (X,‖·‖) associated with aK-order is called an ordered real Banach space, abbreviated by OBS and denoted by (X,K,‖·‖), ifKis closed.

One can define increasing (decreasing) operators and convex (concave) operators as in [29] in an ordered real vector space (X,K). An operatorf:D?X→Xis said to be increasing (resp. decreasing) in the sense of theK-order ifx≤Kyimpliesf(x)≤Kf(y) (resp.f(x)≥Kf(y)). An operatorf:D→X, whereD?Xis a convex subset, is said to be convex (resp. concave) in the sense of theK-order iff(λx+(1-λ)y)≤Kλf(x)+(1-λ)f(y) (resp.f(λx+(1-λ)y)≥Kλf(x)+(1-λ)f(y)) for allλ∈[0,1] and for every pair of distinct comparable pointsx,y∈D(i.e., eitherx≤Kyorx≥ky).

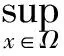
C+(Ω,m,M):={f∈C(Ω,X):f(Ω)?Ω,

m(y-x)≤Kf(y)-f(x)≤KM(y-x) ifx≤Ky,

and ‖f(y)-f(x)‖≤M‖y-x‖

ifxandyare not comparable},

C-(Ω,m,M):={f∈C(Ω,X):f(Ω)?Ω,

m(y-x)≤Kf(x)-f(y)≤KM(y-x) ifx≤Ky,

and ‖f(y)-f(x)‖≤M‖y-x‖

ifxandyare not comparable},

fis convex onΩinK-order},

fis concave onΩinK-order}.

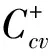
As shown in [28-29], an order coneKin an ordered real Banach space (X,‖·‖) is said to be normal if there exists a constantN>0 such that ‖x‖≤N‖y‖ ifθ≤Kx≤KyinX. The smallest constantN, denoted byN(K), is called the normal constant ofK. In order to prove our main results, we list the following lemmas.

Lemma1.1[18]Let (X,K,‖·‖) be an ordered real Banach space. Then compositionf°gis convex (resp. concave) if bothfandgare convex (resp. concave) and increasing. In particular, for increasing convex (resp. concave) operatorf, the iteratefkis also convex (resp. concave).

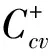
?k=1,2,….

Lemma1.3[18]Let (X,K,‖·‖) be an ordered real Banach space and letf∈C-(Ω,m,M), where 0≤m≤M<+∞. Then

-M2n-1(y-x)≤Kf2n-1(y)-f2n-1(x)≤K

-m2n-1(y-x),n=1,2,…,

(3)

m2n(y-x)≤Kf2n(y)-f2n(x)≤K

M2n(y-x),n=1,2,…,

(4)

for allx≤KyinΩ.

2 Increasing and decreasing solutions

In order to study convexity of solutions, we first investigate the existence of increasing and decreasing solutions of equation (2) in the ordered real Banach space (X,K,‖·‖) such thatKis normal andN(K)≤1. Consider equation (2) with the following hypotheses:

(H1)λ1>0,λn≤0,n=2,3,…,k,…,

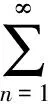
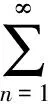
(5)

for a constantM∈(0,+∞), then equation (2) has a solutionf∈C+(Ω,0,M).

ProofUnder the hypotheses (H1) and (H2), we can rewrite equation (2) as

where

(6)

Define a mappingLonC+(Ω,0,M) by

(7)

We first prove thatLis well defined and is a continuous function onΩ. Compactness ofΩimplies thatΩis a bounded set. Hence, by definition ofC+(Ω,0,M) andf∈C+(Ω,0,M) we have

?x∈Ω.

Thus

?x∈Ω.

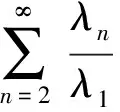
Next we claim thatLis a self-mapping onC+(Ω,0,M). By (6), for allx∈Ω,

conv{F(x),f2(x),f3(x),…}?Ω

becauseΩis a compact convex set. SoLf(Ω)?Ω. Further, whenx,y∈Ωare not comparable, i.e.,x-y?Kandy-x?K, by the definition ofC+(Ω,0,M) we have

‖Lf(x)-Lf(y)‖=

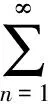
‖Lf(x)-Lf(y)‖≤M‖x-y‖

(8)

because of inequality (5). Whenx,y∈Ωare comparable, suppose thatx≤Ky. Since

n=2,…,k,…

is convergent. Hence, by the definition ofC+(Ω,0,M),

θ≤KLf(y)-Lf(x)=

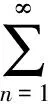
θ≤KLf(y)-Lf(x)≤KM(y-x)

(9)

because of the inequality (5). Thus, (8) and (9) together imply thatLis a self-mapping onC+(Ω,0,M).

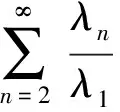
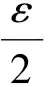
‖Lf-Lg‖C(Ω,X)=

SoLis continuous. SinceC+(Ω,0,M) is a compact convex subset, by Schauder’s fixed point theorem we see thatLhas a fixed pointf∈C+(Ω,0,M). Thusfis an increasing solution of the equation. The proof is completed.

The existence of decreasing solutions is given as following.

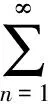
By Lemma 1.3, the proof is similar to Theorem 2.1, we omit it here.

3 Convex and concave solutions

Based on the last section we can discuss the convexity of continuous solutions for equation (2) in the ordered real Banach space (X,K,‖·‖) with a normal coneKsuch thatN(K)≤1.

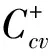
(10)

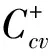
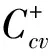
Lf(tx+(1-t)y)≤KtLf(x)+(1-t)Lf(y),

?t∈[0,1],

(11)

for every pair of distinct comparable pointsx,y∈Ω. In fact, eachfn,n=2,…,k,… is convex in the sense ofK-order becausefis increasing and convex by Lemma 1.1. Furthermore,

are convergent onΩand

for alln≥ 1. Hence,

tLf(x)+(1-t)Lf(y),

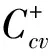
Similarly, we can prove the existence of concave solutions.

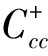
(12)

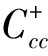
Example3.1Consider the equation

?(x1,x2)∈Ω,

(13)

where

Clearly, equation (13) is of the form (2), where

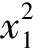
for |M|<3 and

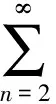
We consider another example in the infinite-dimensional setting.

Example3.2LetX=C([0,1],R) equipped with the norm ‖x‖=supt∈[0,1]|x(t)| forx∈X. Let

Ω:={x∈C([0, 1], [0, 1]):

|x(t1)-x(t2)|≤|t1-t2|,t1,t2∈[0,1]},

a subset ofX. Then, the equation

?x∈Ω,

(14)

is an iterative equation of the form (2) in the infinite-dimensional setting, whereλ1=13/12,λn=-1/4nandF(x):=sinx. Note that

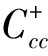
for |M|<4 and

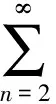
We end our paper with some remarks on not discussing the uniqueness and stability of convex solutions in the sense ofK-order for equation (2) because we do not know whether the mapping defined as (7) is contraction mapping and on not considering the same form mapping P(f) as in [20] because of difficulties in discussing inverse of the function in infinite-dimensional spaces.

[1] Kuczma M, Choczewski B, Ger R. Iterative functional equations[C]//Encyclopedia Math Appl. Cambridge:Cambridge University Press,1990,32.

[2] Targonski G. Topics in Iteration Theory[M]. G?ttingen:Vandenhoeck & Ruprecht,1981.

[3] Baron K, Jarczyk W. Recent results on functional equations in a single variable, perspectives and open problems[J]. Aequationes Math,2001,61:1-48.

[4] 張景中,楊路,張偉年. 關(guān)于函數(shù)方程的若干進(jìn)展[J]. 數(shù)學(xué)進(jìn)展,1995,24(5):385-405.

[5] Dhombres J G. Itération linéaire d'ordre deux[J]. Publ Math Debrecen,1977,24:177-187.

[6] Jarczyk W. On an equation of linear iteration[J]. Aequationes Math,1996,51:303-310.

[7] Matkowski J, Zhang W. On linear dependence of iterates[J]. J Appl Anal,2000,6:149-157.

[8] Mukherjea A, Ratti J S. On a functional equation involving iterates of a bijection on the unit interval[J]. Nonlinear Anal,1983,7:899-908.

[9] Mukherjea A, Ratti J S. On a functional equation involving iterates of a bijection on the unit interval II[J]. Nonlinear Anal,1998,31:459-464.

[10] Tabor J, Tabor J. On a linear iterative equation[J]. Results Math,1995,27:412-421.

[11] Yang D, Zhang W. Characteristic solutions of polynomial-like iterative equations[J]. Aequationes Math,2004,67:80-105.

[12] Malenica M. On the solutions of the functional equationφ(x)+φ2(x)=F(x)[J]. Mat Vesnik,1982,6:301-305.

[13] 趙立人. 關(guān)于函數(shù)方程λ1f(x)+λ2f2(x)=F(x)的存在唯一性定理[J]. 中國科學(xué)技術(shù)大學(xué)學(xué)報,1983,32(S1):21-27.

[15] 麥結(jié)華,劉新和. 一類迭代函數(shù)方程的Cm解的存在性、唯一性和穩(wěn)定性[J]. 中國科學(xué),2000,30(2):129-144.

[18] Gong X, Zhang W. Convex solutions of the polynomial-like iterative equation in Banach spaces[J]. Publ Math Debrecen,2013,82:341-358.

[19] Zhang W. Solutions of equivariance for a polynomial-like iterative equation[J]. Proc Roy Soc Edin,2000,A130:1153-1163.

[20] Kulczycki M, Tabor J. Iterative functional equations in the class of Lipschitz functions[J]. Aequationes Math,2002,64:24-33.

[21] Li X, Deng S. Differentiability for the high dimensional polynomial-like iterative equation[J]. Acta Math Sci,2005,25:130-136.

[22] Song W, Yang G, Lei F. On series-like iterative equation with a general boundary restriction[J]. Fixed Point Theory:Theory and Applications,2009,2009:892691.

[23] Tabor J, Zoldak M. Iterative equations in Banach spaces[J]. J Math Anal Appl,2004,299:651-662.

[24] Kuczma M, Smajdor A. Fractional iteration in the class of convex functions[J]. Bull Acad Pol Sci:Sci Math Astron Phys,1968,16:717-720.

[25] Trif T. Convex solutions to polynomial-like iterative equations on open intervals[J]. Aequationes Math,2010,79:315-325.

[26] Xu B, Zhang W. Decreasing solutions and convex solutions of the polynomial-like iterative equation[J]. J Math Anal Appl,2007,329:483-497.

[27] Zhang W, Nikodem K, Xu B. Convex solutions of polynomial-like iterative equations[J]. J Math Anal Appl,2006,315:29-40.

[28] Zeidler E. Nonlinear Functional Analysis and Its Applications I: Fixed Point Theorems[M]. Wadsack P R. New York:Springer-Verlag,1986.

[29] Amann H. Fixed point equations and nonlinear eigenvalue problems in ordered Banach spaces[J]. SIAM Rev,1976,18:620-709.