結(jié)構(gòu)方陣秩虧為1的可信性驗(yàn)證

李 喆,周 蕊

(長(zhǎng)春理工大學(xué) 理學(xué)院,長(zhǎng)春 130022)

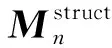
定理1[10]設(shè)A∈n×n.若對(duì)某個(gè)b∈n,c∈n,(n+1)×(n+1)矩陣非奇異,則rankA=n-1當(dāng)且僅當(dāng)線性方程組的解滿足條件f=0.

定理2[11]輸入一區(qū)間矩陣A∈In×n及區(qū)間右端列向量b∈In,若Verifylss函數(shù)[12]成功輸出區(qū)間向量X?In,則X滿足條件對(duì)某個(gè)?X.

利用區(qū)間牛頓迭代法可以驗(yàn)證非線性方程的解.

定理3[11]令f:為可微函數(shù),X=(x1,x2)∈I且給定假設(shè)0?f′(X),利用區(qū)間運(yùn)算,定義若?X,則X內(nèi)包含f的唯一解.若?,則對(duì)所有的x∈X,f(x)≠0.

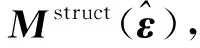
定義邊界矩陣

(1)

其中b,c∈n.則當(dāng)時(shí),矩陣非奇異,且在向量附近,線性方程組

(2)

本文利用隱行列式方法[13]計(jì)算梯度f(wàn)(ε),其理論基于數(shù)值二分法[8,10].對(duì)線性方程組(2)關(guān)于每個(gè)變量εi求導(dǎo),得

(3)

因此可以通過求解k個(gè)具有相同系數(shù)矩陣,但不同右端列向量的線性方程組得到f(ε).

下面基于文獻(xiàn)[14]的結(jié)果通過將非線性方程f(ε)=0的某些變?cè)鎏囟ɑ椒?將驗(yàn)證f(ε)=0的解轉(zhuǎn)化為驗(yàn)證具有一個(gè)變?cè)蔷€性方程的解.設(shè)

(4)

定義

(5)

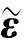
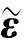
1) 選擇i0滿足式(4).

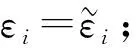
3) 若步驟2)不收斂,則輸出算法失敗.

引入?yún)?shù)向量ε=(ε1,ε2,ε3,ε4,ε5,ε6),定義參數(shù)區(qū)間對(duì)稱矩陣

1) 確定i0=1;

2) 令E1=(-0.088,-0.086);

3) 計(jì)算參數(shù)向量U=(0.077 4,0.077 5);

[1] Rump S M.Verified Bounds for Singular Values,in Particular for the Spectral Norm of a Matrix and Its Inverse [J].BIT Numerical Mathematics,2011,51(2):367-384.

[2] Nishi T,Rump S M,Oishi S.On the Generation of Very Ill-Conditioned Integer Matrices [J].Nonlinear Theory and Its Applications,2011,2(2):226-245.

[3] Rump S M.Verified Bounds for Least Squares Problems and Underdetermined Linear Systems [J].SAIM J Matrix Anal Appl,2012,33(1):130-148.

[4] Rump S M.Accurate Solution of Dense Linear Systems,Part Ⅰ:Algorithms in Rounding to Nearest [J].Journal of Computational and Applied Mathematics,2013,242:157-184.

[5] Rump S M.Accurate Solution of Dense Linear Systems,Part Ⅱ:Algorithms Using Directed Rounding [J].Journal of Computational and Applied Mathematics,2013,242:185-212.

[6] Govaerts W.Bordered Matrices and Singularities of Large Nonlinear Systems [J].Internat J Bifurcation Chaos,1995,5(1):243-250.

[7] Griewank A,Reddien G W.Characterisation and Computation of Generalised Turning Points [J].SIAM J Numer Anal,1984,21(1):176-185.

[8] Griewank A,Reddien G W.The Approximate Solution of Defining Equations for Generalized Turning Points [J].SIAM J Numer Anal,1996,33(5):1912-1920.

[9] Rabier P J,Reddien G W.Characterization and Computation of Singular Points with Maximum Rank Deficiency [J].SIAM J Numer Anal,1986,23(5):1040-1051.

[10] Griewank A,Reddien G W.The Approximation of Generalized Turning Points by Projection Methods with Superconvergence to the Critical Parameter [J].Numer Math,1986,48(5):591-606.

[11] Rump S M.Verification Methods:Rigorous Results Using Floating-Point Arithmetic [J].Acta Numerica,2010,19:287-449.

[12] Rump S M.Kleine Fehlerschranken Bei Matrixproblemen [D].Karisruhe:Karlsruhe University,1980.

[13] Spence A,Poulton C.Photonic Band Structure Calculations Using Nonlinear Eigenvalue Techniques [J].J Comput Phy,2005,204(1):65-81.

[14] CHEN Xiao-jun,Womersley R S.Existence of Solutions to Systems of Underdetermined Equations and Spherical Designs [J].SIAM J Numer Anal,2006,44(6):2326-2341.

(責(zé)任編輯：趙立芹)

研究簡(jiǎn)報(bào)