幾類緊集的box維數(shù)
陳飛燕, 李同興
(南京財(cái)經(jīng)大學(xué) 應(yīng)用數(shù)學(xué)學(xué)院, 江蘇 南京 210046)
幾類緊集的box維數(shù)
陳飛燕, 李同興
(南京財(cái)經(jīng)大學(xué) 應(yīng)用數(shù)學(xué)學(xué)院, 江蘇 南京 210046)
分形幾何中非空有界集的box維數(shù)是應(yīng)用最廣泛的分形維數(shù)之一. 研究了三類緊集的box維數(shù),給出了它們的box維數(shù)的計(jì)算公式,從而推出了三個(gè)常用緊集的box維數(shù)值.
有界集; 緊集; 覆蓋; Hausdorff維數(shù); box維數(shù)
0 引言
維數(shù)是空間和集合建立如何度量的關(guān)鍵,如在經(jīng)典的歐氏空間中,點(diǎn)是0維的,直線是1維的,而平面和立方體的維數(shù)分別是2維和3維的.有時(shí)我們把維數(shù)看作自由度,直線上的點(diǎn)可用一個(gè)實(shí)數(shù)表示,平面上的點(diǎn)可用2個(gè)實(shí)數(shù)表示,一般的n維歐氏空間有n個(gè)自由度,其中的點(diǎn)需要用n個(gè)實(shí)數(shù)(x1,x2,…,xn)來表示.Poincare和Lebesgue都曾對(duì)維數(shù)進(jìn)行過深入研究,但是總的來說效果不夠理想.然而使維數(shù)研究取得重要進(jìn)展的,首先應(yīng)歸功于Hausdorff,他于1919年在測(cè)度基礎(chǔ)上,引入了適用于任何集合的Hausdorff維數(shù)的概念.但是要想計(jì)算一個(gè)一般集合的Hausdorff維數(shù)確實(shí)比較困難.因此人們就提出了計(jì)算及經(jīng)驗(yàn)估計(jì)相對(duì)簡(jiǎn)單的而且應(yīng)用最廣泛的集合的box維數(shù).下面先回顧一下box維數(shù)的概念.
定義設(shè)F?Rn是一個(gè)非空有界集,用N(δ,F)表示直徑最大為δ,可以覆蓋F的集合的最小個(gè)數(shù),則F的下,上box維數(shù)分別定義為
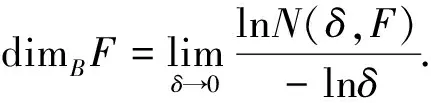
1 主要結(jié)論及其證明
以下我們研究實(shí)數(shù)集R中三類常用緊集的box維數(shù)的規(guī)律性.

證明設(shè)U是一個(gè)區(qū)間,其長(zhǎng)度

取k是滿足

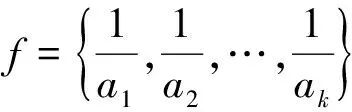
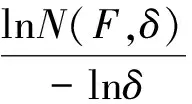
利用洛必達(dá)法則[4]知,極限
所以
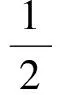

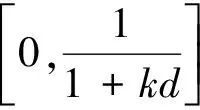
于是可以得到
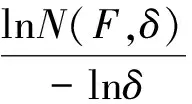
從而有
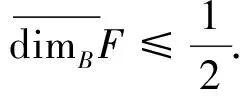
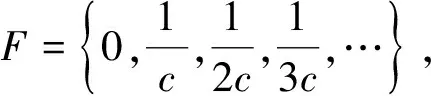

故
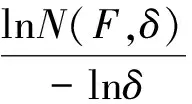
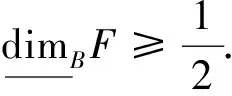
所以
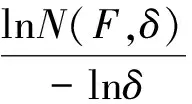
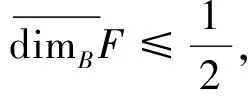
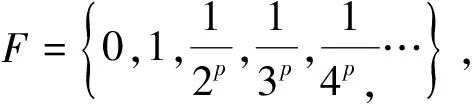
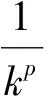
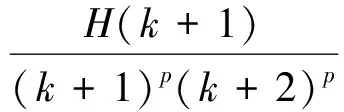
另一方面,

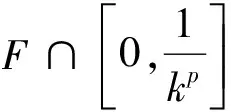
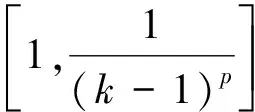
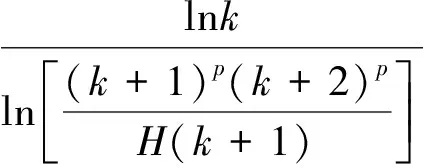
再利用洛必達(dá)法則求極限可得,
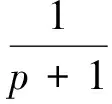
3 簡(jiǎn)單實(shí)例
通過求解以上三類緊集的box維數(shù),我們發(fā)現(xiàn)了它們具有一定的規(guī)律性.利用這些結(jié)果我們可以給出下列三個(gè)常用的特殊緊集的box維數(shù).
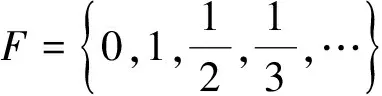
[1] Falconer K. Fractal Geometry: Mathematical Foundations and Applications[M]. New York: Wiley, 1990.
[2] 李水根. 分形[M]. 北京: 高等教育出版社, 2004.
[3] 沙震,阮火軍. 分形與擬合[M]. 杭州: 浙江大學(xué)出版社, 2005.
[4] 華東師范大學(xué)數(shù)學(xué)系. 數(shù)學(xué)分析[M]. 上冊(cè). 3版. 北京: 高等教育出版社,2001.
BoxDimensionsofSeveralCompactSets
CHEN Fei-yan, LI Tong-xing
(School of Applied Mathematics, Nanjing University of Finance and Economics, Nanjing Jiangsu 210046, China)
The box dimension of a nonempty bounded set is one of the most widely used fractal dimensions in the fractal geometry. In this paper, we study and calculate the box dimensions of three kinds of compact sets, and then from which we present the box dimensions of three common compact sets
bounded set; compact set; cover; hausdorff dimension; box dimension
2013-02-13
陳飛燕(1989-), 女, 江蘇鎮(zhèn)江人, 碩士研究生, 研究方向?yàn)榉蔷€性分析及其應(yīng)用.
O175
A
1671-6876(2013)02-0117-03
[責(zé)任編輯李春紅]
 淮陰師范學(xué)院學(xué)報(bào)(自然科學(xué)版)2013年2期
淮陰師范學(xué)院學(xué)報(bào)(自然科學(xué)版)2013年2期
- 淮陰師范學(xué)院學(xué)報(bào)(自然科學(xué)版)的其它文章
- 碳納米管修飾碳糊電極同時(shí)測(cè)定銅和鉛
- 福建省寧德市中職學(xué)校學(xué)生課外籃球運(yùn)動(dòng)情況調(diào)查
- 新媒體視閾下高校中外合作辦學(xué)國(guó)內(nèi)外黨建對(duì)接模式回顧及展望
——以南京郵電大學(xué)海外教育學(xué)院為例 - 淮安市新農(nóng)村建設(shè)綜合評(píng)價(jià)研究
- 洪澤湖周邊地區(qū)生態(tài)系統(tǒng)服務(wù)價(jià)值對(duì)土地利用變化的響應(yīng)
- 2-(4,5-二苯基-1H-咪唑)-4-噻吩Cu(I)配合物的合成及晶體結(jié)構(gòu)
