SUPERCAVITY MOTION WITH INERTIAL FORCE IN THE VERTICAL PLANE*

YU Kai-ping

School of Astronautics, Harbin Institute of Technology, Harbin 150001, China, E-mail: yukp@hit.edu.cn ZOU Wang

School of Astronautics, Harbin Institute of Technology, Harbin 150001, China

Saint Anthony Falls Laboratory, University of Minnesota, Minneapolis, USA

ARNDT Roger

Saint Anthony Falls Laboratory, University of Minnesota, Minneapolis, USA

ZHANG Guang

School of Astronautics, Harbin Institute of Technology, Harbin 150001, China

(Received March 12, 2012, Revised May 4, 2012)

SUPERCAVITY MOTION WITH INERTIAL FORCE IN THE VERTICAL PLANE*

YU Kai-ping

School of Astronautics, Harbin Institute of Technology, Harbin 150001, China, E-mail: yukp@hit.edu.cn ZOU Wang

School of Astronautics, Harbin Institute of Technology, Harbin 150001, China

Saint Anthony Falls Laboratory, University of Minnesota, Minneapolis, USA

ARNDT Roger

Saint Anthony Falls Laboratory, University of Minnesota, Minneapolis, USA

ZHANG Guang

School of Astronautics, Harbin Institute of Technology, Harbin 150001, China

(Received March 12, 2012, Revised May 4, 2012)

The curvilinear motion in a vertical plane is one of the most important features of the supercavitating vehicle. It is of great significance to study the controllability and the maneuverability of the supercavitating vehicle. Models are built for the effects of the angle of attack, the gravity and the inertial force in the curvilinear motion in the vertical plane. Numerical simulations are carried out for the supercavity motion based on these models combined with the Logvinovich model. It is shown that the maximum deviation displacement in the outward normal direction of the trajectory with a constant curvature, which occurs in the tail of the supercavity, increases as the cavitation number or the curvature radius of the supercavity trajectory decreases under the condition that other model and flow parameters are kept constant. For a varied curvature, the supercavity shape changes evidently because of the change of the ambient pressure, but with the same trend as in constant curvature. The deviation displacement increases along the supercavity length gradually.

supercavity, inertial force, curvilinear motion, curvature radius

Introduction

The supercavitation is an extreme state of the cavitation when the cavity envelopes the underwater vehicle fully. There is an increasing interest in the supercavitation because of the potential for a significant drag reduction, especially when the ventilatied supercavity is found to make it possible to realize the controllability and the maneuverability of the supercavity and its vehicle. But, it is a very complicated problem because it not only involves the liquid, the vapor and the gas, related with difficult issues, such as turbulence, viscosity, compressibility and phase change, but also involves the gas-leakage mechanism that re-mains a not well explored field. There is still no mathematical model that considers all the above characteristics that can be used to simulate supercavitating flows so far.

However, research progresses have made on the modeling and the simulation of supercavitating flows. Some methods were developed to study supercavitating flows, including the flat linear theory, the Logvinovich principle, the slender body theory, the singular integral difference method, the variational method and the small perturbation theory. Fridman and Achkinadze[1]presented a brief review of basic theoretical approaches for two-dimensional nonlinear supercavitating flows based on the potential flow theory to some extent. Some mathematical models were developed for the unsteady supcavity based on the Logvinovich principle[2-4]. Yuan et al.[5]studied the asymmetry of the ventilated supercavity by experiment. Serebryakov[6,7]further developed the linearizedtheory for the axisymmetric supercavity by Tulin. Paryshev[8]developed the well known theory of pulsations of axisymmetric cavities.

The related numerical methods can be mainly divided into three kinds, i.e., the interface tracking methods based on the multiphase flow model, the interface capturing methods based on the single-phase flow model and the bubble dynamics methods based on the Logvinovich model. The former two kinds of methods were widely studied and reviewed in the paper[9]. In recent years, numerical studies of supercavitating flows saw a further development. Nouri and Eslamdoost[10]developed an iterative algorithm to capture a two-dimensional symmetric flow using the Boundary Element Method (BEM). Li et al.[11]observed the supercavitation around a hydrofoil using a high-speed video camera and the PIV technique in order to develop a better computational model. The natural cavitating flow around a 2-D symmetrical wedge in shallow water was simulated to analyze the influence of the free surface and the rigid bottom on the supercavity based on a single-phase mixture model[12]. The first numerical simulation of unsteady cavities was carried out by Paryshev in 1978 based on the Logvinovich model. Then, simulations[13-15]were carried out for the supercavity in making vertical motion or with variable ambient pressures.

However, there were not many studies of the supercavity in a curvilinear motion so far. In this paper, models for effects of gravity, angle of attack and inertial force on the supercavity in making a curvilinear motion in a vertical plane are developed. Further, based on the Logvinovich model combined with the above models, a numerical method is adopted to simulate the supercavity, and the effects of the trajectory curvature of the supercavity on the supercavity are analyzed. The results may provide a technological and theoretical support for realizing the controllability and the maneuverability of the supercavity and its vehicle.

1. Mathematical model

The Logvinovich model is applied combined with the models for effects of the angle of attack, the gravity and the inertial force, as shown in Fig.1. If the gas in the supercavity is regarded as incompressible, the section equation of the supercavity with the use of these effect models, the balance equation of the gas mass in the supercavity and the gas state equation will constitute a closed set of equations describing the supercavity at the given ventilation and gas-leakage rates.

1.1 Section equation of the supercavity

The Eq.(1) was introduced in 1974 as a mathematical corollary of the Logvinovich principle, and derived by Serebryakov[16]within the framework of the theory of slender axisymmetric cavities. This section equation can also be obtained by using the principle of conservation of energy on each continuous plane perpendicular to the trajectory of the cavitator in an inertial reference frame[13].

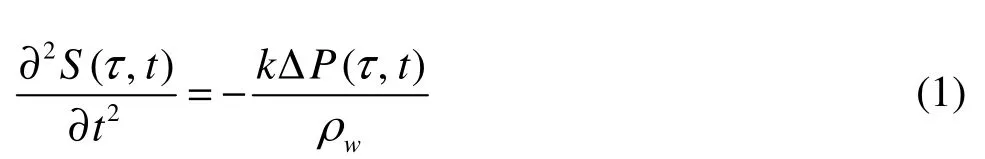
where Δp(τ,t)=p∞(τ,t)+p＇(τ,t)-pc(τ,t ),p∞(τ, t)is the ambient pressure, p＇(τ,t) is the ambient perturbation pressure, pc(τ,t) is the internal pressure of the supercavity, τ is the time of the cavitation inception at a given point x on the trajectory, ρwis the water density; S(τ,t) is the cross section area of the supercavity at time t, perpendicular to the trajectory, at the given point where the cavitation occurs at time τ, k=4πC/a2,Cis the cavita

x

xtion drag coefficient, a is a variable depending on the cavitation number, which is expressed asa= σLc/Dnfor the steady supercavity, where Lcis the supercavity length,Dnis the cavitator diameter. Besides, it must be noted that the value of a is regarded as an empirical constant usually selected within the range 1.5-2 for the supercavity in unbounded flows.

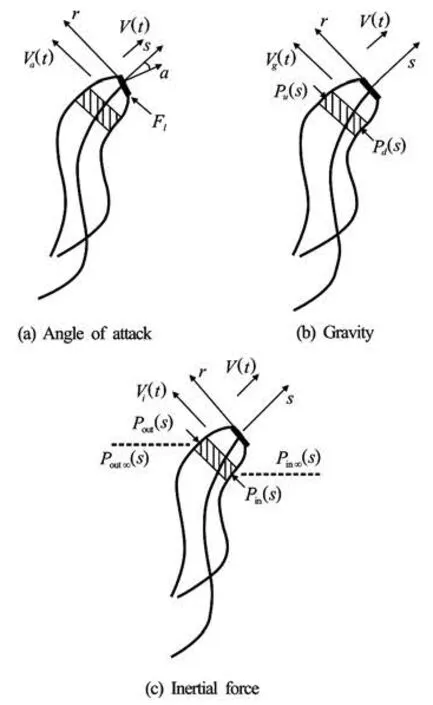
Fig.1 Supercavity deformation with various influencing factors

For Eq.(1), the initial conditions are

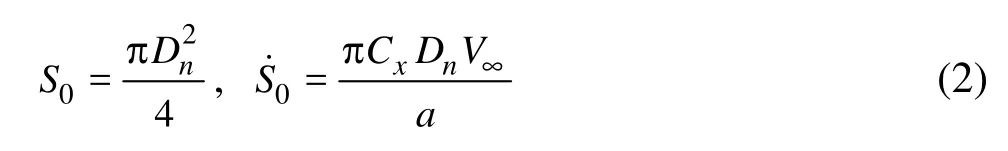
where V∞is the incoming flow velocity. The flow velocity is equivalent to the motion velocity of the supercavitating vehicle in an inertial reference frame.

In the above equations, it is reasonable to assume that the following relation Cx=Cx0(1+σ) holds for the drag coefficient, whereCx0is the drag coefficient at zero cavitation number[17], and is usually taken a value as Cx0=0.82.

1.2 Balance equation of the mass in the supercavity

where ρgis the gas density in the supercavity,Qcis the supercavity volume, m˙inand m˙outare, respectively, the mass flow rates of the gas injecting into and escaping from the supercavity.

The gas may be assumed to be isothermal as well, and the gas state equation may be expressed as ρ= cpk, where c and k are constants, and k may be taken as 1. Because the ventilation holes are enclosed in the head of the supercavity, with a high gas velocity, the gas pressure is slightly smaller than the mean pressure in the supercavity according to the Bernoulli equation. Also, considering that its tail is directly linked with external flows, the gas pressure in the region would approach the ambient pressure. Thus, Eq.(3) can be transformed into the following equation approximately

For the ventilation rate, although some formulas were proposed[18,19], which are mainly for the steady supercavity, which have a great theoretical significance in the supercavity stability, the ventilation rate is regulated as a control variable in actual applications with a great flexibility, different from the actual sense of these formulas. Hence, in this paper, we do not adopt any special formula and the rate is determined according to the actual background as a known parameter or a function of time.

Some studies[18-20]were concerned with the gasleakage regime of the ventilated supercavity, among which the early research achievements on the gasleakage of the supercavity made by Epshtein are noteworthy. Here, the unsteady formula of the gas-leakage rate proposed by the author[15]is used, as follows

where Vwand Sware, respectively, the re-entrant jet velocity and the area in the supercavity tail,Vw=. C1and C2are the constants related to the initial cavitation number

1.3 Modeling for the effect of the angle of attack

Considering a differential supercavity section from the separation point of the supercavity on the cavitator and assuming that the effects of the angle of attack, the gravity and the inertial force on the supercavity can be separately considered, the section control volume is acted by lift force and the radial component of self weight force in the lateral direction of the supercavity.

For the lift force, as is shown in Fig.(1a), we have

where Fdis the drag at the zero angle of attack, and Fd=0.5ρwV2SnCs, Snis the cross section area of the cavitator,Csis the drag coefficient, α is the angle of attack, positive when the longitudinal axis of the cavitator is directed on the left side of the direction of the motion velocity, and negative otherwise for the disk cavitator; Flis the lift force at the angle of attack α.

Hence, according to the momentum theorem and without considering the gas gravity in the supercavity because the gas density is far less than the water density, we have

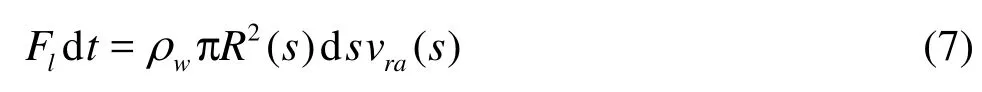
where s, R(s) and vra(s) are the curvilinear coordinate, the radius and the radial velocity of the differential supercavity section, respectively.

Further, combining formula (6) with Eq.(7) we have

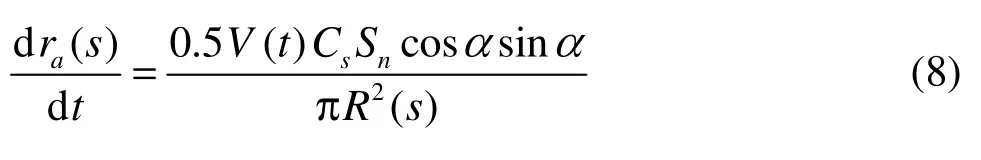
where ra(s) is the radial floatation displacement of the centerline of the differential supercavity section caused by the angle of attack.

Making a variable substitution, Eq.(8) can be written as

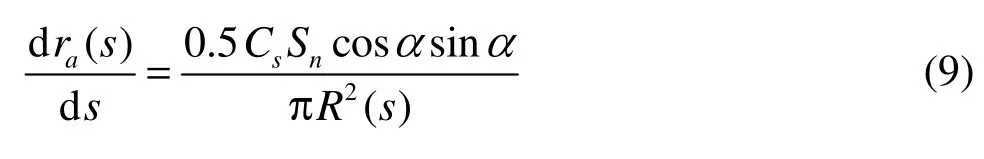
Hence, the displacement in r direction is

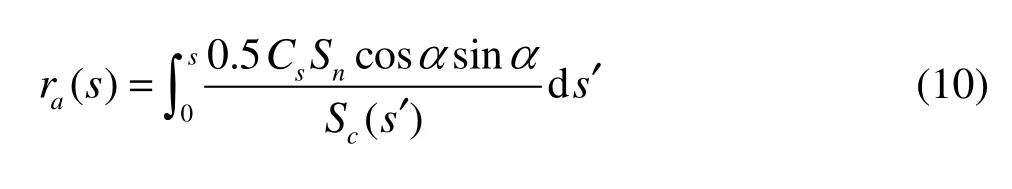
where Sc(s) is the area of the cross section of the supercavity,(s)=πR2(s).

1.4 Modeling for the gravity effect

The gravity effect is significant when the Froude number is not great, defined aswhere g is the gravity acceleration, which denotes the magnitude of the gravity effect. But, the ambient pressure is asymmetric in each supercavity section for the supercavity moving in the vertical plane because of the difference of the water depth to cause a deformed supercavity, which is regarded as the gravity effect. The gravity effect on the supercavity is mostly shown on the deviation of the centerline of the supercavity from the trajectory.

Without consideration of viscosity, considering the unit length of the supercavity, applying the momentum theorem to this unit in r direction, it is assumed that the differential supercavity section is symmetric at the initial time, i.e. the deviation and the expansion of the supercavity section are considered as two independent processes, and the difference between the inclination angle of the supercavity traje ctory and the inclination angle of the upper and lower surfaces of the supercavity is very small in reality, as is showed in Fig.(1b). Also, the gas gravity impulse item may be neglected because the gas density is far less than the water density. Hence, we have

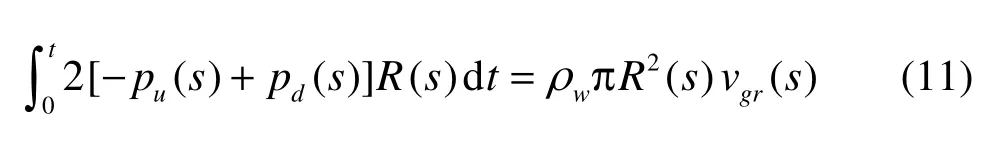
where pu(s) and pd(s) are, respectively, the static pressures on the upper and lower differential surfaces of the supercavity, vgr(s) is the lateral velocity of the differential supercavity section.

Besides, the pressure difference on the upper and lower surfaces is expressed as

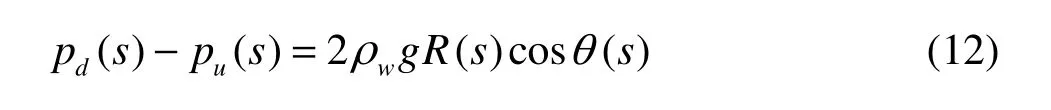
Substituting formula (12) into Eq.(11), we have

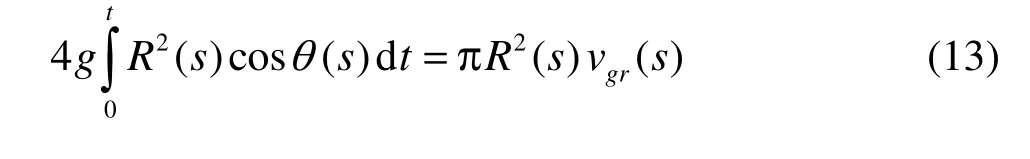
where ()sθ is the angle between the tangent line of the differential section surface of the supercavity and the trajectory.

Further, we have

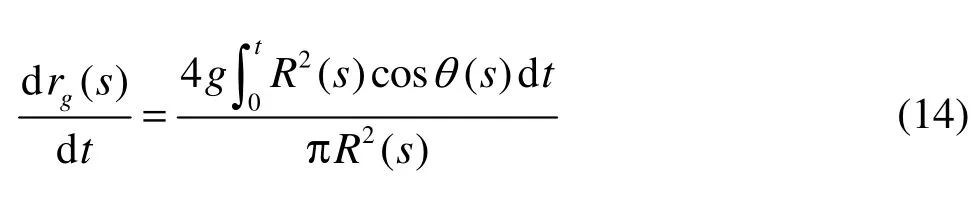
where rg(s) is the radial displacement of the differential supercavity section caused by gravity.

Then with a variable substitution, formula (14) is shown to be equivalent to

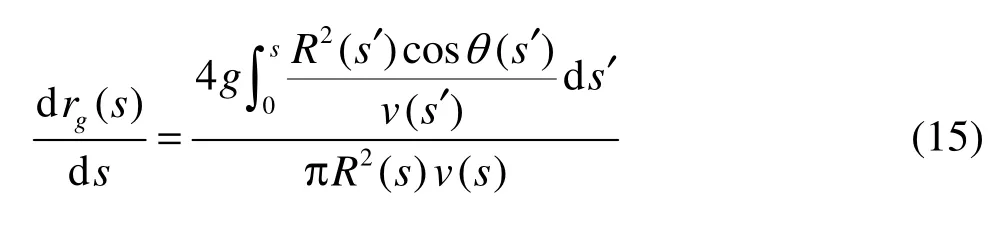
Integrating formula (15) with respect to variable s again, we have

1.5 Modeling for the inertial force effect

The supercavity is acted by the inertial force as a body force when it makes a curvilinear motion. The force is caused by the difference between the inner and outer pressures on the supercavity surface in the vertical plane, and makes the supercavity deviate from its trajectory toward the outward normal direction of the trajectory of the supercavity in Fig.(1c).

Applying the Bernoulli equation to the inner and outer surfaces of the supercavity, we have

where vin(s) and vout(s) are the flow velocities on the inner and outer surfaces of the supercavity, respe-ctively, pin∞(s ) and pout∞(s ) are the ambient pressures on the inner and outer surfaces of the supercavity at infinity.

Similarly, considering the unit length of the supercavity and assuming that the angle between the inclination lines of the upper and lower surfaces of the differential supercavity section and the inclination line of the supercavity trajectory are very small in reality, applying the momentum theorem to this unit in r direction, we have

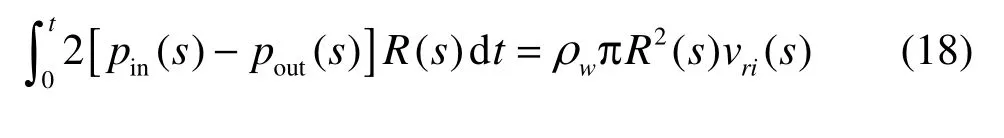
where vri(s ) is the radial velocity of the differential supercavity section.

Substituting formula (17) into Eq.(18) yields

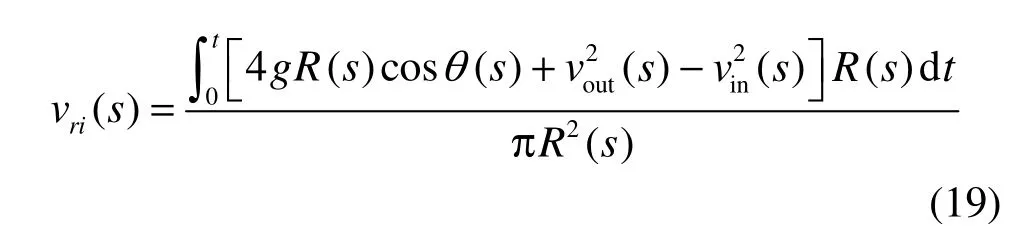
With the supercavity making a curvilinear motion, there are the following relations.

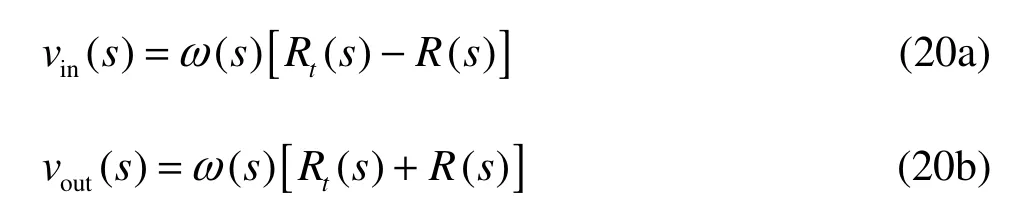
where ω(s)is the angular velocity of the supercavity, ω(s)=v(s)/Rt(s), Rt(s) is the curvature radius of the supercavity trajectory,

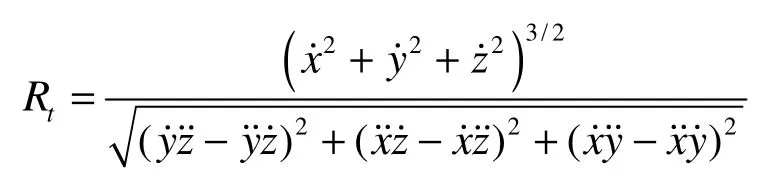
where x, y and z are the coordinate components of the supercavity trajectory in the inertial frame.

Substituting formula (20) into (19), we have

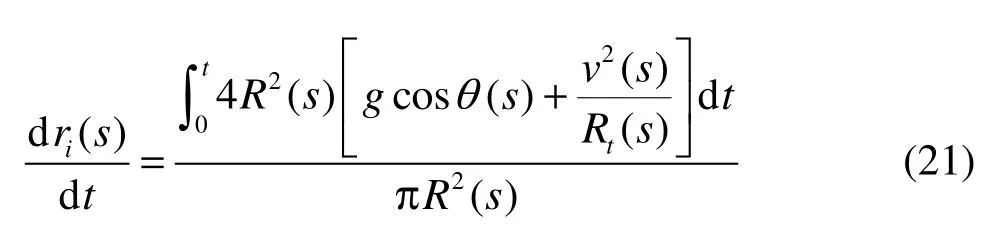
where ri(s) is the radial displacement of the differential supercavity section caused by the inertial force.

A variable substitution yields

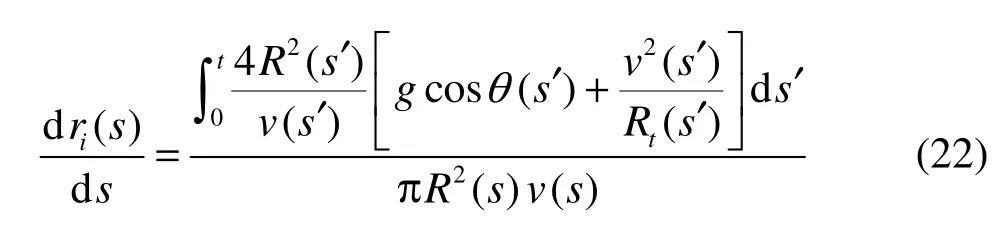
Integrating formula (22), we obtain

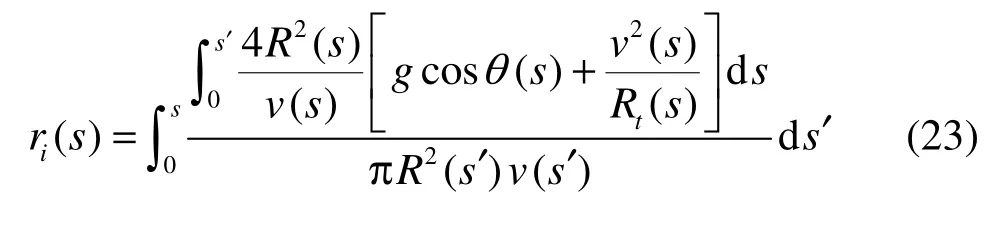
2. Numerical simulation

The effect of the trajectory curvature on the supercavity in the vertical curvilinear motion is analyzed numerically. The trajectory curvature is considered in two cases here, i.e. constant and variable, for the convenience of analysis. In the former case, the flow and model parameters are taken as constant. Although it is an ideal process, the case is of great significance in theory. In fact, the supercavity in the curvilinear motion of the vertical plane is unsteady on the one hand, and some flow or model parameters are varied in order to keep the motion in the vertical plane on the other hand. For these reasons, as a more general case, one has to consider the variable trajectory curvature. The trajectory may be described in the form of the motion Eq.(24).

where u, v and w are the velocity components of the supercavity in the body frame of the supercavity, whose origin is in the geometric center of the cavitator, θ,ψ and φ are the pitch angle, the yaw angle and the roll angle of the supercavity, respectively.

Besides, it is assumed that the cavitator has one degree of freedom, i.e., the cavitator can rotate in the longitudinal plane of the body frame, and the transformation from the velocity coordinate frame to the body coordinate frame is as follows

where

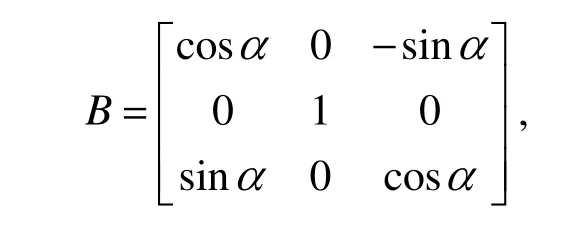
α is the angle of attack.

Combining Eqs.(25) and (24), we have

However, in order to keep the supercavity motion in the vertical plane, we must have

where c is a constant.

For the trajectory Eq.(26), its initial condition may be ascribed as

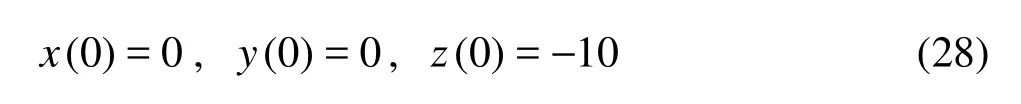
According to the initial condition (28), we may determine the vertical plane as

Theoretically, c may be taken as any constant because there are numerous vertical planes. But, it does not influence the results in this paper, i.e., the effects of the trajectory curvature on the supercavity. For a given variation of the supercavity trajectory,c may be taken as 1.

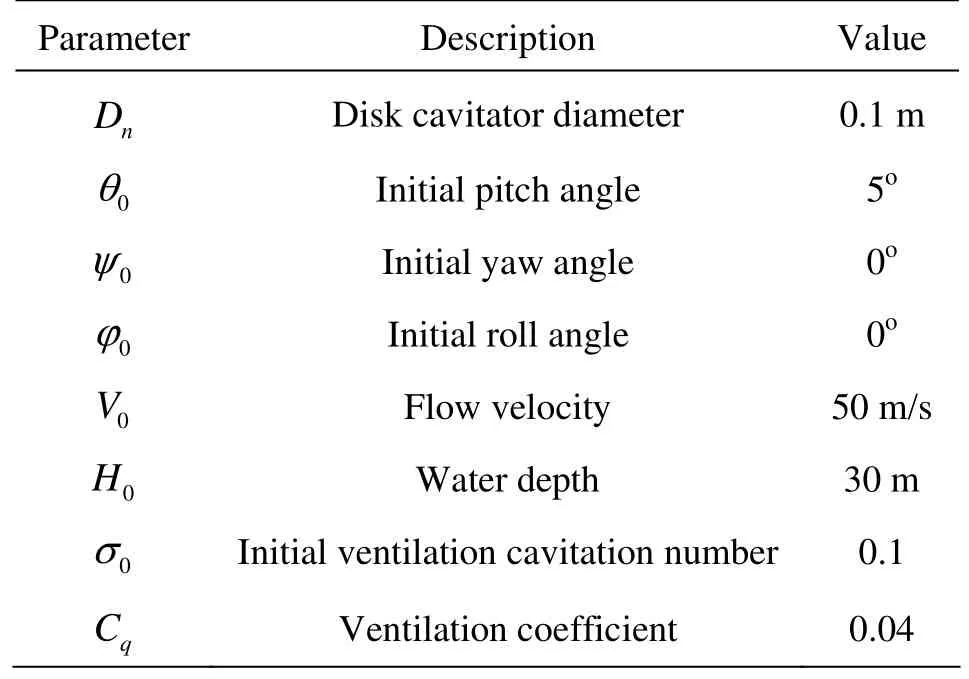
Table 1 Basic model and initial flow parameters

Assume that the flow and model parameters are constant except the pitch angle and the angle of attack. The pitch angle is adjusted to realize the curvilinear motion of the supercavity as a control variable in general, i.e., to climb up and descend. The angle of attack is another variable to satisfy the constraint Eq.(27). The basic model and initial flow parameters are given in Table 1.

2.1 Numerical method

The whole numerical method involves a cavitation number correction algorithm[15,21]. It is divided into two layers: the outer and the inner layers. In the outer layer, the explicit space marching is used, in each space step, the cavitation number correction algorithm together with Eqs.(1), (2), (4) and (5) are used to get the supercavity, and the supercavity is shaped again to reflect the effects of the angle of attack, the gravity and the inertial force based on Eqs.(10), (16) and (23) in the process, i.e., the resultant deformation is the sum of components caused by these effects at each control point in the body frame with the right hand rule in each time step. The initial value of the coefficient a is set to be 2.0 and the initial relaxation factor α=0.4 is applied in all iterative processes. If the iteration number exceeds 20, the factor is reduced by 50%.

2.2 Numerical results

In the first case, the flow velocity and the model parameters are applied in the simulation, as is shown in Table 1.

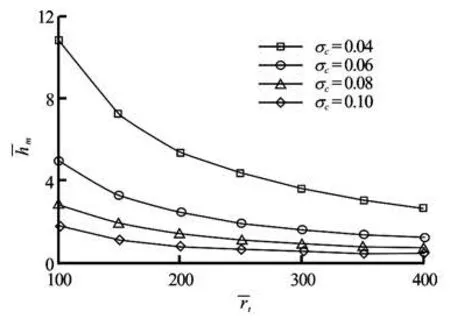
Fig.2 The maximum deviation displacement versus curvature radius

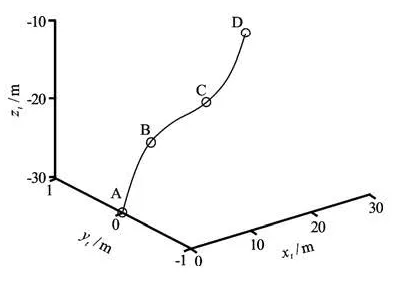
Fig.3 Supercavity trajectory

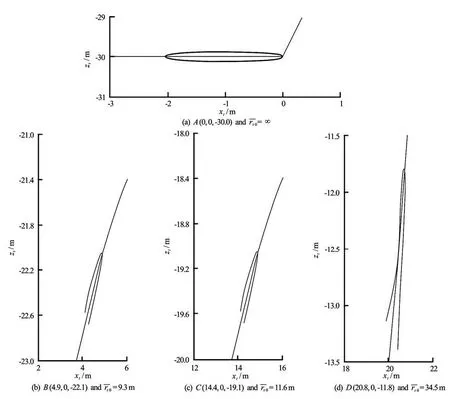
Fig.4 Supercavity in a curvilinear motion in the vertical plane

In the case of the variable curvature trajectory, the supercavity is simulated based on the above analysis, i.e., the pitch angle is used to realize a curvilinear motion as the control variable, whereas the angle of attack is just applied to satisfy the Eq.(27) to guarantee the motion in the vertical plane.

It is assumed that the pitch angle varies in a harmonic form without loss of generality in the simulation, θ(t)=θcos(ωt ), ω=50s-1. The trajectory is

0 given in Fig.3 based on the parameters in Table 1, which describes the process in which the supercavity climbs up and descends in the designed vertical plane determined by the constant c and the initial condition in Eqs.(27) and (28).

The simulation results are shown in Fig.4 based on the parameters given in Table 1, where rt0is the dimensionless curvature radius of the supercavity trajectory at the position of the cavitator, hiis the deviation displacement of the supercavity toward the outer normal direction of the supercavity trajectory. The figure gives the development process of the supercavity at four different locations on the trajectory. It can be seen that the supercavity deviates towards the outer normal direction of the trajectory as a result of the inertial force of the supercavity, and the maximum deviation displacement still occurs in the tail of the supercavity. Besides, the supercavity dimensions change suddenly because the ambient pressure decreases to cause the decrease of the cavitation number when the supercavity climbs up with a constant velocity.

3. Conclusions

A mathematical model of the supercavity in a curvilinear motion in the vertical plane, including the models for the effects of the angle of attack, the gravity and the inertial force and the corresponding calculation method are proposed in this paper. On this basis, the supercavity is simulated when it climbs up in the form of a curvilinear motion.

In the case of constant curvature, the maximum deviation displacement towards the outward normal direction of the trajectory, which occurs in the tail of the supercavity, increases as the cavitation number or the curvature radius decreases when other model and flow parameters are constant. For the variable curvature, the supercavity shape changes evidently because the trajectory curvature and the ambient pressure are variable, and the angle of attack also changes, accompanied by the change of the cavitation number in order to maintain the motion in the vertical plane, with the same trend as in the case of constant curvature. The deviation displacement increases along the supercavity length. But, to determine the exact variation of the displacement is a very complicated matter because the trajectory curvature is time-varying and the flow parameters are unsteady. It is not done here, but it is extremely important for controlling the supercavity and its vehicle and realizing its maneuverability, which requires the understanding of the supercavity shape in the curvilinear motion in detail, where more researches are still in process.

In a word, this paper provides a theoretical foundation and some technical guidance for realizing the controllability and the maneuverability of supercavitating vehicles.

[1] FRIDMAN G. M., ACHKINADZE A. S. Review of theoretical approaches to nonlinear supercavitating flows[C]. RTO-AVT Lecture Series on “Supercavitating Flows”. Brussels, Belgium, 2001.

[2] PARYSHEV E. V. Mathematical modeling of unsteady cavity flows[C]. Proceedings of the 4th International Symposium on Cavitation. Osaka, Japan, 2003.

[3] PELLONE C., FRANC J. P. and PERRIN M. Modeling of unsteady 2D cavity flows using the Logvinovich Independence Principle[J]. Comptes Rendus Mécanique, 2004, 332(10): 827-833.

[4] PARYSHEV E. V. Approximate mathematical models in high-speed hydrodynamics[J]. Journal of Engineering Mathematics, 2006, 55(1-4): 41-64.

[5] YUAN Xu-long, ZHANG Yu-wen and WANG Yu-cai et al. On asymmetry of ventilated supercavity of underwater vehicle[J]. Acta Mechanica Sinica, 2004, 36(2): 146-150(in Chinese).

[6] SEREBRYAKOV V. V. The models of the supercavitation prediction for high speed motion in water[C]. Proceedings of International Summer Scientific School“High Speed Hydrodynamics”. Cheboksary, Russia, 2002.

[7] SEREBRYAKOV V. V. Some models of prediction of supercavitation flows based on slender body approximation[C]. Proceedings of the 4th International Symposium on Cavitation. Pasadena, CA USA, 2001.

[8] PARYSHEV E. V. The dynamic theory of supercavitation[C]. Proceedings of International Summer Scientific School “High Speed Hydrodynamics”. Cheboksary, Russia, 2002.

[9] KINZEL M. P. Computational techniques and analysis of cavitating-fluid flows[D]. Ph. D. Thesis, State College, USA: The Pennsylvania State University, 2008.

[10] NOURI N. M., ESLAMDOOST A. An iterative scheme for two-dimensional supercavitating flow[J]. Ocean Engineering, 2009, 36(9-10): 708-715.

[11] LI X. B., WANG G. Y. and ZHANG M. D. et al. Structures of supercavitating multiphase flows[J]. International Journal of Thermal Sciences, 2008, 47(10): 1263-1275.

[12] CHEN Xin, LU Chuang-jing and LI Jie et al. Properties of natural cavitation flows around a 2-D wedge in shallow water[J]. Journal of Hydrodynamics, 2011, 23(6): 730-736.

[13] VASIN A. D. The principle of independence of the cavity sections expansion (Logvinovich’s principle) as the basis for investigation on cavitation flows[C]. RTOAVT Lecture Series on “Supercavitating Flows”. Brussels, Belgium, 2001.

[14] ERIC R. W., TIMOTHY F. M. A Serendipitous application of supercavitation theory to the water-running basilisk lizard[J]. Journal of Fluids Engineering, 2010, 132(5): 054501.

[15] ZOU Wang, YU Kai-ping and WANG Xiao-hui. Research on the gas-leakage rate of unsteady ventilated supercavity[C]. Proceedings of the 9th International Conference on Hydrodynamics. Shanghai, China, 2010, 778-783.

[16] SEREBRYAKOV V. V. Ring model for calculation of axisymmetric flows with developed cavitation[J]. Journal of Hydromechanics, 1974, 27: 25-29(in Russian).

[17] SAVCHENKO Y. N. Experimental investigation of supercavitating motion of bodies[C]. RTO-AVT Lecture Series on “Supercavitating Flows”. Brussels, Belgium, 2001.

[18] KINZEL M., LINDAU J. and KUNZ R. Air entrainment mechanisms from artificial supercavities: Insight based on numerical simulations[C]. Proceedings of the 7th International Symposium on Cavitation. Ann Arbor, Michigan, USA, 2009.

[19] SEREBRYAKOV V. V. Physical-mathematical bases of the principle of independence of cavity expansion[C]. Proceedings of the 7th International Symposium on Cavitation. Ann Arbor, Michigan, USA, 2009.

[20] SPURK J. H. On the gas loss from ventilated supercavities[J]. Acta Mechanica, 2002, 155(3-4): 125-135.

[21] ZOU W., YU K. P. and ARNDT R. E. A. et al. On the stability of supercavity with angle of attack[C]. Proceedings of the 8th International Symposium on Cavitation. Singapore, 2012.

10.1016/S1001-6058(11)60300-4

* Project supported by the National Natural Science Foundation of China (Grant No. 10832007).

Biography: YU Kai-ping (1968-), Male, Ph. D., Professor