APPROXIMATION OF INTERVAL BEZIER SURFACES

Huang Lin,Hou Jian,Lai Junfeng

(1.Collegeof Science,China Jiliang University,Hangzhou,310018,P.R.China;2.College of Science,Inner Mongolia University of Technology,Hohhot,010051,P.R.China)

INTRODUCTION

Rational curves and surfaces,as a class of important approximation functions, are extensively applied in CAD/CAM.The NURBS model of curves and surfaces representation in CAD/CAM system is an exact form.However,according to the blueprint or the sample surfaces obtained from model measurement,curves and surfaces of the product shell are impossible to be an unique exact form.Caps between curves or surfaces are lack of stability because of the limit exact float computation used in algorithms,which results in the loss of some cross points in computation.Based on the above reasons,the concept interval curves and interval surfaces are presented in approximation theory.

In the theory of approximations,the classic polynomial approximation methods for rational expression have a variety of interpolations and operator approximations, such as Lagrange interpolation,Hermite interpolation and hybrid approximation[1].These approximation methods converge too slowly or even cannot converge[2-4].Chen and Lou[5]presented the control method for net perturbations to approximate the rational curves,and it is a local method.Meng and Wang[6]used the control method for a rational surface in the rectangular domain.

This paper presents an approximation approach for th e interval Bezier surfaces using a global energy minimization method[7-10]. The rational perturbation is used for a rational surface to make it become polynomial surface and make its certain module reach the minimum,so the polynomial surface is a kind of rational surface approximation.According to the biggest control point of perturbation rational surface,a rational surface included by the interval Bezier surfaces is obtained.On the other hand,the approach also makes more confinements to the perturbation surface,such as the requirement for smoothing at the end points.So the polynomial approximation is obtained,which has_×h orders interpolation at the end points.Finally,the approximation surface and the global approximation with certain continuity are obtained.

1 SHAPE MODIFICATION USING ENERGY MINIMIZATION

During the study of CAD/CAM problems,various types of curves and surfaces appear.The cusp point is used to show the shortage of control net perturbation method.Fig.1 shows a curve with a cusp point.When the perturbation is applied to the curve in Fig.1,it is assumed to become the curve in Fig.2.When the control net perturbation method is applied to the curve in Fig.2,it is shown in Fig.3,where the straight lines are the control nets.Apparently,the cusp point perturbation is large,but the control net method does not include the cusp point round.The perturbation is small when using the control net method, so the control net perturbation method fails to accurately estimate the perturbations.

Fig.2 Perturbated curve

Fig.3 Control-net-perturbated curve

The shape modification of the surface is considered with different constraints by using energy minimization.The thin plate energy of a surface R(u,v)is usually defined as

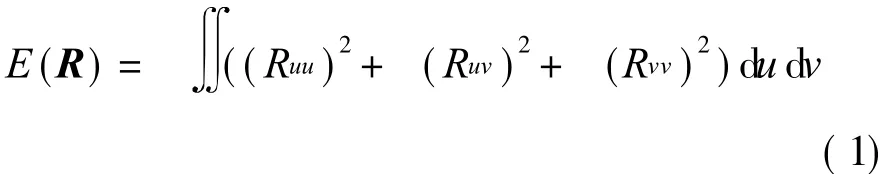
The energy of a parametric surfaceimplies its global properties in a sense,so that it is often used in surface fitting and fairing for smooth and natural shape[1,4-6].Here it is intended to change the control points of surfaces,so the thin plate energy of error surface is minimized.

Supposing that the control points p ij(0≤ i≤m,0≤ j≤ n)are changed,the perturbations X ij(0≤ i≤m+p,0≤ j≤n+qare chosen for those control points,such that the modified surface S (u,v) satisfies some geometric constraints.

It is intended to determine X(u,v)by the constrained optimization method,such that

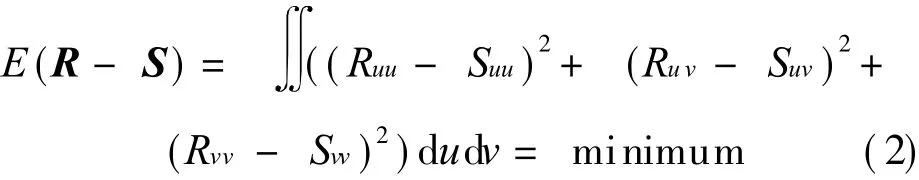
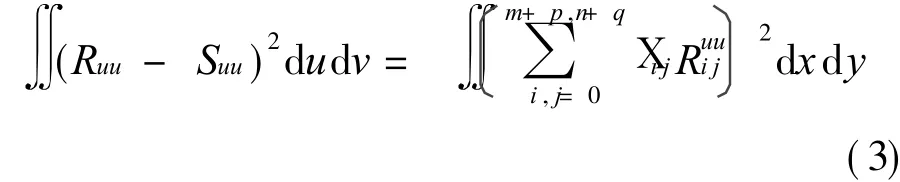
2 APPROXIMATION BUILDING

An m×n rational surface is given as

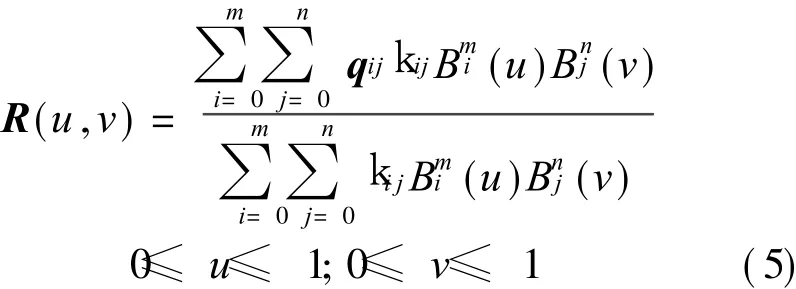
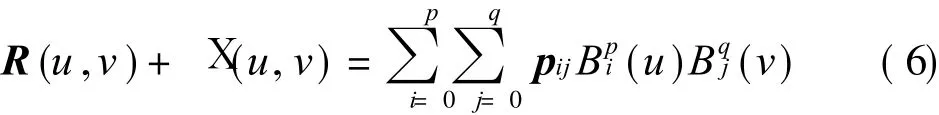
where p ij(i=0,1,… ,m;j=0,1,… ,n)are the control points.

Making a rational perturbation[5]to the parameter surface,we have

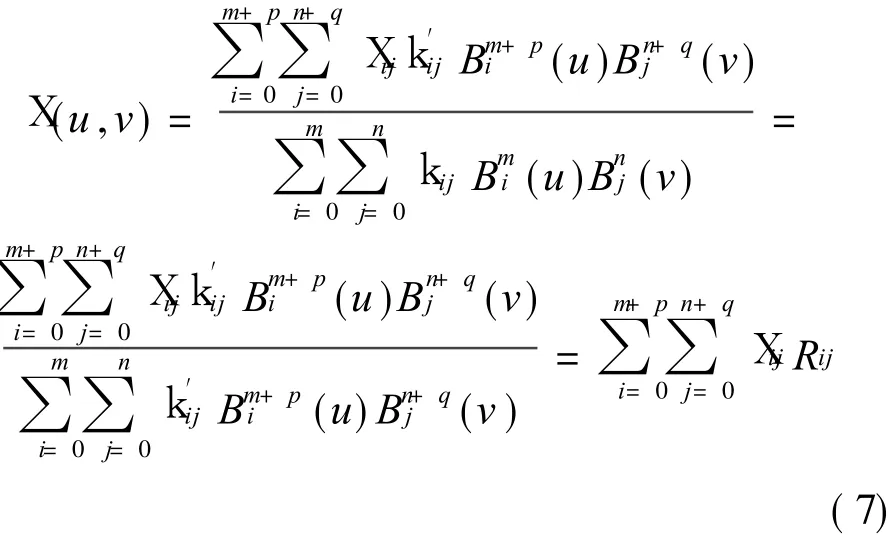
where

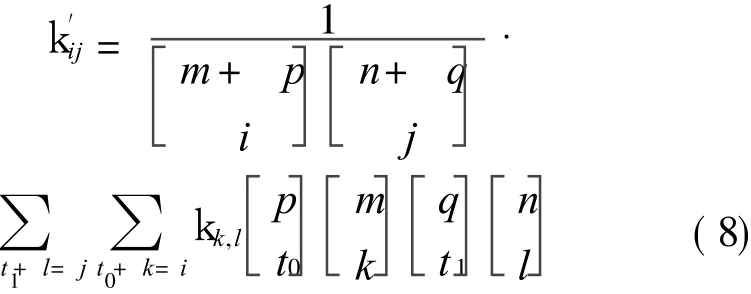
Making R(u,v)+X(u,v)just be a polynomial surface of degree p×q,S(u,v)is defined as

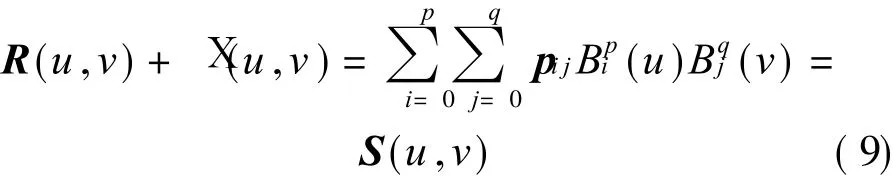
From Eqs.(7,9),we have

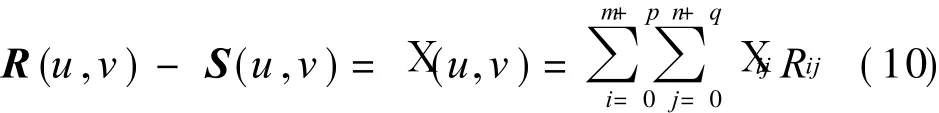
From Eq.(6),we have

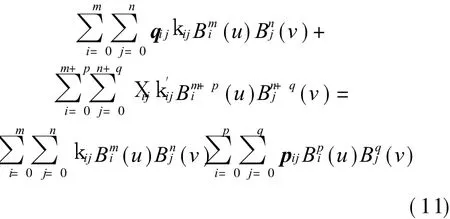
By using the Degree Elevation Formula,two sides of Eq.(11)can be written to the Bezier surface of(m+ p)×(n+q)orders,so Eq.(11)is rewritten to that

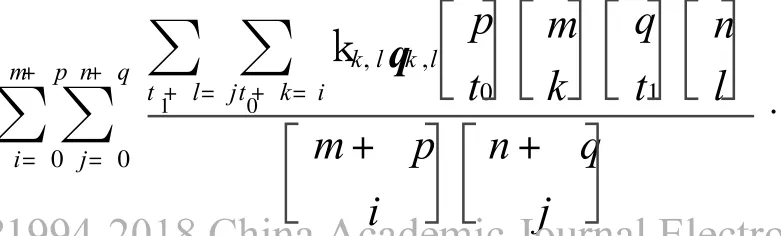
To compare coefficients of both sides,the perturbations are given as follows

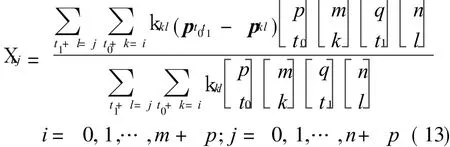
At the same time,it is expected the norm of X(u,v)in some senses reaches the minimum.

In this paper, Eq.(4)is chosen as the optimal target function as follows

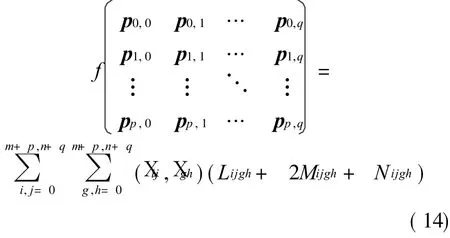
So the problem is transformed into determining

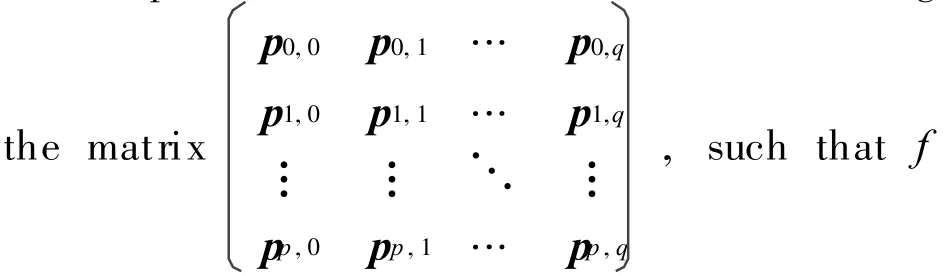
reaches the minimum.

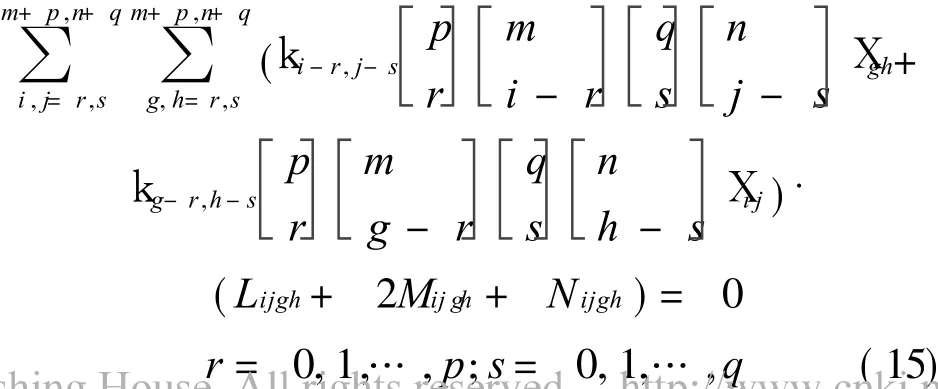
By computing Eq.(15), the matrix

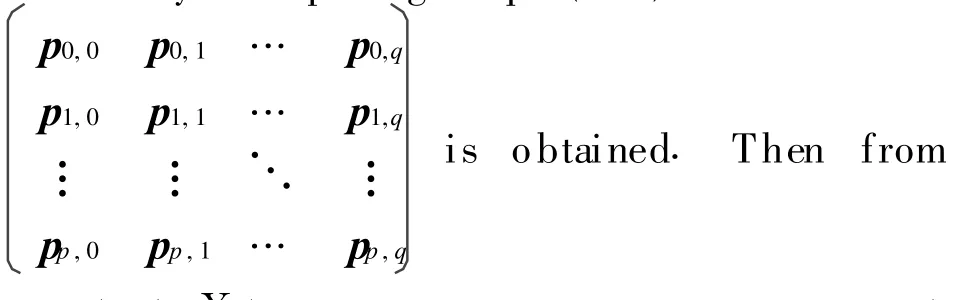
Eq.(13),X ij(i=0,1,… ,m+p;j=0,1,… ,n+q)are also obtained.

The energy minimization method is compared with the control net perturbation method[6],and the major difference is found that the energy minimization method needs to compute Lijgh+2Mijgh+ Nij gh.

Setting

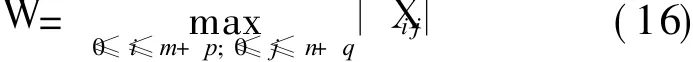
where the maximum value of vector denotes the maximum absolute value of every component.Whereas from Eq.(6),we can deduce[5]

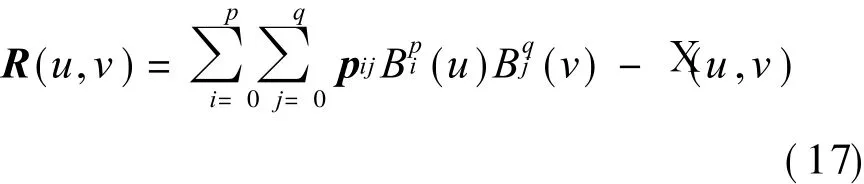
So

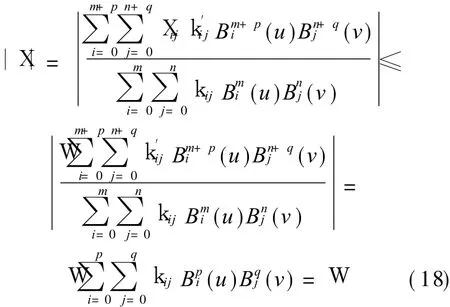
This error may be taken as the half of control interval of interval polynomial.Then we have

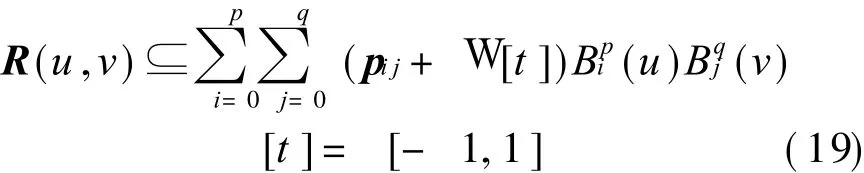
This is the center form of interval polynomial. Then the rational surface can be deduced,which is contained in a p×q degree interval polynomial.

3 APPROXIMATION WITH END POINT INTERPOLATION

Firstly,for edge curves the interval Bezier polynomial can be used for approximating with end point interpolation.Taking R1(u,0)as an example

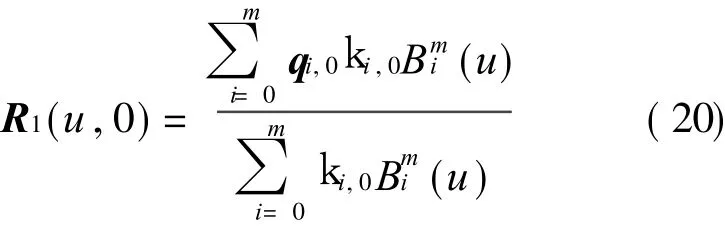
From Eq.(13),we have

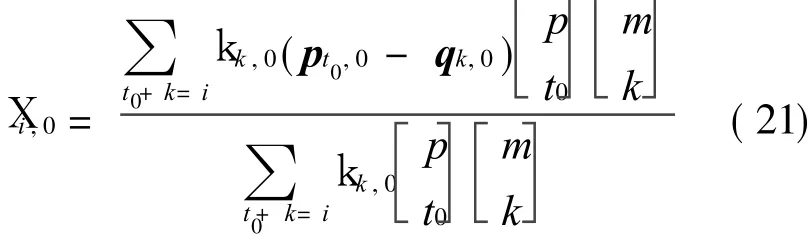
and simultaneously Eq.(21)satisfy that

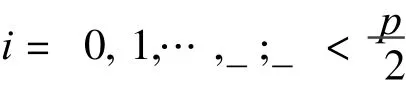
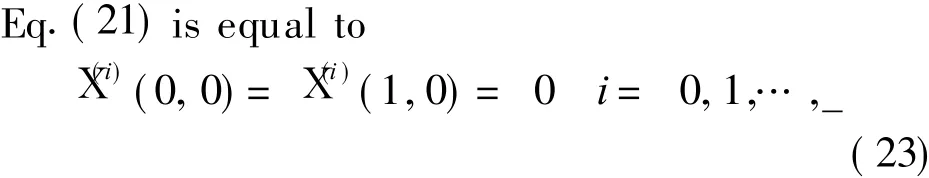
or

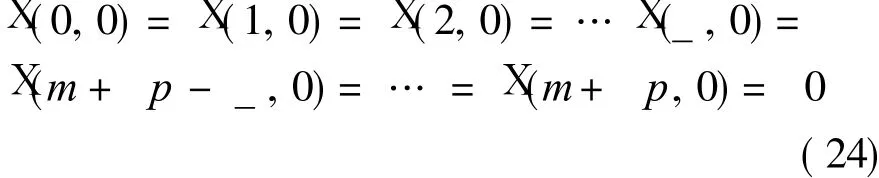
Thus control points p t0,0(t0=0,1,…,_,p-_,p-_+ 1,…,p)of approximation polynomial p1(u,0)which satisfy the interpolation condition(Eq.(21))are determined by Eqs.(21,23).Therefore the objective function is transformed into determining pt0,0(t0=_+ 1,…,p-_-1),then determining(i=_+1,…,m+ p-_),which makes thevalueof thefunction minimum.That is f(p_+1,0,… ,p p-_-1,0)= ?(Ruu- Suu)2d u d v=

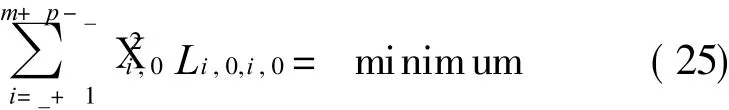
Because p i,0(i=0,1,… ,_,p-_,… ,p)are already deduced by Eq.(24).By computing the set of equations above,p_+1,0,…,p p-_-1,0 can be obtained,then X i,0(i=_+1,…,m+p-_-1)are obtained as follows

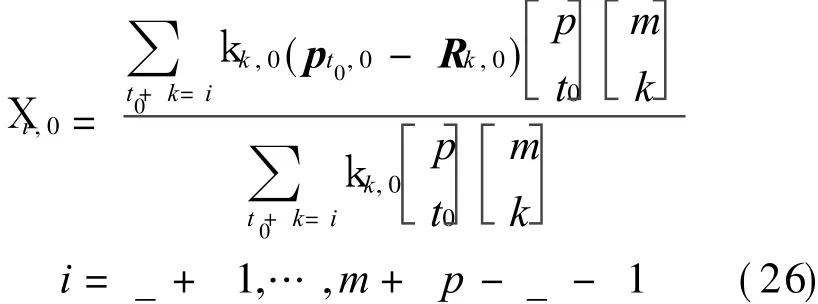
Assuming that

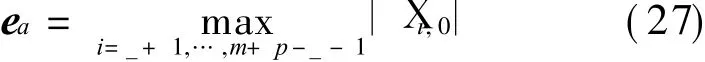
then

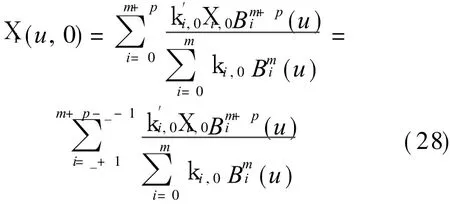
From Eq.(28),we have

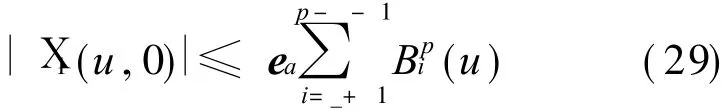
Therefore

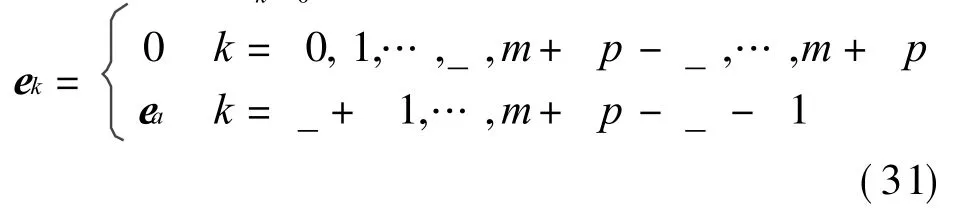
Thus interval polynomial approximation of p orders can be obtained for a rational curve which preserves the interpolation of_ orders at end points.The other three edges are approximated using the same method(the two edges of v direction are interpolated,which preserve the interpolation of h orders at end points).Now four edges are determined,then the corresponding control points and the control interval of four edges can be obtained.The others are solved by using the method in Section 2.Consequently,the polynomial of p×q degrees is determined,which approximates or contains the initial rational surface preserving the interpolation of_ and h orders at the end points,respectively.

4 EXAMPLES

The control points and corresponding weights of a bicubic rational surface(Fig.4)are given as follows(Ri,j)=

where i=0,1,2,3;j=0,1,2,3.

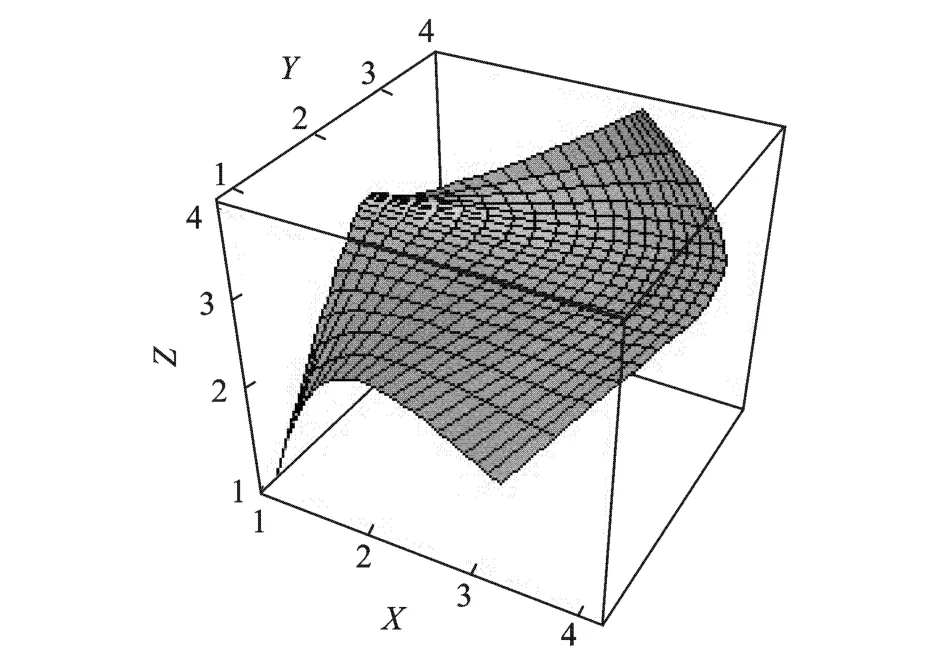
Fig.4 Bicubic rational surface

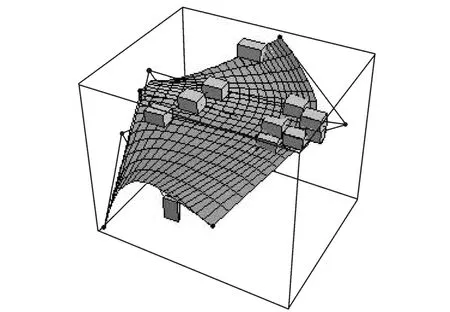
Fig.5 Biquartic interval Bezier surface

By using the presented method,a biquartic interval Bezier approximation is obtained,which preserves theinterpolation of_=1 and h=1 order at two end points,respectively(Fig.5).Fig.6 is a bicubic Coons surface approximation for the initial rational surface. Fig.7 is the interval control grid.The surface in Fig.5 is produced by central control points. Fig.5 demonstrates the generating procedure of biquartic interval Bezier surface. From the examples,it can be easily seen that the interval surface approximation remains the fundamental shape of the initial rational surface,which is produced by the central control points and is almost the same as the initial surface.Furthermore, the approximation surface is polynomial interval surface.The interval surface produced by interval control points has a well approximation.So its property is better than the Coons surface approximation. Because of the considering global property, the interval approximation obtains a better result than the classic methods. Curves and surfaces of the product shell,according to the blueprint or the sample surfaces obtained from the model measurement,belong to a variable domain of the exact curves and sur-faces.The method can be used to describe the variable domain when the polynomial approximation is performed for a rational curve or surface.

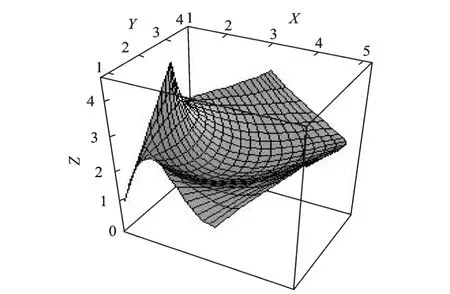
Fig.6 Bicubic Coons surface

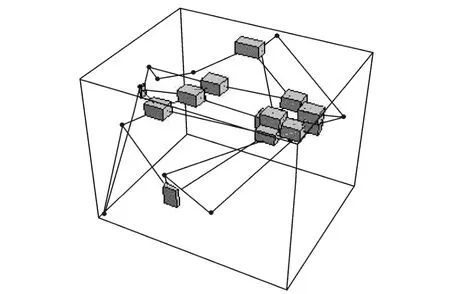
Fig.7 Interval control grid

5 CONCLUSION

Based on the conception of perturbation,an approach is presented for the interval Bezier surfaces approximating the rational surfaces by using energy minimization method.The approach makes the perturbation surfaces have more restrictions than the original surfaces.The result can be combined with the subdivision method to obtain a piecewise interval polynomial approximation for a rational surface.In this paper,the convergence of the approach is not given,and it is worthy of researching further more.

[1] Sederbeg T W,Kakimoto M.Approximating rational curves and surfaces using polynomial curves[C]∥NURBS for Curve and Surface Design.Philadelpha:SIAM,1991:144-158.

[2] Wang Guojin, Wang Guozhao, Zheng Jianmin.Computer aided geometry design[M].Beijing:Higher Education Press,2001.(in Chinese)

[3] Wang Guojin,Sederberg T W.On the convergence of polynomial approximation of rational function[J].Jof Approx Theory,1997,89(3):267-288.

[4] Liu Ligang,Wang Guojin.Two types of polynomial approximation to rational surfaces and their convergence[J]. Journal of Software,2001,12(5):650-655.

[5] Chen Xiaoqun,Lou Wenping.Interval Bezier curves approximation of rational curves[J].Journal of USTC,2001(4):379-386.(in Chinese)

[6] Meng Xiangguo,Wang Renhong. Interval Bezier surfaces approximation of rational surfaces[J].Journal on Numerical Methods and Computer Applications,2003,4(12):247-256.(in Chinese)

[7] Hu Shimin,Li Youfu,Ju Tao,et al.Modifying the shape of NURBS with geometric onstraints[J].Computer-Aided Design,2001,33(5):903-912.

[8] Volin O,Bercovier M,Matskewish T.A comparison of invariant energies for free-form surface construction[J].Visual Computer,1999,15:199-210.

[9] Tian Kuan,Ma Lizhuang,Marc A.Tessellation using loyd relaxation on the surface[J].Journal of Computer-Aided Design and Computer Graphics,2009,21(8):1138-1142.

[10]Zhe Bian,Hu Shimin,Martin R R.Evaluation for smallvisual difference between conforming meshes on strain field[J].Journal of Computer Science and Technology,2009,24(1):65-75.