基于多GPU的大型線性和非線性方程組的求解

劉 沙1 鐘誠(chéng)文1,2 陳效鵬3

(1.西北工業(yè)大學(xué)翼型葉柵空氣動(dòng)力學(xué)國(guó)防科技重點(diǎn)實(shí)驗(yàn)室,西安,710072,中國(guó);2.西北工業(yè)大學(xué)高性能計(jì)算中心,西安,710072,中國(guó);3.西北工業(yè)大學(xué)力學(xué)與土木工程學(xué)院,西安,710072,中國(guó))

INTRODUCTION

Mathematical modeling of engineering problems often leads to systems of linear or nonlinear equations.The solution of such resulting equations utilizing numerical tools via digital computational devices is usually of very time-consuming,because most real-world engineering applications are often of extremely large size for computation.In this paper,with the Inexact Newton method and the preconditioned bi-conjugate gradient stable(PBi-CGstab)method,linear and nonlinear solvers based on muti graphic processunits(GPUs)are proposed for large scale problems.

General purpose GPU(GPGPU)technique denotes the implementation of general purpose computing by using programmable GPUs[1].It has been widely applied in many computational areas owing to its more powerful floating calculation abilities and wider bandwidth compared with the traditional CPU[2-3].Furthermore,the inherent single-instruction-multiple-data (SIMD)mechanism for GPGPU operation renders this technique suitable for massively loaded calculations.

A serial of GPU-based linear algebra operations were proposed by Krüger et al in 2003[4].T he first GPU-based conjugate gradient solver for unstructured matrices was proposed by Bolz et al[5].Buatois et al proposed a general sparse linear solver using CG method in 2 0 0 9[6].Cevahir et al developed a fast CG based on GPUs with some novel optimization techniques[7].These articles show great speedup ratio of GPU to CPU.

In early work,Zhong and Liu proposed a fast solver which has a great speedup ratio about 30 on single GPU[8].In this paper,multi-GPUs are used to obtain more data storage space that large size problems need.In the case of linear solver,the Bi-CGstab method can afford to solve the sys-tem of linear equations with non-symmetric matrix which cannot be solved by the CG method.A better convergence of the method is achieved by using the precondition strategy.For the nonlinear solver,Inexact Newton method is utilized.T he grid generation project in computational fluid dynamics is used to test the practicability of linear and nonlinear solvers,in which systems of linear and nonlinear equations are solved in order to obtain the coordinates of grid nodes.

1 COMPUTE UNIFIED DEVICE ARCHITECTURE

The compute unified device architecture(CUDA)[9]is a GPU architecture manufactured by NVIDIA.CUDA GPU contains a number of SIMD multiprocessors. Each multiuprocessor contains its own shared memory,read-only constant,and texture caches that are accessible by all processors on the multiprocessor.GPU has a device memory which is accessible by all multiprocessors.

CUDA GPU devices run a high number of threads in parallel.Threads are grouped together as thread blocks.Each block of threads is executed on the same multiprocessor and can communicate through fast shared memory.

Threads in different blocks can communicate only through device memory.Access to the device memory is very slow compared with the shared memory.Device memory accesses should be as refrained as possible,and these accesses should be coalesced to attain high performance.Coalescing is possible if the threads access consecutive memory addresses of 4,8 or 16 bytes and the base address for such a coalesced access should be multiple of 16(half warp[9])times size of the aforementioned memory types accessed by each thread.

2 SYNCHRONIZATION

Using Win64 API,a thread is created for each GPU on board in the program.Each thread manages the data input and output of GPU,and calls the GPU kernel functions and synchronizes with other threads.When creating and ending threads,CUDA codes"cutStartT hread"and"cutWaitForThreads"based on Win64 API can also be used for simplification.

T he multi-GPUs solver works as this pattern:Firstly,CPU distributes data and tasks to GPUs;T hen,set barriers to GPU managing threads.A GPU managing thread to run in front of its barrier means that its GPU has finished computational work,renewed its own data on device memory along with its host memory counterpart,and now,it is waiting for the data needed to be renewed by other GPUs.When all threads have run in front of their barriers,the barriers are released,then,each GPU obtains renewed data that they want and continues to work.The whole process consisting of setting and releasing barriers is one time of synchronization.

In this paper,the semaphores are used to manage the synchronization among threads.The synchronization process is shown in Fig.1.Define an array of semaphores(Sem[GPU-NUM])for GPU managing threads with initial value 0 and activation value GPU-NUM:

HANDLE Sem[GPU-NUM];

Sem[device-num]= CreateSemaphore(NULL,0,GPU-NUM,NULL)

When a thread reaches barrier, its semaphore is activated by adding GPU-NUM to initial value 0:

ReleaseSemaphore (Sem [device-num],GPU-NUM,NULL)

T hen the thread waits for the activation of semaphores corresponding to other threads:

WaitForMultipleObjiect(GPU-NUM,Sem,true,INFINIT E)

T he first parameter of this function is the number of semaphores.The second parameter is"Sem",the first word address of semaphores.T he third parameter is set"true",it means the function cannot return until all semaphores are activated.T he fourth parameter is the maximum waiting time,which is set to"INFINIT E"to insure the logic correctness of multi-GPUs solvers.When the demand of this function is fulfilled,the synchronization process is finished.

Fig.1 Threads controlling muti-GPUs and their synchronization

3 LINEAR SOLVER

3.1 PBi-CGstab method

Bi-CGStab is an iterative algorithm for solving a large,sparse,non-symmetric system of linear equations Ax=f.The method attempts to find approximate solutions in Krylov subspaces[10]appropriately generated by A and initial residual r0=f-Ax0.Bi-CGstab combines the advantages of both the Bi-CG and the general minimal residual(GMRES)methods[11],which basically follows the Bi-CG procedure while the residual is minimized in each step by using the GMRES method.The Bi-CG converges fastly but exhibits somehow numerical instability.T he main goal of Bi-CGstab is to retain,in attempt to keep the fast rate of convergence,the coefficients resulted from the Bi-CG method while improving the numerical stability by absorbing the GMRES advantage in its numerical stability.As demonstrated in Ref.[12],the Bi-CGstab method has achieved both fast convergence and numerical stability.

The idea of preconditioning for a system of linear equations is elementary:Precondition of the system for any non-singular matrix M means to pre-multiply both sides by the inverse of the matrix M(the left preconditioning matrix is precise),i.e.,M-1Ax=M-1f,which delivers a system with the same solution.The convergence of the iterative solution of M-1Ax=M-1f depends on the properties of M-1A instead of A.The preconditioner should be chosen in orderthat M-1Ax=M-1f may be solved more rapidly than Ax=f.In this paper,the Jacobi preconditioner is chosen for convenience of parallel computing[13].T he process of PBi-CGstab method is shown as follows:

3.2 Data blocking on multi-GPUs

T he data is blocked and the blocking information is recorded in multi-GPUs solvers as shown in Fig.2.The functions of threads managing GPUs allow transmitting only one parameter.So the blocking information is stored in an architecture body named Solverplan:

Fig.2 Packed matrix and vector blocking process

T he thread can use the information that"Solverplan"provides to exchange data with other threads.In the solver,a vector A stored in blocks is defined like this

So"array d-vectorA[n]"is the nth partition of vector A.The thread function is coded carefully to ensure it can be called by all GPU-managing threads.Defining vector in such a manner will fit the generality of the thread function.T he more complex matrix blocking will be presented in Section 4.2 along with matrix generation.

3.3 Linear solver on multi-GPUs

The aforementioned thread function that can be applied to all GPU-managing threads is the core algorithm of the solvers.This paper presents the detail of it for the linear solver.Fig.3 shows the process of thread function called by the nth thread.

InFig.3,d-f[n],d-r[n],d-r 0[n],d-p[n],d-v[n],d-t[n],d-s[n]are the nth partition of vectors f,r,r0,p,Ap*,As*,and s.They are stored in the nth GPU.Their lengths are all equal to plan[n].dataN shown in Fig.2.Part algorithm of kernel function of product of y=Ax is shown as follows:

Fig.3 PBi-CGstab on GPUs

In the above algorithm,the vectors x,p*,s*are needed by matrix-vector multiply,so theyare stored in entire lengths without blocking.But they are updated on the nth GPU only the nth partition.So,when they need to be updated,all threads should be synchronized.Then the data of updated partition can be exchanged.temp[n],temp2[n]and roub[n]are used to save the dot products of the nth partition of vectors temporarily.sum-temp,sum-temp2and sum-roub are the summation of them.Before calculate sum-temp,sum-temp2 and sum-roub,threads need to be synchronized.T here are five synchronization barriers in thread function shown in Fig.3.

There are three kinds of kernels(functions processing on GPU)which can be called by all thread functions in the solver.These kernels named MVP,IP,VSP are utilized to do the four matrix-vector products,four inner products,six vector summations shown in Fig.3.When thread functions calling kernels,the elements of Solverplan are transferred to them in order to specify which part of data they are dealing with.

4 NONLINEAR SOLVER

4.1 Inexact Newton method

In practice,a system of nonlinear equations should first be linearized,and then,iteration methods are employed to seek the solutions of the set of linearized equations.T hislinearization strategy is widely used in engineering applications for its proved effectiveness and usefulness[14-16].The Newton method serves as basis of the linearization approaches.T he procedure of Newton iteration method is as follows.

For a set of nonlinear equations

where f=(f1,f2,…,fn)T,x=(ξ1,ξ2,…,ξn)T.Its tensor form is fi(ξ1,ξ2,…,ξn)=0(i=1,2,3,…,n).T he equations can be expanded at xk(value of x at kth iteration step)using the T aylor′s series,and only the 1st order terms of the series are retained

T he solution of the system of linearized equations,xk+1,is sought in an iterative manner as follows

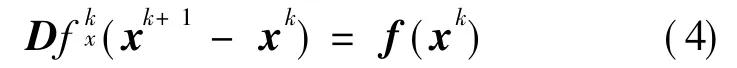
where xk+1is the new solution vector of the system of nonlinear equations.The vector x is updated using Eq.(4)until the convergence is satisfactory.

It is computationally expensive to obtain the accurate solution of the system of linear equations since the number of variables is usually fairly large in practical engineering applications.The solution of the system of linear equations resulted from the Newton method is only an intermediate step of the entire process for solving a system of nonlinear equations.Therefore,one might not always seek an accurate solution of the system of linear equations intermediately encountered.This leads to the Inexact Newton method practically sharing the same form of the original Newton method.T he Inexact Newton method has been routinely used in many engineering applications.As reported in Refs.[17-19],the Inexact Newton method can achieve a satisfactory balance between the solution accuracy of the system of linear equations and the computational cost incurred by the solution process,thus eventually yielding the solution of the system of nonlinear equations to a satisfactory degree of accuracy.

4.2 Nonlinear solver based on multi-GPUs

In engineering application problems,after linearizating,the resultant coefficient matrix is usually a sparse matrix that needs a formatted storage forstorage efficiency. Such process should be mapped to GPUs.

Almost every nonlinear function fi(x)in the system of nonlinear equations f(x)=0 has the same form in engineering applications.For example,when using the finite difference method for solving nonlinear partial differential equations,each fi(x)is a polynomial and all of fi(x)s share an identical structure,except a limited number of fi(x)that describe the boundary conditions.T herefore,when the program deals with the generation and the formatted storage of the coefficient matrix,only a few branch predictions are required.It becomes obvious that the processes used for generation and formatted storage of the coefficient matrix ideally fit the mechanism of SIMD of GPU.

The generation and formatted storage of a n*n matrix is carried out through n threads divided by several GPUs.Each row of the matrix corresponds to a thread.The non-zero elements in a row are counted,and then such non-zero values are sequentially placed into the matrix for formatted storage use.

The formatted storage matrix owns the same number of rows as the original coefficient matrix.The number of columns of the formatted storage matrix is set equal to the non-zero element number of the row which has the most non-zero elements.Hence,some zero-elements might remain in the formatted storage matrix.T his arrangement facilitates all threads in the SIMD mechanism of GPUs by providing threads of GPUs with an identical addressing pattern.It can be noted that,in most cases,the loss of computational resources because the space used for storage of zero-elements is of minor nature.

Since the multiplication of matrix and vector is involved in the computation,the column-wise storage appears more advantageous for coalescing to attain high performance[9,20],which leads to the formatted matrix eventually stored in the form of a vector.In this work,all non-zeros in the matrix are shifted to the left.Nonzero values of the compressed matrix are stored in an array in column order.Corresponding column indices of each nonzero in the original matrix are written in another array.Fig.4 depicts a formatting example with col-ind standing for column indices and the two arrays are divided into three parts stored on different GPUs.

A core part of kernel function of matrix-vector product y[n]=A[n]x[n]for a sub-matrix of A with plan[device-num].dataN rows and m columns are shown in the algorithm in Section 3.3,which is needed in the PBi-CGstab method.After the coefficient matrix A is generated,PBi-CGstab method based linear solver is used to solve the system of linear equations.And then generate the matrix again,keep doing this until achieving convergence.

5 EXPERIMENT

5.1 Computation platform

In this paper,Intel(R)Xeon(R)E5520 2.27 GHz CPU is chosen.DRAM is 12 GB.Four chips of NVIDIA QUADRO FX 3700 graphic card,with video memory of 512 MB,core frequency of 500 MHz, are chosen and driver version is 6.14.11.9038.OS is Windows Server 2003 X64.Statistics is done based on different number of GPUs for comparison use.

5.2 Experiment and data analysis

In this paper the grid generation project[21-23]in computational fluid dynamics is used to test the practicability of linear and nonlinear solvers.A NACA0012 airfoil is utilized in the numerical experiment in Fig.5.T he speed up ratio in different scales is tested.Using same solvers,an O-type grid is generated for a cross-section out of a F6 body-wing configuration with more industrial interests in Fig.6 to ensure the correctness of solvers.

5.3 Linear solver

Fig.5 Grids around NACA0012airfoil

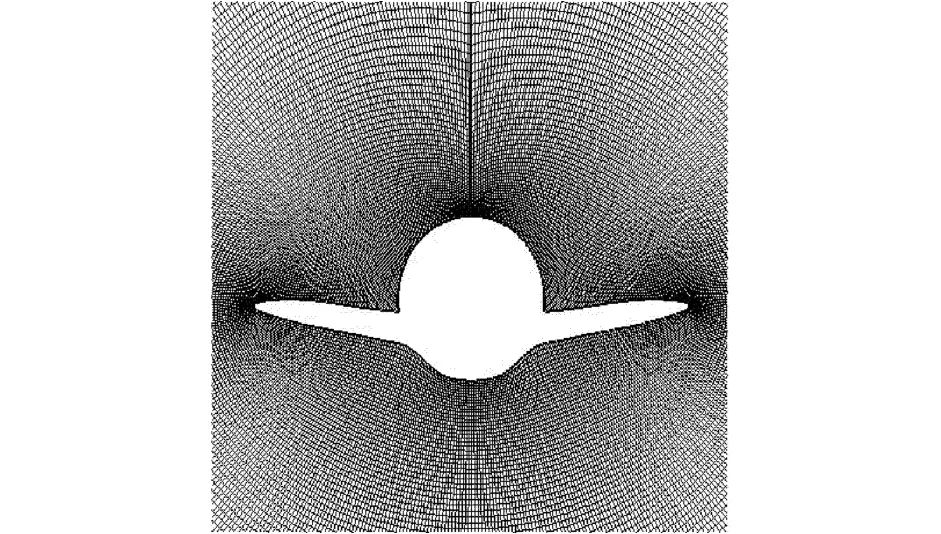
Fig.6 Grids around cross-section out of F6 body-wing

T he average time cost of one iteration in linear solver versus the number of variables on one,two and four GPUs is shown in Fig.7.In this grid generation project,the coefficient matrix is non-symmetric with a maximum row length of nine elements.

Fig.7 Time per step versus number of variables

The factors impacting on one iteration time cost are mainly the data exchanging between the host memory(memory)and the device memory(video memory),the utilization ratio of GPU units and the consumption of synchronization.With the enlargement of scales the multiprocessors are given more data blocks and utilization ratio of GPU rises correspondingly.When there is sufficient computing time,the consumption of data exchanging and synchronization become insignificance.T he limitation scale of gird generation problem on one GPU is about 2 800 000,so the speed up ratios of multi-GPUs are calculated under this limitation . When scale is below 2 000 000,there are only a few GPU resources utilized for two GPUs and four GPUs cases,so the scale-dependent blocking process will induce some fluctuation in the speed up ratio calculations in Fig.8.For instance,when scale is 1 605 632,the speed up ratio is relatively low compared with the results of other scales.In spite of this fluctuation,the rising trend of speed up ratio is evident and the stable ratios are:Two GPUs speed up one GPU by 1.5 and four GPUs by 2.2 as shown in Fig.8.

Fig.8 Linear solver speed up ratio of multi-GPUs to single-GPU

5.4 Nonlinear solver

In each iteration ofthe Inexact Newton method for nonlinear solver,the coefficient matrix is generated and a system of linear equations is solved.T ime consumptions of the two parts are compared in Fig.9:T he time cost of matrix generation and preconditioning time is 9%of the time of one loop of linear solving step.This test is specially taken on two NVIDIA T esla C1060 GPUs with lager video memory to illustrate the result of wild range of variable numbers.It also implies that Jacobi preconditioner fits the multi-GPUs solvers well.

Fig.9 Time consumptions per linear solve step and matrix generation versus number of variables

T he average time cost of one iteration in nonlinear solver versus the variable number on one,two and four GPUs is shown in Fig.10.Similar to the linear case,the speed up ratio rises with the enlargement of scales.The stable ratios are that two GPUs speed up one GPU by 1.6 and four GPUs by 2.5 as shown in Fig.11.

Fig.10 Time per step versus number of variables

Fig.11 Nonlinear solver speed up ratio of multi-GPUs to single-GPU

6 CONCLUSION

In this paper,multi-GPUs linear and nonlinear solvers using the PBi-CGstab method with Jacobipreconditionerand the InexactNewton method are proposed and computational fluid dynamics(CFD)grid is generated by the proposed methods.With multi-GPUs on board,engineering application problems with large scales are able to be solved.Multi-GPUs also provide excellent speed up to single-GPU.

T his paper focuses on managing GPUs on single board.It also can be anticipated that using the Ethernet network connecting computers with multi-GPUs on board can achieve huge computing capability.And with the development of GPU chip and GPGPU technique,more optimized solvers can be proposed.

[1] Luebke D,Mark H,Govidaraju N,et al.GPGPU:general-purpose computation on graphics hardware[C]∥Proceedings of the 2006 ACM/IEEE Conference on Supercomputing.New York,USA:Association forComputing Machinery,2006:10.114/1198555.1198765.

[2] Liu Y Q,Liu X H,Wu E H.Real-time 3D fluid simulation on GPU with complex obstacles[J].Journal of Software,2006,17(3):568-576.

[3] Zhou J F,Zhong C W,Xie J F,et al.Multiple-GPUs algorithm for lattice Boltzmann method[C]∥International Symposium on Information Science and Engineering.New York,USA:IEEE,2008:793-796.

[4] Krüger J,Westermann R.Linear algebra operators for GPU implementation of numerical algorithms[J].ACM T ransactions on Graphics,2003,22(3):908-916.

[5] Bolz J,Farmer I,Grinspun E,et al.Sparse matrix solvers on the GPU:conjugate gradients and multigrid[J].ACM Transactions on Graphics,2003,22(3):917-924.

[6] Buatois L,Caumon G,Levy B.Concurrent number cruncher:a GPU implementation of a general sparse linear solver[J].International Journal of Parallel,Emergent and Distributed Systems,2009,24(3):205-223.

[7] Cevahir A,Nukada A,Matsuoka S.Fast conjugate gradients with multiple GPUs[C]∥Computational Science, ICCS.Heidelberg,Germany:Springer,2009,5544:893-903.

[8] Liu S,Zhong C W,Chen X P,et al.A GPU implementation of fast solver for large scale nonlinear e-quations[C]∥2010International Colloquium on Computing,Communication,Control,and Management. Hongkong, China: Intelligent Information T echnology Application Research Association,2010:23-26.

[9] NVIDIA Corporation.NVIDIA CUDA compute unified device architecture programming guide[EB/OL].www.nvidia.com,2009.

[10]Van der Vorst H A.A fast and smoothly converging variant of BI-CG for the solution of nonsymmetric linear systems[J].SIAM Journal on Scientific and Statistical Computing,1992,13(2):631-644.

[11]Saad Y,Schultz M H.GMRES:a generalized minimal residual algorithm for solving nonsymmetric linear systems[J].SIAM Journal on Scientific and Statistical Computing,1986,7(3):856-869.

[12]Sogabe T,Sugihara M,Zhang S L.An extension of the conjugate residual method to nonsymmetric linear systems[J].Journal of Computational and Applied M athematics,2009,226:103-113.

[13]Mansfield L.Damped jacobi preconditioning and coarse grid deflation for conjugate gradient iteration on parallel computers[J].SIAM Journal on Scientific and Statistical Computing,1991,12(6):1314-1323.

[14]Fokkema D R,Sleijpen G L G,Van der Vorst H A.Accelerated inexact Newton schemes for large systems of nonlinear equations[J].SIAM Journal on Scientific,1998,19(2):657-674.

[15]Martí nez J M,Qi L.Inexact Newton methods for solving nonsmooth equations[J].Journal of Computational and Applied Mathematics,1995,60(1/2):127-145.

[16]Kalashnykova N I,Kalashnikov V V,Franco A A.Inexact Newton algorithm to solve nonlinear complementarity problems[C]∥8th International Conference on Intelligent Systems Design and Applications,ISDA.T aiwan China:[s.n.],2008,3:67-71.

[17]Elias R N,Coutinho A L G A,M artins M A D.Inexact Newton-type methods for non-linear problems arising from the SU PG/PSPG solution of steady incompressible navier-stokes equations[J].Journal of the Brazilian Society of Mechanical Sciences and Engineering,2004,26(3):330-339.

[18]Rizzoli V,M astri F,Cecchetti C,et al.Fast and robust Inexact Newton approach to the harmonic-balance analysis of nonlinear microwave circuits[J].IEEE M icrowave and Guided Wave Letters,1997,7(10):359-361.

[19]Hwang F N,Cai X C.A parallel nonlinear additive Schwarz preconditioned inexact Newton algorithm for incompressible Navier-Stokesequations[J].Journal of Computational Physics,2005,204(2):666-691.

[20]Harris M.Optimizing parallel reduction in CUDA[EB/OL].http:∥www.nvidia.com,2007/2010-9.

[21]Sorenson R L.A computer program to generate two-dimensional grids about airfoils and other shapes by the use of poisson′s equation[R].NASA TM 81198,1980.

[22]Zhang Z,Tsai H M.Comparison of Eca′s method with Hilgenstock′s method in 2-D grid generation[C]∥10th ISGG Conference on Numerical Grid Generation.New York,USA:Curran Associates Inc.,2007:59-75.

[23]T hompson J F,Weatherill N P.Aspects of numerical grid generation:current science and art[R].AIAA-93-3539-CP,1993.