一類新廣義Jordan(α,β)-導(dǎo)子的刻畫

杜衛(wèi)平,王素芹

(陜西職業(yè)技術(shù)學(xué)院計算機(jī)科學(xué)系,陜西西安 710100;2.棗莊三中,277160)

一類新廣義Jordan(α,β)-導(dǎo)子的刻畫

杜衛(wèi)平1,王素芹2

(陜西職業(yè)技術(shù)學(xué)院計算機(jī)科學(xué)系,陜西西安 710100;2.棗莊三中,277160)

設(shè)Tn(R)是一個含單位元的可交換環(huán)R上的上三角形矩陣代數(shù),M是Tn(R)的-雙模,引進(jìn)了廣義Jordan (α,β)-導(dǎo)子,刻畫了上三角形矩陣代數(shù)上的廣義Jordan(α,β)-導(dǎo)子的特征性質(zhì).

導(dǎo)子;廣義(α,β)-導(dǎo)子;廣義Jordan(α,β)-導(dǎo)子.＊

0 引言及預(yù)備知識

導(dǎo)子和廣義Jo rdan導(dǎo)子在代數(shù)上是一個重要的課題,本文在文獻(xiàn)[1]的基礎(chǔ)上,引進(jìn)了另外一類廣義Jo rdan(α,β)-導(dǎo)子的概念,并且刻畫了上三角形矩陣代數(shù)上的廣義Jo rdan(α,β)-導(dǎo)子的特征性質(zhì),為了敘述的方便,我們給出以下概念:

設(shè)R是一個含單位元的可交換環(huán),A是環(huán)上的含單位元I的代數(shù),M是A的-雙模,我們稱一個從A到M上的映射Δ是R-線性的,即對任意的r∈R,a,b∈A,我們有Δ(a+ b)=Δ(a)+Δ(b),Δ(ra)=rΔ(a),設(shè)α,β是A上的自同構(gòu).本文假設(shè)所有的雙模M都是2-非撓的.

定義:(1)設(shè)φ:A→M是一個R-線性映射,如果對任意的a,b∈A有φ(ab)= φ(a)β(b)+α(a)φ(b),則稱φ是(α,β)-導(dǎo)子.

(2)設(shè)φ:A→M是一個R-線性映射,如果對任意的a,b∈A有φ(ab)=φ(a)β(b) +α(a)(b),則稱φ是廣義(α,β)-導(dǎo)子,其中是(α,β)-導(dǎo)子.

(3)設(shè)δ:A→M是一個R-線性映射,如果對任意的a,b∈A有δ(ab)=δ(b)β(a) +α(b)(a),則稱是廣義(α,β)-反導(dǎo)子,其中是(α,β)-反導(dǎo)子.

(4)設(shè)Δ:A→M是一個R-線性映射,如果對任意的

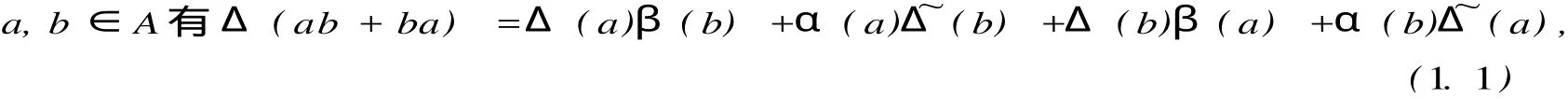
1 主要結(jié)論

引例1.1 設(shè)Δ是一個-線性映射,下列命題是等價的

(1)Δ是廣義Jo rdan(α,β)-導(dǎo)子;

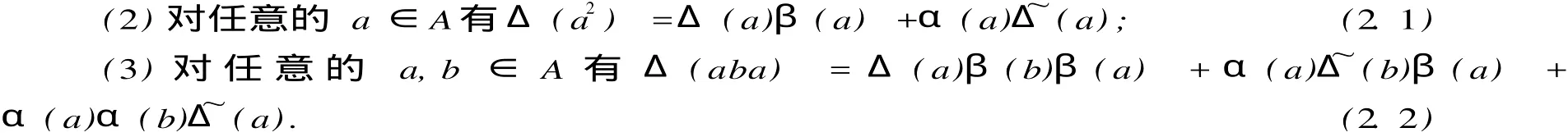
證明 (1)?(2),令a=b,我們就得到(2.1),因為所有的模都假設(shè)是2-非撓的. (2)?(1),假設(shè)Δ(a2)=Δ(a)β(a)+α(a)(a),那么

(1)?(3),假設(shè)Δ是廣義Jo rdan(α,β)-導(dǎo)子,那么

由(2.5),(2.6)展開可知(2.2)成立.

(3)?(2),令b=I知(2.1)成立,這樣引理2.1成立.

由引理2.1知,假設(shè)ab=ba=0,

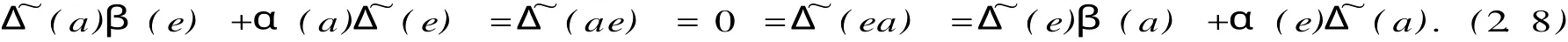
設(shè)Tn(R)是一個含單位元的可交換環(huán)R上的上三角形矩陣代數(shù),M是Tn(R)的-雙模,若Δ:Tn(R)→M是廣義Jo rdan(α,β)-導(dǎo)子,令eij∈Tn(R),且eij表示第(i,j)個元素為1其余元素均為0的n×n矩陣.由(2.7)我們得到下面兩個式子

對任意的1≤i

并且當(dāng)k,j≠i時,由(2.8)知

根據(jù)(2.9)我們得到φ(eii)=Δ(eii),1≤i≤n.

引例1.2 線性映射φ:Tn(R)→M是廣義(α,β)-導(dǎo)子.

情形1 j≠k時,那么φ(eijekl)=0,我們只要證明φ(eij)β(ekl)+α(eij)?φ(ekl)=0.由(2.12)知

若i≠k時,那么由(2.11)知上式等于α(eii)[(eij)β(ekk)+α(eij)(ekk)]β(ekl)= 0.

若i=k時,

這樣情形(1)成立.

情形2 j=k時,我們需要證明

若i

若i=j

若i

若i=j=l時,那么φ(eii)=Δ(eii)=Δ(eii)β(eii)+α(eii)(eii)=φ(eii)β(eii)+ α(eii)(eii).

這樣對所有的i≤j,k≤l我們有φ(eijekl)=φ(eij)β(ekl)+α(eij)(ekl).對任意的a,b∈Tn(R),設(shè)a=aijeij,b=bklekl,其中aij,bkl∈R易證φ(ab)=φ(a)β(b)+ α(a)(b).所以φ是廣義(α,β)-導(dǎo)子,這樣引理2.1成立.令δ=Δ-φ,則δ(eij)= Δ(eij)-φ(eij),并且δ(eii)=Δ(eii)-φ(eii)=0,所以δ(Dn)=0.其中Dn是對角矩陣.

引例1.3 線性映射δ:Tn(R)→M是一個廣義(α,β)-反導(dǎo)子,并且δ(Dn)=0.

證明 我們已經(jīng)知道δ(Dn)=0,由(2.10)與(2.12)知,當(dāng)i

所以δ(eij)=Δ(eij)β(eii)+α(eij)(eii)=(φ(eij)+δ(eij))β(eii)+α(eij)(eii)+ δ?(eii))

=φ(eij)β(eii)+δ(eij)β(eii)+α(eij)(eii)+α(eij)(eii)=φ(eijeii)+δ(eij)β(eii)

=δ(eij)β(eii).由δ是廣義Jo rdan(α,β)-導(dǎo)子知

所以

我們要證明δ是廣義(α,β)-反導(dǎo)子,只要證明對任意的i≤j,k≤l都有δ(eijekl)=

成立即可.

情形1 j≠k時,那么δ(eijekl)=0我們只需證明δ(ekl)β(eij)+α(ekl)(eij)=0.

若i=k并且j=l時,那么由δ也是廣義Jo rdan(α,β)-導(dǎo)子知δ(eijeij)=δ(eij)β(eij) +α(eij)(eij)=0.若i≠k并且j≠l時,那么

若i=k并且j≠l時,由(2.14)和(2.16)知

若i≠k并且j=l時,由(2.14)和(2.16)知

知δ(ekj)β(eij)+α(ekj)(eij)=α(ekj)(eij)=α(ekk)(ekjeij+eijekj)=α(ekk)(eij)=0.

情形2 j=k時,若i=j=l,那么δ(eii)=0=δ(eii)β(eii)+α(eii)(eii).

若i

那么δ(ejl)β(eij)+α(ejl)?δ(eij)=δ(ejl)β(ejj)β(eij)+α(ejl)α(ejj)(eij)=0,

又因為δ(eil)=δ(eijejl+ejleij)=δ(eij)β(ejl)+α(eij)?δ(ejl)+δ(ejl)β(eij)+ α(ejl)?δ(eij)

=δ(eij)β(eii)β(ejl)+α(eij)α(ell(ejl)+δ(ejl)β(ejj)β(eij)+α(ejl)α(ejj)(eij)=0.

所以δ(ejl)β(eij)+α(ejl)(eij)=0=δ(eil).所以由情形1,情形2知(2.15)成立.

所以δ是一個廣義(α,β)-反導(dǎo)子.

定理1.4 如果Δ:Tn(R)→M是一個廣義Jo rdan(α,β)-導(dǎo)子,則它可以分解成一個廣義(α,β)-導(dǎo)子φ和一個廣義(α,β)-反導(dǎo)子δ之和,即Δ=φ+δ,其中δ(Dn)= 0.

證明:由引理(2.2)和(2.3)即可證明.

推論1.5 如果Δ:Tn(R)→M是一個廣義Jo rdan(α,α)-導(dǎo)子,則它可以分解成一個廣義(α,α)-導(dǎo)子φ和一個廣義(α,α)-反導(dǎo)子δ,即Δ=φ+δ,其中δ(Dn)=0.

[1]孫亮吉,吉國興.上三角形矩陣代數(shù)上的Jordan導(dǎo)子和廣義Jordan導(dǎo)子[J].山東大學(xué)學(xué)報(理學(xué)版),2007,10:100 -105.

[2]孫亮吉,廣義Jordan-導(dǎo)子和Jordan-同態(tài)的穩(wěn)定性的刻畫[J].山東大學(xué)學(xué)報(理學(xué)版),2008,12:77-79.

[3]FeiMa,Guoxing Ji.Generalized Jordan derivations on triangular matrix algebras[J].Linear and multilinear Algebra, 2007,55:355-363.

[4]D.Benkovic.Jordan derivations and an tiderivations on triangular matrices[J].Linear Algebra Appl,2005,397:235-244.

[5]M.Brecar.Jordan derivationson semi prime rings[J].Algebra1989,127:218-228.

Abstract:Let R be a commutative ring and let Tn(R)be an upper triangular matrix algebra over R,the concept of generalized Jordan(α,β)derivation is introduced and the properties of generalized Jordan(α,β)-derivation on upper triangular matrix algebras.

Keywords:Derivation;Generalized(α,β)-derivation;Generalized Jordan(α,β)-antiderivation.

Characterizations of a New Generalized Jordan Derivation

DUWei-ping;WANG Su-qin
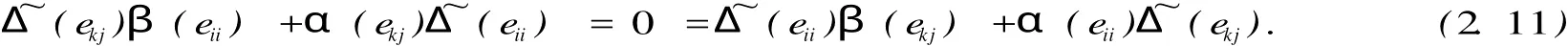
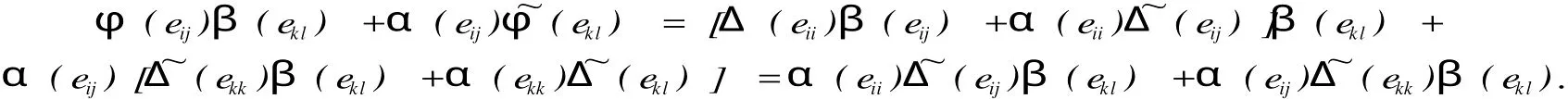
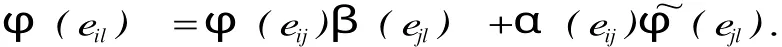
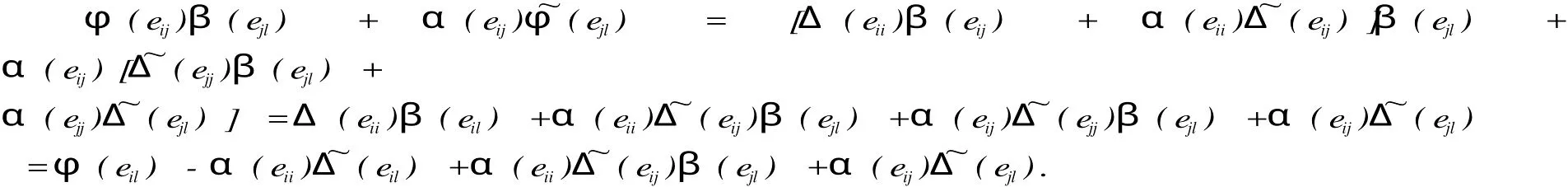
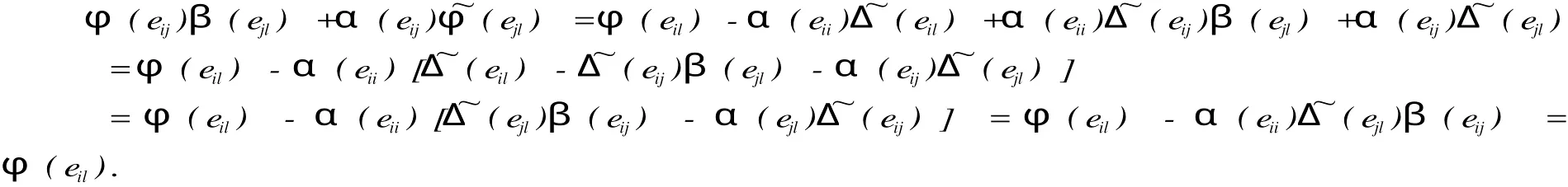
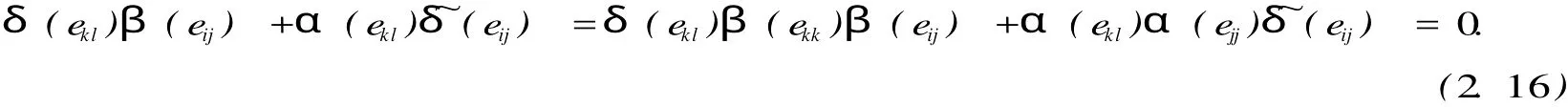
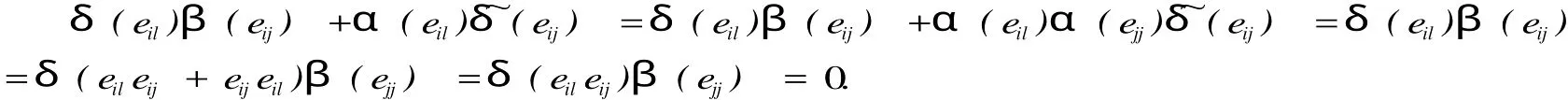
(Computer Science Department,Shaanxi Insititute of Ocational and Technical, X i’an 710100,China)

O 177

A

1004-7077(2010)02-0019-04

2009-11-28

杜衛(wèi)平(1979-),男,山東棗莊人,講師,碩士,主要研究方向為算子代數(shù).

[責(zé)任編輯:陳慶朋]