有限群的可補(bǔ)置換子群與 p-冪零性

晁 芳, 郭秀云

(上海大學(xué) 理學(xué)院,上海 200444)

有限群的可補(bǔ)置換子群與 p-冪零性

晁 芳, 郭秀云

(上海大學(xué) 理學(xué)院,上海 200444)

有限群 G的子群 H稱為 G的 SS-擬正規(guī)子群,如果存在 G的子群 B,使得 G=HB且對(duì) B的每個(gè) Sylow子群 Q,都有 HQ=QH.利用冪指數(shù)等于 Sylow p-子群冪指數(shù)的交換 p-子群的 SS-擬正規(guī)性,來研究有限群的 p-冪零性,推廣和改進(jìn)了一些已有的結(jié)果.

有限群;SS-擬正規(guī)子群;p-冪零群

Abstract:A subgroup H of a finite group G is said to be SS-quasinormal in G if there existsa subgroup B of G such that G=HB and H permutesw ith every Sylow subgroup of B.In thispaper,some conditions for a finite group to be p-nilpotent are given using SS-quasinormality of some abelian subgroup sw ith p rime power order,and several known results are generalized and improved.

Key words:finite group;SS-quasinormal subgroups;p-nilpotent groups

本研究所涉及的群均為有限群,采用標(biāo)準(zhǔn)記號(hào).利用子群的某些性質(zhì)來研究群的結(jié)構(gòu)是許多群論學(xué)者感興趣的課題.群 G的一個(gè)子群 H稱為 G的 S-擬正規(guī)子群,如果對(duì) G的每個(gè) Sylow子群 Q,都有 HQ=QH.自 1962年 Kegel[1]引入這一概念以來,許多研究人員應(yīng)用這一概念研究有限群的結(jié)構(gòu)[2-6].為進(jìn)一步拓廣這方面的研究,Li等[7]又引進(jìn)一個(gè)新的概念——SS-擬正規(guī)子群,即群 G的子群 H稱為 G的SS-擬正規(guī)子群,如果存在 G的子群 B,使得 G=HB且對(duì) B的每個(gè) Sylow子群 Q,都有 HQ=QH.Li等[7-8]運(yùn)用 Sylow子群的極大與極小子群的 SS-擬正規(guī)性研究有限群的結(jié)構(gòu),獲得許多有意義的結(jié)果.本工作主要研究素?cái)?shù)冪階子群的 SS-擬正規(guī)子群對(duì)有限群結(jié)構(gòu)的影響,其中著重考慮與 Sylow子群的冪指數(shù)相同的交換子群的 SS-擬正規(guī)性.

1 預(yù)備知識(shí)

為引用方便,本節(jié)給出 SS-擬正規(guī)子群的一些基本性質(zhì)和重要引理.

引理 1[7]設(shè) K為群 G的一個(gè)子群,N為群 G的一個(gè)正規(guī)子群,H為群 G的一個(gè) SS-擬正規(guī)子群,那么

(1)如果 H≤K,則 H為 K的 SS-擬正規(guī)子群;

(2)HN/N為 G/N的 SS-擬正規(guī)子群;

(3)如果 N≤K且 K/N是 G/N的 SS-擬正規(guī)子群,則 K為 G的 SS-擬正規(guī)子群.

引理 2[7]設(shè) P為群 G的一個(gè) p-子群,則下列條件等價(jià):

(1)P為 G的 S-擬正規(guī)子群;

(2)P≤F(G)且 P為 G的 SS-擬正規(guī)子群.

引理 3[7]設(shè) P為群 G的一個(gè) p-子群且 P為群G的 SS-擬正規(guī)子群,則對(duì) G的每個(gè) Sylow q-子群Q(q≠p),都有 PQ=QP.

引理 4[9]設(shè) H為群 G的一個(gè) p-子群且 H為 G的 S-擬正規(guī)子群,則 Op(G)≤NG(H).

引理 5[10](Burnside定理)設(shè) p為群 G的階的最小素因子,P為群 G的一個(gè) Sylow p-子群且 P為循環(huán)群,則 G有正規(guī) p-補(bǔ).

2 主要結(jié)果

首先考慮 p為群 G的階的最小素因子的情況.

定理 1 設(shè) p為群 G的階的最小素因子,P為群G的一個(gè) Sylow p-子群且 exp P=pe(e≥1).若F={H|H≤P,H′=1,exp H=pe}中的每一元都是 G的SS-擬正規(guī)子群,則 G為 p-冪零群.

證明 假設(shè)定理不真,G是一個(gè)極小階反例.

顯然 T′≤Op′(G). 又 T為 p-群 ,從而 T′=1.注意到exp T =exp T=pe,即 T∈F.由定理假設(shè)條件可知,T為 G的 SS-擬正規(guī)子群.再由引理 1知,T為 G的SS-擬正規(guī)子群.G的選擇隱含著 G/Op′(G)為 p-冪零群,從而 G為 p-冪零群,矛盾.

(2)任取 F中的一元 H,則 Op(G)≤CG(H).

令 Q為 G的任意 Sylow q-子群 (q≠p).由定理假設(shè)條件可知,H為 G的 SS-擬正規(guī)子群.由引理 3得 HQ=QH,即 HQ為群 G的一個(gè)子群.又 H為交換p-子群,則 H可由 H中最高階元素生成,設(shè) H=〈a1,a2,…,as〉,其中 o(ai)=pe,i=1,2,…,s.由假設(shè)及引理 3知 ,〈ai〉Q=Q〈ai〉. 由引理 5可得 ,〈ai〉Q=

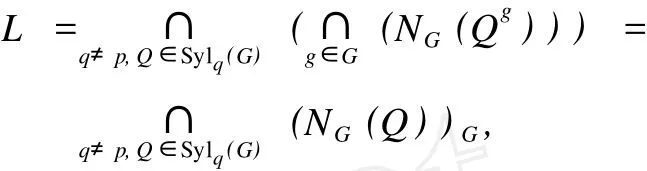
顯然 L?—G且 L∩Q?—L.注意到 L∩Q≤Op′(L)≤Op′(G)=1,故 L為 p-群.另一方面 ,顯然有 H≤L,從而 H≤L≤Op(G).H為 G的 S-擬正規(guī)子群,故 H次正規(guī)于 HQ,從而 HQ=H ×Q,故Op(G)≤CG(H).

(3)最后的矛盾.

取 F中階最大的一元 H,由 (2)可得,Op(G)≤CG(H).

假設(shè) CG(H)≠G,由于 P1=P∩CG(H)為CG(H)的 Sylow p-子群且 exp P1=pe,令

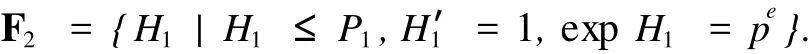
由假設(shè)及引理 1知,F2中每一元都是 CG(H)的SS-擬正規(guī)子群,所以 CG(H)滿足定理假設(shè),G的選擇隱含著 CG(H)為 p-冪零群,從而 Op(G)為 p-冪零群,由此即得 G為 p-冪零群,矛盾.

假設(shè) CG(H)=G,這時(shí) H≤Z(G),由 H的選擇隱含著 P≤Z(G),故 NG(P)=CG(P).由引理 5知G為 p-冪零群,矛盾.

由定理 1,有如下推論.

推論 1 設(shè) G為一個(gè)群,π(G)={p1,p2,…,pn},其中 p1>p2>… >pn.Pi為群 G的一個(gè) Sylow pi-子群且 exp Pi=pei,i=2,3,…,n.若 Fi={H|H≤Pi,H′=1,exp H=(pi)ei}(i=2,3,…,n)中每一元都是 G的 SS-擬正規(guī)子群,則 G為 Sylow塔群.

證明 由定理 1知 G為 pn-冪零群.設(shè) K為 Pn在群 G中的正規(guī) pn-補(bǔ).由歸納法知 K為 Sylow塔群,因此,G為 Sylow塔群.

推論 2 設(shè) p為群 G的階的最小素因子,N?—G,P為群 N的一個(gè) Sylow p-子群且 exp P=pe(e≥1),G/N為 p-冪零群.若 F={H|H≤P,H′=1,exp H=pe}中每一元都是 G的 SS-擬正規(guī)子群,則 G為 p-冪零群.

證明 假設(shè)定理不真,G是一個(gè)極小階反例.由定理 1知 N為 p-冪零群,從而由定義可知,N存在正規(guī) p-補(bǔ)子群 K.假設(shè) K≠1,考慮G=G/K,則P=PK/K為G的 Sylow p-子群且 exp P=pe.G/K/N/K?G/N為 p-冪零群.令

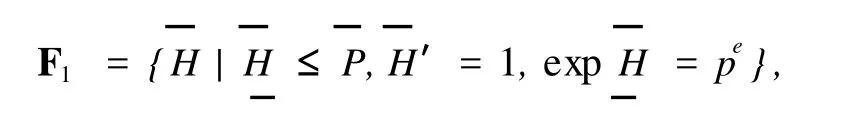
任取 F1中一個(gè)元T,則存在 T≤P,使T=TK/K.由于

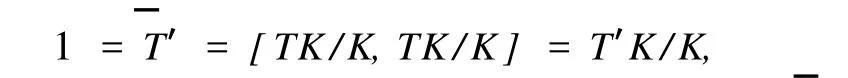
顯然 T′≤K.又 T為 p-群,從而 T′=1.注意到 exp T=exp T=pe,即 T∈F.由定理假設(shè)條件可知,T為 G的SS-擬正規(guī)子群.再由引理 1可知,T 為G的 SS-擬正規(guī)子群.G的選擇隱含著 G/K為 p-冪零群,從而 G為 p-冪零群,矛盾.

若 K=1,此時(shí) P=N,即 N為 p-群.若 N為 G的Sylow p-子群,根據(jù)定理 1可知,G為 p-冪零群,矛盾.若 N不為 G的 Sylow p-子群,設(shè) M/N為 G/N的正規(guī) p-補(bǔ).由歸納假設(shè),M為 p-冪零群.令 M1為 M的正規(guī) p-補(bǔ),從而M1也為 G的正規(guī) p-補(bǔ) ,即 G為 p-冪零群,矛盾.

下面考慮另一種情況,設(shè) P為 p-群,記

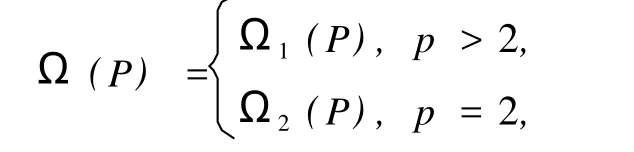
其中

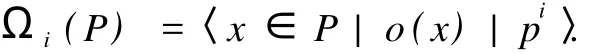
定理 2 設(shè) p為群 G的階的最小素因子,P為群G的一個(gè) Sylow p-子群,且 expΩ(P)=pe(e≥1).若F={H|H≤Ω(P),H′=1,exp H=pe}中每一元都是G的 SS-擬正規(guī)子群,則 G為 p-冪零群.

證明 假設(shè)定理不真,G是一個(gè)極小階反例

(2)任取 F中一元 H,有 Op(G)≤NG(H).

令 Q為 G的任意 Sylow q-子群 (q≠p).由定理假設(shè) H為 G的 SS-擬正規(guī)子群,根據(jù)引理 3可得HQ=QH,從而 HQ為群 G的子群.

又 H為交換 p-子群,則 H可由 H中最高階元素生成,設(shè) H=〈a1,a2,…,as〉,其中 o(ai)=pe,i=1,2,…,s.由假設(shè)及引理 3知 ,〈ai〉Q=Q〈ai〉. 再根據(jù)引理 5,〈ai〉Q=〈ai〉|×Q,進(jìn)一步有 HQ=H|×Q.令

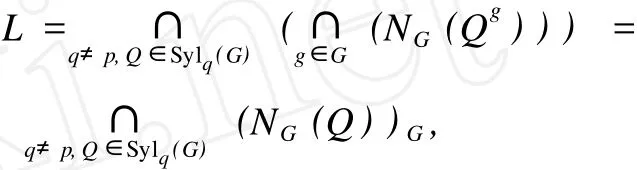
顯然 L?—G且 L∩Q?—L.注意到 L∩Q≤Op′(L)≤Op′(G)=1,知 L為 p-群.另一方面顯然有 H≤L,從而 H≤L≤Op(G).根據(jù)引理 2知,H為 G的 S-擬正規(guī)子群,Op(G)≤NG(H).

(3)最后的矛盾.

由 (2)知,Op(G)≤NG(H),有 HOp(G)≤NG(H)≤G.

(i)首先考慮 HOp(G)≤NG(H)

令 P1=P∩HOp(G),P1為 HOp(G)的一個(gè) Sylow p-子群.從而 P1≤P∩HOp(G)≤P,expΩ(P1)=pe.下面考慮

F2={H1|H1≤Ω(P1),H′1=1,exp H1=pe},任取 F2中一元 T,顯然 T∈F,從而 T為 G的 SS-擬正規(guī)子群.利用引理 1可得,T為 HOp(G)的 SS-擬正規(guī)子群.由歸納法可知,HOp(G)滿足定理假設(shè),因此HOp(G)為 p-冪零群.令 K為 HOp(G)的正規(guī) Hall p′-子群 ,則 K也為 Op(G)的正規(guī) Hall p′-子群.

因?yàn)?K為 Op(G)的特征子群,所以 K?—G.顯然G/Op(G)為 p-群 ,從而 K為 G的正規(guī) Hall p′-子群 ,于是 G為 p-冪零群,矛盾.

(ii)其次考慮 NG(H)=G.

假設(shè) G不是 p-冪零群,由 Frobenius定理知,存在 G的一個(gè)非平凡 p-子群 L,使得 NG(L)/CG(L)不為 p-群.由 Sylow定理,可以假設(shè) L≤P且 r為群 NG(L)的階的任意一個(gè)素因子 (r≠p).考慮群 NG(L)的任一 Sylow r-子群 R,顯然 R正規(guī)化 L.又Ω(L)為L的特征子群,從而 Ω(L)?—NG(L),故Ω(L)R為NG(L)的子群,進(jìn)一步可知,HΩ(L)R為群 G的子群.由定理 1知,HΩ(L)R有正規(guī) p-補(bǔ),從而Ω(L)R有正規(guī) p-補(bǔ).

因?yàn)棣?L)R有正規(guī) p-補(bǔ) R,且 R正規(guī)化Ω(L),所以Ω(L)R=Ω(L)×R.根據(jù)文獻(xiàn) [10]第Ⅶ章的定理 4.3,R中心化 L,因此,對(duì)于群 NG(L)的階的任意素因子 r(r≠p),群 NG(L)的每一個(gè) Sylow r-子群都中心化 L,于是 NG(L)/CG(L)為 p-群,G為 p-冪零群,矛盾.

由定理 2,有如下推論.

推論 3 設(shè) G為一個(gè)群且π(G)={p1,p2,…,pn},其中 p1>p2>…>pn.又設(shè) Pi為群 G的一個(gè)Sylow pi-子群且 expΩ(Pi)=(pi)ei,i=2,3,…,n.若 Fi={H|H≤Ω(Pi),H′=1,exp H=(pi)ei}(i=2,3,…,n)中每一元都是 G的 SS-擬正規(guī)子群,則 G為Sylow塔群.

證明 設(shè) K為 Pn在群 G中的正規(guī) pn-補(bǔ),由歸納法可知,K為 Sylow塔群,因此 G也為 Sylow塔群.

推論 4 設(shè) p為群 G的階的最小素因子,N?—G,P為群 N的一個(gè) Sylow p-子群,且 expΩ(P)=pe(e≥1),G/N為 p-冪零群.若 F={H|H≤Ω(P),H′=1,exp H=pe}中每一元都是 G的 SS-擬正規(guī)子群 ,則 G為 p-冪零群.

證明 類似推論 3可證.

[1] KEGEL H O. Sylow-Gruppen and subnormalteiler endlicher Gruppen[J].Math Z,1962,78:205-221.

[2] SHAALAN A.The influence of S-quasinormality of some subgroup s[J].Acta Math Hungar,1990,56:287-293.

[3] PETER S.Subgroupspermutablewith all sylow subgroups[J].Journal of Algebra,1998,207:285-293.

[4] RAMADAN M.The influence of S-quasinormality of some subgroup s of prime power order on the structure of finite groups[J].Arch Math,2001,77:143-148.

[5] BALLESTER-BOL INCHES A,PEDRAZA-AGUILERA M C.Sufficient conditions for super-solvability of finite groups[J].Pure App l Algebra,1998,127:113-118.

[6] ASAAD M,RAMADAN M,SHAALAN A.Influence ofquasinormality on maximal subgroupsof Sylow subgroups of fitting subgroup of a finite group[J].Arch Math,1991,56:521-527.

[7] L I SR,SHEN Z C,L IU J J,et al.The influence of SS-quasinormality of some subgroups on structure of finite groups[J].Journal of Algebra,2008,319:4275-4287.

[8] L I S R,SHEN Z C,KONG X H.On SS-quasinorma subgroup s of finite group s[J]. Communications in Algebra,2008,36:4436-4447.

[9] DESKINS E W.On quasinormal subgroups of finite groups[J].Math Z,1963,82:125-132.

[10] 徐明曜.有限群導(dǎo)引[M].北京:科學(xué)出版社,2001.

(編輯:孟慶勛)

SS-quasinormality of Subgroupsand the p-n ilpotency of Fin ite Groups

CHAO Fang, GUO Xiu-yun
(College of Sciences,ShanghaiUniversity,Shanghai200444,China)

O 152.1

A

1007-2861(2010)04-0376-04

10.3969/j.issn.1007-2861.2010.04.009

2009-06-03

國家自然科學(xué)基金資助項(xiàng)目(10771132);高等學(xué)校博士點(diǎn)基金資助項(xiàng)目 (200802800011);上海大學(xué)研究生創(chuàng)新基金資助項(xiàng)目(SHUCX092004)

郭秀云 (1956～),男,教授,博士生導(dǎo)師,博士,研究方向?yàn)橛邢奕?E-mail:xyguo@shu.edu.cn