On the improved dynamics approach in loop quantum black holes

Hongchao Zhang,Wen-Cong Gan,Yungui Gong and Anzhong Wang

1 Institute for Theoretical Physics &Cosmology,Zhejiang University of Technology,Hangzhou,310023,China

2 United Center for Gravitational Wave Physics(UCGWP),Zhejiang University of Technology,Hangzhou,310023,China

3 College of Physics and Communication Electronics,Jiangxi Normal University,Nanchang 330022,China

4 GCAP-CASPER,Physics Department,Baylor University,Waco,TX 76798-7316,United States of America

5 School of Physics,Huazhong University of Science and Technology,Wuhan,Hubei 430074,China

6 Department of Physics,School of Physical Science and Technology,Ningbo University,Ningbo,Zhejiang 315211,China

Abstract In this paper,we consider the B?hmer–Vandersloot (BV) model of loop quantum black holes obtained from the improved dynamics approach.We adopt the Saini–Singh gauge,in which it was found analytically that the BV spacetime is geodesically complete.We show that black/white hole horizons do not exist in this geodesically complete spacetime.Instead,there exists only an infinite number of transition surfaces,which always separate trapped regions from antitrapped ones.Comments on the improved dynamics approach adopted in other models of loop quantum black holes are also given.

Keywords: loop quantum gravity,black hole,dynamics approach

1.Introduction

In Einstein’s general relativity (GR),two different kinds of spacetime singularities appear,one is the Big Bang singularity of our universe,and the other is the internal singularity of a black hole.It is commonly understood that the spacetime curvatures become Planckian when very closed to these singularities,and GR ceases to be valid,as quantum gravitational effects in such small scales become important and must be taken into account.It is our cherished hope that these singularities will be smoothed out after such quantum effects are taken into account.

In the past two decades,it has been shown that this is indeed the case for the Big Bang singularity in the framework of loop quantum cosmology(LQC)[1–3].LQC is constructed by applying loop quantum gravity (LQG) techniques to cosmological models within the superminispace approach [4],and the resulting quantum corrections to classical geometry can be effectively described by semiclassical effective Hamiltonian that incorporate the leading-order quantum geometric effects[5].The effective model works very well in comparison with the full quantum dynamics of LQC even in the deep quantum regime[3],especially for the states that are sharply peaked on a classical trajectory at late times[6].LQC can resolve the Big Bang singularity precisely because of the fundamental result of LQG: quantum gravity effects always lead the area operator to have a non-zero minimal area gap[7].It is this non-zero area gap that causes strong repulsive effects in the dynamics when the spacetime curvature reaches the Plank scale and the big bang singularity is replaced by a quantum bounce [8].

The semiclassical effective Hamiltonian can be obtained from the classical one simply by the replacement

wherecdenotes the moment conjugate of the area operatorp(∝a2,whereais the expansion factor of the Universe),and μ is called the polymerization parameter.Clearly,when μ →0,the classical limit is obtained.While when μ ?0,the quantum gravitational effects become large,whereby a mechanism for resolving the Big Bang singularity is provided.In LQC,there exist two different quantization schemes,the so-called μoandschemes,which give different representations of quantum Hamiltonian constraints and lead to different effective dynamics[3].The fundamental difference of these two approaches rises in the implementation of the minimal area gap mentioned above.In the μoscheme,each holonomyhk(μ)is considered as an eigenstate of the area operator,associated with the face of the elementary cell orthogonal to thek-th direction.The parameter μ is fixed by requiring the corresponding eigenvalue to be the minimal area gap.As a result,μ is a constant in this approach[4]

However,it has been shown [9] that this quantization does not have a proper semiclassical limit,and suffers from the dependence on the length of the fiducial cell.It also lacks of consistent identified curvature scales.On the other hand,in thescheme[2],the quantization of areas is referred to the physical geometries,and when shrinking a loop until the minimal area enclosed by it,one should use the physical geometry.Since the latter depends on the phase space variables,now when calculating the holonomyhk(μ),one finds that the parameter μ depends on the phase space variablep[2]

In parallel to the studies of LQC,loop quantum black holes(LQBHs) have also been intensively studied in the past decade or so (See,for example,[10–15] and references therein.).In particular,since the spacetime of the Schwarzschild black hole interior is homogeneous and the metric is only time-dependent,so it can be treated as the Kantowski–Sachs spacetime

whereLodenotes the length of the fiducial cell in thex-direction,and dΩ2≡ dθ2+sin2θd?2.Then,some LQC techniques can be borrowed to study the black hole interiors directly.In particular,LQBHs were initially studied within the μoscheme[16–18].However,this LQBH model also suffers from similar limitations as the μoscheme in LQC [11,19,20].Soon thescheme was applied to the Schwarzschild black hole interior by B?hmer and Vandersloot (BV) [21] with the replacements

in the classical Hamiltonian,wherebandcare the moment conjugates ofpbandpc,with{c,pc}=2Gγ,{b,pb}=Gγ,and δband δcare the corresponding two polymerization parameters,given by [21]

To understand the quantum effects,let us first note that in the interior of the Schwarzschild black hole we have [22]

for which the black hole singularity is located atT=–∞,while its horizon is located atT≡ ln (2m).Thus,near the singular point we have δb∝e-T→∞,although δc∝eT/2→0.Then,we expect that the quantum effects become so large that the curvature singularity is smoothed out and finally replaced by a regular transition surface [21].On the other hand,near the black hole horizon,we haveand? 0,so that δc→∞(although now δbremains finite).Then,we expect that there are large departures from the classical theory very near the classical black hole horizon even for massive black holes,for which the curvatures at the horizon become very low [11,19–21].As a matter of fact,recently we found that the effects are so large that black/white horizons never exist in the BV model [22].

It should be noted that in [22],the lapse function was chosen asin which the coordinateTdoes not represent the cosmic time.Then,one may wonder ifTcovers the whole spacetime of the BV model.On the other hand,in [23] the proof that the BV model is geodesically complete was carried out in the cosmic time coordinate,in which the lapse function was set to one.In this paper,we shall adopt the Saini-Singh (SS) gauge,N=1,and show that indeed black/white horizons never exist in the BV model,as expected from what we obtained in [22],since the physics should not depend on the choice of the gauge.

The rest of the paper is organized as follows: in the next section,section 2,we first re-derive the corresponding field equations in the SS gauge,and correct typos existing in the literature.Then,we re-confirm the result obtained in[23]that the BV spacetime is geodesically complete even without matter.After that,from the definitions of black/white hole horizons we show explicitly that they do not exist in the BV model.Instead,there exist infinite regular transition surfaces that always separate a trapped region from an anti-trapped one.Finally,in section 3,we present our main conclusions and provide comments on other models of LQBHs,adopting thescheme.In particular,the models studied recently by Han and Liu [24,25] are absent of the above pathology.

2.BV model with SS gauge

To show our above claim,we first note that the Kantowski–Sachs metric (4) is invariant under the gauge transformations

via the redefinitions of the lapse function and the length of the fiducial cell,

wheref(τ) is an arbitrary function of τ,and α andxoare arbitrary but real constants.Using the above freedom,we can always choose the SS gauge [22]

For this particular choice of the gauge,we denote the timelike coordinateTby τ.Then,the corresponding effective BV Hamiltonian reads [23]

from which we find the equations of motion(EoMs)are given by

Note that in writing down the above equations,we had used the Hamiltonian constraintHeff≈0.It should be also noted that there exists a typo in the EoM ofc(τ)given in[23],where the last term should beinstead of[cf equation (3.6) of [23] and recall that now we consider the vacuum case ρ=0].From equations (14) and (15),we find that

within any given finite time τ [23].As a result,the range of τ ∈(–∞,∞)cover the whole spacetime,and the corresponding BV universe is geodesically complete in the (τ,x,θ,?)-coordinates.In particular,pc(τ=∞)=∞corresponds to the spacetime casual boundaries,and no extensions beyond it are needed.

In figures 1 and 2,we plot the four physical variables(b,c,pb,pc) for -3 ＜τ ＜415 andm/?pl=1 with the initial time being chosen at τi=-2.15018,and the initial data(b,c,pb,pc)as those given in [22].In order to compare the results obtained in this two papers,whereτT?1.11068corresponds to the location of the first transition surface of the BV model,and 0=to the location of the classical Schwarzschild black hole horizon.In particular,we find thatpcandpbare indeed finite and non-zero.This is true also forb,c,gxxand the Kretchmann scalarK≡RαβγδRαβγδ.When τ ?τi,we find thatpc(τ) is exponentially increasing.To monitor the numerical errors,we also plot outN2andHeff∣ ∣,from which one can see that ∣Heff∣ ≤6 ×10-12over the whole range of τ.To compare our results with those given in[21],in figure 3 we also plot out the corresponding physical quantities forτ＜τT.From it,it can be seen that our results match very well with those presented in[21].We also consider other choices of the mass parameter,and similar results are obtained.In review of all the above,one can see that our numerical code is quite trustable.

In the following,we shall show that in the geodesically complete BV model,black/white horizons never exist.Instead,only regular transition surfaces exist.To show these claims,let us first introduce the unit vectors,andThen,we construct two null vectorswhich define,respectively,the in-going and out-going radially-moving null geodesics.Then,the expansions of them are defined by [11]

wheremμν≡gμν+uμuν-sμsν.

Definitions[26–28]: a spatial 2-surfaceS is said untrapped,marginally trapped,trapped,or anti-trapped according to

A black(white)hole horizon is a marginally trapped that separates an untrapped region from a trapped one [26–28],while a transition surface is a marginally trapped that separates an anti-trapped region from a trapped one [11].

From equations (18) and (19) we can see that a black or white hole horizon does not exist,as now the BV spacetime is already geodesically complete,and no untrapped regions(Θ+Θ-＜0) in such a spacetime exist.However,transition surfaces could exist atpc,τ=0,and such surfaces shall always separate trapped(pc,τ＞0)regions from anti-trapped(pc,τ＜0)ones.From equation (14),on the other hand,it can be seen that this becomes possible when

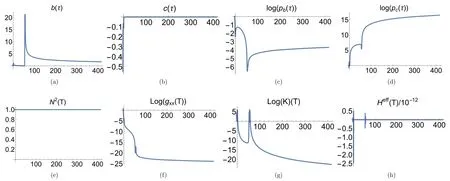
Figure 1.Plots of the four physical variables (b ,c,pb ,pc )for-3 ＜τ ＜415 and =1,for which we have τT ?1.110 68and =0.The initial time is chosen at τi=-2.15018.

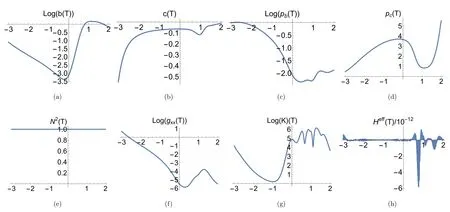
Figure 2.Plots of (b ,c,pb ,pc ) for -3 ＜τ ＜2.The same initial time and conditions are chosen as those of figure 1.

wherenis an integer.Numerically,we find that such surfaces indeed exist in the BV model.In fact,there exists an infinite number of such surfaces.In particular,in figure 3(d)we show that two of such surfaces exist for τ ∈(-3,2).

3.Conclusions and remarks

In this brief report,we adopted the SS gauge[23],in which the lapse function is set to one,so the time-like coordinate becomes the cosmic time.Then,we found that black/white hole horizons do not exist.This conclusion is consistent with what we obtained previously by adopting a different gauge [22].This is quite expected,as the physics should not depend on the gauge choice.The advantage of the SS gauge is that one can easily show analytically that the BV spacetime is geodesically complete.

The above conclusion is important,as now thescheme has been widely used in recent studies of LQBHs [24,25].Therefore,several comments now are in order.In particular,in [24] the authors considered the Lemaitre–Tolman–Bondi(LTB) spacetime in which the Schwarzschild black hole solution is given by

Figure 3.Plots of (b ,c,pb ,pc)for-24 ＜τ ＜0 and δcc(τ)for-3 ＜τ ＜2 with =1.The same initial time and conditions are chosen as those of figure 1.

Note that the advantage of writing the Schwarzschild black hole solution in the LTB form is that it covers both inside and outside regions of the black hole.In particular,the spacetime singularity now locates atx-t=0,while the black hole horizon atx-t=4m/3.Denoting the moment conjugates ofExandEφbyKxandKφ,respectively,Han and Liu considered the following replacements [24]

Clearly,near the singularity,we have (δx,δφ)→(0,∞).Then,it is expected that quantum gravitational effects become very large,so in the reality the singularity used to appear classically now is smoothed out by these quantum effects,and a non-singular transition surface finally replaces the singularity.On the other hand,near the location of the classical black hole horizon,we havewhich are all finite.Yet,for massive black holes,they are all very small,so quantum effects near the horizons of these massive black holes are expected to be negligible.These are consistent with the results obtained in [24].Similar considerations were also carried out in[25],so we expect that in this model black/white hole horizons also exist,and quantum effects near these horizons of massive black holes are expected to be negligible,too.

Acknowledgments

The numerical computations were performed at the public computing service platform provided by TianHe-2 through the Institute for Theoretical Physics &Cosmology,Zhejiang University of Technology.YG is partially supported by the National Key Research and Development Program of China under Grant No.2020YFC2201504.AW is partially supported by a NSF grant with the grant number:PHY2308845.

ORCID iDs