An Incentive Mechanism for Federated Learning: A Continuous Zero-Determinant Strategy Approach

Changbing Tang ,,, Baosen Yang , Xiaodong Xie , Guanrong Chen ,,, Mohammed A.A.Al-qaness , and Yang Liu ,,

Abstract—As a representative emerging machine learning technique, federated learning (FL) has gained considerable popularity for its special feature of “making data available but not visible”.However, potential problems remain, including privacy breaches, imbalances in payment, and inequitable distribution.These shortcomings let devices reluctantly contribute relevant data to, or even refuse to participate in FL.Therefore, in the application of FL, an important but also challenging issue is to motivate as many participants as possible to provide high-quality data to FL.In this paper, we propose an incentive mechanism for FL based on the continuous zero-determinant (CZD) strategies from the perspective of game theory.We first model the interaction between the server and the devices during the FL process as a continuous iterative game.We then apply the CZD strategies for two players and then multiple players to optimize the social welfare of FL, for which we prove that the server can keep social welfare at a high and stable level.Subsequently, we design an incentive mechanism based on the CZD strategies to attract devices to contribute all of their high-accuracy data to FL.Finally, we perform simulations to demonstrate that our proposed CZD-based incentive mechanism can indeed generate high and stable social welfare in FL.

I.INTRODUCTION

THE emergence of artificial intelligence and the rapid development of 5G technologies have made the Internet of Things gradually evolve into the Internet of Intelligences[1].Many studies on the machine learning (ML) and the iterative learning control of multi-agents once attracted everyone’s attention [2]-[4].However, issues such as data silos and privacy security directly hindered their development [5], [6].As a representative distributed ML technique, federated learning(FL) has attracted considerable attention for its characteristic of “making data available but not visible” [7]-[9].In FL, all participants work in a collaborative manner [10], [11].There is no need to upload private personal data during training [12],and the devices only need to use the shared model for local iterative learning, global aggregation [13] and updating [14].

However, when applying FL in real applications, devices are often reluctant to contribute relevant data, or even refuse to participate in FL, as they are faced with sensitive issues such as privacy risks and break-even results.There are some studies considering these issues.For example, in [15] an incentive scheme was designed to maximize the collective utility while minimizing the inequality among data owners.However, some studies were based on unreasonable assumptions, such as mobile devices voluntarily participating in FL without receiving any rewards [15], [16], which is unrealistic in real-life scenarios.Furthermore, risks such as resource consumption and privacy leakage make the devices more reluctant to participate in FL.Therefore, an important and also challenging issue is:Determining how to design an effectiveincentive mechanism that not only optimizes the social welfare of FL,but also encourages devices to contribute all of their high-quality data to FL.

To address the aforementioned problem, game theory offers an ideal approach since it is an effective tool for competition and cooperation of individuals participating in an interacting process [17]-[19], such as FL, or more generally, ML.There are already some works using game theory to design effective incentive mechanisms, for example to optimize social welfare[20]-[24].To select reliable devices participating in FL, in[20] a reputation-based incentive mechanism was proposed based on contract theory.Some studies combine effective computational algorithms with game theory to enhance FL efficiency [25]-[29].Nevertheless, further research is still needed to balance schematic efficiency and social welfare.

As a new methodology for studying various strategies in game theory, zero-determinant (ZD) strategies [30] have found many applications.By using ZD strategies, a player can unilaterally control the opponent’s expected utility, regardless of the opponent’s strategy used.On one hand, some work aims to enhance the applicability of ZD strategies through theoretical analysis [31]-[34].For example, in [31] the ZD strategies were classified into three types (fairness, extortion,and generosity) to study cooperation and control in social dilemmas.On the other hand, some work incorporates practical consideration into modeling and their performances[35]-[38].For instance, in [36] a collective extortion strategy was developed to accelerate the learning process.Notably,very few work focuses on continuous strategy games, especially in multi-player continuous strategy game scenarios of FL.This motivates us to design an incentive mechanism for FL based on continuous ZD (CZD) strategies.

In the practical FL scenario, there are some advantages of considering CZD strategies.First of all, the incomplete cooperation of contributing a portion of high-quality data is widely present in FL.That is, the continuous action space is more practical than the discrete action space in FL.Actually, the ZD strategies are special cases of CZD strategies.The CZD strategies maintain the control effect of the ZD strategies and extend the action spaces from discrete to continuous.Secondly, as continuous strategies contain more complete information compared to discrete strategies, the CZD strategies have broader incentive ranges than the ZD strategies.Therefore, compared with the ZD strategies, the incentive mechanism designed by the CZD strategies can more effectively motivate the participating FL devices to contribute high-quality data.At last, the fair distribution of rewards can be achieved by adjusting the parameters in the CZD strategies.That is, the incentive mechanism designed by applying the CZD strategies can effectively achieve “no pain no gain”, in which devices contributing high accuracy data can receive high rewards and the server gains a high-quality global model.Therefore, the incentive mechanism designed by the CZD strategies can lead to a win-win situation in FL.

In this paper, we consider the continuous strategy game scenario in FL and propose an incentive mechanism based on the CZD strategies.We first model the interaction between devices and servers during FL as an iterative game.We then design an incentive mechanism to optimize social welfare.We further apply CZD with two players, and then multiple players, to optimize social welfare in FL.Based on theoretical analysis, we demonstrate that servers can control social welfare at a high and stable level by applying the CZD strategies with refinement.

The main contributions of this study are summarized as follows:

1) We model the interaction between the server and the devices in the FL process as a continuous iterative game,based on which the ZD strategies are extended to the CZD strategies.Practically, the CZD strategies cover more complete information than the ZD strategies, which results in problem where the CZD strategies are more suitable to demonstrate the incomplete cooperation scenario of FL.Our work further develops ZD theory and enriches the application of ZD strategies in continuous strategy scenarios.

2) Based on the CZD strategies with two-player and multiplayer scenarios, we design an incentive mechanism for FL.This mechanism can not only motivate as many devices as possible to contribute high-quality data in FL, but also enhance the efficiency of FL.Compared with the existing ZDbased studies, our proposed approach can achieve broader incentive range, more efficient motivation, more effective incentive compatibility, and more accurate fair distribution of rewards.

3) We combine numerical and real experiments to validate the advantages of the proposed method in simulations.On one hand, the strengths of the CZD strategies are proved by numerical experiments.On the other hand, the effectiveness of the CZD-based incentive algorithm is verified by FL experiments with real datasets.To our knowledge, among the existing FL incentive mechanisms based on the ZD strategies, we are the first to perform both numerical and real experiments.

The remainder of the paper is organized as follows.In Section II, a literature review is presented.In Section III, the system model based on the CZD strategies in FL is established.In Section IV, by applying the CZD strategies to the continuous scenarios with two players and then multiple players, an incentive mechanism algorithm is designed for resolving the dilemma in FL.Finally, in Section V, simulation results are demonstrated, and in Section VI the investigation is concluded.

II.RELATED WORK

Several works [20]-[24] designed effective incentive mechanisms based on game-theoretic analyses.To optimize the system payoff, a hierarchical incentive framework based on coalitional and contractual games was proposed in [21].In[22], the stackelberg game was applied from the perspective of communication efficiency to optimize FL.In [23], an incentive mechanism was designed for FL based on the auction theory.Moreover, some works combined computational algorithms with game theory [25]-[29], aiming to optimize social welfare and solve the incentive problem in FL.However, the aforementioned works are either from a theoretical perspective to improve FL efficiency or from an algorithmic perspective to optimize the social welfare, which did not or were unable to balance the efficiency and effectiveness through the FL process.

As a new approach in game theory, the ZD strategies [30]led to extensive research in recent years.In [32], the ZD strategies were applied to both discrete and continuous strategy scenarios for wireless resource sharing, where the number of players was extended from two toN.Also, in [33] the fairness of the ZD strategies was studied and in [34] the ZD strategies were refined to a ruling strategy in a repeated game with a limited number of players and action sets.Furthermore,to encourage collaborative mining in PoW-based blockchain networks, an incentive mechanism based on the ZD strategies was proposed in [35].In [37], the ZD strategies were applied to solve the reward allocation problem in mobile crowdsourcing.The multi-player multi-action ZD (MMZD) strategy was applied in [38] to address social dilemmas in cross-silo FL.However, it was noticed that some factors such as high incentive costs and the random nature of device' strategies could still reduce FL efficiency and even harm social welfare.

Inspired by the above works, we consider the continuous strategy game scenarios in FL and propose an incentive mechanism based on the CZD strategies.Compared with the existing works, our proposed approach has several differences.Firstly, continuous strategies cover more complete information than discrete strategies, which is caused by the dynamic interaction between FL participants.Therefore, we apply CZD strategies to solve the incentive problem in FL.This differs from existing studies [30]-[38] who focused on discrete ZD strategies.Secondly, the CZD strategies can promote full cooperation of FL participants, which is confirmed by theoretical derivations in two-player and multi-player scenarios.Based on this, the designed CZD-based incentive algorithm can optimize social welfare and also improve FL efficiency.This is different from the existing studies.In [20]-[24], game methods were adopted to optimize social welfare; in[25]-[29], several efficient computational algorithms were applied to improve FL efficiency.Thirdly, the effectiveness of the CZD-based incentive algorithm is verified by FL experiments with real datasets.This is different from existing studies [36]-[38] which were verified by numerical experiments without real experiments.

III.PROBLEM FORMULATION

A. System Model

Fig.1 shows an FL scenario consisting of one server andNdevices.First, the server issues the FL task (including the global model, deadline, and expected reward), and the devices choose whether to join based on whether their local data matches the FL task sufficiently.Secondly, the server selects candidate devices by pre-training and sends the global model.The candidate devices do not need to upload any sensitive data, but only need to receive the global model for local training.Third, if the model parameters and gradient values meet the thresholds set by the server, which were obtained after several rounds of local iterative computation, the devices can apply to upload the local models.Finally, after local model aggregation and global model updating, the server will distribute rewards to the devices participating in FL.

However, due to the lack of trust and the unavoidable information gap, selfish devices may resort to “cheating” (e.g.,contributing their incomplete or irrelevant data during FL) to save computational resources and demand rewards that do not match their contributions.Obviously, it is more effective to prevent and control problems by taking preventive measures than to solve them during the working process.Therefore, to avoid selfish behavior of a device, the server can dynamically modulate rewards based on the contribution of the device.Conveniently, we summarize the notations in Table I.

B. Game Formulation

In the FL process, all participants have their own preferences for the choice of strategies and make decisions independently by combining their costs and benefits.In fact, the devices and the server involved in FL have no way to obtain strategy information of others in interaction, and there are multiple decision participants.Therefore, the interaction between devices and the server can be modeled as a multiplayer synchronous game.

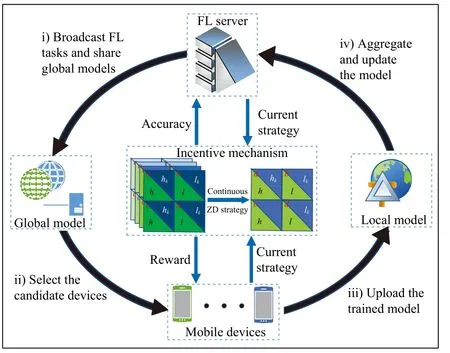
Fig.1.System model.The process of the FL task can be divided into four stages: i) Broadcasting of the FL task and initialization of the global model;ii) Selection of candidate devices and transmission of the global model; iii)Training and uploading of local models; iv) Model aggregation and updating,and reward distribution.During the FL process, devices may resort to cheating to save their computational resources.To enhance the efficiency of FL, it is necessary to design an effective incentive mechanism that can encourage devices to contribute their high-quality data to FL.

In addition, in terms of the participants’ strategies, they will have more than just two discrete outcomes.Specifically, for the server, it will not foolishly choose to pay in full in any situation, nor will it recklessly choose a zero-payment strategy.For the devices, they can contribute partial data instead of participating or not participating during FL.Therefore, in this paper, we focus on the continuous strategy scenario in FL,which is more comprehensive and realistic in practice.

The strategy of thek-th device (k=1,2,...,N) in the current round can be defined asxk∈[lk,hk], that is, local data accuracy is controlled by the device and chosen to invest in the FL task for model training.Using incomplete information among FL participants,lkandhkcan be obtained by pre-training.The strategy of the server in the current round can be defined asy∈[l,h]; that is, the reward is given to all devices under the control of the server, which is effective on the accuracy of the trained global model.

Based on the experimental validation reported in [27], the strategy of thek-th device can be modeled by the following function via curve fitting:

Similarly, the mixed strategy of the server has a constraint where

To compensate for the devices’ costs in FL, a payment strategyis determined by the server to eachk-th device involved in the FL task, as a reward to its contribution,where ?kandτare adjustment scalars controlled by the server.Then, the utility equation of thek-th device can be expressed as

where σk,δk>0 are the weight parameters for balancing revenue and cost, andCkis the total cost of thek-th device,which is monotonically increasing inxk.

Correspondingly, the utility equation of the server can be expressed as

where σsand δs>0 are the weight parameters to balance the model accuracy and the total payment,νis the expected return of the server corresponding to the unit global model accuracy,ρis a positive adjustment parameter, andRis the transmission and aggregation expense of the server in FL.

Based on the interaction between the server and the devices,the FL game can be precisely defined as follows.

Definition 1(FL Game): In the FL scenario consisting of one server andNdevices, the devices can determine the quality and quantity of data, and the server can control the rewards to the devices.The interaction between the devices and the server is equivalent to a multiplayer synchronous repetitive game, called the FL Game,G=(N∪{s},[lk,hk]∪[l,h],{uk}∪{us}) withk∈{1,2,...,N}.

C. Dilemma in the FL Game

Optimal actions of rational players correspond to actions that maximize their own profits.However, this is a dilemma in the FL game, as further discussed below.

Proposition 1: In the FL game described in Definition 1, the best actions of thek-th device and server arelkandl, respectively.

Proof: For thek-th device, according to (5), if the server’s strategyyis fixed, the utilityukis a monotonically decreasing function aboutxk.That is, whatever the server’s action is, the best action of thek-th device is alwayslk.

Without loss of generality, two extreme cases are considered here to verify the conclusion.Ify=h, thenrkin (5) is taken to the maximum value.Considering the total costCk(lk)uk(hk), which leads to the best action ofxk=lk.Ify=l, so it will not gain more by choosingxk=hk.

Similarly, for the server, if thek-th device’s strategyxkis fixed, the utilityusis a monotonically decreasing function abouty.Sincerk(l)us(h).According to(6),uscan be maximized only ifrkbecomes as small as possible, which corresponds toy=l.

In other words, regardless of the action taken by the device,the best action for the server isy=l.

It follows from Proposition 1 that the best action of the device is to contribute incomplete high-accuracy data, and the best action of the server is to set a lower level of reward.

This dilemma will seriously harm the social welfare or even hinder the implementation of FL.As the initiator and manager of FL, the server has the motivation and ability to take precautions (e.g., an incentive mechanism) to attract contribution from the device so as to avoid the dilemma.

However, on one hand, the utility of the server is affected by the strategies of all participants, which makes it difficult to unilaterally adopt optimal strategies.On the other hand, the additional costs of the preventive measures are critical challenges.Inspired by [30], the ZD strategies can help the adopter unilaterally control the proportional relationship between the expected utilities of two participants, which is expected to resolve the FL dilemma.With this consideration,in [36] the ZD strategies were extended to multiplayer discrete strategy scenarios for accelerating the learning process.

Notice that the traditional ZD strategies are applicable to discrete strategy games with two players, while the strategies of participants in FL are usually continuous.Therefore, this paper studies continuous strategy scenarios with two players and then multiple players, and designs an incentive algorithm for FL based on the CZD strategies to attract contributions from devices.

IV.INCENTIVE MECHANISM IN FL BASED ON THE CZD STRATEGIES

A. CZD Strategies With Two Players

WhenN=1, the strategy functions of the devices and the server arexkandy, respectively, and the utility of the devices and the server areuk(xk,y), andus(xk,y), respectively.The probability of thek-th device and the server to choose strategiesx′kandy′in the previous round and the current round arez(x′k,y′) andz(xk,y), respectively.

If the steady-state vector satisfiesthe expected utility of thek-th device within each round can be expressed as

and the expected utility of the server within each round can be expressed as

Based on the theory of the ZD strategies, the following lemma is established.

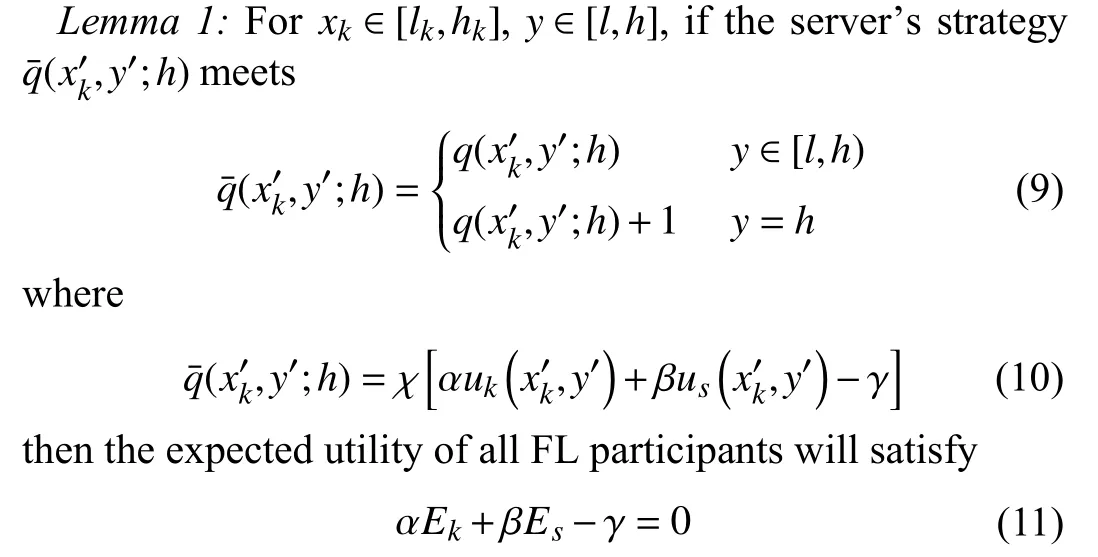
where the factorχis a non-zero scalar,αandβare weight factors, andγis a parameter.

Proof: The proof is given in Appendix A.■

When the server takes the CZD strategies as in (9) and (10),social welfare can always be kept at the desired level, whatever the strategies of the devices are.The objective can be transformed to the following optimization problem:

By solving the problemP1, the following theorem can be established.

Theorem 1: When the strategy of the server satisfies

the social welfareγwill reach a maximum value, as

Proof: The proof is given in Appendix B.

At this point, the social welfare of the FL can be unilaterally controlled at γmax.That is, by applying the CZD strategies, the server can unilaterally control the social welfare of the FL at the desired level whatever the devices’ strategies are.

B. CZD Strategies With Multiple Players

In this subsection, consider a scenario where there is one server andNdevices playing the game with their continuous strategies in the FL iterative task, i.e., ?xk∈[lk,hk] (k=1,2,...,N), ?y∈[l,h].

The corresponding formula in the continuous strategy setting with two players is extended toN+1 dimensions.

According to Definition 1, when the strategy functions of thek-th device and the server arexkandy, respectively, the utility of thek-th device can be defined asuk=uk(x1,...,xN,y)(k=1,2,...,N).Additionally, the utility of the server can be defined asus=us(x1,...,xN,y).

To reveal the relationship between the variables more intuitively, set

Consequently, one has

If the steady-state vector satisfiesz(x1,...,xN,y), the expected utility of thek-th device can be expressed as

and the expected utility of the server can be expressed as

The total utilities of all the players with weight factors αk(k=1,2,...,N)andβcan be defined as the social welfare, i.e.,

Similar to the previous section, the following lemma can be established based on the theory of the ZD strategies.

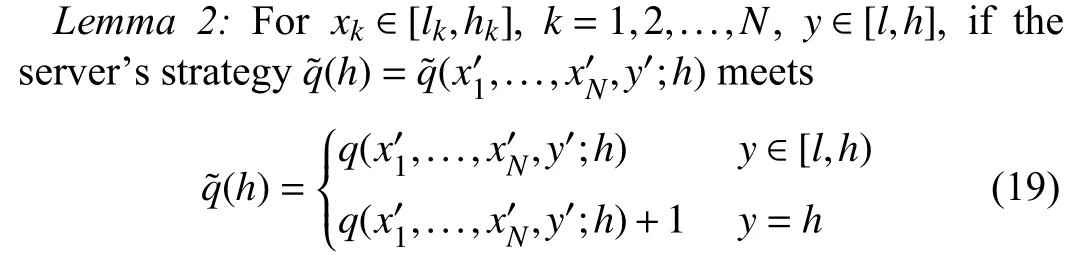
where

then the expected utility of all FL participants will satisfy

where the factorχis a non-zero scalar, αk(k=1,2,...,N) andβare weight factors, andγis a parameter.

Proof: The proof is given in Appendix C.

Algorithm 1 Incentive Algorithm Input: Threshold value , deadline ;q(y)Θk T Input: The CZD strategies ;r={r1,r2,...,rn}Output: Reward vector.1: Initialize parameters, post FL tasks and recruit devices 2: for all devices that have sent requests do Ξk ≥Θk 3: if the sample data accuracy of the k-th device then 4: Evaluate the k-th device’s accuracy upper bounds , lower bounds , and weight , and then update 5: end if 6: end for k=1 hk lk ?k Θk 7: for to N do 8: Compute and update local models xk ≥Θk 9: if then 10: Upload the local model to the server 11: end if 12: end for Tk ≤T 13: while do 14: Model aggregation θ ≥Θ θ ←θ= 1 N∑Nk=1(?k·xk)15: if then 16: Calculate by the CZD strategies r={r1,r2,...,rn}

17: end if 18: end while 19: return Reward vector.r={r1,r2,...,rn}

When the server takes the CZD strategies as in (19) and(20), the social welfare could always be kept at the desired level, whatever the strategies of the devices are.Accordingly,the optimization problem to be solved can be expressed as

By solving the problemP2, the following theorem can be established.

Theorem 2: When the strategy of the server satisfies

the social welfareγcan reach a maximum value as

Proof: The proof is given in Appendix D.

At this point, social welfare can be controlled unilaterally to the value of γmax, regardless of the strategies adopted by the devices.

In summary, when the server applies the CZD strategies, it can unilaterally control the expected utility of all participants,which makes the social welfare of FL stable at a high level.

C. Incentive Algorithm

Considering the selfishness of the FL game players and the continuity of the adopted strategies, we propose a CZD-based incentive mechanism as follows with the illustration in Fig.2 and the pseudo-code in Algorithm 1.

1)Initialization:The server initializes model parameters,publishes the FL task and recruits devices (Line 1).

2)Selection: In pre-training, if the accuracy of thek-th device’s sample data satisfies the threshold value Θk, the server can evaluate its accuracy upper boundhk, the lower boundlk, and weight ?k, and then update Θk(Lines 2-6).

3)Model Training: The selected devices calculate and update the local model by applying their high-quality data.If the trained local model meets the requirements, it can be sent to the server (Lines 7-12).

4)Model Aggregation and Reward Distribution: During local model aggregation, thek-th device’s contributionxkis recorded.And the server assigns the rewardrkby applying the CZD strategies (Lines 13-19).

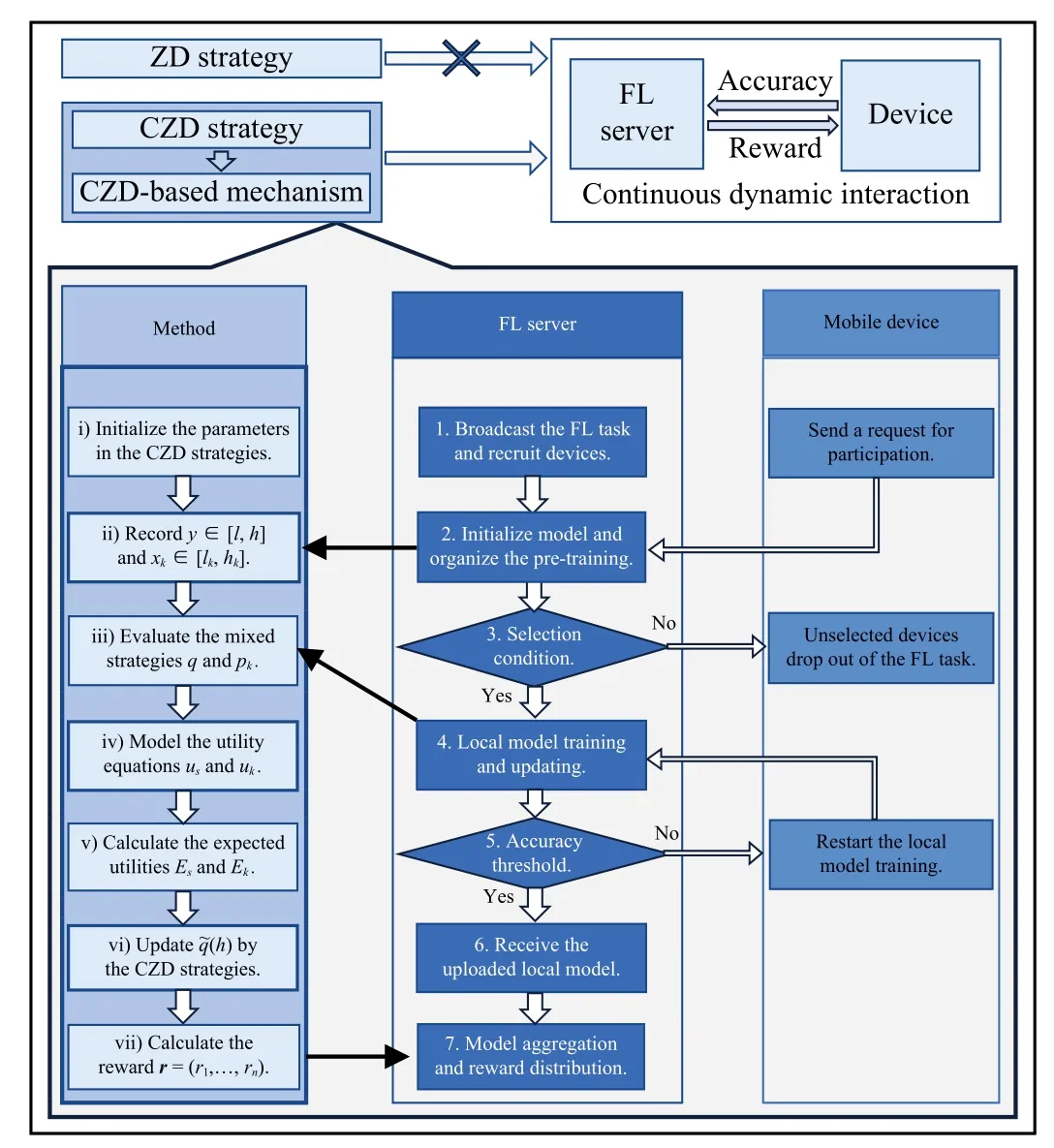
Fig.2.Flowchart of the CZD-based incentive mechanism.

Since allxkandyare continuous bounded variables, the water-filling algorithm [39] in complexity ofO(N) is commonly used to approach the optimal solution.Since this algorithm is equivalent to a traversal of all participating devices,the complexity of Algorithm 1 is alsoO(N).

V.SIMULATIONS

In this section, to evaluate the performance of the proposed incentive algorithm, the datasets used for the experimental tests are MNIST [40] and CIFAR-10 [41].MNIST contains 10 000 test samples and 60 000 training samples.CIFAR-10 contains 10 000 test samples and 50 000 training samples.

The deep learning models to be trained are the multilayerperceptron (MLP) [42] and ResNet-18 [43] models.The minibatch stochastic gradient descent (SGD) [44] optimizer is used.The codes of the incentive algorithm are edited in Python 3.7.3 with PyTorch 1.2.0.The machine used for simulation is a desktop PC with an Intel Core i5 running at 2.7 GHz.To enhance the confidence of the numerical simulation and eliminate errors, the corresponding data in the correlation diagram is obtained by repeating the experiment 20 times and then taking the average values.

A. Effectiveness of the CZD Strategies

To show the effectiveness of the CZD strategies, as displayed in Table III, the characteristics of the strategies CE[36] and MMZD [38] are compared with CZD.Note that both CE and MMZD are based on the discrete strategy scenarios,while the CZD strategies are based on the continuous strategy scenarios with two players and multiple players, respectively.

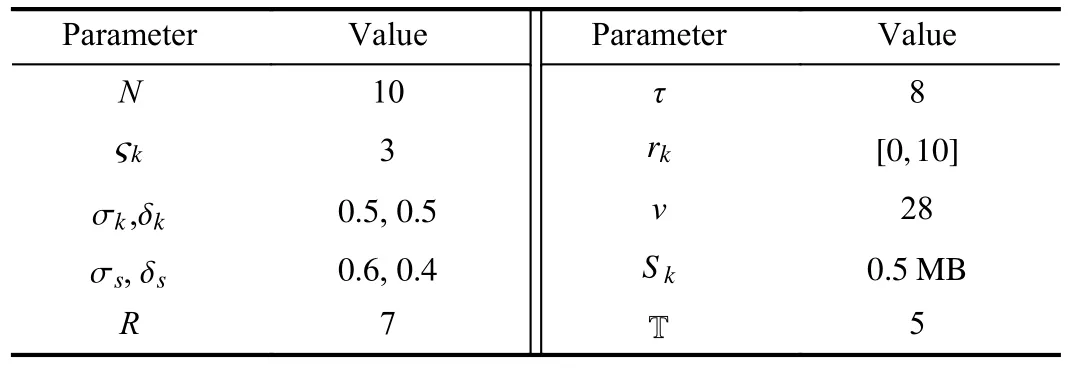
TABLE II PARAMETER SETTINGS

TABLE III COMPARISON OF CHARACTERISTICS

Observing that MMZD has a similar setup to this paper, so we take MMZD as an example for performance comparison to show the effectiveness of CZD.In Table IV, we record the average accuracy of FL models based on different incentive mechanisms with different models and different datasets.To represent the performance of the different methods more concretely, we create real FL experiments by taking the MLP model based on the datasets MNIST and CIFAR-10, the results are represented in Tables V and VI, respectively.The data in Tables V and VI are the average accuracy of FL models, and running time.

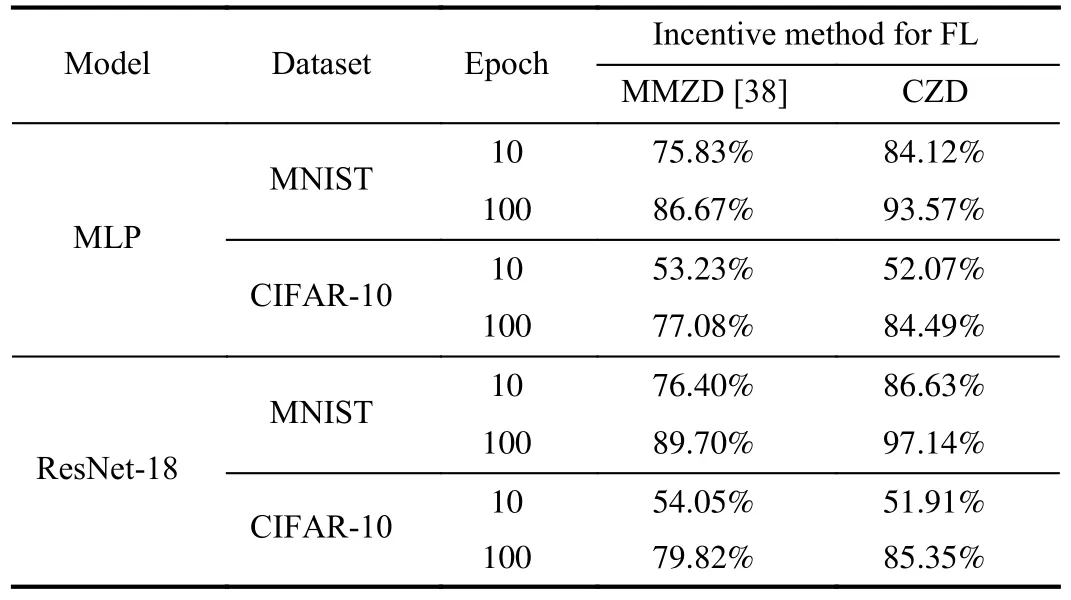
TABLE IV AVERAGE ACCURACY OF FL MODELS BASED ON DIFFERENT INCENTIVES

In Table IV, it can be seen that CZD outperforms MMZD regardless of the dataset or training model applied.For example, when we choose model ResNet-18 with dataset CIFAR-10, CZD improves model accuracy by 5.53% over MMZD.The results in Tables V and VI are consistent with those in Table IV.In Table V, it can be seen that the proposed method improves model accuracy to about 90% after 20 epochs, and the difference in model accuracy between the two methods after 10 epochs of training is 8.29%.Based on our proposedmethod, about 400 s of training time is saved in 200 epochs.Compared to MNIST, CIFAR-10 is more complex, which directly hinders the performance of FL during model training.In Table VI, CZD improves accuracy by 7% compared to MMZD in 100 epochs of FL and saves 3000 s of training time.In other words, when the player’s strategy is extended from discrete to continuous, devices not only can choose whether to participate or not but also can control their contribution specifically in conjunction with some conditions such as revenues and costs.Therefore, compared with strategies in discrete scenarios, CZD strategies that cover more complete information will be more valuable in practical applications.

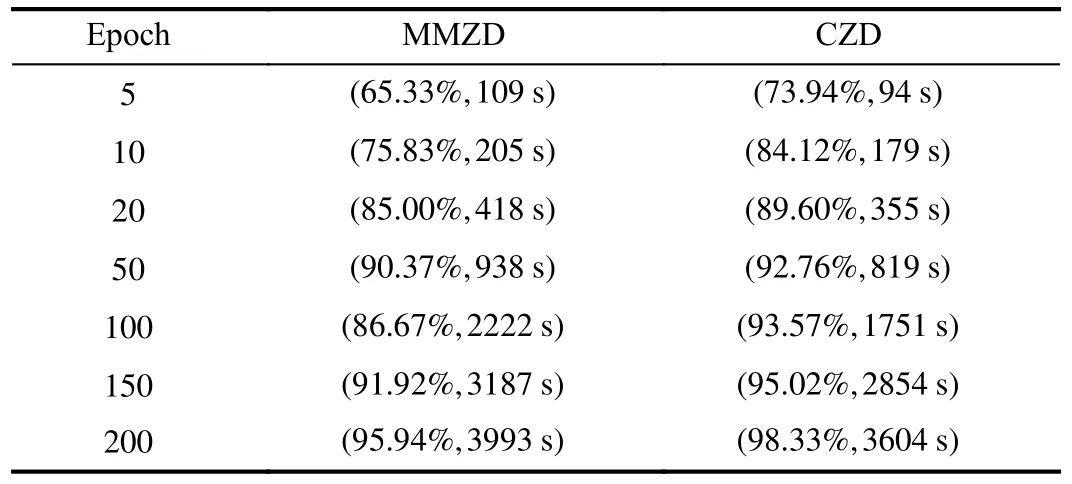
TABLE V PERFORMANCE COMPARISON WITH MMZD BASED ON MNIST

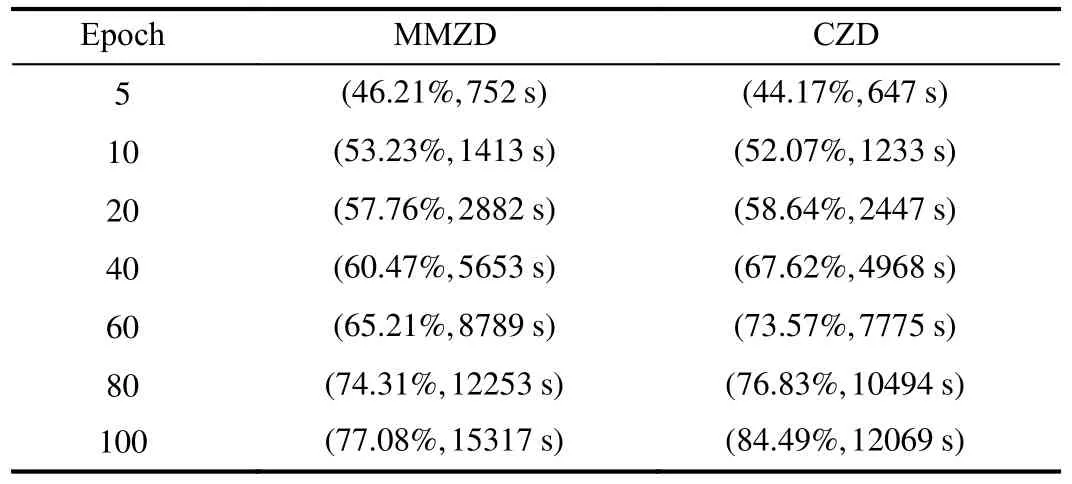
TABLE VI PERFORMANCE COMPARISON WITH MMZD BASED ON CIFAR-10

To confirm that the server can control any evolutionary device to fully cooperate after adopting the CZD strategies, it is now compared with the classical strategies, such as TFT(tit-for-tat), WSLS (win-stay-lose-shift) [45] and GTFT (generous TFT, TFT with forgiveness) [46].

In TFT, the player acts according to the opponent’s previous actions.In WSLS, the player holds an action if it would lead to a high benefit; otherwise, its makes a switch.Similar to TFT, players who take GTFT will repeat their opponent’s choice from the previous round, but have the probability to choose to forgive when betrayed.Here, we set this probability as 1/3.

Figs.3 and 4 show the variation of social welfare with the global model epochs in the cases ofN=1 andN=10, respectively, where the server adopts the CZD strategies, TFT,WSLS and GTFT, and the devices apply TFT, WSLS and GTFT.For example, CZD vs TFT corresponds to the case where the server adopts the CZD strategies while the devices adopt TFT.As GTFT was shown to be effective in promoting cooperation in heterogeneous groups [46], we specifically compare GTFT with other strategies in Figs.3(a) and 3(b).

In the two-player continuous strategy scenario, Fig.3(a)shows that the social welfare is unstable when the devices adopt the TFT strategy while the server takes WSLS or TFT.If the devices take WSLS while the server adopts WSLS or TFT, the social welfare will be stabilized at a low level.When the server applies CZD strategies, social welfare will converge to a high and stable value, regardless of the strategies adopted by the devices.In Fig.3(b), it can be seen that the forgiveness of GTFT does increase the social welfare of FL.However, social welfare converges to the optimal value only in the case of CZD vs GTFT and GTFT vs GTFT, and CZD is 70 epochs ahead of GTFT.

In Fig.4, the number of devices participating in FL is expanded from 1 to 10.Compared with Fig.3, social welfare converges to a higher stable value in all cases.In particular,when the server adopts the CZD strategies, social welfare increases from 1 0 to 16 asNchanges.GTFT can be effective in promoting cooperation, but forgiveness may hurt adopters’gains.Similar to Fig.3(b), in Fig.4(b), the performance of GTFT is better than that of TFT and WSLS.Social welfare can reach an optimal value in the case of CZD vs GTFT and GTFT vs GTFT.However, CZD shows a stronger control effect than other strategies.

B. Fairness of the CZD Strategies

To prove the fairness of CZD strategies, Fig.5 describes the stable values of FL participants’ relative utilities when the server and devices takes different strategies.The value of the relative utility is equal to the quotient of the actual utility divided by the utility in ALLC (all cooperative).

Figs.5(a) and 5(b) show that only the CZD strategies can make the relative utility of the devices and the server steadily go towards 1.As for GTFT, the relative utility of FL participants converge to 1 only when the GTFT player faces opponents who adopt the same strategy.The strategies TFT and WSLS push the relative utility below 1 and can even reduce the server’s revenue.

Fig.6 shows the variation of the relative utility when all devices take the WSLS strategy and the server adopts different strategies.Similar to Fig.5, the relative utilities of FL participants steadily converge to 1 only when the server adopts the CZD strategies.For GTFT, the relative utility can converge to 1 only if it encounters an opponent who adopts the same strategy, otherwise it will be below 1.The strategies TFT and WSLS make the relative utility tend to stabilize at a value lower than 1.

C. Effect of System Parameters

Fig.3.Social welfare with global model epochs in the continuous strategy setting when N=1.(a) Comparison of CZD, TFT, and WSLS; (b) Comparison of CZD, TFT, WSLS, and GTFT.

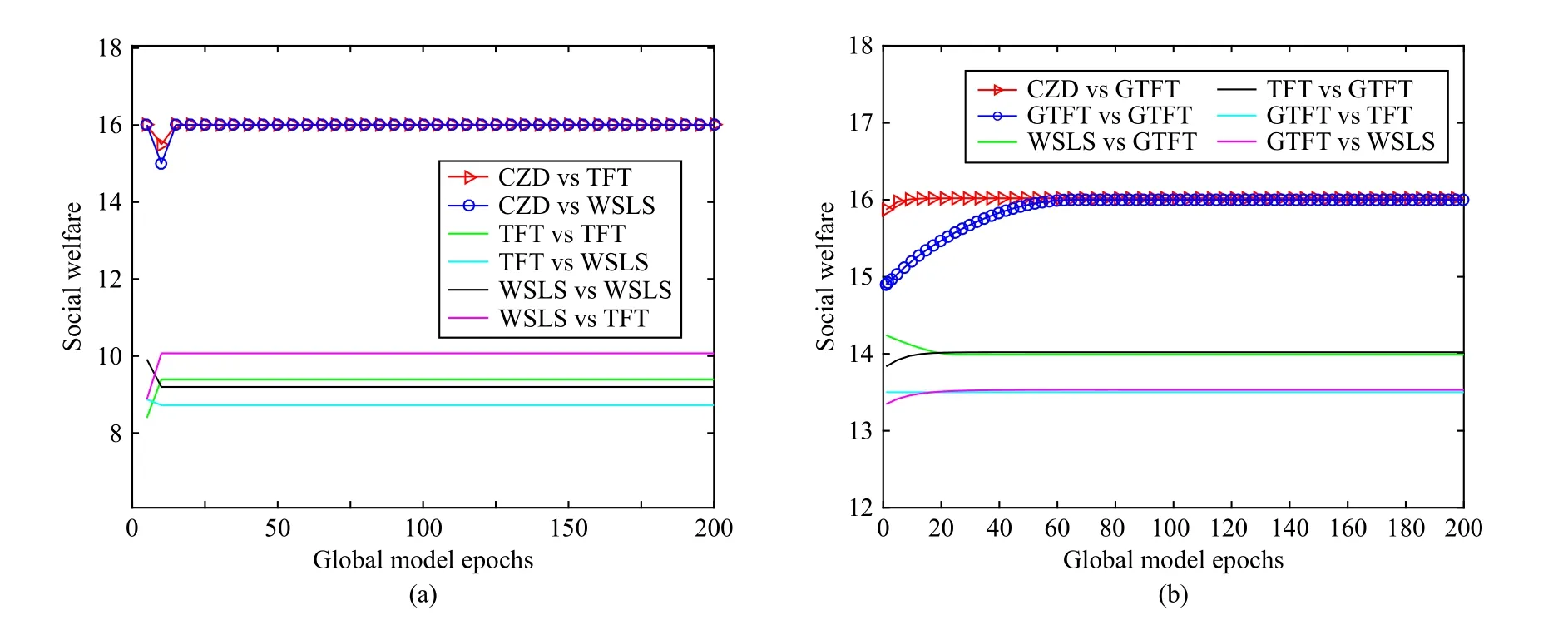
Fig.4.Social welfare with global model epochs in the continuous strategy setting when N =10.(a) Comparison of CZD, TFT, and WSLS; (b) Comparison of CZD, TFT, WSLS, and GTFT.

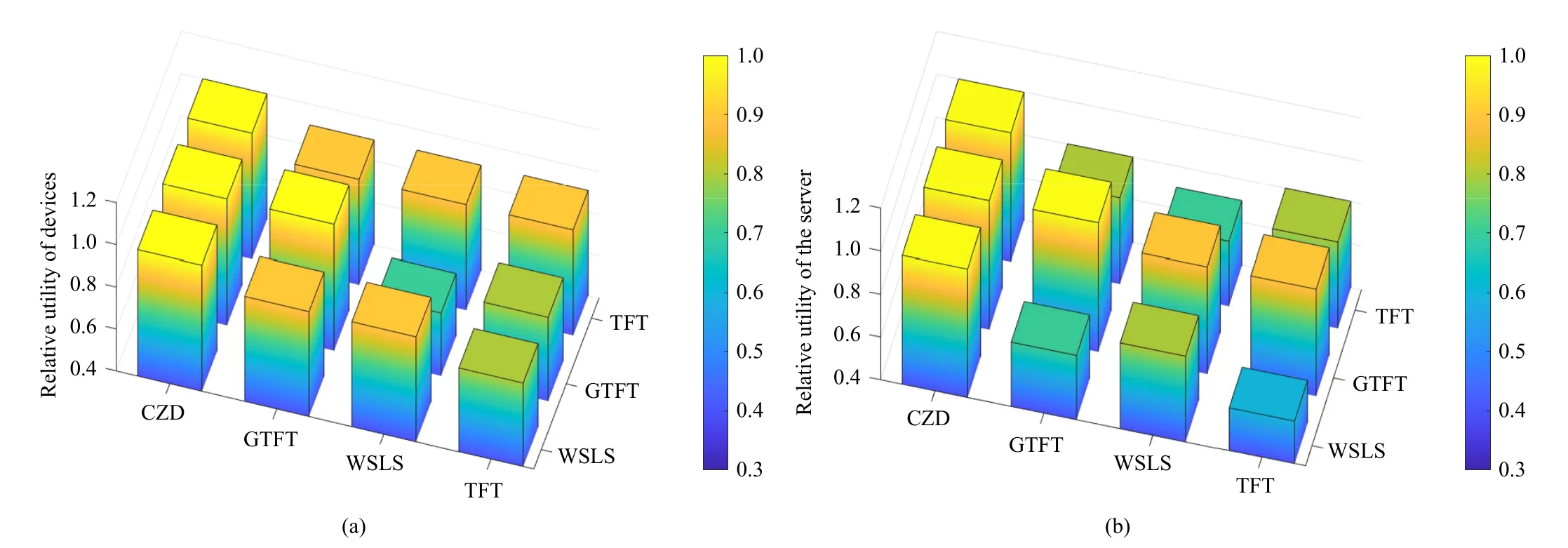
Fig.5.Stable values of FL participants’ relative utilities when the server and devices adopt different strategies, where the strategies of the server are CZD,GTFT, WSLS and TFT, and the strategies of devices are WSLS, GTFT and TFT.(a) Relative utility of devices; (b) Relative utility of the server.

As seen in Section IV, system parameters play an essential role in regulating the utility relationship between the devices and the server.To reveal the effect of the system parameters on the FL game, Fig.7 shows the variation of social welfare with the global model epochs when the system parameters take different values.It can be observed that the change of theχvalue will lead to fluctuation of social welfare, while the change of theβvalue will affect the convergence rate of social welfare.However, the social welfare of FL will eventually stabilize at an identical level.This is because the CZD strategies can regulate the actions of the devices and make them contribute their high-accuracy data, which in turn guarantees that the expected utility of all participants tends to be stable,resulting in the social welfare converging to the same level.

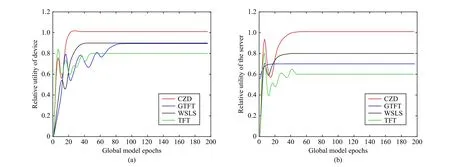
Fig.6.Variation of the FL participants’ relative utility when all devices take the WSLS strategy and the server adopts different strategies.(a) Variation of the devices’ relative utility; (b) Variation of the server’s relative utility.

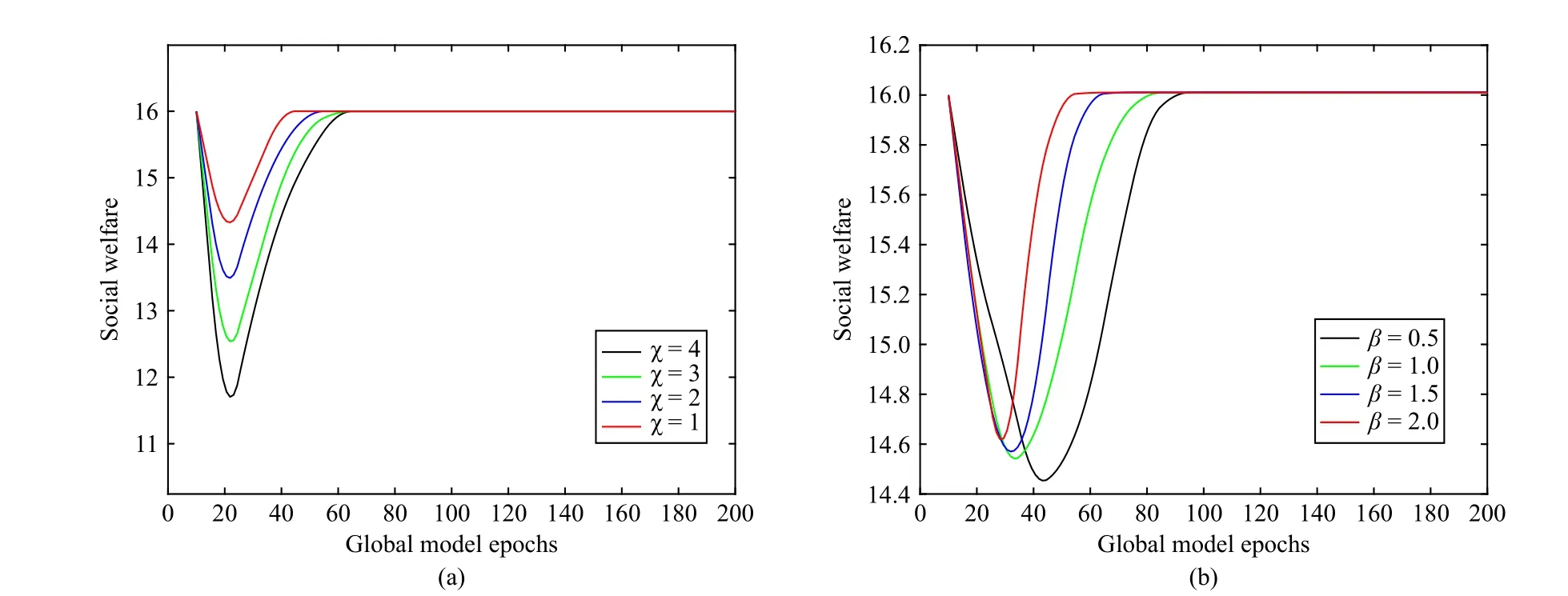
Fig.7.Variation of the social welfare with global model epochs.(a) When the factor χ takes different values; (b) When β takes different values.

In summary, the designed CZD-based incentive algorithm has several advantages.Firstly, our proposed method can be effective in avoiding anyone to increase their own interests by harming the collective interests.Secondly, the CZD strategies extend the action spaces of the ZD strategies from discrete to continuous.Compared with the discrete action space, the continuous action space covers all incomplete cooperative behaviors including full cooperation and full defection.Thirdly, in FL, the continuous strategy contains more complete information than the discrete strategy.As the objects considered by the CZD strategies are more comprehensive, the CZD-based incentive algorithm can more effectively motivate the full contribution of FL participants.Fourthly, the fair distribution of rewards can be achieved by adjusting the system parameters.

VI.CONCLUSION AND DISCUSSION

In this paper, to investigate the issue of incentive mechanisms in FL, we model the interaction between the devices and the server as a continuous multi-player iterative game.We apply the CZD strategies to the continuous strategy scenarios with two players and multiple players.Then, we demonstrate that the server can unilaterally control social welfare regardless of the strategies adopted by the devices.Based on this, we develop a CZD-based incentive algorithm which can motivate as many devices as possible to participate in FL and contribute high-quality data.Furthermore, by comparing strategies of TFT, GTFT and WSLS in game theory and other methods in existing works, we present some simulations to verify the advantages of the CZD-based incentive algorithm.Our proposed approach can attract devices to contribute all their high-accuracy data in FL, and then effectively optimize the social welfare and improve the efficiency of FL.

It is noticed that we have considered the case of one server in this paper, but the situation is more complex in real applications.As the number of servers increases, the interaction among FL participants will become more complex, and the competition among FL participants will also become more competitive.Thereby, the malicious competitive behavior among servers will also become more prominent, and even pose a serious threat to the sustainability of the FL system.Furthermore, the proposed CZD-based incentive mechanism can motivate participants to invest in FL, but has limited effect on the optimization of the learning algorithm.Thus, it is meaningful to consider the balance between the incentive effect and learning efficiency.

In the future, we intend to expand the number of servers from one to multiple, and consider dynamic interactions between multiple servers and multiple devices in FL, which corresponds to a more complex network structure.Under this scene, we will consider applying the ZD alliance theory to overcome the effect of increased servers and avoid malicious competitive behaviors.In addition, we will consider using the reinforcement learning method to optimize the strategies selection in the FL process of decision making, where the balance between the incentive effect and the learning efficiency can be achieved.

APPENDIX

A. Proof of Lemma 1

and

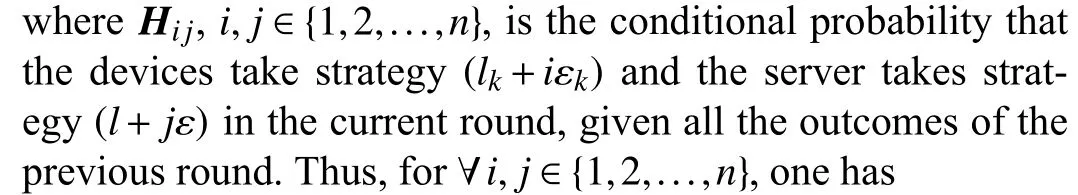
The payoff matrix of the device can be defined as

and the payoff matrix of the server can be defined as

it can be seen that the result depends on the strategy of only one participant, i.e.,

Whenf=αUk+βUs-γ1, withαandβas weight factors,andγis a nonzero scalar, one has

When

using properties of the determinant, one obtains

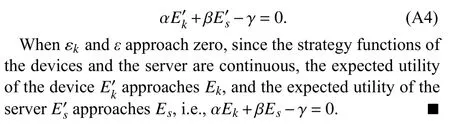
B. Proof of Theorem 1

Proof: Based on the existing conditions and the strategy of the server, the problemP1can be solved by solving the following problem:

where

C. Proof of Lemma 2

Based on mathematical induction, it follows that inN-player FL games (N≥2), when the server adopts the CZD strategies,it can control the expected utility of all participants unilaterally, which can keep the social welfare at a high and stable level.

D. Proof of Theorem 2

The problemP2can be solved by solving the following problem:

Similar to the Proof ofTheorem 1, one has

Therefore, to optimize the social welfare of FL, the CZD strategies adopted by the server need to satisfy