Anomaly-Resistant Decentralized State Estimation Under Minimum Error Entropy With Fiducial Points for Wide-Area Power Systems
Bogang Qu , Zidong Wang ,,, Bo Shen ,,, Hongli Dong ,,, and Hongjian Liu ,,
Abstract—This paper investigates the anomaly-resistant decentralized state estimation (SE) problem for a class of wide-area power systems which are divided into several non-overlapping areas connected through transmission lines.Two classes of measurements (i.e., local measurements and edge measurements) are obtained, respectively, from the individual area and the transmission lines.A decentralized state estimator, whose performance is resistant against measurement with anomalies, is designed based on the minimum error entropy with fiducial points (MEEF) criterion.Specifically, 1) An augmented model, which incorporates the local prediction and local measurement, is developed by resorting to the unscented transformation approach and the statistical linearization approach; 2) Using the augmented model, an MEEF-based cost function is designed that reflects the local prediction errors of the state and the measurement; and 3) The local estimate is first obtained by minimizing the MEEF-based cost function through a fixed-point iteration and then updated by using the edge measuring information.Finally, simulation experiments with three scenarios are carried out on the IEEE 14-bus system to illustrate the validity of the proposed anomaly-resistant decentralized SE scheme.
I.INTRODUCTION
FOR a few decades, power systems have been undergoing dramatic changes due to the penetration of renewable power generations, the widespread use of demand-response devices as well as access to dynamic loads [1], [2].In order to monitor power systems under complex working conditions, a new generation of infrastructure, namely, wide area monitoring systems (WAMS), has been increasingly deployed in modern power systems [3].As a key part of the WAMS, the state estimation (SE) algorithm has been playing a vitally important role in raising situation awareness, facilitating realtime control and enhancing security assessment and protection [4]–[6].
So far, the SE algorithms based on the data collected from the phasor measurement unit (PMU) have spurred tremendous interest (see e.g., [7], [8]) because of PMU’s merits of providing synchronized, accurate yet timely sensing data.Nevertheless, due primarily to unaffordable implementation costs and the limited communication resources, it is difficult to deploy the PMU widely in the foreseeable future [9], [10].Therefore, one would need to make use of the measurements from both the advanced PMUs and conventional supervisory control and data acquisition (SCADA) in order to reach the tradeoff between communication/implementation cost and estimation accuracy.
There have been three typical SE frameworks, namely, centralized, hierarchical and decentralized frameworks, which have appeared in [11]–[13].In the centralized SE framework,the global estimates can be generated in the estimation center by utilizing the measurement data from the entire power grid[14], [15].Such a centralized framework might suffer from computation costs and/or communication burdens, and this is especially true when the power grid is scaled up [16], [17].The hierarchical SE framework, on the other hand, disperses the computation/communication burdens by dividing the power grids into several areas and then generating the local estimates of each area which are finally fused in the estimation center [9], [10].Note that hierarchical frameworks are very much dependent on the efficiency and reliability of the SE schemes (executed at the estimation center), which might not be always guaranteed for large-scale power systems [17],[18].Compared to its centralized and hierarchical counterparts, the decentralized SE framework aims to further save limited computation/communication resources by dividing the power grid into several areas and conducting state estimation in each individual area based on the information from the local area as well as the edges which are shared with its neighboring areas.
In the past decades, the decentralized SE problem for power systems has attracted increasing research interest, see [3],[16]–[19] for some representative works.For instance, in [3],a fully distributed static SE algorithm has been designed for wide-area power systems based on the weighted-least-square(WLS) method.In [18], an efficient distributed SE algorithm has been developed with the aid of the WLS method, where the Gauss-Newton step is achieved without inner iteration.It should be noted that the WLS-based SE method is inherently a static one, and is therefore incapable of capturing the dynamic behaviors most likely caused by sudden load changes or the penetration of renewable power generations.
As with the increasing demand of monitoring dynamic behaviors of large-scale power systems, the so-called decentralized dynamic state estimation (DDSE) problem has created great enthusiasm from researchers leading to the development of three mainstream DDSE-based schemes, namely, the model-decoupling-based scheme [8], [20], consensus-based scheme [21], [22] and maximum-a-posteriori-based scheme[23].Briefly speaking, the model-decoupling-based scheme is computationally efficient at the cost of sacrificing certain estimation performance since the neighboring information of each synchronous generator is not effectively utilized.For a given area, although the consensus-based DDSE scheme improves the estimation efficiency, it may not be able to fully utilize the available data since the information of the indirectly connected areas is largely ignored.The distributed maximum-aposteriori-based DSE algorithm, on the other hand, can achieve an adequate tradeoff between information utilization efficiency and state estimation accuracy since the information of entire power grid can be accessed through finite steps of iteration.
It is worth pointing out that most existing SE algorithms for power systems have been developed in the minimum meansquare-error (MMSE) sense, and the corresponding estimation performances are therefore prone to contaminated measurement data due to anomalies (e.g., outliers, communication impulses, quantization errors and instrument failures)[24]–[28].To enhance the resistance against anomalies, some novel SE schemes have been proposed based on the minimum error entropy (MEE) criterion and the maximum correntropy(MC) criterion, see e.g., [29] for the MEE-based unscented Kalman filter (UKF), [30] for the MC-based extended Kalman filter and [31] for the novel Cauchy-kernel-based MC filter.In many situations, the MEE-based SE scheme outperforms the MC-based one, but the shift-invariant of the MEE criterion introduces a bias to make sure that the estimation error goes to zero [32].In hopes of combining the merits of both MC and MEE criteria, the so-called minimum error entropy with fiducial points (MEEF) criterion has been proposed in [32] without having to add a bias after training.
Based on the above discussions, it can be found that there is a lack of adequate investigation into the SE problem for a wide-area power system with anomaly, and the main purpose of this paper is therefore to shorten such a gap.In doing so,the technical challenges can be identified as threefold: 1)Determining how to implement the SE algorithm in a decentralized style to decrease the computation/communication cost; 2) Determining how to improve data redundancy in the case of a decentralized SE framework where only the local measurement is available; and 3) Determining how to reduce the negative influences of the measurement with anomalies on the SE performance in the estimator design.
In connection with the challenges identified above, the main contributions are highlighted as follows.1) For the purpose of implementing the SE in a decentralized manner, the wide-area power system is divided into several non-overlapping areas,and the state of a given area is first estimated by using local measuring information and then updated by using the edge measurements which are shared with its neighboring areas.2)To improve the data redundancy, an augmented model which involves both the local prediction and the local measurement is constructed by resorting to the unscented transformation approach as well as the statistical linearization approach.3) A local MEEF-based UKF is proposed based on the MEEF criterion so as to enhance resistance against measurement with anomalies.
The remainder of this paper is outlined as follows.Section II formulates the decentralized model of power systems.In Section III, a brief review of the error entropy criterion and the correntropy criterion is first given, and then the MEEF criterion is introduced.Section IV describes the proposed anomaly-resistant decentralized SE algorithm.In Section V,simulation studies and detailed discussions are carried out on the IEEE 14-bus power system.Finally, some conclusions are drawn in Section VI.
Notations: The notation used here is fairly standard except where otherwise stated.Rnrepresents then-dimensional Euclidean space.The superscript “T” represents the transpose operation.diag{···} represents the block-diagonal matrix.E{x}is the expectation of the stochastic variablex.[A]ijrepresents the element at thei-th row and thej-th column of the matrixA.//·//stands for the Euclidean norm of a vector.
II.PROBLEM FORMULATION
A. Preliminaries
In this paper, an undirected acyclic graph G =(V,E) is used to reveal the connections of different areas of a wide-area power system.Specifically, V={1,2,...,M} represents the set of areas, and E ∈V×V is the set of edges.The edge(m,n)∈Erepresents them-th area of the wide-area power system and is interconnected with then-th area.The set of neighbors of aream∈V plus the node itself are denoted byNm={m∈V:(m,n)∈E}.
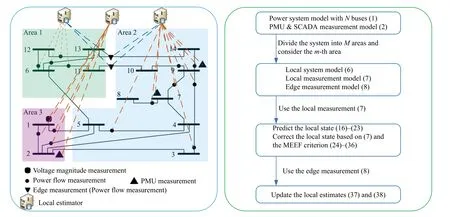
Fig.1.Schematic view of the proposed decentralized SE for wide-area power systems.
B. Power System Model
Consider a power system which containsNbuses (an example is shown in Fig.1), where the dynamic equation of thei-th bus with the quasi-steady state is described by [10], [33]

Remark 1: In this paper, the power system under consideration belongs to the widely used quasi-steady paradigm in which the loads and generators are assumed to operate stably without sudden changes in a short time interval [34], [35].For the purpose of revealing the quasi-steady paradigm, a famous dynamic model (1) is used in which the bus magnitudes and phase angles are chosen as the state variables, the matrixAidescribes how fast the transitions between the states are andBirepresents the trend behavior of the state trajectory.It should be pointed out that the parameters ofAiandBican be identified in an online style and such a method is sufficient for the characterization of the quasi-steady behavior of the power systems [35].
C. SCADA and PMU Measurement Models
In this paper, the mixed SCADA and PMU measurements are used to monitor the power system (an example is shown in Fig.1).The voltage magnitude of each bus and the power flows between two interconnected buses are measured by the SCADA units, and the voltage phasors of the selected buses are measured by the PMUs.It should be pointed out that all of the buses are installed with the SCADA units, and selected buses are installed with the PMUs since the implementation cost of the PMUs is much higher than that of the SCADA units [10].
The voltage magnitude of thei-th bus measured by the SCADA unit at time instantσis expressed as

wheregsi+jbsirepresents the admittance of the shunt branch connected to busi, andgi j+jbi jis the admittance of the series branch connecting busesiandj.Taking the measurement noise into account, a compact SCADA-based measurement model of the power flows is of the following form:
where
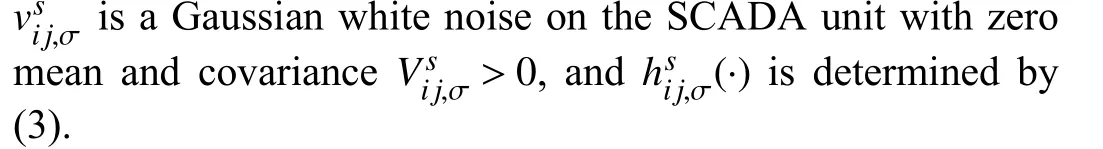
Letting thei-th bus be equipped with the PMU, the corresponding measurement model for the voltage phasor can be expressed as
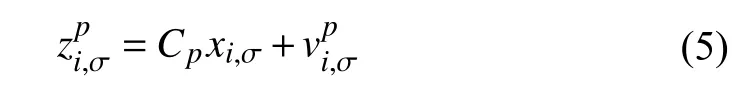
whereCpisanidentitymatrix, andisa zero-mean Gaussian whitenoiseonthePMU withcovariance>0.
D. Decentralized Model
In this subsection, we divide the power system (1) intoMnon-overlapping areas and assume that the topology of such a divided system is acyclic.The system model and the corresponding measurement model for each area as well as the edge measurement model for two interconnected areas are given as follows:
1)Local S ystem Model: The dynamic equation of them-th area (m=1,2,...,M) can be given as


2)Local Measurement Model: The local measurement of them-th area can be expressed as
where


3)Edge Measurement Model: Since some buses of one area are often connected with other areas, the measurements related to these buses are treated as edge measurements in this paper.To be specific, for them-th area, the edge measurement model can be represented by
where

Remark 2: In actual power systems, the inducements of the measurement anomalies (e.g., stealthy attacks, communication impulses, instrument fails or packet losses) are numerous and the features of these anomalies (e.g., the type, occurring occasionality/probability, intermittency) are often unknown[7], [36].As such, it is difficult and even impossible to reveal the measurement anomalies by using specific models, and this motivates us to improve the robustness of the estimator by adopting some novel methods.
E. Problem Statement
The aim of this paper is to develop an anomaly-resistant SE algorithm for power systems such that
1) The proposed SE algorithm is deployed in a decentralized manner by dividing the large-scale interconnected power system into several non-overlapping areas;
2) The decentralized state estimate is calculated iteratively by using the local measurement and edge measuring information; and
3) The resistance of the proposed algorithm against measurement with anomalies is enhanced by adopting the MEEF criterion.
III.MINIMUM ERROR ENTROPY WITH FIDUCIAL POINTS CRITERION
In this section, the error entropy criterion and the correntropy criterion are briefly reviewed, and then an error entropy with fiducial points criterion is developed.
A. Error Entropy Criterion
Letebe the error between the actual statexand the desired statey, (i.e.,e=x-y).The Rényi’s quadratic error entropy is defined as

whereG?(·) is the kernel function and?is the kernel bandwidth [38].Without loss of generality, we choose the Gaussian kernel as the kernel function, i.e.,
Then, the Rényi’s quadratic error entropy in (9) can be approximated as
with
representing the information potential of the errore[39].Obviously, the MEE criterion is actually equivalent to the maximization of the information potentialIP(e).
B. Correntropy Criterion
LettingXandYbe stochastic variables, the correntropy between these two variables is defined as

As such, the so-called MC criterion is actually equivalent to the maximization of the cost function given in (14).
C. Minimum Error Entropy With Fiducial Points Criterion
As discussed in [32], [37], the MEE is shift-invariant and one has to add a bias to guarantee that the estimation error goes towards zero.In order to overcome such a shortcoming,an improved approach called the MEEF criterion has been proposed in [32].Specifically, the MEEF criterion is established by combining MEE and MC criteria through a cost function

Remark 3: Due to the unique merits in enhancing robustness against anomalies, the MEE and MC criteria have attracted a surge of research enthusiasm and some representative results have appeared, see e.g., [29]–[31].For example, a novel MC-based filter has been designed in [31] where the inherent shortages of Gaussian kernels have been overcome with the aid of the Cauchy kernel.It is worth pointing out that the shift-invariant property of the MEE criterion makes it difficult to guarantee that the mean of the error PDF tends to zero[40].As such, the MEEF criterion has been proposed in [40]where the MC term is used to fix the peak of error PDF at origin and the MEE term is adopted to minimize the error entropy [32], [41].In this paper, the MEEF criterion will be used in the subsequent anomaly-resistant state estimator design.
IV.ANOMALY-RESISTANT DECENTRALIZED STATE ESTIMATOR DESIGN
In this section, we aim to study the anomaly-resistant SE problem for wide-area power systems in the presence of measurement with anomalies.First, a local UKF-based state estimation scheme is developed by using the local sensing data,where the MEEF criterion is utilized in the cost function design to enhance the resistance of the local state estimator against the measurement with anomalies.Then, the local estimate is updated by exploiting the edge measuring information.The schematic view of the proposed decentralized SE scheme is outlined in Fig.1.
A. Design of the MEEF-Based Local State Estimator

and
2)Update: Based on the statistical linearization approach proposed in [42], the local measurement function (7) can be linearized aroundX?m,σ|σ-1as

By integrating local prediction and local measurement into a compact form, we obtain the following augmented model:
where

Moreover, it can be seen that
Remark 4: It has been proven in [43] that, for an arbitrary nonlinear function, the results obtained from the statistical linearization are equivalent to those from the unscented transformation.As such, for the purpose of improving data redundancy, an effective way is to construct an augmented model(i.e., (25)) to process the local prediction and local measurement simultaneously with the aid of unscented transformation approach and statistical linearization approach.
According to the MEEF criterion given in (15), the cost function of the MEEF-based local estimator can be written as
By maximizing the cost function (29), we can obtain the local estimate ofXm,σ.To be specific, taking the partial derivative ofJ(Xm,σ) with respect toXm,σand letting the derivative be zero, we have
where
with
Based on the fixed-point iteration technique [41], the solution of (30) can be expressed as

with
and then reformulate (31) as
where
By resorting to the matrix inversion lemma, (33) can be rearranged in the following recursive form:
with
where
Then,thelocal estimation covariance ofcan be ex pressed as

B. Design of Decentralized State Estimator
In this subsection, the maximum-a-posteriori state estimation method in [23] is extended to update the local estimate recursively by using the edge sensing information.For arean∈Nm, the pseudo measurement matrix of the edge measurementzmn,σcan be expressed as
where
with
Then, for aream∈V, the estimate and the estimation error covariance ofXm,σare of the following form:
where
As discussed in [23], for each aream∈V, the decentralized SE algorithm will converge at eachσafter finite iterations.As such, an inner loop is added in the update of the local estimate.In summary, the pseudo code of the proposed anomalyresistant decentralized SE for wide-area power systems is outlined in Algorithm 1.
Remark 6: In this paper, the anomaly-resistant decentralized SE algorithm is designed for the wide-area power systems.For the purpose of improving computational efficiency,the SE for power system is executed in a decentralized manner where the whole power grid is divided into several nonoverlapping areas which are interconnected through transmission lines.In the design of the anomaly-resistant SE algorithm, an augmented model is established by employing the unscented transformation technique and the statistical linearization technique.Then, an MEEF-based cost function is designed based on the augmented model where the local prediction errors of states and measurements are all reflected.Finally, the local estimate is obtained by iteratively solving an optimization problem with the MEEF-based cost function and such an estimate is then updated by using the edge measurement.
Remark 7: In comparison with the existing SE schemes for wide-area power systems, the main novelties of this paper lie in the following aspects: 1) The scheme we adopted is novel since the state is first estimated in a decentralized manner by using the local measurement and then updated with the aid of edge measurements shared with the neighboring areas; 2) The augmented model we developed is novel since it not only reflects the local prediction errors of the state and measurement but also improves the data redundancy; and 3) The MEEF criterion we adopted in the estimator design is novel since it is more comprehensive than the MEE and MC criteria in the sense of enhancing the resistance of the proposed SE scheme against the anomalies in the measurements.
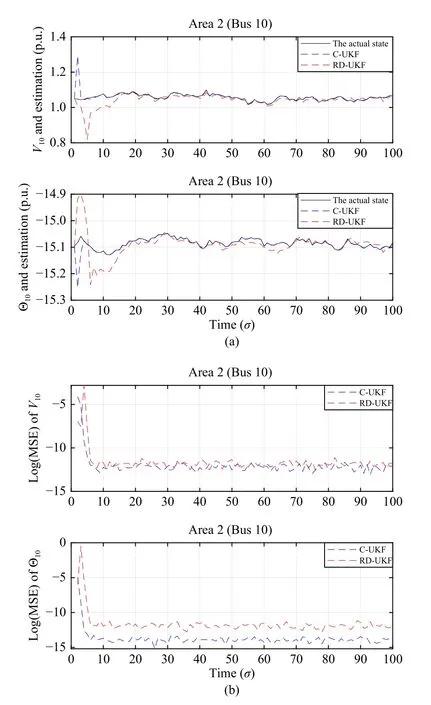
V.SIMULATION EXAMPLE


TABLE I EXPECTED STATES OF IEEE 14-BUS SYSTEM

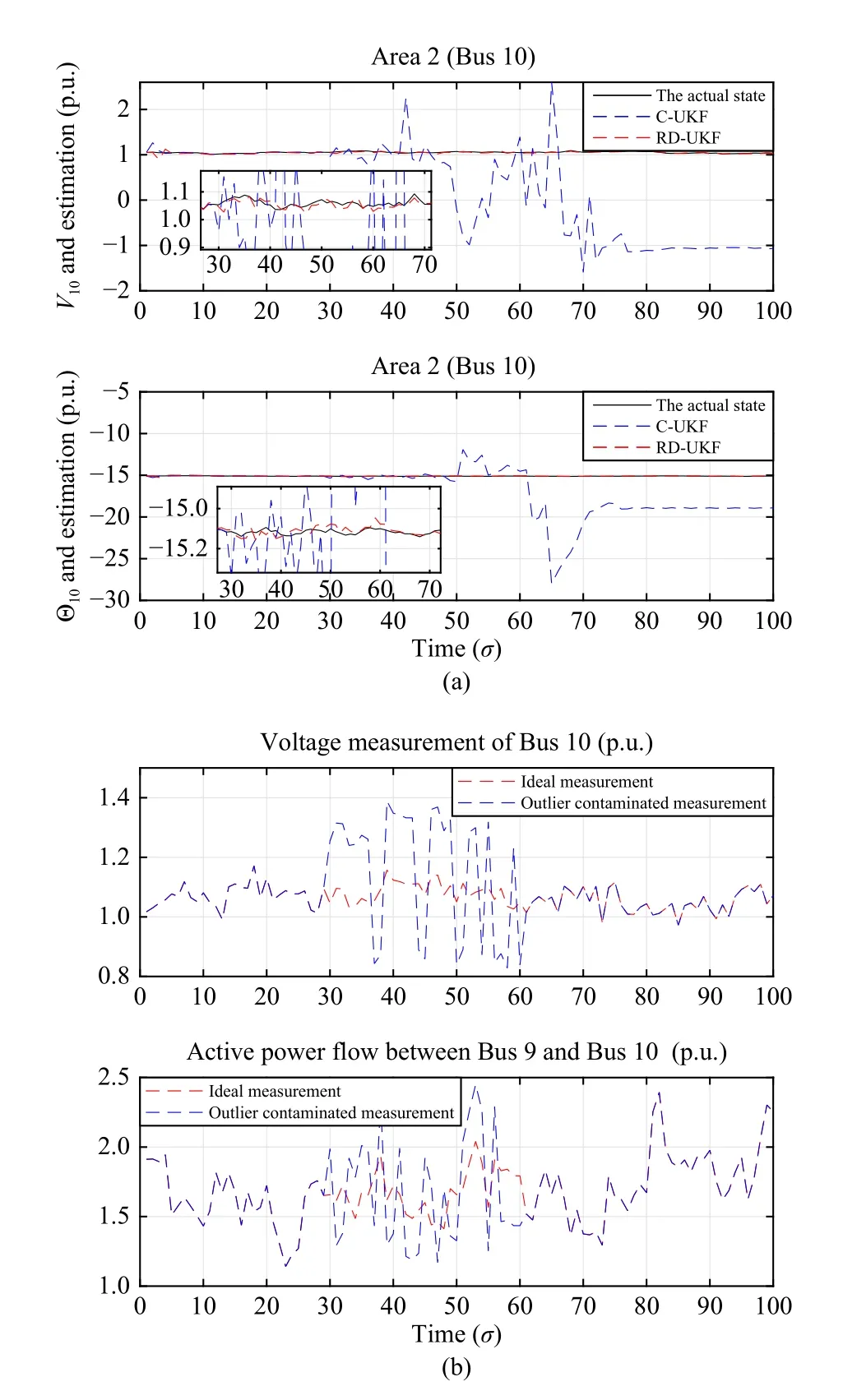
Algorithm 1 Anomaly-Resistant Decentralized SE Algorithm for Wide-Area Power Systems.m ∈V ?Xm,0|0 Pxx Initialization: For each area , initialize the parameters and and choose the weighted coefficients μ, and.In addition, set the kernel widths and and select the positive scalars and.Recursion:σ=1,2,...m,0|0 ωjm θjm(j=0,1,...,4τm) ?1 ?2 ζ? t?1: for do χj 2: Compute the sigma points with known via (16).?Xm,σ|σ-1 Pxx m,σ-1|σ-1(j=0,1,...,4τm)?Xm,σ-1|σ-1 3: Compute the local prediction state and the corresponding covariance matrices , and in terms of (18)-(23).?Xm,σ|σ-1 4: Linearize the local measurement function (7) around via (24).m,σ|σ-1 Pzzm,σ|σ-1 Pxzm,σ|σ-1 5: Construct the augmented model (25) and use the Cholesky decomposition to calculate , and in (26).ym,σ Fm,σ ξm,σ SPm,σ SVm,σ S m,σ 6: Compute , and via (28).t=0 (ˇXm,σ|σ)t(ˇXm,σ|σ)0= ?Xm,σ|σ-1 7: Set and let be the estimate at the fixed-point iterative step t.Denote as the initial iteration value.ζ>ζ? t 19: Area m computes the current state estimate and its covariance(?Xm,σ|σ)h=(Lm,σ)-1 h (ηm,σ)h(Pxx m,σ|σ)h=(Lm,σ)-1h with∑(ηm,σ)h=ˇηm,σ+HTmn,σ(ˉVnm,σ)-1h (?znm,σ)h n∈Nm(Lm,σ)h=ˇLm,σ+∑HTmn,σ(ˉVnm,σ)-1h Hmn,σ.n∈Nm 20: For each area , area m computes n ∈Nm(υnm,σ)h=Hmn,σ(Lnm,σ)-1h (ηnm,σ)h(Υnm,σ)h=Hmn,σ(Lnm,σ)-1h HTmn,σ with(ηnm,σ)h=(ηm,σ)h-HTmn,σ(ˉVnm,σ)-1h (?znm,σ)h(Lnm,σ)h=(Lm,σ)h-HTmn,σ(ˉVnm,σ)-1h Hmn,σ and sends and to area n.21: end for 22: end for(υnm,σ)h (Υnm,σ)h whereTrepresents the number of Monte Carlo simulations andT=100. In this scenario, the standard UKF-based centralized SE scheme (labeled as C-UKF) is considered for the purpose of comparison with our proposed anomaly-resistant UKF-based decentralized SE scheme (labeled as RD-UKF).In order to save space, the state trajectories of Bus 11 (in Area 1) and the state trajectories of Bus 10 (in Area 2) are taken for illustration.The simulation results are given in Figs.2 and 3.To be specific, Fig.2(a) shows the real curves of the states and the associated estimates of bus 11 in area 1, the corresponding MSEs are plotted in Fig.2(b).Similarly, the corresponding results for bus 10 in area 2 are shown in Figs.3(a) and 3(b),respectively. Fig.2.Scenario 1: Simulation results of Bus 11 for Area 1: (a) Estimated states; (b) MSE. It can be found from Figs.2 and 3 that: 1) The estimation accuracy of the C-UKF is higher than that of the RD-UKF since the measurement redundancy of the former is higher than that of the latter; and 2) The estimation accuracy of our proposed RD-UKF is acceptable. For the purpose of verifying the resistance of the developed anomaly-resistant decentralized SE scheme to the measurement outliers caused by the non-Gaussian noises, in this scenario, the following two cases are considered: Case1: The local measurements of 3 areas and their corresponding parts in the centralized measurement model are contaminated with consecutive measurement outliers.Specifically, from σ =30 to σ =60, a two-component Gaussian mixture sequence, which has zero means and covariance matrices of 0.1Iand 1 0-2Iwith weights 0.9 and 0.3, is used to model the outliers. Fig.3.Scenario 1: Simulation results of Bus 10 for Area 2: (a) Estimated states; (b) MSE. Case2: In this case, the randomly occurring measurement outliers caused by the non-Gaussian sequence are considered.The detailed parameters of the non-Gaussian sequence are similar to the one in Case 1. Similarly, only the states of Bus 11 (in Area 1) are taken for illustration in this scenario.Fig.4 shows the simulation results under Case 1.Specifically, Fig.4(a) shows the true state trajectories and the associated estimates of Bus 11 in Area 1, and the corresponding measurement curves contaminated with consecutive measurement outliers are plotted in Fig.4(b).Similarly, for Case 2, the corresponding results are plotted in Fig.5. From Figs.4-7, it can be concluded that: 1) The estimation performance of the C-UKF degrades severely in the presence of consecutive measurement outliers, while our proposed RDUKF is anomaly-resistant to such kind of measurement outliers; and 2) When the randomly occurring measurement outliers occur, the estimation performance of the C-UKF degrades severely, and the RD-UKF is still anomaly-resistant to these kinds of measurement outliers. Fig.4.Scenario 2: Simulation results of Bus 11 for Area 1 under Case 1:Consecutive measurement outliers caused by non-Gaussian noises.(a) Estimated states; (b) Measurement curves. Due to the presence of sensor saturations, gross errors and/or instrument failures, the measurements in power systems can be contaminated with bad measurements [46].In order to assess the resistance of the developed SE algorithms,the following two cases are considered: Case1: The local measurements of 3 areas and their corresponding parts in the centralized measurement model are contaminated with instantaneous errors.Specifically, when σ=50, the measurements are corrupted with 20% errors. Case2: In this case, the local measurements of 3 areas and their corresponding parts in the centralized measurement model are contaminated with consecutive errors.Specifically,from σ=30 to σ=60, the measurements are corrupted with 20% errors. For the sake of saving space, only the states of Bus 10 (in Area 2) are taken for illustration in this scenario.The simulation results under Case 1 are plotted in Fig.6.To be specific,the trajectories of the states and the associated estimates of Bus 10 in Area 2 are plotted in Fig.6(a), and the corresponds measurement curves contaminated with consecutive gross errors are plotted in Fig.6(b).Similarly, the corresponding results for Case 2 are plotted in Fig.7. Fig.5.Scenario 2: Simulation results of Bus 11 for Area 1 under Case 2:Randomly occurring measurement outliers caused by non-Gaussian noises.(a) Estimated states; (b) Measurement curves. It can be confirmed from Figs.6 and 7 that: 1) When the instantaneous bad measurements occur, the estimation performance of the C-UKF degrades severely, and the proposed RDUKF is anomaly-resistant to such kinds of gross errors; and 2)The estimates of the C-UKF are non-convergent when the consecutive bad measurements occur, while the proposed RDUKF performs well under such kinds of gross errors. The average running times (ARTs) of the above three scenarios are given in Table II.It can be confirmed from Table II that the proposed decentralized SE has much higher computational efficiency than the centralized one. Fig.6.Scenario 3: Simulation results of Bus 10 for Area 2 under Case 2:Instantaneous bad measurements.(a) Estimated states; (b) Measurement curves. Fig.7.Scenario 3: Simulation results of Bus 10 for Area 2 under Case 2:Consecutive bad measurements.(a) Estimated states; (b) Measurement curves. TABLE II AVERAGE COMPUTING TIME UNDER THREE SCENARIOS AT EACH ITERATION In this paper, the anomaly-resistant decentralized SE problem has been investigated for wide-area power systems.For the purpose of lighting the computation costs and computation burdens, a model decomposition approach has been adopted to facilitate the SE in a decentralized manner.To enhance the resistance of the proposed decentralized SE scheme against measurement with anomalies, the MEEF criterion has been utilized in the estimator design.Specifically,1) By using the augmented model which reflects the information of the local prediction errors of state and measurement, a MEEF-based cost function has been developed; 2) By solving the MEEF-based cost function with the aid of the fixed-point iteration technique, local estimates have been obtained; and 3) By integrating the edge measuring information gradually with the iterative method, the decentralized estimates have been calculated.Finally, based on the IEEE 14-bus system,three test scenarios have been considered in the simulation to verify the effectiveness of our proposed anomaly-resistant decentralized SE scheme.One of the future research directions would be to extend the main SE approach developed in this paper to other more sophisticated systems such as networked systems [47]–[53].

A. Scenario 1: Centralized Scheme Versus Decentralized Scheme
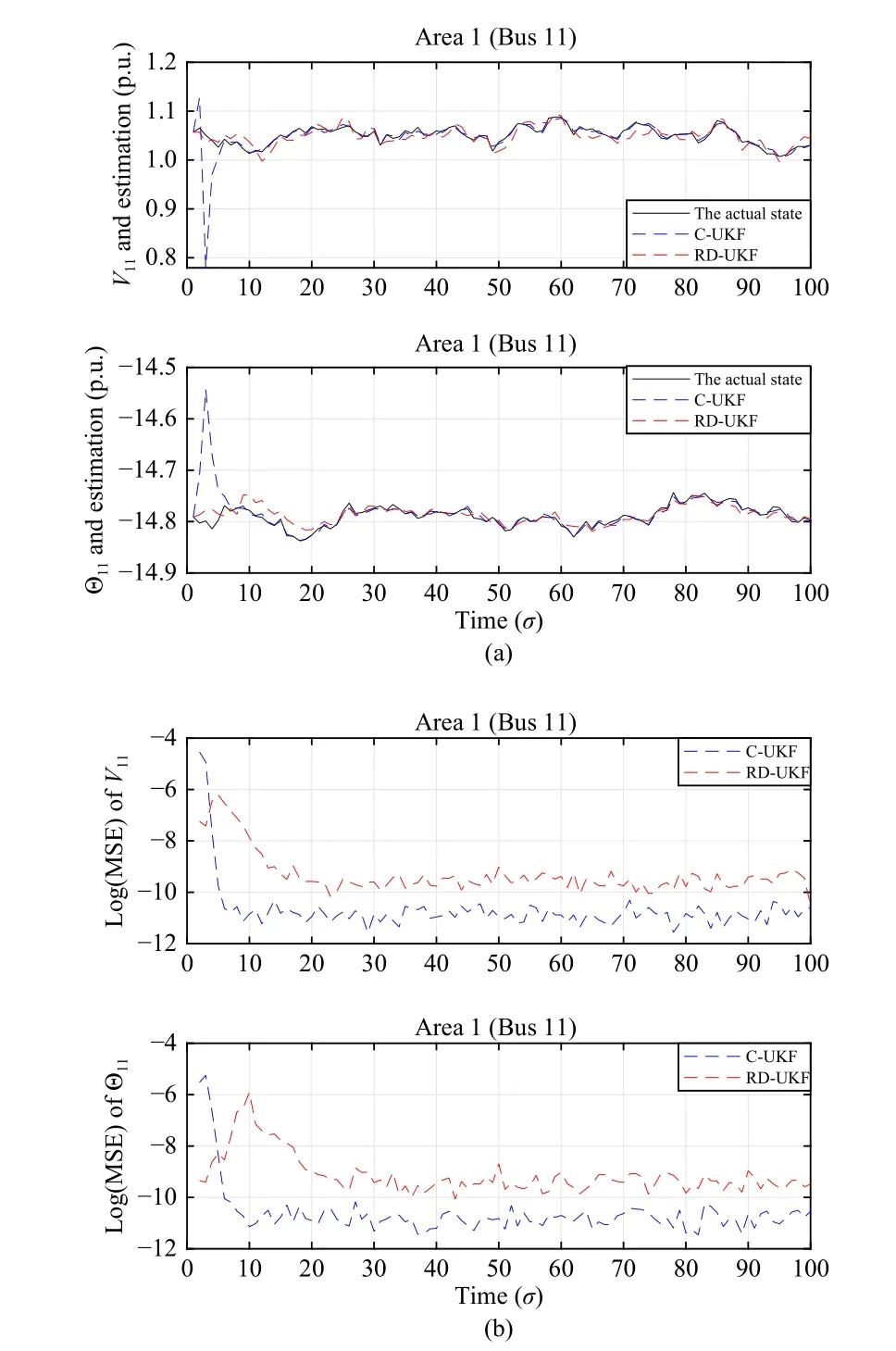
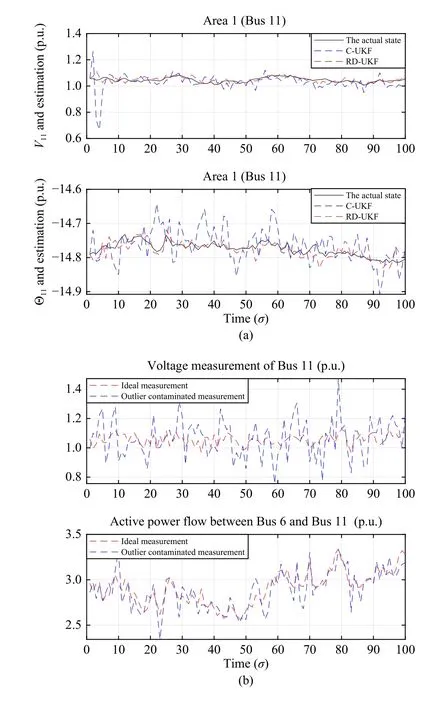
B. Scenario 2: Resistance to Measurement Outliers Caused by Non-Gaussian Sequences
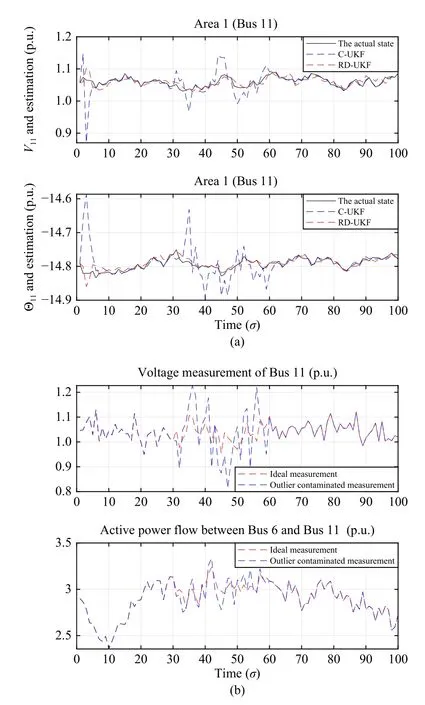
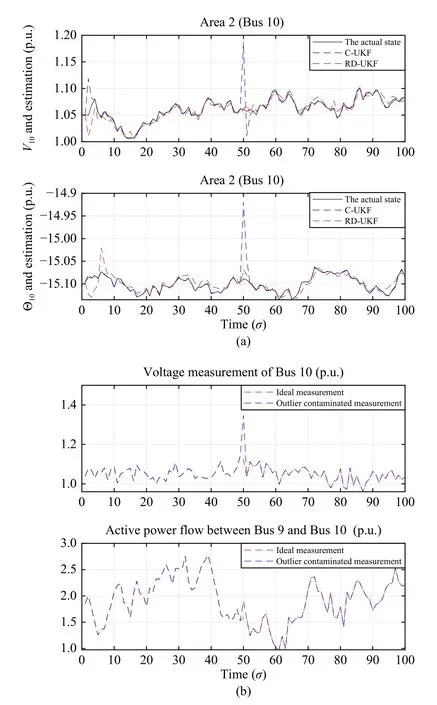
C. Scenario 3: Resistance to Bad Measurement Data
D. Computational Efficiency
VI.CONCLUSION

 IEEE/CAA Journal of Automatica Sinica2024年1期
IEEE/CAA Journal of Automatica Sinica2024年1期
- IEEE/CAA Journal of Automatica Sinica的其它文章
- Sustainable Mining in the Era of Artificial Intelligence
- Distributed Optimal Formation Control for Unmanned Surface Vessels by a Regularized Game-Based Approach
- Fixed-Time Consensus-Based Nash Equilibrium Seeking
- Control of 2-D Semi-Markov Jump Systems: A View from Mode Generation Mechanism
- Autonomous Recommendation of Fault Detection Algorithms for Spacecraft
- An Incentive Mechanism for Federated Learning: A Continuous Zero-Determinant Strategy Approach
