人口轉(zhuǎn)型中生育觀念傳播模型的建立與分析
劉子建 ,劉 銘 ,譚遠順 ,楊 金 ,龐建華
(1.重慶交通大學(xué) 數(shù)學(xué)與統(tǒng)計學(xué)院,重慶 400074;2.廣西科技大學(xué) 理學(xué)院,廣西柳州 545006)
§1 引言
人口轉(zhuǎn)型(Demographic Transition),是指一個國家或地區(qū)從工業(yè)化前的經(jīng)濟體制向工業(yè)化經(jīng)濟體制過渡時,伴隨著的從高出生率高死亡率到高出生率低死亡率,再到低出生率低死亡率的現(xiàn)象[1-3].人口轉(zhuǎn)型與生育率和老齡化,與人力資本和經(jīng)濟增長,與技術(shù)進步和農(nóng)業(yè)人口轉(zhuǎn)化,與收入分配和教育特別是女性教育等關(guān)系密切,眾多學(xué)者已詳細研究了人口轉(zhuǎn)型的原因及所帶來的經(jīng)濟和社會影響[4-10].文獻[4]分析我國第七次人口普查數(shù)據(jù),發(fā)現(xiàn)我國人口發(fā)展的主要矛盾正在從數(shù)量性壓力向結(jié)構(gòu)性壓力轉(zhuǎn)化,提出我國應(yīng)明確人口新國情定位,順應(yīng)人口新國情要求,普及人口新國情教育,深化體制機制改革,創(chuàng)新社會治理新格局的重要建議.文獻[5]分析了黑龍江省人口老齡化特征及老齡問題的成因,討論了老齡化在勞動力供給,政府財政和創(chuàng)新創(chuàng)業(yè)方面對黑龍江省社會經(jīng)濟產(chǎn)生的負向效應(yīng),建議從優(yōu)化勞動力供給結(jié)構(gòu),增強財政可持續(xù)性,鼓勵“銀色創(chuàng)業(yè)”三個方面進行應(yīng)對.文獻[6]綜述了中國人口與經(jīng)濟問題的關(guān)系,指出人口結(jié)構(gòu)而非人口總量才是影響經(jīng)濟增長的主要因素.文獻[8]指出了農(nóng)業(yè)人口的轉(zhuǎn)型提高了農(nóng)業(yè)勞動力的人力資本水平,帶來了人口,物質(zhì),資本等農(nóng)業(yè)技術(shù)進步所需的保障,推動了技術(shù)的進步,保證了農(nóng)業(yè)的可持續(xù)增長.文獻[9]利用具有內(nèi)生儲蓄和人力資本投資決策的代際重疊模型評估了中國人口變化對人力資本積累和總產(chǎn)出的影響.結(jié)果表明,與現(xiàn)狀相比,教育份額和人均收入將隨著生育率的反彈而下降,教育政策在減輕與高生育率相關(guān)的不良后果方面有效.文獻[10]從理論和實證兩方面研究了發(fā)展中國家的教育,性別差距和人口轉(zhuǎn)型的關(guān)系,得到了技術(shù)進步解放了家務(wù)勞動從而導(dǎo)致了最初人口出生率增加,女性參加社會勞動的增加提升了教育的機會成本進而導(dǎo)致生育率下降,女孩教育投入的增加,性別教育差距的降低,提高了平均人力資本,加速了技術(shù)進步和經(jīng)濟增長的結(jié)論.
人口轉(zhuǎn)型的直接結(jié)果是出生率和死亡率的變化.發(fā)達國家諸如美國,日本,德國等國家均在工業(yè)革命后進入了人口轉(zhuǎn)型期.目前絕大多數(shù)發(fā)達國家已接近或完成人口轉(zhuǎn)型,其死亡率和出生率均處于新的低水平上[3].我國因為較長一段時間的計劃生育政策,出生率呈快速下降趨勢.人口死亡率隨著生活和醫(yī)療技術(shù)的提高,也呈下降趨勢,但人口的自然增長率在近10 年下降較快,尤其2020 年僅有1.45 ‰(如圖1 (a)).我國不同省份的人口自然增長率差距也較大,且并不樂觀(如圖1 (b)),這其中有人口流動的影響,但出生率的影響更為重要.聯(lián)合國《世界人口發(fā)展展望(2019)》采用高,中,低三個方案(總和生育率—每個婦女育齡期生育孩子的總數(shù)—水平分別取2.3,1.8,1.3)對我國的總和生育率進行了預(yù)測(如圖2),顯示我國未來生育水平既有實現(xiàn)適度生育水平的可能性,更有停留在超低生育率水平的風(fēng)險,表明未來生育政策優(yōu)化及生育友好環(huán)境的重構(gòu)將是關(guān)鍵.因此,研究群體生育觀念及國家生育政策的改變對生育觀念的影響具有現(xiàn)實意義.本文將具體研究人口轉(zhuǎn)型過程中生育觀念的傳播對我國低生育率現(xiàn)象和人口增長的影響.
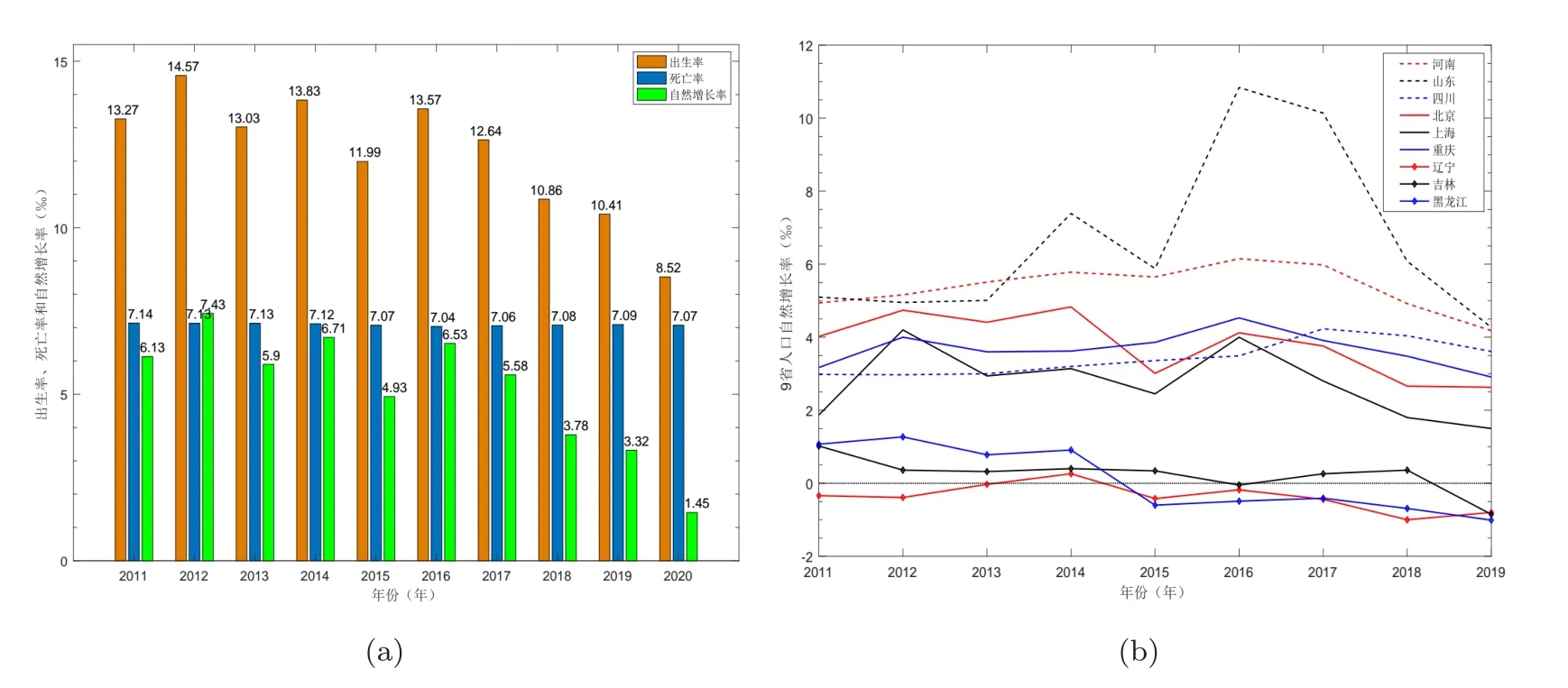
圖1 (a) 2011-2020年我國人口的出生率,死亡率和自然增長率(數(shù)據(jù)來源:國家統(tǒng)計局) (b) 2011-2019年河北,山東,四川,北京,上海,重慶,遼寧,吉林,黑龍江9省市的人口自然增長率情況(數(shù)據(jù)來源:國家統(tǒng)計局)
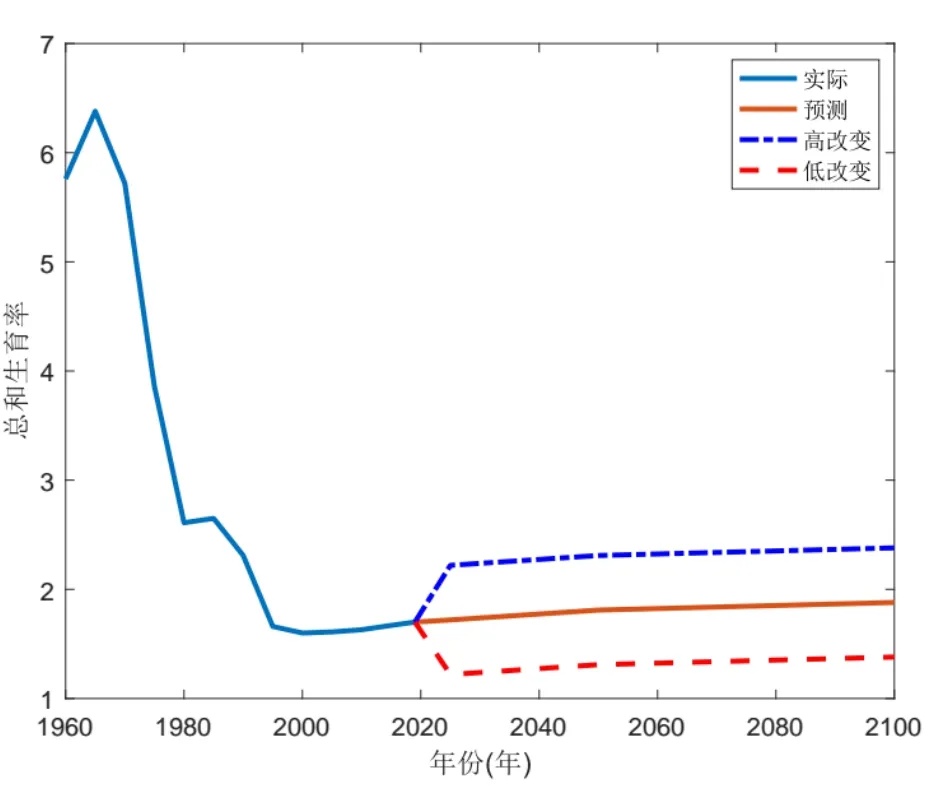
圖2 1960-2100年我國總和生育率變化及未來走向(數(shù)據(jù)來源:World Population Prospects 2019)
§2 模型建立
觀念的傳播和擴散問題,可以借助傳染病模型進行建模研究.基于傳染病模型并考慮個體接觸傳播這一假設(shè),越來越多的學(xué)者利用傳染病模型研究具有社會互動影響行為的諸如成癮行為[11-13](吸煙,吸毒,飲酒等),觀念認同度[14-17](幸福觀,生育觀,社會輿論,媒體影響)和飲食失衡或肥胖現(xiàn)象[18-19]等的傳播特性,傳播規(guī)律及社會影響.文獻[14]建立了具有自發(fā)行為的SIRS謠言傳播微分方程模型,指出了影響謠言傳播的主要因素并提出謠言治療策略.文獻[20]建立SIS模型研究了具有從眾偏見的文化特質(zhì)傳播問題,并將研究結(jié)果應(yīng)用到酗酒行為.文獻[21]結(jié)合傳染病模型和Lotka-Volterra系統(tǒng),建立模型
來刻畫數(shù)量增加或衰減種群中生育觀念的傳播問題.其中S(t)表示t時刻高生育群體個體數(shù)量,即易感群體個體數(shù)量,I(t)表示t時刻低生育群體個體數(shù)量,即感染群體個體數(shù)量.b1和b2分別是易感群體和感染群體的Malthus增長參數(shù),滿足b1>b2.β>0為傳染系數(shù).作者研究指出,當(dāng)生育觀念侵入指數(shù)大于1 時,生育觀念侵入成功,人口轉(zhuǎn)型將會發(fā)生.本文考慮國家人口政策對我國人口出生率和總和生育率的影響[22-24],改進Inaba的模型,建立了考慮國家生育政策且具有飽和發(fā)生率的生育觀念傳播模型
(1)式中,a為國家對生育政策的干預(yù)力度.N=S+I.假設(shè)模型(1)中參數(shù)滿足條件
(JS1)b1>0,b1>b2,β>0,k>0,a ≥0.
注1b2可正可負,b2>0表示低生育群體的出生率大于死亡率,b2<0表示低生育群體的出生率小于死亡率,a>0指國家采取鼓勵生育的政策.
若無特別說明,本文總是假設(shè)條件(JS1)成立.記(1)式中第一個式子右端為g1(S,I),第二個式子右端為g2(S,I).論文首先研究了在無國家生育政策干預(yù)下生育觀念傳播模型的動力學(xué)行為.進一步討論了國家實施鼓勵生育政策后,生育觀念的傳播特性及我國人口的變化情況.最后通過數(shù)值例子討論了國家生育政策干預(yù)力度對我國人口增長的影響.
§3 主要結(jié)論
本節(jié)將分析在無或有國家鼓勵生育政策情況下(1)式的動力學(xué)行為,并說明這些動力學(xué)行為所蘊含的實際意義.
首先說明解的非負性.對任意非負初值(S(0),I(0)),由系統(tǒng)(1),對?t>0有
假設(shè)(JS1)保證a ≥0,從而
即對任意非負初值,系統(tǒng)(1)的解非負.此結(jié)論亦完全符合實際生物學(xué)意義.
3.1 無國家生育政策干預(yù)(a=0)
此時模型(1)變?yōu)?/p>
(2)式中令g1(S,I)=g2(S,I)=0,有g(shù)1(S,I)+g2(S,I)=b1S+b2I=0.顯然系統(tǒng)(2)必存在零平衡點E0=(0,0).進一步,因為b1>0,易知b2≥0時,系統(tǒng)(2)無正平衡點;而當(dāng)b2<0時,有S=-b2I/b1,此時可建立系統(tǒng)存在正平衡點條件.
(1A) b2 >0
令v=I/N,顯然0≤v ≤1.此時u=S/N=1-v.系統(tǒng)(2)兩方程相加有
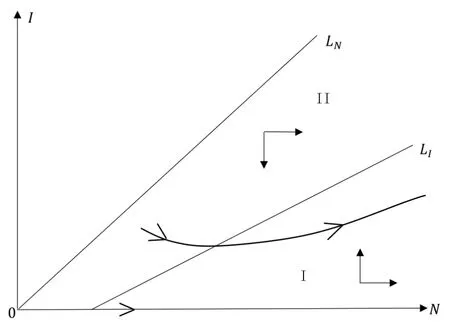
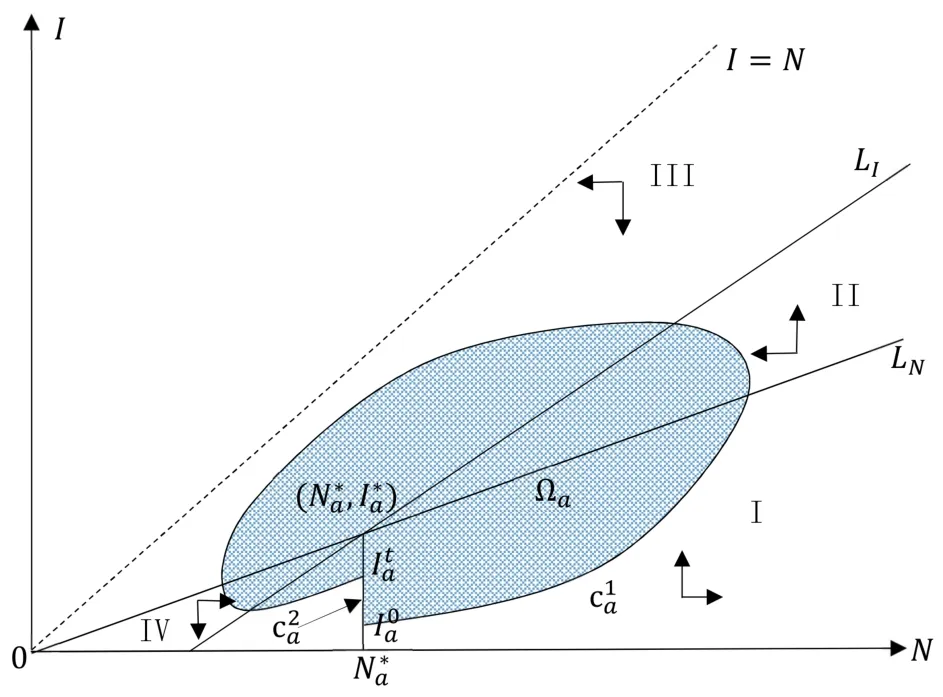
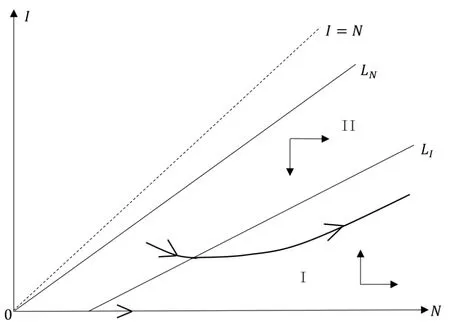
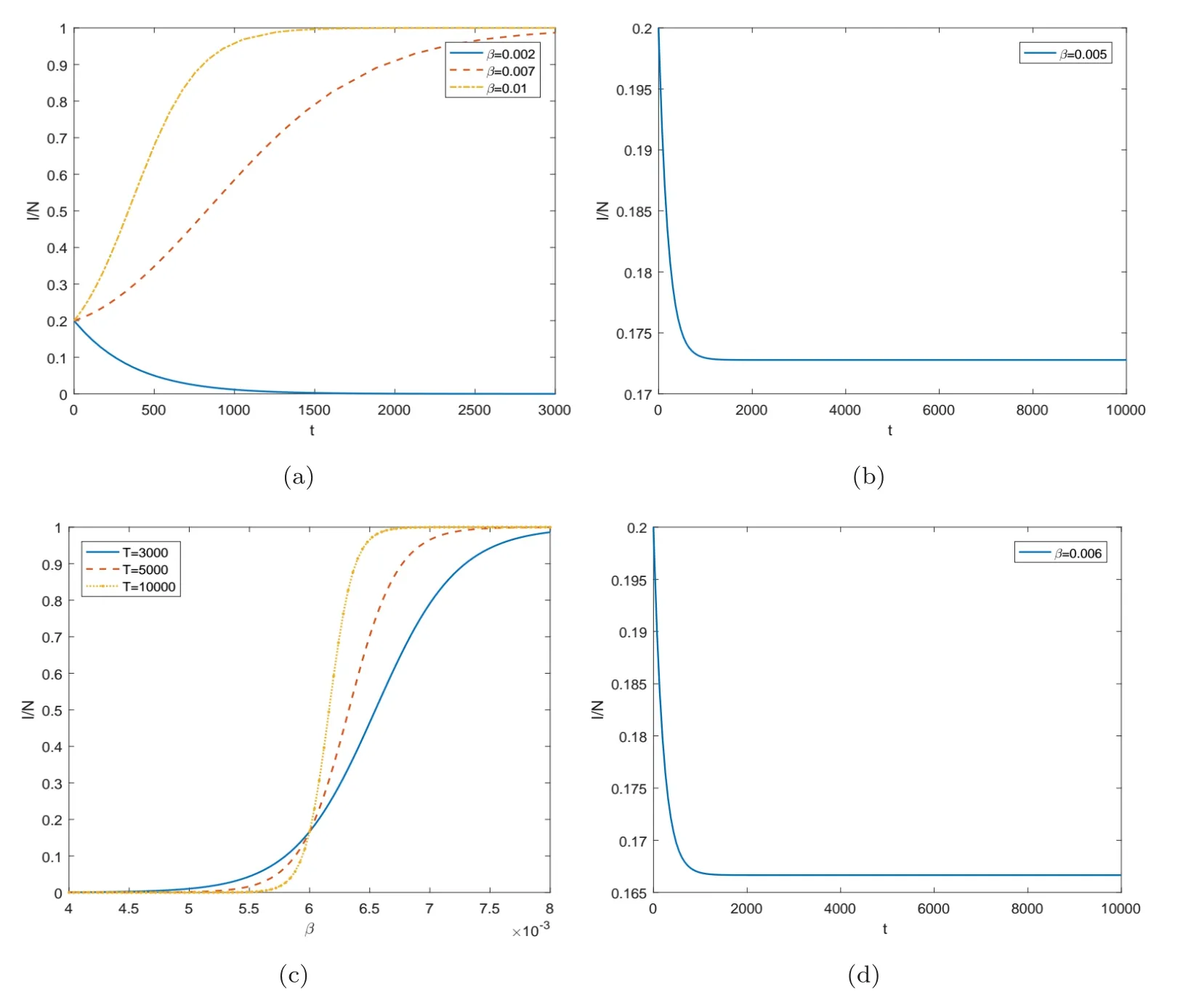
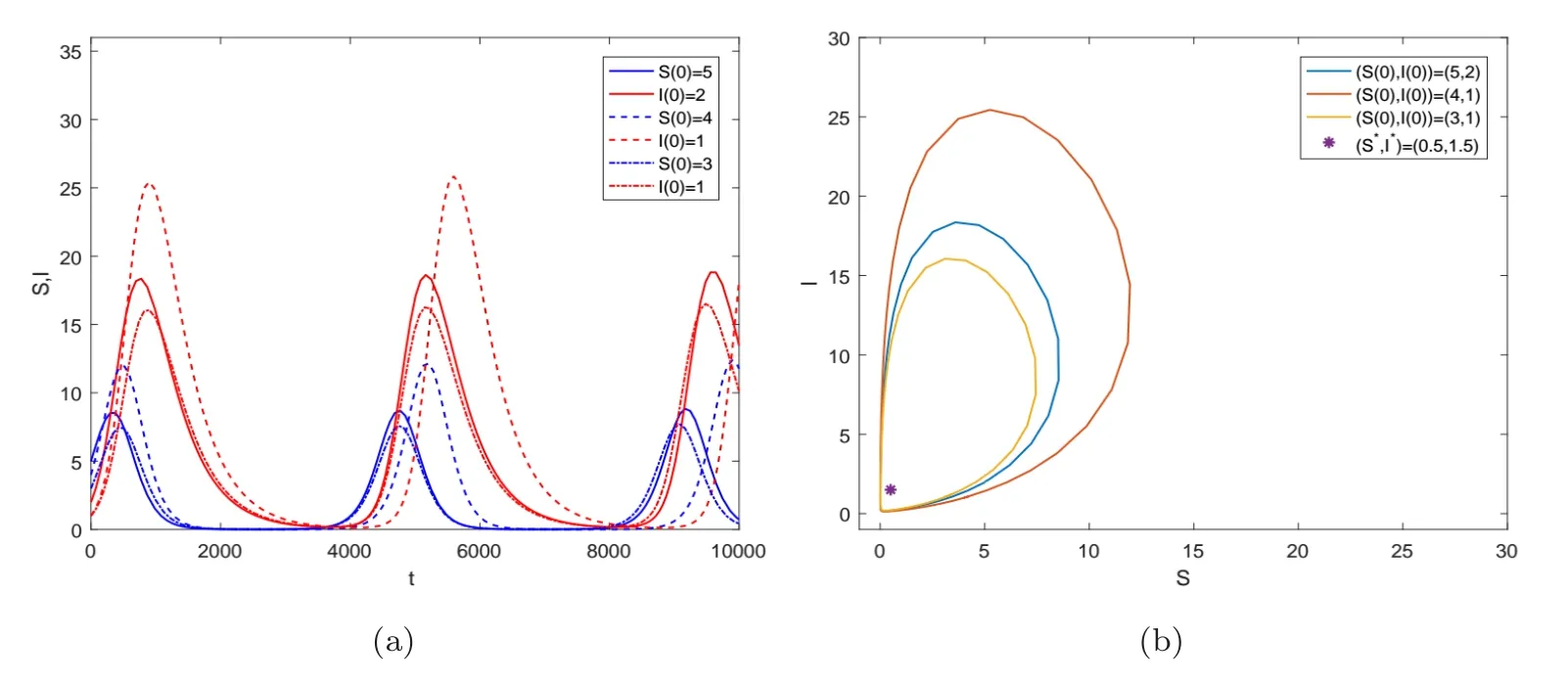
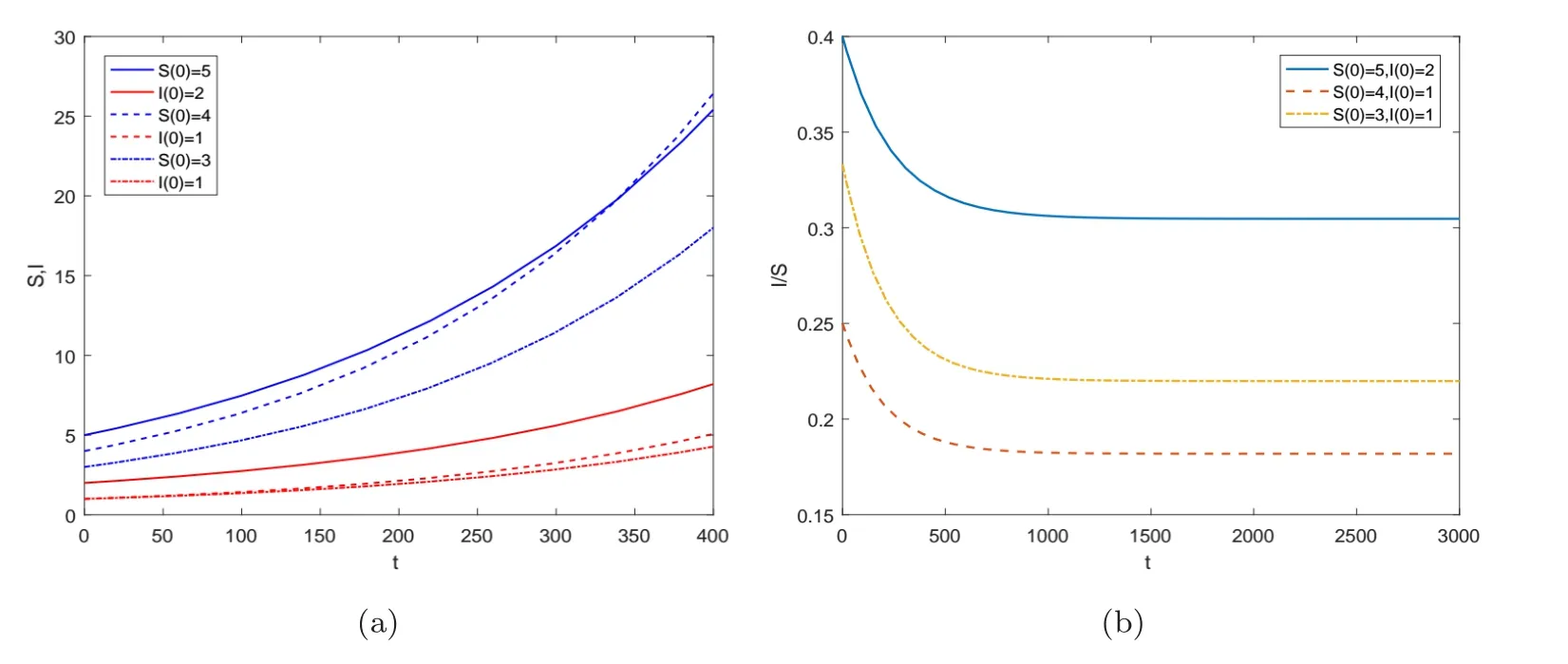
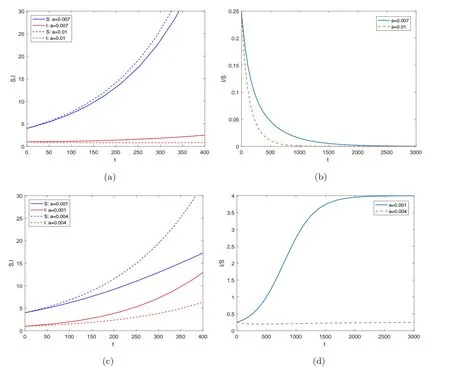
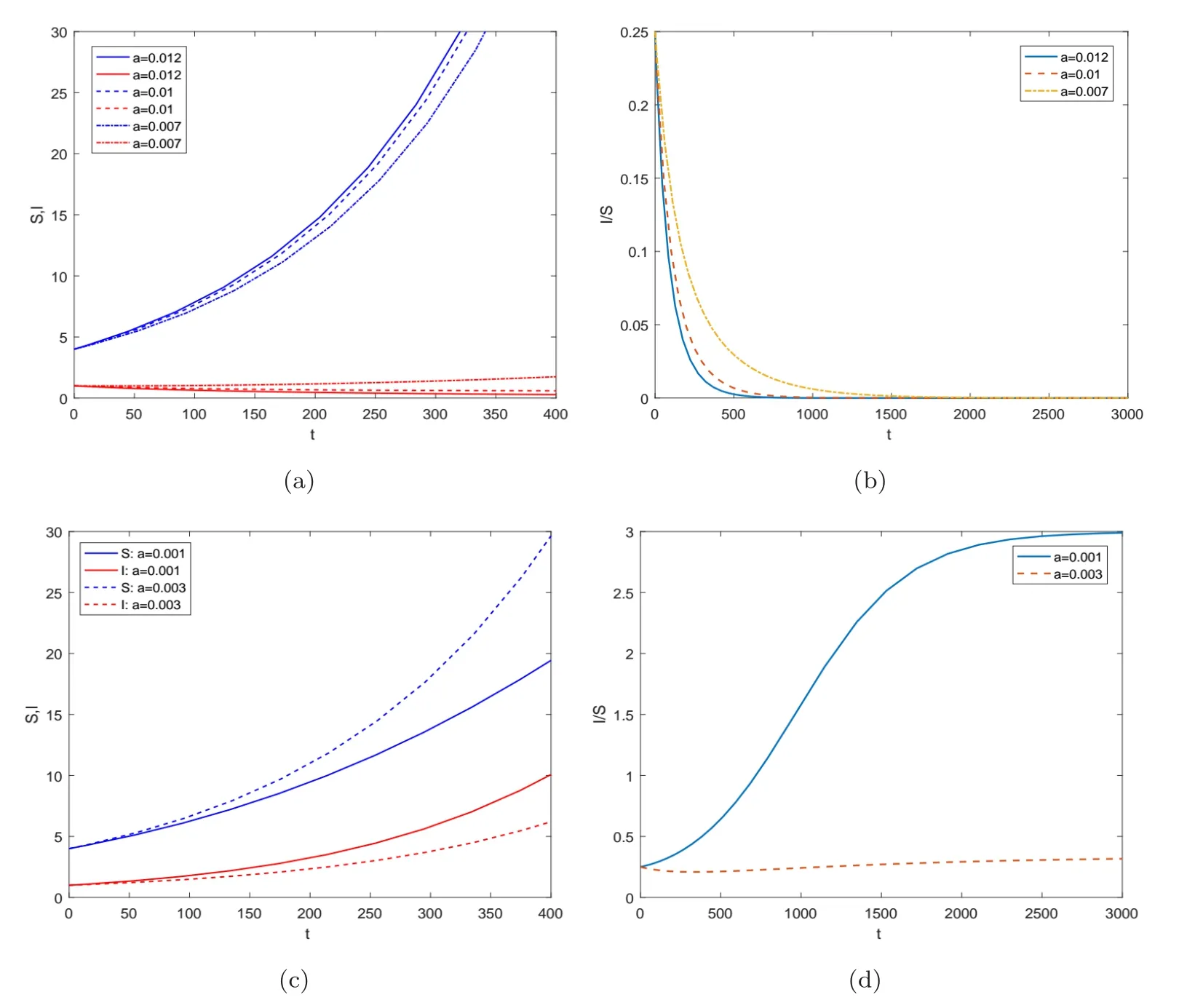
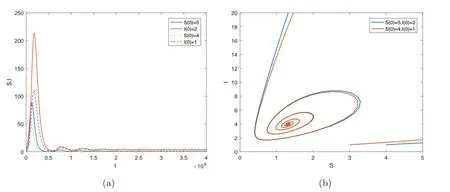
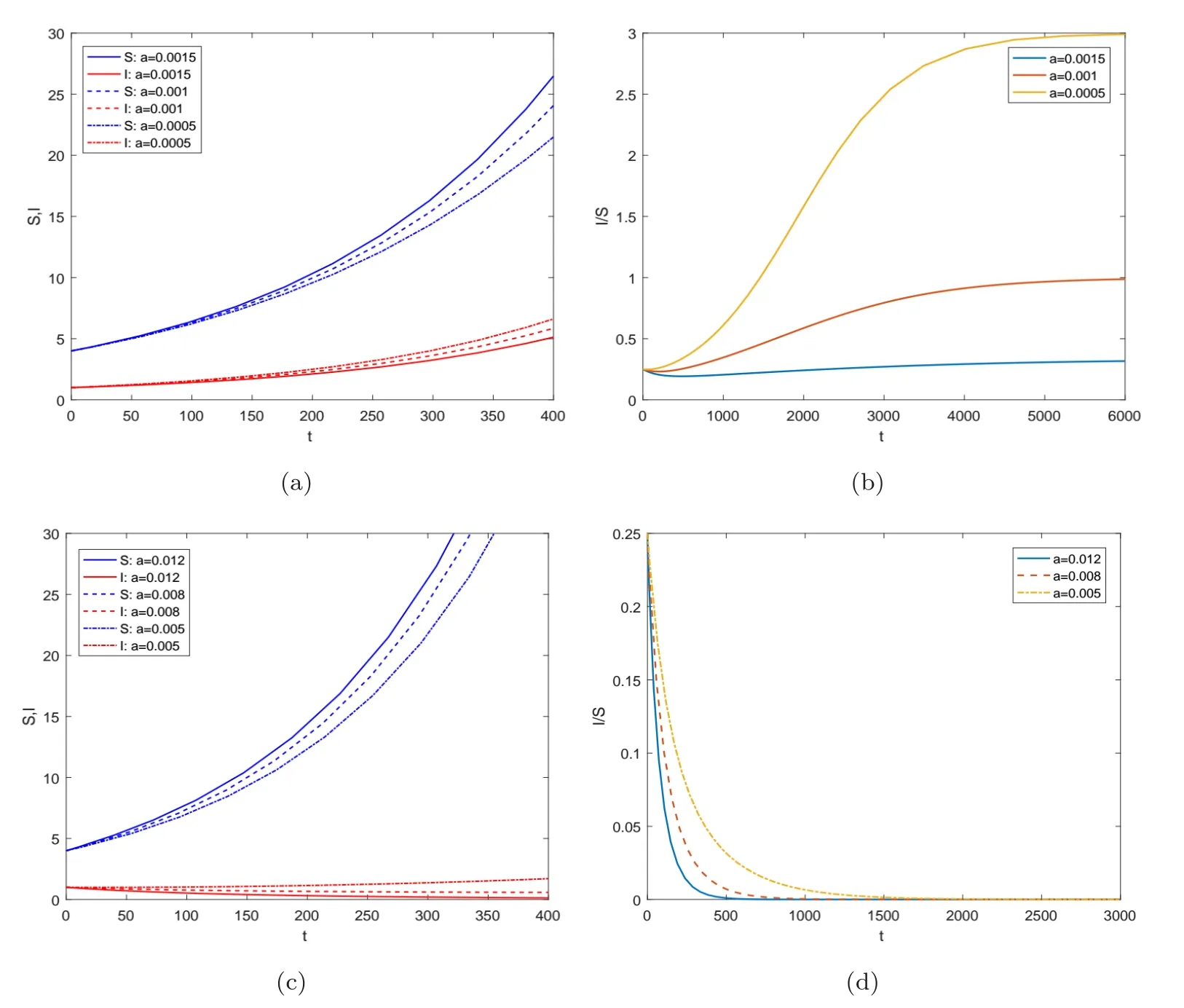
這里h(N)=b1-b2-β(1/N+k)-1.假設(shè)0 記h∞=limN→∞h(N)=b1-b2-β/k,則對所有N>0 都有h(N)≥h∞. 當(dāng)h∞>0時 當(dāng)h∞<0時,存在?0>0 使得h∞+?0<0.此?0,(3)式說明存在T>0,當(dāng)t>T時,N(t)滿足h(N(t)) 綜上,當(dāng)t →∞時有 定義生育觀念侵入指數(shù) 顯然 依據(jù)低生育群體在總?cè)丝谥腥丝跀?shù)量占比,給出生育觀念侵入成功的定義. 定義1若limt→∞v(t)=1,則稱生育觀念侵入成功且為完全侵入.若0 有如下結(jié)論. 定理1當(dāng)?shù)蜕后w自然增長率b2>0時,若生育觀念侵入指數(shù)R>1,則低生育群體的生育觀念完全侵入到高生育群體;若R<1,則生育觀念侵入不成功. 注2若b2>0,R=1,未能理論證明確切結(jié)論.數(shù)值實驗可證明其會發(fā)生不完全的生育觀念侵入,如圖9 (b).注意到,例證雖具有局限性,但卻能夠說明會發(fā)生不完全生育觀念侵入這一事實. 注3當(dāng)b2=0時,若傳染系數(shù)小于高生育群體的自然增長率,即β (1B) b2 <0 將S=-b2I/b1代入g1(S,I)=0,易解得 為(6)式定義的侵入指數(shù).顯然,在假設(shè)(JS1)和(1B)下,系統(tǒng)(2)正平衡點E?=(S?,I?)存在的充要條件為R>1.下面分析系統(tǒng)(2)在E0和E?處的穩(wěn)定性情況. 系統(tǒng)(2)的Jacobian矩陣為 對于平衡點E0=(0,0),有=J(0,0)=diag(b1,b2).又b1>0,b2<0,易得如下定理. 定理2系統(tǒng)(2)的零平衡點E0=(0,0)恒存在,且是不穩(wěn)定的鞍點. 若生育觀念侵入指數(shù)R>1,則正平衡點E?=(S?,I?)存在.對于正平衡點E?,有 設(shè)JE?的兩個特征值分別為λ1和λ2,有 可見在正平衡點E?存在的條件下,JE?的兩個特征值為一對純虛根.E?是一個中心.下面定理進一步表明E?的全局性態(tài). 定理3當(dāng)?shù)蜕后w的自然增長率b2<0時,若生育觀念侵入指數(shù)R>1,則系統(tǒng)(2)的正平衡點E?=(S?,I?)存在,且是一個全局中心,即除(S?,I?) 外的所有軌線都是包含(S?,I?)的周期軌. 為證明此結(jié)論,先證明下面兩個命題. 命題1假設(shè)R>1,任取一從(S?,I0) (I0 圖3 b2 <0, R >1時系統(tǒng)(2)的等傾線及軌線走向示意圖 最終p(x)=0在區(qū)間(-I0,I?-I0)內(nèi)有唯一解x=0,即p(I1-I0)=0當(dāng)且僅當(dāng)I1=I0時成立.證畢. 命題2假設(shè)R>1,則從區(qū)域I出發(fā)的軌線必與等傾線LS相交進入?yún)^(qū)域II,如圖3所示.這里L(fēng)S的表達式為 證一方面,若軌線不離開區(qū)域I,則它將保持在LS下方,此時I/S必有上界. 則易得limt→∞I/S=∞,進而與I/S有界矛盾.下證(11)式成立. 對任意z>S?,記Gz={(S,I):S>z,I 下面證明定理3. 證設(shè)I0 ①進入?yún)^(qū)域III 然后趨向于(S?,I?),如圖4 (a). 圖4 b2 <0, R >1時系統(tǒng)(2)的等傾線及軌線走向示意圖(a) 經(jīng)區(qū)域III然后趨向于(S?,I?) (b) 經(jīng)區(qū)域III和IV進入?yún)^(qū)域I,然后趨向于(S?,I?) ②經(jīng)區(qū)域III 和IV 進入?yún)^(qū)域I,然后趨向于(S?,I?),如圖4 (b). ③經(jīng)區(qū)域III 和IV 進入?yún)^(qū)域I,然后交S=S?于I1.由命題1 知,I1=I0,即Γ為一周期軌. 下說明情況①和②不成立. 這里α=β(kb1)-1.由命題1的分析知,(12)式成立當(dāng)且僅當(dāng)I?-I0=0.這與I0 至此得,所有與線段M={(S?,I) :I ∈(0,I?)}相交的軌線必是周期軌.由命題1和命題2,從任意點出發(fā)的軌線如果不與M相交,則必趨向于(S?,I?).那么它必交于從(S?,I0)(I0 下面考慮生育觀念侵入指數(shù)R<1時,系統(tǒng)的動力學(xué)行為.有如下結(jié)論. 定理4當(dāng)?shù)蜕后w的自然增長率b2<0時,若β<-kb2+kb1,即生育觀念的侵入指數(shù)R<1,則低生育群體到高生育群體的生育觀念侵入不成功.具體為 (i) 若β<-kb2,則I(t)→0,S(t)→N(t)→∞,t →∞,即若生育觀念的傳染力度無法抵消低生育群體的人口減少時,低生育群體人口數(shù)量將趨向于0,高生育群體人口數(shù)量將趨向于總?cè)丝跀?shù)量且最終以Malthus 增長指數(shù)b1進行指數(shù)增長; (ii) 若β=-kb2,則I(t)≤I(0),S(t)→N(t)→∞,t →∞,即若生育觀念的傳染力度恰好抵消低生育群體的人口減少時,低生育群體人口數(shù)量將不再增加,高生育群體人口數(shù)量將趨向于總?cè)丝跀?shù)量且最終以Malthus 增長指數(shù)b1進行指數(shù)增長; (iii) 若β>-kb2,但β<-kb2+kb1,則 即若生育觀念的傳染力度能夠抵消低生育群體的人口減少速度但其余力不足以影響高生育群體的出生率時,低生育群體和高生育群體人口數(shù)量最終將分別以Malthus 增長指數(shù)b2+β/k和b1進行指數(shù)增長,低生育群體的人口增長速度將緩于高生育群體,生育觀念侵入不成功. 即S(t)→∞,t →∞.從而N →∞且v=I/N →0,t →∞,由(5)式易得結(jié)論成立. (ii)β=-kb2.對任意初值(S(0),I(0))>0,由系統(tǒng)(2) 知≤I(b2+β/k),即I(t)≤I(0)對所有t ≥0 成立.進而有 下證S(t)→∞,t →0. 知I(t)→0,t →∞.從而易得S(t)→∞,t →0.故在β=-kb2時,有N →∞且v=I/N→0,t →∞,由(5)式立得結(jié)論成立. (iii)β>-kb2.下面將分三種情況說明S(t)→∞,t →∞. (iii-a) 若β 知,S(t)→∞,t →∞成立. (iii-b) 若β=kb1,則系統(tǒng)(2)的兩條等傾線分別為I軸和 如圖5 (a)所示.易知系統(tǒng)(2)只有唯一的零平衡點,且無閉軌.由于(0,0)是以I軸為穩(wěn)定流形的鞍點,故沒有軌線趨于(0,0).由Poincare-Bendixson定理[25,26],所有軌線必?zé)o界.而區(qū)域II中有<0,故區(qū)域II中所有軌線必會隨S增加穿過LI進去區(qū)域I.在區(qū)域I中,有I<-S(β+kb2)/(kb2)-1/k.故從區(qū)域區(qū)I出發(fā)的解滿足 圖5 b2 <0, R <1時系統(tǒng)(2)的等傾線及軌線走向示意圖(a) 無內(nèi)部平衡點,區(qū)域II的軌線均進入?yún)^(qū)域I (b) 無內(nèi)部平衡點,區(qū)域III和區(qū)域II的軌線均進入?yún)^(qū)域I 圖6 系統(tǒng)(20)的等傾線及軌線走向示意圖 圖7 b2 <0,>1時系統(tǒng)(24)的等傾線及軌線走向示意圖 從而有S(t)→∞,t →∞. (iii-c) 若β>kb1但β<-kb2+kb1,則系統(tǒng)(2)兩等傾線分別為 如圖5 (b).同(iii-b)的分析,從區(qū)域II和區(qū)域III出發(fā)的軌線必進入?yún)^(qū)域I,從而最終有S(t)→∞,t →∞成立. 故β>-kb2時,均有S(t)→∞,t →∞.進而有N →∞且v=I/N →0,t →∞,由(5)式易得結(jié)論成立. 注4在b2<0時,若生育觀念的傳染力度在抵消低生育群體的人口減少速度后其余力仍與高生育群體的自然增長率相當(dāng),即β=-kb2+kb1時,則R=1,理論上無法證得低生育群體到高生育群體的生育觀念侵入情況.但第四節(jié)數(shù)值例子表明,此種情況下,低生育群體和高生育群體的人口數(shù)量最終將以相同的Malthus 增長指數(shù)進行增長,見圖12.此時,發(fā)生不完全的生育觀念侵入. 此時,在條件(JS1)下研究模型(1)的動力學(xué)行為,并分析這些動力學(xué)行為所蘊含的實際意義. (2A) b2 >0 令v=I/N,顯然0≤v ≤1.此時u=S/N=1-v.類似(C1-B)的分析易知 從而,有如下結(jié)論. 定理5在國家采取鼓勵生育政策下,即a>0,若低生育群體自然增長率b2>0,則當(dāng)生育觀念侵入指數(shù)Ra ≤1時,低生育群體對高生育群體的的生育觀念侵入不成功,低生育群體和高生育群體的人口數(shù)量最終將分別以Malthus增長指數(shù)b2-a+β/k和b1進行指數(shù)增長.而當(dāng)生育觀念侵入指數(shù)Ra>1時,低生育群體到高生育群體有生育觀念侵入,但不能完全同化高生育群體,即發(fā)生生育觀念的不完全侵入.隨著時間增大,低生育和高生育群體人口數(shù)量將以比例:a達到平衡并都指數(shù)增長,其最終的指數(shù)增量率均為 注5定理5表明,在國家采取鼓勵生育政策下,不會出現(xiàn)低生育群體的生育觀念完全侵入高生育群體的情形,即v →1,t →∞的情形. 注6由生育觀念侵入指數(shù)Ra的表達式 及定理5可知,國家鼓勵生育政策的力度a的大小直接影響到生育觀念是否能夠侵入.在參數(shù)β,k,b1,b2固定的情況下,國家鼓勵生育政策的力度越大,即a越大,越不易發(fā)生低生育群體到高生育群體的生育觀念侵入. (2B) b2=0 此時系統(tǒng)(1)變?yōu)?/p> 由(19)中I的方程易知,β/k與a的大小關(guān)系將決定I群體的人口數(shù)量.類似定理4的分析: 當(dāng)β 當(dāng)β=ka時,有I(t)≤I(0),S(t)→N(t)→∞,t →∞,從而v=I/N →0,t →∞; 當(dāng)β>ka時,考慮輔助系統(tǒng) 這里N=S+I.該系統(tǒng)的兩條等傾線為 定理6當(dāng)?shù)蜕后w的自然增長率b2=0時,低生育群體到高生育群體的生育觀念侵入不成功.具體為 (i) 若a>β/k,則I(t)→0,S(t)→N(t)→∞,t →∞,即若國家鼓勵生育政策的力度大于生育觀念的傳染力度時,低生育群體人口數(shù)量將趨向于0,高生育群體人口數(shù)量將趨向于總?cè)丝跀?shù)量且最終以Malthus 增長指數(shù)b1進行指數(shù)增長; (ii) 若a=β/k,則I(t)≤I(0),S(t)→N(t)→∞,t →∞,即若國家鼓勵生育政策的力度恰好與生育觀念的傳染力度相當(dāng)時,低生育群體人口數(shù)量將不再增加,高生育群體人口數(shù)量將趨向于總?cè)丝跀?shù)量且最終以Malthus增長指數(shù)b1進行指數(shù)增長; (iii) 若a<β/k.進一步,若a ≥β/k-b1,此時≥0,則 即若國家鼓勵生育政策的力度不小于低生育群體的生育觀念對高生育群體自然增長率的影響力度時,低生育群體和高生育群體人口數(shù)量最終將分別以Malthus增長指數(shù)-a+β/k和b1進行指數(shù)增長. 若a<β/k-b1,此時<0,則 即若國家鼓勵生育政策的力度未能彌補低生育群體的生育觀念對高生育群體自然增長率的影響時,低生育群體和高生育群體人口數(shù)量最終將以相同的Malthus增長指數(shù)-ab1/(-a)進行指數(shù)增長,其人口數(shù)量比例穩(wěn)定在:a. (2C) b2 <0 當(dāng)b2<0時,系統(tǒng)(1)的非零平衡點為 系統(tǒng)(1)的Jacobian矩陣為 必有λ1<0,λ2<0,從而有如下定理. 基于N=S+I,考慮輔助系統(tǒng) 命題3系統(tǒng)(24)無周期軌. 這里α=-b1/b2.下尋找(25)中不等式成立的條件. 證一方面,若軌線不離開區(qū)域I,則它將保持在LN下方,此時I/N必有上界. 則易得limt→∞I/N=∞,進而與I/N有界矛盾.下證(26)式成立. 基于命題3-命題5,可證明如下結(jié)論. 由命題6,易得系統(tǒng)(1)正平衡點的全局穩(wěn)定性. 定理10當(dāng)?shù)蜕后w的自然增長率b2<0時,若a ≥β/k+b2-b1-b1(β/k/(b1-b2)-1),即≤1,則 (i) 若a>β/k+b2,則I(t)→0,S(t)→N(t)→∞,t →∞,即國家鼓勵生育政策的力度大于生育觀念的傳染力度與低生育群體的人口增長速度之和時,低生育群體人口數(shù)量將趨向于0,高生育群體人口數(shù)量將趨向于總?cè)丝跀?shù)量且最終以Malthus增長指數(shù)b1進行指數(shù)增長,此時低生育群體到高生育群體的生育觀念侵入不成功; (ii) 若a=β/k+b2,則I(t)≤I(0),S(t)→N(t)→∞,t →∞,即國家鼓勵生育政策的力度與生育觀念的傳染力度和低生育群體的人口增長速度之和相當(dāng)時,低生育群體人口數(shù)量將不再增加,高生育群體人口數(shù)量將趨向于總?cè)丝跀?shù)量且最終以Malthus增長指數(shù)b1進行指數(shù)增長,此時低生育群體到高生育群體的生育觀念侵入不成功; (iii) 若a<β/k+b2.進一步,若a ≥β/k+b2-b1,此時≥0,則 即若國家鼓勵生育政策的力度雖不及生育觀念的傳染力度與低生育群體的人口增長速度之和但足以彌補他們對高生育群體出生率的影響時,低生育群體和高生育群體人口數(shù)量最終將分別以Malthus增長指數(shù)b2-a+β/k和b1進行指數(shù)增長,此時低生育群體到高生育群體的生育觀念侵入不成功; 若a<β/k+b2-b1但a ≥β/k+b2-b1-b1(β/k/(b1-b2)-1),此時<0時,則 即若國家鼓勵生育政策的力度未能彌補生育觀念的傳染力度與低生育群體的人口增長速度之和對高生育群體出生率的影響時,低生育群體和高生育群體人口數(shù)量最終將以相同的Malthus增長指數(shù)(-ab1+)/(-a)進行指數(shù)增長,其人口數(shù)量比例穩(wěn)定在:a,此時會發(fā)生低生育群體到高生育群體的生育觀念的不完全侵入. 證結(jié)論(i)和(ii)的證明完全類似于定理4中結(jié)論(i)和(ii)的證明.結(jié)論(iii)的證明需要輔助方程 其軌線走向如圖8.類似定理4 中(iii)的證明即可得本定理結(jié)論(iii). 圖8 b2 <0, ≤1時系統(tǒng)(28)的等傾線及軌線走向示意圖 綜合定理9和定理10,可得如下結(jié)論. 定理11當(dāng)生育觀念侵入指數(shù)Ra>1時,定理9和定理10 (iii)的第二部分說明將發(fā)生低生育群體到高生育群體的不完全生育觀念侵入;而當(dāng)生育觀念侵入指數(shù)Ra ≤1時,定理10的(i),(ii)和(iii)的第一部分說明低生育群體到高生育群體的生育觀念侵入不成功. 本節(jié)通過數(shù)值例子驗證結(jié)論的正確性,并討論未能理論證得確切結(jié)論的注釋.例子中,取定人口年凈增長率b1=0.006,b2=0.001,0,-0.002 (數(shù)據(jù)來源參考于圖1),取定k=1.傳染系數(shù)β的值取自于0.001~0.02,國家鼓勵政策a的值取自于0.0005~0.012(數(shù)據(jù)取值范圍參考了人口凈增長率,無確切參考文獻).初值取定為(S(0),I(0))=(4,1)[3-4].人口數(shù)量單位為“億”,時間長度單位為“年”.圖9-圖12為無國家鼓勵生育政策(a=0)時,傳染系數(shù)β的變化對低生育群體的生育觀念對高生育群體能否(完全)侵入的影響;圖13-圖16為傳染系數(shù)β=0.01取定時,國家鼓勵生育政策的力度a的變化對低生育群體的生育觀念對高生育群體能否侵入的影響. 圖9 (a) 對定理1的例證, b2=0.001時, I/N在不同β下的時間序列圖(b) 對注2 的例證, b2=0.001, R=1時,I/N趨向于一定值約為0.1725 (c) 對注3 的討論, b2=0時, I/N的最終規(guī)模(I(T)/N(T))隨β的變化趨勢(d) 對注3 的討論, b2=0, R=1時, I/N趨向于一定值約為0.167 圖9 (a)為對定理1的例證.在低生育群體自然增長率b2=0.001>0下,由(6)中生育觀念侵入指數(shù)的定義知,當(dāng)β取值0.002,0.007,0.01時,R值分別為0.25,1.4,2.由圖可見,R>1時,低生育群體到高生育群體的生育觀念侵入成功,R<1時,生育觀念的侵入不成功.而當(dāng)β=0.005即R=1時,圖9 (b)顯示I/N將趨向于一定值約為0.1725,故此時會發(fā)生不完全的生育觀念侵入.圖9 (c),(d)為對注3的討論.由圖9 (c)可見,在低生育群體自然增長率b2=0時,若傳染系數(shù)β 定理3表明,當(dāng)?shù)蜕后w的自然增長率為負值時,系統(tǒng)(2)在生育觀念侵入指數(shù)R>1下將存在唯一全局中心.取定低生育群體的自然增長率b2=-0.002,由文化規(guī)范侵入指數(shù)的表達式知β=Rk(b1-b2),進而有β>0.008?R>1,β=0.008?R=1,β<0.008?R<1.圖10例證了傳染系數(shù)β=0.012時(此時,R=1.5>1),三個不同初值下,系統(tǒng)(2)存在一個全局中心(S?,I?)=(0.5,1.5).圖11例證了生育觀念侵入指數(shù)R<1時,生育觀念侵入不成功.圖12例證了生育觀念侵入指數(shù)R=1時,低生育群體和高生育群體的人口數(shù)量比值將趨向于一具體數(shù)值,即具有相同的Malthus增長指數(shù).所以在低生育群體自然增長率b2<0且生育觀念侵入指數(shù)R=1時,生育觀念侵入成功但不能完全侵入. 圖10 對定理3的例證, b2= -0.002且R >1時,三個不同初值下系統(tǒng)(2)存在唯一正平衡點(S?,I?),且是一個全局中心(a) S, I周期變化的時間序列圖(b) S, I周期變化的相圖 圖12 對注4的討論, b2= -0.002且R=1時,三種不同初值下S, I隨時間變化的時間序列圖(a)和I/S隨時間變化的時間序列圖(b),由圖可知,生育觀念侵入成功但不能完全侵入 取定傳染系數(shù)β=0.01,下面例證在有國家鼓勵生育政策下,鼓勵生育政策力度a的大小對生育觀念能否侵入的影響. 若低生育群體的自然增長率b2=0.001>0,那么鼓勵生育政策的力度a ≥0.005可保證生育觀念的侵入指數(shù) 此時低生育群體到高生育群體的生育觀念侵入不成功,如圖13 (a)和(b).但若鼓勵生育政策的力度不夠,即若a<0.005,此時將有R>1,則會發(fā)生生育觀念的侵入.由于有國家鼓勵生育政策的存在,不會發(fā)生完全的生育觀念侵入.隨著時間的增大,低生育和高生育群體的人口數(shù)量最終將以比例4:1 (a=0.001)和1:4 (a=0.004)達到平衡并以相同的Malthus增長指數(shù)進行指數(shù)增長,兩種情況下的指數(shù)增長率分別為0.002和0.005,如圖13 (c)和(d).圖13表明,國家鼓勵生育政策的力度越大,越不易發(fā)生低生育群體到高生育群體的生育觀念侵入.當(dāng)其他參數(shù)有確切數(shù)值時,可計算出國家鼓勵生育政策力度的參考值,從而可更合理的制定國家的鼓勵生育政策. 圖13 對定理5的例證, b2=0.001,(a)和(b)分別為Ra ≤1時S, I及I/S的時間序列圖,(c)和(d)分別為Ra >1時S, I及I/S的時間序列圖,由圖可見, Ra ≤1時生育觀念的侵入不成功;而Ra >1時發(fā)生不完全的生育觀念侵入 若低生育群體的自然增長率b2=0,則鼓勵生育政策力度的閾值a=0.004.當(dāng)a ≥0.004時有Ra ≤1,此時低生育群體到高生育群體的生育觀念侵入不成功,如圖14 (a)和(b).但若a<0.004,則會發(fā)生生育觀念的不完全侵入,如圖14 (c)和(d). 圖14 對定理6的例證,(a)和(b)分別為不發(fā)生生育觀念侵入時S, I及I/S的時間序列圖,(c)和(d)分別為發(fā)生生育觀念侵入但不完全時S, I及I/S的時間序列圖 在低生育群體的自然增長率b2=-0.002<0下,若國家采取鼓勵生育政策的力度不夠,即 此時,發(fā)生低生育群體到高生育群體的不完全生育觀念侵入.若a=0.0001,則低和高生育群體的人口數(shù)量最終將穩(wěn)定在(1.3125,3.9375)處,如圖15.若國家加大鼓勵生育政策的力度但仍未能彌補生育觀念的傳染力度與低生育群體的人口增長速度之和對高生育群體出生率的影響即a<β/k+b2-b1=0.002 時,則會發(fā)生不完全的生育觀念侵入.隨著時間的增大,低生育和高生育群體的人口數(shù)量最終將以比例3 :1 (a=0.0005),1 :1 (a=0.001)和1 :3 (a=0.0015)達到平衡并以相同的Malthus 增長指數(shù)進行指數(shù)增長,三種情況下的指數(shù)增長率分別為4.2352×10-19,0.002和0.004,如圖16 (a)和(b).但若國家鼓勵生育政策的力度足以彌補文化規(guī)范的傳染力度與低生育群體的人口增長速度之和對高生育群體出生率的影響時,即a ≥0.002時,低生育群體到高生育群體的生育觀念侵入不成功,如圖16 (c)和(d). 圖15 對定理9的例證,當(dāng)國家鼓勵生育政策的力度a=0.0001時,系統(tǒng)(1)存在唯一正平衡點(1.3125,3.9375)且是全局漸近穩(wěn)定的,(a)和(b)分別為兩組初值下S, I的時間序列和相圖 圖16 對定理10的例證,(a)和(b)分別為發(fā)生不完全生育觀念侵入時S, I及I/S的時間序列圖,(c)和(d)分別為生育觀念侵入不成功時S, I及I/S的時間序列圖 低生育率在我國某些地區(qū)已表現(xiàn)的非常明顯,對生育觀念在個體間傳播的研究也就非常有必要.本文考慮包括生育觀念在內(nèi)的導(dǎo)致低生育率的更廣義的生育觀念,借助傳染病模型的思想,建立了一類簡單的人口轉(zhuǎn)型中生育觀念的傳播模型,給出了生育觀念是否傳播的充分必要條件.具體為,在無國家鼓勵生育政策時,定義出生育觀念侵入指數(shù)R=β/(k(b1-b2)),理論證得當(dāng)R<1時,低生育群體到高生育群體的文化規(guī)范侵入不成功;當(dāng)R>1 且低生育群體的自然增長率b2>0時,發(fā)生完全的生育觀念侵入,b2<0 時,發(fā)生不完全的生育觀念侵入.數(shù)值實驗例證了當(dāng)R>1且b2=0時,發(fā)生完全的生育觀念侵入;R=1時,對任意的低生育群體自然增長率b2均發(fā)生不完全的生育觀念侵入.在有國家鼓勵生育政策時,給出生育觀念侵入指數(shù)Ra=β/(k(b1-b2+a)),理論證得當(dāng)Ra ≤1 時,低生育群體到高生育群體的生育觀念侵入不成功;當(dāng)Ra>1時,發(fā)生不完全的生育觀念侵入. 本文所建立的生育觀念模型較簡單,從理論證明和數(shù)值例證兩方面全面的討論了系數(shù)不同取值時模型的各種動力學(xué)行為.鑒于部分特殊情況未理論證明出結(jié)果,只是通過數(shù)值例子進行了討論,如注2-注4,故模型的完全理論討論是我們需要努力之處.同時,在本文模型基礎(chǔ)上,還有許多思考值得進一步的深入研究. 1.本文考慮全國人口中生育觀念的傳播模型,忽略了出國與歸國的人口流動.若考慮國內(nèi)具體地區(qū),則人口流動的因素不可避免,可針對具體地區(qū)考慮具有人口流動的生育觀念傳播模型. 2.本文只考慮了生育觀念的傳播結(jié)果,并未考慮其傳播方式,如生育觀念的垂直傳播,水平傳播和傾斜傳播[27-28].傳播方式的不同會影響傳播系數(shù)的變化,可細分傳播方式進行更細致的建模研究. 3.本文假設(shè)了固定的常數(shù)傳播系數(shù),而個體內(nèi)在價值觀的改變,社會生育,養(yǎng)育成本的增加等等因素會影響傳播強度[9-10],可根據(jù)實際影響傳播強度因素的不同考慮變系數(shù)的生育觀念傳播模型. 4.本文只考慮了生育觀念的傳播對人口數(shù)量的影響,而眾多對人口轉(zhuǎn)型問題的研究都考慮其與經(jīng)濟增長,教育進步,技術(shù)進步,農(nóng)業(yè)向工業(yè)化轉(zhuǎn)變,消費習(xí)慣,儲蓄率等的關(guān)系[3,4,6,8-10],故可考慮從不同角度融入相關(guān)因素的較復(fù)雜的生育觀念傳播模型. 5.本文考慮低生育和高生育兩群體總?cè)丝诘淖兓闆r,但不能準確反應(yīng)適齡群體人口數(shù)量.人口的老齡化,適齡生育群體年齡范圍的增大等現(xiàn)象與人口的年齡結(jié)構(gòu)密切相關(guān)[21],考慮具有年齡結(jié)構(gòu)的生育觀念傳播模型具有明顯的現(xiàn)實意義.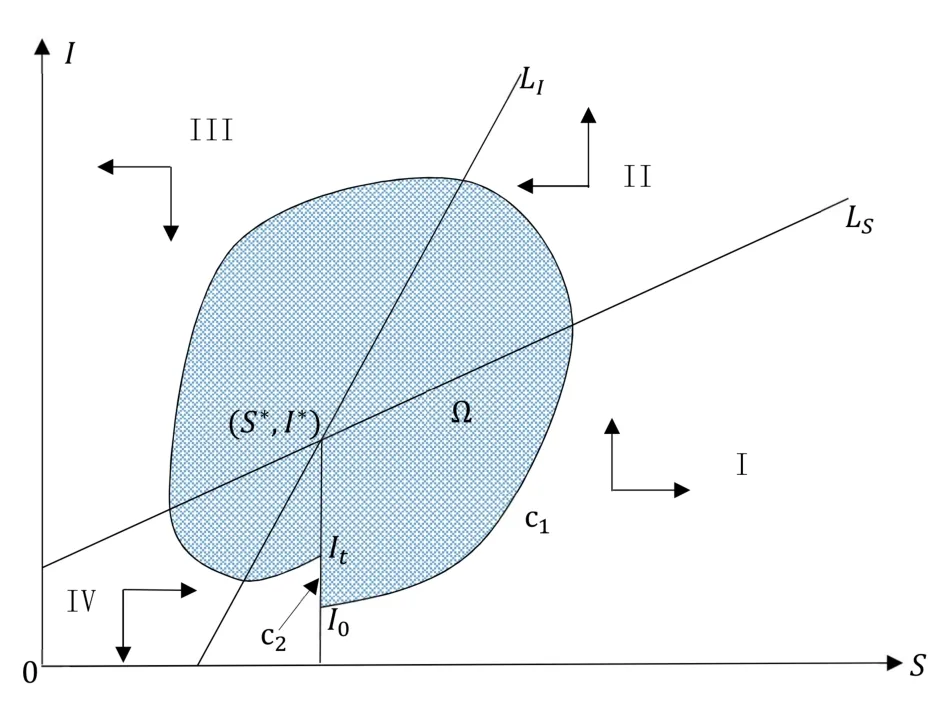

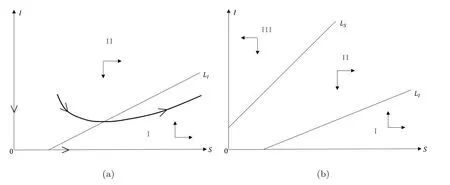
3.2 有國家生育政策干預(yù)(a >0)
§4 數(shù)值例子
§5 結(jié)論

