關于G?llnitz小分拆定理的連分式展開式的一個注記

蔡華蓉

(重慶師范大學數(shù)學科學學院,重慶 401331)

1 預備知識

Gu等人[1]在2011年通過猜測相對量并證明遞歸關系給出了一些Rogers-Ramanujan型的連分式展開式.2013年,Oliver等人[2]又在他們的基礎上,根據(jù)G?llnitz小分拆定理得到了7個新的結果,本文將對其中結果的輔助級數(shù)sk作出進一步改進.

對于給定的q級數(shù)F(z)和G(z)以及遞歸關系sk+1=(sk-1-aksk)/z(k=0,1,2,…),其中sk是輔助級數(shù),數(shù)ak由sk唯一定義.那么,令F(z)=s0和G(z)=s-1時,可以得到下面關于級數(shù)商的連分式

這意味著,如果要得到級數(shù)商的連分式的展開式,就只需要給出輔助級數(shù)sk,這樣數(shù)ak自然也就可以求得.

根據(jù)G?llnitz小分拆定理[3]:

Oliver等人[2]給出了下面兩個q級數(shù)F(z)和G(z)的結果.對其中的輔助級數(shù)sk,本文給出了改進.

2 主要結果及證明

關于Oliver等人[2]在2013年根據(jù)G?llnitz小分拆定理所得的定理2中原本所用的輔助級數(shù)sk如下.本文也在下面定理2.1中給出相應的更正.

定理2.1

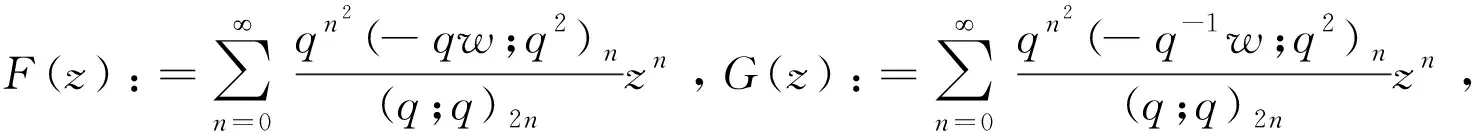
其輔助級數(shù)為

證明：首先,為了得到輔助級數(shù)sk的一般形式,本文先根據(jù)遞歸關系sk+1=(sk-1-aksk)/z

(k=0,1,2,…)求出其前面的幾項,本文求出了前7項s-1,s0,s1,s2,s3,s4,s5,以及被sk唯一定義的數(shù)ak的前5項a0,a1,a2,a3,a4,這里僅對s1,s2,s3進行詳細說明,其余情況類似.按照前面的方法,令F(z)=s0和G(z)=s-1,并記冪級數(shù)sk的zn項的系數(shù)為[zn]sk,其中當n<0時,規(guī)定[zn]sk=0.下面對k=0,1,2,3,4的情況依次計算.

當k=0時,由遞歸關系得

(1)

在(1)式中,令n=0,有0=1-a0,求得a0=1.將所求的a0代入(1)式,對?n>0有

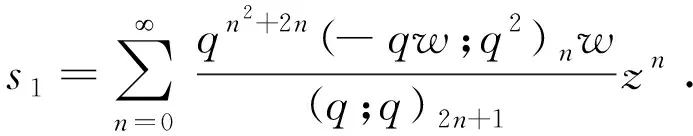
當k=1時,由遞歸關系得

(2)

在(2)式中,令n=0,有0=1-a1w(q;q)1-1,求得a1=(1-q)w-1.將所求的a1代入(2)式,對?n>0有

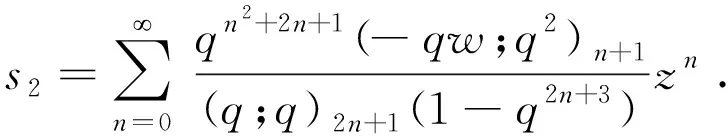
當k=2時,由遞歸關系得

(3)

在(3)式中,令n=0,有0=w(q;q)1-1-a2q(-qw;q2)1(q;q)1-1(1-q3)-1,求得

a2=q-1(1+qw)-1(1-q3)w.將所求的a2代入(3)式,對?n>0有

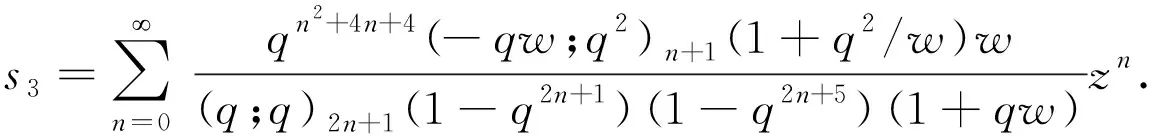
在文獻[4]的式1.2.39中,令a=q有

(q;q)2n=(q2;q2)n(q;q2)n.

(4)

因此使用(4)式,可以將s0,s1,s2,s3進一步改寫為如下形式

同理可得

綜上,可以猜測s2k和s2k+1即為定理2.1中的形式,并且由sk所定義的數(shù)a2k,a2k+1恰好也滿足定理2.1中的形式;其次,還需要證明所猜測的輔助級數(shù)滿足遞歸關系.

當k≥1,n≥1時有

則s2k+1=(s2k-1-a2ks2k)/z(k≥1)成立,且當k=0時,有s1=(s-1-a0s0)/z成立.

同理,當k≥0,n≥1時有

則s2k+2=(s2k-a2k+1s2k+1)/z成立.

綜上所述,所猜測的輔助級數(shù)s2k,s2k+1滿足遞歸關系sk+1=(sk-1-aksk)/z(k=0,1,2…),并且相應的數(shù)a2k,a2k+1也為定理2.1中的形式,故定理2.1證畢.

3 結語

一方面,本文對關于G?llnitz小分拆定理的其中一個連分式展開式的輔助級數(shù)sk進行了更正,并給出了證明.

另一方面,定理2.1中的級數(shù)商zF(z)/G(z)所對應的連分式有如下形式的展開式

其中通過對數(shù)a2k和a2k+1計算可知,當k≥0時有

a2ka2k+1=(1-q4k-1)(1-q4k+1)(q2k+w)-1,

a2k+1a2k+2=(1-q4k+1)(1-q4k+3)(q2k+1+q4k+2w)-1.

故此連分式可進一步改寫為

在后續(xù)的研究中,也可以使用Worpitzky-Pringsheim[5]等定理繼續(xù)研究由此類方法構造的連分式zF(z)/G(z)的收斂性.