SLGC:Identifying influential nodes in complex networks from the perspectives of self-centrality,local centrality,and global centrality

Da Ai(艾達(dá)), Xin-Long Liu(劉鑫龍), Wen-Zhe Kang(康文哲), Lin-Na Li(李琳娜),2,Shao-Qing L¨u(呂少卿), and Ying Liu(劉穎)

1School of Communication and Information Engineering,Xi’an University of Posts and Telecommunications,Xi’an 710121,China

2Network Ecological and Environmental Governance Research Center,Xi’an University of Posts and Telecommunications,Xi’an 710121,China

Keywords: influential nodes,self-influence,local and global influence,complex networks

1.Introduction

Social structures,road systems,social networks,etc.can be abstracted as complex networks consisting of nodes and connected edges.[1]The opening of the metaverse era, where the node data in complex networks may be virtual and digital, and the connections between nodes may also be virtual,digital, or connected to the real world, has increased the heterogeneity and uncertainty of complex networks while increasing the difficulty of mining important nodes in complex networks.[2]The critical node detection problem (CNDP) is typical in complex network analysis, where its enhancement or failure will significantly improve or degrade the functionality of the target network and can better understand or control the behavior of nodes in complex networks.[3]Identifying a set of influential and important nodes in complex networks plays a crucial role in advertising placement,[4]rumor control,[5]epidemic prevention and control,[6]etc.With the complexity of human society and the increasing demand for large-scale, complex systems, the study of the importance of complex network nodes has received increasing attention.The study of mining important nodes in complex networks has important research significance and practical value for network data science and mining network functions.

In complex networks, different types of network nodes have specific properties,and some special nodes that can manipulate the entire network data transmission and information dissemination are called important nodes,[7,8]for example,predictive dissemination of financial risk research institutions in the field of finance,[9]online social networking platforms with a strong ability to disseminate online bloggers,[10]and important transportation hubs that undertake transportation in road traffic networks.[11]Thus, several ranking algorithms have been proposed to evaluate the importance of nodes based on network features or node attributes, which can be broadly classified into categories such as node neighborhood-based,node path-based, node feature vector-based, node locationbased,and node multi-attribute decision-based methods.[12]

Measuring the importance of a node based on its local neighborhood primarily involves evaluating its significance by considering its own information within the local neighborhood structure of the network and the importance of neighboring nodes within that neighborhood.Degree centrality(DC)[13]and H-index[14]are classical algorithms based on the node neighborhood,which mainly consider the number or degree of one-hop neighboring nodes to measure the importance of nodes and are an intuitive and simple node ranking algorithm, but because only one-hop neighboring nodes are considered,the influence of more distant nodes and network topology information is ignored, resulting in the accuracy rate of identifying important nodes not high.[15]

Although algorithms based on local neighborhood node importance sorting can quickly and intuitively reflect the importance of nodes,their low accuracy leads to ranking results that are not suitable for practical applications.Subsequently,researchers proposed a class of path-based sorting algorithms that measure the importance of nodes in the global network based on the number of shortest paths between nodes.[16]The representative node-path-based algorithms are betweenness centrality(BC)[17]and closeness centrality(CC),[18]BC by calculating the number of shortest paths between nodes in the network and CC by calculating the inverse of the average distance from nodes to other nodes in the network, this type of node-centricity algorithm focuses on the global structure of the network and only considers the shortest path information between nodes without considering the path, which will not be able to describe the importance of the nodes for unconnected networks and lead to the high computational complexity of the model, which has some limitations for large-scale networks.[19]

The importance of a node depends not only on the number of its neighboring nodes but also on the importance of those neighbors.The idea behind feature vector-based sorting algorithms is to calculate the weight value of a node based on the eigenvector of the network adjacency matrix.It emphasizes both the quantity and quality of neighboring nodes in the network where the node resides.The importance of a node is evaluated by considering the relationship between its own weight and the weights of its neighboring nodes.Eigenvector centrality (EC)[20]and PageRank (PR)[21]algorithms are representative algorithms based on the node eigenvector centrality.However,due to the involvement of matrix operations,this type of algorithm has high computation complexity and slow convergence speed, making it unsuitable for large-scale networks and prone to being trapped in loops.[22]

In addition,by decomposing the complex network structure, the importance of a node is determined based on its position in the network.The classical algorithms based on node location areK-shell decomposition,which divides the nodes in the network into different levels according toK-shell values,and the closer a node is to the center of the network,the more influential that node is,but this method cannot distinguish the importance of nodes in the same level.[23]

With the increase of uncertainty in complex networks, researchers have proposed a node centrality measure based on the multiple attribute decision-making methods(MADMs).[24,25]The idea of this algorithm is to define node centrality as a combined performance under multiple attribute perspectives,or to use the technique for order of preference by similarity to ideal solution(TOPSIS)to perform weighted calculations based on different attribute weights, and ultimately obtain a comprehensive ranking result for the nodes.[26]Wanget al.[27]proposed a centroidal of centripetalism to evaluate the importance of nodes more comprehensively from their global,local, and semi-local topological information.Qiuet al.[28]improved the traditional degree centrality by introducing the concept of local clustering coefficients to measure the local influence of nodes, improving the classicalK-shell algorithm to measure the global influence of nodes,and proposing a local and global influence(LGI)algorithm for identification and ranking of influential nodes in complex networks.

In the aforementioned method based on the multiattribute decision-making for nodes, the comprehensive consideration of local and global features of nodes overlooks the self-influence of nodes.In this paper,we propose a new node importance ranking algorithm called SLGC algorithm from the perspective of multi-attribute decision-making for nodes,considering the self-influence of nodes.Compared to existing methods based on the multi-attribute decision-making for nodes, the proposed SLGC algorithm takes into account the self-influence of nodes, defines a new metric for local influence by considering the quantity and quality of the neighboring nodes within the node’s local neighborhood, and introduces the concept of Shannon entropy.Additionally,it defines a new metric for global influence based on the node’s position in the overall network and the topology structure between nodes.By integrating these three dimensions of metrics —node’s self-influence,local-influence,and global-influence—the SLGC algorithm comprehensively determines the node’s importance in a complex network and identifies influential nodes.The main innovation of our research in the SLGC algorithm lies in:

(i) From the perspective of the self-influence of nodes.Starting from the node’s own attributes, we introduce an eexponential function to limit the overestimation of the node’s own importance due to large differences in node degrees.Based on the degree of the node and the maximum degree of the network, we define a new metric for self-influence of nodes,constraining it between(1, e).

(ii)From the perspective of the local influence of nodes.Within the node’s local neighborhood, we consider the quantity and quality of the node’s first-order and second-order neighboring nodes to define a new metric called node’s local average degree.Then, we calculate the node’s local decision probability and introduce Shannon entropy to construct the node’s entropy-weighted local degree centrality as an evaluation of the node’s local influence.

(iii)From the perspective of the global influence of nodes.In the global topological structure of the network, we assign each node with a correspondingK-shell value based on its position in the network.Simultaneously,we calculate the shortest path between any two nodes in the network to evaluate the node’s global influence.

The rest of this article is composed as follows.Section 2 briefly introduces the basic concepts of complex network graph data and node centrality ranking algorithm.Section 3 outlines the SLGC algorithm proposed in this paper.Section 4 analyzes the experimental results, including the data set, node distinguishability experiments, node propagation ability experiments,and network model efficiency experiments.And Section 5 summarizes our research results and algorithm highlights.

2.Preliminaries

Mathematically,any complex network can be represented as a graphG=(V,E), where the set of nodes is denoted asV={v1,v2,v3,...,vn}and the set of connected edge relations between nodes is denoted asE={e1,e2,e3,...,em}.

Without loss of generality,we assume that the graphG=(V,E) is an undirected and unweighted complex graph network data,and the information of nodes and edges in the complex network is described by the adjacency matrixThe adjacency matrix describes the connection relationship between each node, and for the undirected and unweighted complex network,the adjacency matrix of the nodes is a symmetric matrix,and bothai jandajiin the adjacency matrix are 1 if there is a connection between nodeviand nodevj,otherwise they are 0.

2.1.Degree centrality

The degree of a node is defined as the number of neighboring nodes that are directly connected to it.According to the degree of a node,the more neighboring nodes that are directly connected to it,the greater its influence in the network[13]

whereaijdenotes the existence of a connection between nodeviand nodevjin the network adjacency matrix.

Normalized degree centrality

wherekidenotes the degree of nodeviandNis the total number of nodes in the network.

2.2.Betweenness centrality

Betweenness centrality is a node centrality measure based on the global topology of the network,and the importance of a node is measured by the shortest path of the node,according to which the more the shortest path, the more important the node is[17]

wheregjkis the number of the shortest paths between nodevjandvk.gjk(vi)is the number of shortest paths between nodevjand nodevkthrough nodevi.

2.3.Closeness centrality

Closeness centrality is a centrality measure based on the global topology of the network,where the closeness centrality of a node is calculated as the reciprocal of the sum of the shortest paths between the node and other nodes,and the closeness centrality of a node is defined based on the reciprocal of the average shortest path of the node[18]

whereNdenotes the number of nodes in the network anddijis the shortest path between nodeviand nodevj.

2.4.Eigenvector centrality

The importance of a node takes into account not only the information of the node itself but also the information of neighboring nodes.Feature vector centrality defines node importance based on the centrality of neighboring nodes.Based on the adjacency matrixAof a given network,the feature vector centrality is defined as[20]

whereλis the maximum eigenvalue of the adjacency matrix of the network and 1/λis used as a scaling constant,only the eigenvector corresponding to the maximum eigenvalue is required for the centrality measure, andxT={x1,x2,...,xn}is the corresponding eigenvector.

2.5.PageRank centrality

The PageRank algorithm is a variant of eigenvector centrality,which was initially used by Google to rank web pages.The algorithm is calculated based on the structure and number of connections of nodes in the network,and the PR of a node is not simply calculated with the number of its neighboring nodes,but the sum of the weights of the related nodes,which are derived based on the iterative formula of the PageRank,which is calculated as follows:[21]

where PRC(vi)denotes the PageRank value of nodevi,dis the damping factor,Nis the total number of the network nodes,PR(vj) denotes the PageRank value of nodevj, Out(vj) denotes the number of connections from nodevito other nodes.

2.6.Clustered local-degree centrality

The algorithm calculates the sum of the degrees of the nearest neighbors of a given node and introduces the clustering coefficients of the nodes to propose a new centrality measure called clustering local degree centrality for identifying important nodes in the network,defined as follows:[29]

wherekidenotes the degree of the node,C(vi) denotes the clustering coefficient of the node, andLidenotes the number of contiguous edges existing between the neighboring nodes of nodevi.

2.7.Global structure model

The algorithm proposes a new node centrality metric for identifying influential nodes based on the node global structure model, which considers the node’s self influence while emphasizing the node’s global influence in the network topology,defined as follows:[30]

whereKs(vi) denotes theK-shell value of the node anddijdenotes the shortest distance between nodesviandvj.

2.8.Local-and-global centrality

The algorithm considers the degree of nodes and the shortest distance between nodes and proposes a new algorithm based on local and global centrality measures of nodes to identify key nodes by processing the local and global topology of nodes in the network,defined as follows:[31]

whered(vi) denotes the degree of the node,di jdenotes the shortest distance between nodesviandvj, andα, as the degree of influence of the adjustable parameter control network,lies in the range between 0 and 1.

3.The proposed method

The importance of nodes in a complex network is determined by three key factors: the influence of a node, the local influence of a node,and the global influence of a node.The influence of a node is mainly provided by the degree of the node,while the influence of a node is measured by introducing the exponential function of e.Local influence is determined based on the node’s one-hop neighboring nodes and two-hop neighboring nodes jointly,and the concept of information entropy is introduced to reflect the information sharing ability between the node and its one- and two-hop neighboring nodes.The global influence considers the information dissemination ability of the node in terms of the global structure of the whole network,i.e.,the location and shortest path of the node in the network.

3.1.Definitions related to the SLGC algorithm

To describe the node importance evaluation index in complex networks, the following definitions of node’s selfinfluence, local influence, and global influence are given in this paper.

Definition 1.Self-influence of node(SIN)The degree of a node can directly reflect its information dissemination capacity.Nodes with higher degrees tend to be more important.However, this may lead to the neglect of nodes with lower degrees.To avoid this situation, we introduce the eexponential function to limit the node’s self-influence within the range of (1, e), thereby preventing an excessive evaluation of the node’s own importance, defining SIN, the node’s self-influence is calculated as

whered(vi)is the degree of the node andkmaxis the maximum degree of the node in the network.

Definition 2.Local-influence of nodes (LIN)The importance of a node depends not only on the number of nodes it directly connects to but also on the quality of its immediate neighbors and second-order neighbors.The larger the degree of a node’s immediate neighbors and second-order neighbors,the more significant the node is considered to be.Therefore,a new local degree centrality method is proposed as follows by introducing the Shannon entropy[32]in the local information dimension of the node.

(i) Local average degreeThe local average degree of a node reflects the average level of connectivity within its local neighborhood, revealing the node’s capacity for information sharing and propagation with its neighboring nodes.The local average degree is calculated as the ratio of the sum of the degrees of a node’s first-order and second-order neighboring nodes to the degree of the node itself,denoted byknnand defined as follows:

whered(vi)denotes the degree of the nodevi,d(vj)andd(vk)denote the degree of the node’s one-hop neighboring nodesvjand two-hop neighboring nodesvk, andΓ(vi) andΓ(vj) denote the set of nearest neighbor nodes and two-hop neighboring nodes of the nodevi.

(ii)Local decision probabilityBased on the node’s own attributes and the network structure between its first-order and second-order neighboring nodes, the local decision probability of a node is defined to evaluate its level of connectivity within the local neighborhood network, thereby revealing its importance in information dissemination or control.The local decision probability of a node is defined as the reciprocal of the local average degree and is expressed as follows:

(iii) Node local information entropyShannon entropy is a concept in information theory used to measure the uncertainty of a random variable.In the context of ranking the importance of nodes in complex networks,nodes can be seen as information sources,and their neighboring nodes can be seen as information related to that source.By introducing the definition of the Shannon entropy,we can evaluate the information transmission capacity of a node within its local neighborhood.Based on the local decision probability of each node involved in information propagation, the definition of node’s local information entropy is as follows:

where the probability of the local information entropy of a node is represented by the local decision probability of the node,andΓ(vi)denotes the set of one-hop neighboring nodes of nodevi.

(iv) Node local influenceOn the basis of the node degree centrality measurement method,the node information entropy is introduced to construct the entropy-weighted local degree centrality as an indicator to measure the local influence of nodes,which is defined as follows:

whereE(vi)is the information entropy of nodevi,d(vi)is the degree of nodevi, andNis the total number of nodes in the network.

Definition 3.Global-influence of node (GIN)When considering only the local influence of a node often loses information about the topology of the node network, the time and ability of the node to spread information with other nodes as one of the indicators to measure the global influence of the node,theK-shell value of the node’s direct neighbors also indirectly increases the influence of the node,theK-shell value measures the nucleus of each node in the network from the global dimension of the network, the shortest path between any two nodes in the network directly affects the ability of the node to share information with other nodes, the shortest distance between two nodes is inversely proportional to the node,so the global dimension influence is defined as follows:

whereKs(vj) denotes the value ofK-shell of nodes anddijdenotes the shortest path between nodeviand nodevj.

Definition 4.Total influence of nodeAccording to the above-proposed node’s self-influence,local influence,and global influence, the product of the three is used as the basis for assessing the importance of the node by the SLGC method proposed in this paper,therefore,the SLGC value of the node is defined as

Algorithm 1 provides the algorithmic description of SLGC.

Algorithm 1 SLGC Input: A network G=(V,E)//G is an undirected and unweighted graph with V as the set of nodes and E as the set of edges.Output: A ranking list of node’s influence.Begin Initialize the information For each node v in V do For each node u in V do Calculate the degree deg(v)and the max degree kmax Calculate the Ks(v)using K-shell decomposition Using Dijkstra calculate the shortest distance duv End for End for SIN= /0//self influence LIN= /0//local influence GIN= /0//global influence For each node in V do Calculate self influence SIN(v)using Eq.(11).End for For each node v in V do Calculate the knn using Eq.(12).For each(u,v)∈E do puv=1/knn Huv=-puv log puv For each node v in V do Ev=∑u∈Γv Huv Calculate local influence LIN(v)using Eq.(15).End for End for For each node v in V do Calculate global influence GIN(v)using Eq.(16).?indices i/= j for Eqs.(16)and(17).End for For each node v in V do Calculate SLGC(v)using Eq.(17).End for Sort the nodes in descending order based on SLGC scores to obtain the ranking list.End

3.2.Example of SLGC algorithm

The procedure of the proposed method is illustrated below using a simple random network.The random network is shown in Fig.1, which contains 16 nodes and 21 edges.By using the SLGC algorithm for this random network, the important nodes in the network are identified and the nodes are ranked.

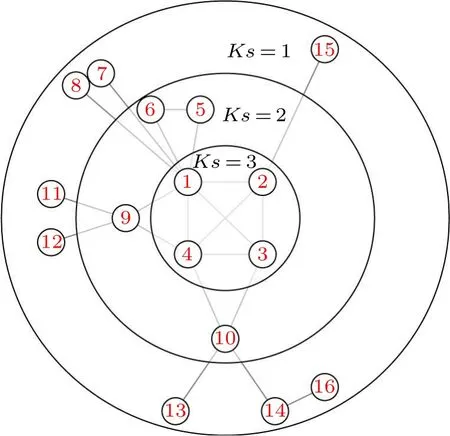
Fig.1.The random network for illustration.

Calculate step-by-step according to the SLGC algorithm flow.

Step 1: in a given network,the first step is to performKshell decomposition by partitioning the network based on the position of nodes within the network, resulting in each node being assigned aK-shell value.Simultaneously, the degree value of each node is calculated.The values are shown in the following table.

Table 1.Degree and Ks values of nodes.

Step 2: by calculating the degree values of nodes in the given random network,we obtain the maximum degree valuekmaxas 8.Based on the degree values of each node obtained in the first step and the maximum degree value in the network,we can calculate the SIN value of nodes in the random network using the e-exponential function.

Table 2.SIN value of the node.

Step 3: to calculate the local average degree and local clustering probability of each node in a random network based on the node’s degree within its local neighborhood and the network structure,we introduce the concept of Shannon entropy to compute the local information entropy of each node.Subsequently,we can calculate the LIN value of nodes in the random network.

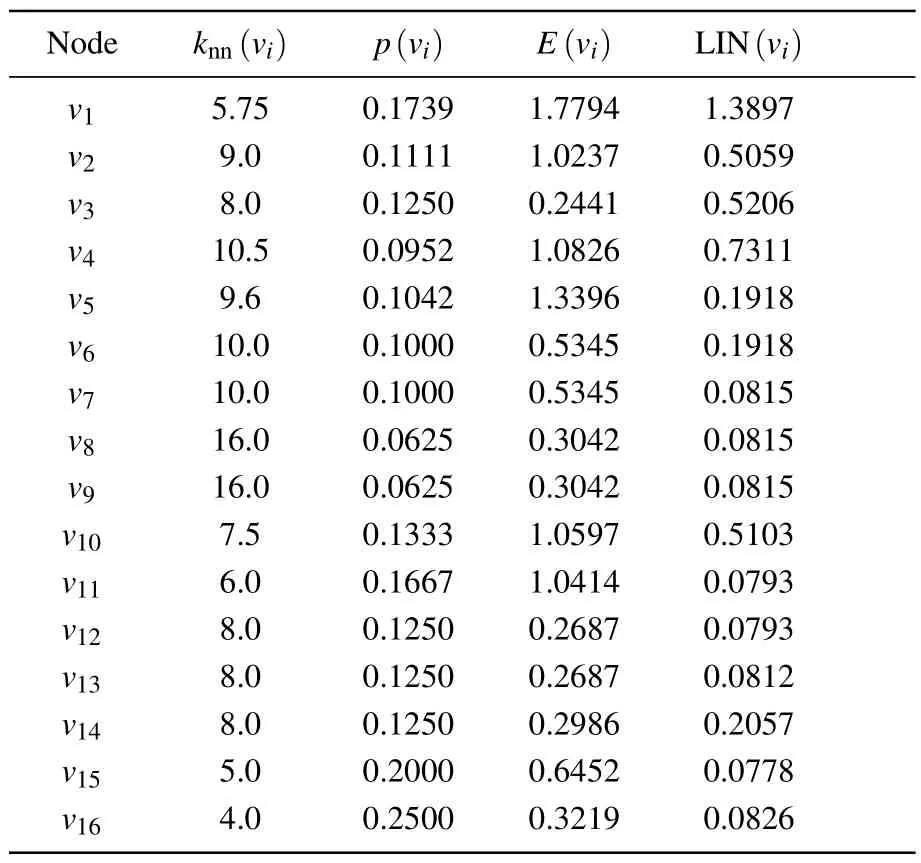
Table 3.LIN value of the node.

Step 4: based on the degree andK-shell values of nodes in the random network obtained in step one, we can use Dijkstra’s algorithm to calculate the shortest paths between any two nodes in the network,and then calculate the GIN value for each node in the random network.

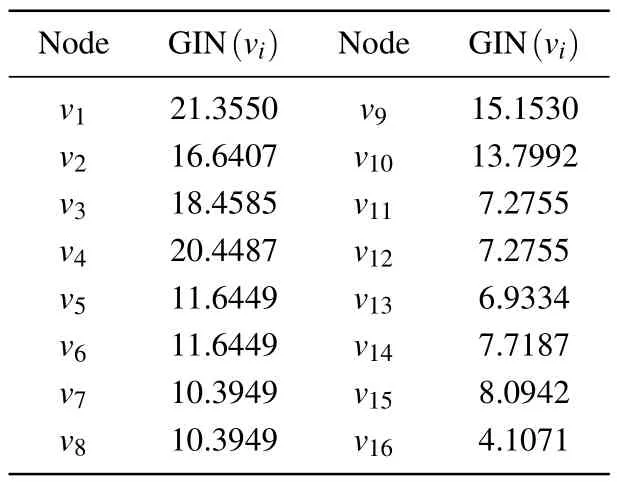
Table 4.GIN value of the node.

Step 5:based on the above-obtained node SIN value,LIN value,and GIN value,calculate the SLGC value of the nodes and sort the nodes.

From Table 5, it can be seen that nodev1has the largest SLGC value, indicating that it has the strongest importance;nodesv5andv6,nodesv7andv8,and nodesv11andv12have the same SLGC value,indicating that they have the same importance; in Table 1,nodev9and nodev10have the same degree value andK-shell value,therefore,the traditional method cannot distinguish the importance of the two nodes; whereas,from Table 3, it can be seen that the local influence of nodev9is slightly higher than that of nodev10, and Table 4 shows that the global influence of nodev9is higher than that of nodev10,which leads to a more obvious differentiation between the influence of nodev9and nodev10in Table 5, indicating that the accuracy of the proposed method for node identification is better than that of the existing methods.The detailed experimental analysis will be given in Section 4.

3.3.Computational complexity analysis of SLGC

Time complexity is an important indicator to measure the quality of an algorithm.The proposed SLGC algorithm consists of three main components: computing the self-influence,local influence,and global influence of nodes.The time complexity of the SLGC algorithm is given below.

(i) For an undirected graph, when computing the selfinfluence of nodes,it is necessary to traverse all nodesn,calculate the degree value of each node and perform exponential function computation once,with a time complexity ofO(n).

(ii)When calculating the sum of degrees of one-and twohop neighboring nodes for each node, it is necessary to traverse the first- and second-order neighboring nodes of each node once,resulting in a time complexity ofO（n2）.

(iii)When calculating the information content of a node,it is necessary to perform a local average degree calculation on the neighboring nodes of each node,with a time complexity ofO（n2）.

(iv)When computing the information entropy of nodes,it is necessary to traverse each node’s neighbor nodes and accumulate information value during the traversal process, with a time complexity ofO（n2）.

(v) Using Dijkstra’s algorithm to calculate the shortest path between two nodes or calculate theK-shell value of a node has a time complexity ofO（n2）.

(vi) When computing the self-influence, local influence,and global influence of nodes, it is necessary to perform one computation for each node,with a time complexity ofO(n).

Therefore,the time complexity of the SLGC algorithm isO（n2）.

4.Experiment and analysis

In this section, we use six real-world complex networks with different properties as test datasets to verify the effectiveness of our proposed method.We compare our method with a total of eight most commonly used and latest node centrality measures,including degree centrality,betweenness centrality,closeness centrality, eigenvector centrality, PageRank, cluster local degree centrality(CLD),global structure model(GSM),and local-and-global centrality(LGC).

The following three metrics are used to evaluate the proposed SLGC node centrality metric.

Differentiation This reflects the ability of the method to distinguish the node influence ranking, mainly including the monotonicity function, the distinct metric based evaluation criterion,and the complementary cumulative distribution function.

Accuracy This reflects that the node ranking obtained by the method can be more conducive to the dissemination of information and mining the nodes with strong dissemination ability in the network.

Efficiency This reflects the network running time of the algorithm in identifying important nodes.

4.1.Datasets

In this experiment,six real-world networks with different properties are selected,including Jazz,[33]EEC,[34]Email,[35]Hamster,[36]Facebook,[37]and PGP.[38]As Table 6 shows the relevant statistical characteristics of the six real networks,where|N|and|M|are the number of edges and nodes,〈K〉is the average degree.The last two columns indicate the maximum degreeKmaxand average cluster coefficients〈C〉 of the networks.

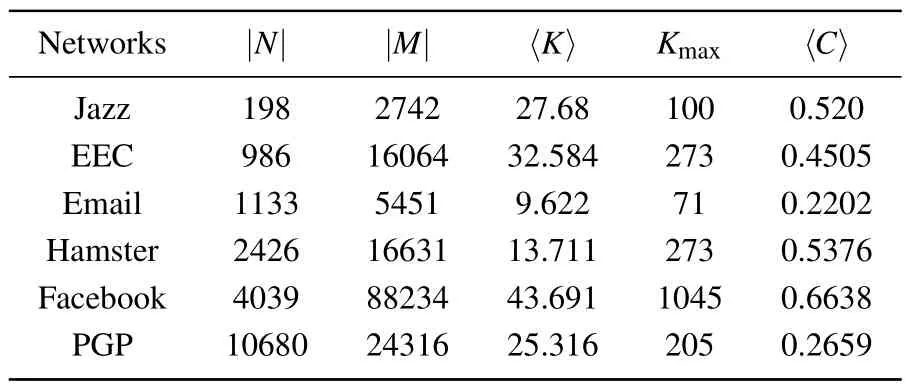
Table 6.The statistical features of six real-world networks.

4.2.Differentiation

4.2.1.Monotonicity based evaluation criterion

In this experiment, the discriminative power of the proposed method versus other methods on the generated ranking results is studied by using the monotonicity function[39]

whereRis the ranked list of node importance generated by different methods,|V|rdenotes the number of nodes assigned to the ranked listr,and|V|denotes the total number of nodes in the network.If the ranking listRhas better discriminative power,then a higher value indicates that the method has better node ranking performance.

Table 7.The M values of different methods on six real-world networks.

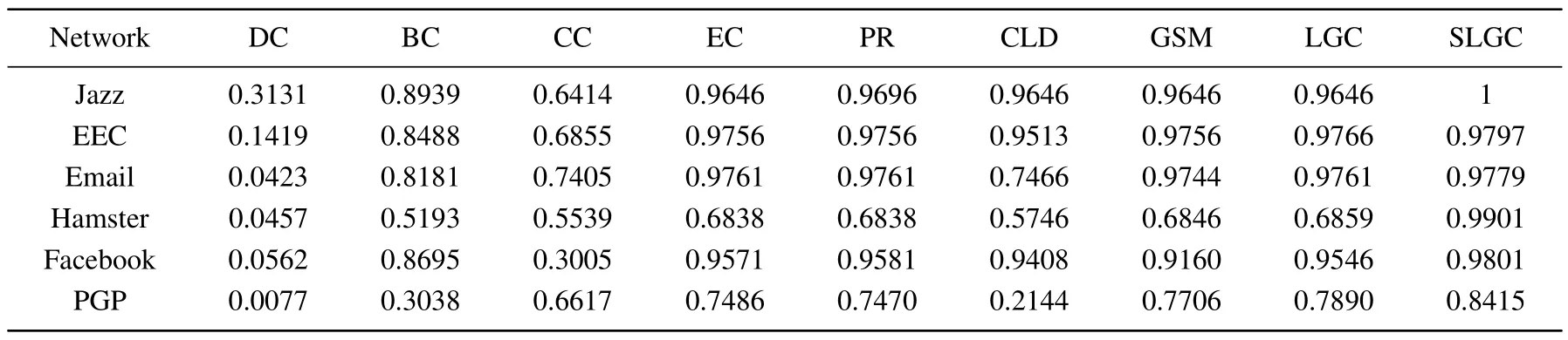
Table 8.DM values of different methods on six real-world networks.

Table 7 shows the monotonicity values of eight different node centrality measures for six real complex networks.The monotonicity value of SLGC tends to be 1 on each network,which is significantly higher than other methods,verifying the goodness and monotonicity of the proposed method for node ranking performance.

4.2.2.The distinct metric based evaluation criterion

The distinct metric(DM)of nodes is another metric used to test the ability to distinguish nodes differentiation by performing statistics on the ranking results of nodes, defined as follows:[40]

whereRdenotes the ranking list generated by different methods,|V|denotes the total number of nodes in the network,and DM takes values in the range of[0,1],the higher the value of DM indicates that the method has a better ability to differentiate the nodes in the network.

According to the display in Table 8, it can be concluded that the DM values of SLGC are higher than other methods on all six complex networks,which indicates that the nodes in the network are resolved to be assigned to different ranks and have high differentiation ability for nodes.

4.2.3.Complementary cumulative distribution function based evaluation criterion

The complementary cumulative distribution function(CCDF) further standardizes the node ranking distribution of the ranking methods by generating node rankings for different node centrality metrics to better assess the differences in node ranking lists between methods and the node importance capabilities.The mathematical definition of CCDF is as follows:[41]

whereRdenotes the node ranking list andndenotes the number of network nodes.According to this formula, from the perspective of distinguishing nodes’differentiation ability,the more nodes are assigned different ranks for ranking the better the method can show and the stronger the method’s ability to distinguish nodes,which helps to select the more effective topNnodes from the network node ranking for disseminating information; if each node is assigned a different rank,the CCDF curve result will gradually converge to zero with a smooth slope,and if all nodes are assigned the same rank,the CCDF curve result will rapidly converge to zero.

As Fig.2 shows the CCDF curve results on six real network datasets,it can be concluded that due to the degree centrality assigning node ranking ranks according to node degrees, which leads to most nodes in the same rank, the corresponding CCDF curve results will also converge to zero rapidly; the CCDF curve graph of the SLGC algorithm proposed in this paper converges to zero gently,reflecting that the algorithm has the optimal node.The CCDF curve of the proposed SLGC algorithm tends to zero gently,which reflects that the algorithm has optimal node distribution and monotonicity performance,and better distinguishes the differences between node rankings.

4.3.Accuracy

The SIR model is a common mathematical model used to describe the spread and control of infectious diseases, which is applied to describe the spreading process of a disease in a closed population.In this experiment,the SIR epidemic transmission model is used to model the transmission of infectious diseases for ranked lists generated by different methods, in order to identify the transmission capacity and efficiency of nodes in complex networks.In the SIR model, nodes are divided into three states: susceptible, infected, and recovered.A susceptible person can be infected by contacting with an infected person with a certain probability.The infected node remains infected for a certain period and then enters the recovered state with a certain recovery probability and no longer infects other nodes.The SIR model can be described by a set of differential equations,whereS,I,andRdenote the number of susceptible, infected, and recovered individuals, respectively.The differential equations of SIR are[42]

wheres(t),i(t),andr(t)denote the number of nodes in susceptible, infected, and recovered states, respectively;βdenotes the infection probability andμdenotes the recovery probability.

The performance of the proposed algorithm can be measured by the spreading capability of the selected initial nodes.Based on the SIR model,the network infection quantityF(t)at timetis defined as the ratio of the sum of infected nodes and recovered nodes within a unit of time to the total number of nodes in the network.It is defined as follows:

whereF(t) represents the network infection level at timet,nI(t)represents the number of infected nodes at timet,nR(t)represents the number of recovered nodes at timet,andNrepresents the total number of nodes in the network.

In this experiment, the first ten nodes of each method are selected as the initially infected nodes,and the remaining nodes are in the susceptible state.During the simulation experiment, the node overview in the network is the sum of the number of infected nodes and the number of recovered nodes,and the infected nodes infect the surrounding nodes in the susceptible state with the infection probabilityβ.The infection probabilityβis set to 0.1, and the recovery probability is set toμas 1.The propagation time is denoted byt,and each experiment is run 100 times independently.As shown in Fig.3,the number of infected nodesF(t)is used as the size of the infection ability of the selected initial node in a specific period,and the largerF(t)is in the same propagation time,the larger the size of the node’s impact under the method,which further indicates the stronger own influence of the node’s initial test infected node selected according to the method.

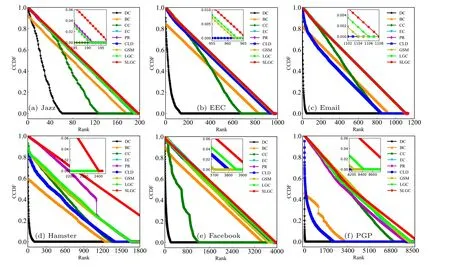
Fig.2.The CCDF plots for ranking lists were obtained by different methods on six real-world networks.

4.4.Efficiency

In this experiment, the running time of each method on six real network datasets is investigated,and a shorter running time for a certain method indicates better efficiency.The efficiency of each method in identifying and ranking important nodes is reflected in terms of the running time.As shown in the figure,each node centrality measure is independently executed 100 times on each network,and the average run time is taken to quantify the efficiency of each method for node identification and ranking.

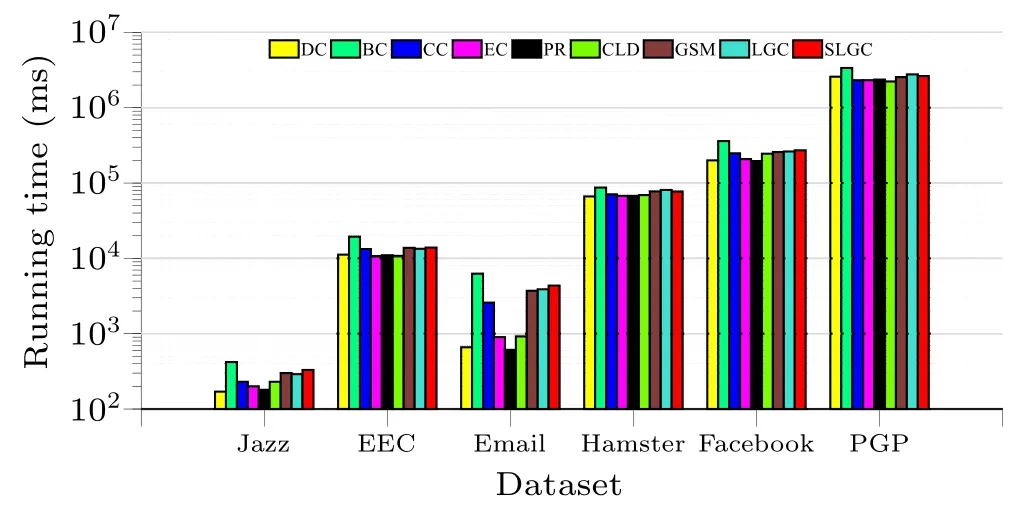
Fig.4.Running time of different methods on six datasets.

As shown in Fig.4, the SLGC algorithm takes less time to run than BC on all six datasets.On Jazz, EEC, and Email datasets, the SLGC algorithm takes the same amount of time as GSM and LGC, and on Facebook and PGP large-scale datasets, the SLGC algorithm not only takes less time than BC,but also takes less time than LGC algorithm.It is obvious that although DC takes little time to calculate node centrality,DC only considers the number of connected edges of nodes as an evaluation index and has a lower monotonicity value,while BC algorithm is a slower algorithm on most data and data pairs because it considers the shortest path and number of nodes in the data.As a whole,the SLGC algorithm increases the computing time relatively by a small amount on the basis of improving the accuracy of the node centrality metric;therefore,in terms of network running time,the SLGC algorithm is in a relatively intermediate position among all methods.

5.Conclusion

Mining and ranking of important nodes of complex networks has become one of the research hotspots of complexity theory.In this paper, we propose a new node centrality measurement method,the SLGC algorithm.In response to the limitations of traditional classical algorithms that only consider single-dimensional node features and the inaccurate results of existing node centrality measurement algorithms,we adopt the idea of multi attribute decision making for node importance ranking.We explore influential nodes in complex networks by considering the node’s own attributes,the quantity and quality of neighboring nodes within its local neighborhood,and introducing information entropy to study the node’s local influence.Additionally,we calculate the global influence throughK-shell decomposition and the shortest paths between nodes.

By applying the SLGC algorithm to six different types and scales of real-world complex networks, we fully demonstrate its effectiveness in partitioning nodes into different ranks and better distinguish the influence of nodes from three aspects: monotonicity value, ranking value, and complementary cumulative distribution function.Furthermore, we validate the effectiveness of the proposed algorithm by simulating the spread of nodes in practical scenarios using the SIR model.The proposed method measures the importance of nodes from multiple dimensions and statistical features,and its time complexity is intermediate among node centrality measurement methods.This method improves the ranking of node importance in complex networks while ensuring network operational efficiency,and it can be applied to complex networks of various sizes and scales.

Experimental results show that the proposed method effectively differentiates and propagates nodes, outperforming existing benchmark methods.However,the current SLGC algorithm is limited to unweighted networks.Therefore, in future research, we will incorporate the study of weighted networks into the proposed method, which could present one of the challenges for developing a more accurate and widely applicable algorithm for ranking the importance of nodes in complex networks.

Acknowledgments

Project supported by the Natural Science Basic Research Program of Shaanxi Province of China (Grant No.2022JQ-675)and the Youth Innovation Team of Shaanxi Universities.