Deterministic remote preparation of multi-qubit equatorial states through dissipative channels

Liu-Yong Cheng(程留永), Shi-Feng Zhang(張世鳳), Zuan Meng(孟鉆),Hong-Fu Wang(王洪福), and Shou Zhang(張壽)

1School of Physics and Information Engineering,Shanxi Normal University,Taiyuan 030031,China

2Department of Physics,College of Science,Yanbian University,Yanji 133002,China

Keywords: remote state preparation,dissipative channel,equatorial state,fidelity

1.Introduction

Quantum communication and quantum information technology demonstrate prominent advantages in many modern information processing tasks with enhanced security,fast speed,and high transmission efficiency.As a unique resource,quantum entanglement has been widely used in many quantum information processing protocols, such as quantum teleportation (QT),[1,2]quantum secret sharing,[3,4]quantum secure direct communication(QSDC),[5–8]and remote state preparation (RSP).[9–11]Quantum teleportation is a typical quantum process that allows one to send an unknown quantum state to another one through local operations and classical communication(LOCC)without physically transporting particles.Remote state preparation is another unique quantum process, in contrast to QT, which is used to transmit a known state between sender and receiver.Therefore,RSP schemes consume less qubit resources.So far,RSP has gained extensive interest and research, such as deterministic RSP (DRSP),[12,13]joint RSP(JRSP),[14–18]controlled RSP(CRSP),[19–25]and continuous variable RSP.[26,27]Several RSP programs have been experimentally implemented in linear optical systems,[28]cavity QED,[29–31]and nuclear magnetic resonance systems.[32]However,in long-distance quantum communication,quantum states or quantum channels inevitably interact with the external environment, and environmental noise and noise-induced decoherence may lead to deviations in quantum information processing tasks.In actual quantum communication,five types of noise are often encountered,which are amplitude damping noise, phase damping noise, bit flip noise, phase flip noise,and depolarizing noise.[33]Remote state preparation schemes in noisy environments have also been studied.[34–42]

Equatorial state is a special class of quantum states of the Bloch sphere.In contrast to general quantum states,some of the equatorial state’s information is known.So they have some special properties and are easy to prepare.These quantum states have many specific applications in quantum information processing, such as remote realization of unitary operations,[43,44]and phase-covariant quantum cloning machines.[45–47]In recent years, remote preparation of equatorial states has been proposed.In 2011, Chenet al.proposed probabilistic joint remote preparation of two-particle high-dimensional equatorial states.[48]Choudhuryet al.proposed a JRSP scheme for preparing two-qubit equatorial states in 2015.[49]In the same year, Liet al.proposed a joint remote preparation scheme of multi-qubit equatorial states.[50]In 2017, Adepojuet al.proposed a JRSP scheme of twoqubit equatorial state in noisy channels.[51]In 2018, Sunet al.proposed an asymmetric controllable bidirectional JRSP method for single-qubit and three-qubit equatorial states in a noisy environment.[52]In the same year, Weiet al.proposed a DRSP scheme of arbitrary multi-qubit equatorial states.[53]Later, Sunet al.realized asymmetric synchronous bidirectional transmission of equatorial states.[54,55]In 2020, Zhaet al.proposed the remote deterministic preparation of arbitrarynqubit equatorial states using the maximally entangled state channel.[56]Very recently,Wanget al.proposed bidirectional three-qubit and four-qubit CRSP schemes.[57]

It should be noted that there are few comprehensive studies on the remote preparation of multi-qubit equatorial states in a noisy environment.To our knowledge, Adepojuet al.proposed a JRSP scheme of two-qubit equatorial state for six noisy channels in 2017.[51]Subsequently, Sunet al.proposed an asymmetric controllable bidirectional JRSP method for single-qubit and three-qubit equatorial states in a noisy environment with nine-qubit entangled state as the quantum channel.[52]Here, we investigate the effect of diverse quantum noises on the RSP of multi-qubit equatorial states with Bell state channels.The effects of amplitude damping noise,phase damping noise,bit flip noise,phase flip noise,bit-phase flip noise,depolarizing noise,and non-Markov environmental noise on the remote preparation of three-qubit and four-qubit equatorial states are analyzed in detail.The fidelities of the final states are quantitatively analyzed.The results show that the fidelities are related to the noise factors and the parameters of equatorial states.A comparative analysis shows that there are many differences in the influence of different noises on the state preparation.This makes it possible to better understand the influence of ambient noise on RSP and distributed quantum communication networks.

This article is organized as follows.In Section 2, we review the RSP of multi-qubit equatorial states under ideal conditions.Then,in Sections 3,4,and 5,the three-qubit and fourqubit equatorial states are taken as examples to expound the influence of environmental noise on the remote preparation of expected states.Finally, our discussions and conclusions are given in Section 6.

2.Remote state preparation of general multiqubit equatorial states

We first introduce the RSP process without considering noise.Suppose that there are two spatially distant participants,Alice and Bob.Alice wants to help Bob prepare a generalnqubit equatorial state in form of

whereal ∈{0,1}, 0≤θj ≤2π,j=∑nl=1al·2l-1is the corresponding decimal number of binary stringan···a2a1.Initially,Alice and Bob sharensets of two-qubit maximally entangled Bell states as quantum channels.The channels can be expressed as

where particles belonging to Alice have subscript A and particles belonging to Bob have subscript B.According to the conventional RSP process, Alice needs to performn-qubit projection measurement using a set of orthogonal measurement basis{|Γd〉,d=1,2,...,2n}to help Bob prepare the target state.Under this set of measurement basis,the entangled state of the entire system can be rewritten as

After Alice completes the projection measurement of the particles in her hand, she announces the measurement results through classical channel.According to Alice’s measurement results,Bob can perform the corresponding unitary operations to achieve the target state to be prepared.

It should be pointed out that the form of Alice’s measurement basis is not unique theoretically.For instance, the measurement basis{|Γd〉}can take the form of[56]

Taking the first form of measurement basis as an example, if Alice’s measurement result is|Γ2n〉A(chǔ)1···An,then Bob’s particles will collapse into state|φ2n〉B1···Bn.Bob can then perform appropriate unitary operationsσB1z ?σB2z ?σB3z ?···?σBnzon the particles in his hand to realize the target state|χ〉.

However, in a practical communication process, a quantum system will inevitably interact with the environment.The environmental noise will have a certain impact on the success or performance of the quantum communication schemes.Therefore, it is instructive to research the effect of quantum noise on the RSP process.Here, we first study the influence of six common quantum noises, which are amplitude damping noise,bit flip noise,phase damping noise,phase flip noise,bit-phase flip noise, and depolarizing noise, followed by the analysis of non-Markovian effects on the RSP schemes.The effects of quantum noises can be mathematically regarded as some specific kinds of quantum operation, expressed in the form of corresponding operators.In addition, we can determine the information loss due to noise during RSP by calculating the fidelity of the obtained state.The formula for calculating the fidelity of the final system is

The fidelity ranges from 0 to 1 and the smallerFmeans more information is lost in a noisy environment.Next,we will illustrate the RSP processes of three-qubit and four-qubit equatorial states in different kinds of noisy environment and deduce the fidelity of the final states.

3.RSP of three-qubit equatorial states in common noisy environments

To elaborate the influence of environmental noise on the RSP of multi-qubit equatorial states, we begin to take the three-qubit equatorial state as an example.Here,Alice wants to help Bob remotely prepare the three-qubit equatorial state expressed as

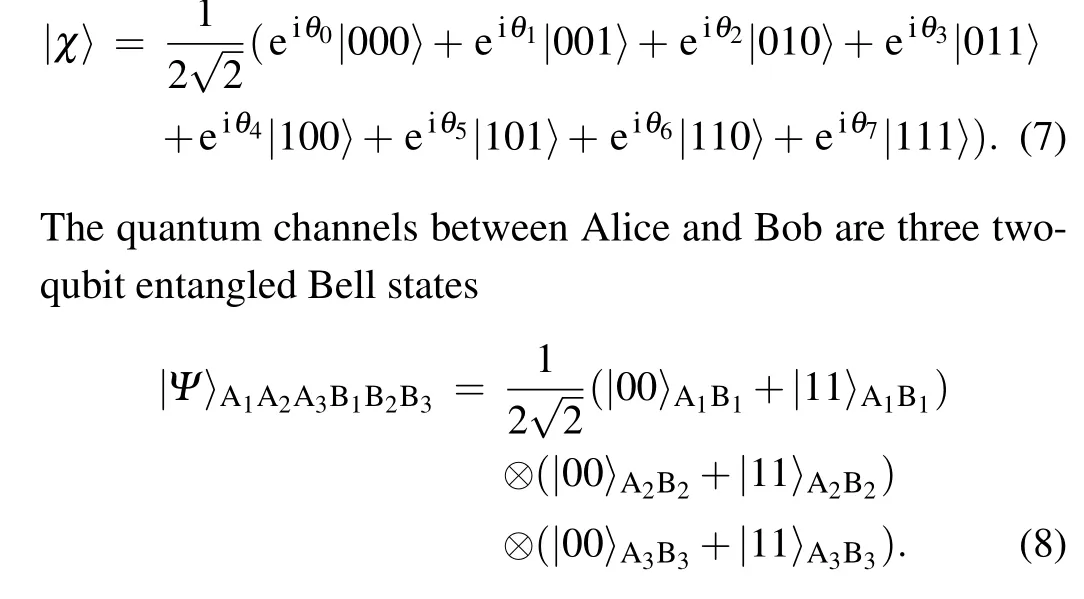
Consider that Bob is the generator of the entangled resource|Ψ〉A(chǔ)1A2A3B1B2B3.He keeps the particles{B1, B2, B3}and sends the particles{A1, A2, A3}to Alice through the noisy channel.Therefore,in the subsequent RSP process,we only consider the influence of noise on particles{A1, A2, A3}.For simplicity, we assume that all particles experience the identical noise.

3.1.The amplitude damping noise

The amplitude damping noise can be used to describe the energy dissipation effects due to energy loss in a quantum system.In quantum optics, the spontaneous radiation of a twolevel atom from excited state to ground state and the decay of a single photon from a micro-cavity can be described by this noise mechanism.The general behavior of amplitude damping noise can be represented by the following Kraus operators:

whereκindicates the decoherence rate of amplitude damping noise.In such a noisy transmission environment, the density matrix of quantum system evolves asρ →ε(ρ) =E?0ρE0+E?1ρE1.

Under the influence of amplitude damping noise, the quantum channels between Alice and Bob evolve as

The density matrix of the final state after Alice’s measurements and Bob’s unitary operations becomes

The explicit measurement results of Alice and the corresponding unitary operations of Bob are given in Appendix A.

We can then calculate the fidelity of the final state under the influence of amplitude damping noise as

It can be seen directly from Eq.(12) that the fidelity of state preparation depends on the decoherence rate of noise.And whenκ=0,F=1, corresponding to the perfect preparation process under ideal environment.The specific relationship between fidelity and decoherence rate is shown in Fig.1.As can be seen from the figure,the fidelity decreases asκincreases, and the decline rate is slow at first and is then fast,which show that the amplitude damping channel has a great influence on the results of the RSP.Whenκ=1, the fidelity reached the minimum value of 1/8.

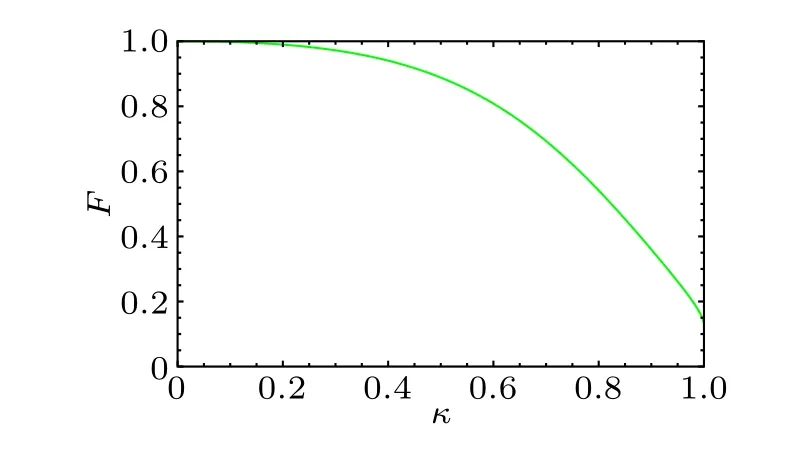
Fig.1.The fidelity of RSP of three-qubit equatorial state with decoherence rate κ in amplitude damping noise.

3.2.The bit flip noise

The Kraus operators of bit flip noise can be represented as

whereλindicates the decoherence rate of bit flip noise.The physical effect of bit flip noise is to change a qubit state as|0〉→|1〉or|1〉→|0〉with the probabilityλ.In such a noisy transmission environment,the quantum channels between Alice and Bob evolve into

As a result, the density matrix of the final state obtained by the remote preparation of the three-qubit equatorial state becomes

The fidelity of the final state under the influence of bit flip noise is

As can be seen from the above formula, the fidelity of state preparation under bit flip noise is related not only to the noise factor but also to the phase information of the target state.To unambiguously analyze the relationship between fidelity and the noise factor,we chooseθ7-θ0=θ6-θ1=θ5-θ2=θ4-θ3=θ.Figure 2(a)gives two-dimensional diagrams of fidelity changing with noise factorλwhenθ=π/4,π/2 andπ, respectively.As shown in the figure, whenθ=π/4 orπ/2, the fidelity value has three changing stages as slow decrease, dramatic decrease, and gentle change for the noise factor intervals 0<λ<0.3,0.3<λ<0.6 and 0.6<λ<1,and gets the minimum value 0.5 or 0 forλ=1.But whenθ=π(or integer multiples ofπ),no matter how the noise factor changes,the fidelity is always equal to 1,so that the remote state preparation is not affected by the bit flip noise for target states with this special phase relationship.

Fig.2.(a)The fidelity of RSP of three-qubit equatorial state with decoherence rate λ in bit flip noise for θ =π/4,π/2 and π.(b)The fidelity of RSP of three-qubit equatorial state with decoherence rate λ and phase parameter θ in bit flip noise.

To show the relationship between decoherence rate,phase information of equatorial state,and fidelity of final state more visually, in Fig.2(b), we demonstrate the three-dimensional diagram of bit flip noiseλ, phase informationθ, and fidelityF.As can be seen,the remote preparation fidelity of equatorial states with different phase relationships is not the same in the bit flip noise environment,especially when the noise factor is large.Furthermore,for the sameλvalue,the fidelity curve has a rising-falling turning point atθ=π/2(F=0)in 0<θ<π.This is due to the periodic property of the cosine function in the fidelity Eq.(16).

3.3.The phase damping noise

In contrast to amplitude damping noise, phase damping noise describes the interaction of quantum system with the surrounding environment when no energy loss is involved.The behavior of this noise can be characterized by the following Kraus operators:

whereμindicates the decoherence rate of phase damping noise.In such a noisy transmission environment, the density matrix of quantum system evolves asρ →ε(ρ)=E?0ρE0+E?1ρE1+E?2ρE2.

Therefore, under the influence of phase damping noise,the quantum channels between Alice and Bob evolve as

After Alice’s projection measurements,the density matrix of the final state obtained by Bob becomes

Figure 3 shows the relationship between decoherence rateμand fidelity in the phase damping noise environment.As can be seen from Eq.(20) and Fig.3, the fidelity depends on the decoherence rateμ.Whenμ=0, the maximum fidelity is 1,and the fidelity gradually decreases with the increase ofμ.Specifically,the fidelity decreases slowly with the increase ofμin 0<μ<0.4,decreases rapidly in 0.4<μ<0.8 and becomes less steep in 0.8<μ<1.Whenμ=1, the fidelity reaches the minimum value of 1/8.

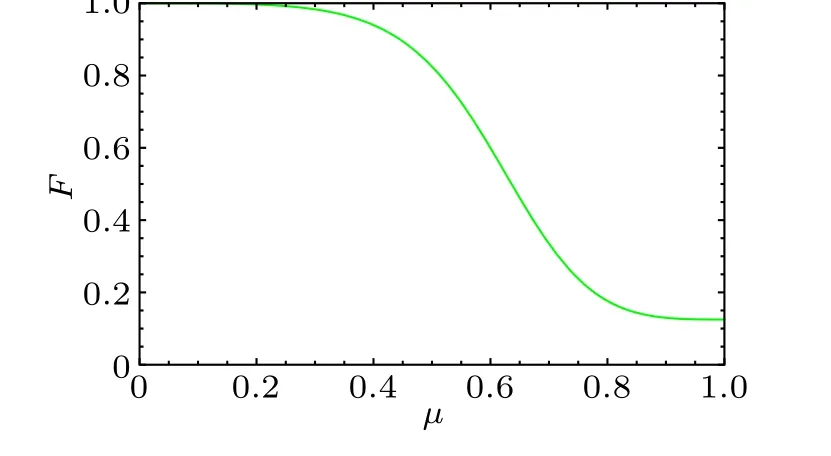
Fig.3.The fidelity of RSP of three-qubit equatorial state with decoherence rateμ in phase damping noise.

3.4.The phase flip noise

The Kraus operators of phase flip noise can be represented as

whereηindicates the decoherence rate of phase flip noise.In the phase flip noise environment, the quantum channels between Alice and Bob evolve into

After Alice’s measurements,the density matrix of the final state obtained by Bob becomes

The fidelity of the final state under the influence of phase flip noise is

Figure 4 is a two-dimensional diagram of fidelity changing with noise factorη.As can be seen,the fidelity gradually decreases with the increase ofη.Whenη=0, the fidelity reaches the maximum value 1.When 0<η<0.3,the fidelity decreases slowly with the increase ofηand changes quickly in 0.3<η<0.7.Finally, the fidelity gradually reaches 0 whenη=1.

Fig.4.The fidelity of RSP of three-qubit equatorial state with decoherence rate η in phase flip noise.

3.5.The depolarizing noise

The Kraus operators of depolarizing noise can be represented as

whereωindicates the decoherence rate of depolarizing noise.The physical effect of depolarizing noise is to keep the original state unchanged with probability 1-ω, and to have a bit flip,phase flip,or bit-phase flip with probabilityω/3,respectively.In such a noisy transmission environment,the quantum channels between Alice and Bob evolve into

As a result, the density matrix of the final state obtained by the remote preparation of the three-qubit equatorial state becomes

The fidelity of the final state under the influence of depolarizing noise is

The fidelity of state preparation under depolarizing noise is related not only to the noise factor but also to the phase information of the target state.For simplicity, we first chooseθ7-θ0=θ6-θ1=θ5-θ2=θ4-θ3=θto analyze the relationship between fidelity and the noise factor.Figure 5(a)gives two-dimensional diagrams of fidelity changing with noise factorωwhenθ=π/4,π/2 andπ, respectively.As shown in the figure, whenθ=π/4 orπ/2, the fidelity value gradually decreases with the increase ofωand gets the minimum value 0.5 or 0 forω=1.And whenω=π(or integer multiples ofπ), no matter how the noise factor changes, the fidelity is always equal to 1.We show the three-dimensional relationship between fidelity,depolarizing noise factorω,and phase factorθin Fig.5(b).The results shown in the figure are similar to the results shown in Fig.2(b).

Fig.5.(a)The fidelity of RSP of three-qubit equatorial state with decoherence rate ω in depolarizing noise for θ =π/4, π/2 and π.(b) The fidelity of RSP of three-qubit equatorial state with decoherence rate ω and state parameter θ.

3.6.The bit-phase flip noise

Next,we study the influence of bit-phase flip noise on the remote preparation of three-qubit equatorial states.The Kraus operators of this noise can be represented as

whereγindicates the decoherence rate.It is observed that the bit-phase flip is the combination of a phase flip and a bit flip.In bit-phase flip noisy transmission environment,the quantum channels between Alice and Bob evolve into

ξA1A2A3B1B2B3(ρ)

The final state obtained by Bob after the measurement and recovery operations gives

We calculate that the fidelity of the final state under the bitphase flip noise is

Obviously, the fidelity of state preparation under bitphase flip noise is related to both the noise factor and the phase information of the target state.We chooseθ7-θ0=θ,andθ6-θ1=θ5-θ2=θ4-θ3= 0 for simplicity, to analyze the relationship among fidelity and the noise factorγand phase factorθin Fig.6.Figure 6(a) shows that the fidelity decreases with the increase ofγbut will have a slight fluctuation with the change ofθ.To exhibit the fluctuation of the fidelity more clearly, we capture a small range illustration forγ ∈[0.8,1.0], as shown in Fig.6(b).For a givenγ, the fidelity curve has a inflection point and a small peak value atθ=π/2.Another thing to note is that if we chooseθ7-θ0=θ6-θ1=θ5-θ2=θ4-θ3as in Subsections 3.2 and 3.5,then the fidelity under bit-phase flip noise is consistent with the fidelity under phase flip noise.

To facilitate the comparison of the influence of different noise channels on the remote preparation of three-qubit equatorial states,the relationship between noise factors and the fidelities of the final states are drawn in Fig.7 under the same phase parameters.As can be seen, the fidelity changes under bit flip noise,phase damping noise,depolarizing noise,phase flip noise, and bit-phase flip noise tend to be consistent.But when the noise factors equal 1, only the fidelities under bit flip noise, phase flip noise, depolarizing noise, and bit-phase flip noise equal to 0.When the noise factors are in the interval 0–0.4, the fidelities of remote state preparation under the six types of noise can almost be maintained above 0.8.Moreover,the fidelity under depolarizing noise is almost invariably greater than that of other noise for small noise factor(0–0.7),while the fidelity under amplitude damping noise is almost invariably greater than that of other noise for large noise factor(more than 0.7).

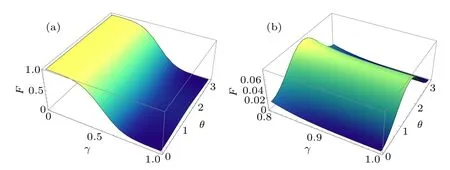
Fig.6.(a) The fidelity of RSP of three-qubit equatorial state with decoherence rate γ and state parameter θ.(b) The fidelity of RSP with decoherence rate γ ∈[0.8,1.0]and θ.

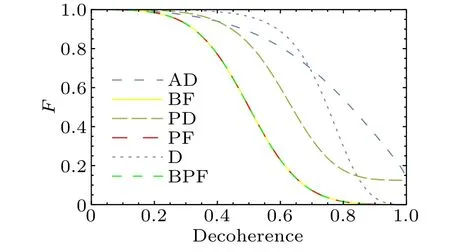
Fig.7.The contrastive fidelities of RSP of three-qubit equatorial state in amplitude damping(AD)noise,phase damping(PD)noise,bit flip(BF)noise, phase flip (PF) noise, bit-phase flip (BPF) noise, and depolarizing (D) noise with decoherence rate for θ7-θ0 =θ6-θ1 =θ5-θ2 =θ4-θ3=π/2.

4.RSP of four-qubit equatorial states in common noisy environments

Next, we explore the RSP of four-qubit equatorial states in six common noisy environments.Here,the target four-qubit equatorial state can be expressed as

Consider that Bob is the generator of the entangled resource|Ψ〉A(chǔ)1A2A3A4B1B2B3B4.He keeps the particles{B1, B2, B3, B4}and sends the particles{A1, A2, A3, A4}to Alice through the noisy channel.Therefore, in the subsequent RSP process,we only consider the influence of noise on particles{A1, A2, A3, A4}.For simplicity, we assume that all particles experience the identical noise.

According to the similar steps in Section 3,we can calculate the prepared final states of the four-qubit equatorial state under the six types of environmental noise, i.e., amplitude damping noise,bit flip noise,phase damping noise,phase flip noise, depolarizing noise, and bit-phase flip noise.The final states of RSP of four-qubit equatorial states in noisy environments are given in the Appendix B.Thus, we can obtain the six fidelities of the final states as follows:

Therefore,we can compare the fidelities of the final fourqubit equatorial states under different noisy channels in Fig.8 under the same phase parameters.As can be seen,the fidelity curves under amplitude damping noise,phase damping noise,bit flip noise, phase flip noise, depolarizing noise, and bitphase flip noise are similar with the three-qubit equatorial state preparation results in Fig.7.Compared with the three-qubit scheme, there are just different minimum values for fidelities under amplitude damping noise and phase damping noise.We also plot the fidelity diagrams of RSP of four-qubit equatorial state with decoherence rates and phase parameterθin bit flip noise and depolarizing noise in Fig.9.The trends of fidelities are also similar to those in Figs.2(b)and 5(b).

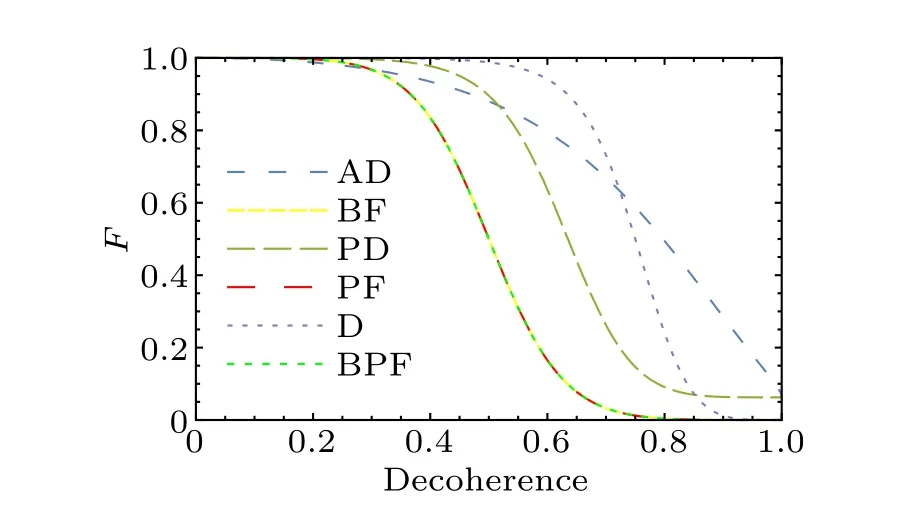
Fig.8.The contrastive fidelities of RSP of four-qubit equatorial state in amplitude damping noise,phase damping noise,bit flip noise,phase flip noise,bit-phase flip noise,and depolarizing noise with decoherence rate for θ15-θ0 =θ14-θ1 =θ13-θ2 =θ12-θ3 =θ11-θ4 =θ10-θ5 =θ9-θ6=θ8-θ7=π/2.

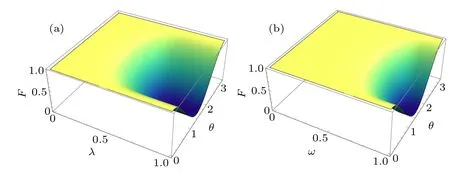
Fig.9.(a)The fidelity of RSP of four-qubit equatorial state with decoherence rate λ and state parameter θ in bit flip noise.(b)The fidelity of RSP of four-qubit equatorial state with decoherence rate ω and state parameter θ in depolarizing noise.Here, we have taken θ15-θ0 =θ14-θ1 =θ13-θ2=θ12-θ3=θ11-θ4=θ10-θ5=θ9-θ6=θ8-θ7=θ.

5.RSP process in a non-Markov environment

Next,we consider the RSP schemes of multi-qubit equatorial states under the influence of non-Markov environments,which are markedly different from the the previous six noise mechanisms.Due to the memory effect of the non-Markov environment, when an open quantum system evolves in it, part of the information flowing from the system to the environment will flow back from the environment to the system,which oscillates the decoherence process of quantum state.

Similar to the above sections, we consider that only the particles in Alice’s hand are affected by non-Markov noise in the remote preparation process of the three-qubit and fourqubit equatorial states, and qubits are resonantly coupled to their own local non-Markov environments.We assume that the environment has a spectral density of the Lorentzian form

Hence,the quantum channel between Alice and Bob under the influence of non-Markov noise evolves into

The final state after Alice’s measurements and Bob’s unitary operations becomes

Figure 10 shows the fidelity diagram of the three-qubit equatorial states in non-Markov environmental noise.As can be seen,there will be an up-and-down oscillation phenomenon with the increase ofλ0t.Even for long evolution time,the fidelity gradually approaches 0.1 rather than 0.Damping oscillation is a characteristic of the non-Markov process,which reflects the information flow back and forth between the system and the environment.

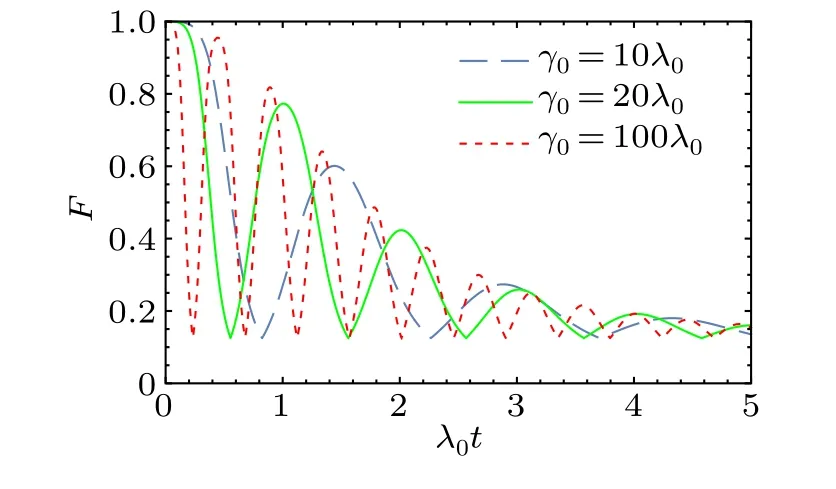
Fig.10.The fidelity diagram of the three-qubit equatorial states in non-Markov environmental noise with γ0=10λ0,γ0=20λ0 and γ0=100λ0.

For the RSP of four-qubit equatorial states, the effect of non-Markov environmental noise on the process is similar to that of the three-qubit equatorial state.Through direct calculation, the quantum channel of four-qubit scheme under the influence of non-Markov noise gives

The density matrix of the final state after Alice’s measurements and Bob’s unitary operations becomes

The fidelity of the final state under the influence of non-Markov environmental noise is

Figure 11 shows the fidelity diagram of the four-qubit equatorial states in non-Markov environmental noise withλ0t.As can be seen, the fidelity also shows oscillatory variation.With the increase oft, the fidelity gradually approaches 0.05 after several damping oscillations.Compared to Fig.10, the fidelity minimum is smaller.This happens because the target state has a higher number of particles and more channel particles are subjected to noise,and the fidelity is affected more.

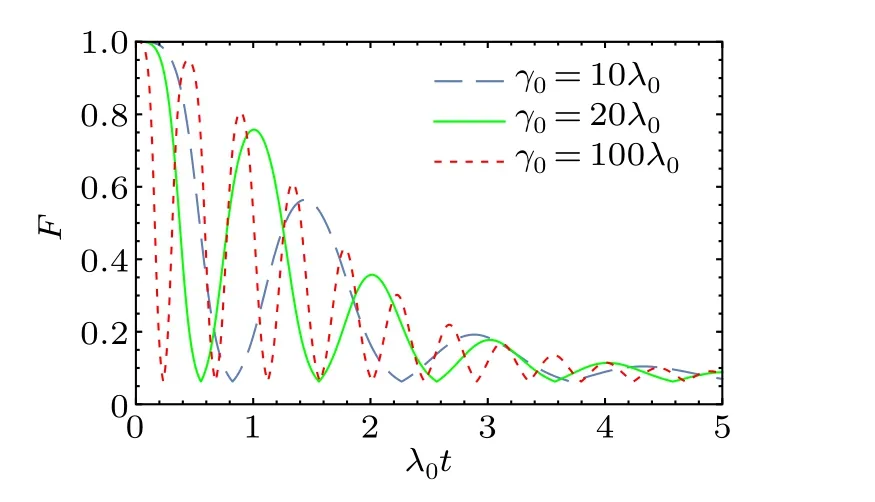
Fig.11.The fidelity diagram of the four-qubit equatorial states in non-Markov environmental noise with γ0=10λ0,γ0=20λ0 and γ0=100λ0.

6.Discussion and conclusion

RSP schemes are significant for the construction of distributed quantum communication and quantum network.In the actual environment,information will inevitably be affected by different types of environmental noise in the storage and transmission processes.In this paper,by studying the remote preparation of multi-qubit equatorial states in noisy environments, we find that the fidelities of the schemes depend on the decoherence rates of the environmental noises.Generally,the fidelity decreases as the decoherence rate increases.For the six types of common noise,i.e.,amplitude damping noise,bit flip noise,phase damping noise,phase flip noise,bit-phase flip noise and depolarizing noise, when the noise factors are equal, the influence of bit flip noise and phase flip noise are similar.When the noise factors are in the small range, the effect of depolarizing noise on RSP is minimal.The information loss caused by amplitude damping noise is less than other noises when the noise factors are large.In particular,when the target state has specific phase information, the bit flip noise and depolarizing noise may have more complex effects on our RSP schemes,even for the ideal cases where the fidelity values are always 1.For the non-Markov environment,owing to the back and forth of information between the environment and systems, fidelities exhibit oscillating behavior and the minimum value may stay greater than zero for a long evolutionary time.These results may have important implications for future research on how to avoid the influence of noise on distributed quantum communication.

Here, our RSP schemes mainly focus on the effects of various types of environmental noise on multi-qubit equatorial states.The results show that noise inevitably reduces the fidelities of the RSP process.In fact,we can design appropriate operations to reduce the negative effects of noises and improve the fidelities of state preparation schemes.For example,it has been proven that weak measurements and quantum reversing measurements of qubits can suppress the influence of environmental noises on quantum states and improve the fidelities of remote preparation of quantum states.[25,29]In our schemes,performing appropriate weak measurements and quantum reversing measurements on transmitted particles in the quantum channel can theoretically improve the fidelities, and the cost of the improved fidelities may be reduced successful probabilities of state preparations.Moreover, the schemes that we considered are remote realization of states preparation by two spatially distant participants.In fact, when it comes to the remote preparation schemes of multi-qubit states,we can theoretically extend the schemes to the controlled RSP schemes or joint RSP schemes.That is,the initial particles can be distributed in the hands of more than one sender or controller.The final success requires the cooperation of multiple senders or controllers.Such schemes are more valuable for the confidentiality of long-distance quantum communication networks.

Appendix A: The explicit derivation procedure from Eq.(10)to Eq.(11)

Under the influence of amplitude damping noise, the quantum channel of participants evolves into the state of Eq.(10).Subsequently,Alice carries out projection measurement of particles in her hand, and the basis vectors of measurement can be expressed as follows:

According to the eight different measurement results,the particles in Bob’s hand collapse into one of the following eight states:

From this, it can be seen that if Bob performs a set of corresponding unitary operationsIB1?IB2?IB3,σB1z ?IB2?IB3,IB1?σB2z ?IB3,IB1?IB2?σB3z,σB1z ?σB2z ?IB3,σB1z ?IB2?σB3z,IB1?σB2z ?σB3zorσB1z ?σB2z ?σB3zon the particles in his hand,then the final state can be obtained as Eq.(11).

For the other noisy environments, the measurement and recovery processes of multi-qubit equatorial state RSP are similar.The tedious derivations of the expressions are not shown here.

Appendix B:The final states of RSP of four-qubit equatorial states in a noisy environment

According to the Kraus operators of six types of noise in Eqs.(9),(13),(17),(21),(25),and(29),we can work out the density matrices of the four-qubit final states obtained by Bob after Alice’s projection measurements,respectively.

(i)The final state under amplitude damping noise

(ii)The final state under bit flip noise

(iii)The final state under phase damping noise

(iv)The final state under phase flip noise

(v)The final state under depolarizing noise

(vi)The final state under bit-phase flip noise

Finally, we can get the fidelities of prepared four-qubit equatorial states in a noisy environment as shown in Eqs.(35)–(40).

Acknowledgment

Project supported by the Fundamental Research Program of Shanxi Province(Grant No.202203021211260).