Activated dissociation of H2 on the Cu(001)surface:The role of quantum tunneling

Xiaofan Yu(于小凡), Yangwu Tong(童洋武), and Yong Yang(楊勇)

1Key Laboratory of Photovoltaic and Energy Conservation Materials,Institute of Solid State Physics,HFIPS,Chinese Academy of Sciences,Hefei 230031,China

2Science Island Branch of Graduate School,University of Science and Technology of China,Hefei 230026,China

Keywords: H2, Cu(001), dissociation, quantum tunneling, density functional theory (DFT), transfer matrix method

1.Introduction

As a clean energy source, hydrogen mainly exists in the form of molecules in nature.Materials involving metal elements are commonly utilized as catalysts for hydrogen production and storage to harvest hydrogen-based energy.[1-3]The elementary dynamics (e.g., adsorption and diffusion) of hydrogen on transition metal surfaces are closely related to some important physical and chemical processes such as crystal growth,hydrogen embrittlement,and surface corrosion,as well as technological applications like radiation protection in fusion reactor, electrode reactions in fuel cells, and surface catalysis.[4-19]When H2molecules approach a metal surface,depending on the energetics,they may remain in the molecular form, or they can dissociate with the H atoms attached separately on the metal surface.The key factor determining the energetics is the energy path, in particular the energy barrier associated with the dissociation process, i.e., the dissociation barrier.It is found that the dissociation barriers of hydrogen molecules on metal surfaces depend on the types of metals.For instance,the H2molecules adsorbed on the surfaces of Pt and Rh can spontaneously decompose into H atoms.[20-22]By contrast,the H2molecules adsorbed on the surface of Cu and Ag[23]cannot decompose into H atoms spontaneously.Additional energy consumption is required for the dissociation process,which is usually referred to as an activated process,with an energy barrierEb＞0, as compared withEb=0 for the spontaneous process.The dissociation barriers of hydrogen are also quite different for different crystallographic planes.The existence of an activation barrier is commonly believed to be due to the full occupation of d orbitals,which induces Pauli repulsion when molecules encounter surfaces.[24,25]Consequently, the dissociation processes of H2on the surfaces of the metals that have fully-occupied d orbitals tend to be activated processes (Eb＞0), while the dissociation on the metals with partially-occupieddorbitals is more likely to be a spontaneous process(Eb=0).There have been many experiments reported[6,8,10,14,15]for the adsorption,dissociation and diffusion processes of hydrogen on different metal surfaces.For example,the nozzle beam experiment,with sticking coefficient measurements for monoenergetic molecular beams as a function of energy and the angle of incidence, was carried out to study the adsorption and desorption kinetics of H2on Cu surfaces.[6]Using thermal desorption with work function and low-energy electron diffraction (LEED) measurements,the adsorption state and adsorption energy for the H/Pd(100)system was determined.[8]Molecular beam techniques were utilized to control the kinetic energy and the incident angle of H2molecules,and to explore in detail the nature of the dissociation barriers on copper surface.[10]

As a typical prototype system for the activated reactions of H2with metal surfaces, H2/Cu has been the subject of immense theoretical investigations, primarily on the dissociation and sticking dynamics,[26-49]and the thermal desorption spectra,[50]which are directly related to the energy pathway governing the dissociation/desorption processes.Generally, the collision between a diatomic molecule with a surface involves at least six degrees of freedom, if the surface is as assumed to be rigid.For an accurate description of the process, a study of six-dimensional (6D) dynamics is usually required.Such a study is feasible for classical mechanics, but it is relatively challenging for quantum-level simulations.Based on the potential energy surface (PES) constructed within the Born-Oppenheimer approximation,multidimensional(3D to 6D)quantum dynamics calculations have been carried out to study the activated dissociation of H2on Cu surfaces,[28-41]with a focus on the role of the vibrational and rotational states of H2, as well as the coupling between both degrees-of-freedom.[29-40]Using 6D quantum simulations, it is found that[33-35]the dissociation probability depends on the orientation of the axis-of-rotation of the incident H2molecule.The so-called “helicopter” orientation(where the angular momentum vectors are perpendicular to the surface, or the line joining the H-H bond is parallel to the surface) yields a reaction probability that is dramatically larger than for the “cartwheel” orientation, where the angular momentum vectors of H2are parallel to the surface.Recently, special attention has been paid to the development of chemically-accurate PES for the interactions between H2and the copper and other metal surfaces.[42-49]Notable progress in this field includes, for instance, the implementation of the semi-empirical specific reaction parameter(SRP)approach to the density functional theory (DFT),[42-47]and the recentlydeveloped machine learning PES.[48,49]

As compared with other elements,hydrogen has a smaller mass, and therefore more significant nuclear quantum effects are expected in its dynamical process.[51-54]In recent years,the important role of atomic quantum tunneling in the reaction rates and the selectivity of chemical processes involving small molecules has been increasingly reported.[55,56]For instance,it is found that nuclear quantum effects account for the facile activation and dissociation of H2on Cu(111) surface which is alloyed with 1%monolayer of Pd.[57,58]Analysis based on model potentials has shown that quantum tunneling is essential to the sticking of H2on metal surfaces.[26]Despite the enormous number of experimental and theoretical investigations,there still lack of systematic and in-depth studies on the role of quantum tunneling in the activated dissociation of H2on metal surfaces.In this paper,we revisit this topic by studying the activation and dissociation of H2molecules on Cu(001).The effects of quantum tunneling are investigated based on first-principles calculations combined with the transfer matrix method, for which the minimum energy pathway (MEP) of dissociation is extracted fromab initiopotential energy surface(PES).During the activation process of H2on Cu(001), it is shown that the charge transfer between the Cu surface and the H2molecules is the key for the breaking of H-H bond and the formation of Cu-H bonds.Bistability of the adsorption states is identified in the vicinity of the critical point of dissociation.The probability of dissociation and the corresponding rate constants due to the translational (H2tunneling as a whole unit)and the vibrational motions of H2molecules are quantitatively evaluated.The obtained activation barrier and the threshold kinetic energy for detectable dissociation events agree with experimental observations.The effective dissociation barrier is evaluated as a function of temperature,whose magnitude is found to be significantly reduced owing to the quantum tunneling of H atoms.For the dissociation of hydrogen isotopes H2and D2,the crossover from the high-temperature classical dynamics to low-temperature quantum dynamics is recognized.

This paper is organized as follows.Following the introduction, Section 2 presents the technical details of the firstprinciples calculations and the transfer matrix (TM) method employed in this study.In Section 3, the results for the energy path of the activated dissociation of H2on Cu(001), the role of charge transfer, and the role of quantum tunneling in shaping the kinetic process are presented and compared with experiments.Section 4 summarizes the main findings of this paper.

2.Methods

2.1.First-principles calculations

The Viennaab initiosimulation package (VASP)[59,60]based on density functional theory(DFT)is employed for the first-principles calculations.The Perdew-Burke-Ernzerhof(PBE) functional within the generalized gradient approximation(GGA)[61,62]is used to describe the exchange correlation of electrons,in combination with the PAW potentials[63,64]to describe the electron-ion interactions.The energy cutoff for the plane-wave basis sets is 600 eV.The initial atomic configurations are constructed with the aid of VESTA,[65]which models the Cu(001)surface as a six-layerp(3×3)supercell repeating periodically along thexyplane with a vacuum layer of about 15 °A along thezdirection.In all the calculations, the Cu atoms in the bottom three layers are fixed while the atoms in the upper layers are relaxed.We employ a dipole correction for the total energy to eliminate the artificial dipole-dipole interaction caused by the upper and lower asymmetric slab surfaces.A 4×4×1 Monkhorst-Packk-mesh[66]is generated to sample the Brillouin zone(BZ)in performing structural relaxation and total energy calculations.These sets of parameters ensure the total energy calculations converge within an error bar of～0.5 meV/atom.The vibrational properties of the relaxed structures are analyzed using the density functional perturbation theory(DFPT).[67]

2.2.Transfer matrix method

The probability of a quantum particle passing through a potential barrier of arbitrary shape can be obtained using the transfer matrix (TM) method.By numerically slicing an arbitrarily-shaped potential, it is transformed into a stack of multiple rectangular potential barriers(potential wells).[54]The transmission of a particle through each rectangular potential barrier (potential well) can be represented by a matrix of coefficients that describe the transmitted and the reflected amplitudes of the wave function.Multiplying the coefficient matrices in turn one obtains a transition matrix representing the transition relationship between the initial and the final states.For the transmission across a potentialV(x),the incoming(AL,BL) and outgoing amplitudes (AR,BR) of the wave functions can be related as follows:[54]

The advantage of the TM method is that the obtained transmission probabilities are numerically accurate as compared with that calculated by the Wentzel-Kramers-Brillouin(WKB)approximation.[68]For instance,when the incident energy of a classical particle is higher than the potential barrier,the probability of the particle passing through the barrier is 1.Such a deficiency of traditional WKB is partly amended by an improved version.[69]For a quantum particle,due to the existence of quantum interference, even if the energy of the particle is greater than the barrier height, there may be a certain probability of reflection,which makes the probability of passing through the potential barrier to be smaller than 1.The TM method deals with the transport of quantum particles through a given potential field in a unified manner,and it fully considers the quantum effects in the process of crossing a potential barrier.

3.Results and discussion

3.1.Mechanistic analysis of the interaction between H2 and Cu(001)

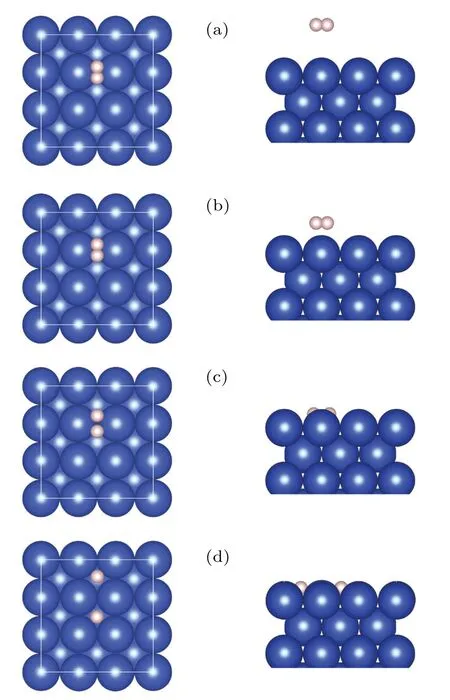
Fig.1.Top(left)and side views(right)of the typical H2/Cu(001)configurations,from the molecular state(a)to the dissociative state(d).The blue(large)balls represent Cu atoms,while the pink(small)ones are for H atoms.This convention applies to all the figures.

We begin by investigating the atomistic process of the dissociation and adsorption of H2on the Cu(001)surface.Figure 1 shows some typical configurations representing the dissociation process of a H2molecule approaching the Cu(001)surface along the normal(z)direction.The orientation line of H-H bond is parallel to Cu(001), and the midpoint of H-H bond is right above one of the bridge sites of Cu(001), with the projection of H-H bond perpendicular to the surface of Cu-Cu bond.Such an initial configuration gives rise to the largest possibility of dissociation.[17,25,33-35]Our calculations found that,when the distance between the H2molecule and the Cu(001) surface decreases to a critical value (zc=0.947 °A),the covalent bonds in the H2molecules tend to break, and the molecule decomposes into two adsorbed H atoms on the Cu(001) surface.The corresponding PES is obtained by the following procedure: At the height of the center-of-massZH2,the H2bond lengthdH-His gradually varied, and the configuration space is sampled point-by-point with the energy of each configuration at the coordinates (ZH2,dH-H) given by the DFT calculations.The PES is shown in Fig.2(a), with its 2D projection onto the parameter planeZH2-dH-Hshown as a contour plot in Fig.2(b).The MEP is indicated by the scattered dots in Figs.2(a)and 2(b),with four typical configurations labeled by A, B, C, and D.The top and side views of the MEP are schematically shown in Fig.1.The relative energy with respect to the initial molecular state (configuration A) is shown in Fig.2(c), as a function of the distance(|Z0-Z|) traveled by the center-of-mass of H2approaching the Cu(001) surface.Compared to Figs.2(a) and 2(b), the relative energies for the configurations near the critical point shown in Fig.2(c)are refined by the calculations with relaxed H2bond length (dH-H) at a given heightZH2.Therefore, the refined MEP represents a set of energy local minima along the reaction path.Figure 2(d)shows the variation of total energyE0(with respect to configuration A)as a function of the bond lengthdH-Hat a series of heightsz(=ZH2),from the gaseous molecular state(z～2.813 °A)to near the critical height of dissociation(zc～0.947 °A).The local minima of the curves correspond to the dynamically stable configurations locating on the MEP,yielding the stable bond lengthsdH-Hat a given height.Compared with the otherE0-dH-Hcurves of molecular state,the most remarkable feature of the curve(z=0.968 °A)at the vicinity of the critical height(zc=0.947 °A)is the existence of two stationary points,as indicated by the two local minima atdH-H=0.990 °A and 2.772 °A,respectively.The two minima are separated by a small barrier of ΔE～3 meV.This small barrier implies that a weak perturbation will switch the molecular state(C)to the dissociative state(Cd),leading to an abrupt change in the bond lengthdH-H.At temperaturesT ≤300 K,the H2molecule is frozen at its vibrational ground state, and the translational motion along the surface normal direction(z)therefore plays a major role.Near the critical height, a slight increase in the kinetic energy of the center-of-mass and consequently a small decrease in the H2-Cu(001)distance will result in an abrupt breaking of the H-H bond.

Before the onset of the dissociation,the energy of the system continuously rises with the decreasing of H2-Cu(001)distance.At the critical point of bond breaking, there is a sudden change,and the energy of stationary states drops abruptly,as indicated by theC-Cdline shown in Fig.2(c).Accordingly, the energy drop (from configurationCtoD) in this process corresponds to the desorption barrier of chemicallyadsorbed H on Cu(001).The height of the barrier (Eb～0.586 eV) is in good agreement with that from the previous works(Eb～0.58 eV)[17,46,70]at the GGA level,but it is lower than the barrier height (Eb～0.74 eV) calculated using the SRP-DFT method.[43,45,46]The desorption barrier and the desorption rate of H2on the Cu(001) surface[15]are commonly measured in experiments using temperature-programmed desorption(TPD);they can be numerically simulated based on the DFT calculations in combination with kinetics analysis.[50]

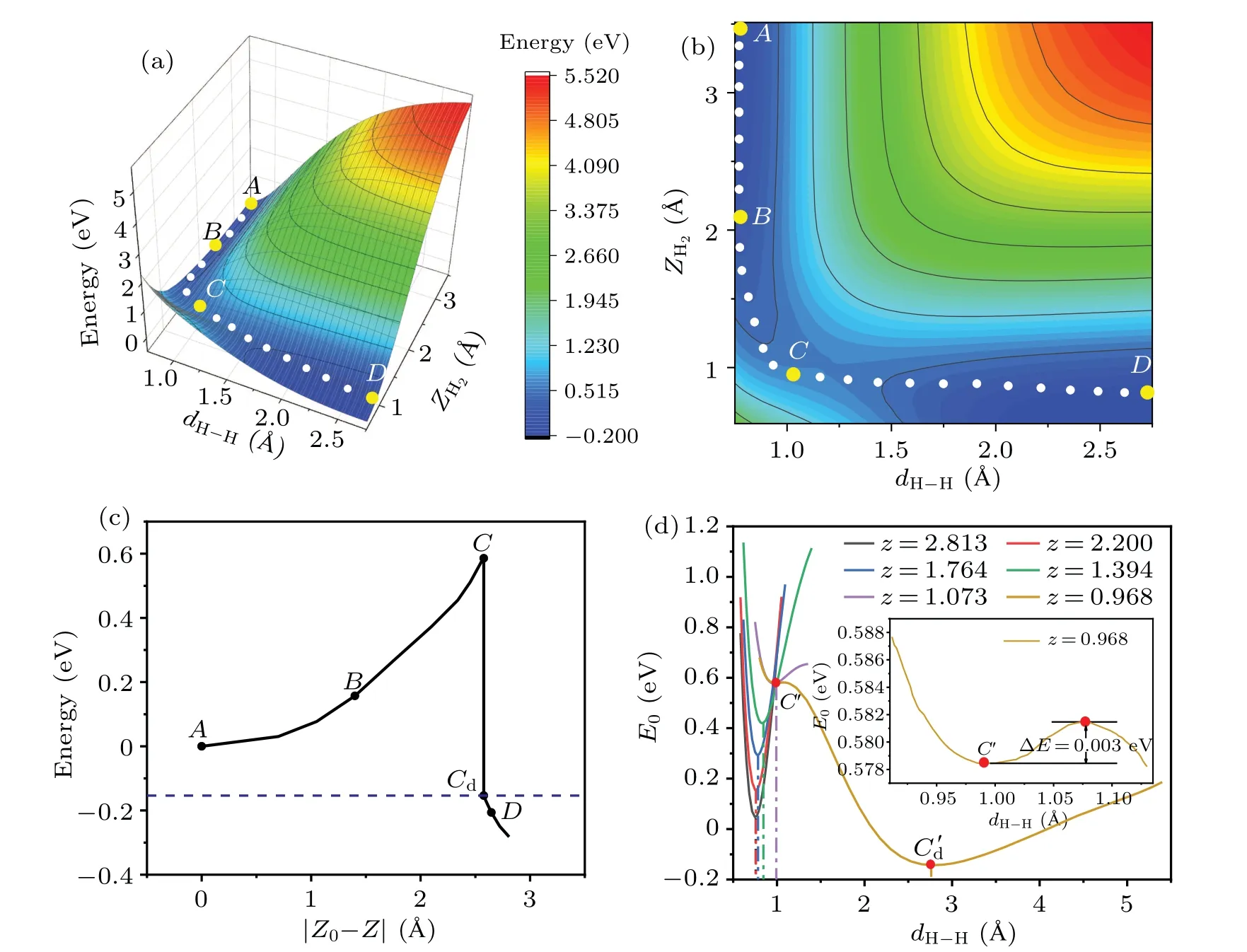
Fig.2.Calculated PES(a),its 2D contours(b),and the refined MEP(c)for the activated dissociation of H2 on the Cu(001)surface.(d)Variation of the relative energy (E0) with the bond lengths (dH-H) at a given height z.The energy of the initial configuration at gaseous phase(configuration A)is set as zero point.The points A-D in(c)correspond to the atomic configurations shown in Figs.1(a)-1(d),respectively. Z0 is the initial height of H2 and|Z0-Z|is the distance traveled.The points C and Cd represent the two stationary states at the critical height zc.

To understand the bond breaking from the level of electron, we have calculated the charge density differences for a number of typical adsorption configurations,including the initial molecular state, the intermediate and transition states of dissociation, and the final fully-dissociated state on Cu(001).Practically,the charge density difference(Δρ)of a given configuration is obtained by subtracting the charge density of the substrate and two individual H atoms from the total charge density of the adsorption system.The formula is as follows:

whereρ[H2/Cu(001)] is the charge density of the system of H2/Cu(001),ρ[H 1]andρ[H2]denote respectively the charge densities of the two H atoms,ρ[Cu(001)]is the charge density of the Cu(001)system.

The isosurfaces of charge density differences are shown in Fig.3.When the H2molecule is far away from the Cu(001)surface, there is no charge transfer between H2and the substrate.Instead, one sees mainly the charge difference with positive values in-between the two H atoms(Fig.3(a)),which is a clear evidence of the H-H covalent bond.As the distance between H2and Cu(001) decreases, the electrons from substrate Cu start to be transferred to the H atoms.The closer they are, the larger the amount of charge transfer is found.When the H2-Cu(001)distance isz=0.749 °A,the two H atoms are separated from each other and the H-H covalent bond is broken.The H atoms are located between four nearest neighboring Cu atoms and exchange charges with them.The H atoms gain electrons while the Cu atoms lose electrons.The electrons gather around the H atoms,indicating some characteristics of ionic bond between H and Cu atoms.Figures 4(a)-4(d)show the two-dimensional (2D) contours of charge distributions,which are sliced along the surface normal plane through the centers of the two H atoms.When the H2-Cu(001) distance isz= 0.592 °A, the covalent bond is completely broken.It is worth noting that the H-H bond is very weak atzc=0.947 °A,but it is still not broken.This can be regarded as the critical state.The breaking of the H-H bond is observed instantaneously when the H2-Cu(001)distance exceeds the critical value(zc=0.947 °A).

To get more insights into the dynamical process associated with charge transfer,we study the charge transfer between H2molecule and the substrate using the Bader analysis.[71]The results are shown in Fig.4(e).When an H2molecule gradually approaches the Cu(001)surface,electrons from the underlying Cu substrate are gradually transferred to the two H atoms.The critical distance between the hydrogen molecule and the surface of Cu(001) isZH2-Cu(001)≈0.947 °A, corresponding to a decrease in the height|Z0-Z|≈2.576 °A.As seen from Fig.2(c), the total energy of the system drops steeply at this distance.Meanwhile, a sharp increase in the charge transfer to H atoms is observed(Fig.4(e)).The abrupt changes in both the total energy and the number of transferred electrons indicate that the dissociation of hydrogen molecules at the critical point may be an ultrafast process.

Figures 4(f)-4(i) show the variation of 2D charge distributions between one of the H atoms(the other one is geometrically equivalent)and the nearest neighboring Cu atoms.At the initial distancez=2.460 °A,the H-Cu bond does not exist.As the distance between the H2molecule and the Cu(001)surface decreases, the H-Cu bond gradually forms and strengthens.Finally,the H atoms form H-Cu bonds with the nearest neighboring Cu atoms.The charge contours clearly demonstrate the formation of H-Cu bonds when a H2molecule approaches the Cu(001)surface.

From the analysis above, one may conclude that the adsorption and dissociation of H2molecules on Cu(001) is essentially a competition between H-H and H-Cu bonds.Regarding the forces governing this process, the nuclear (ion core)-electron interactions are attractive, while the nuclear(ion core)-nuclear (ion core) and electron-electron interactions are repulsive.The balance between the attractive and repulsive forces leads to the formation of the chemical bonds.The strength of the attraction is largely related to the extent of the overlap of electron wave functions.As a result, the strength of the attraction and the bonding between two atoms are largely determined by the overlap of wave functions of electrons that participate in the bond formation.For a given atom in a molecule,when the attraction from an atom of a foreign species is larger than that from the one it is bonded with,breaking of the old bond and the formation of a new bond are therefore expected.

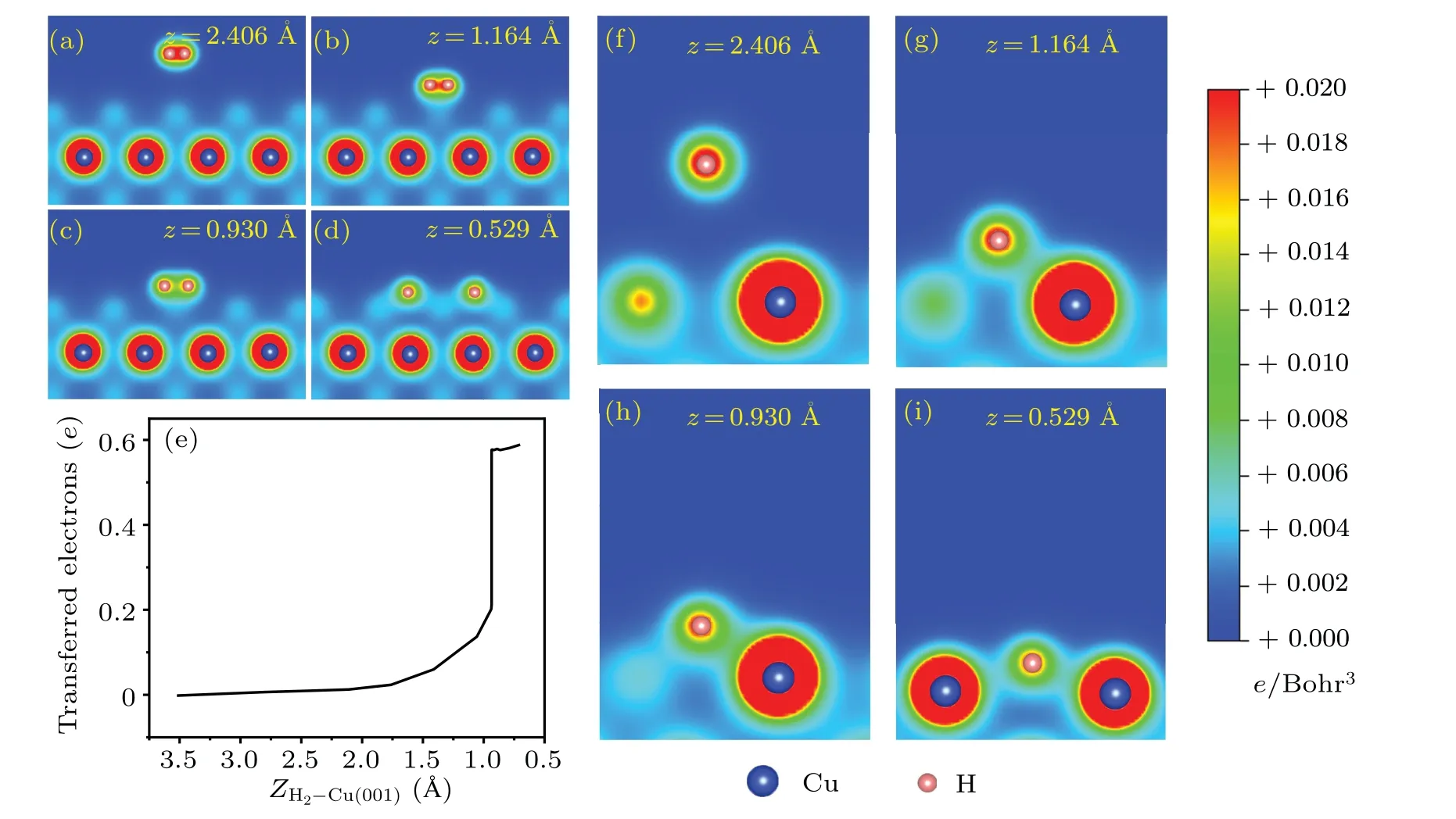
Fig.4.The 2D contours of the charge densities associated with the breaking of H-H bond, from the molecular state(a), the transition states(b)and(c),to the dissociative state(d).(e)Charge transfer from Cu(001)to H2,obtained from a Bader analysis,as a function of the distance from the center-of-mass of H2 to Cu(001).(f)-(i) 2D contours of charge densities, illustrating the formation of H-Cu bonds for the same configurations as that for(a)-(d),but viewed from different perspective angles.

3.2.Role of quantum tunneling in the dissociation processes

For a hydrogen molecule incident on the Cu(001)surface,the line joining the H-H bond can be either parallel or perpendicular to Cu(001).Generally, the orientation of the H-H bonds with respect to the Cu(001)surface can be described by an angleα, which varies in the range of 0≤α ≤90°.Previous studies based on semi-empirical andab initiomethods have shown that the barrier for H2dissociation on Cu(100)depends on the orientation angle.[17,33-35]Dissociation occurs more easily when the H-H axis is parallel to the surface.This is because the H2molecule of this orientation has the largest contact with the surface when it is close to the Cu(001) surface.Thus,it has the biggest chance of reaction and dissociation.Therefore,we only consider the case ofα=0,for which the axis of the H-H bond is parallel to Cu(001),with the two H atoms and the center-of-mass sharing the samezcoordinates.From the point of view of dynamical motions,the dissociation of H2molecules on Cu(001)is mainly due to the contribution of two processes.The first process is the dissociation due to the translational motion of H2in the vertical direction along the MEP,the most probable reaction path which is determined with the variation of H-H bond length(dH-H)intrinsically included in our DFT calculations.As shown in Fig.5(a),an H2molecule approaches the Cu(001) surface along thezdirection by overcoming the potential barrierU(z), i.e., the MEP,and finally it reaches the state of dissociation and chemisorption.The second process is the dissociation due to the stretching vibrations of H atoms in the horizontal direction (which is parallel to the Cu(001)surface).These two processes consist with the concept of overcoming the early and the late barriers, respectively, in the dissociative attachment of diatomic molecules on surfaces.[72]As shown in Fig.5(b), when the H atoms approach the Cu(001) surface alongzdirection, the lateral vibration of each H atom provides an additional probability of breaking the H-H bond by overcoming the lateral potential barrierU(x,y).This can be determined by standard DFT calculations.For a given temperatureT,the dissociation probabilities of the two processes can be calculated separately,and then the total dissociation probability is obtained by summing up the probabilities of the two processes.Unless otherwise stated,both H2molecules and single H atoms are treated as quantum particles in our study of the role of tunneling.

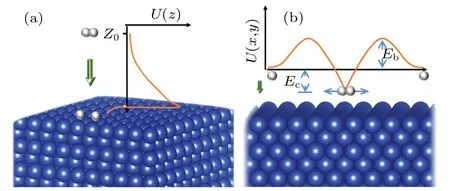
Fig.5.Schematic diagrams for the dissociation of H2 molecules incident along (a) the surface normal (z) directions and (b) the transverse direction.Here, ZC and Z0 correspond to the initial and the critical positions of H2 (point C in Fig.2), respectively.The potential energy difference between the instantaneous ground state of H2 at height z and the zero point(completely dissociative state)of the potential energy is marked as Ec.The potential barrier height,with respect to the potential energy zero,is marked as Eb.

For the first process,the probability of dissociation is

whereis the kinetic energy distribution function;[73]it is suitable for the particles in thermal equilibrium systems where the parabolic momentumenergy relation exists and the scalar potentials dominate the interactions.[54]Here,Tis the absolute temperature,Eis the incident energy,andkBis the Boltzmann constant.The quantityTr(E) is the transmission probability of the H2molecule(as a whole unit)across the potential barrierU(z)(Fig.5(a)),at a certain energyE; it is calculated by the transfer matrix(TM)method.In practice,an upper bound(Em)is set for the evaluation of the integral,and it ensures the numerical results converge to desired precisions.

For the second process,the probability of dissociation is

wherez0is the initial height of H2, andz1is the minimum height for H2to remain at molecular state (i.e., the critical height,zc),as shown in Fig.5(a).The lengthL=(z1-z0)is a normalization factor; it represents a decrease in the height with respect to Cu(001).The integration of the kinetic energy function is considered only for the case whenE ≥U(z).The quantityTr(z)is the probability that a H2molecule passes through the transversal potentialU(x,y)(Fig.5(b))at temperatureTand heightz;it can be obtained by the transfer matrix(TM) method combined with the calculations based on statistical mechanics.Quantum tunneling is possible only if the vibrational energyEn ≥Ec,whereEcis the energy difference between the molecular and the dissociated states at a heightz(Fig.5(b)).The mathematical expression for the transmission probability is

The quantityTr(En-Ec,z)is the probability of a H2molecule passing through the transversal barrierU(x,y)with an incident energy ofEn-Ecand a height ofz.Similarly, the transmission probability can be calculated using the TM method.The barrier height isEb, as depicted in Fig.5(b).For a numerical evaluation with energy sampling interval in the order of magnitude of 0.1 meV, a good convergence (with a relative deviation of less than 0.1%) of the integral is obtained whenEm≈5Eb.

At a given heightz, the energy of the system is set to be the zero point of potential energy when the H-H bond is broken(Fig.5(b)).The difference between the lowest potential energy point at this height and the potential energy zero is labeled asEc.It should be emphasized that only the energy levels withEn ≥Eccan produce effective quantum tunneling,and the corresponding vibrational energy level is labeled as thencth excited state.The subscript of the summation is thereforen ≥nc.In the case ofEn ＜Ec, evanescent waves of incident particles are expected,and the waves decay exponentially with the distance traveled.Finally,at temperatureT,the total probability of H2dissociation on Cu(001)as a quantum particle is given byPQ(T)=P⊥(T)+P‖(T).

The role of quantum tunneling can be demonstrated by assuming the H2molecule to be a classical particle and then comparing the probabilities of dissociation at given temperatures.The dissociation can be considered to be due to the contributions from two processes.The first process is to overcome the potential barrierU(z)to reach the decomposed adsorption state when H2gradually approaches the Cu(001)surface along thezdirection.The probability corresponding to this process can be calculated as follows:[53]

As mentioned above,is the kinetic energy distribution function at a given temperatureT,Ekis the kinetic energy,andEb⊥corresponds to the height ofU(z),which is～0.586 eV.

The second process is the dissociation due to the thermal motions of a single H atom overcoming the constraint of H-H bond.The probability of this process is given by,whereEb‖=EH-His the H-H bond energy,which was experimentally determined to be～436 kJ/mol or 4.51 eV.[74]This value is well aboveEb⊥and thus one hasPC⊥?PC‖.Therefore, the dissociation in the horizontal direction is negligible as compared with that in the vertical(surface normal)direction due to the translational motions of H2.In summary, as a classical particle, the dissociation probability of H2is given byPc=PC⊥+PC‖～=PC⊥.The calculated transmission probabilities are presented in Fig.6, as a function of temperature.It is seen that both quantum and classical probabilities increase with elevating temperatures.BelowT=1350 K,the transmission probability considering quantum tunneling effects(PQ)is always higher than that for the case of treating the H2molecule as a classical particle(PC).This phenomenon is even more pronounced at room temperature and below, at which the quantum transmission probabilityPQis well above its classical counterpartPC.In the lower panels of Fig.6 the contributions of the two processes are compared.It is found that the first process plays a major role in the overall dissociation,especially at low temperatures.AtT ≤18 K,the probability of the first process is more than 100 orders of magnitude higher than that of the second one.In low energy region,the corner-cutting effects,[75-79]due to which the tunneling pathway deviates from the MEP, can be important for H2dissociation.Such effects have been partly included in the calculation of MEP,for which the constraint of symmetric configurations of H2is imposed(see texts above).

Using the calculated dissociation probability of the H2molecule on Cu(001), we can estimate the rate constants of dissociation.The reaction rate constantkcan be obtained via the relation,[54]k=νP, whereνis the attempting frequency andPis the corresponding dissociation probability.For the first process,νcan be expressed as the reciprocal of the timeτ(E)for traveling from the starting pointz0to the end pointz1(Fig.5(a)).The dissociation rate constant for the first process is

whereEis the kinetic energy of the incident particle,U(z)is the dissociation potential along the vertical direction as shown in Fig.5(a), andmis the mass of H2molecule.The traversal timeτ(E)of tunneling across the barrier is obtained using Eq.(2) presented in Ref.[80].The reaction rate constant of the first process is

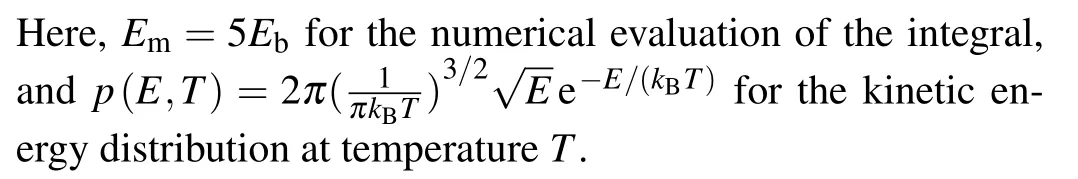
For the second process,the frequency of the H-H stretching mode in the transverse direction,ν‖(z),is used in the calculation of the rate constant.The frequency varies with the heightz,in fact,it gets progressively smaller with decreasing heightz.The rate constant for the second process is given by

where the vibrational frequencyν‖(z) can be obtained from the DFPT calculations.Ultimately,the total rate constant is

The results for the rate constants are shown in Fig.7,indicating that the dissociation in the vertical direction dominates the whole process.On the other hand, it is seen that (insets of Fig.7)the dissociation due to the H-H vibrations(horizontal stretching)plays a nontrivial role atT ≥300 K,for which both the translational and the vibrational motions of H2contribute significantly to the breaking of H-H bond.

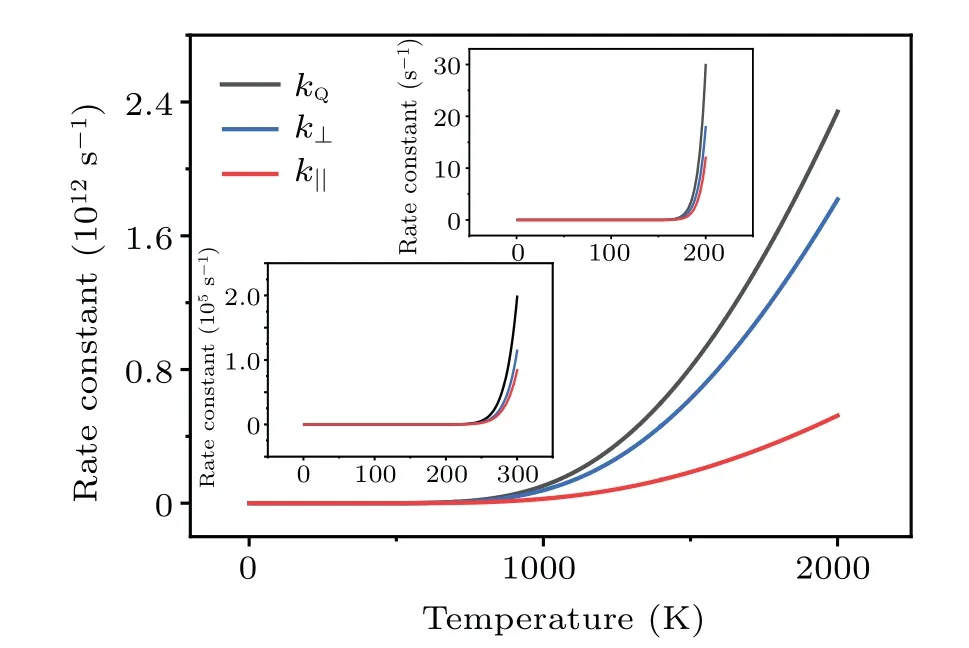
Fig.7.Temperature dependence of the quantum rate constant kQ, and their vertical and transverse components.

At the temperatureTd=220 K(insets of Fig.7),the rate constant of dissociation iskQ～300/s, which corresponds to a dissociation number ofNH2≈1.08×106within one hour.The smallest face-centered two-dimensional(2D)surface unit cell for Cu(001)is a square with the sizea～3.61 °A and the surface areaSCu(001)=a2～=13.03 °A2.Periodically extending 1000 times along the two basis vectors yields a square substrate with a side length ofL～0.361 μm, which is comparable to the size of the samples employed in experiment.On average, each 2D surface unit cell can adsorb 1.08×2 H atoms.If we define a surface coverage of one monolayer(ML) for the adsorption of one H to one surface Cu atom,then atTd=220 K, the surface coverage on Cu(001) within one hour is estimated to be～1.13 ML.This coverage is experimentally measurable.Nontrivial dissociation of H2is expected to take place on Cu(001) atT ≥Td.The predicted temperature for the onset of the nontrivial dissociation of H2isTd=220 K, which is comparable to previous experimental observations of the thermal desorption of dissociated H from Cu(001) (Td～218 K).[15]A significant increase in the reaction rate constant is found when the temperature reaches 1000 K and above(Fig.7).At such temperature the dissociation due to the stretching mode of H-H vibrations starts to play a nontrivial role.This is also in good agreement with the previous experimental measurements.When the kinetic energies of the hydrogen molecules ejected from the molecular beam nozzle reached about an equivalent temperature of～1000 K and above,it was observed that hydrogen began to adsorb instantaneously on the copper surfaces with measurable sticking coefficients.[6]

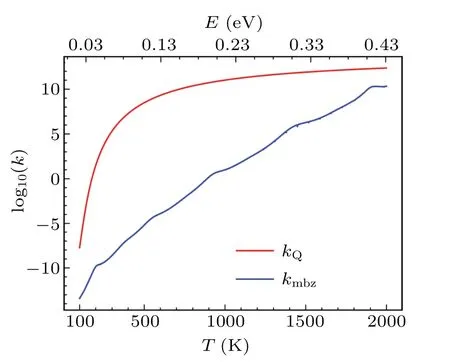
Fig.8.Calculated rate constants kQ and kmbz (in logarithmic scales)for the dissociation of H2 on Cu(001) under the thermal equilibrium condition and from molecular beam experiments,respectively.

The kinetic processes studied above are based on the precondition that the dosed H2molecules are in thermal equilibrium, with a well-defined kinetic energy distribution.[54]The situation changes significantly when the incident H2molecules are produced by a molecular beam nozzle,[6,10]where the kinetic energy of H2molecules has a very narrow distribution[10]and it can be as assumed to be single-valued.For the monoenergetic molecular beams of H2with kinetic energyE,the probability of tunneling is given by the transmission coefficientTr(E),which is readily computed using the TM method.For a H2molecule which penetrates the barrierU(z) and arrives at the Cu(001) surface, the rate constant of dissociation iskmbz(E) =ν⊥(E)×P⊥(E) =ν⊥(E)×Tr(E).We have compared the rate constant of dissociation of H2under thermal equilibrium with that for the non-equilibrium molecular beam experiment.The characteristic temperature for the activation of the rotational degree-of-freedom of a H2molecule isθr～85 K.[81]By contrast,the vibrational degree-of-freedom of H2is largely frozen at its ground state due to the very high characteristic temperature(θv～6100 K).[81]For temperatures aboveθr, both the translational and rotational degreesof-freedom of H2are activated,and the equivalent temperature of the incident H2molecular beam with the kinetic energyEcan therefore be estimated to beT=2E/(5kB).The calculated rate constants are shown in Fig.8, as a function of the temperature and the kinetic energy of each H2from molecular beams.It is clearly seen that at the same temperature the rate constant under thermal equilibrium(kQ)is larger than that for molecular beams (kmbz).Unlike the monoenergetic molecular beam with the translational kinetic energyEt, the H2molecules at thermal equilibrium have a nontrivial probability of being at the energy statesE ≥Et.This probability is

In the caset=1 s, we havend,H2(E)～=18.4×kmbz(E).For the kinetic energyE=0.176 eV andkmbz(E)～=0.073 s-1,our calculations yieldnd,H2(0.176)～=1.3, which implies that the surface coverage of dissociatively adsorbed H is～1 ML.This is expected to give detectable signals for experimental measurements.The threshold valueE=0.176 eV for measurable dissociative adsorption of H2on Cu(001) is comparable to the experimental measurementE=0.2 eV from molecular beam experiment.[6]This result shows the key role of quantum tunneling in the activated dissociation of H2on Cu(001).

3.3.Effective barrier and isotope effects

For the barrier-crossing process of a microscopic particle that satisfies the Van’t Hoff-Arrhenius relation, the total transmission probability (Ptot) can be generally expressed as follows:[54]

whereE?bis the effective barrier,andkBThave the usual meanings as before.Therefore,the value of the effective barrierE?bcan be obtained as follows:

Clearly, the effective barrieris a function of temperature.Using the probabilityPtot(T) obtained by the TM method, the values ofat different temperatures are calculated, and the results are shown in Fig.9.The data for the dissociation of H2and D2are presented, to show the isotope effects.It is seen that the effective barrier,which includes the effects of quantum tunneling,is appreciably lower than the classical barrier height(dissociation along the surface normal,U(z)),which is deduced by treating the incident H2molecules as classical particles.ForT ≥200 K, the effective dissociation barriers of both H2and D2increase smoothly withTand reach their maxima at～500 K,then they decrease slowly with further increasing temperatures.The nearly steady gap(ΔE=～0.02 eV) between the effective barriers of H2and D2is a consequence of quantum tunneling, whose probability decreases with increasing particle mass.Our calculations found that, forT ≥1000 K the gap (ΔE) decreases gradually and vanishes at～3500 K, beyond which the system approaches the classical limit.The existence of a maximum forE?bcan be qualitatively understood based on Eq.(14),where the competition between the termskBTand lnarrives at a compromise.[54]The weak temperature dependence ofE?batT ≥300 K indicates that it is usually sufficient to use one barrier parameter to describe the temperaturedependent kinetic process of atoms.

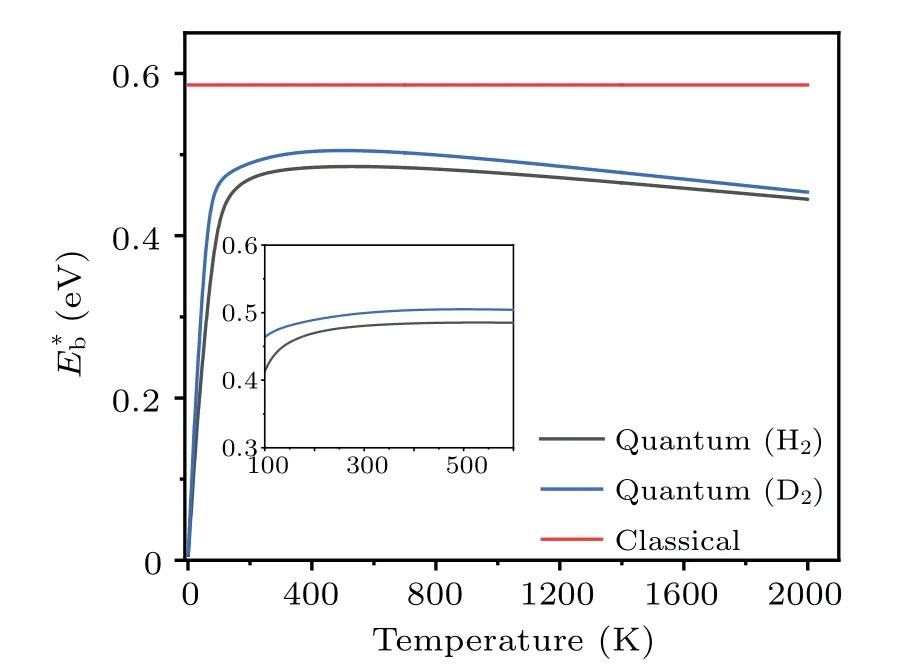
Fig.9.The energy barriers for the dissociation of H2 and D2 on Cu(001).The original barrier height calculated using adiabatic approximation is referred to as“classical”.The effective barriers(E?b)due to quantum effects are presented as a function of temperature.

The effective barriers for both H2and D2increase with temperature slightly, forT～200 K to 260 K.In this temperature range, the barrier for H2varies fromE?b～0.47 at 200 K to 0.48 eV at 260 K.Similarly, the corresponding values for D2increase from 0.49 eV to 0.50 eV.This is comparable to the data from the thermal desorption (the reverse process of dissociation) measurements in the same temperature range,in which the activation barriers of dissociation are determined to be 48±6 kJ/mol(or～0.50±0.06 eV)for H2and 56±8 kJ/mol (or 0.58±0.08 eV) for D2.The situation is much different forT ≤200 K, where the effective barrier drops almost linearly with decreasing temperature.The effective barrier for H2decreases quickly fromE?b～0.47 eV at 200 K to 0.06 eV at 10 K,while the barrier for D2varies from 0.49 eV to 0.08 eV in the same temperature range.When the temperatureTapproaches 0,E?btends to be zero, indicating that quantum tunneling effects may have a significant impact on the atomic-scale dynamics even at extremely low temperatures.

The significant role of quantum tunneling can be further demonstrated by investigating the isotope effects on the transmission probability and rate constant of H2and D2dissociation on Cu(001).In the calculations based on the TM method,both H2and D2are treated as quantum particles,for temperatureT ≤300 K.The results are shown in Fig.10.In the low temperature region,particularly forT ≤100 K,significant differences between the transmission probabilities and rate constants are found.Using the relationk=νP, the natural logarithm of the reaction constant, ln(KQ), may be expressed as follows:

where the negative slope of the lnline is simply due to the effective barrierE?bat a given temperatureT.As seen from Fig.10(d), at the turning pointT～100 K the rate constants for H2and D2depart from each other significantly,as an indication of the crossover from classical to quantum regimes.Moreover, the trends of the two curves can be roughly described by a combination of two lines that have the slopes being equivalent to the two effective barriers,as shown by the dash lines in Fig.10(d).Similar characteristics ofTdependent rate constant are found in the case of H diffusion on the Cu(001)and Pt(111)surfaces;[82-84]these characteristics may be also expected for the diffusion processes on the surface of other metals.In the phenomenological description of the effects of quantum tunneling,[69,85]two sets of parameters for the activation barriers (for both classical and quantum motions) together with two prefactors are introduced to roughly account for the dynamics at high and low temperature regions.By contrast,our method produces the major features of the variations of rate constant with temperature in a logically natural and unified manner, and it provides a promising way for including quantum tunneling effects in the chemical dynamics of many-body systems.

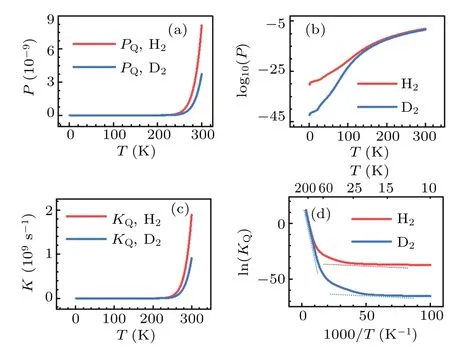
Fig.10.Calculated quantum probabilities(upper panels)and rate constants(lower panels)for H2 and D2 dissociation on Cu(001),as a function of temperature.The crossover from classical to quantum regimes is schematically indicated by the dash lines in(d).

The transmission coefficientsTr(E), the total transmission probabilityPtot(T)at a given temperatureT,the rate constantsk, and the corresponding effective barrierE?bare deduced from the PES calculated at the DFT-GGA level.Further corrections can be made by introducing more accurate PES for the H2-Cu(001) interactions (e.g., the PES calculated by the semi-empirical SRP-DFT approach[42-45]),the van der Waals corrections, or the interactions due to surface phonons.All these corrections may be taken as perturbations to the PES obtained by DFT-GGA calculations.As has been shown in Ref.[54] the perturbations or small changes to the original PES would only result in minor modifications on the transmission coefficientsTr(E),and therefore the quantities derived based onTr(E).Consequently,the main results regarding the role of quantum tunneling in the dissociation kinetics of H2on Cu(001)qualitatively remain unchanged.

4.Conclusion

In summary, the activation and dissociation processes of H2molecules on the Cu(001) surface have been studied based on the first-principles calculations and the transfer matrix (TM) method.It is found that charge transfer from the substrate Cu atoms to H2plays an essential role in activating and breaking the H-H bond.Near the critical point of bond breaking, the adsorption configurations are characterized by the existence of two stationary states,and an abrupt change of H-H bond length is expected upon small perturbations to the translational motions of H2.Using the MEP determined by the DFT calculations, the probabilities of H2molecules passing through the dissociation energy pathways are calculated using the TM method,which explicitly takes into account the effects of quantum tunneling.The probabilities and rate constants of dissociation due to the translational and the vibrational motions are evaluated and distinguished.Both translational and vibrational motions contribute nontrivially to the dissociation of H2at high temperatures.For the conditions when the Van’t Hoff-Arrhenius relationship applies,the effective potential for the dissociation and adsorption of H2on Cu(001)is calculated.After the effects of quantum tunneling are considered,the barrier height is significantly reduced as compared with that of the barrier which treats the H2as a classical particle within the Born-Oppenheimer approximation.In the studies on the situation of thermal equilibrium and the non-equilibrium molecular beam of H2, the calculated temperatures for the onset of measurable dissociation of H2on Cu(001)agree with the experiments.To further demonstrate the role of quantum tunneling, we have computed the effective barriers of dissociation for both H2and D2,which are found to be comparable to the experimental data.The role of quantum effects is found to be remarkable in low-temperature region where the crossover from the classical to quantum regimes is identified.The results are expected to be tested by future experiments.

Acknowledgements

Project supported by the National Natural Science Foundation of China(Grant Nos.11474285 and 12074382).We are grateful to the staffs at the Hefei Branch of Supercomputing Center of Chinese Academy of Sciences, and the Hefei Advanced Computing Center for the support of supercomputing facilities.