Recent Advances in China on the Predictability of Weather and Climate※
Wansuo DUAN ,Lichao YANG ,Mu MU ,Bin WANG ,Xueshun SHEN ,Zhiyong MENG ,and Ruiqiang DING
1LASG,Institute of Atmospheric Physics,Chinese Academy of Sciences,Beijing 100029,China
2Collaborative Innovation Center on Forecast and Evaluation of Meteorological Disasters (CIC-FEMD),Nanjing University of Information Science &Technology,Nanjing 210044,China
3Department of Atmospheric and Oceanic Sciences/Institute of Atmospheric Sciences,Fudan University,Shanghai 200438,China
4CMA Earth System Modeling and Prediction Center,China Meteorological Administration,Beijing 100081,China
5CMA Tornado Key Laboratory,Department of Atmospheric and Oceanic Sciences,School of Physics,Peking University,Beijing 100871,China
6Faculty of Geographical Science,Beijing Normal University,Beijing 100875,China
ABSTRACT This article summarizes the progress made in predictability studies of weather and climate in recent years in China,with a main focus on advances in methods to study error growth dynamics and reduce uncertainties in the forecasting of weather and climate.Specifically,it covers (a) advances in methods to study weather and climate predictability dynamics,especially those in nonlinear optimal perturbation methods associated with initial errors and model errors and their applications to ensemble forecasting and target observations,(b) new data assimilation algorithms for initialization of predictions and novel assimilation approaches to neutralize the combined effects of initial and model errors for weather and climate,(c) applications of new statistical approaches to climate predictions,and (d) studies on meso-to small-scale weather system predictability dynamics.Some of the major frontiers and challenges remaining in predictability studies are addressed in this context.
Key words: predictability,target observation,data assimilation,ensemble forecasting
1.Introduction
High-impact weather and climate events [e.g.,typhoons,rainstorms,monsoon,El Nino—Southern Oscillation(ENSO),and Indian Ocean Dipole (IOD) events] have serious adverse effects on society,the economy,and people’s lives in China and elsewhere across the globe,and thus predicting such events has always been a key concern of governments and the general public.Although initial errors due to insufficient observations at present,and model errors due to imperfect descriptions of atmospheric and oceanic processes,inevitably exist in numerical forecasts,governments and the public still expect relevant agencies to provide high quality weather forecasting and climate prediction services in a timely manner.A key question posed to meteorologists,therefore,is how can we maximize the forecasting capability for weather and climate using current numerical prediction systems?
To address this question,one first needs to recognize the reasons and mechanisms responsible for prediction uncertainties and identify the major sources of forecast uncertainties.Thereafter,one can then study how to effectively reduce those forecast uncertainties.Such studies belong to the research field of predictability (Mu et al.,2004b,2017a).Since a high forecast skill is closely related and important to everyone’s lives,the predictability of high-impact weather and climate events has long been recognized as a frontier research topic in the atmospheric and oceanic sciences.Indeed,it is listed as the core research subject in the “World Weather Research Program” (https://public.wmo.int/en/programmes/world-weather-research-programme) and the“World Climate Research Program” (https://www.wcrp-climate.org/clivar).
Studies on predictability dynamics generally provide useful guidance to improve the forecasting skills for weather and climate (Palmer et al.,1998;Mu et al.,2002;Duan and Mu,2015).They generally focus on estimation of the predictability time,identification of the predictability sources and associated uncertainties,and recognition of the mechanism responsible for error growth (Kalnay,2002;Mu et al.,2017a;Duan and Mu,2018).These concerns are often explored by investigating the growth dynamics of forecast errors caused by initial and/or model uncertainties.Then,an effective forecasting strategy can be constructed to predict the weather and climate events of concern.
Data assimilation (DA) is recognized as one of the most important forecast strategies to reduce the prediction uncertainties induced by initial errors (Bauer et al.,2015).It combines a limited number of observations with numerical models and their respective error statistics to provide an improved estimate (or analysis) of the present state (Talagrand,1997).Bauer et al.(2015) pointed out that the advances in numerical weather prediction (NWP) have undergone a quiet revolution in the past 30 years,resulting in the forecasting skill having increased by nearly 30% during this period,and the improvement is even more substantial in the Southern Hemisphere.Such a breakthrough was achieved through exploiting satellite data and the variational DA approach (Bauer et al.,2015).It is obvious that DA plays an important role in achieving high-quality forecasts in modern NWP.
In addition to advanced DA methods,targeted observations are essential to obtain a high-quality forecast (Mu et al.,2015;Parsons et al.,2017).Actually,if an advanced DA approach together with additional targeted observations (Snyder,1996) is used to predict high-impact weather or climate events,a more accurate initial state can be obtained,and their forecasting skill can be increased to a large extent.In targeted observation strategies,to better predict an event occurring in an area (i.e.,the verification area) at a given future time t1,additional observations are deployed at a much earlier time t0(i.e.,the target time;t0 Tennekes (1991) pointed out that a complete forecast includes not only a deterministic forecast but also an estimation of its uncertainty.Therefore,reliable estimation of uncertainties is indispensable for complete forecasts.Ensemble forecasting is a useful method that provides estimation of uncertainties by evaluating ensemble spread (Du et al.,2018;Duan et al.,2019).The idea of ensemble forecasting is that the perturbations that reflect the uncertainties of the initial states are superimposed on the initial condition in the control run to generate an initial ensemble,and then the forecast error of the ensemble mean can be quantified using the spread of the forecast ensemble (Leith,1974).These members can also be used to calculate the probability for the occurrence of the weather or climate events of concern [see the review by Kriz (2019)].Since the analysis errors in the control forecasts often grow quickly,the perturbations for ensemble forecasting should present fast-growing dynamical behaviors;in this situation,the optimally growing perturbations are useful for improving the ensemble forecast skill.Due to the abundance of forecast products of ensemble forecasting,this method plays an irreplaceable role in numerical prediction and has been listed as one of the main development strategies of current numerical prediction by the WMO (Majumdar et al.,2021). Consequently,a complete high-quality forecast should contain an accurate forecast result and a reliable estimation of its uncertainties.To produce an accurate forecast result,in addition to using a superior numerical model,one should also use advanced DA methods and targeted observations.Furthermore,a reliable ensemble forecast system is also essential to obtain an effective estimation of the forecast uncertainties.Therefore,to greatly improve the forecasting skill for high-impact weather and climate events,meteorologists should synthesize theoretical and practical research on targeted observations,DA,and ensemble forecasting under the framework of an advanced numerical model,based on the guidance of theoretical studies on predictability dynamics.In recent years,Chinese scientists have made great progress in this field and some of their results have been implemented in operational centers in China.This paper summarizes this progress,as well as future prospects,especially on major frontiers and challenges in research on methods to study error growth dynamics and to reduce the uncertainties in forecasting weather and climate. Consensus has been reached that the best methods for predicting geophysical dynamical systems are optimization methods (e.g.,DA);however,such methods for estimating forecast uncertainty remain controversial (Smith et al.,1999).Currently,there are two approaches to optimization methods for error growth estimations.One is to solve the optimally growing initial perturbation during a given period of prediction,while the other searches for the optimally growing perturbations during a time period before the initialization of prediction.One representative example in the former approach is that of singular vectors (SVs,Lorenz,1965),and one in the latter approach is Lyapunov vectors (Toth and Kalnay,1993).However,these two approaches are both linear and do not contain the effects of nonlinearity that exist in atmospheric and oceanic motions or land surface processes (Mu,2000;Kalnay,2002).In this section,we summarize the advances made in studies of nonlinear optimal perturbations achieved by Chinese scientists via these two approaches. As mentioned above,SVs (Lorenz,1965) are traditional approaches to estimating the growth of initial errors,and work by simplifying nonlinear systems to be linear and allowing exploration of the initial error that causes the largest prediction error during a given time period.Although SVs have been widely used to address the error growth dynamics of atmospheric and oceanic predictability and even to yield initial perturbations of ensemble forecasting for weather and climate events and identify sensitive areas for targeted observation (Mu et al.,2015,Majumdar,2016;Duan and Mu,2018),they do not consider the modulation effect on optimal perturbations of nonlinear processes (Mu,2000;Sévellec and Fedorov,2013;Winkler et al.,2020).To overcome this limitation,Mu et al.(2003) proposed a novel approach of conditional nonlinear optimal perturbation (CNOP) in the field of atmospheric sciences.Similar optimal perturbation also subsequently appeared in the fields of fluid mechanics (see Pringle and Kerswell,2010;Kerswell et al.,2014).Such perturbations often describe the initial perturbation that satisfies a certain constraint condition and have the largest departure from the reference state at a given future time.The CNOP has been applied to find the optimal precursor (OPR) for the occurrence of high-impact oceanic—atmospheric environmental events such as ENSO and IOD events (Duan et al.,2004;Duan and Zhao,2014;Mu et al.,2017b;Yang et al.,2020),as well as explore the optimally growing initial errors(OGEs) for targeted observations associated with the forecasts of tropical cyclones (TCs;Mu et al.,2009;Qin et al.,2013;Qin and Mu,2014),the season-dependent predictability barrier for ENSO and IOD events (Mu et al.,2007;Duan et al.,2009;Feng and Duan,2014;Duan and Mu,2018;Liu et al.,2018a),and the stability and sensitivity analyses of both thermohaline circulation and terrestrial ecosystems (Mu et al.,2004a;Sun and Mu,2014;Zu et al.,2016).All these works not only reveal the important role of considering nonlinear effects,but also provide useful guidance for improving weather and climate predictions.In particular,in recent years,the CNOP has been extended to applications in ensemble forecasting for weather and climate forecasting and field campaigns for targeted observations associated with TC forecasting;furthermore,it has been extended from the original CNOP representing the OGEs [for convenience,hereafter referred to as CNOP-I (Mu et al.,2003,2010)] to the additional CNOP-P for addressing the influences of optimal model parametric error (Mu et al.,2010),CNOP-B for revealing the boundary uncertainties that have the largest effect on forecasts (Wang and Mu,2015),and CNOP-F [i.e.,the nonlinear forcing singular vector (NFSV) proposed in Duan and Zhou (2013)] for exploring combined effects of various model errors.Thus,a family of CNOPs has been achieved,including CNOP-I,-P,-B and -F (Wang et al.,2020a).All these perturbations fully consider the effects of nonlinear physical processes and have been shown to represent the optimally growing mode in their respective scenarios.To facilitate readers,we summarize the CNOP family and their respective benefits in Table 1. 2.1.1.Ensemble forecasting In applications of CNOPs,CNOP-I was recently applied to ensemble forecasting,and orthogonal CNOPs(i.e.,O-CNOPs),which is a new approach to yield initial per-turbations for ensemble forecasting,were proposed (Duan and Huo,2016).O-CNOPs have been used to provide skillful forecasts for TC tracks.For example,Huo et al.(2019)demonstrated that the ensembles generated by O-CNOPs,as compared with those made by traditional SVs,Bred Vectors(BVs),and Random Perturbations (RPs),can present much larger spreads;moreover,they tend to appear on both sides of real TC tracks and have high prediction reliability for TC tracks,ultimately providing much higher forecasting skill for TC tracks (Huo and Duan,2019). Table 1.The CNOP family and their respective benefits. CNOP-P,which was proposed to address optimal parametric perturbation,has also been used in ensemble forecasting,based on its recognized sensitivity to parameter uncertainties.As is well known,a convection-allowing model cannot yet well resolve convective cells as well as turbulence diffusion and has limitations in forecasting severe weather events.Even if ensemble techniques are used,the ensembles generated by the stochastically perturbed physics tendencies(SPPT;Buizza et al.,1999) used in operational centers still face new scientific challenges,especially the problem of under-dispersion.To address this under-dispersion issue,Wang et al.(2020b) applied the CNOP-P approach to the Global and Regional Assimilation and Prediction Enhanced System (GRAPES),which is a convection-scale ensemble prediction model,to detect the most sensitive model parameters.They then formulated the model uncertainty by adding a group of stochastic perturbations on these sensitive parameters and conducted ensemble forecast experiments on relevant variables of convective scales.They showed that these new members,as compared with those generated only by the SPPT,bring about much larger spread for humidity and temperature over the troposphere and yield much more reliable forecasting skill for near-surface variables and precipitation.In view of this,we conclude that CNOP-P is more applicable than SPPT in describing model uncertainties for convectivescale forecasting.Of course,it is easily recognized that CNOP-P only accounts for the effect of model parameter errors,and there are other model error sources that also severely influence weather and climate predictions;furthermore,these model errors are interactive.Considering this situation,Xu et al.(2022a) further adopted the CNOP-F approach [i.e.,the NFSV in Duan and Zhou (2013)] for measuring the combined effect of various model errors to explore the ensemble forecast of convective scales [also see Xu et al.(2022b)].They superimposed the NFSV on the SPPT perturbations and formulated new tendency perturbations (denoted by SPPT_NFSV) for ensemble forecasts.With these new perturbations,Xu et al.(2022b) conducted ensemble experiments using the GRAPES convection-scale ensemble prediction model as adopted in Wang et al.(2020b).They illustrated that the overall probabilistic skills were significantly improved at the 99.99% significance level as estimated by a Student’s t-test,and have an advantage over the SPPT (Fig.1).Particularly,they demonstrated that the use of the NFSV enhances the forecasting skill for precipitation accuracy.It is inferred that additional state-independent nonlinear perturbations (e.g.,the NFSV) superimposed on the SPPT can better represent model uncertainties in convection-scale ensemble forecasts and ultimately contribute to a more comprehensive characterization of model error for convective-scale forecasts. Fig.1.The probabilistic skill for 500-hPa zonal wind (left column) and temperature (right column).Panels (a) and(b) show the domain-averaged RMSE of the control forecast (gray line),the SPPT_NFSV experiment (red line),and the SPPT experiment (blue line),together with the ensemble spread for the SPPT_ NFSV (red bar) and the SPPT (blue bar).Panels (c) and (d) represent the spread-error consistency,and (e) and (f) show the continuous ranked probability score.Panels (g) and (h) are Talagrand rank histograms,and (i) and (j) show the outlier scores.The model adopted height-based terrain-following coordinates with 51 vertical levels and covered the domain of South China (19.99°—25.99°N,106.5°—117°E) with a horizontal resolution of 0.03°.The forecasts were integrated for 24 h,initialized at 0000 UTC of each day during the period 1—30 May 2020 over South China.[Reprinted from(Xu et al.,2022b)]. In addition,the CNOP-F (i.e.,NFSV) was also extended to yield a group of combined modes of initial and model perturbations that are mutually independent and can cause the largest departure from the control forecast in their respective sub-phases,which offers a novel ensemble forecasting method of C-NFSVs (Duan et al.,2022a).The CNFSVs reveal the important role of the dynamically coordinated growth of initial and model perturbations in improving the ensemble forecasting skill,thus yielding much more reliable ensembles compared with O-CNOPs for measuring only initial error effects in terms of spatiotemporal variability(Duan et al.,2022a).C-NFSVs are under investigation for TC track and intensity forecasting with encouraging preliminary results.It is expected that future papers will address the usefulness of C-NFSVs in producing much more realistic forecasts for high-impact weather and climate events. 2.1.2.Targeted observations Another type of application of CNOPs is to provide the sensitive area for targeted observations associated with highimpact weather and climate events by revealing their precursory disturbance and/or fastest-growing initial errors.Although CNOP-I has always been used to explore the OPRs and OGEs and their growth dynamics for some typical weather and climate events since it was proposed in 2003(Mu et al.,2003),as summarized in section 2.1,its applications in recent years have been focused on identifying sensitive areas for targeted observations by OPRs and OGEs,especially for the forecasting of high-impact oceanic—atmospheric environmental events.For example,CNOP-I was applied to identify the OPRs for the sudden shifts in the Antarctic circumpolar current transport through the Drake Passage(Zhou et al.,2021),the occurrence of large meanders in the track of the Kuroshio (Liu et al.,2018b),the initiation of the primary Madden—Julian Oscillation (MJO;Wei et al.,2019),and the determination of El Ni?o types (Duan et al.,2018;Hou et al.,2019,Hou et al.,2023);plus,it was also used to determine the OGEs for predictions of the oceanic flows in the Kuroshio extension (Geng et al.,2020;Wang et al.,2020c),and the sea surface height,with a key focus on the role of mesoscale eddies,as well as forecasts of high-impact weather events such as TCs (Qin et al.,2013;Jiang et al.,2022),heavy rainfall (Yu and Meng,2016,2022;Zhang and Tian,2022),and the southwest vortex (Chen et al.,2021).All these identified OPRs or OGEs provide useful indications for the sensitive areas for targeted observations associated with corresponding weather and climate event forecasting.Particularly,motivated by the important role of the meteorological initial field in air quality forecasts,Yang et al.(2022) made a first attempt at applying CNOP-I to determine the sensitive area for targeted observations associated with improving PM2.5forecasts in a heavy air pollution event that did not have a warning issued in time by the Beijing Municipal Ecological and Environmental Monitoring Center.In particular,greater improvements in PM2.5forecasts were obtained by assimilating targeted observations in the sensitive areas,relative to those after assimilating the additional observations in the key areas suggested by previous studies.Therefore,even if the strategy of targeted observation was initially proposed for forecasting high-impact weather and ocean events,the study of Yang et al.(2022) suggests that this strategy,especially when determined by the CNOP-I,is also useful in greatly improving air quality forecasts. In addition,the similarities between OPRs and OGEs and their application in targeted observations in recent applications of CNOP-I should be particularly emphasized.Specifically,when oceanic—atmospheric ENSO events and IOD events were explored using the CNOP-I method,they were shown to have similar OPRs and OGEs in terms of spatial variability;plus,their large perturbation values were demonstrated to often be concentrated within a small area (Mu et al.,2014,2017b;Hu and Duan,2016).Therefore,when additional observations are carried out over these areas and assimilated into the initial fields,one can not only improve the accuracy of the initial fields and then decrease the prediction errors,but also detect the precursory signals of the events in advance,which may substantially improve the forecasting skill for such events (Mu et al.,2014).It is clear that these studies provide support for a new approach in identifying the sensitive area for targeted observations by considering the similarity between the OPRs and OGEs. Another great advance in targeted observations is that CNOP-I has been applied in several realistic TC field campaigns to determine the observation area of the Fengyun-4A satellite (FY-4) and locations of dropsondes.From 2020 to 2022,a total of eight field campaigns were implemented by using FY-4 and/or dropsondes (Chan et al.,2022;Feng et al.,2022;Qin et al.,2023).Six TCs,including Higos(202007),Maysak (202009),Chan-Hom (202014),Conson(2022113),Chanthu (202114) and Mulan (202207),were observed using FY-4 from the China Meteorological Administration (CMA),and simultaneously,these TCs were also observed using dropsondes from Hong Kong Observatory.Particularly,in TC Mulan from 8 to 10 August 2022 over the South China Sea,the first ever ground—space—sky observing system experiment (OSE) of a TC with enhanced observations,including GIIRS microwave soundings,round-trip radiosondes and aircraft-launched dropsondes,was conducted through collaboration between meteorological authorities and research institutes on mainland China with the meteorological service in Hong Kong.Furthermore,these data were assimilated in real time into the operational numerical prediction system of the CMA (Chan et al.,2022).The observational and forecast results were presented in “the CMA weather conferences”,which demonstrated that assimilating the additional data collected in this way shows a positive impact on TC forecasts of both track and intensity (see Fig.2),as well as improves the forecasting skill for heavy rain in southern China. Fig.2.(a) The track forecasts before (red) and after (green) assimilating additional observations,and the best track(black) of TC Mulan,which is often derived using the available observations and represents a subjectively smoothed representation of a TC’s location and intensity over its lifetime.(b) The forecast errors of the maximum wind speed(Vmax) before (blue) and after (red) assimilating additional observations.The forecast was initialized at 0600 UTC 8 August 2022 with a lead time of 36 h.[Reprinted from (Chan et al.2022),Reproduced with permission from Springer Nature]. CNOP-I was also applied to identify the sensitive area for targeted observations in an oceanic field campaign conducted in summer 2019 for prediction of the vertical thermal structure in continental shelf seas in the Yellow Sea (Hu et al.,2021;Liu et al.,2021).It was found that the sensitive area is northeast—southwest-oriented to the northeast of the verification area.The associated targeted observations obtained in the field campaign further helped in refining the structure of the initial vertical thermal structure,thereby greatly improving predictions of the vertical thermal structure at a lead time of 7 days.Liu et al.(2021) also extended CNOP-I to a new application in the field campaign for vertical thermal structure predictions favorable for recognizing circulation patterns and enhancing fishing and submarine expeditions. The above discussion shows that targeted observations determined by CNOP-I have been transferred from theoretical studies of OSSEs (observing system simulation experiments)to OSEs.The use of CNOP-I in these OSEs represents a realistic implementation of self-developed targeted observation technology in China to support meteorological or oceanic observational campaigns in order to improve atmospheric and oceanic forecasts.But is there a particular kind of weather or climate event that is not sensitive to targeted observations? A study on the sensitive area for targeted observation of a heavy rain event in South China in June 2008 attempted to answer this question (Huang and Meng,2014).Specifically,the authors expressed a perspective that designing a particular observation plan based on an estimated target area could be unnecessary or useless for heavy rainfall forecasts when the focus is on forecasting a heavy rain case by using a piece-by-piece DA targeting strategy.Whether or not such a perspective still holds for most other rainfall cases may need further investigation,especially by using the CNOP-I approach,which considers the interaction among the regiondependent uncertainties of the initial field and then automatically determines the most sensitive initial error. 2.1.3.Analyses of sensitivities and uncertainties Sensitivities to initial fields and model parameters are one of the reasons for prediction uncertainties.Studies on parametric sensitivity are especially important for the simulation and prediction of land surface processes.It is known that the parametric errors depicting climate change uncertainties are one of the main model error sources that severely influence the prediction skill for land surface processes.Scientists often explore the effects of climate change uncertainties by superimposing on the climatology a time-invariant perturbation without consideration of the effect of climate variability.However,Sun and Mu (2013) superimposed the parameter perturbations featured by CNOP-P to explore the response of the uncertainties in land surface process prediction and found that the resultant perturbations provided a possible climate change scenario including the changes in both the climatology and climate variability possibly induced by the frequency of occurrence of extreme events.Furthermore,these perturbations,compared with the traditional way,have helped to fully address the impact of climate change on the simulated net primary production and soil carbon in China(Sun and Mu,2013,2017a).Sun and Mu (2017b) also demonstrated that the use of CNOP-P reveals the possibility of the terrestrial ecosystem as a carbon sink in China.In addition,Sun and Mu (2017a) applied CNOP-P to identify a subset of physical parameters whose accuracy was much more important in reducing prediction uncertainties.They applied this new strategy to simulating and predicting the net primary production in arid and semi-arid regions over the Tibetan Plateau and revealed significant effects of nonlinear interactions among parameters on projecting the sensitivity of a group of parameters,which compensated for the deficiencies of traditional approaches and also greatly helped in determining the parameter set that should be preferentially calibrated by additional observations to improve the simulation and prediction (Sun et al.,2020).These works indicate that the idea of targeted observation for improving initial fields can be extended to calibrate the values of sensitive parameters by digesting additional observations. Another factor that causes prediction uncertainties is the boundary condition error;and Wang and Mu (2015),as mentioned in section 2,proposed the CNOP-B approach to explore the boundary condition errors that have the largest impact on forecast uncertainties.Furthermore,they applied CNOP-B to an ocean ecosystem model and identified two nutrient errors at the bottom boundary of the water column.These two nutrient errors have similar spatial pattern but opposite signs,and have significantly asymmetric nonlinear effects on the simulated deep chlorophyll maximum [which is a ubiquitous phenomenon in oligotrophic waters in the global ocean (Navarro and Ruiz,2013)].More recently,Ma et al.(2022) further used the CNOP-B method to investigate the effect of Arctic Sea ice uncertainties (as a boundary) on the prediction of atmospheric Ural blocking events.They found that the use of CNOP-B allows one to identify the uncertainties in the sea-ice concentration of the Greenland Sea,Barents Sea,and Okhotsk Sea as the dominant contributors to the forecast uncertainties of strong and long-lasting Ural blocking formation in four pentads.Furthermore,the local characteristics of perturbation distribution provided by these boundary uncertainties are able to provide the area where the additional observations should be preferentially implemented for the sea-ice concentration in order to improve the forecasting skill of Ural blocking events. As mentioned in section 2,one approach to obtaining the optimal initial perturbations is to evaluate the evolution of initial perturbations during the time period before the prescribed time interval of prediction.The vectors derived from the Lyapunov exponents are the representatives.The traditional Lyapunov vectors and relevant Lyapunov exponents are established under the framework of linear systems and,similar to SVs,limitations exist in revealing the effect of nonlinearity on predictability.To address this issue,Ding and Li (2007) proposed the nonlinear local Lyapunov exponent(NLLE) method,theoretically inherited from the Lyapunov exponent in a linear framework.The NLLE measures the growth rates of initial errors averaged over a given time period in a nonlinear dynamical system and can be used to quantify an averaged predictable time of the system.Over the past decade,the NLLE has been applied to determine the predictable times of weather and climate on various time scales.For different reference states of weather or climate events of concern,their respective analogous states can be extracted from the historical observational time series according to a locally dynamical analogs algorithm proposed by Li and Ding (2011),and then the error growth between the reference states and analogous states can be estimated,with the predictable time range ultimately being determined according to the spread of the time when the error growths are saturated.Such an idea has been adopted to estimate the predictable time ranges of TC tracks (Zhong et al.,2018a,b,2021),the quasi-biweekly oscillation (QBO;Shi and Ding,2012),the MJO (Ding et al.,2010,2011;Lu et al.,2020),the East Asian summer monsoon (Ai et al.,2017;Li et al.,2018),ENSO (Hou et al.,2018a,Hou et al.,2022),and the Pacific Decadal Oscillation (PDO,Ding et al.,2016).By combining these studies in terms of predictable time,a predictability diagram ranging from synoptic to decadal time scales was obtained.For convenience,we plot this in Fig.3.It is obvious that the predictable time of weather and climate phenomena depends on their time scale,with the predictable times increasing with the timescale length.This predictability diagram serves as a useful reference for improving seamless predictions. Fig.3.A diagram of the predictable time range of weather and climate systems at various time scales estimated using the NLLE method.The weather and climate phenomena include TC track,eastern Pacific oscillation (EP),western Pacific Oscillation (WPO),North Atlantic Oscillation (NAO),Pacific—North American teleconnection (PNA),Arctic Oscillation (AO),Antarctic Oscillation (AAO),Blocking High (Block),Madden—Julian Oscillation MJO,monsoon,Victoria Mode (VM),Indian Ocean Dipole (IOD),El Ni?o—Southern Oscillation(ENSO),Quasi-Biweekly Oscillation (QBO),Pacific Decadal Oscillation (PDO),and Atlantic Multidecadal Oscillation (AMO). The above studies provide a means to understand how far forward one can predict atmospheric and oceanic motions and associated weather and climate events.Li et al.(2019) named such predictability as “forward predictability”.In fact,for a weather or climate event that has happened,the back-tracking time with which one can trace it is also useful for understanding the predictable time and improving predictions (Mu et al.,2002).This predictable time was termed “backward predictability” by Li et al.(2019).The NLLE method was also applied to explore the backward predictability and,eventually,a backward NLLE method was developed to determine the backward predictability of extreme weather and climate events,e.g.,an extreme hightemperature event (Li et al.,2019,2020,2021a;Li and Ding,2022).This method can quantitatively provide the maximum lead time for predictions of specific states or extreme weather and climate events.In addition,to examine the effects of different external forcing (e.g.,ENSO events,the PDO) on the atmospheric predictability,a conditional NLLE was also introduced to separate the effect of each external forcing on the predictability,which can therefore quantitatively estimate the relative contribution of each external forcing to the predictability of the nonlinear dynamical system(Li and Ding,2011).Combining these NLLEs may provide insight into predictability dynamics and the effect of external forcing,which serves as a reference to evaluate the skillful lead times of numerical weather forecasting and climate predictions. In addition,the vectors corresponding to the NLLEs were named the nonlinear local Lyapunov vectors (NLLVs),which represent a group of vectors of orthogonal directions in phase space and have different growth rates with time.NLLVs have been used to yield ensemble forecasting members through a hierarchy of models (Feng et al.,2014,2016;Hou et al.,2018b).They have been demonstrated as able to perform better and more reliably than BVs in ensemble forecasting (Feng et al.,2014).A comparison of the ensemble forecasting skills of NLLVs and Ensemble Transform Kalman filter (ETKF) schemes suggested that the skill achieved by NLLVs is comparable to that made by the ETKF,but the former can be computed far more easily and with less computation time (Feng et al.,2014).Consequently,NLLVs not only have potential for improving the ensemble forecasting skill,but are also easily implemented in complex models,which shows a potential for application in operational forecasts. It should be noted that NLLVs are different from OCNOPs as reviewed in section 2.1,although they can both be applied in ensemble forecasts to address the effect of initial uncertainties.The former searches for the optimally growing initial perturbations before the initialization time of the forecasts to estimate the growing-type perturbations employed in the ensemble forecast,whereas the latter directly estimates the growing-type perturbations during the forecast period.In other words,one method concerns the lasting effect of historical information on the present state estimation,while the other directly estimates the present state according to the evolutionary behavior of initial uncertainties during the forecast period.Actually,these two kinds of information are both important for estimation of the present state and forecasting of the future state.It is therefore inferred that combining NLLVs and O-CNOPs may lead to a better ensemble forecasting skill,which is worth investigating in the future. Four-dimensional variational (4DVar) and the Ensemble Kalman filter (EnKF) are two commonly used DA methods for providing high-quality initial conditions for operational forecasts (Evensen,1994;Talagrand,1997).A few major operational NWP centers around the world have successfully applied 4DVar,EnKF,or a hybrid of both,to generate global and/or regional analyses and/or reanalyses.In terms of 4DVar,there are still two main challenges that have to be faced in real-time forecasts: one is the high computational cost,and the other is the lack of a global flow-dependent background error covariance (BEC) matrix [hereafter referred to as the “B matrix” (Liu et al.,2011)].One of the strategies to address these difficulties is to develop a four-dimensional ensemble variational (4DEnVar) algorithm by referring to the idea of EnKF,which adopts a pure ensemble covariance predicted dynamically in DA cycles as per the EnKF to provide the flow-dependent B matrix for the 4DVar cost,and obtains the analysis without tangent linear and adjoint models(Liu et al.,2008;Tian et al.,2008).Thus,4DVar becomes much more easily realized and economical owing to the 4DEnVar algorithm,and has been applied in some operational centers with high forecast skill (Buehner et al.,2010a,b;Kleist and Ide,2015;Lorenc et al.,2015).Despite the progress made with this algorithm,it has not yet been applied operationally in most of the world’s major NWP centers,including the CMA.Furthermore,relevant challenges regarding the flow-dependent B matrix and the localization for dealing with spurious correlation between the model and observation still need to be faced,due to limited ensemble sizes and the difficulties of reasonably determining the vertical coordinates of satellite radiance observations and the localization radius,for instance.Therefore,one has to develop a corresponding 4DEnVar algorithm based on specific forecast models,such as the CMA Global Forecast System of GRAPES (GRAPES-GFS) in China.Although the hybrid 4DVar-EnKF DA method has gained great attention and become a research trend,the EnKF itself is still a popular DA method presently.Furthermore,many studies have explored its efficiency and effectiveness in simulations and predictions of weather and climate.One of the main difficulties in implementing the EnKF is that one has to generate an ensemble to estimate the forecast-error statistics in performing DA.The large ensembles in the EnKF always mean more numerical integration,and it therefore comes at huge computational cost.However,the limited ensemble members are usually insufficient to represent the statistics of background flows at different time scales,especially the slow-varying part,which can lead to filter drift due to the misfit of slow-varying signals and a decrease in the DA efficiency.Moreover,it is known that model error is another major source of forecast errors (Duan and Zhou,2013;Duan and Mu,2018).Concerning the approaches to reduce model error effects,one has to improve numerical models by updating and/or improving physical parameterization schemes,or increase their spatiotemporal resolutions.However,model errors have diverse sources;moreover,they are nonlinearly interactive.Therefore,it is difficult to separate and debug them to reduce their negative effects.Although the stochastic physical perturbations used in ensemble forecasts can partly consider model errors in the ensemble covariance of 4DEn-Var,they are unable to reduce the model errors in DA significantly.To overcome the above difficulties in using DA,Chinese scientists have invested great effort in recent years in the development of new 4DVar and EnKF algorithms and novel DA approaches in order to reduce model error effects(see the overview in Table 2). 3.1.1.DRP-4DVar DA Dimension-Reduced-Projection 4DVar (DRP-4DVar;Wang et al.,2010;Liu et al.,2011) is one of the representative 4DEnVar methods developed by Chinese scientists.This algorithm uses a limited numbers of ensemble forecasting members to project the optimization problem in model space onto a low-dimensional subspace spanned by these ensemble members;and the necessary localization is directly applied to the ensemble samples based on the leading eigenvectors of the localization correlation function in zonal,meridional and vertical directions,rather than being applied to the Kalman Gain matrix as the EnKF does (Wang et al.,2018).As a result,the DRP-4DVar algorithm is not only time-saving and easily implemented,but also realizes low dependence in the B matrix that is applicable either inside the assimilation window (implicitly) or from window to window (explicitly)(Wang et al.,2010). DRP-4DVar has been successfully applied in regional and global weather forecasts.The high-quality initial conditions produced by this algorithm have led to obvious improvements in predicting regional heavy rainfall and typhoons in China (e.g.,Liu et al.,2009;Zhao et al.,2012).In particular,a 4DEnVar DA system for medium-range numerical weather forecasts in GRAPES-GFS has been developed in recent years (Zhu et al.,2022).This DA system has two unique advantages.First,the system dynamically estimates the BEC during the DA cycle instead of adopting a pre-estimated static BEC as 4DVar does;and second,an inflationtechnique,by which the current predictions of the ensemble covariance are initiated from the linear combinations of previous analysis increments produced by the 4DEnVar system and balanced RPs generated using the static climate BEC,is utilized to alleviate the underestimation problem of the B matrix during the DA cycle (Zhu et al.,2022).The system,with all its advantages,created resultant smaller errors in the ensemble mean analysis and better skill in the ensemble mean forecast than 4DVar in a single analysis and deterministic forecast (Zhu et al.,2022).In fact,the DRP-4DVar embedded in GRAPES-GFS can be used not only to conduct ensemble DA independently,but also to provide flow-dependent ensemble covariance for the 4DVar system,by which an ensemble 4DVar (En4DVar) DA system for GRAPES-GFS was additionally established.Furthermore,this En4DVar system achieved a more accurate analysis and higher forecast skill than the 4DVar in GRAPES-GFS.It should be noted that using the DRP-4DVar (4DEnVar) approach to provide the ensemble covariance for the En4DVar system differs from most of the presently available En4DVar systems internationally,which estimate the dynamic covariance via the EnKF-class algorithms or the 4DVar approach.Therefore,this is a novel algorithm for generating the dynamic ensemble covariance for En4Dvar. Table 2.Overview of the improvements in DA methods achieved by Chinese scientists. In addition to its applications in regional and global NWPs,DRP-4DVar has also been applied in the initialization of decadal climate predictions by the Flexible Global Ocean—Atmosphere—Land System model,gridpoint version 2 (FGOALs-g2),developed by LASG,Institute of Atmospheric Physics,Chinese Academy of Sciences (He et al.,2017,2020a,b).Actually,it is one of the world’s first 4DEn-Var-based initialization systems for decadal predictions.Due to better dynamically coordinated behavior between the initial conditions of different component models obtained by DRP-4DVar in the coupled framework of FGOALS-g2,the tough initial shock problem was greatly alleviated.Furthermore,a much higher decadal prediction skill for surface air temperature anomalies was achieved (He et al.,2017;Fig.4).In addition,since DRP-4DVar has the ability to incorporate the constraint of air—sea—land interactions during the process of initialization,a high prediction skill for the PDO,East Asian summer monsoon,Sahel rainfall,and surface air temperature and precipitation over the Tibetan Plateau and Europe has also been attained on interannual to decadal time scales [for further details,readers are referred to He et al.(2020a,b),Li et al.(2021b,c),and Shi et al.(2021,2022)]. Fig.4.Taylor diagrams for the 10-year averaged global mean surface air temperature anomaly (SATA),with trend (top) and without trend (bottom).The first member is shown on the left and the ensemble mean of the first three members is shown on the right.Each circle represents one model.The radial coordinate means the standard deviation of the SATA normalized by the standard deviation of the corresponding observed SATA.The red filled circle and red open circle correspond to the DRP-4DVar and nudging results based on the hindcasts from the FGOALS system,respectively.The red open triangles are for the 20th historical simulation (20C) made by the FGOALS system without any initialization.The violet semicircles represent the RMSE of the hindcasts,which is also normalized by the observed standard deviation.The correlation between the hindcast and observation is indicated by the azimuthal variable.For the single member,the simulation from the historical experiment by FGOALS-g2 is also plotted.Only the models with positive correlations are shown.[Reprinted from (He et al,2017)]. Fig.5.The winter SST pattern of central Pacific (CP) El Ni?o in the (a) observations,(b) ICM predictions and (c) NFSVICM predictions,where the lead time is six months.[Reprinted from (Tao and Duan,2019),? American Meteorological Society.Used with permission]. Enlightened by these studies,ongoing projects are focusing on investigating the ability of DRP-4DVar for initializing the difficult but urgent issue of subseasonal-to-seasonal(S2S) prediction.Furthermore,in view of the great advantages of DRP-4DVar,it is expected that high skill in S2S predictions (e.g.,the MJO,monsoon) and related extreme events (e.g.,extreme precipitation,heatwaves) will be achieved.Of course,with these potential applications,more challenging problems for the 4DEnVar algorithm may be revealed,and more effort will be needed to optimize the performance of 4DVar in predicting high-impact weather and climate events. 3.1.2.NLS-4DVar DA The nonlinear least-squares 4DVar (NLS-4DVar) algorithm,which was proposed by Chinese scientists and attracted a lot of attention due to its success,is another 4DEn-Var DA approach.The idea of NLS-4DVar is to convert the 4DEnVar optimization problem into a nonlinear leastsquares problem that can be solved using an efficient Gauss—Newton iteration scheme,and then the nonlinear effect including the 4DVar cost function can be handled naturally and accurately (Tian and Feng,2015;Tian et al.,2018).Based on this,a multigrid NLS-4DVar was further developed to correct multi-scale errors and enhance assimilation performance with reduced computational costs via the multigrid iterative algorithm of NLS-4DVar (Zhang and Tian,2018).In addition,Tian et al.(2021) considered the influence of both initial and model errors and provided an integral correction 4DVar algorithm to correct them simultaneously and then reduce the impact of model errors on the performance of DA (Zhang and Tian,2022). With the above progress regarding NLS-4DVar algorithms,these methods have also been applied in meteorological and environmental simulations and forecasts.Specifically,Zhang et al.(2020a) constructed the SNAP system (i.e.,the system of multigrid NLS-4DVar DA for NWP) by embedding the multigrid NLS-4DVar in the Weather Research and Forecasting (WRF) model.This system borrows the data processing and observation operator modules from the operational Gridpoint Statistical Interpolation and has the ability to assimilate multi-source and multi-scale observations from conventional,satellite and Doppler radar observations (Zhang et al.,2020a,b;Zhang and Tian,2021).Furthermore,Zhang et al.(2021,2022a) applied NLS-4DVar to the atmospheric chemical transmission model WRF-CMAQ (WRF-Community Multiscale Air Quality Modeling System) and constructed a joint assimilation system that can simultaneously optimize initial conditions and emission fluxes for improving PM2.5concentration forecasts.In addition,a Tan-Tracker global CO2flux inversion system was established to optimize the terrestrial and ocean carbon fluxes through assimilating space-based and/or groundbased CO2observations using NLS-4DVar,where a novel dual-pass strategy was proposed for initialization (Jin et al.,2021).Recently,NLS-4DVar was further upgraded to a big data—driven version,which provides superior performance to the standard NLS-4DVar without additional computational costs (Tian and Zhang,2019). All these applications of NLS-4DVar have shown that this approach greatly reduces the computational cost and performs well in simulations or forecasts for relevant climate events based on realistic forecast models.It is therefore expected that NLS-4DVar will make important contributions to operational forecast systems,especially in terms of mesoand micro-scale systems,because of its ability in handling the strong nonlinearity that exists in these systems. The EnKF,as discussed above,is limited in terms of its multiscale representation of BEC.To address this issue,Wu et al.(2015) developed an adaptive compensatory approach to improve the performance of the EnKF in the multiscale analysis (MSA).The approach adaptively triggers a multigrid analysis (MGA) to extract multiscale information from the observational residual after the EnKF without inflation is completed at each analysis step.In this way,the MGA can extract multiscale information through refining the analysis grid;furthermore,it does not introduce any correlation scale.Particularly,Wu et al.(2015) demonstrated that the MGA also helps reduce the computational cost of the original MSA by 93%;and on the assimilation quality,they illustrated that the EnKF with the adaptive MGA shows an incremental improvement over the original EnKF-MSA and the adaptive EnKF-MGA works for a broader range of impact radii than the standard EnKF (i.e.,the EnKF with inflation).For extreme impact radii,the adaptive EnKF-MGA causes much smaller assimilation error than the standard EnKF;particularly,it shortens the spin-up period by 53%.Regarding the accurate representation of the slow-varying part of background error statistics,Yu et al.(2019) designed a multitimescale,high-efficient approximate EnKF (MSHea-EnKF)to increase the representation of low-frequency background error statistics and then enhance its computational efficiency.MSHea-EnKF uses model simulations over a long period to construct background statistics and adopts the frequency split technique to address different time scales;thus,the performance of coupled DA on large-scale dynamics can be expected to improve.In fact,Yu et al.(2019)adopted a hybrid coupled ocean circulation model and showed that MSHea-EnKF only requires a small fraction of computing resources to present a comparable performance to the standard EnKF.This new EnKF scheme allows one to assimilate multisource observations into any high-resolution coupled Earth system model that is intractable with current computing power for weather and climate analysis and predictions. Given the huge computational cost of the EnKF,the Ensemble Optimization Interpolation (EnOI) approach is also used in realistic numerical forecasts.The EnKF adopts the B matrix derived from a real-time computed ensemble,while EnOI just uses a B matrix estimated by a statistic historical ensemble and can be regarded as an approximation to the EnKF.However,EnOI has only one forward integration and remarkably reduces the computational costs in the EnKF (Oke et al.,2002;Evensen,2003),consequently often being applied in operational forecasts.Recently,Wu et al.(2018) developed an initialization scheme for FGOALS based on EnOI.In this scheme,the observed oceanic temperature and salinity profiles from the EN4 dataset produced by the Hadley Center (Good et al.,2013) and the grid sea surface temperature (SST) from HadISST (Rayner et al.,2003) are assimilated to the model with an assimilation window width of 1 month.The feature of this initialization scheme is that it adopts a combination of EnOI and the incremental analysis update (IAU),where the assimilation increments are calculated by EnOI and then introduced into the model integration by the IAU.Compared with the traditional EnOI method that directly adds analysis increments to model states,the EnOI-IAU approach gradually superimposes the analysis increments generated by EnOI to model tendency equations during the model integration,which enhances constraints of the assimilation on the time dimension of the model and ultimately greatly suppresses the shortwave noise in the assimilation runs (Bloom et al.,1996).Based on this scheme,Wu et al.(2018) built a decadal climate prediction system,referred to as IAP-DecPreS,which was used to conduct decadal prediction experiments serving the Climate Prediction Project(DCPP;Boer et al.,2016),and showed significant predictive skill for SST anomalies in the North Atlantic and subtropical Pacific (Hu et al.,2023).In addition,Hu et al.(2019)adopted IAP-DecPreS to study the impacts of initialization approaches and full-field and anomaly assimilation on the seasonal to interannual climate prediction skill (see also Hu et al.,2020).They demonstrated that the anomaly assimilation scheme greatly reduced the model initial shocks in predictions and thus improved the seasonal to interannual prediction skill for ENSO and Indian Ocean basin modes. The EnKF,as emphasized above,is hugely expensive in computational terms,but with the advances in computing capacity,it will benefit from improved computational platforms,and we could therefore profit further from these new EnKF schemes.Accordingly,we can easily achieve more ensemble members and make higher quality assimilation.It may also be possible,in the near future,to have a global EnKF configuration that approaches a higher spatial model resolution.As shown above,the hybrid 4Dvar and EnKF approach makes it possible to implement a global flow-dependent B matrix and enhance the assimilation performance.Alongside this,if 4DVar is reasonably combined with more advanced and newly developed EnKF schemes as above,then higher quality initial fields and higher forecasting skill can be expected. As discussed above,DA plays a key role in current weather forecasting and climate prediction.However,the classical DA methods,as reviewed in sections 3.1 and 3.2,were mainly established on the assumption of a perfect model with only initial error effects considered.In recent years,Duan and Zhou (2013),as reviewed in section 2,proposed the NFSV approach to reveal the model error that causes the largest prediction error.Actually,the NFSV suggests adopting a total tendency perturbation for depicting the combined effect of different kinds of model error sources.Inspired by the NFSV,Duan et al.(2022b) formulated an NFSV data assimilation (NFSV-DA) approach for neutralizing not only the initial error effect but also the model error effect (Tao and Duan 2019;Tao et al.,2020).It should be noted that NFSV-DA,which is different from the above NFSV that consists of a maximum problem that solves the total tendency perturbation that causes the largest departure from a reference state,is relevant to a minimization problem that calculates the optimal tendency perturbation to offset the prediction errors caused by initial and model errors by assimilating a limited number of observations.This is the exact reason why it is regarded as a DA approach. NFSV-DA has been applied to El Ni?o predictions.Particularly,it helped to make a breakthrough in alleviating the effect of the “spring predictability barrier” phenomenon for ENSO (Tao and Duan,2019).Results have also shown that NFSV-DA has great capacity in revealing which type of El Ni?o will occur in predictions.Figure 5 provides the predictions for central (CP) El Ni?o events made by an intermediate ENSO model (ICM;Zhang et al.,2003) and its corrected version by NFSV-DA.[For eastern Pacific (EP) El Ni?o events,readers can refer to Fig.4 in Tao et al.(2020)].Furthermore,NFSV-DA has been applied in real-time predictions of El Ni?o events in recent years.Together with ICM (Zhang et al.,2003),NFSV-DA shows superiority in predicting the 2015/16 strong El Ni?o event and its subsequent double La Ni?a variability from 2016 to 2018.For the 2019 CP El Ni?o event,many models predicted a strong EP El Ni?o event at the beginning of the year;and for the following 2021/22 La Ni?a event,quite a few models did not make successful forecasts.However,NFSV-DA performs well in predicting the warm and cold phases and even the types of those events (Duan et al.,2022b). Despite NFSV-DA having been applied successfully in the prediction of El Ni?o,it remains unknown whether it might be useful when applied to the forecasting of other weather and climate events.Therefore,more weather and climate phenomena should be investigated to explore the robustness and usefulness of NFSV-DA in improving predictions.It is anticipated that NFSV-DA could prove highly effective when applied in numerical weather forecasting and climate predictions. In addition to numerical predictions of weather and climate,significant progress has also been made by Chinese scientists in studies of data-driven predictions made by statistical approaches,including traditional statistics,emerging complex networks,and machine learning (ML).They have identified the sources of climate predictability via a complex network and conducted prediction experiments on high-impact climate events.In addition,they have also proposed new statistical prediction methods for achieving high levels of forecasting skill.Besides these advances,the progress made in the use of ML in climate predictions is also summarized in this section. In the past few years,a number of studies have been carried out to explore the possible relationships between climate patterns/variables of concern and external forcing,as well as the dynamical mechanisms of different interactions of coupled systems,but little attention has been paid to the effects of climate memory.In view of the potential mix of different predictable sources,neglecting the effects of climate memory may induce uncertainties in the subsequent climate prediction.In order to quantify the effects of climate memory and increase the prediction skill,Yuan et al.(2014) proposed a strategy for identifying predictable sources [also see Yuan et al.(2019)].Specifically,this strategy adopts the recently proposed fractional integral statistical model,which is a generalized version of the classical stochastic climate model proposed by Hasselmann (1976),to decompose a given climatic time series into the memory part M(t) and the residual partε(t);and then,by calculating the variance explained by M(t),the climate memory effects—in other words,the contributions of climate memory to predictability—can be quantified.Regarding the residual partε(t),the strategy can further use a variance decomposition method to extract the relatively slow-varying covariance matrix,which may contain signals related to external forcing and dynamical interactions of multiple climate processes;and in this way,different predictable sources on multiple time scales can be obtained. With the above strategy,Nian et al.(2020) analyzed the seasonal predictability in observational monthly surface air temperatures over China from 1960 to 2017.They found that the climate memory component,as expected,contributes to a large portion of the seasonal predictability in the temperature records;and after removing the memory component,the residual predictability stems mainly from teleconnections,where the residual predictability is closely related to SST anomalies in the eastern tropical Pacific and the northern Indian Ocean in summer.It is obvious that the strategy and its application to the seasonal predictability of surface air temperature provides a new way to estimate climate predictability,and more importantly,by employing this strategy,the different predictability sources can be better recognized.Meanwhile,it is also necessary to emphasize the different climate memories over the corresponding temporal scale since the long-term persistence of some climate variables [i.e.,precipitation (Yang and Fu,2019)] is process dependent.It is obvious that these predictability sources can be regarded as the predictors to predict the relevant climate phenomenon by a statistical model or,as recently popular,a deep learning model.It is therefore expected that this strategy to identify the predictability sources can be further used to carry out real predictions and improve prediction skill. The novel complexity-based technique of climate networks has been developed rapidly and implemented to advance our knowledge of the Earth system,especially with respect to extreme climate events.The key idea of the method is that the locations in a longitude—latitude spatial grid can be regarded as nodes in the climate network and the connections between the time series at different nodes are recognized as edges (Tsonis and Roebber,2004;Donges et al.,2009).Using statistical filtering facilities,one can interactively filter for nodes and edges,thereby highlighting structures of particular importance for matter and energy flow in the climate system,which promotes a deeper understanding of climate science and even substantially improves the prediction of high-impact climate events [see the review by Fan et al.(2021)].Here,we highlight the applications of climate networks in improving the forecasting skill of the Indian summer monsoon. The Indian summer monsoon is an intense rainy season lasting from June to September and delivers more than 70%of the country’s annual rainfall.Despite the development of sophisticated statistical and dynamical climate models,a relatively long-term and reliable prediction of the Indian summer monsoon rainfall (ISMR) has remained a challenging problem.Fan et al.(2022) constructed a series of dynamical climate networks based on the global near-surface air temperature (NSAT) field,showing that there are characteristics of the directed and weighted climate networks that can serve as efficient long-term predictors for ISMR forecasting.Specifically,they uncovered the Southwest Atlantic as a hotspot for predicting the Indian precipitation,due to the strong connection through the chain of main atmospheric circulation patterns.Based on this,Fan et al.(2022) developed a climate network prediction method for ISMR,which produced a forecasting skill of 0.54 (Pearson correlation) with a 5-month lead time by using the previous calendar year’s data (Fig.6).This level of skill is higher than that of operational forecast models,even with quite a short lead time.It is clear that the climate network method can capture useful predictors for ISMR and provide much higher forecast skill.This network approach allows the all-India rainfall to be predicted,as well as the rainfall in different homogeneous Indian regions,which is crucial for the country’s agricultural production. Fig.6.(a) The correlation coefficients between observed All Indian Rainfall Index (AIRI) in summer (June—September,JJAS) and the network predictor during the training period (1950—88) for all nodes.The regions with statistical significance exceeding the 95% confidence level (Student’s t-test) are marked in black.The region with the maximal correlation coefficient is marked by the yellow box.(b) Scatterplot between the observed JJAS AIRI and the optimized network predictor (i.e.,only using the NSAT information in the yellow box) in the training period.(c) Scatterplot between the observed JJAS AIRI and the predicted AIRI during the forecast period (1989—2019).[Reprinted from (Fan et al.,2022),?American Meteorological Society.Used with permission]. The climate network approach was also successfully applied to improving the forecasting skill for IOD events(Lu et al.,2022) and exploring the weakening tropical circulations (Geng et al.,2021),the relationship between the CO2concentration and surface air temperature (Ying et al.,2021),and the transportation and clustering of PM2.5concentrations(Ying et al.,2022).Although the application of climate networks has achieved successes in climate predictions,improvement of the prediction level is still limited. A promising methodology that has emerged in recent years and could play an instrumental role in demystifying climate change is ML.Due to the enhanced data availability,ML has been shown to have ability in making up for the deficiency of traditional forecast methods.Owing to the limited prediction skill for the IOD achieved by traditional dynamical and statistical methods,Ling et al.(2022) developed a multitask deep learning model named MTL-NET to challenge the current IOD prediction skill.The deep learning method can extend reliable IOD predictions out to 7 months ahead,which exceeds the original 3 months in the traditional predictions.By investigating the precursors revealed by MTLNET for strong IOD events,their studies also help us deepen our understanding of the nonlinear mechanisms of the IOD,and of the complex climate variabilities in the Earth system.Aside from helping enhance prediction levels,ML may also have potential in reducing computational costs in ensemble forecasts.Since the computational cost of large ensemble members is always a challenge in the realtime operational chain of ensemble forecasts,Duan et al.(2022a) applied deep learning to learn the dependence relationship of the control runs and ensemble forecasting members,and then expected to produce efficient ensemble members in real-time forecasts.The numerical results showed that the ensemble forecasts made by the deep learning models could not only reduce the computational costs in real-time forecasts,but also achieve comparable forecasting skill to the original ensemble forecast system.Therefore,the application of ML may be a new research topic of interest in ensemble forecasting. As an emerging method of climate prediction,climate networks show ability in identifying spatial information about cooperativity and provide a new possibility of revealing precursory signals of climate or even entire causal chains of climate phenomena.However,some latent processes and relationships of climate systems cannot yet be identified by the climate network method,and the relevant climate prediction level is still limited from this perspective.However,the promise of ML is superior to that of the climate network method in learning the complex nonlinear relationships in data.Therefore,combining the climate network method with ML may have the potential to deepen the physical understanding and improve the prediction skill of weather and climate events. Fan et al.(2008) proposed the year-to-year increment prediction approach (referred to as the DY approach) based on the quasi-biennial oscillation of climate variables.The DY includes both the predictand and predictor in the year-toyear increment,rather than only the predictor in the anomaly of the traditional climate prediction approach.The DY can then amplify the signal against that in traditional anomaly prediction;plus,it can capture multi-timescale variabilities of climate variables.As a result,the DY not only shows high predictive skill for the interannual variability of climate variables,but also reproduces their interdecadal variability (Fan et al.,2008).In recent years,Fan et al.(2012),based on the DY,combined dynamic model predictions and further proposed a new idea of statistical—dynamical hybrid climate prediction approach.Furthermore,the idea was realized in predictions of summer precipitation over China (Liu and Fan,2012;Dai and Fan,2021),spring drought in China(Tian and Fan,2022),the summer extreme precipitation frequency in the Yangtze River basin (Tian and Fan,2020),and the number of landfalling TCs in summer in China(Tian and Fan,2019).Moreover,satisfying levels of prediction skill benefiting from available predictors and,particularly,from inheriting the contribution of dynamical coupled model predictions for large-scale atmospheric circulation anomalies,were achieved not only for mid—high-latitude climate systems such as Arctic sea ice,Eurasian snow cover,and SST over the North Pacific,but also tropical climate systems such as ENSO and SST over the tropical Indian and Atlantic oceans. It is clear that the DY,which uses the difference in a variable between the current year and preceding year,is able to provide higher prediction skills of the interannual and decadal component,,as compared with traditional anomaly prediction,especially when it is inherited from the superiority of a dynamically coupled model in predicting large-scale circulations.Evidently,this further illustrates the great strength of the statistical—dynamical hybrid approach in climate predictions.Consequently,it can be expected that this approach will play a more important role in climate predictions,especially in the forecasting of high-impact climate events. The above sections have reviewed the advances made in predictability studies associated with the identification of optimally growing errors and the development of dynamical and statistical methods to reduce the prediction uncertainties of weather and climate.In fact,in the evolution of prediction errors,the errors of different variables and at different temporal and spatial scales interact with each other,and thus revealing the key factors that have large impacts on these prediction uncertainties and identifying the dominant scale responsible for error growth will have important implications on improving the forecast skill for weather and climate events.In recent years,Chinese scientists have made contributions towards understanding these aspects of error growth and multi-scale interactions,particularly in meso-to small-scale weather systems,which range from several meters to around 2000 km spatially,and from seconds to days temporally,which in particular can encompass certain types of disastrous weather events,such as squall lines,supercells and convection (Orlanski,1975).Such studies can help us to optimize observational networks,assimilation algorithms,and model configurations in order to maximize the forecasting accuracy for various types of disastrous weather and climate events.Studies on meso-to small-scale error growth carried out by Chinese scientists can be summarized into two aspects,as follows: One aspect is the identification of the key factors for an accurate forecast through either ensemble-based sensitive analysis or DA.Studies show that the formation of a squall line in China is most sensitive to the initial moisture,with a linear response to the initial moisture error (Wu et al.,2013),which is different from the nonlinear response in squall lines over the United States.The mesoscale convective vortex(MCV) has been demonstrated to be a key factor in producing extremely heavy rainfall in China (Yu and Meng,2016;Zhang et al.,2022b),and operational models carry larger uncertainty in predicting the behavior of MCVs owing to the juxtaposition between the direction of MCV movement and the low-level jet (Zhang and Meng,2018).In addition to MCVs,the predictability of TCs has also been examined,revealing that the TC intensity forecast error is closely related to the intensity (as well as the rate of intensity change) of TCs and a number of environmental parameters(Zhang et al.,2014).A TC’s intensity and precipitation forecast largely depends on the initial relationship between the TC intensity and location and the initial steering flow (Zhu et al.,2016). Another aspect is to understand the error growth dynamics.A pioneering study on storm-scale predictability revealed that small yet realistic uncertainties in boundary layer and topographical influence,or errors much smaller than what can be observed,may lead to considerable differences in the initiation and subsequent organization and intensity of the mesoscale convective system and its embedded supercells (Zhang et al.,2015,2016).The forecast errors remained nearly unchanged even when the initial perturbations were reduced by 90%,which suggests an inherently limited predictability for lead times as short as 3—6 h. The relative importance of errors at different spatial scales has been a hot topic in error growth dynamics.There has been disagreement on whether small-scale or large-scale error is more important.The former claims that small-amplitude,small-scale errors will grow up-scale,saturate at smaller scales,and transfer to progressively larger scales,while the latter claims that errors grow up-amplitude at all model-resolved scales simultaneously rather than transfer up-scale.This disagreement is actually equivalent because the important scale should be determined by the dominant error growth dynamics.In this regard,how sensitive the forecast error growth is to different amplitudes and horizontal scales of flow-dependent unobservable initial uncertainties in a high-resolution convection-permitting ensemble forecast on a real high-impact rainfall event in China was examined by Zhang et al.(2022b).The dominance of up-scale rather than up-amplitude error growth was demonstrated under the regime of k-5/3power spectra by revealing the inability of large-scale errors to grow until the amplitude of small-scale errors has increased to an adequate amplitude.An apparent transfer of the fastest growing scale from smaller to larger scales with a slower growth rate at larger scales was revealed.In addition,initial perturbations with different structures have different error growth features at larger scales in different variables in a regime transitioning from the k-5/3to k-3power law;and the error growth featured by the CNOPtype initial error mentioned in section 2 tends to be more upamplitude relative to perturbations of the NCEP’s Global Ensemble Forecast System or sub-grid-scale perturbations. The advances made in predictability studies in China in recent years have been reviewed in this article,mainly from the perspectives of new methods for targeted observation,DA,ensemble forecasting,and statistical predictions and their applications to weather and climate predictions.The article emphasizes the great progress made in studies of nonlinear optimal perturbations for targeted observations and ensemble forecasting,and a family of CNOPs are presented,including CNOP-I for measuring the initial error effect,CNOP-P for estimating the model parametric error effect,CNOP-B for evaluating uncertainties in boundary conditions,and CNOPF for investigating the combined effect of various model errors (see section 2).Among the many studies on the sensitive areas for targeted observations associated with the forecasting of high-impact ocean—atmosphere environmental events,several field campaigns for the forecasting of TCs and predictions of the vertical thermal structure in continental shelf seas in the Yellow Sea are highlighted to demonstrate the real-time implementation of the CNOP-I technique independently developed in China to support meteorological and oceanic observational campaigns for the needs of weather and climate predictions.In ensemble forecasting,CNOPs have been found to be able to represent initial uncertainties for TC track forecasting through orthogonal CNOP-Is,and to estimate model parametric uncertainties and even the combined effect of different kinds of model errors for convection-scale forecasting using CNOP-P and -F,respectively(see section 2.1).Another approach,the NLLE,was proposed to quantify the predictable time of atmospheric and oceanic motions and associated weather and climate,and a predictability diagram from daily weather,through monthly,sub-seasonal,and seasonal,to interannual and even decadal climate phenomena was achieved for reference in improving the level of seamless predictions.Furthermore,the vectors featured by the NLLE (i.e.,NLLVs),were applied to provide the lasting effect on initial uncertainties of the ensemble forecasting of past information,which favored a better performance and higher reliability than that of traditional BVs and presented a skill comparable to the ETKF;due to the features of NLLVs in the form of easier realization and less computational time,this approach prevails over the ETKF in terms of ensemble forecast performance (see section 2.2).All these methods on targeted observation and ensemble forecasting indicate that fully considering the nonlinear effects is necessary in order to correct prediction biases.Concerning DA,new 4DVar and EnKF algorithms for initialization and approaches to reduce the combined effect of model and initial errors are reviewed (see section 3).These new algorithms include DRP-and NLS-4DVar,both of which are focused on 4DEnVar to address the challenge of 4DVar posed by the flow-dependent B matrix and computational efficiency problem (see section 3.1).The former algorithm projects the optimization problem in model space onto a low-dimensional subspace,using a particular localization technique to deal with spurious correlation between the model field and observations,and was eventually embedded in GRAPES-GFS to provide flow-dependent ensemble covariance for 4DVar,which ultimately led to the establishment of an En4DVar DA system for GRAPES-GFS.This latter algorithm focuses on another perspective to treat the nonlinear effect included in the 4DVar cost function by considering nonlinear leastsquares.It furthermore uses a multigrid interactive technique to correct multi-scale errors and reduce the computational cost,which was eventually applied in quite a few models to address relevant practical concerns.Besides 4DVar algorithms,Chinese scientists have also developed new EnKF schemes to reduce the computational costs and address the multiscale background error statistics (see section 3.2).With the newly-developed adaptive EnKF-MGA,it is possible to address the multiscale information from the observational residual by adaptively triggering an MGA,thus producing smaller assimilation errors and shortening the spin-up period;but with the further improved MSHea-EnKF,it is possible to use long-term simulations and the frequency split technique to derive the low-frequency background error statistic and use less computing resource to provide comparable performances to the standard EnKF. Along with the development of dynamical forecasting,statistical approaches are also thriving in terms of acquiring high levels of forecast skill for high-impact weather and climate events (see section 4).Chinese scientists have continued to invest great effort in exploring new and effective statistical forecasts methodologies.Particularly,based on the classical stochastic climate model,a fractional integral statistical model was built to quantify the predictable sources and help us to purposely design better prediction models (see section 4.1).Meanwhile,the network theory,which emerged from complex system science,has been recently applied in climate science,providing critical predictive power for scientific challenges,which is sometimes even superior to dynamical forecasts (see section 4.2).Chinese scientists have also tried using ML algorithms to improve IOD predictions and increase the efficiency of ensemble forecasting in real-time forecasts,eventually showing that ML has the ability to make up for the deficiency of traditional forecast methods.In addition,different from the traditional statistical prediction approach based on climate anomalies,a year-to-year increment prediction approach (DY approach) was proposed,which amplifies the climate signal and shows high prediction skill for interannual and interdecadal climate variabilities(see section 4.3).Nevertheless,the dynamical and statistical approaches have their respective advantages and limitations.How to effectively combine the dynamical and statistical approaches and improve the forecast skill may be a prospective research subject in need of further study. Table 3.Main advances in predictability studies in China in recent years. It is clear that Chinese scientists have made some outstanding contributions to the development of new methods that address the forecasting uncertainties for weather and climate.To facilitate readers,we summarize in Table 3 these contributions from the perspective of targeted observation,DA,ensemble forecasting,and statistical predictions.In this context,the hot topics related to the importance of errors at the different spatial scales of meso-to small-scale weather systems are also highlighted (see section 5).An apparent transfer of the fastest growing scale from smaller to larger scales with a slower growth rate at larger scales was revealed under the regime of k-5/3power spectra,and the dominant role of up-scale rather than up-amplitude error growth was demonstrated.The error growth featured by the CNOPI error was shown to be more up-amplitude in a regime transitioning from the k-5/3to k-3power law,relative to perturbations of the NCEP’s Global Ensemble Forecast System or sub-grid-scale perturbations.These studies contribute to addressing the controversy regarding whether small-scale or large-scale error is more important in meso-to small-scale weather systems.Furthermore,understanding the error growth dynamics can help to optimize observational networks,assimilation algorithms,and model configurations in order to maximize the forecasting accuracy of various disastrous weather events. Besides these above advances,there studies have also been conducted on controversial issues of predictability,and these should be mentioned here.For example,on the issue “whether the approaching limit of predictability for TC track prediction is near or has already been reached”,proposed by Landsea and Cangialosi (2018),Zhou and Toth(2020) and Yu et al.(2022) used TC forecast data in the Atlantic basin and in the western North Pacific basin,respectively,to explore what the past trend was in the reduction of TC forecast track error,and how such errors may be further reduced in future decades.Both showed that the improvements of TC track forecast skills in the past 10 years have mainly been due to the reduction in analysis errors rather than the reduction in the error growth rate.They also pointed out that if the current trend continues,a further twoday improvement in TC track forecast lead times may be projected for the coming 20 years in the Atlantic basin,and 15 years in the western North Pacific basin.It is therefore clear that we have not yet reached the limit of TC track predictability in both basins. Although great progress has been made in the predictability and even practical forecasting of weather and climate,there are greater requirements for numerical weather forecasting and climate prediction related to disaster prevention and national security with the development of society and the progress of technology.For example,it is necessary to strengthen the development of seamless forecasting systems from traditional weather scales to decadal climate scales,the development of coupled forecasting systems from single atmosphere to multi-spherical interactions between the atmosphere,sea,land and ecology,and the coordinated development of an observation—assimilation—model forecasting system instead of an independent observation system or numerical forecast model.These requirements undoubtedly pose new challenges to the study of predictability for highimpact weather and climate events,particularly in the study of targeted observation,DA,and ensemble forecasting with the consideration of multiple temporal and spatial scales and their associated interactions.Although international communities have developed various strategies to deal with the above challenges and made progress—particularly,a few NWP centers have established weather forecasting and climate prediction systems that are able to address some of the new challenges to certain extent—their DA systems,ensemble forecasting systems and other technologies are not open to the public.Therefore,in order to meet the new requirements in forecasting and predictions in China,Chinese scientists must try to study multi-scale error analysis theory for dealing with multi-scale problems in DA and ensemble forecasting,establish new theories that accurately quantify the sensitivities in observations and uncertainties,improve current hybrid assimilation techniques or develop new filtering techniques based on current particle or mixed filtering algorithms,and construct new models that incorporate the advantages of big data analysis and artificial intelligence.It is expected that a much advanced numerical forecasting system can be established in China in the near future,thus addressing the challenges of numerical weather forecasting and climate predictions due to the effects of multiple temporal and spatial scales and their interactions. Acknowledgements.The authors greatly appreciate the useful comments and suggestions of the editor and two anonymous reviewers.The authors would also like to thank Drs.Ke FAN,Xiangjun TIAN,Guodong SUN,Qiang WANG,Feifan ZHOU,Jingfang FAN,Juanjuan LIU,Naiming YUAN,Guokun DAI,Xinrong WU,Bo WU,and Ms.Lu WANG and Zhizhen XU for providing materials.This article was sponsored by the National Natural Science Foundation of China (Grant Nos.41930971,42105061 and 42030604).2.Advances in studies of nonlinear optimal perturbations for weather and climate predictability dynamics
2.1.Conditional nonlinear optimal perturbation:applications to ensemble forecasting and targeted observations



2.2.Nonlinear local Lyapunov exponents: applications to estimate the predictability time and yield ensemble forecasting members

3.New DA algorithms and novel assimilation approaches to address the combined effect of initial and model errors
3.1.New 4DVar algorithms and their applications

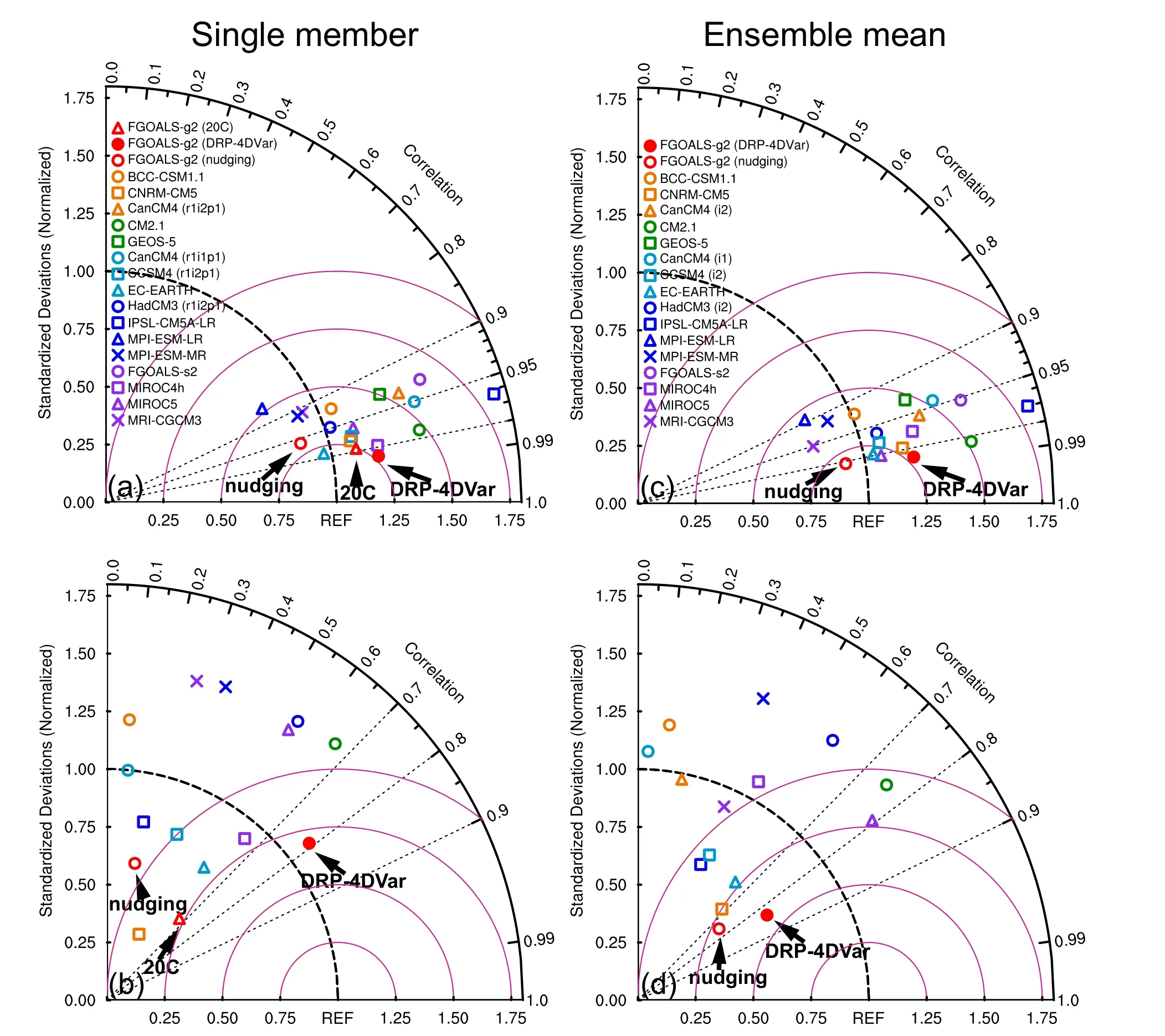

3.2.Improvement of the EnKF scheme
3.3.NFSV-DA and its applications
4.Statistical approaches to improving prediction skill
4.1.An approach to identify sources of climate predictability considering the impact of climate memory
4.2.Complexity-based forecasting of climate phenomena
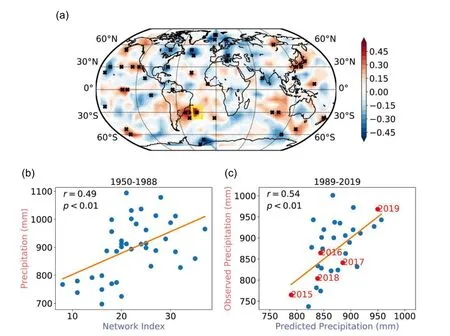
4.3.The year-to-year increment prediction approach and its role in enhancing climate predictions
5.Predictability dynamics associated with meso-to small-scale weather systems
6.Summary and discussion

 Advances in Atmospheric Sciences2023年8期
Advances in Atmospheric Sciences2023年8期
- Advances in Atmospheric Sciences的其它文章
- Preface to the Special Issue on the National Report to the 28th IUGG General Assembly by CNC-IAMAS (2019-2022)※
- Seamless Prediction in China: A Review※
- A Review of Research on the Record-Breaking Precipitation Event in Henan Province,China,July 2021※
- A Review of Atmospheric Electricity Research in China from 2019 to 2022※
- Recent Advances in Understanding Multi-scale Climate Variability of the Asian Monsoon※
- China’s Recent Progresses in Polar Climate Change and Its Interactions with the Global Climate System※
