Rapid stabilization of stochastic quantum systems in a unified framework
Jie Wen(溫杰), Fangmin Wang(王芳敏), Yuanhao Shi(史元浩),Jianfang Jia(賈建芳), and Jianchao Zeng(曾建潮)
1School of Electrical and Control Engineering,North University of China,Taiyuan 030051,China
2State Key Laboratory of Precision Measurement Technology and Instruments,Department of Precision Instrument,Tsinghua University,Beijing 100084,China
3School of Computer Science and Technology,North University of China,Taiyuan 030051,China
Keywords: rapid stabilization,state feedback,stochastic quantum systems,switching control
1.Introduction
The Nobel Prize in Physics 2022 was awarded to Alain Aspect, John Clauser, and Anton Zeilinger for their pathfinding work in quantum mechanics and quantum information science.At present, quantum information science has become a hot research field,where the transfer of quantum systems from any initial state to the target state,i.e.,the preparation or global stabilization of quantum states,is one of the basic tasks.In order to prepare the target quantum state rapidly and accurately,numerous classical control methods have been introduced into control of quantum systems,e.g.,optimal control[1–3]and Lyapunov control.[4–7]
For the better robustness, feedback controls, which need the system information through measurement, are recommended to apply.Although measurement operations can cause collapse of quantum states, quantum filter theory[8,9]helps to overcome this obstacle by using measurement-based feedback control, where quantum filter states described by an It?o stochastic differential equation, instead of the actual quantum states, are used.Based on quantum filter theory,for the stabilization of stochastic quantum systems, switching control strategy, which was proposed in Ref.[10] first,is one of the main control strategies and has been used to achieve global stabilization of eigenstates forN-level quantum systems,[10–12]Bell states for two-qubit systems[13,14]and Greenberger–Horne–Zeilinger(GHZ)state for multi-qubit systems.[15,16]The idea of the switching control strategy is that the state space is divided into two state subspaces, then to design two controls to form the switching control strategy such that one control can make the system state converge to and evolve permanently in the state subspace that contains the target state, and the other control can make the system state converge to the target state.Of course, the state trajectory may travel back and forth between the two subspaces under the switching control.To improve the convergence rate,Vuet al.used the coupling Lyapunov functions to design a switching control to reduce the travel number of system trajectory between two subspaces.[13]Recently, Lianget al.designed a state feedback to achieve the local exponential stabilization of both eigenstates forN-level quantum angular momentum systems and GHZ states for multi-qubit systems, whose robustness analyses were presented in Ref.[17].In addition, Cardonaet al.proposed noise-assisted feedback strategy that can also achieve the exponential stabilization ofN-level quantum systems.[18]Considering that state feedback has been applied in the real physical experiment,[19]we mainly focus on the state feedback control in this paper.
Due to the rapidity requirement in quantum manipulations,the rapid convergence of quantum states is of great significance.According to the review of related literature, state feedback has been used to achieve the rapid stabilization of stochastic quantum systems, even local exponential stabilization.In order to improve the convergence rate of system states further,we present a unified framework to combine the existing techniques of rapidly stabilizing stochastic quantum systems in this paper, i.e., the reduction of the travel number of system trajectory between state subspaces and the local exponential stabilization of quantum states.For this goal, we study the rapid stabilization of a class of nonlinear stochastic systems and introduce a Lyapunov–LaSalle-like theorem for the general stochastic differential equations by extending the results in Ref.[13].Based on the proposed Lyapunov–LaSalle-like theorem, a unified framework with five steps for the rapid stabilization of the general stochastic quantum systems is presented and is applied to the rapid stabilization of single-qubit systems,two-qubit systems,andN-qubit systems,which show the effectiveness and universality of the unified framework.According to the proposed unified framework,the state space should be divided into two state subspaces first,and the switching state feedback controls designed based on the constructed coupling Lyapunov functions can make the system trajectory only transit the boundary between the two state subspaces no more than two times,and the target state is globally asymptotically stable in probability.In particular,the system state can converge exponentially in(all or part of)the state subspace where the target state is located.Thus,the main contributions of this paper can be concluded as follows: (i)A Lyapunov–LaSalle-like theorem is introduced for the rapid stabilization of a class of nonlinear stochastic systems.(ii)A unified framework is presented for the rapid stabilization of stochastic quantum systems based on the proposed Lyapunov–LaSalle-like theorem.(iii)The unified framework is applied to the rapid stabilization of single-qubit systems, two-qubit systems,andN-qubit systems.
The rest of this paper is organized as follows.The stochastic differential equation describing the quantum filter state and the problem of rapid stabilization by state feedback are described in Section 2.We introduce a Lyapunov–LaSallelike theorem for a class of nonlinear stochastic systems in Section 3.In Section 4,the proposed Lyapunov–LaSalle-like theorem is applied to the rapid stabilization of single-qubit systems,two-qubit systems,andN-qubit systems.We take threequbit systems as an example to verify the effectiveness of the proposed state feedback strategies in numerical simulations in Section 5.Finally,we present conclusions and discuss the possible future directions in Section 6.
NotationR and C denote the set of real numbers and complex numbers, respectively; tr(·) is the trace of matrices;A?is the conjugate transpose of matrixA; [A,B]=AB ?BAis the commutator of matricesAandB; P{·}represents the probability of event.E[·] denotes the expected value of random variables;are the Pauli operators alongx,yandzaxes, respectively, with;diag[λ1,...,λn]represents then×ndiagonal matrix with diagonal elementsλ1,...,λn;?represents the Kronecker product of matrices.In=diag[1,...,1]is then×nidentity matrix.
2.Preliminaries
In this paper, we consider the rapid stabilization of stochastic quantum systems via measurement-based feedback control, where the quantum filter state, instead of the state of the actual quantum system, is used in the feedback control.According to the quantum filter theory,[8,9]the evolution of quantum filter state can be described by the It?o stochastic differential equation, i.e., stochastic master equation (SME),which can be written as[20]
whereρtis the density matrix describing quantum state, andρt ∈S={ρt ∈Cn×n:ρt=ρt?≥0,tr(ρt)=1}in whichSrepresents the state space;H0andHkare free Hamiltonian and control Hamiltonian,respectively;Ljis the measurement operator;ΓL jandηLjare the measurement strengths and efficiencies, respectively;ωL j,tis the standard Wiener process,while dωL j,tis the independent Wiener increment that satisfies dωLi,tdωL j,t=δijdt,in whichδijis the Kronecker delta;uk,t ∈R is the control input;yj,tis the measurement record of the output;superoperatorsD(Lj,ρt)and?(Lj,ρt)are defined as
For SME (1), the existence and uniqueness of solutions can be guaranteed by constructing the appropriate control HamiltonianHkand the control inputuk,t.[10]It should be noticed that SME (1) can be used to describe many physical experiment systems, for example, an ensemble of laser-cooled Cesium atoms confined to a cavity mirror,[10,21,22]and a twoqubit system consisting of a couple of two-level atoms placed in two distant cavities and interacting through a radiation field in a dispersive way.[23]In particular,the theoretical study carried out in Ref.[10] was extended to discrete-time quantum systems,[24,25]and has been applied to the first physical experiment of achieving real-time quantum measurement-based feedback control in the photon box of the Kastler Brossel Laboratory,[19]from which the study of continuous-time quantum systems considered in this paper is the first step towards the practical quantum manipulation and has an important potential practical value.
Measurement-based feedback has been used to achieve the stabilization of stochastic quantum systems, where the feedback architectures of designing the control inputuk,tinclude static output feedback,[26,27]state feedback,[10,12,17,21,28]and noise-assisted feedback.[18,29]Considering the practicability, we focus on the state feedback architecture here.For state feedback, the control inputuk,tin Eq.(1) can be written asuk(ρt).Therefore, the goal of this paper is to achieve the rapid stabilization of stochastic quantum systems by using state feedback controluk(ρt), which is described in the following.
Rapid stabilization by state feedbackFor the quantum filter (1), design the state feedback controluk(ρt) to globally rapidly asymptotically render the system stateρtfrom any initial stateρ0to the target stateρfalmost surely, i.e.,P{limt→∞ρt=ρf}=1,?ρ0∈S.
In fact, several state feedback strategies have been proposed for the rapid stabilization of stochastic quantum systems, e.g., Refs.[13,16,20,30,31].However, the state feedback controls designed in Refs.[3,16,20,30,31]are either for a certain class of quantum systems or for a certain class of target quantum states.In this paper,we aim to propose a unified architecture of designing state feedback controls that can be applied to the rapid stabilization of multiple types of stochastic quantum systems and different types of quantum states.
The SME(1)describing quantum filter state is a nonlinear stochastic differential equation.In order to design the state feedback control of rapidly stabilizing stochastic quantum systems, we introduce a Lyapunov–LaSalle-like theorem for the rapid stability in probability of a class of nonlinear stochastic systems in the next section,and then present the unified framework of rapidly stabilizing stochastic quantum systems proposed in this paper and apply the unified framework to Eq.(1)in Section 4, where we take single-qubit systems (eigenstate as the target state),two-qubit systems(Bell state as the target state),and multi-qubit systems(GHZ state as the target state)as examples.
3.Rapid stability of stochastic differential equations
Consider the nonlinear stochastic systems described by the stochastic differential equation
wherextis the system state;f:Rn×Rn →Rnandg:Rn×Rn →Rn×rare Borel-measurable, locally bounded, and locally Lipschitz continuous functions;f(0,0)=0,g(0,0)=0;ωtis anr-dimensional standard Wiener process.
Based on the concept of stability in probability as shown in Ref.[32], we have the following theorem, which is an extension of Theorem 1 in Ref.[13].
Theorem 1For the nonlinear stochastic systems (3), if there exists a partition of Rn,which is denoted as{φ1,φ2},and there exists the coupling Lyapunov functionsV1(x),V2(x) :Rn →R+, which are defined inφ1andφ2, respectively, and both nonnegative differential and continuously twice differential satisfy the following conditions:
C.I:V1(x) is constant on the boundary of the sets{φ1,φ2}.
C.II:α1(|x|)≤V1(x)≤α2(|x|),?x ∈Rn.
C.III:?V1(x)≤?λV1(x),?x ∈φ1.
C.IV:?V2(x)≤?M,?x ∈φ2.
Here,α1(·) andα2(·) areK∞-class functions;λandMare positive constants;?is the infinitesimal operator associated with Eq.(3)and defined as
Then, the equilibriumx= 0 of the system (3) is globally asymptotically stable in probability, and the system trajectoriesxtwill only transit through the boundary betweenφ1andφ2no more than two times for any initial statex0∈Rn.In particular, E[V1(xt)]≤V1(xT)e?λ(t?T)whent ≥T, whereTis the time after thatxtevolves inφ1permanently.
ProofAccording to Theorem 1 in Ref.[13],if we let
it is easy to verify thatW(x)is a continuous positive function defined inφ1due to the fact thatV1(x) is a continuous positive function as well asλ>0,then the conditions C.1–C.3 of
Theorem 1in Ref.[13] hold true, such thatx=0 is globally asymptotically stable in probability andxttransits the boundary betweenφ1andφ2no more than two times.
On the other hand,according to Theorem 3 in Ref.[18],ifV1(x),T,andφ1are regarded asV(x),t0,andS,respectively,we can directly conclude that E[V1(xt)]≤V1(xT)e?λ(t?T).The proof is completed.
Remark 1 In Theorem 1,it is necessary thatV1(x)is constant on the boundary betweenφ1andφ2, regarded as an independent condition,which is denoted as condition C.I.From the proof of Theorem 1 in Ref.[13],the condition C.I is used to guarantee that there is no sliding motion of the system trajectory on the boundary and help to prove the conclusion thatxtwill evolve inφ1permanently after a finite time for any initial statex0.Therefore,when applying Theorem 1,we need to deliberately check the condition C.I to avoid misusing Theorem 1 to obtain wrong conclusions.
4.Rapid stabilization of stochastic quantum systems
In this section, we present the unified framework of rapidly stabilizing stochastic quantum systems based on Theorem 1 and Ref.[13]first,and then apply the unified framework to the rapid stabilization of single-qubit systems, two-qubit systems, andN-qubit systems, to demonstrate the effectiveness and universality of the proposed unified framework.
4.1.The unified framework of rapidly stabilizing stochastic quantum systems
Comparing SME(1)and the stochastic differential equation (3), SME (1) is a special class of stochastic differentialequation withthus
Theorem 1is suitable for SME (1).According to Theorem 1 in this paper and Theorem 1 in Ref.[13],we proposed a unified framework for the rapid stabilization of stochastic quantum systems,which is shown in Fig.1.
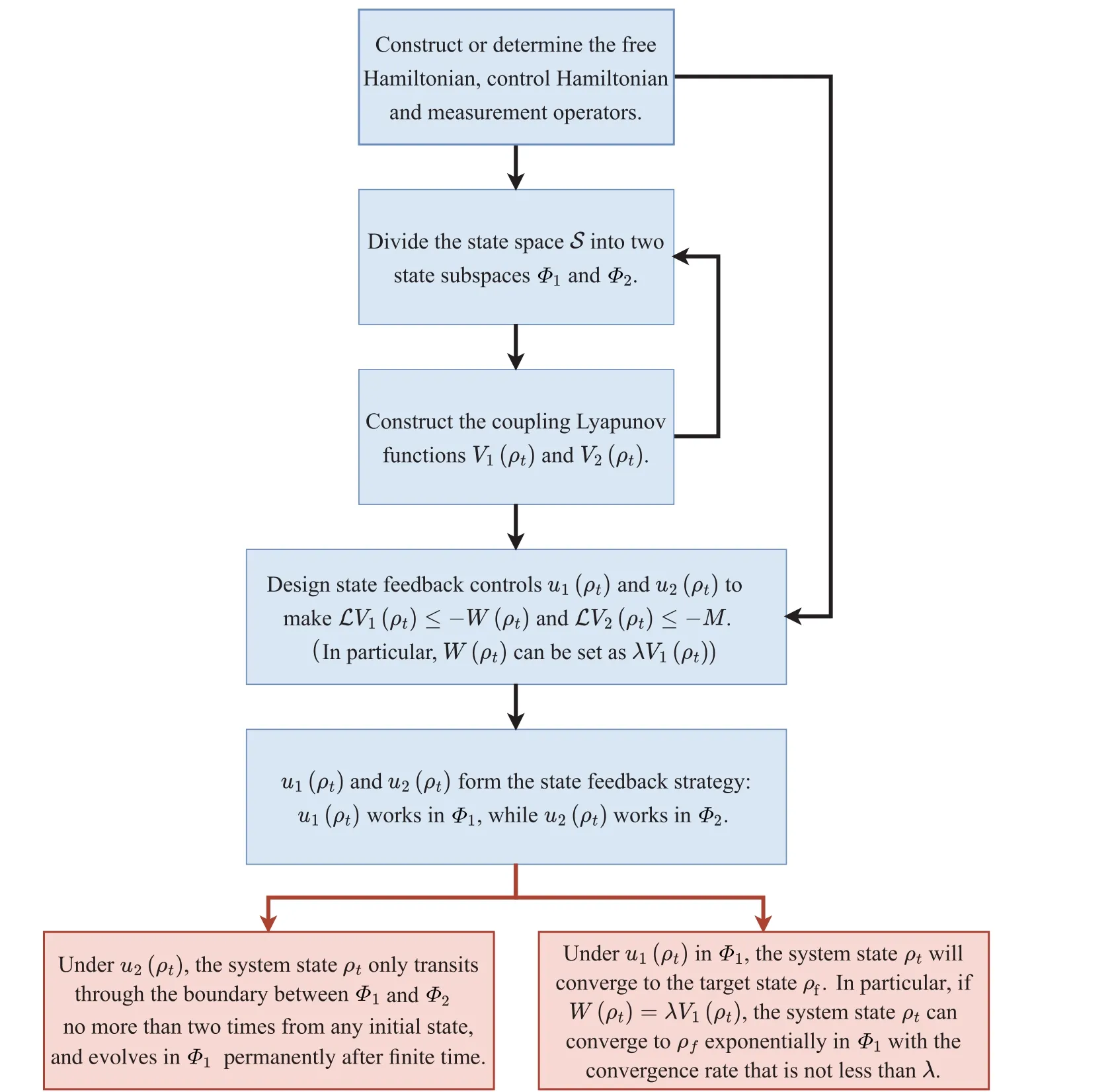
Fig.1.The diagram of the unified framework proposed in this paper for the rapid stabilization of stochastic quantum systems, where the blue blocks represent the operations, the pink blocks represent the results of stabilization control, while the lines with arrow describe the relationships between different blocks.
From Fig.1, it is necessary to perform five steps for the design of state feedback controls to rapidly stabilize stochastic quantum systems.The specific details of each step are described as follows.
Step 1Construct or determine Hamiltonians and measurement operators.For the stabilization of stochastic quantum systems, the solvability is the first problem to be solved.The system Hamiltonians(including free HamiltonianH0and control HamiltoniansHk)and measurement operatorsLjneed to be constructed reasonably to guarantee the solvability of the stabilization problem of quantum systems.For example,in Ref.[11], under the setting of Hamiltonians and measurement operator presented in Assumptions 2–3 of Ref.[11]the target state belongs to system equilibria, and the controlled quantum system has a finite number of equilibrium states due to the fact that the measurement operator in Ref.[11]is nondegenerate.However, if the measurement operator is degenerate, the number of the system equilibria may be infinite, as shown in Refs.[16,30,31].On the other hand,if the controlled quantum system is the actual physical system,the first step is also to determine Hamiltonians and measurement operators.No matter what is the case, Hamiltonians and measurement operators should be constructed or determined to ensure that the target state belongs to the system equilibria,such that the solvability of the stabilization problem of quantum systems is guaranteed.
Step 2Divide the state spaceSinto two state subspaces,which are denoted asΦ1andΦ2.The state spaceScan be divided artificially and directly, or can also be divided based on the Lyapunov functionV1(ρt) constructed in Step 3.No matter what is the division method, the partition ofSshould satisfy the following conditions:
If the number of system equilibria is finite,the target state is located inΦ1while the other equilibria are located inΦ2.
If the number of system equilibria is infinite, the target state is only the state that simultaneously located in the LaSalle invariant set andΦ1.
Step 3Construct the coupling Lyapunov functionsV1(ρt) andV2(ρt).V1(ρt) is defined inΦ1, whileV2(ρt) is defined inΦ2.BothV1(ρt)andV2(ρt)should be nonnegative differentiable and twice continuous differentiable.In particular,V1(ρt)must be constant on the boundary between the state subspacesΦ1andΦ2.Moreover,V1(ρt)can be used to divide the state spaceSin Step 2.
Step 4Design state feedback controlsu1(ρt)andu2(ρt)to make?V1(ρt)≤?W(ρt) and?V2(ρt)≤?M.In particular,W(ρt) can be set asλV1(ρt).If the designed state feedback controlu1(ρt) cannot make?V1(ρt)≤?λV1(ρt)hold in all ofΦ1, we can design another state feedback control denoted as ?u1(ρt) to make?V1(ρt)≤?W(ρt) hold in the state subspace denoted as ?Φ1, whereu1(ρt) cannot make?V1(ρt)≤?λV1(ρt)hold,andu1(ρt)still works inΦ1??Φ1.
Step 5u1(ρt) andu2(ρt) form the state feedback strategy:u1(ρt)works inΦ1,whileu2(ρt)works inΦ2.Ifu1(ρt)cannot make?V1(ρt)≤?λV1(ρt) hold in all ofΦ1,u1(ρt),?u1(ρt) andu2(ρt) form the state feedback strategy:u1(ρt)works inΦ1??Φ1,u2(ρt) works inΦ2, while ?u1(ρt) works in ?Φ1.
Following the above design process, the state feedback strategy can be applied to achieve:
Underu2(ρt),the system stateρtonly transits through the boundary betweenΦ1andΦ2no more than two times from any initial state, and evolves inΦ1permanently after finite time.
Underu1(ρt)inΦ1,the system stateρtwill converge to the target stateρf.In particular,ifW(ρt)=λV1(ρt),the system stateρtcan converge toρfexponentially inΦ1with the convergence rate that is not less thanλ, which means that the target state is stabilized globally and rapidly.In Subsections 4.2, 4.3, and 4.4, we apply the unified framework to achieve the rapid stabilization of single-qubit systems, twoqubit systems,andN-qubit systems,respectively.
4.2.Rapid stabilization of single-qubit systems
For single-qubit systems, the time evolution ofndimensional quantum filter state is described by the following SME:[11,33]
which corresponds to the case ofq=1,m=1,L1=Le, andΓLe=1 in SME(1).
Similar to Ref.[11],the target stateρfis set as an eigenstate of the measurement operatorLe.For the rapid stabilization of single-qubit systems(6),we follow the five steps in the unified framework as shown in Subsection 4.1 to design the state feedback controlut.
To guarantee the solvability, the measurement operatorLeis self-adjoint, non-degenerate, and commutative withH0,while the control HamiltonianH1is connected, under which the system equilibria are all the eigenstates of the measurement operatorLeand the target state belongs to the system equilibria,such that the number of the system equilibria is finite,i.e.,n.
Now, we should divide the state spaceSinto two subspaces.Consider the following coupling Lyapunov functions
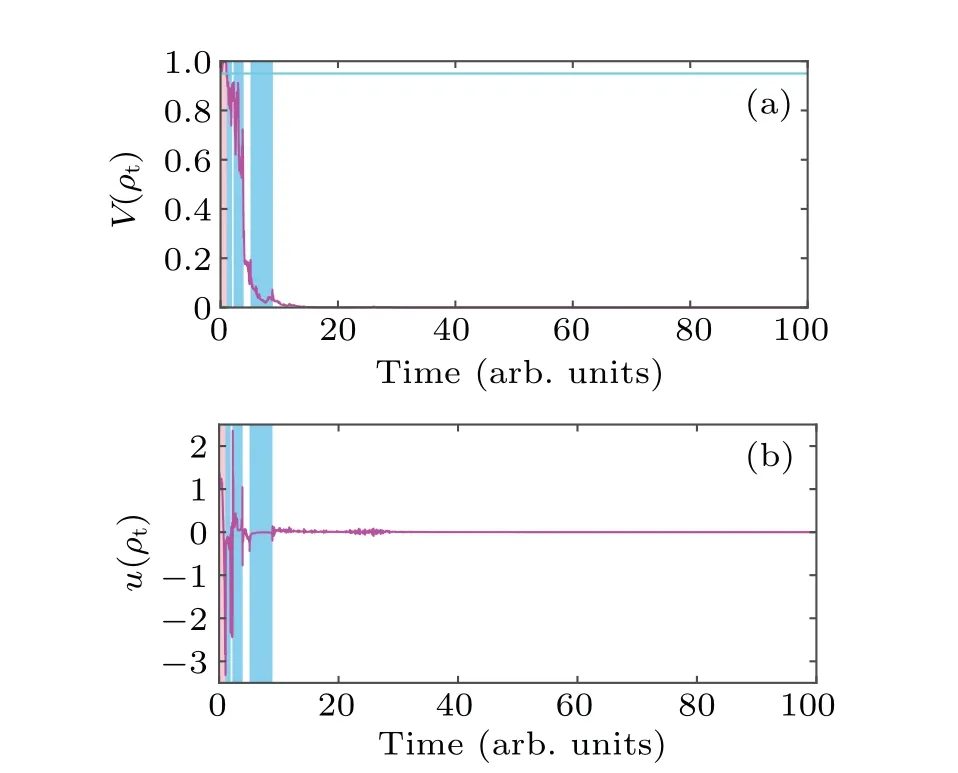
with 0 Based onVe(ρt) andVc(ρt), the feedback controlsue,1(ρt)andue,2(ρt),which are regarded asu1(ρt)andu2(ρt),can be designed.According to It?o’s product rule and Eq.(4),the infinitesimal generator associated with Eq.(6) acting onVe(ρt)andVc(ρt)are respectively,with From Eqs.(8) and (9), the feedback controlsue,1(ρt) andue,2(ρt)can be designed as respectively, which make?Ve(ρt)≤ ?λeVe(ρt) and?Vc(ρt)≤?Mehold,where 0<λe≤ˉλeand 0 and Fortunately, Eq.(13) can hold by constructingXbased on the algorithm proposed in Ref.[16], and Eq.(12)holds in the state subspaceΦe,1?Φe,3, whereΦe,3={ρ ∈Φe,1:ge(ρ)/=0} ??Φe,1={ρ ∈Φe,1:|ge(ρ)|≤εe}withεe>0.For the state subspace ?Φe,1, we design another state feedback control as wherese>0 is the strength of the feedback control,andηe>0 is a parameter used to adjust the hardness of the control.The state control(14)is called the approximate bang-bang control,which was proposed in Ref.[5] first for closed quantum systems.Here,,1(ρt)can make?Ve(ρt)≤?We(ρt)hold,with(ρt)being a continuous positive definite function defined onS. Finally,ue,1(ρt),ue,2(ρt), ande,1(ρt) form the switching state feedback strategy,which can be expressed as From Theorem 1,underue,2(ρt),the system stateρtonly transits through the boundary betweenΦe,1andΦe,2no more than two times from any initial state, and evolves inΦe,1permanently after finite time.InΦe,1,ue,1(ρt) and ?ue,1(ρt) make?Ve(ρt)≤?λeVe(ρt) and?Ve(ρt)≤?We(ρt) hold, which means that the system trajectory will converge to the invariant set?e={ρ ∈Φ1:?Ve(ρ)=0}from LaSalle’s invariance principle.Due to the fact that the target stateρfis only the equilibrium inΦe,1,thus?e={ρf}and the system stateρtwill converge to the target stateρfwith probability 1,thus the target stateρfis globally asymptotically stable in probability under the switching controlue(ρt).In addition, the system stateρtcan converge exponentially inΦe,1??Φe,1with the convergence rate that is not less thanλedue to?Ve(ρt)≤?λeVe(ρt) andλe≤ˉλeaccording to Theorem 1 in this paper and Theorem 3 in Ref.[18]. Remark 2As shown in Eq.(15),we use different feedback controls in the corresponding different state subspaces.However, under switching state feedbackue(ρt), there is no sliding motion of the system trajectory on the boundaryΛebetweenΦe,1andΦe,2as well as the boundary ?Λeof ?Φe,1,which are defined asΛe={ρ ∈S:Ve(ρ)=ke}and ?Λe={ρ ∈Φe,1:|ge(ρ)|=εe}, respectively.The conclusions can be proved by contradiction as follows. If there exists sliding motion ofρtonΛe,then?Ve(ρt)=0 for someρt ∈Λe.On the other hand,?Ve(ρt)≤?λeVe(ρt)or?Ve(ρt)≤?We(ρt) holds inΦe,1.It is obvious that bothVe(ρt)andWe(ρt)are positive definite onΦe,1andρfis not onΛe,such thatVe(ρt)>0 andWe(ρt)>0 for?ρt ∈Λe,therefore?Ve(ρt)<0,which contradicts with?Ve(ρt)=0.Thus,there is no sliding motion of the system trajectory on the boundaryΛe. For two-qubit systems,the time evolution of quantum filter state is described by the following SME:[13] which corresponds to the case ofH0= 0,q= 1,m= 2 in SME (1).Bell states are the maximally entangled states of two-qubit quantum systems,which are written as and the target stateρfis set asφ+in this subsection. In order to divide the state spaceSinto two subspaces,we use the following Lyapunov function: with 0 Then,VB(ρt) andVc(ρt) form the coupling Lyapunov functions, based on which we can design the feedback controlsuB,1(ρt) anduB,2(ρt) for the rapid stabilization of Bell states.The infinitesimal generator associated with Eq.(16)acting onVB(ρt)andVc(ρt)are where andU12(ρt)==1tr(Ljρt).From Eqs.(18) and (19), the control lawsuB,1(ρt)anduB,2(ρt)can be designed as which make?VB(ρt)≤?λBVB(ρt)and?Vc(ρt)≤?MBhold,where 0<λB≤ˉλBand 0 Therefore,uB,1(ρt),uB,2(ρt),and ?uB,1(ρt)form the state feedback strategy of rapidly stabilizing Bell states,which can be expressed as Through a discussion similar to that in Subsection 4.2,we can conclude that the target stateρfis globally asymptotically stable in probability under the switching state feedback controluB(ρt)and the system stateρtcan converge exponentially inΦB,1??ΦB,1with the convergence rate that is no less thanλB. In this subsection, we consider the rapid stabilization ofN-qubit systems,whereN ≥3.Without loss of generality,the target state is set as the GHZ state,i.e., where|φf(shuō)〉 =(|00···0〉+|11···1〉) andn= 2N.Similar to Ref.[31], a diagonal measurement operator is chosen, whereli /=ljfori,j ∈{1,2,...,n/2}andi/=j, which makes the target stateρfbe one of the eigenstates ofLG.Due to the fact thatLGis degenerate,two control Hamiltonians should be used,such that the corresponding SME describingN-qubit systems is described as Here,we choose the distance function asV1(ρt),i.e., which is used to form the coupling Lyapunov functions withVc(ρt) for design of the state feedback controlsuG,1(ρt) anduG,2(ρt) of rapidly stabilizing GHZ states and to divide the state spaceSinto two state subspaces as where 0 BecauseLGis degenerate, the number of system equilibria is infinite, so we construct the HamiltonianH1such thatholds to simplify the control design.Similar to Subsections 4.2 and 4.3, the switching state feedback control can be designed as wheresG>0,ηG>0,and withεG> 0, which makes?VG(ρt)≤?λGVG(ρt) or?VG(ρt)≤?WG(ρt)and?Vc(ρt)≤?MGhold with 0<λG≤.For the feedback controluG(ρt)in Eq.(29), ?uG,1(ρt)is used to avoid the denominators ofuG,1(ρt) too small, while the denominators ofuG,1(ρt)cannot be zero by constructingXandH2based on the algorithm in Ref.[16]. Remark 3The stabilization of multi-qubit systems was also studied in Ref.[31],where the proposed feedback control is a special case of the feedback controluG(ρt) in Eq.(29)withεG=+∞.The main difference betweenuG(ρt)and the feedback control in Ref.[31] is thatuG(ρt) can make the system stateρtconverge exponentially inΦG,1?G,1, which cannot be guaranteed in theory by the feedback control in Ref.[31]. Remark 4In Subsection 4.2 (4.3, 4.4), we only make the system stateρtconverge exponentially inΦe,1?e,1(ΦB,1?B,1,ΦG,1?G,1, respectively) rather thanΦe,1(ΦB,1,ΦG,1,respectively), which can be avoided if the feedback controlue,1(ρt) (uB,1(ρt),uG,1(ρt), respectively) is designed more properly.For example, the state feedback controls in Refs.[28,34] can achieve the GHZ states and local exponential stabilization of eigenstates for multi-qubit systems andNlevel quantum angular momentum systems, respectively.If the feedback controls in Refs.[28,34] are applied instead ofuG,1(ρt) andue,1(ρt), respectively, and the state subspaces that the system state converge exponentially in Refs.[28,34]are regarded asΦG,1andΦe,1, respectively, then the system state can be converge more faster,which means that the results of exponential stabilization for quantum systems and the unified framework proposed in this paper can be combined reasonably to obtain better control performance. In this section,we take a three-qubit system with a degenerate measurement operator as an example to verify the effectiveness and rapidity of the proposed state feedback controls by stabilizing a target GHZ state. In the simulations,the target GHZ state is chosen as where|φf(shuō)〉=(|000〉+|111〉), while the initial state is set asρ0=diag[0,1,0,0,0,0,0,0].The system parameter settings are listed as[16] Fig.2.Simulation results of rapidly stabilizing GHZ state by using the switching feedback control (29) and the feedback control proposed in Ref.[16].(a) The curves of V(ρt).(b) The semi-lon version of (a).In(a)and(b),the grey curves,blue curve and purple curve represent the sample trajectories, the mean value of 1000 arbitrary sample trajectories under the feedback control (29), and the feedback control in Ref.[16], respectively; the red curve and the cyan line represent the exponential reference with exponent λG and the boundary between ΦG,1 and ΦG,2,respectively. The control parameters in Eq.(29)are set asλG=0.15,MG=1,sG=0.5,andηG=0.05.The state spaceSis divided intoΦG,1={ρ ∈S:V1(ρ)≤kG}andΦG,2=S?ΦG,1,wherekG=0.95.The state subspace,where the control lawG,1(ρt)works,is set asG,1={ρ ∈ΦG,1:|tr([H2,ρ]ρf)|≤εG}withεG=0.05.The simulation results of 1000 sample trajectories under the switching feedback control(29)are shown in Fig.2.One can see thatV(ρt) converges to zero, which means that the stabilization of the target GHZ state is achieved and verifies the effectiveness of the proposed switching state feedback control.On the other hand, the convergence rate of quantum states under the switching feedback control (29) is more thanλG, which means the rapidity of stabilizing target state.Moreover, the feedback control proposed in Ref.[16], i.e.,usingG(ρt) =?KGtr(i[H2,ρt]ρf) instead ofuG,1(ρt) andG,1(ρt) inΦG,1, is also applied to stabilize the target GHZ state.The results withKG=0.02 are also shown in Fig.2.One can see from Fig.2 thatV(ρt)converges to zero faster under the switching feedback control (29) than that under the feedback control proposed in Ref.[16],which shows the advantage of the designed feedback control in this paper.A sample trajectory is presented in Fig.3,from which one can see that the state trajectory transits the boundary betweenΦG,1andΦG,2no more than two times,which is consistent with the theoretical analysis. Fig.3.Simulation results of arbitrary sample trajectory.(a)The curves of V(ρt),(b)The curves of u(ρt).In(a)and(b),the purple curves represent VG(ρt) and uG(ρt), while the blue, pink and white background present the time domain of ρt ∈ΦG,1,ΦG,2 and ?ΦG,1,respectively. In summary, we have studied the rapid stabilization of stochastic quantum systems.In order to rapidly stabilize the target state, we propose a unified framework for design of state feedback controls based on the Lyapunov–LaSalle-like theorem, which is suitable for the It?o stochastic differential equation.The proposed unified framework is applied to the rapid stabilization of single-qubit systems,two-qubit systems,andN-qubit systems.Moreover, we take three-qubit systems as an example to verify the effectiveness and rapidity of the designed state feedback controls based on the proposed unified framework by stabilizing GHZ states in numerical simulations. In the near future, we will consider the further work as follows:(i)design of state feedback controls for the global exponential stabilization of the general stochastic quantum systems instead of some special quantum systems;[34](ii)robustness analysis of the state feedback strategies proposed in this paper when the physical parameters or the initial state are uncertain, as the work in Ref.[17]; (iii) exponential stabilization of stochastic delay quantum systems,specially the case of time-delay control,i.e.,ut=u(ρt?τ)with constant delay timeτorut=u(ρt?τ(t))with time-varying delay timeτ(t). Acknowledgements Project supported in part by the National Natural Science Foundation of China (Grant No.72071183), and Research Project Supported by Shanxi Scholarship Council of China(Grant No.2020-114).
4.3.Rapid stabilization of two-qubit systems

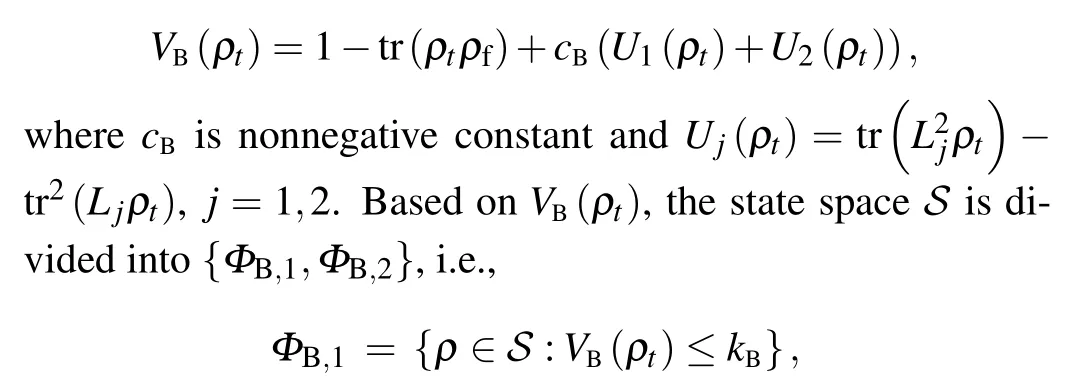
4.4.Rapid stabilization of N-qubit systems

5.Numerical simulations

6.Conclusions

