First-order quantum phase transition and entanglement in the Jaynes–Cummings model with a squeezed light
Chun-Qi Tang(湯椿琦) and Li-Tuo Shen(沈利托)
Fujian Key Laboratory of Quantum Information and Quantum Optics,College of Physics and Information Engineering,Fuzhou University,Fuzhou 350116,China
Keywords: Jaynes–Cummings model,quantum phase transition,entanglement
1.Introduction
Quantum phase transition is a fundamental research object in physics.Either in quantum optics or in condensed matter physics, quantum phase transition has been widely used,such as heavy fermions,[1–5]magnetism,[6–9]and superconductivity.[10–12]Different from the classical phase transition occurring in a finite temperature,the quantum phase transition occurs between two stable phases as the temperature tends to absolute zero degree due to the enhanced quantum fluctuations.[13–16]Quantum phase transition is generally divided into the first-order phase transition and the second-order phase transition.[17–19]For the first-order phase transition, it is a cross-boundary jump caused by two robust phases due to quantum fluctuations, and the two phases can coexist when they are at the critical point.At present, the study of nonequilibrium dynamics of quantum phase transition is still in a state of uncertainty because the physical information behind it is not completely clear.
Traditionally, the experimental study of quantum phase transition mainly focuses on the thermodynamic limit,and the number of components of the system is infinite, such as the Dicke model.[20–26]The Dicke model consists of a quantized single-mode field that couples to infinite qubits simultaneously.A recently noteworthy work shows that the thermodynamic limit may be no longer a limit.[27]When the system only consists of a qubit and a single-mode field, namely the Rabi model,[28–31]based on the trapped ion Yb+,it is found that the quantum phase transition of the Rabi model may still be observed without following the thermodynamic limit.However,this experiment still needs to be carried out under the condition of infinite frequency ratio between the qubit and field,[32]which restricts the perfect implementation and application of quantum phase transition.
In a recent theoretical study,[33]it was found that in a high-quality cavity driven by a squeezed light, a quantum phase transition occurs in the qubit collective system,and the process does not require ultrastrong coupling between each qubit and the field.By controlling the intensity of squeezed light, the system can realize the transition from the normal phase to superradiative phase.However, this study uses the standard mean field theory method, so it is difficult to extend and to determine the specific form and entanglement of the ground state.A very recent work[34]shows that the Jaynes–Cummings model induced by squeezed optical nonlinearity will exhibit a second-order quantum phase transition at a critical boundary.However, this work still needs to satisfy the condition that the qubit frequency is far larger than the field frequency.Whether there is a quantum phase transition in the squeezed Jaynes–Cummings model under the near-resonance condition remains unknown.In order to study the quantum phase transition and ground-state entanglement of the squeezed Jaynes–Cummings model under the near-resonance condition, we propose a diagonalization method,[35,36]which first uses the squeezing transformation and then uses the displacing transformation, to map the original Hamiltonian into a Hamiltonian with the form of an asymmetric Rabi model.The analytical ground state is in good agreement with the numerical solution.We show that the ground state undergoes a first-order quantum phase transition at a critical point linearly induced by squeezing strength.The ground state has the maximum qubit-field entanglement when the qubit-field coupling strength is large enough.The study of the squeezed Jaynes–Cummings model is interesting because it adds the deeper understanding of the Jaynes–Cummings model with squeezed light under near-resonance condition, reveals a new critical point,explains the role of squeezing strength in the first-order quantum phase transition,and provides a basis for related experiments.
2.Ground state
The Hamiltonian of the Jaynes–Cummings model with a squeezed light reads(ˉh=1)[34]
where?is the detuning of qubit andωis the detuning of the single-mode field, compared to the driving frequency of the squeezed light;λis the coupling strength between the qubit and field mode;Gis the strength of squeezed light;a?(a)is the creation(annihilation)operator of the field mode;
σ+=|e〉〈g|,σ?=|g〉〈e|, andσz=|e〉〈e|?|g〉〈g| are called the Pauli spin operators with|g〉and|e〉being the ground and excited states of the qubit,respectively.The eigenstates ofσzare|g〉and|e〉,i.e.,σz|e〉=|e〉andσz|g〉=?|g〉.The eigenstate of field mode is the Fock state|n〉(n ∈N).
Our main goal is to obtain the analytical ground state|g0〉and the ground-state energyEgof the Hamiltonian (1) of the system.In order to eliminate the two-photon terma?2+a2,we first use the method of squeezing transformation withsrepresenting a squeezing operator, i.e.,s=(a?2?a2), whereis the chosen squeezing parameter.Then, we obtain
Note thatHshas a similar mathematical form with that of the asymmetric Rabi model.[29]WhenG/ω=0.5,λ1=λg1=λ·+∞andλ2=λg2=λ·+∞.Therefore,λ1?λ2, which returns to the symmetric Rabi model and does not have a firstorder quantum phase transition atG/ω=0.5.
To remove the counterrotating-wave terms inHs,we then use a displacing transformation toHs,i.e.,
with
whereξis the displacement parameter to be determined.Then,we can divide the HamiltonianHuinto three parts
with
whereη=〈0|cosh[2ξ(a??a)]|0〉= e?2ξ2is the average of vacuum feild, andO(a?2,a2)=σz(g1?g2)ηξ(a?2+a2) is the higher-order term ofaanda?,which represents the doublephoton transition processes.Whenξand|λ(g1±g2)| are much smaller than the sum of qubit’s and field’s frequencies?+ω, where? ≈ω, higher-order termO(a?2,a2) can be neglected.Thus,Hu ?+.
Let parameterξsatisfy the following condition:
Then,the coupling between qubit and oscillator becomes
It is easy to find that|g〉|0〉is the ground-state eigenvector of the approximate transformed HamiltonianHu.Thus,we obtain the corresponding ground-state energy
The approximate ground state of the original Hamiltonian becomes
3.Quantum phase transition
In Fig.1, we plot the variation of ground-state energyEand its first derivative dE/dGwithG/ω.We find that the quantum phase transition of the system occurs at the critical pointGc==1.Only whenω ≥2G,ω′is a real number.Whenω<2G,ω′is an imaginary number.Eis continuous at the phase transition boundaryGc=1, while dE/dGis discontinuous, which reveals the first-order nature of this quantum phase transition.This result is different from the previous work,[34]where the squeezed Jaynes–Cummings model underwent a second-order quantum phase transition under the large-detuning condition.
When the qubit is weakly coupled to the field,η ?1.Then, we can approximately obtain the analytical solution ofξas follows:
In Fig.2,we compare the numerical and analytical solutions ofξ.The analytical solution ofξis in good agreement with the numerical solution under the near-resonance condition.WhenG=0.4ωandλ=0.3ω,the relative error between the numerical solution and the analytical solution ofξis only 2.7% at?=ω.Based on Eq.(15),Egapproximates to?(?+),which indicates that the ground-state energyEghas a quadratic dependence on the squeezing strengthG,and the main reason for this result is the two-photon excitation in the squeezing drive.When the limitGc=→1 andω+2G →2ω,ω ?2Gcan be considered as a small quantity,soξis approximated as
ForGc→1, ˉn →∞.This result is consistent with the numerical solution of ˉnshown in Fig.3(a),where ˉnis divergent.
We determine the entropy of a qubit subsystem by tracing out the freedom degree of field,
whereρqis the reduced density matrix of the system.The numerical solution ofSqis plotted in Fig.3(b).WhenGc→1,the entropySqof the system increases to its maximum when the ratio ofλ/ωincreases to 0.3.This indicates that the entanglement between the qubit and the field can reach its maximum in the ground state when the qubit-field coupling strength is large enough at the critical point.

Fig.1.Numerical solution of ground-state energy E versus G/ω under different λ/ω values:(a)0.01,(b)0.1,(c)0.5,(d)1.The first derivative dE/dG versus G/ω under different λ/ω values: (e)0.01,(f)0.1,(g)0.5,(h)1.These numerical solutions are given under resonance condition ? =ω.
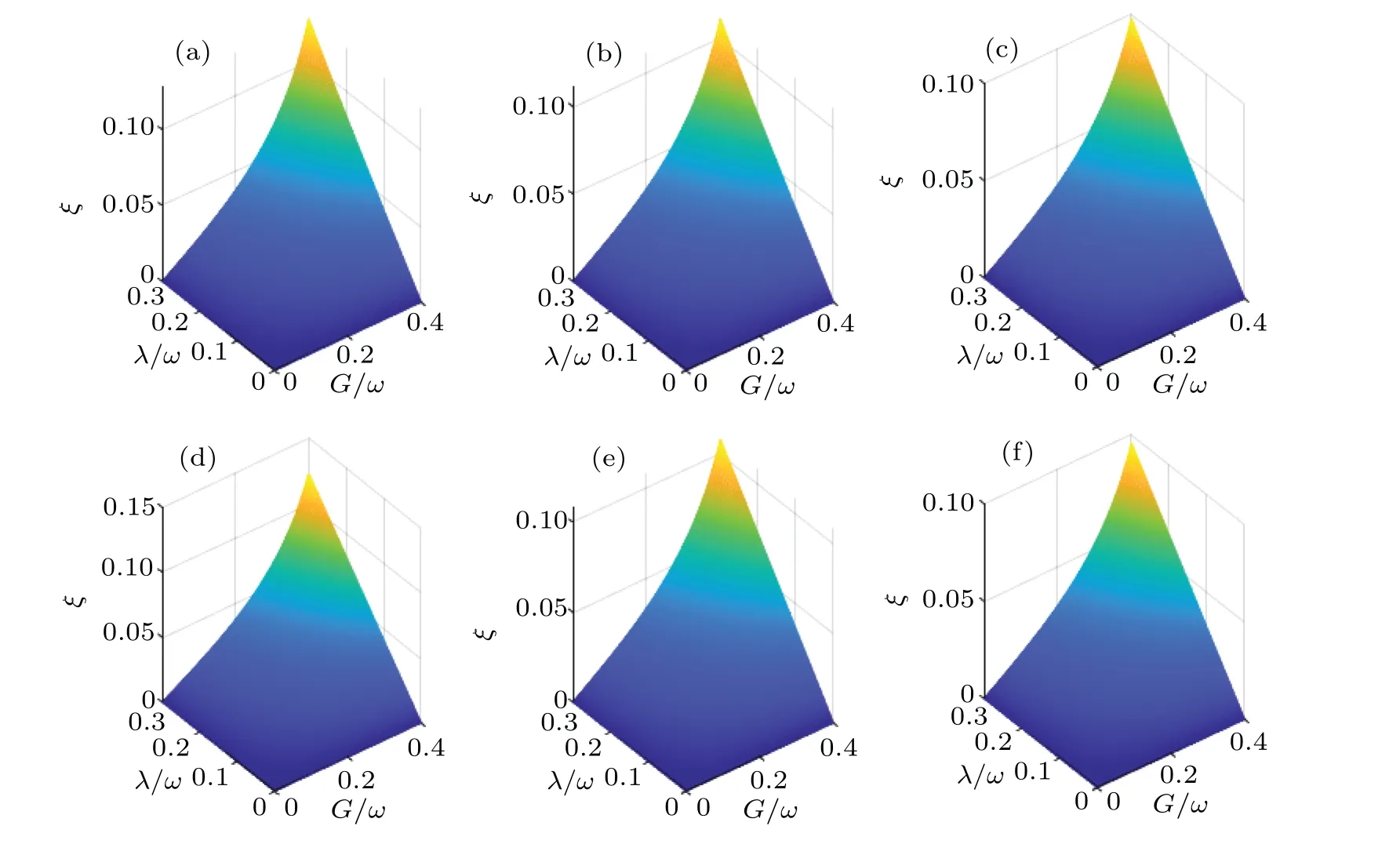
Fig.2.Numerical solution of ξ in Eq.(11)versus G/ω and λ/ω under different ?/ω values: (a)0.8,(b)1.0,(c)1.2.Analytical solution of ξ in Eq.(15)versus G/ω and λ/ω under different ?/ω values: (d)0.8,(e)1.0,(f)1.2.
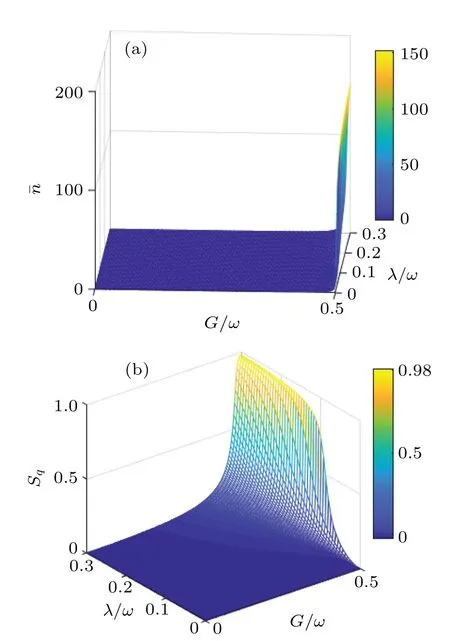
Fig.3.(a)Numerical solution of ˉn.(b)The entropy Sq obtained by the numerical simulation versus the coupling strength λ and the squeezing strength G.Both(a)and(b)are under the resonance condition of ? =ω.
The standard deviation of position quadratureX=a+a?for the field is
and the standard deviation of momentum quadratureP=i(a??a)is
For(?X)2·(?P)2≤1/4,the field mode is squeezed.?Xand?PversusG/ωandλ/ωare plotted in Fig.4.The analytical solutions of ?Xand ?Pcoincide with their corresponding numerical solutions under the resonance condition.WhenGc→1, ?Xincreases sharply while ?Pis slightly squeezed.Whenλ/ωis small,the condition of ?X·?P ?1 is satisfied,indicating that the ground state becomes a minimum uncertainty state.
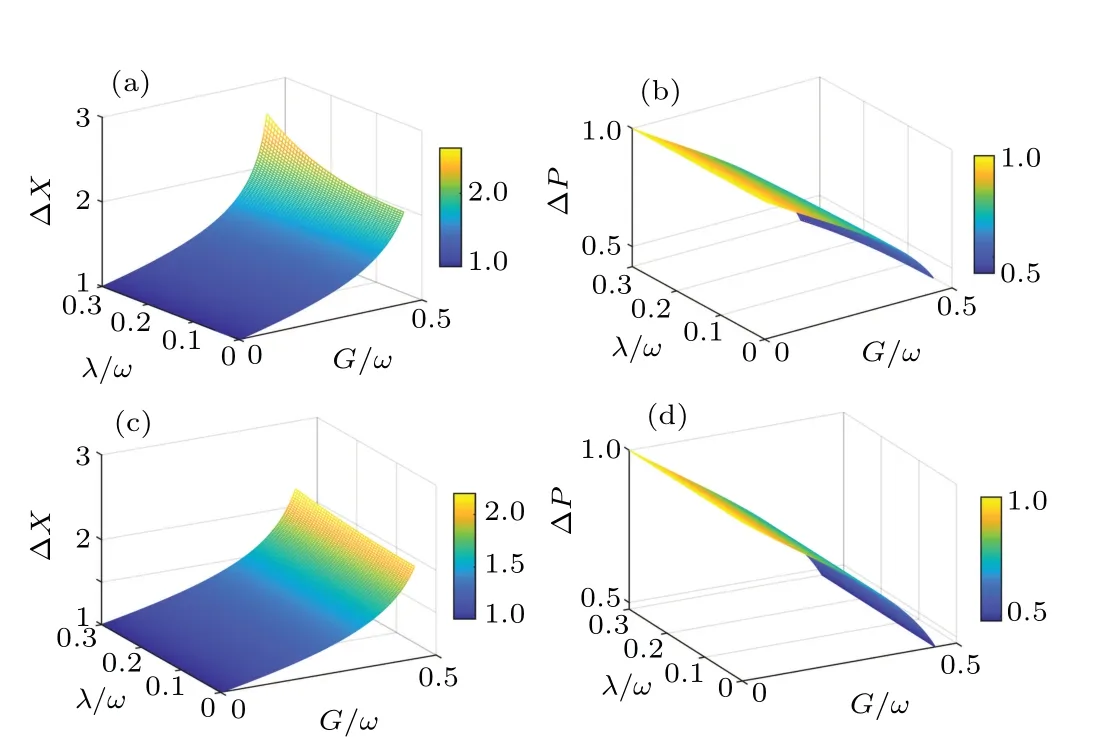
Fig.4.?X versus λ/ω and G/ω at ? =ω: (a)numerical solution,(c)analytical solution in Eq.(19).?P versus λ/ω and G/ω at ? =ω: (b)numerical solution,(d)analytical solution in Eq.(20).
4.Validity
In Fig.5, we compare the uniformity between analytical and numerical solutions of ground-state energyEgwithin the near-resonance regime? ?ωunder different squeezing strengthsG/ω.When the squeezing strength isG=0.2ω,even in the ultrastrong-coupling regimeλ=0.8ω,the analytical solution of the ground-state energyEgis in good agreement with the numerical solution under the near-resonance condition.Whenλ= 0.8ωandG= 0.2ω, the relative errors between the analytical solution and numerical solution at?=0.8ω,?=ω,and?=1.2ωare 2.2%,1.4%,and 0.9%,respectively.We plot the fidelityF=〈g0|gn〉 versusGandλunder the near-resonance condition in Fig.6, where|gn〉is the ground state obtained by numerical solution.The result shows that whenλ=0.1ωandG=0.2ω,a high fidelity withF>99%can be obtained.This means that with smallλandGvalues,|g0〉can be perfectly approximated as a ground state.
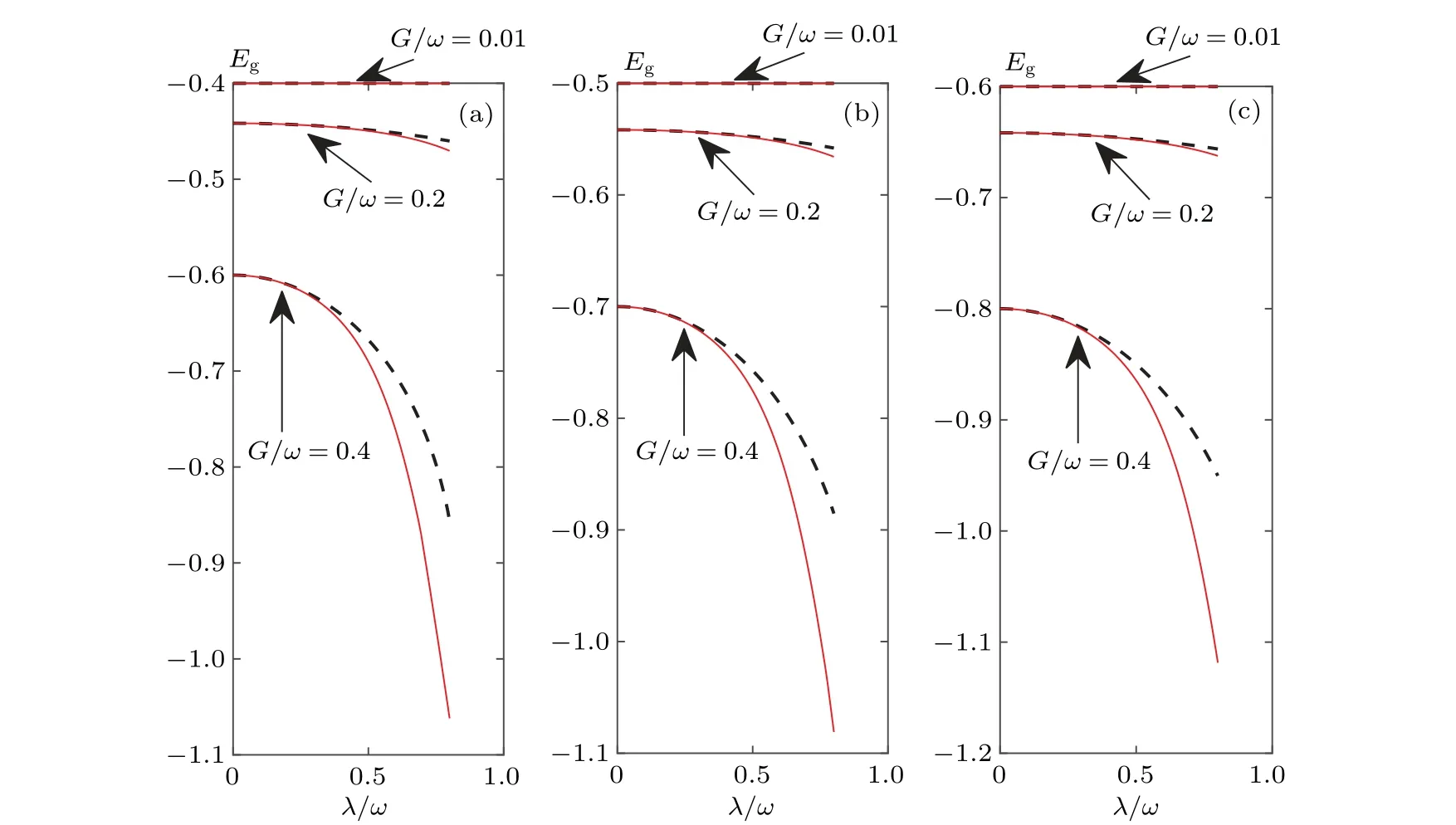
Fig.5.Ground-state energy by the transformation method Eg (black dotted line) and by numerical solution (red solid line) versus λ/ω and G/ω under the different ?/ω values: (a)0.8,(b)1.0,(c)1.2.
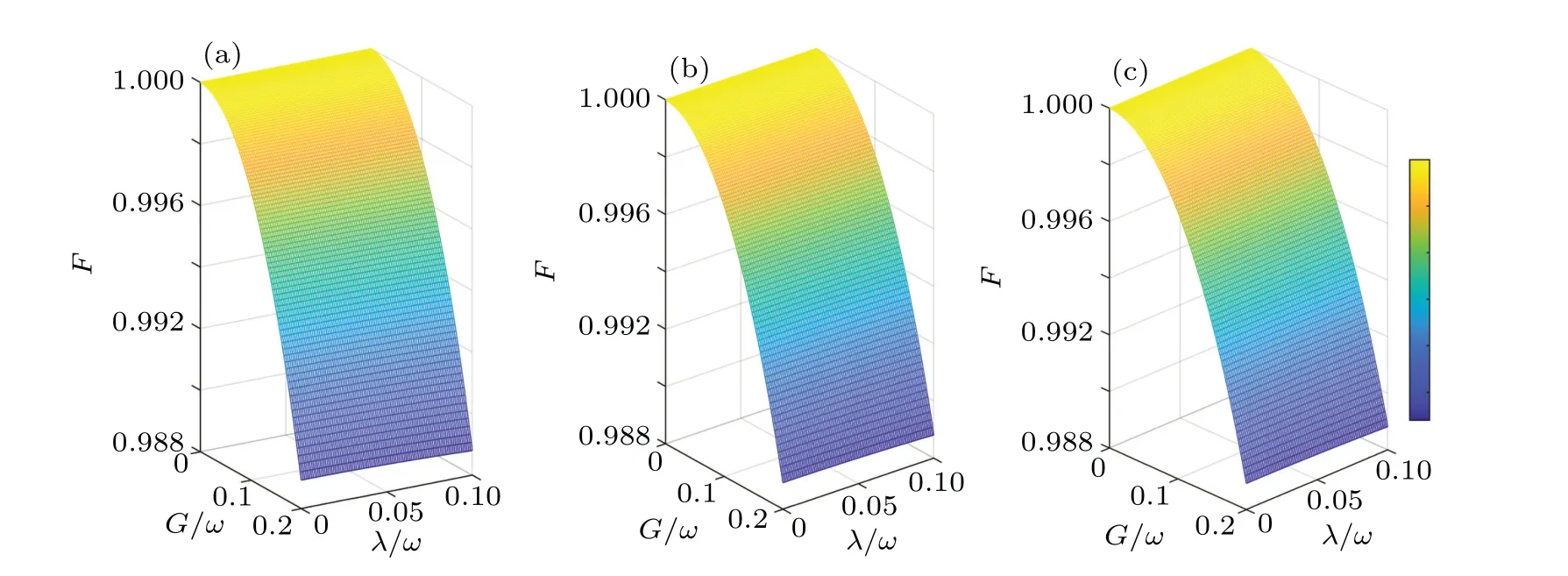
Fig.6.The fdielity F of the ground state versus λ/ω and G/ω with different ?/ω values: (a)0.8,(b)1.0,(c)1.2.These numerical solutions have a cutoff photon number of 200.
5.Conclusion
In summary,we have found the first-order quantum phase transition in the squeezed Jaynes–Cummings model within the near-resonance regime.We eliminate the non-integrable squeezing interaction by the special transformation method,and transform the original Hamiltonian into an asymmetric Rabi Hamiltonian.Our analytical ground state is in good agreement with the numerical solution under the nearresonance condition.When the qubit-field coupling strength is large enough at the critical point,the maximum entanglement in the ground state is obtained.In the future, we will extend this method to the multi-qubit Jaynes–Cummings model with a squeezed light to understand the effects of the increasing number of qubits on the first-order quantum phase transitions.
Acknowledgement
Project supported by the Natural Science Foundation of Fujian Province,China(Grant No.2021J01574).
- Chinese Physics B的其它文章
- First-principles calculations of high pressure and temperature properties of Fe7C3
- Monte Carlo calculation of the exposure of Chinese female astronauts to earth’s trapped radiation on board the Chinese Space Station
- Optimization of communication topology for persistent formation in case of communication faults
- Energy conversion materials for the space solar power station
- Stability of connected and automated vehicles platoon considering communications failures
- Lightweight and highly robust memristor-based hybrid neural networks for electroencephalogram signal processing

