Tolerance-enhanced SU(1,1)interferometers using asymmetric gain

Jian-Dong Zhang(張建東) and Shuai Wang(王帥)

School of Mathematics and Physics,Jiangsu University of Technology,Changzhou 213001,China

Keywords: SU(1,1)interferometer,asymmetric gain,Heisenberg limit,quantum Cramer–Rao bound

1. Introduction

In practical applications,the measurement of many physical quantities, such as temperature, concentration and magnetic field, can be transformed into phase estimation.[1–5]In view of this, optical interferometers are an important tool to realize precision measurements. A classical scheme deploys a linear interferometer fed by a single-mode coherent state;in turn, its phase sensitivity is bounded by the shot-noise limit 1/withNbeing the average photon number inside the interferometer. By employing exotic input states,the phase sensitivities of quantum schemes can break through the shot-noise limit and even reach the Heisenberg limit 1/N. On the other hand,nonlinear interferometers,also known as SU(1,1)interferometers,have also received a lot of attention. This kind of interferometer, making use of two nonlinear elements in lieu of two beam splitters in Mach–Zehnder interferometers, was first proposed by Yurkeet al.[6]and experimentally realized by Jinget al.[7]Due to the squeezing and entanglement introduced by nonlinear elements, SU(1,1) interferometers generally have advantages over linear interferometers in phase sensitivity.

In recent years, many schemes based on SU(1,1) interferometers were proposed. With coherent states as inputs,Plicket al.proved that the phase sensitivity of intensity detection can surpass the shot-noise limit in a lossless scenario.[8]Related to this,Marino and Xinet al.studied the phase sensitivities of intensity detection and parity detection in the presence of photon losses respectively.[9,10]With respect to coherent and squeezed vacuum states, Ou discussed the effects of photon losses on the phase sensitivity of balanced homodyne detection.[11]Further, Liet al. showed that the Heisenberg limit can be achieved by using balanced homodyne detection and parity detection without photon losses.[12,13]The schemes using other quantum states[14–17]and related experimental demonstrations[18–21]have also been studied.

In addition, many studies are committed to the modified SU(1,1) interferometers. Szigetiet al. showed a pumped-up SU(1,1)interferometer assisted by the pump beam.[22]Andersonet al.proposed a truncated SU(1,1)interferometer,which directly measure the state after the estimated phase with balanced homodyne detection.[23,24]Subsequently, Guptaet al.optimized this scheme and designed a tunable balanced homodyne detection.[25]A degenerate SU(1,1) interferometer and an SU(1,1)interferometer based on entanglement-assisted inputs have also been analyzed.[26,27]Konget al.reported a hybrid SU(1,1)interferometer,in which a beam splitter replaces the second nonlinear element[28]and recently we generalized this configuration.[29,30]More recently, Duet al. designed an SU(2)-in-SU(1,1) nested interferometer in experiment.[31]These schemes can efficiently improve the phase sensitivity or loss tolerance with respect to some specific inputs. The sensitivity limit given by quantum Fisher information can be also saturated. The detailed and comprehensive review can be found in Ref.[32].

For practical purposes, many of the above schemes analyzed the phase sensitivity in the presence of photon losses.However, almost no method is proposed to resist photon losses. In this paper,we report a modified SU(1,1)interferometer based on asymmetric gain.Two vacuum states are injected into the interferometer and on–off detection is performed at the output. The effects of internal and external losses on the phase sensitivity are analyzed.The asymmetric gain can improve the loss tolerance,which shows a feasible method to downplay the effects of photon losses.

2. Estimation scheme and optimal phase sensitivity

In Fig.1,we show the schematic of the modified SU(1,1)interferometer using asymmetric gain. Two vacuum states are used as the inputs and injected into the first optical parametric amplifier(OPA).After the OPA1,the two-mode squeezed vacuum states are prepared and pass through the estimated phaseθ. Subsequently,the states are recombined by the OPA2. Finally,we perform on–off detection at the two output ports. In our scheme, the phase and gain parameter of OPA1 (OPA2)are 0(π)andg1(g2),respectively.

The transformation relationship of OPA to the mode operators is given by

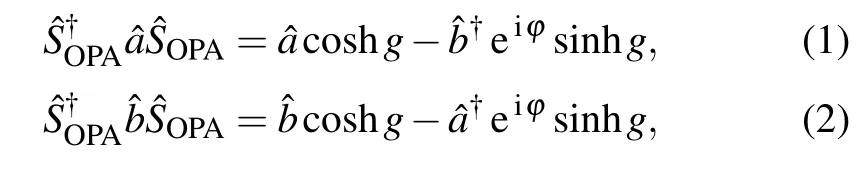
withg ∈{g1,g2}andφ ∈{0,π}. Further,the average photon number inside the interferometer is found to be

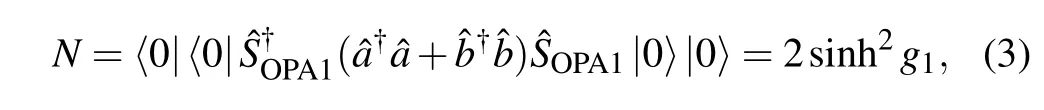
irrespective of the gain parameter of OPA2. This is because all devices after the estimated phase including OPA2 are considered as the detection. In addition, refer to Ref. [33], the quantum Cramer–Rao bound for our scheme turns out to be

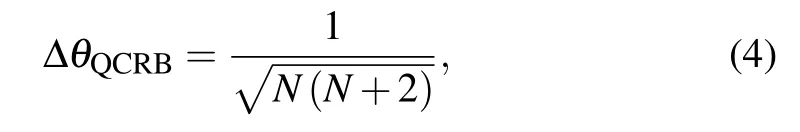
which is superior to the Heisenberg limit.

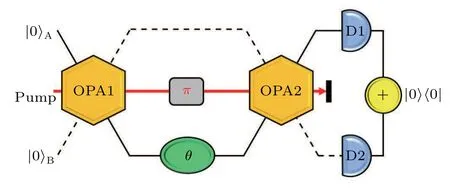
Fig.1. Schematic of estimation scheme based on a modified SU(1,1)interferometer. OPA,optical parametric amplifier;D,detector.

Here we calculate the phase sensitivity through the method of symplectic geometry.[34]Since the inputs are Gaussian states and all operations are Gaussian operations,we can write them as symplectic matrices in the phase space. The inputs, two vacuum states, are zero-mean and, as a result, all calculations can be completed by the covariance matrices.

For our scheme, the covariance matrix of the inputs is found to be

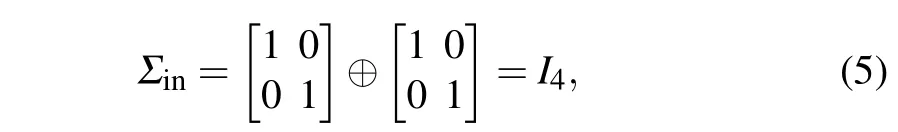
whereI4is the identity matrix.

The evolution matrix of the phase shift can be written as

and those of OPA1 and OPA2 are

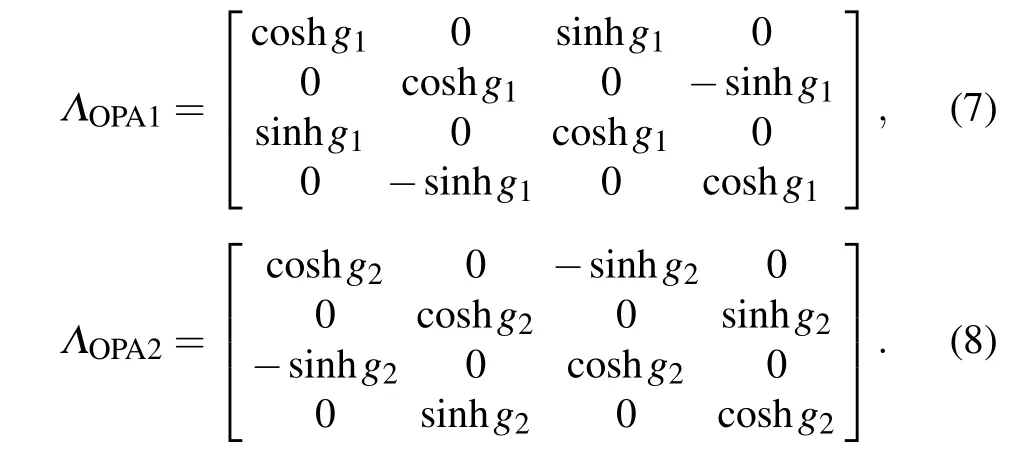
Using Eqs.(5)–(8),one can obtain the covariance matrix of the outputs through the following relationship:

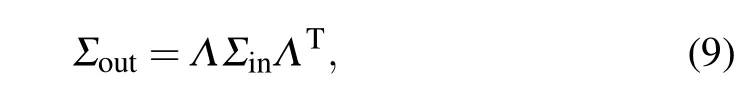
whereΛ=ΛOPA2ΛPSΛOPA1is the whole evolution matrix.

On–off detection is a simple photon-number detection,which records only zero-photon events. Accordingly, the expectation value of the detection operator equals the probability of zero-photon events. This can be calculated as[35]

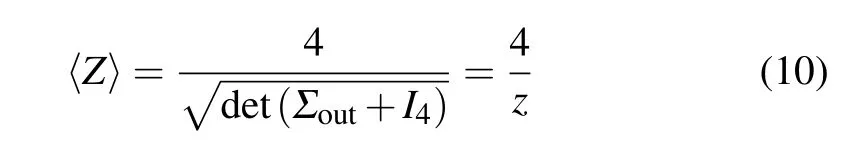
with

In particular,the expectation value sits at 1 when the estimated phase is 0.This is because,forθ=0,the whole interferometer is equivalent to identity operation and the outputs are always two vacuum states.

Using operator property〈Z2〉=〈Z〉and error propagation formula,we get the phase sensitivity

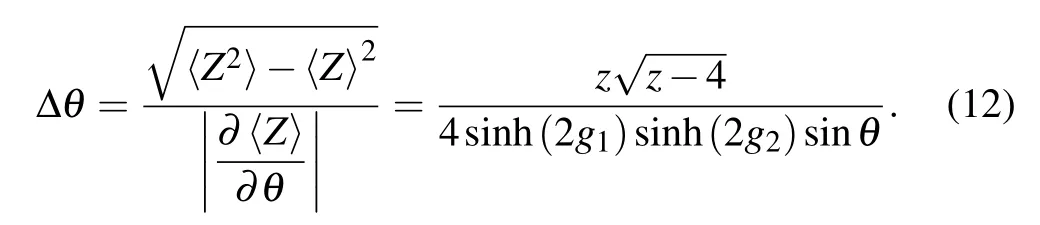
For a lossless scenario,we consider symmetric gaing1=g2=g. Based on Taylor expansions of cosine and sine functions approaching 0, cosθ ?1-θ2/2 and sinθ ?θ-θ3/6,we can obtain the optimal phase sensitivity

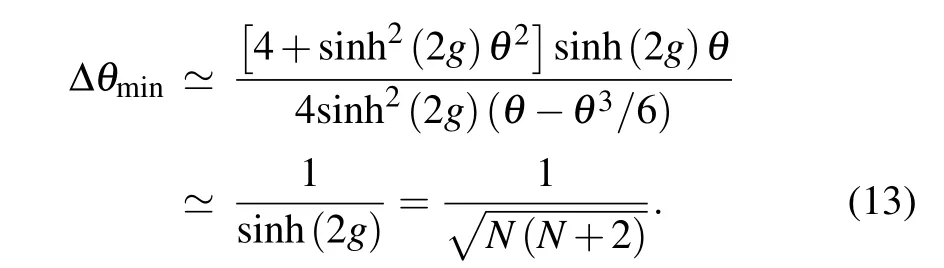
It can be found that the optimal phase sensitivity is equal to the quantum Cramer–Rao bound. This result suggests that symmetrical gain and on–off detection are the optimal detection strategy. For a small average photon number,the optimal phase sensitivity is superior to the Heisenberg limit. With the increase of the average photon number,the optimal phase sensitivity approximately equals the Heisenberg limit.

3. Phase sensitivity in the presence of photon losses

In a realistic scenario,photon losses are inevitable due to the collision between photons and air molecules or optical elements. According to the theory of quantum open systems,for the conservation of photon number,all the lost photons are assumed to enter the surrounding environment. Physically, this process can be modeled by placing two virtual beam splitters in the interferometer. Mathematically, the photon losses can be calculated through the use of Kraus operator. Upon leaving a lossy channel, the covariance matrixΣof a quantum state becomes

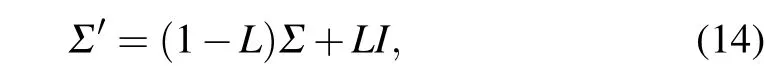
whereLis the lossy rate andIis the identity matrix.

Because OPAs in the SU(1,1) interferometer are nonlinear elements,the photon losses at different stages have different effects on the phase sensitivity. In what follows, we analyze the effects of internal and external losses,respectively.

3.1. The effects of internal losses

Internal losses refer to the photons that lost inside the SU(1,1)interferometer. Without loss of generality,we assume that the losses occur before the estimated phase. At this time,the covariance matrix of the outputs can be written as

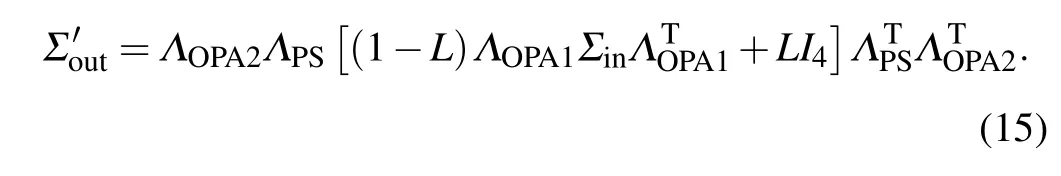
Further, the expectation value of detection operator is given by

with

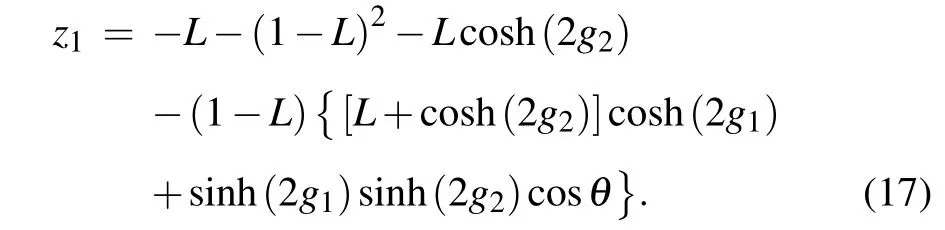
Using error propagation formula,the phase sensitivity can be obtained by

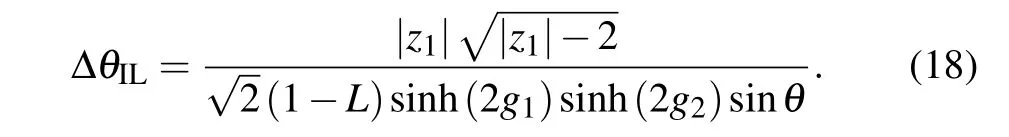
In this section,we also analyze the conventional SU(1,1)interferometer with symmetric gaing1=g2=g. Based on Eq.(18),the optimal phase sensitivity in the presence of internal losses can be calculated. For practical purposes, we consider the maximally tolerable lossy rate defined as the lossy rate for the optimal phase sensitivity degenerating to the shotnoise limit. When the internal lossy rate of the system exceeds this threshold,the optimal phase sensitivity is inferior to the shot-noise limit. In order to show the quantum advantage,the lossy rate of the system needs to be controlled below this threshold in the realistic detection.

Figure 2 shows the maximal tolerable lossy rate as a function of the gain parameter. It can be seen from the figure that the maximally tolerable lossy rate decreases with the increase of the gain parameter. That is,the low-photon scheme is more robust than the high-photon scheme. This is because that,for the same lossy rate,the entanglement between the two modes in the high-photon scheme is destroyed more seriously. Interestingly, the decrease in the maximally tolerable lossy rate is approximately linear. Overall,the estimation scheme is sensitive to internal losses. In the realistic detection,low lossy rate should be guaranteed as far as possible.

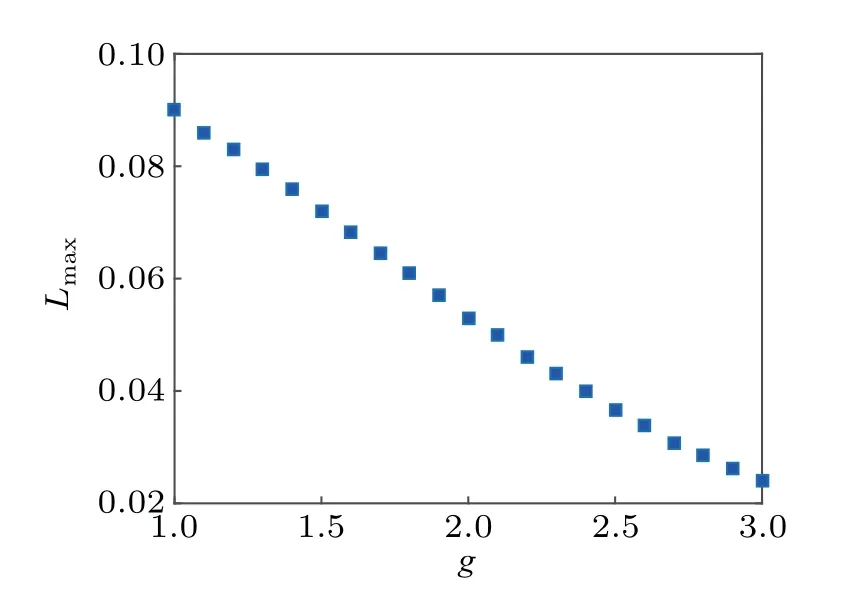
Fig.2. Maximally tolerable lossy rate Lmax against gain parameter g in the presence of internal losses.

3.2. The effects of external losses

External losses can be divided into preparation losses and detection losses. For our scheme,the inputs are vacuum states and, as a result, the preparation losses have no effect on the phase sensitivity. In the following,we merely consider the detection losses originating from imperfect detection efficiency.In the presence of external losses,the covariance matrix of the outputs can be written as

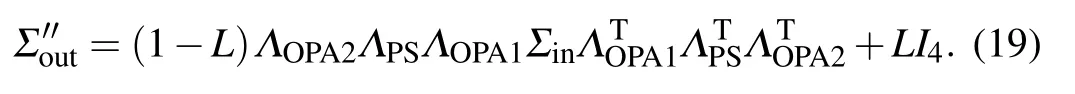
Further,the expectation value of the detection operator is given by

with

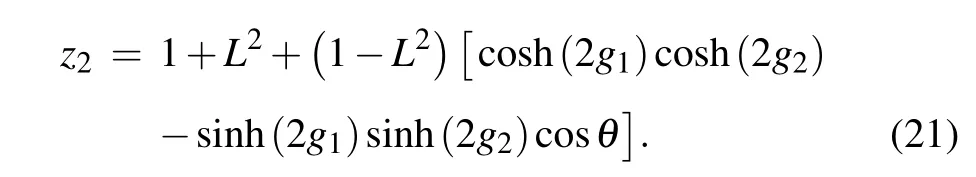
Through the use of error propagation formula, the phase sensitivity is found to be

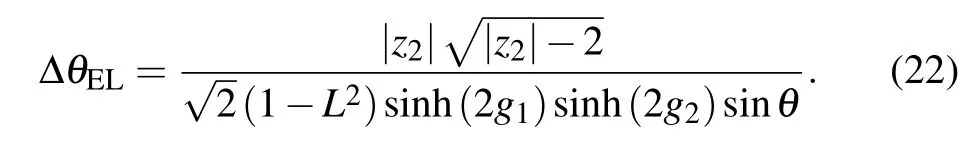
Now we turn our attention to the effects of external losses on the optimal phase sensitivity. In Fig.3,we give the dependence of the maximally tolerable lossy rate on the gain parameter. The results suggest that our scheme is very robust against external losses in that the loss tolerance can exceed 90%. In addition, the loss tolerance increases with the increase of the gain parameter. That is, the high-photon scheme is more robust than the low-photon scheme,which is contrary to the case of internal losses.

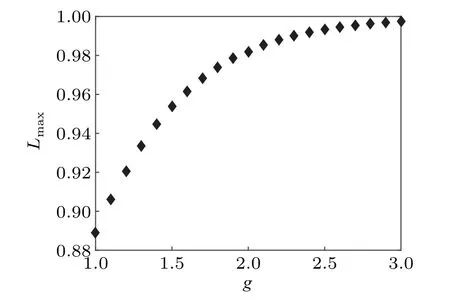
Fig.3. Maximally tolerable lossy rate Lmax against gain parameter g in the presence of external losses.

In fact, this phenomenon is not difficult to understand.Due to external losses, the component state|m,n〉in the outputs ∑cmn|m,n〉turns into|m′,n′〉. As long as the sum ofm′andn′is not equal to 0,the expectation value of detection operator will not be affected. With the increase of the average photon number, the probability ofm′+n′=0 decreases. Therefore,the high-photon scheme has strong tolerance,which originates from the property of on–off detection. In addition, the above results show different loss tolerance behaviors of internal losses and external losses. This is because the fact that external losses are linear whereas internal losses are nonlinear due to the amplification of OPA2.

4. Optimal asymmetric gain and enhancement of loss tolerance

In the previous sections,we analyzed the phase sensitivity of the conventional SU(1,1) interferometer without and with photon losses. Here we discuss the phase sensitivity of the modified SU(1,1)interferometer with asymmetric gain. In the lossless scenario, the SU(1,1) interferometer using symmetric gain has been proved to realize the quantum Cramer–Rao bound. On the other hand, our scheme is of strong tolerance with respect to external losses. Hence,we focus on the phase sensitivity with asymmetric gain in the presence of internal losses.

For given gain parameterg1and lossy rateL, one can determine the optimal gain parameterg2by minimizing the phase sensitivity. Figure 4 shows the optimal asymmetric gain differenceg2-g1as a function of the gain parameterg1.Since the tolerance of our scheme to internal losses is within 10%,we analyze the lossy rate in the same range. The results indicate that, for a small lossy rate, the optimal asymmetric gain difference increases at first and then decreases with increasing the gain parameterg1. When the lossy rate increases,the optimal asymmetric gain difference decreases with the increase of the gain parameterg1. In addition,for the gain parameter less than 1.5,the optimal asymmetric gain differences with different lossy rates are close. When the gain parameter is greater than 2,there is a distinct contrast among the optimal asymmetric gain differences with different lossy rates.

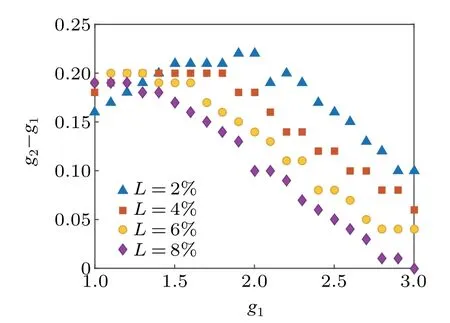
Fig.4. The optimal asymmetric gain differences g2-g1 against the gain parameter g1 with different lossy rates.

Here three points deserve mention. The first point is the reason why asymmetric gain is superior to symmetric gain in a lossy scenario. According to the theory of quantum parameter estimation, at the optimal working point, the phase sensitivity can generally reach the quantum Cramer–Rao bound if the operations before and after the estimated phase are reversed.For a lossless scenario, OPA2 completely undoes the operation on the inputs imposed by OPA1. However, in a lossy scenario,OPA2 no longer has such capability in the presence of symmetric gain. To obtain improved phase sensitivity,one can deploy asymmetric gain to restore the outputs to the inputs as much as possible. The second point is the reason whyg2is greater thang1, as shown in Fig. 4. A quantitative calculation is quite complicated and we show a qualitative analysis from a physical perspective. Indeed,OPA1 is a two-mode squeezer and the state inside the interferometer is a two-mode squeezed vacuum. Upon leaving a lossy channel, the resultant state can be expressed as an infinite mixture of two-mode squeezed Fock states|m,n〉.[36]For a low lossy rate,it is feasible that the gain of the anti-squeezer,OPA2,is slightly greater than that of the squeezer,OPA1.The action of OPA2 is divided into two parts;one part is used to offset the squeezing effect of OPA1 and the other part is used to partially convert the Fock state to vacuum. The third point is the reason why there are some jumping points in Fig. 4. As mentioned above, the resultant state becomes a definite mixed state with an equivalent mixed squeezing factorr ＜g1. For a given lossy rate,with the increase of gaing1,the squeezing factorris not a monotonic function since it consists of infinite weights.[36]That is,there is no simple positive correlation betweeng1andr.Overall,the optimal asymmetric gain is a trade-off between the degrees of squeezing and mixing,resulting in some jumping points.

In order to quantify the enhanced tolerance arising from asymmetric gain,we define the enhancement factor as follows:

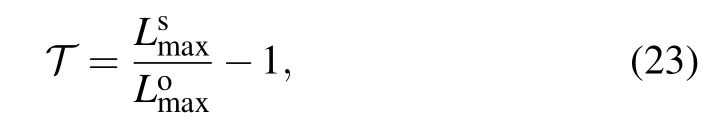
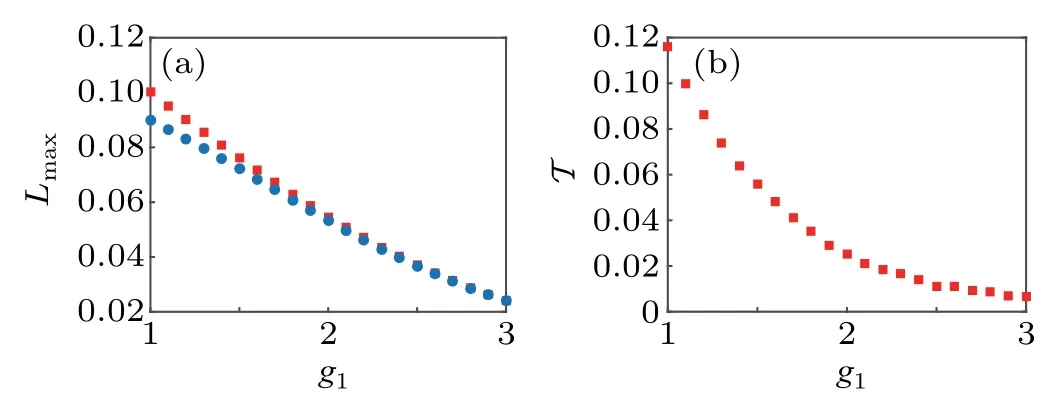
Fig.5. (a)The maximally tolerable lossy rates with the optimal asymmetric gain(red squares)and symmetric gain(blue circles)against the gain parameter g1. (b)Enhancement factor T against the gain parameter g1.

In Fig. 5, we show the maximally tolerable lossy rates and enhancement factor against the gain parameterg1,respectively. One can find that the maximally tolerable lossy rate with the optimal asymmetric gain is superior to that with symmetric gain. The corresponding enhancement factor varies roughly from 1% to 12% and decreases with the increase of the gain parameter, as shown in Fig. 5(b). This result verifies that asymmetric gain is a feasible method to resist photon loss.Although this improvement is not remarkable,our results provide an instructive idea for other estimation schemes using SU(1,1) interferometers. In addition, it is not difficult to understand that the enhancement factor is small for a high gain.After a lossy channel,there are infinitely incoherent two-mode squeezed Fock states|m,n〉.[36]Only whenn=mis it possible for OPA2 to convert the state to two vacuum states. For a high gain, the probability of large values ofnandmincreases and that ofn=mdecreases. At this point, the function of OPA2 becomes so weak that it can hardly provide the enhancement of loss tolerance.

5. Conclusion

In summary, we proposed an estimation scheme using a modified SU(1,1)interferometer. The inputs are two vacuum states and on–off detection is implemented at the output. In a lossless scenario,the optimal phase sensitivity with symmetric gain can surpass the Heisenberg limit and reach the quantum Cramer–Rao bound. For practical purposes, we analyzed the effects of internal and external losses on the phase sensitivity. The results suggest that our scheme is sensitive to internal losses but extremely robust against external losses. The use of asymmetric gain generally improves the loss tolerance and the physical interpretation is given. Our method provides a feasible idea for resisting photon losses, which may take a step towards practical quantum metrology.

Acknowledgments

Project supported by Leading Innovative Talents in Changzhou (Grant No. CQ20210107), Shuangchuang Ph.D Award (Grant No. JSSCBS20210915), Natural Science Research of Jiangsu Higher Education Institutions of China(Grant No.21KJB140007), and the National Natural Science Foundation of China(Grant No.12104193).