Characterizing entanglement in non-Hermitian chaotic systems via out-of-time ordered correlators
Kai-Qian Huang(黃愷芊) Wei-Lin Li(李蔚琳) Wen-Lei Zhao(趙文壘) and Zhi Li(李志)
1Guangdong Provincial Key Laboratory of Quantum Engineering and Quantum Materials,SPTE,South China Normal University,Guangzhou 510006,China
2School of Science,Jiangxi University of Science and Technology,Ganzhou 341000,China
3Guangdong-Hong Kong Joint Laboratory of Quantum Matter,Frontier Research Institute for Physics,South China Normal University,Guangzhou 510006,China
4Guangdong Provincial Key Laboratory of Nuclear Science,Institute of Quantum Matter,South China Normal University,Guangzhou 510006,China
Keywords: out-of-time ordered correlators,quantum entanglement,non-Hermiticity
1. Introduction
Out-of-time ordered correlators (OTOCs),C(t) =-〈[A(t),B]2〉, have attracted extensive investigations in the field of gravity physics,[1-3]quantum chaos[4-6]and quantum information.[7-9]Growth of OTOCs characterizes the spread of local information over many degrees of freedom. For chaotic systems, OTOCs exhibit exponential dependence on time with growth rate being determined by the Lyapunov exponent.[1]In addition, OTOCs constitute a robust alternative to measure information scrambling, as it can be detected by nuclear magnetic resonance systems.[10]More importantly,since OTOCs are related to the second R′enyi entropy[11-13]and quantum Fisher information,[10]quantum entanglement can be indirectly reflected by the measurement of OTOCs.
Non-Hermitian physics has been accepted as a complement of traditional quantum physics. In has been found that Hamiltonian with parity-time(PT)symmetry owns real eigenspectra.[14-16]Such a fascinating feature motivates research in optical waveguides,[17-27]cold atom systems,[28-32]Floquet systems,[32-42]etc. In particular, a lot of exotic phenomena have been found in kicking systems (systems subject to periodical pulses) withPT-symmetry. For example, the quantum state of aPTkicked particle will evolve to one of the localized quasieigenstate (QES) with complex quasieigenvalue (QEV).[37]This localization can be destroyed by nonlinearity-induced self-interaction, which leads to superexponential growth of the mean energy, i.e.,〈p2〉=exp[exp(αt+β)].[40]Interestingly,the non-Hermitian kicking potential can protect the quantum coherence in chaotic systems since the quantum state evolves to the localized QES with maximum imaginary part of the QEV.[41]Recent investigation has reported the quantized response of OTOCs to thePTsymmetric kicking potential.[42]
So far, the characterization of the entanglement with OTOCs in non-Hermitian systems is still an open problem. In this work, we investigate it via a bipartite system withPTsymmetric kicking potential. We find that, in the Hermitian case,the OTOCs increase in a power law of time. Intriguingly,when the non-Hermitian driving strength is strong enough,the growth of OTOCs is suppressed and the freezing of OTOCs occurs. The linear entropy increases from zero to almost unity with time in the Hermitian case,which indicates entanglement production. However, the non-Hermitian driving can effectively suppress the growth of linear entropy. We further investigate the long-time averaged value of both OTOCs and linear entropy. Our result shows that there is a turning point where both the time-averaged OTOCs and linear entropy exhibit a sharp decrease from the plateau,thus the occurrence of disentanglment is demonstrated. More interestingly, the transition point is in the vicinity of thePT-symmetric breaking point.The paper is organized as follows.In Section 2,we present the model. Section 3 shows the result of the OTOCs and entanglement.The physics mechanism is given in Section 4. Summary is presented in Section 5.
2. Model
The Hamiltonian of the bipartite system reads


For simplicity,we consider the case that the two particles are identical, i.e.,K1=K2=Kandλ1=λ2=λ. In fact, we have investigated the case thatλ1=0 andλ2varies. There is no essential difference between the two cases. In numerical simulation, we set the initial state as the product state of the ground stateψ(x1,x2,0)=2cos(πx1/L)cos(πx2/L)/L.
3. Characterizing entanglement with OTOCs
3.1. OTOCs dynamics


Fig.1. OTOCs versus time,corresponding to(a)C11=-〈[p21(t),p21]2〉and (b) C12 = -〈[p21(t),p22]2〉. The dashed lines indicate the fitting function of the form C11 ∝t4 (C12 ∝t4). Other parameters are K =5,ˉheff=0.25,μ =0.5,and L=2π.
3.2. Entanglement entropy
During the process of QCC, the entanglement between the subsystems grows due to the interaction. To measure the entanglement,we investigate the linear entropy of the system as follows:

With the generation of entanglement, a pure state evolves to a mixed one,during which the value ofSincreases from zero to almost unity[53,54][see Fig. 2(a) forλ=0]. This process is accompanied by the disappearance of quantum coherence.Therefore, the decoherence effect induced by interaction results in the QCC of diffusion dynamics.
Intriguingly,for a specificλ,the linear entropy increases during the initially short time interval [see Fig. 2(a) forλ=0.01], which indicates that the quantum state is a mixed one.After the initial growth, the linear entropy decreases to a saturation value and the quantum state becomes actually a pure state. This clearly demonstrates that the quantum coherence,which is initially destroyed, will partially revive due to the non-Hermitian kicking potential. Therefore, under the effect of non-Hermitian kicking potential,an initially pure state becomes mixed during short time evolution, and eventually evolves to a pure state. This process corresponds to the transition from the decoherence to coherence recovery and entanglement production to disentanglement as time evolves. Note that the decreasing process of the valueSto saturation indicates the back flow of information from the environment to the system.[55]

Fig.2. (a)Linear entropy S versus time withμ=0.5. (b)The averaged value〈S〉t in the parameter space(λ,μ). Other parameters are the same as those in Fig.1.
Moreover, to clearly show the entanglement with different parameters, we further numerically investigate the longtime average ofS,i.e.,

by varying the interaction strengthμand the non-Hermitian kicking strengthλ. Figure 2(b) shows that, for extremely small value ofμ,Sis almost zero,and the reason is that weak interaction is not enough to thermalize the system.[56]With the increase of interaction,Sincreases due to the decoherence and quantum entanglement. However, for a certain value ofμ,Sdecreases with largeλ. This demonstrates that,though the interaction leads to quantum entanglement and decoherence,the non-Hermitian kicking potential results in the decrease of entanglement and prevents the decoherence,mitigating the effect of interaction.
3.3. Featuring PT-symmetric breaking with OTOCs and linear entropy

Figure 3(b)shows that as the value ofλincreases,〈C11〉tand〈C12〉tstay at a plateau and then decrease in a power law.Moreover,the turning point is aboutλ=10-3,which is equal toλc. This also shows that the QESs with non-zero complex QEVs contribute to the suppression of the OTOCs increase.The discovery that the non-Hermitian kicking potential leads to the saturation of OTOCs opens a new prospect in the field of information scrambling for conventional theory,believing that the many-body localization induces the logarithmic growth of TOCs.[57]
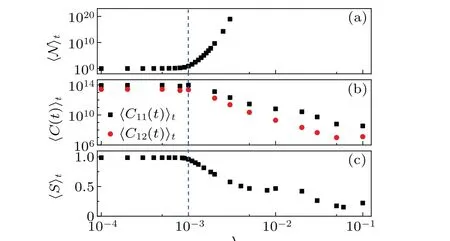
Fig. 3. Dependence of 〈N〉t (a), 〈C11〉t (squares) and 〈C12〉t (circles)(b),and〈S〉t (c)on λ. The parameters are the same as those in Fig.1.
In addition, our numerical results show that the value ofSis equal to almost unity for〈S〉tsmaller than a critical value, beyond which the value of〈S〉tis less than unity,which indicates the coherence recovery and disentanglement.Moreover, it gradually decreases with the increase ofλ[see Fig. 3(c)]. This indicates that the appearance of the QES with complex QEV contributes to the recovery of coherence. The recovery will be more salient with stronger non-Hermitian kicking potential,and the saturation of OTOCs decreases with the increase ofλ[see Fig. 1]. Thus, the above findings again prove that the OTOCs are closely relevant to entanglement,[9-12,58-66]even in the non-Hermitian case.
4. Physics mechanism
Previous research suggests that in a non-Hermitian system, the inherent physics of the localization of the state is such that the quantum state evolves to one of the eigenstates of the Floquet operator.[37,41]We also investigate the QESs and QEVs of the Floquet operator. The eigenequation of the Floquet operator reads

whereNis the norm of|ψ(t)〉. The numerical results(Fig.4)show that the fidelity of most QESs is quite small and only one of them is approximately 1, whose imaginary part of QEV is maximum. This indicates that the dynamically evolved state evolves to the QES with the maximum imaginary part of the QEV.Furthermore,we compare the two states. It can be seen that both of them are localized states and they are in good agreement. All these indicate the reason of the localization such that the quantum state evolves to the localized QES with maximum imaginary part of QEV.
Then let us consider the case ofλ >λc. Since interaction will lead to decoherence and entanglement between the two subsystems,both OTOCs and linear entropy increase versus time at the beginning. The corresponding quantum state evolves into a mixed state. However, as time goes by, the effect of non-Hermitian kick gradually becomes apparent. The eigenstate with the maximum imaginary part of the eigenvalue begins to dominate the dynamical behavior of the whole system,where localization has been induced and,simultaneously,the increase of OTOCs and linear entropy has been suppressed.Finally, the two particles disentangle partially, and the quantum state eventually evolves to a pure state.

Fig. 4. (a) The fidelity F between the dynamically-evolved state and the QESs versus the imaginary part of the QEV.The dot marks the QES with F ≈1. (b) Comparison of the probability density distribution in energy space between the dynamically-evolved state (solid curve)and the QES(dashed curve)with F ≈1. The parameters are t =300,λ =0.1. Other parameters are the same as those in Fig.1.
5. Summary
We have investigated the quantum entanglement in a bipartite non-Hermitian kicking system. In the Hermitian case,the OTOCs,bothC11andC12,exhibit the power-law increase with time. In the non-Hermitian case, the growth of OTOCs can be suppressed by the non-Hermitian kicking potential.The linear entropy increases quickly to unity in the Hermitian case. For strong enough non-Hermitian driving strength, the growth of the linear entropy is suppressed. More importantly,we find that, with the increasing non-Hermitian strength, the long-time averaged values of both OTOCs and linear entropy have the same transition point where they exhibit the sharp decrease from the plateau,demonstrating the disentanglment.This indicates that the OTOC can characterize entanglement.The reason is that there exist localized QESs with complex QEV in thePT-symmetric broken regime. The system will evolve to the localized QES with maximum imaginary part of the QEV,leading to the suppression of the increase of OTOCs and linear entropy. Our work gives an insight into quantum information,quantum communication and other related fields.
Acknowledgements
W. Zhao was supported by the National Natural Science Foundation of China (Grant No. 12065009) and Science and Technology Planning Project of Ganzhou City(Grant No. 202101095077). K. Q. Huang and Z. Li were supported by the National Natural Science Foundation of China(Grant Nos.11704132,11874017,and U1830111),the Natural Science Foundation of Guangdong Province,China(Grant No.2021A1515012350),and the KPST of Guangzhou(Grant No.201804020055).
- Chinese Physics B的其它文章
- Erratum to“Accurate determination of film thickness by low-angle x-ray reflection”
- Anionic redox reaction mechanism in Na-ion batteries
- X-ray phase-sensitive microscope imaging with a grating interferometer: Theory and simulation
- Regulation of the intermittent release of giant unilamellar vesicles under osmotic pressure
- Bioinspired tactile perception platform with information encryption function
- Quantum oscillations in a hexagonal boron nitride-supported single crystalline InSb nanosheet

