Dynamical quantum phase transition in XY chains with the Dzyaloshinskii–Moriya and XZY–Y ZX three-site interactions
Kaiyuan Cao(曹凱源) Ming Zhong(鐘鳴) and Peiqing Tong(童培慶)
1Department of Physics and Institute of Theoretical Physics,Nanjing Normal University,Nanjing 210023,China
2Jiangsu Key Laboratory for Numerical Simulation of Large Scale Complex Systems,Nanjing Normal University,Nanjing 210023,China
Keywords: dynamical quantum phase transition,gapless phase,asymmetry excitation spectra
1. Introduction
Quantum phase transitions (QPTs) are one of the most significant phenomena in quantum many-body physics.[1,2]It is characterized by a nonanalytic behavior of some physical observable at a quantum critical point due to the change of the external control parameter. Recently,the dynamical quantum phase transitions(DQPTs)that in the quantum many-body systems have attracted extendedly both the theoretical[3–31]and experimental[32–37]interests. Unlike the QPTs driven by the external control parameters, the DQPTs describe the nonanalytic behavior of the Loschmidt echo (LE) during the time evolution, where a common protocol for driven a system out of equilibrium is called quantum quench. In many cases, the DQPTs are found to have a strong connection with the QPTs. The DQPTs are present in the cases of sudden quenches crossing the quantum critical points[3,4]and the topology changes,[5,8]although it is also found that the DQPTs occur in the cases of quenches without crossing any quantum critical point.[6,12]Therefore,it is still an open and debated issue whether the quench crossing the critical points of QPTs is a necessary condition to induce a DQPT.[22,27]
Up to now, many works have investigated the quench from gapped phase to gapped phase,whereas few studies have focused on the case of quench from the gapless phase. The gapless phase is of general existence in the quantum systems,such as theXYchain with the Dzyaloshinskii–Moriya (DM)interaction,[38–41]theXYchain withXZY–YZXtype of threesite interactions[42,43]and Kitaev model.[44]Unlike the case of the gapped phase, the ground states of the system in the gapless phase corresponds to the configuration where all the states with negative excitation spectra are filled and nonnegative are empty.[45–47]Recently, Cheraghi and Mahdavifar studied the DQPTs in the quantum Ising chain with DM interaction.[16]They only considered the case of quench from gapped phase to gapped phase and did not consider the quench from the gapless phase,so that they concluded that the DM interaction does not affect the DQPT.In a recent paper,[27]the authors studied the DQPTs in theXYchain with DM interaction in the alternating external transverse field. They also did not discuss the case of quench starting from the gapless phase, because they said that it is difficult to study the initial condition in the gapless phase in their models.[27]Therefore, it is still unknown when the quench is from the gapless phase.
Recently, Jafari has studied the DQPTs in the extendedXYchain withXZX+YZYtype of three-site interaction in the staggered transverse field.[22]He found that the DQPTs may not occur when the quench is from the gapped phase to gapless phase. The model has the gapless phase due to the staggered external field and the quasiparticle excitation spectra are symmetrical.[22]In this paper,we investigate the DQPTs in the extendedXYchains with DM interaction andXZY–YZXtype of three site interactions. Both the models have asymmetrical quasiparticle excitation spectra(εk/=ε-k),which are different from the model in Ref.[22].We study all possible situations of ground states of pre-quench Hamiltonian and obtain the general expression of LE for the systems with gapless phases(see Section 2). This allows our discussion to be generalized to the general quantum spin models. For the homogeneous system,the LE can be given byL(t)=∏k>0Lk(t),whereLk(t)equals unity corresponding to the quasiparticle excitation spectra of pre-quench Hamiltonian satisfyingεk·ε-k <0 in the momentum subspacek >0. Therefore,we obtain general conditions for the occurrence of DQPTs. In Sections 3 and 4,we discuss the behaviors of DQPTs for two extendedXYchains by given numerical results. It is found that the DQPTs may not occur in the quench across the quantum phase transitions regardless of whether the quench is from the gapless phase to gapped phase or from gapped phase to gapless phase. A brief conclusion is given in Section 5.
2. Models and DQPT
We consider two kinds of the extendedXYchains (with periodic boundary) in a transverse field: one with the added DM interaction and the other with addedXZY–YZXtype of three-site interaction. The Hamiltonian is written as




Fig.1. (a)The typical phase diagram of the XY chain with DM interaction in the (h,γ) plane for D=0.2. (b) Three typical quasiparticle excitation spectra εk for points A,B,and C in(a). (c)The typical phase diagram of the XY chain with XZY–YZX type of three-site interaction for ξ =0.5. (d)Three typical εk for points A,B,and C in(a). Regions CP,PM,FMx and FMy between the solid lines correspond to the gapless chiral phase, gapped paramagnetic phase, gapped ferromagnetic phase along x direction and gapped ferromagnetic phase along y direction,respectively.The orange areas denote the negative quasiparticle excitation spectrum intervals(εk <0).
In Figs.1(a)and 1(c),we show the phase diagrams in the(h–γ)plane for theXYchain with DM interaction(D=0.2)[47]andXZY–YZXtype of three-site interaction (ξ= 0.5),[48]respectively. Both the phase diagrams consist of four parts[see Figs. 1(a) and 1(c)]: gapless chiral (CP) phase, gapped paramagnetic(PM)phase,gapped ferromagnetic phase alongx(FMx) direction, and gapped ferromagnetic phase alongy(FMy)direction,where for gapless CP phase,εk <0 for somek, but for gapped phases,εk >0 for allk. In Figs. 1(b) and 1(d),we show three typical excitation spectra for points A,B,and C(see Figs.1(a)and 1(c))for theXYchain with DM interaction(D=0.2)andXZY–YZXtype of three-site interaction


3. The DQPT in the XY chain with DM interaction
For the quench from theH(h0,γ0) toH(h,γ), we define the domain?(h0,γ0)in the plane(h,γ),where the conditions(17) and (18) are satisfied. The domain?(h0,γ0) covers all the parameters of the post-quench Hamiltonian, in which the DQPT will occur for the quench from(h0,γ0). In the following,we discuss the cases of quenches from the gapless phase and the gapped phase,respectively.
3.1. Quench from the gapless phase
First, we consider the case of quench from the gapless phase. As a typical example, Fig. 2(a) shows the domain?(h0= 0.5,γ0= 0.2) for the quench from the gapless CP phase, where the domain is shown as the red region. It can be seen that the domain?(h0=0.5,γ0=0.2)does not cover all the areas of the PM,FMxand FMyphases,and also covers a part of the area in the CP phase. This means that the DQPT may occur for the quench within the gapless CP phase, and may not occur for the quench from the CP phase to the PM,FMxand FMyphases.
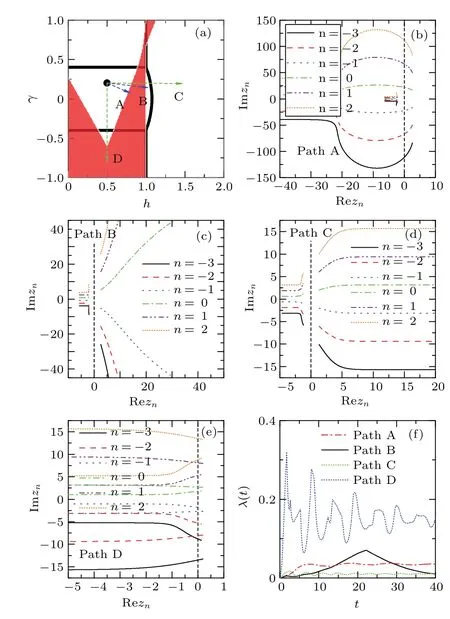
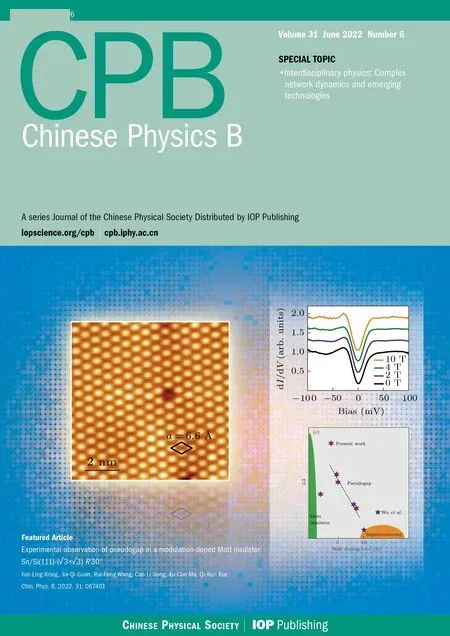
Fig.2. (a)Domain ?(h0,γ0)(the red region)covering the post-quench Hamiltonian parameters where the DQPTs appear for the quench from the initial points(h0,γ0). (b)–(e)The Fisher zeros for the quench paths A–D shown in(a). (f)The corresponding rate functions for the quench paths A–D.
To show the behaviors of DQPTs more clearly,we show four examples of the Fisher zeroszn(k)in Figs.2(b)–2(e)for the quench paths A–D marked in Fig.2(a),and the corresponding rate functions are given in Fig.2(f). The paths A and B are within the CP phase, and the paths C and D are from the CP phase to the PM phase and FMyphase,respectively. It should be noticed that all the Fisher zeros for the paths A–D are separated into two parts,because those wave vectors corresponding toεk·ε-k <0 do not contribute to the Fisher zeros for the quench from the gapless CP phase. For the quench path A,one branch of the Fisher zeroszn(k) is seen to intersect with the imaginary axis in the complex time plane.However,for the quench paths B and C,the Fisher zeroszn(k)have no intersection with the imaginary axis. While for the quench path D,all two branches of Fisher zeroszn(k)will intersect with the imaginary axis. Meanwhile,for the quench paths A and D,we can find the corresponding cusp-like peaks of the rate functions at the critical times of the DQPTs [see Fig. 2(f)], which are in good agreement with the intersections between the Fisher zeros and the imaginary axis. However, for the quench paths B and C,the rate functions are smooth curves.
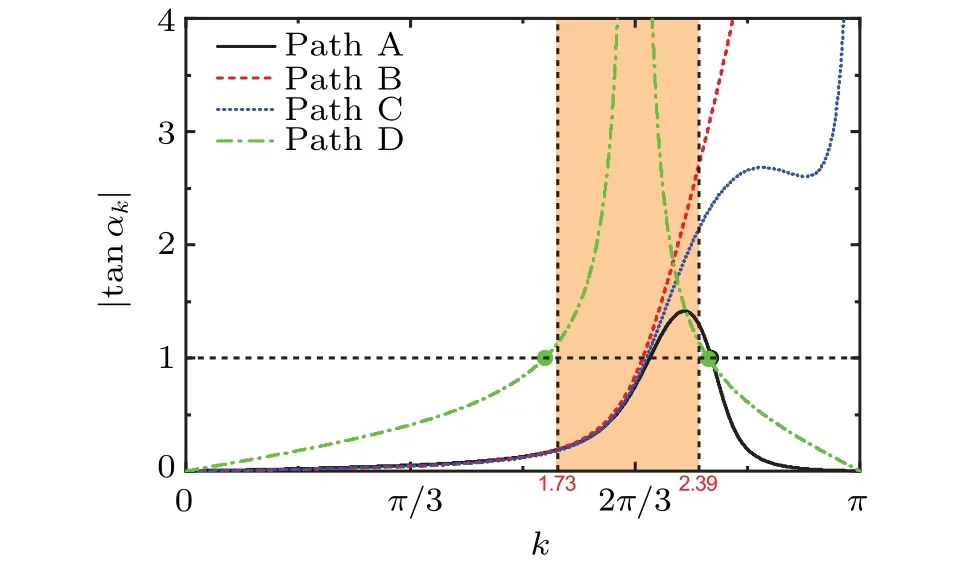
Fig.3. Values of|tanαk|for the paths A,B,C,and D in Fig.2(a),respectively. The orange block denotes the wave vectors k corresponding to εk <0.
To understand the reason of the behavior of DQPT for the quench from the gapless phase,we draw|tanαk|as a function ofkin Fig. 3 for the quench path A to D, respectively. The wave vectors intervalk ∈(1.73,2.39),in whichεk <0 of the pre-quench HamiltonianH(h0=0.5,γ0=0.2), is marked by the orange block. According to Eqs.(17)and(18),the DQPT will occur when|tanαk| reach 1 at the critical wave vectors outside the orange block. For the path A, it can be seen that there are two wave vectors satisfying|tanαk|=1, but one is inside the orange block and the other is outside. Therefore,there is one critical wave vectork*of the DQPT in the quench path A. For paths B and C, the wave vectors for|tanαk|=1 are located in the orange block, so the DQPT can not occur for the quench paths B and C.While for the path D,there are two critical wave vectorsk*for|tanαk*|=1 outside the orange block, which is exactly corresponding to two groups of DQPTs shown in Fig.2(e). In summary,for the quench from the gapless phase, the occurrence of DQPT must satisfy the conditions(17)and(18)simultaneously.
3.2. Quench from the gapped phase
Now, we consider the case of quench from the gapped phase(FM phase and PM phase). It is found that the situation for the quench from the FM phase is essentially the same as that for the quench from the PM phase, so we take the case of quench from the FM phase as an example to discuss the behavior of DQPT in the quench from the gapped phase.
In Fig. 4(a), we display the domain?(h0,γ0) from the ground state of the pre-quench HamiltonianH(h0=0.5,γ0=-0.5), that is, from the FMyphase. It can be seen that the domain?(h0=0.5,γ0=-0.5)does not cover all the area of the CP phase, but cover all the area of the PM phase and the FMxphase. This indicates that the DQPT will always occur for the quench from the FMyphase to the PM phase and the FMxphase,but may not occur for the quench from the gapless CP phase. We find that the case of quench from the gapped phase to the gapped phase is similar to that in theXYchain,[6]so we focus on the case of quench from the gapped phase to the gapless phase.
We consider the case of quench from the FM phase to the gapless CP phase. As two examples, we show the Fisher zeros for the quench paths A and B in the Figs. 4(b) and 4(c),and the corresponding rate functions are shown in Fig. 4(d).Unlike the case of the quench from the gapless phase, the quasiparticle excitation spectraεk >0 for all the wave vectorsk. Therefore, the Fisher zeros lines for the paths A and B are both continuous lines in the complex time plane. For the path A, the Fisher zeros are found having no intersection with imaginary axis[see Fig.4(b)],and the rate function is the smooth function. There is no DQPT in the path A.However,for the path B,each Fisher zeros linezn(k)have two intersections with the imaginary axis.The corresponding critical times of DQPTs are seen as the cusp-like peeks of the rate function[see Fig.4(d)].
Similarly, we show the values of|tanαk| for the quench paths A and B in Fig. 5. For the path A, all the values of|tanαk| are smaller than 1, so the DQPT can not occur because the condition(17)is not satisfied. However,for the path B,there are two critical wave vectorsk*for|tanαk|=1,which is exactly corresponding to two intersections between each Fisher zeros line and the imaginary axis[see Fig.4(c)].Unlike the case of the quench from the gapless phase,the quasiparticle excitation spectra of the pre-quench Hamiltonian satisfyεk >0 for all the wave vectorskwhen the quench is from the gapped phase. Therefore,the occurrence of DQPT is actually determined by the condition(17).
Fig.5. Values of|tanαk|for the paths A and B in Fig.4(a),which are from the FM to the CP phase.
4. The DQPT in the XY chain with three-site interaction
Now, we discuss the behavior of the DQPT in theXYchain withXZY–YZXtype of three-site interaction.
4.1. Quench from the gapless CP phase
First,we consider the case of quench from the gapless CP phase. In Fig. 6(a), we show the domain?(0.5,0.1) which indicates that the DQPTs occur in the case of quench from the ground states of pre-quench HamiltonianH(0.5,0.1). It is found that the domain?(0.5,0.1) does not cover the areah >1, and leaves the blank blocks in the gapped FMxphase and FMyphase [see Fig. 6(a)]. This means that the DQPTs may not occur when the quench is from the ground state ofH(0.5,0.1) and across the QPTs. Similarly, we take four examples of the Fisher zeros for the quenches from gapless phase in Figs. 6(b)–6(e) corresponding to paths A–D in Fig. 6(a),and the rate functions are shown in Fig.6(f). The Fisher zeros lineszn(k)in Figs.6(b)–6(e)are found to be separated into two branches,because for somekthe quasiparticle excitation spectra of the initial Hamiltonian satisfyεk·ε-k <0[see Fig.1(d)].For the paths A and B in which the system is quenched to the covered area by domain?(0.5,0.1),the Fisher zeros lines have intersections with the imaginary axis,and the nonanalytic points can be seen in the rate functions. For the paths B and C,the Fisher zeros do not intersect with the imaginary axis,and the rate functions are seen to be smooth. At this moment,the DQPT does not occur even if the quench crosses the QPTs.
Similarly,we draw the values of|tanαk|in Fig.7 for the paths A, B, C, and D to explain the occurrence and the absence of the DQPTs. It is found that the values of|tanαk|for all four paths have intersections with the line|tanαk|=1.However,for the paths B and C,the intersections are located in the orange block, where the wave vectorskdo not contribute to the Fisher zeros. Therefore,the DQPTs do not occur in the quench paths B and C. For the paths A and D, the values of|tanαk| have one intersection outside the orange block. The corresponding wave vectorsk*of the intersections are exactly the critical wave vectors of the DQPTs.

Fig. 6. (a) Domains ?(h0,γ0) (the red region) for quench from the initial points (h0,γ0) in the XY chain with XZY–YZX type of three-site interaction. The initial point is (h0 =0.5,γ0 =0.1). (b)–(e) The Fisher zeros for the quench paths A–D shown in(a). (f)The corresponding rate functions for the quench paths A–D.

Fig.7. Values of|tanαk|for the paths A,B,C,and D in Fig.6(a),respectively. The orange block denotes the wave vectors k corresponding to εk <0 of the pre-quench Hamiltonian.
4.2. Quench from the gapped phase
Now, we consider the case of quench from the gapped phase. Here we take the case of quench from the FM phase as an example. In Figs. 8(a), we show the domain?(h0=0.5,γ0=-0.5)that is from the FMyphase. It is found that the domain?(h0=0.5,γ0=-0.5)does not cover all the area of the gapless CP phase,but covers all the gapped phases which are not the initial points belonging to. This indicates that the DQPTs may not occur when the quench from the gapped phase to the gapless phase, but will always occur in the case of quench from the gapped phase to the gapped phase.

Fig. 8. (a) Domain ?(h0,γ0) (the red region) for the quench from the FM phase. (b) and (c) Fisher zeros lines zn(k) for the quench paths A and B marked in(a). (d)Corresponding rate functions for the quench paths A and B.

Fig.9. Values of|tanαk|for the paths A and B in Fig.8(a),which are from the FM to the CP phase.
As two examples, we show the Fisher zeros for the quench paths A and B marked in Fig. 8(a). It can be seen that for the quench path A, the Fisher zeros do not cross the imaginary axis. Meanwhile, the corresponding rate function is smooth. For the quench path B, each Fisher zeros lineszn(k) has two intersections with the imaginary axis, and the sharp peaks are seen in the rate function at the critical times of the DQPTs. Similarly, we display the values of|tanαk|for the paths A and B in Fig. 9. It is found that for the path A the values of|tanαk| are smaller than 1. However, for the path B the values of|tanαk| change from zero to the infinity(|tanαk|∈[0,+∞))and have the intersections with the line|tanαk|=1.
5. Summary and conclusion
We study the properties of DQPTs in theXYchains with DM interaction andXZY–YZXtype of three-site interaction,in which the systems have gapless phases and asymmetrical quasiparticle excitation spectra. By considering the quench starting from different initial states, we find that the factorsLk(t) of LE equal unity where the quasiparticle excitation spectra of pre-quench Hamiltonian satisfyεk·ε-k <0. Therefore, we obtain the general conditions for the occurrence of DQPT,that is, the occurrence of DQPT not only requires the Bogoliubov angle to satisfy|tanαk|=1,but also requires the quasiparticle excitation spectra of the pre-quench Hamiltonian to satisfyεk·ε-k ≥0.
Although we consider two specifical models in our paper,the conclusion can also be extended to a group of integral quantum spin chain, which can be mapped into the spinless free fermion model with the quadratic form by the Jordan–Wigner transformation. From the above discussion and the previous results,[22,27]we summarize the connection between the DQPT and the QPT as follows: For the system only with gapped phase,the DQPTs will occur when the quench crosses the critical lines of QPTs. For the system with the gapless phase,the DQPT may not occur in the quench from the gapped phase to the gapless phase or from the gapless phase to the gapped phase. For the systems with symmetrical quasiparticle excitation spectra,the reason for the absence of the DQPT is that there is noksatisfying|tanαk| = 1. However, for the systems with asymmetrical quasiparticle excitation spectra, the reason for the absence of the DQPT is that no wave vectorksatisfies|tanαk|=1,or the wave vectorsksatisfying|tanαk|=1 correspond toεk·ε-k <0.
Acknowledgement
This work was supported by the National Natural Science Foundation of China(Grant Nos.11975126 and 11575087).
- Chinese Physics B的其它文章
- Switchable terahertz polarization converter based on VO2 metamaterial
- Data-driven parity-time-symmetric vector rogue wave solutions of multi-component nonlinear Schr¨odinger equation
- Neutron activation cross section data library
- Multi-phase field simulation of competitive grain growth for directional solidification
- A novel similarity measure for mining missing links in long-path networks
- Effects of electrical stress on the characteristics and defect behaviors in GaN-based near-ultraviolet light emitting diodes