Characteristic Polynomial of Linear Hexagonal Spiders?

YAN Juan ,HOU Jiangxia ,HUANG Qiongxiang

(1.Department of Mathematics,Lishui University,Lishui Zhejiang 323000,China;2.School of Mathematics and System Sciences,Xinjiang University,Urumqi Xinjiang 830017,China)

Abstract:In this paper,we give the explicit expressions of characteristic polynomials of linear hexagonal spiders,which are representation of certain branched catacondensed benzenoid molecules.From our result,the number of perfect matchings of these graphs are easily obtained.Our new method can also be used to calculate the characteristic polynomial of any graph having threefold symmetry.

Key words:linear hexagonal spiders;recurrence relation;characteristic polynomial

0 Introduction

Let G be a graph with n vertices,and A(G)be its adjacency matrix.φG(λ)=|λIn-A(G)|is the characteristic polynomial of G,and the spectrum of G is the n roots of φG(λ).Even though these are classical algebraic concepts,it is amazing that they have close relation with the structure of graphs.Especially,the number of some basic subgraph of G is closely linked to the coefficients of φG(λ).This makes it possible to study the structure of graphs by algebraic methods.Obviously,it is extremely hard to give the spectrum or characteristic polynomial for an arbitrary graph with large n.But there are many results showed the spectra or characteristic polynomials for some special classes of graphs,see[1-3]for example.

A chemical structure can be conveniently represented by a graph.As an important example,benzenoid hydrocarbons can be represented by hexagonal systems naturally.The center graph,denoted by GC,of a hexagonal system is defined to classify hexagonal systems.Each vertex of GCis placed in the center of a hexagon of G,and two vertices are adjacent if the two hexagons are adjacent.A hexagonal system G is called a hexagonal chain if its center graph GCis a path,and it is called a hexagonal spider if GCis a tree with exactly one vertex of degree 3 and other vertices of degree 1 or degree 2.Hexagonal chains are graph representations of unbranched catacondensed benzenoid molecules,while hexagonal spiders are graph representation of branched catacondensed benzenoid molecules.

Denote by m(G)the number of matchings of G,and i(G)the number of independent sets of G.In chemical terminology,m(G)and i(G)are called the Hosoya index and Merrifield-Simmons index,respectively.Details of chemical applications of these two indices can be found in[4].

Chen and Zhao[5]computed the Hosoya index and Merrifield-Simmons index of hexagonal chains.Gutman[6]proved that the extremal graph among hexagonal chains of m(G) and i(G) is linear chain Ln,and Shiu[7]proved that the extremal graph among hexagonal spiders of m(G)and i(G)is linear hexagonal spider Gnshown in Fig 1.These works motivated us to find the spectral or characteristic polynomials of linear hexagonal spiders.

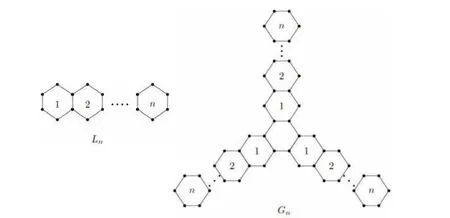
Fig 1 Ln and Gn

The spectrum of Lncan be found in [2],and Gutman determined it in a new way in [3].This paper aim to give the characteristic polynomial of Gn.In very early years,there are several papers introduced some methods which may be used to calculate the characteristic polynomials of linear hexagonal spiders[8].However,none of them gives the explicit expression.We develop a method to calculate the characteristic polynomials of linear hexagonal spiders by using the combinatorial techniques.Namely,the recurrence relation shown in Lemma 1.The proof of our main result involves a new technique.An iterative result is used to obtain the characteristic polynomial of the adjacency matrix of the resultant graph.A special case of Lemma 1 has been used to give the spectra of graphs under some operations[9].This method can also be used to calculate the characteristic polynomial of any graph having threefold symmetry.

Theorem 1Let Gnbe the linear hexagonal spider.Then

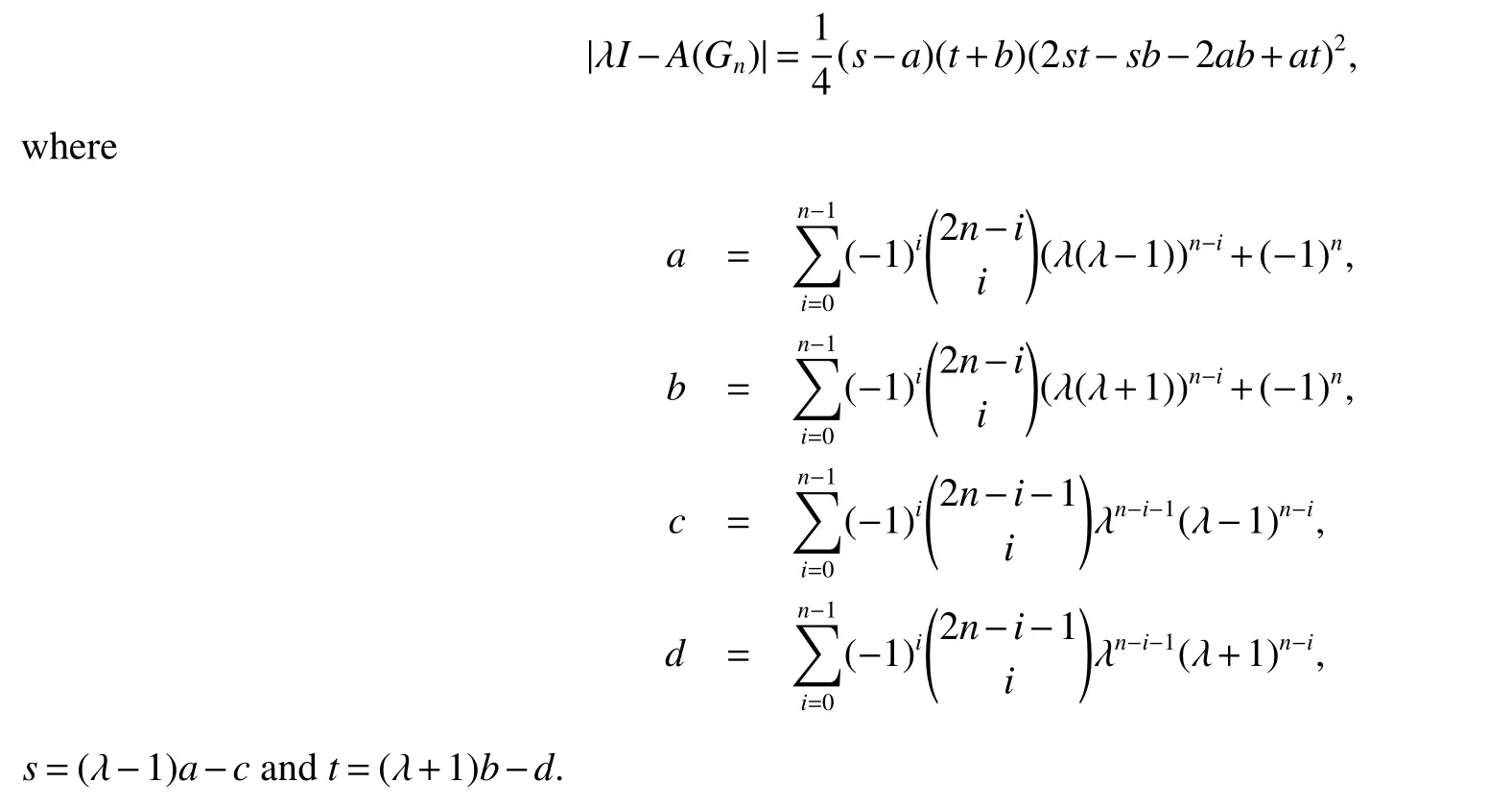
In the next section,we will see that when n=1,s-a=λ3-3λ2+3,t+b=λ3+3λ2-3 and 2st-sb-2ab+at=λ6-6λ4+9λ2-3,it is easy to see from Eisenstein’s Irreducibility Criterion that all of them are irreducible in the rational polynomial ring Q[x].So the expression given in Theorem 1 is best possible in some sense.

We will see from Theorem 1 that for linear hexagonal spider Gn,0 is not an eigenvalue of Gn.In Hu¨ckel molecular orbital theory used in chemistry,this means that the chemical compound whose skeleton is represented by Gnis stable.Also,by Theorem 1,we obtain the number of perfect matchings in Gnis K(Gn)=(n+2)(n2+n+1).

1 Proof of Theorem 1

In this section,we give the proof of Theorem 1.First,we prove Lemma 1,which is the key of our proof.

Lemma 1If a2n=a2n-1D-a2n-2and a2n+1=λa2n-a2n-1,for a0=C and a1=λC-I,where C and D are square matrices with the same order.Then

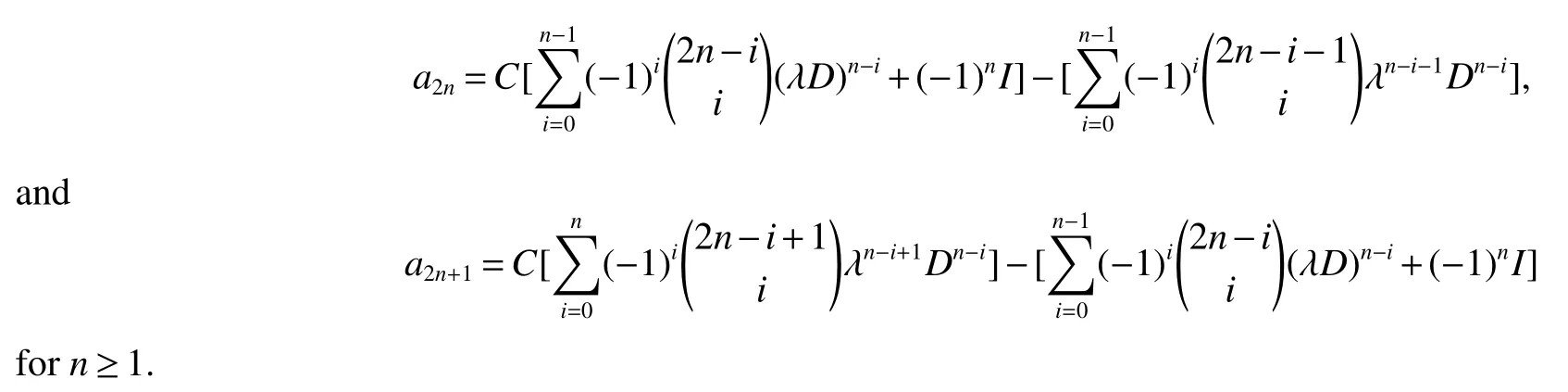
ProofWe prove this lemma by induction on n.Note that a2=a1D-a0=C(λD-I)-D and a3=λa2-a1=C(λ2D-2λI)-(λD-I).We have that Lemma 1 is true for n=1.

Suppose the Lemma 1 is true for n.We have

By the same method,we have

Wondering whence it could come, I was about to call to my maid who slept in the room next mine, when, to my surprise, I felt as if some heavy weight on my chest had taken all power from me, and I lay there unable to utter the slightest sound

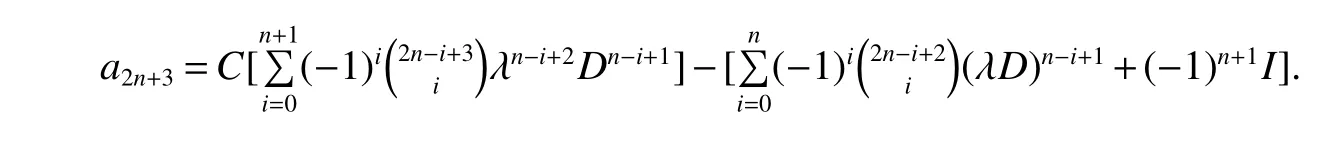
This completes the proof.

Let Gnbe the linear hexagonal spider shown in Fig 1.To calculate the characteristic polynomial of Gn,we first use the recurrence relation in Lemma 1 to drop the order of determinant |λI-A(Gn)|.In the following,we always assume thatand C=λI6-A(C6),where C6is the cycle of 6 vertices.We give the following lemma.

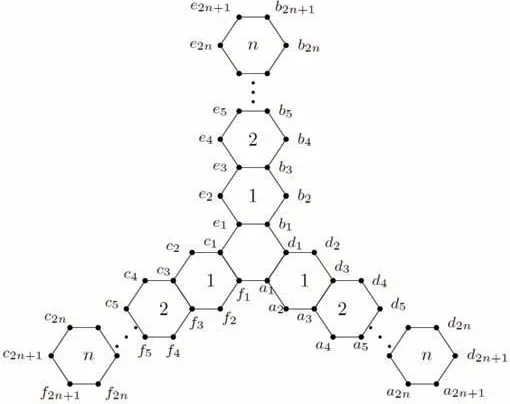
Fig 2 The label

Lemma 2Let Gnbe the spider hexagonal system graph.Then

ProofLet Xi={ai,bi,ci,di,ei,fi}for i=1,2,···,2n+1,see Fig 2.We have

where the submatrix A(Xs,Xt)corresponds the row-Xsand column-Xt,say

Note that A(X1,X1)=A(C6),the adjacency matrix of C6.Now set C=λI6-A(C6)and D=It is easy to verify that|λI-A(Gn)|can be written as

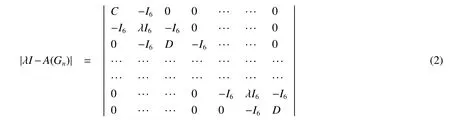
For this block matrix,switch the first row with the others one by one,we get

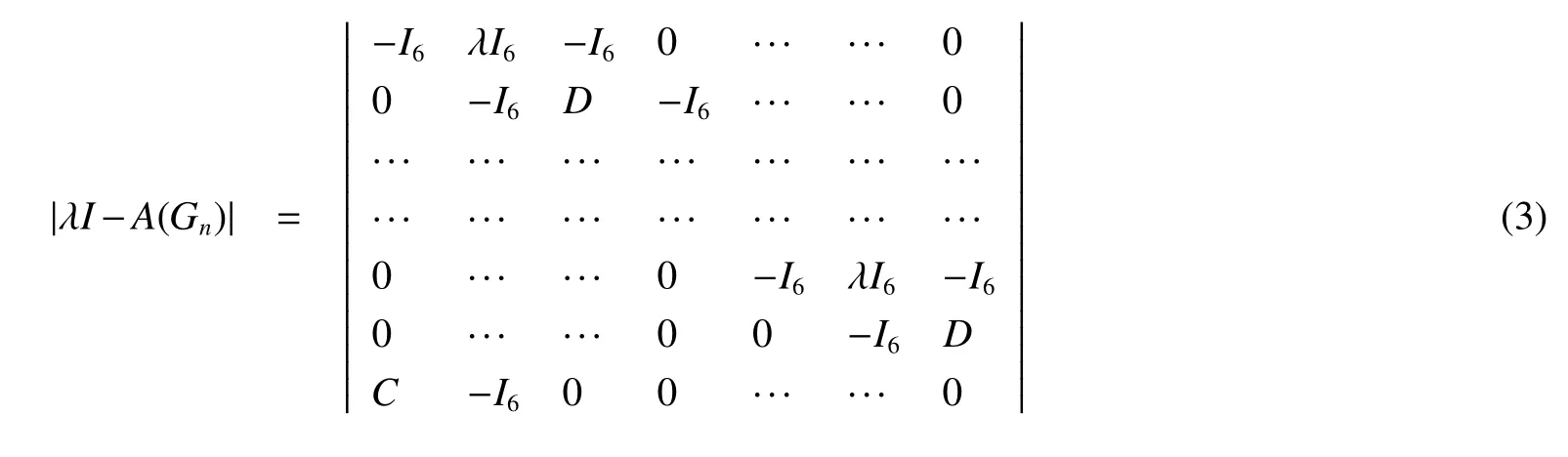
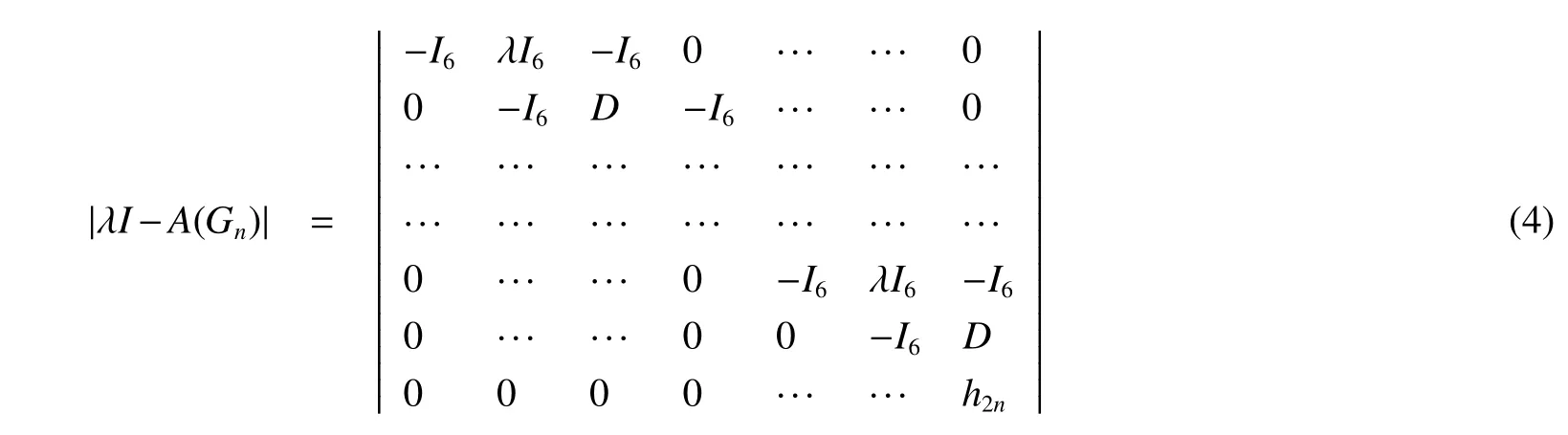
So|λI-A(Gn)|=|a2n|.By Lemma 1,we complete the proof.

The determinant on the right of equation(1)in Lemma 2 is a determinant of a matrix polynomial with respect to D and C,both of them have order six.To compute this determinant we need to diagonalize D.

and T=TT=T-1.

ProofOne can easily verify Lemma 3 by hand.

For the preparation work to calculate the characteristic polynomial of Gn,we firstly define four polynomials with respect to λ bellow.

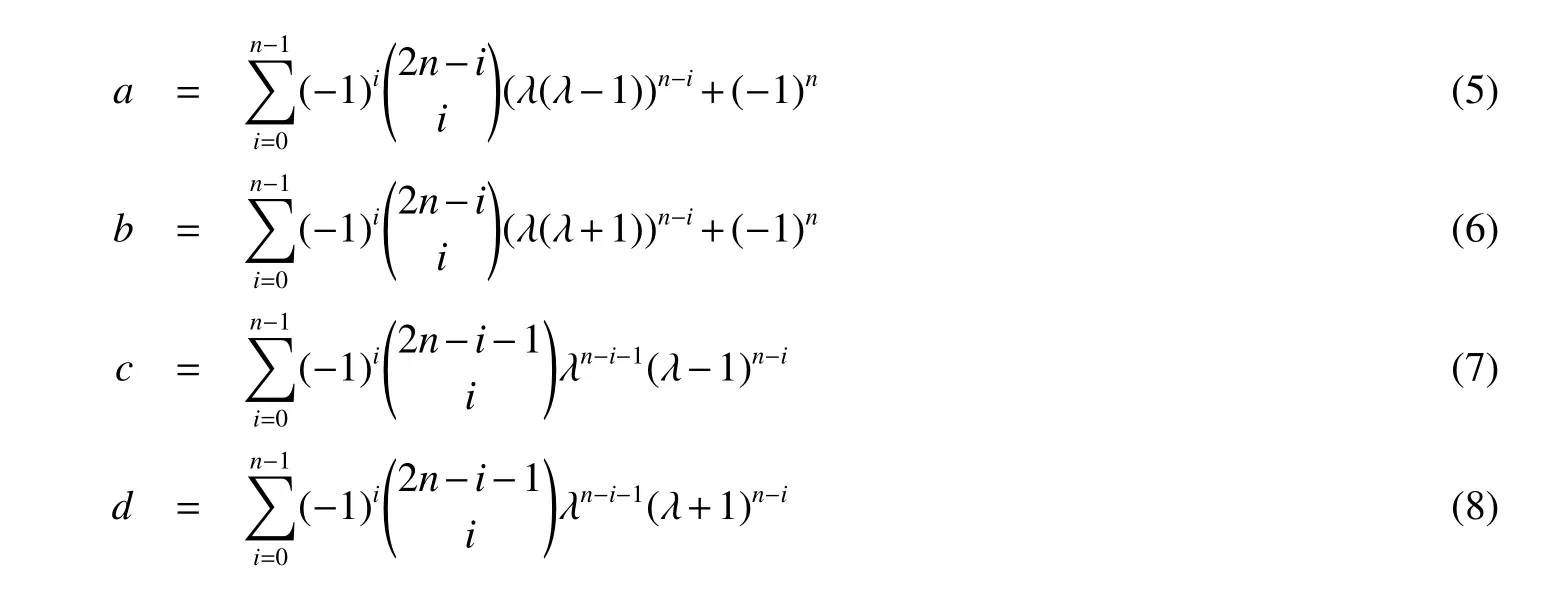
Lemma 4Let Gnbe the spider hexagonal system graph shown in Fig 1.Then

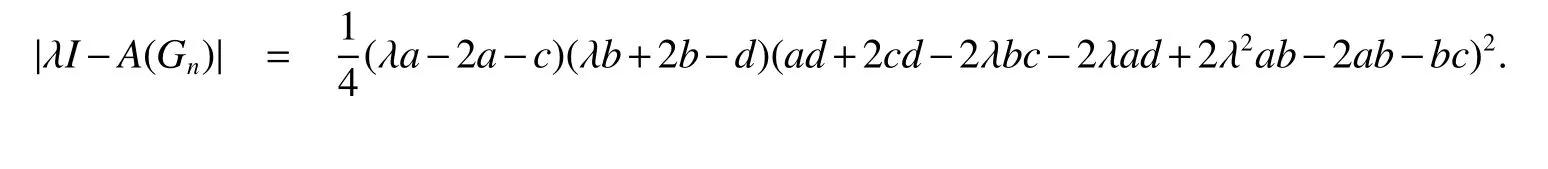
From the definition of a,b,c and d,we can see that a=f1(λ-1),b=f1(λ+1),c=f2(λ-1) and d=f2(λ+1).Then let Λ1=f1(Λ)=diag(a,a,a,b,b,b)and Λ2=f2(Λ)=diag(c,c,c,d,d,d).We have|λI-A(Gn)|=|CTΛ1T-1-TΛ2T-1|,which is a matrix of order six.So the result is easily given by Maple.

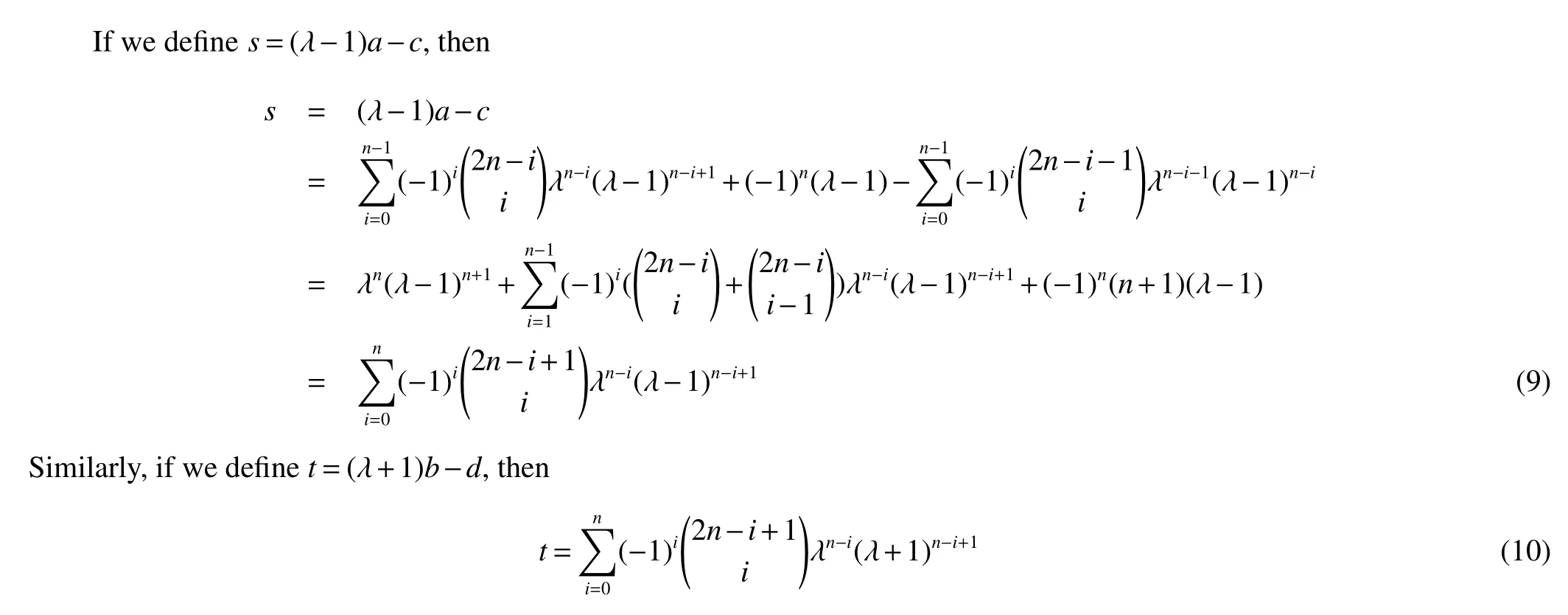
By the definition of s and t,we get Theorem 1 immediately from Lemma 4.

2 Further Discussions

Since each of a,b,s and t in Theorem 1 is a polynomial in λ,they can be written in standard form.For(5),(6),(9)and(10),expanding(λ-1)n-iand(λ+1)n-iby Newton’s binomial theorem gives the coefficients of λk.Define=0 if m ＜0,we obtain the polynomials

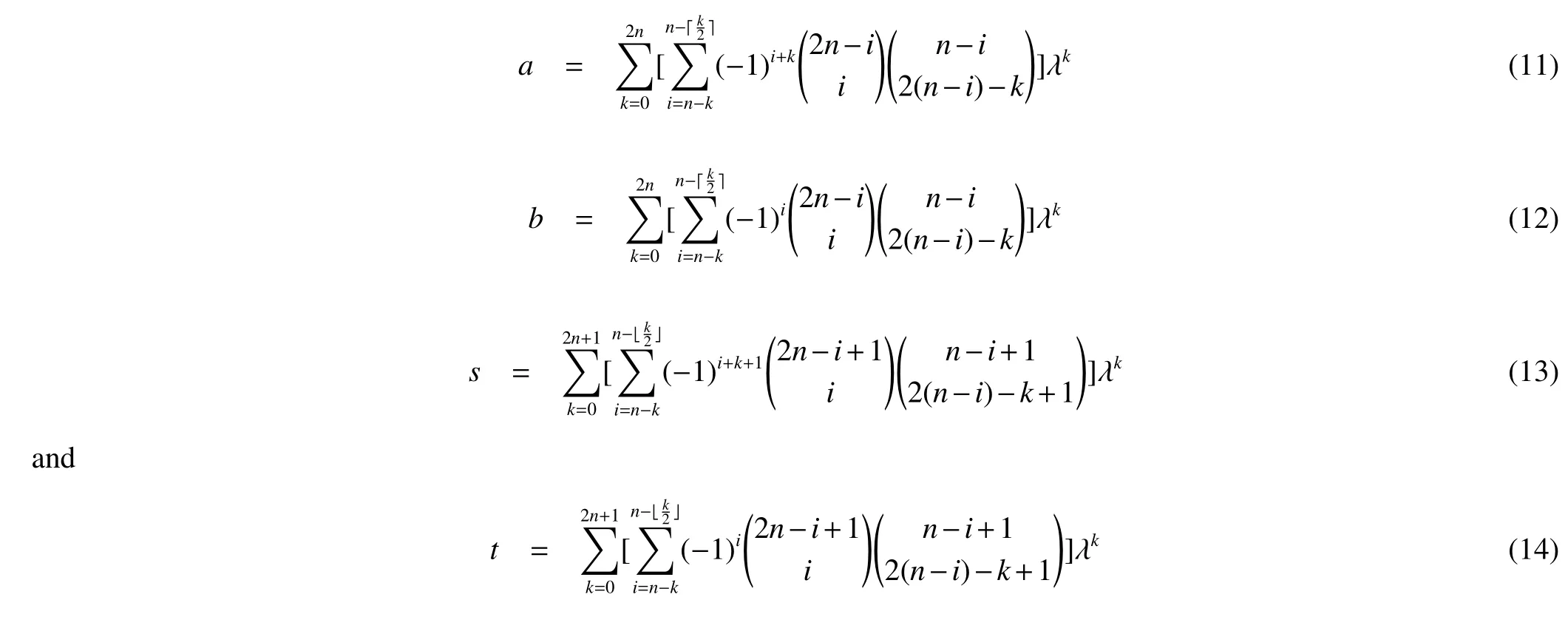
We can see from above that the coefficient of λkin s-a is equal to the coefficient of λkin t+b when k is odd and they are opposite when k is even.So if λiis a root of s-a then -λiis a root of t+b,i.e.,the roots of s-a and the roots of t+b are symmetric about the origin.Meanwhile,from(11)～(14)we can see that ak(a)=-ak(b),ak(s)=ak(t)when k is odd and ak(a)=ak(b),ak(s)=-ak(t) when k is even,where ak(f) is the coefficient of λkin f.So the coefficient of λkin(2st-sb-2ab+at)is zero when k is odd.It means that the roots of(2st-sb-2ab+at)are symmetric about the origin either.

From(11)～(14)we can see that the coefficient of λ0inis equal to-(n+2)2(n2+n+1)2.Thus,we have the following result.

Corollary 1Let Gnbe the linear hexagonal spider Gn.Then 0 is not the eigenvalue of Gn.

From Theorem 1,we can get the number of perfect matchings of linear hexagonal spider.In fact,a perfect matching(1-factor)is a Kekul′e structure of a benzenoid hydrocarbon system.Kekul′e structures are used in resonance theory and ab initio valence bond theory.The number of Kekul′e structures is denoted by K.So,we denote by K(G),the number of perfect matchings in graph G.The remarkable Dewar-Longuet-Higgins formula states that detA(G)=So we have the following corollary.

Corollary 2Let Gnbe the linear hexagonal spider Gn.Then the number of perfect matchings in Gnis K(Gn)=(n+2)(n2+n+1).

ProofBy Dewar-Longuet-Higgins formula,detA(G)=The result follows from the fact that|V(Gn)|=12n+6.

Theorem 1 gives an explicit expression for the characteristic polynomial of linear hexagonal spider Gn.Using this theorem,one can easily calculate the characteristic polynomial of Gnby computer for each given n.For examples,we give the expressions of φGn(λ)for n=1,2,3,4 with the help of Maple.