Fixed point theorems for two new classes of generalized (ψ,φ) weakly contraction mappings in b-metric spaces
,
(College of Mathematics and Systems Science, Shenyang Normal University, Shenyang 110034, China)
Abstract: The Banach contraction mapping principle plays an important role in nonlinear analysis, and it is effective to solve the problem of the existence and uniqueness of fixed points in metric spaces. It has a wide range of applications in both basic mathematics and applied mathematics, and has been extended in many different directions. In recent years, there have been many studies on the fixed point of new weakly contraction mappings in b-metric spaces. Firstly, two new classes of (ψ,φ) weakly contraction mappings with variable exponents are introduced in b-metric spaces. Then, a sequence is defined in X by using variable index, and proved by using reduction to absurdity and contraction condition. It follows from that the sequence is a Cauchy sequence in X. Secondly, combining the completeness of (X,d) and the contraction conditions, we get the conclusion that there exists x*∈X such that Tn(x*)x*=x*. Further, x* is the unique fixed point of T. Finally, we obtain that for any x, the iteration sequence {Tnx converges to the unique fixed point x*. At the same time, an example is given to illustrate the validity of one of our results.
Key words: fixed point; generalized (ψ,φ) weakly contraction; b-metric spaces; Cauchy sequence
0 Introduction
The Banach contraction mapping principle[1]plays an important role in nonlinear analysis, and it is effective to solve the problem of the existence and uniqueness of fixed points in metric spaces. It has a wide range of applications in both basic mathematics and applied mathematics, and has been extended in many different directions. By changing the contraction condition, many new theorems are established, we can refer to [3-4]. On the other hand, in 1993, Czerwik[5]extended the metric space by modifying the third condition in metric spaces and introduced the concept ofb-metric spaces, also the author studied the fixed point theorem of a new class of contraction conditions in theb-metric spaces. Then Kir et al.[6]gave the conclusions that Kannan type and Chatterjea type contraction mapping have a unique fixed point. Popescu[7]has done initial work that stimulated many researchers to prove fixed point theorems for a few (ψ,φ) weakly contraction mappings. More examples and results inb-metric spaces can be found in [8-14].
Based on the results of Zhang[2]and Popescu[7], we introduce two new classes of generalized (ψ,φ) weakly contraction mappings and study the existence and uniqueness of fixed points involving generalized contraction conditions in the framework ofb-metric spaces. Meanwhile, we provide an example to support one of our results.
1 Preliminaries
We introduce some definitions which will be needed in the sequel.
Definition1[5]LetXbe a nonempty set ands≥1 be a given real number. A mappingd:X×X→R+is said to be ab-metric if and only if the following conditions are satisfied:
1)d(x,y)=0 if and only ifx=y;
2)d(x,y)=d(y,x) for allx,y∈X;
3)d(x,z)≤s[d(x,y)+d(y,z)] for allx,y,z∈X.
Then (X,d) is calledb-metric space with parameters≥1.
RemarkWe should note that ab-metric space is a metric space if and only ifs=1.
Definition2[15]Let (X,d) be ab-metric space with parameters≥1. Then, a sequence {xn} inXis called
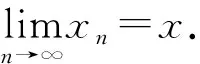
2) a Cauchy sequence if and only ifd(xn,xm)→0 asn,m→∞.
Definition3[15]Let (X,d) be ab-metric space with parameters≥1.
1) The space (X,d) is complete if every Cauchy sequence inXis convergent.
2) A functionT:X→Yis continuous at a pointx∈Xif it is sequentially continuous atx, that is, whenever {xn} is convergent tox, {fxn} is convergent tofx.
Definition4[16]A functionφ:[0,∞)→[0,∞) is called an altering distance function if the following properties hold:
1)φis continuous and nondecreasing;
2)φ(t)=0 if and only ift=0.
2 Main Results
Theorem1 Let (X,d) be a completeb-metric space with parameters≥1. Letψ:[0,∞)→[0,∞) be a continuous and nondecreasing function andφ:[0,∞)→[0,∞) be a altering distance function onX. LetT:X→Xbe a given continuous mapping satisfying that for anyx∈X, there exists a positive integern(x) such that for anyy∈X,
ψ(sd(Tn(x)x,Tn(x)y))≤ψ(N(x,y))-φ(N(x,y))
(1)
where
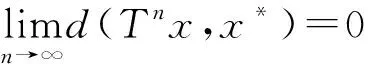
Proof: Letx0∈Xand define the sequence {xm} inXbyxm=Tn(xm-1)xm-1for allm∈N. Ifxm=xm+1for somem∈N, then we havexm+2=Tn(xm+1)xm+1=Tn(xm)xm=xm+1=xm. It is easy to see thatxmis a fixed point ofTn(xm). Now we showxmis the unique fixed point ofTn(xm). Assume thaty*is another fixed point ofTn(xm). Then we haveTn(xm)y*=y*and
where
This implies thatψ(d(xm,y*))<ψ(d(xm,y*)), which is a contradiction. Therefore,xmis the unique fixed point ofTn(xm). Also,Txm=Txm+1=TTn(xm)xm=Tn(xm)Txm, this impliesTxmis a fixed point ofTn(xm). In view of uniqueness of fixed point, we obtainTxm=xm. That is,xmis a fixed point ofT. The uniqueness can be proved by a similar method.
Without loss of generality, assume thatxm≠xm+1for allm∈N. By the contraction condition (1), we have
If we assume that, for somem∈N,N(xm-1,Tn(xm)xm-1)=d(xm,xm+1), then we have
ψ(d(xm,xm+1))≤ψ(d(xm,xm+1))-φ(d(xm,xm+1))
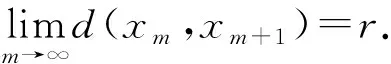
Next, we prove that {xm} is a Cauchy sequence inX. Assume to the contrary that there existsε>0 for which we can find subsequence {xmk} and {xnk} of {xm} satisfyingnkis the smallest index for whichnk>mk>k,
d(xmk,xnk)≥ε,d(xmk,xnk-1)<ε
(3)
In view of triangle inequality and (3), we get
ε≤d(xmk,xnk)≤sd(xmk,xnk-1)+sd(xnk-1,xnk) Taking the upper limit ask→∞ in the above inequality, we deduce (4) Also, Taking the upper limit ask→∞ in (5), we obtain (6) In view of the definition ofN(x,y), one can deduce that Taking the upper limit ask→∞ in (7), we have So there is This implies thatφ(ε)=0 andε=0, which is a contradiction. Therefore {xm} is a Cauchy sequence inX. By completeness ofX, there existsx*∈X, such that (8) The continuity ofTensures that (9) Again, Taking the upper limit asm→∞ in (10) and from (8) and (9), we deduce Now if we takem→∞ in (11), we obtaind(x*,Tn(x*)x*)=0, i.e.,x*is a fixed point ofTn(x*). One can check thatx*is the unique fixed point ofTn(x*). In fact, we assume thaty*is another fixed point ofTn(x*), then we have ψ(d(x*,y*))≤ψ(sd(x*,y*))=ψ(sd(Tn(x*)x*,Tn(x*)y*))≤ψ(N(x*,y*))-φ(N(x*,y*)) where Thenφ(d(x*,y*))=0 andd(x*,y*)=0, sox*is the unique fixed point ofTn(x*). Moreover, one can get thatTx*=TTn(x*)x*=Tn(x*)Tx*, which impliesTx*is a fixed point ofTn(x*)andTx*=x*. Uniqueness can be obtained by referring to the above method. Finally, we prove the last part of the theorem. Letnbe an arbitrary positive integer such thatn>n(x*). Putn=in(x*)+s,i≥1,0≤s ExampleLetX=[0,∞) andd:X×X→[0,∞) be defined byd(x,y)=|x-y|2for allx,y∈Xands=2. Define mappingsT(x) andn(x) by T(x)=1,n(x)=2 for allx∈X. Also we defineψ,φ:[0,∞)→[0,∞) byψ(t)=ktandφ(t)=(k-1)tfor allt∈[0,∞), wherek∈N. Now we show the hypothesis of Theorem 1. By calculation, we have Therefore, all the conditions of Theorem 1 are satisfied. And 1 is the unique fixed point ofT. Theorem2 Let (X,d) be a completeb-metric space with parameters≥1, Letψ:[0,∞)→[0,∞) be a continuous and nondecreasing function andφ:[0,∞)→[0,∞) be an altering distance function onX. LetT:X→Xbe a given continuous mapping and hold that for anyx∈X, there exists a positive integern(x) such that for anyy∈X, ψ(s2d2(Tn(x)x,Tn(x)y))≤ψ(N(x,y))-φ(N(x,y)) (13) where Proof: It following from theorem 1 that we get {xm} and ifxm=xm+1,thenxmis a fixed point ofTn(xm). Similarly, we assume thaty*is another fixed point ofTn(xm). Then we haveTn(xm)y*=y*and which This implies thatψ(d2(xm,y*))<ψ(d2(xm,y*)), which is a contradiction. Therefore,xmis the unique fixed point ofTn(xm). Using the same method to prove Theorem 1, we getxmis the unique fixed point ofT. Without loss of generality, assume thatxm≠xm+1for allm∈N. By the contraction condition (13), we have where If we assume that, for somem∈N,N(xm-1,Tn(xm)xm-1)=d2(xm,xm+1), then we have ψ(d2(xm,xm+1))≤ψ(d2(xm,xm+1))-φ(d2(xm,xm+1)) which gives a contraction. It follows thatN(xm-1,Tn(xm)xm-1)=d2(xm-1,xm) and so {d(xm,xm+1} is a nonincreasing sequence. As the proof of Theorem 1, we have Next, we prove that {xm} is a Cauchy sequence inX. In view of (4), (6), (13) and (14), one can deduce that So there is This implies thatψ(ε2)=0 andε=0,which is a contradiction. As the proof of Theorem 1, we have (15) Again, where Taking the upper limit asm→∞ in (16) and from (15), we deduce where Which yields thatφ(d2(x*,y*))=0 andd(x*,y*)=0. That is,x*is the unique fixed point ofTn(x*). Similarly, we getx*is a unique fixed point ofT. Finally, letnbe an arbitrary positive integer such thatn>n(x*). Putn=in(x*)+s,i≥1,0≤s where From the above inequalities, we derive ψ(d2(x*,Tnx0))≤ψ(d2(x*,Tnx0))-φ(d2(x*,Tnx0)) (17) In this paper, we introduced two new classes of generalized(ψ,φ)weakly contraction mappings and studied the existence and uniqueness of fixed points involving generalized contraction conditions in the framework ofb-metric spaces. Further, we provided an example that elaborated the usability of one of our results.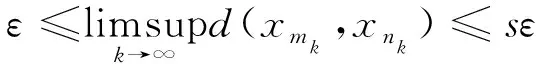
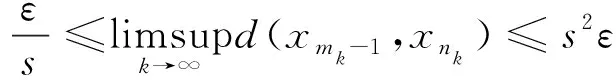
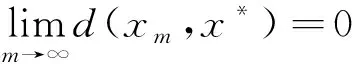
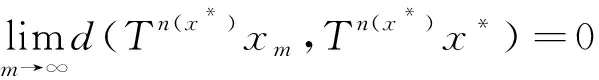
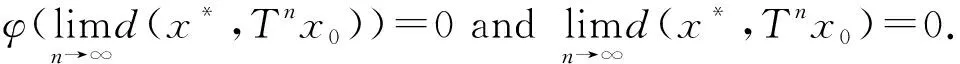
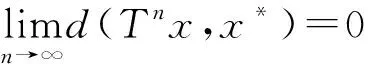
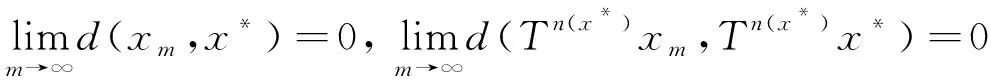
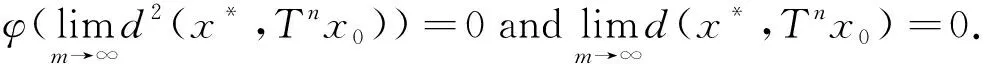
3 Conclusions

