Block-coherence measures and coherence measures based on positive-operator-valued measures

Liangxue Fu, Fengli Yan and Ting Gao

1 College of Physics, Hebei Key Laboratory of Photophysics Research and Application, Hebei Normal University, Shijiazhuang 050024, China

2 School of Mathematical Sciences, Hebei Normal University, Shijiazhuang 050024, China

Abstract We study block-coherence measures based on the resource theory of block-coherence and coherence measures based on positive-operator-valued measures (POVM).Several blockcoherence measures are presented, including the block-coherence measure based on maximum relative entropy, the one-shot block-coherence cost under maximally block-incoherent operations,and the coherence measure based on coherent rank.Their relationships are obtained.Moreover, we describe the deterministic coherence dilution process by constructing blockincoherent operations.Based on the POVM coherence resource theory, we also propose two coherence measures and analyze their relationship.

Keywords: coherence measure, block-coherence measure, positive-operator-valued measure

1.Introduction

Quantum coherence is an important ingredient in quantum information processing [1].Baumgratz et al proposed the theoretical framework (BCP framework) of the resource theory of quantum coherence in 2014 [2].This framework comprises three basic elements:a set of free states that do not contain resource, a corresponding set of free operations that map an arbitrary free state to a free state, and a metric functional [2].

In the resource theory of quantum coherence, the free states are incoherent states,which can be diagonalized under a fixed reference basis [2].Free operations (incoherent operations) are some specified classes of physically realizable operations [2].According to different operational capabilities and physical relevance,the sets of free operations may be:the maximally incoherent operation [3, 4], the dephasing-covariant incoherent operation [3, 5, 6], the incoherent operation[2],the strictly incoherent operation[7,8],and the physically implementable incoherent operation [6].In order to quantify coherence, many coherence measures are proposed in the resource theory of coherence, such as the l1-norm coherence measure [2], relative entropy coherence measure [2],coherence of formation [7, 9], coherence concurrence [10],etc.Coherence measures of different meanings help us better quantify and understand coherence [2-14].

An interesting problem in the resource theory of quantum coherence is the transformation of states via free operations[14, 15], especially the transformation between an arbitrary state ρ and a maximally coherent state [15].In particular, the process of converting a given state ρ to the maximally coherent state by an incoherent operation is referred to as coherence distillation [15-18].In contrast to distillation, the dilution process converts the maximally coherent state into the desired target state [15, 19, 20].The processes of asymptotic dilution and distillation are performed under the independent and identically distributed assumption [15,17-19], which ignores the possible correlation between the different state preparations.Therefore, in order to relax the assumption, it is necessary to consider the one-shot scenario,where only one copy of the state is supplied [15, 17-19].

The resource theory of block-coherence was introduced in[4].Here,we adopt the framework proposed in[21].In the resource theory of block-coherence, the block-incoherent states can be considered to be generated by a von Neumann measurement P={Pi}, i=1, 2, …, d, i.e., the blockincoherent statefor the stateρ∈S, whereS denotes the set of quantum states on the Hilbert spaceH,the rank of the orthogonal projector Piis arbitrary, and the orthogonal projectors form a complete set, i.e.,[4, 21-23].

In 2019, Bischof et al [21] established the positiveoperator-valued measures (POVM) coherence resource theory.It employs the Naimark extension to define the POVM coherence via block-coherence in a larger Hilbert space,where the quantum states act through an embedded channel in thed′ -dimensional (d′ ＞d) Hilbert spaceH′ (Naimark space), and a POVM E is extended to the projective measurement P of the Naimark space H′ [21, 22, 24].We will give detailed description of the resource theory of blockcoherence and the POVM coherence resource theory in the second section of this paper.

In this paper, we study the block-coherence measures based on the resource theory of block-coherence and the coherence measures based on the POVM coherence resource theory,and then analyze the relationship between these blockcoherence measures.

This paper is divided into five sections.In section 2,we introduce some main concepts, and review the resource theory of block-coherence and POVM coherence resource theory.In section 3, we propose two block-coherence measures and the one-shot block-coherence cost in the framework of the resource theory of block-coherence, and analyze their relationship.We illustrate the problem of deterministic coherence dilution by constructing a blockincoherent operation.In section 4, a POVM-based coherence measure and the one-shot block-coherence cost under the maximally POVM-incoherent operations are presented and analyzed.

2.Background

2.1.Block-coherence theoretical framework

In 2006, ?berg introduced the general measurement method of the degree of superposition of mixed quantum states and applied it to the orthogonal decomposition of Hilbert space,and thus created the resource theory of block-coherence.Similar to the theoretical framework of BCP, the resource theory of block-coherence also consists of three elements:the set of block-incoherent states, the set of block-incoherent operations, and the block-coherence measures [4, 21].

The Hilbert spaceH is divided into d orthogonal subspaces, and the projective measurement P={Pi} is performed on the setS of quantum states, where Piis the projector of the ith subspace.Block-incoherent states [4,21-23] are defined as

where Δ denotes the block-dephasing operation.The set of block-incoherent states is denoted as IB( H ).

We refer to the largest class of(free)operations that cannot produce block-coherence as maximally block-incoherent(MBI) operations.A channel ΛMBIonS is free operations if it maps any block-incoherent state to a block-incoherent state [4,21-23], namely,

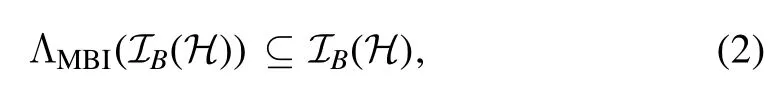
or equivalently

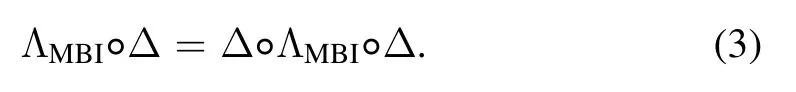
A quantum channel Λ is often expressed by the Kraus operators.Let {Kn} be a set of Kraus operators onH, and satisfy the normalization conditionSome Kraus operators have the form

where f is the index function, and cnis the complex matrix.Knis a block-incoherent Kraus operator, if f is an index permutation.

A real-valued functionC(ρ,P)is called the blockcoherence monotone of quantum state ρ with respect to the projective measurement P, if it satisfies [4, 21-23]:

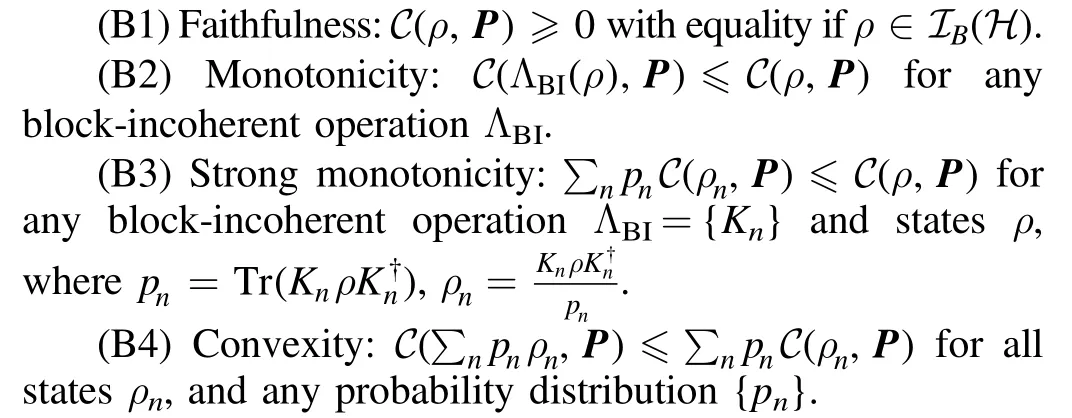
Note that the rank of the above projector Piis arbitrary,and when the rank of Piis 1, the resource theory of blockcoherence is consistent with the standard resource theory of coherence.

2.2.POVM coherence theoretical framework

and

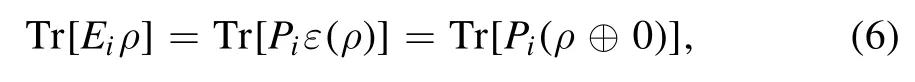
is required for all states ρ in the setS of quantum states.Here, ⊕denotes the orthogonal direct sum, and 0 is the zero matrix of dimensiond′ -d.Any projective measurement P that satisfies equation (6) is called a Naimark extension of E.

The embedding into a larger-dimensional Hilbert space can also be realized via the canonical Naimark extension[21,25]:one attaches a probe,initially in the state |1〉〈1|,via the tensor product ε(ρ)=ρ ?|1〉〈1| [21].A canonical Naimark extension projective measurementof the POVMis described by a unitary matrix V satisfying [21, 22]

and

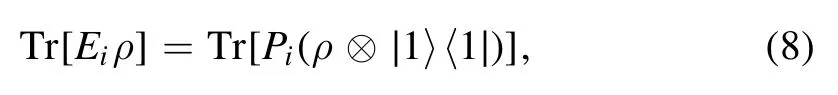
for every state ρ in the quantum state setS.

A state ρ is called a POVM-incoherent state[21,22,24],if

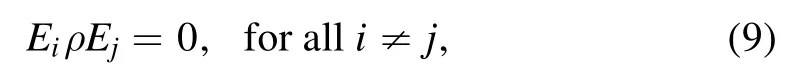
or equivalently

The set of POVM-incoherent states is denoted as IPI.

2.3.Max-relative entropy and the coherent rank

In the theoretical framework of BCP,the max-relative entropy between quantum state ρ ≥0 and quantum state σ ≥0 is defined as [26, 27]

if φi≠0 for i=1, 2,…,R.

3.Block-coherence measures

Based on the max-relative entropy, we first define a blockcoherence measure,which is a generalization of the coherence measure in [19].

Then, we have the following result.

Suppose thatH is a d-dimensional Hilbert space and P={Pk} is a projective measurement.A maximally blockcoherent state is defined by [24]

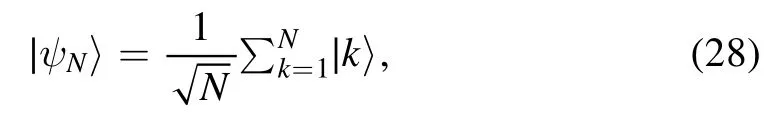
where |k〉 is a state in the spacePkH.Here, the rank of projective measurement Pkis arbitrary and the number of Pkin the projective measurement P is N(N ≤d).

Obviously, for an maximally block-coherent state |ψN〉,we have

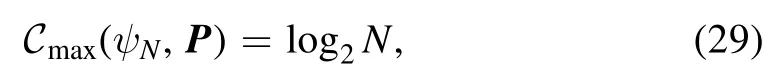
namely,the value ofCmax(ψN,P)depends on the number N of projectors in the space.

The one-shot scenario is the most general conversion case, where the conversion is from an initial state to a final state.The one-shot block-coherence dilution process converts the MBI state |ψN〉 into the desired state ρ via the MBI operation [15, 19, 20].

Now we define a block-coherence measure as the oneshot block-coherence cost of quantifying block-coherence dilution.

Since errors are allowed in one-shot scenarios, in the presence of the error ∈, we use

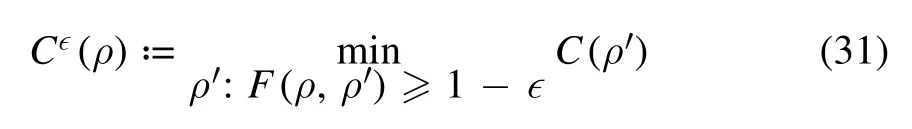
to characterize the coherence measure of state ρ[19].That is,in order to define the coherence cost with a certain error ∈,one can use a smoothing to the measure C(ρ)by minimizing over statesρ′ satisfyingF(ρ,ρ′)≥ 1 -∈to smooth the measureC(ρ).

Next.we discuss the relationship between the coherence measureand the one-shot block-coherence cost

Theorem 1.For∈＞ 0, the coherence measures satisfy

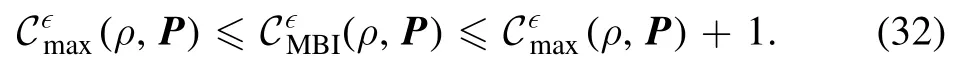
which means

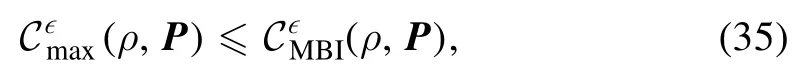
as required.

Next, we prove the second inequality of equation (32).Suppose that the stateρ′ reaches the minimum, then

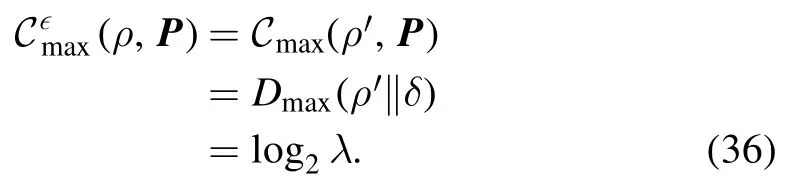
Here, ΛBIis a block-incoherent operation composed by the Kraus operators {Kn}.We choose the block-incoherent Kraus operators[24]

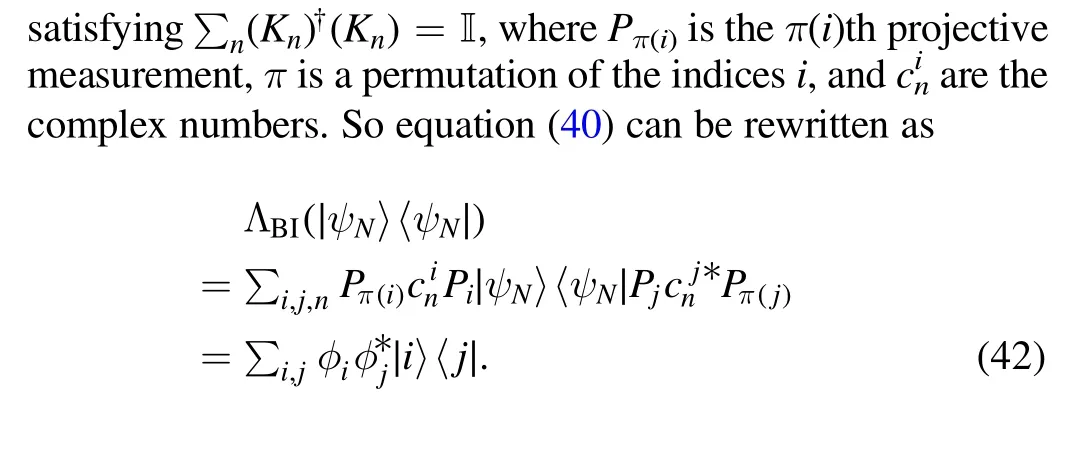
For the sake of simplicity here we only discuss the case of N=d.In this case,deterministic coherence dilution means that the coefficients between the initial state|ψd〉(maximally blockcoherent state) and the final state |φ〉 satisfy the majorization relation[31],i.e.,

The probability distribution is [32]

The set of Kraus operators of the incoherent operation[32]is

where cijis the (ij)-entry element of the d×d matrix c satisfying

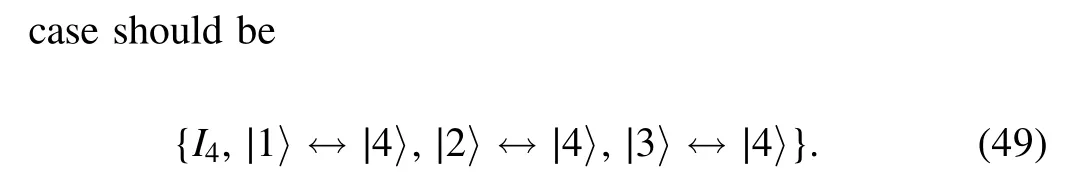
The matrix c corresponding to this set of permutations is

Thus, the probability distribution is

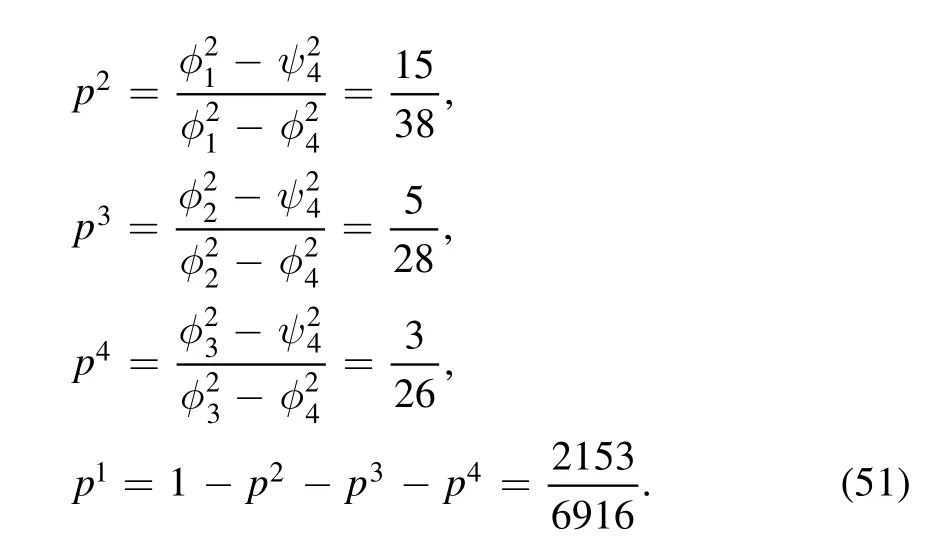
Then, the Kraus operators are

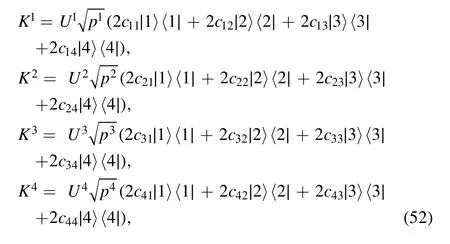
where U1=I4is the identity transformation, U2=|1〉?|4〉,U3=|2〉?|4〉, U4=|3〉?|4〉.The Kraus operators can be expressed as

Next, we define another coherence measure based on coherent rank.

Definition 3.A block-coherence measure based on coherent rank is defined as

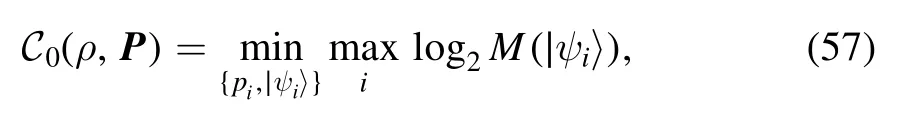
We have the following result.

Then, we prove that for any block-incoherent operation with {Kn}, there is

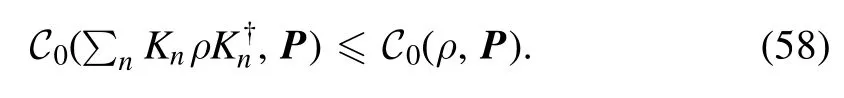
Before we prove the above inequality, let us introduce the following lemma proved in [7].

Clearly, lemma 1 also holds when {Ki} is a block-incoherent operation.

Let {pi, |ψi〉} be the decomposition such that

Therefore, we get

as desired.

4.POVM-based coherence measures

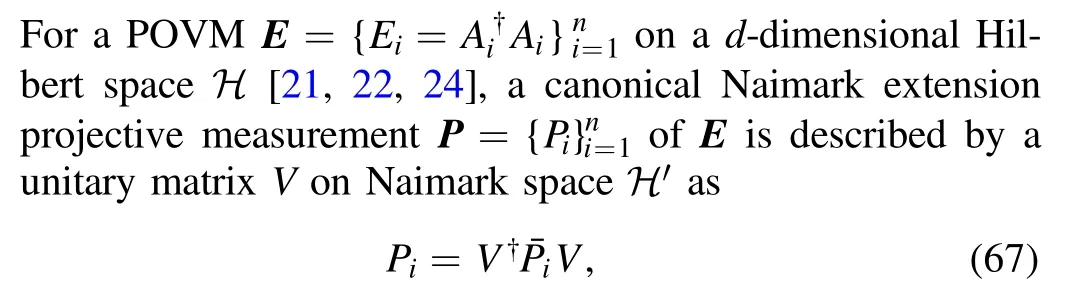
where

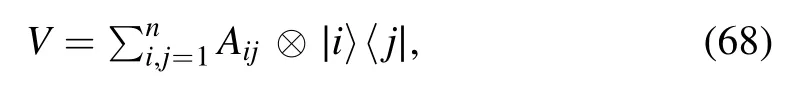
and

LetC(ρ′,a unitary invariant block-coherence measure, that is,

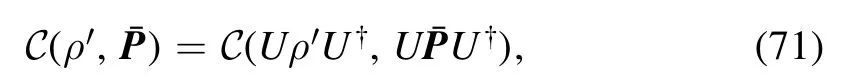
for any unitary transformation U on the Hilbert space [21].The POVM-based coherence measureC(ρ,E)of ρ under POVM E is defined [21] as

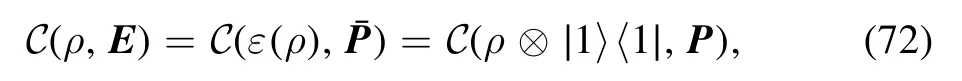
where

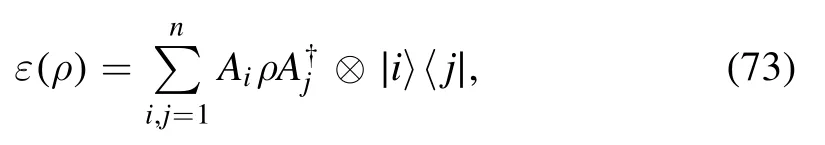
is a state on the embedded state Hilbert space Hε.

From the conclusions in references[21,22,24],we know that the quantityC(ρ,E)is a POVM-based coherence measure satisfying the conditions (P1),…, (P4).

Next, we discuss a concrete POVM-based coherence measure.

Proposition 3.Letbe a POVM on the Hilbert spaceH, the quantity based on the max-relative entropy

where σ is an arbitrary density operator on the state setS (εH ).

For any unitary transformation U onεH , we derive maximally POVM-incoherent operations.For a state ρ and∈≥0, the one-shot block-coherence cost underO is defined as

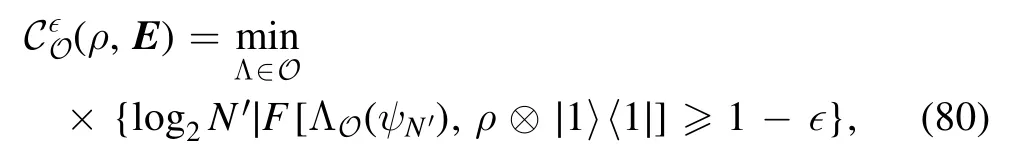
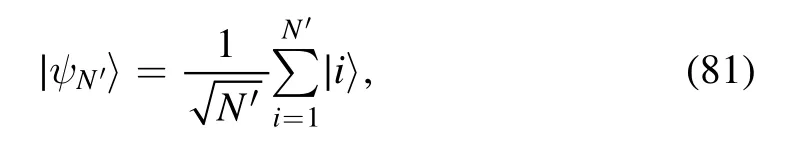
is an maximally block-coherent state in the extended Hilbert space H′.Here, ∣i〉 is a state in the spacePiH′, and ΛOis a block-incoherent operation in the extended Hilbert space,corresponding to the POVM-incoherent operation Λ.

Similar to theorem 1, for the one-shot block-coherence cost under the maximally POVM-incoherent operations, the following is true.

Theorem 3.For quantum state ρ and∈＞ 0, we have

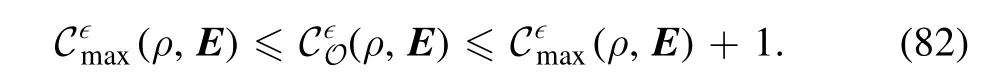
5.Conclusion

In the resource theory of block-coherence,we have presented a block-coherence measureCmax(ρ,P)based on maximum relative entropy, and shown that it is a coherence monotone and quasi-convex under the MBI operations.We have proposed the one-shot block-coherence cost under the MBI operations and found the relationship between the coherence measureCmax(ρ,P)and the one-shot block-coherence cost.We have described the deterministic coherence dilution process by constructing block-incoherent operations based on the resource theory of block-coherence.We also introduced the coherence measureC0(ρ,P)based on coherent rank, and obtained the relationship with the one-shot block-coherence cost.Based on the POVM coherence resource theory, we proposed a POVM-based coherence measure by using the known scheme of building POVM-based coherence measures from block-coherence measures, and the one-shot blockcoherence cost under the maximally POVM-incoherent operations.The relationship between the POVM-based coherence measure and the one-shot block-coherence cost under the maximally POVM-incoherent operations has been analyzed.

Acknowledgments

This work was supported by the National Natural Science Foundation of China under Grant No.12071110, the Hebei Natural Science Foundation of China under Grant No.A2020205014, and the Science and Technology Project of Hebei Education Department under Grant Nos.ZD2020167 and ZD2021066.