Quantum exceptional points of non-Hermitian Hamiltonian and Liouvillian in dissipative quantum Rabi model*

Xianfeng Ou(歐先鋒) Jiahao Huang(黃嘉豪) and Chaohong Lee(李朝紅)

1Guangdong Provincial Key Laboratory of Quantum Metrology and Sensing&School of Physics and Astronomy,Sun Yat-Sen University(Zhuhai Campus),Zhuhai 519082,China

2State Key Laboratory of Optoelectronic Materials and Technologies,Sun Yat-Sen University(Guangzhou Campus),Guangzhou 510275,China

3Synergetic Innovation Center for Quantum Effects and Applications,Hunan Normal University,Changsha 410081,China

Keywords: dissipative quantum Rabi model, non-Hermitian Hamiltonian, Lindblad master equation, exceptional points

1. Introduction

Quantum Rabi model(QRM)is a simplest and most fundamental model describing the light-matter interaction involving a two-level system and a quantized bosonic field.[1,2]Recently, there appear various excellent experimental platforms for realizing QRM ranging from weak to ultrastrong coupling regimes,such as,cavity quantum electrodynamics,[3]trapped ions,[4,5]circuit-QED,[6,7]cold atoms[8]and superconducting circuits.[9,10]In addition to the fundamental interests in quantum optics,QRM has extensively potential applications,such as high-precision weak force measurement.[11-13]

In realistic situations,dissipation inevitably exists during the time evolution. The system is not exactly isolated and it interacts with an environment. Thus, the system and the environment form an open quantum system. In general,the dynamics of an open quantum system can be described by a Lindblad master equation captured by a Liouvillian superoperator?,[14]which consists of a Hermitian Hamiltonian part, and a non-Hermitian part called Lindblad dissipators. The Lindblad dissipators can be divided into two parts.[15-18]The first part represents a non-unitary dissipation of the system,transforming the Hamiltonian to be non-Hermitian. The second part describes the effect of quantum jumps.

Generally,by neglecting the effect of quantum jumps,the system can be described by an effective non-Hermitian HamiltonianH.[19,20]A distinct feature of non-Hermitian systems is exceptional points(EPs),which are the degeneracies at which not only eigenvalues but also the eigenstates coalesce.[21-25]In recent years, notions drawn from EPs in non-Hermitian systems have attracted considerable attention.[26,27]EPs were subsequently observed in microwave cavities,[28-30]optical microcavities,[31-35]coupled atom-cavity systems,[36]photonic lattices,[37]exciton-polariton billiards,[38]and so on.

Among the investigations on EP so far, the majority use the non-Hermitian Hamiltonians. However, the description of non-Hermitian Hamiltonian cannot be completely equivalent to the standard Lindblad master equations. For the Lindblad master equation,the Liouvillian superoperator?is a non-Hermitian matrix,which also possesses EPs. Liouvillian EPs(LEPs)are defined via degeneracies of Liouvillians,i.e.,when two(or more)eigenvalues and the corresponding eigenmatrix of a given Liouvillian superoperator coalesce. In general, the LEPs are not the same with the Hamiltonian EPs (HEPs) of the non-Hermitian HamiltonianH. Thus,in certain scenarios,the processes via HEPs may not be valid in the framework of full quantum description via Lindblad master equations. It is interesting to investigate in what conditions are the HEPs the same as the LEPs[39]and how to characterize the EPs with a quantity.

On the other hand, quantum Fisher information (QFI),which is related to the Bures metric, measures the ability of distinguishing two quantum states.[40]Generally, the QFI gives the ultimate precision bound on the estimation of a parameter encoded in a quantum state. Moreover, the QFI and the Bures metric have been also used for describing the criticality of quantum phase transitions, where they help to distinguish a sudden change of a quantum state when an external parameter is varied.[41-45]Thus,can we use the QFI to capture the signature of the EPs?

This article will be organized as follows. In Section 2,we will introduce the dissipative quantum Rabi model. In Section 3,considering a dissipative quantum Rabi model,we verify that the HEPs and LEPs are consistent in the weak coupling regime. The model can be simplified to the Jaynes-Cummings(JC)model where analytical analysis can be performed.[46]We show the spectral properties with both NHH and Liouvillian.While for a comparison, we find that the HEPs and LEPs are totally different out of the weak coupling regime.In Section 4,we show how to use QFI as a signature to characterize the EPs.In Section 5,we give a conclusion and discussion of the main results.

2. Model

The quantum system we consider consists of a single bosonic mode and a spin system interacting via dipolar coupling. Such a system is described by the Hamiltonian

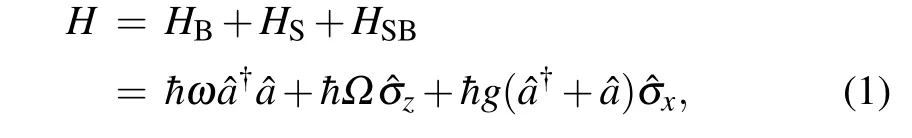
whereHBis the Hamiltonian of a the bosonic field ,HSis the Hamiltonian of the spin system, andHSBis the interaction Hamiltonian between the bosonic field and spin system,and ?a(?a?)is the bosonic annihilation(creation)operator corresponding to the single bosonic mode with frequencyω, ?σi(i=x,y,z)are the Pauli matrices for the two-level system with level splittingΩ,andgis the coupling strength(we set ˉh=1 in the following).

For a weakly coupled Markovian environment,the Lindblad master equation can efficiently capture the dynamics of the open quantum system,which is in the form[14]

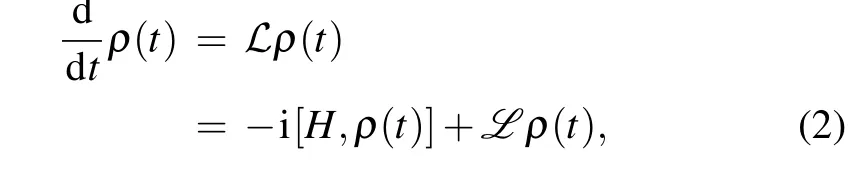
where?is the Liouvillian superoperator,His the Hamiltionian (1),ρ(t) is the density matrix of the quantum Rabi system at timet, andLis the so-called dissipators associated with the jump operators ?a, which describes the system-bath interaction,and has the Lindblad form[14]

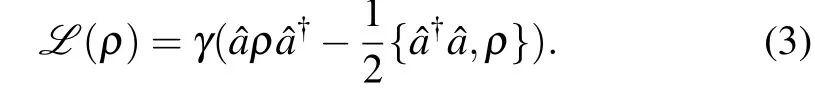
Here,γis the dissipation rate and the annihilation operator ?ais known as the jump operator,which determines the dissipative component of the system’s evolution, while the symbol{·,·}represents the anticommutator. The dissipators can be spilt into two part: the first term is quantum jumps that describe the effect of the measurement performed by the environment on the state of the system,while the second term describes the continuous losses of energy,information,and coherence of the system into the environment.

In the (semi)classical approximation, the quantum jump term from Eq. (3) is neglected. Thus, we can get the corresponding non-Hermitian effective Hamiltonian of the dissipative quantum Rabi model

Recently, quantum simulation of the dissipative QRM has been researched.[47]Moreover,it is worth stressing that dissipative QRM may yield a dissipative phase transition.[48]In the following,we will investigate the EPs of NHH and Liouvillian(i.e., the HEPs and LEPs) in different parameter regimes and find their connections.

3. Exceptional points

For NHH (4), the HEPs are the degeneracy point of the non-Hermitian HamiltonianH, where the eigenvalues and eigenvectors both collapse. In general, we can also get the LEPs of the non-Hermitian Liouvillian superoperator?,which correspond to the degeneracies of the eigenvalues and eigenmatrices of?.

Generally, the HEPs and LEPs have essentially different properties. However, under some specific conditions, they may exhibit similar properties. One trivial condition can be found in the subspace where the action of the annihilation operator has no effect.In this case,the quantum jump term can be exactly neglected.For example,if we considern=0 and in the subspace of{|0〉|e〉;|1〉|g〉},the annihilation operator acted on ?a|0〉|e〉=0,and the effect of quantum jump is eliminated. For the eigenspectrum of?in this subspace, the quantum jump term will not work,and the LEPs and HEPs are identical.

Next, we consider the weak coupling regime whereg ?ω.In this regime,the quantum Rabi model can be transformed to the Jaynes-Cummings (JC) model by using the rotating wave approximation(RWA),[46]which can be readily solved.The Hamiltonian(1)then becomes

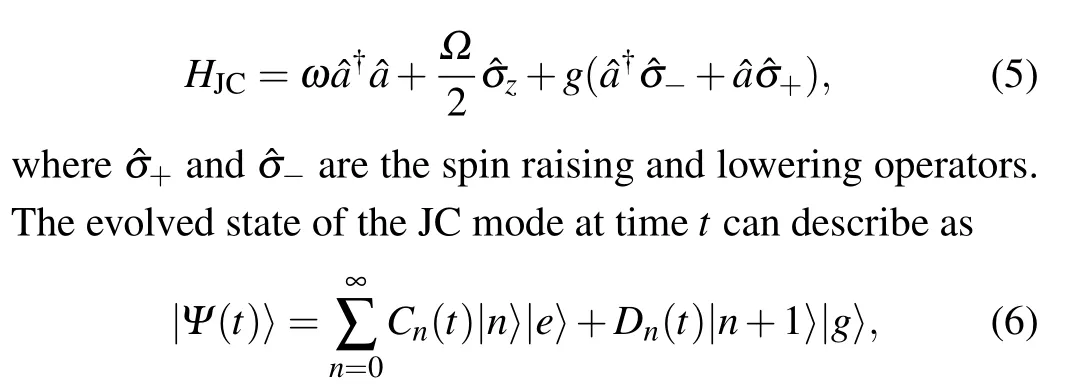
where|n〉is the Fock state of the bosonic field,|3〉(|g〉)stands for the excited (ground) state of the two-level system, andCn(t)(Dn(t))is the coefficient of state|n〉|e〉(|n+1〉|g〉).

For a fixed excitation numberN=n+1,we can decompose into two-dimensional subspace{|n〉|e〉;|n+1〉|g〉}. Further,we can get the analytic results in this subspace

wheren= 0,...,N ?1 withNthe excitation number. For HEPs,the eigenvectors coalesce and the fidelity|〈ψ1|ψ2〉|2=1.

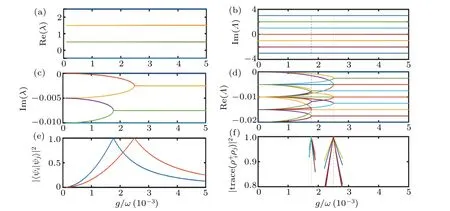
Fig.1.Spectral properties of the dissipative quantum Rabi model in weak coupling regime with excitation number N=2.The HEPs correspond to the LEPs. (a) Real and (c) imaginary parts of the eigenvalues of NHH ? as a function of g/ω. (b) Imaginary and (d) real parts of the eigenvalues of Liouvillian ? as a function of g/ω. (e)Fidelity between the eigenvectors of NHH ? associated with the EPs as a function of g/ω.(f)The trace of the product between the eigenmatrices of Liouvillian ? associated with the EPs as a function of g/ω.Here,the parameters are chosen as ω =1,Ω =ω,and γ =0.01ω.

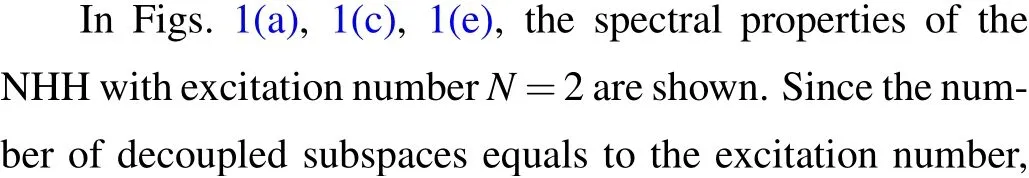
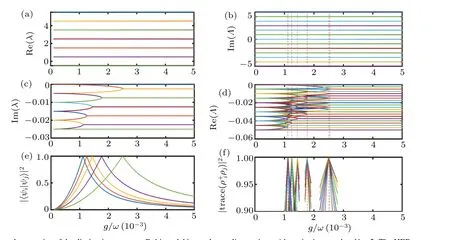
Fig.2.Spectral properties of the dissipative quantum Rabi model in weak coupling regime with excitation number N=5.The HEPs correspond to the LEPs. (a) Real and (c) imaginary parts of the eigenvalues of NHH ? as a function of g/ω. (b) Imaginary and (d) real parts of the eigenvalues of Liouvillian ? as a function of g/ω. (e)Fidelity between the eigenvectors of NHH ? associated with the EPs as a function of g/ω.(f)The trace of the product between the eigenmatrices of Liouvillian ? associated with the EPs as a function of g/ω.Here,the parameters are chosen as ω =1,Ω =ω,and γ =0.01ω.

Fig. 3. Spectral properties in strong coupling regime under γ =0.01ω showing that no EPs exist. (a) Real and (c) imaginary parts of the eigenvalues of NHH ? as a function of g/ω. (b)Imaginary and(d)real parts of the eigenvalues of Liouvillian ? as a function of g/ω. Here,the parameters are chosen as ω =1,Ω =ω and excitation number N=2.

Next, we turn to the regime whereg ?ωdoes not satisfied. In this regime, even the eigenspectrum of NHH cannot be analytically obtained and we find the EPs numerically.Here,we consider the excitation numberN=2 for an example.Whenγis small,no EPs exhibit for both NHH and Liouvillian,as shown in Fig. 3. Whenγis large, the HEPs and the LEPs occur at different places,which shows no correspondence. In Figs. 4 and 5, we show the spectral properties of NHH and Liouvillian in strong coupling regime underγ=100ω. In the region ofg/ω ∈[2,4],five LEPs appear while no HEPs exist,see Fig.4. On contrary,in the region ofg/ω ∈[15,25],there are one HEP while no LEPs appear, see Fig. 5. Our numerical results show that,in the strong coupling regime,either the number or the position of HEPs and LEPs are totally different.

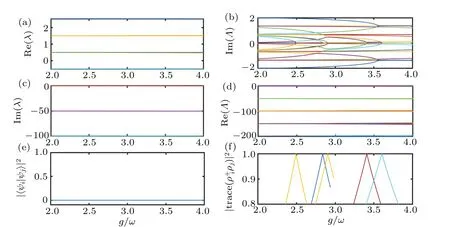
Fig. 4. Spectral properties in strong coupling regime g/ω ∈[2,4] under γ =100ω showing that the HEPs do not correspond to the LEPs. (a) Real and (c)imaginary parts of the eigenvalues of NHH ? as a function of g/ω. (b)Imaginary and(d)real parts of the eigenvalues of Liouvillian ? as a function of g/ω.(e) Fidelity between the eigenvectors of NHH ? associated with the EPs as a function of g/ω. (f) The trace of the product between the eigenmatrices of Liouvillian ? associated with the EPs as a function of g/ω. Here,the parameters are chosen as ω =1,Ω =ω and excitation number N=2.

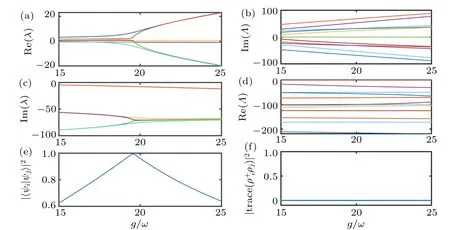
Fig.5. Spectral properties in strong coupling regime where g/ω ∈[15,25]under γ =100ω showing that the HEPs do not correspond to the LEPs. (a)Real and(c)imaginary parts of the eigenvalues of NHH ? as a function of g/ω. (b)Imaginary and(d)real parts of the eigenvalues of Liouvillian ? as a function of g/ω. (e)Fidelity between the eigenvectors of NHH ? associated with the EPs as a function of g/ω. (f)The trace of the product between the eigenmatrices of Liouvillian ? associated with the EPs as a function of g/ω. Here,the parameters are chosen as ω =1,Ω =ω and excitation number N=2.

4. Quantum fisher information as a signature for the exceptional points

As above, we find that the HEPs can be consistent with LEPs in the dissipative quantum Rabi model in the weak coupling regime.In this section,we will show how to characterize the HEPs and LEPs. We find that the QFI can be a signature for the appearance of EPs. The QFI in the vicinity of the EPs blows up indicating the location of EPs, while the QFI associated with the states of no EPs remains a small value unchanged. Despite the definitions of the QFI with NHH and Liouvillian are different, in the weak coupling regime, the QFI of NHH and the Liouvillian are consistent.

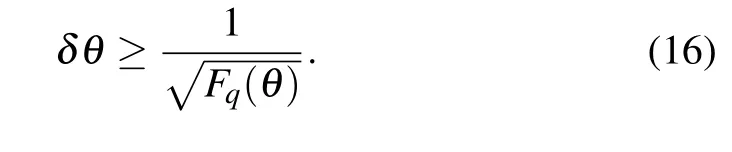
Generally,the standard deviation of an estimate of the parameterθof a single measurement is bounded by the inverse of the QFIFq(θ),[40]i.e.,The QFIFq(θ)characterizes the limit of distinguishing the infinitesimally close quantum statesψθ(ρθ)andψθ+δθ(ρθ+δθ)that differ only by a small variation of the parameterδθ. The discrimination of two close quantum states parameterized byθandθ+δθis equivalent to distinguishing the two close parametersθandθ+δθ,thus the QFI also measures how well the parameterθcan be estimated.

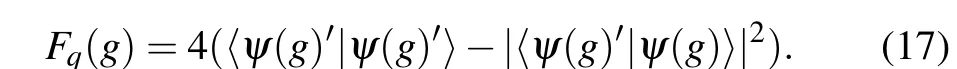
Similarly,one may use QFI to distinguish the states near the EPs and determine the location according to the QFI.Whenγ,ωandΩare fixed, for NHH, the QFIFq(g) can be defined as[49]Here,|ψ(g)〉is the eigenvector of NHH and|ψ(g)'〉is the derivative with respect to parameterg. On the other hand,for Liouvillian,the QFI can be defined via the density matrix,[50]in the form of

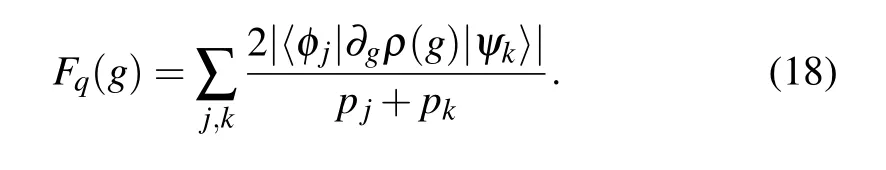
Here,ρis the eigenmatrix of Liouvillian?,φlis thel-th eigenstate of the density matrix,andplis the corresponding eigenvalue. Hereafter, we will calculate via Eq. (17) for the NHHHand Eq.(18)for the Liouvillian?.

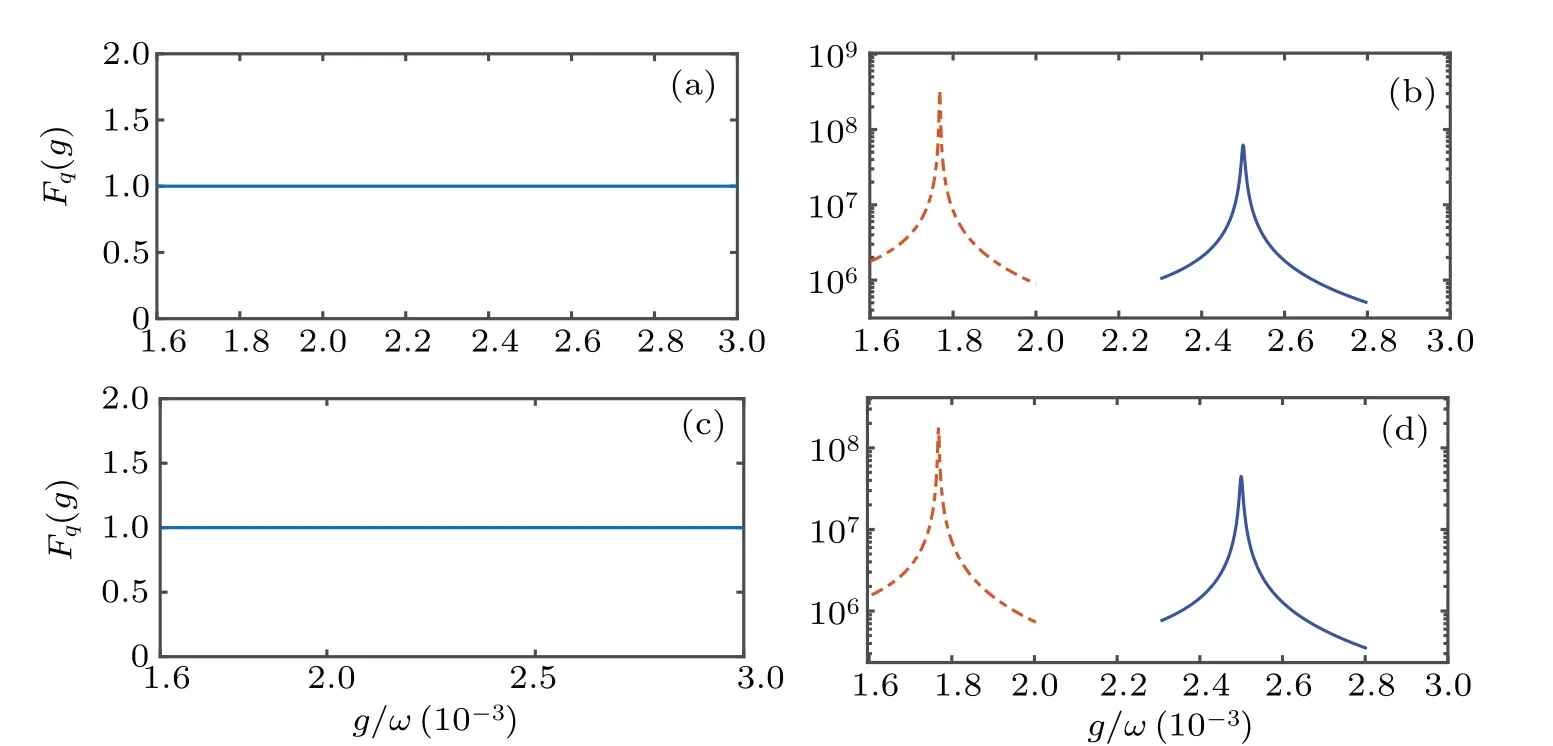
Fig. 6. The QFI of different eigenvectors as a function of g/ω with excitation number N =2. The other parameters are chosen as ω =1,Ω =ω, γ =0.01ω. (a)The QFI of the eigenvectors of NHH ? without HEPs. (b)The QFI of the eigenvectors of NHH ? associated with HEPs. Blue and red lines indicate the two different eigenvectors of NHH.(c)The QFI of the eigenmatrices of Liouvillian ? without LEPs. (d)The QFI of the eigenmatrices of Liouvillian ? associated with LEPs. Blue and red lines indicate the two different eigenvectors of Liouvillian.

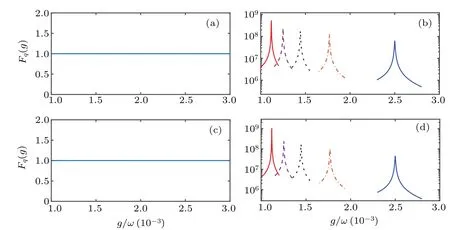
Fig. 7. The QFI of different eigenvectors as a function of g/ω with excitation number N =5. The other parameters are chosen as ω =1,Ω =ω, γ =0.01ω. (a)The QFI of the eigenvectors of NHH ? without HEPs. (b)The QFI of the eigenvectors of NHH ? associated with HEPs. Five colored lines indicate five different eigenvectors of NHH.(c)The QFI of the eigenmatrices of Liouvillian ? without LEPs. (d)The QFI of the eigenmatrices of Liouvillian ? associated with LEPs. Five colored lines indicate five different eigenvectors of Liouvillian.

With excitation numberN=2, we show the QFI versusg/ωin Fig. 6. For the eigenvector that does not exhibit EPs,the QFI of the NHH as well as the Liouvillian is a smooth function versusg/ω, see Figs. 6(a) and 6(c). While for the eigenvector that possesses EPs,the QFI of the NHH as well as the Liouvillian appears sharp peaks at the EPs, see Figs.6(b)and 6(d). Since there will appear the numerical problems in correctly sorting the eigenvectors, we only show the results near the EPs. Because the excitation numberN= 2, there are only two EPs. Here, the different colored lines represent different eigenvectors that have EPs appearing at different location. Similarly, the results of QFI with excitation numberN=5 are shown in Fig. 7. For the eigenvector that does not exhibit EPs,the QFI of the NHH as well as the Liouvillian is a smooth function versusg/ω,see Figs.7(a)and 7(c). While for the eigenvector that possesses EPs, the QFI of the NHH as well as the Liouvillian appears sharp peaks at the EPs,see Figs.7(b)and 7(d). It is obvious that the QFI can be a signature for EPs. For eigenvectors without EPs,the QFI provides no information. However, for eigenvectors at the EPs (15),the corresponding QFI of the NHHHand the Liouvillian?dramatically reaches a maximum. Although the definitions of QFI for NHH and Liouvillian are different which makes their values different,the locations of the peaks at EPs are the same.Thus,one can use QFI for characterizing the EPs.

5. Conclusions

In summary, we have studied the properties of HEP and LEP in a dissipative quantum Rabi model. Firstly, we consider the quantum Rabi model in the weak coupling region

where the model can be approximated as a JC model under RWA. We obtain the analytical conditions for the EPs in the NHH description and show its corresponding spectral properties. Then, for another description based upon a Liouvillian superoperator?, we show its corresponding spectral properties via numerical calculations. We find that the EPs of NHH(HEPs) and the ones of Liouvillian (LEPs) are consistent in this weak coupling regime. While for the regime out of weak coupling, we numerically find that HEPs and LEPs are no longer correspondent.

Further, we show how to characterize the EPs via QFI.For the states without EPs, the QFI provides no information.While for the states associated with EPs,the QFI appears sharp peaks at the EPs indicating that QFI can be used as a signature for EPs. Our study may provide a guidance for investigating the properties of EPs in state-of-the-art experiments.