Propagations of Fresnel diffraction accelerating beam in Schr¨odinger equation with nonlocal nonlinearity*
Yagang Zhang(張亞港) Yuheng Pei(裴宇恒) Yibo Yuan(袁一博)Feng Wen(問峰) Yuzong Gu(顧玉宗) and Zhenkun Wu(吳振坤)
1Institute of Nano/Photon Materials and Application&International Joint Research Laboratory of New Energy Materials and Devices of Henan Province,School of Physics and Electronics,Henan University,Kaifeng 475004,China
2College of Miami,Henan University,Kaifeng 475004,China
3Key Laboratory for Physical Electronics and Devices of the Ministry of Education&School of Science&Shaanxi Key Laboratory of Information Photonic Technique&Institute of Wide Bandgap Semiconductors,Xi’an Jiaotong University,Xi’an 710049,China
Keywords: Fresnel diffraction beams,nonlocal nonlinearity,real space,momentum space,three-dimensional(3D)Schr¨odinger equation
1. Introduction
Accelerating beams have attracted significant theoretical and experimental research interest in the last few decades owing to their unique features of self-acceleration and diffractionfree propagation over several Rayleigh lengths.[1-8]In particular, Airy beams as exact solutions of the Schr¨odinger’s equation[9,10]indicated that all paraxial accelerated beams are related to the Airy function.[11-17]Until quite recently, study of accelerating beam is still an active topic, and the evolution dynamics of these beams in different medium have been reported in Refs. [18-20]. By applying the separation of variables method to the wave equation and the Helmholtz equation,[21]nonparaxial accelerating beams and Mathieu and Weber beams can be obtained, respectively. Notably, these waves exhibit self-acceleration and self-healing. Additionally, accelerating beams have also been discovered in nonlinear media,[22-24]Bose-Einstein condensates,[25]atomic vapors with electromagnetically induced transparency,[26,27]chiral media,[28]and photonic crystals.[29]
With respect to the propagation dynamics of selfaccelerating beams, previous studies have shown that the nonlocality[30,31]and boundary conditions of nonlocal media[32]significantly impact the propagation of solitons. In particular, the spatial properties and anomalous interactions of Airy beams can be modulated considerably via a nonlocal nonlinear potential during propagation.[33-35]Nonlocal optical nonlinearity is observed in nematic liquid crystals[36]and thermal media,[37]where the degree of change induced in the material’s refractive index at a specific location is controlled by the light intensity in a specific neighborhood at that location.[38]Nonlocal nonlinearity also affects the interaction of out-of-phase bright solitons and dark solitons.
Motivated by these previous studies,we investigate a selfaccelerating beam arising from the paraxial propagation of Fresnel diffraction patterns, which, to the best of our knowledge has not been studied thus far. We first show that this beam exhibits self-acceleration and self-healing, and we then investigate the evolution of these properties - first for the one-dimensional (1D) case involving diffraction at a straight edge,and subsequently for the two-dimensional(2D)case involving diffraction at a corner. We also investigate the periodic inversion and phase transition of Fresnel finite diffraction beams propagating in nonlocal nonlinear media via the fourth-order split-step fast Fourier transform(FFT)method in double precision.[39,40]Through the results of numerical simulations, we conclude that the intensity of the period of the Fresnel finite diffraction beam is strongly related to the degree of nonlocality. We also show that the nonlocal nonlinear medium exhibits a harmonic potential under a sufficiently high degree of nonlocality, causing the beam to fluctuate in an approximately cosine mode. In the 2D case,the beam undergoes two-phase oscillation and periodic inversion; during propagation, the process repeats, leading to a quasi-periodic breath-like phenomenon during evolution.
2. Theoretical model
2.1. Properties of Fresnel finite diffraction beam
We first consider the 1D case where we generated the Fresnel diffraction of plane waves from a straight edge located atx= 0. In this case, the equation describing the normalized amplitude of the Fresnel diffraction pattern can be written as[41]

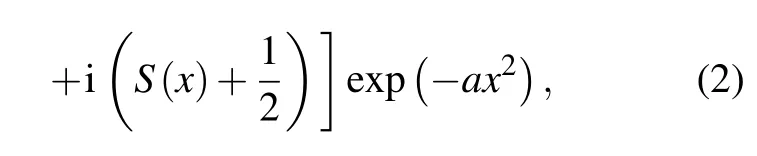
wherea>0 is the attenuation factor associated with the numerical aperture of the system. In Figs. 1(a) and 1(b), we show the diffracting beam intensity distributions and the numerically obtained streaks ofm(x)andn(x),respectively.The energy of the propagating beams described bym(x)is infinite,and the oscillating tails ofm(x)approach unity asx →∞.Contrarily,the oscillating tail of the transmitted beam described byn(x)approaches 0 asx →∞,which leads to a wave packet with finite energy. Moreover,the energy distribution ofn(x)is not symmetric under parity and may exhibit acceleration.
The linear Schr¨odinger equation for the slowly varying envelope of the paraxial wave packet in 1D free space or linear media can be written as
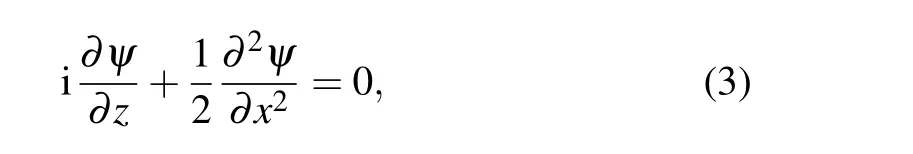
whereψ=n(x) is the Fresnel finite diffraction beam envelope. The variablexis the normalized transverse coordinate,andzis the normalized propagation distance-both of which are scaled by a characteristic transverse widthx0and the corresponding Rayleigh rangekx20. Here,k= 2πn/λ0is the wavenumber,nis the ambient index of refraction,andλ0is the wavelength in free space.[42,43]Figure 1(c) shows the evolution of the finite energy diffraction pattern in a linear medium.As shown by the white dashed curve, it is apparent that the beam accelerates to the left,and the intensity maximum of the beam accelerates during propagation along a parabolic trajectory. All self-accelerating linear beams display the same characteristics: the high-intensity part of the beam is accelerated,while the center of mass of the beam moves along a straight line instead of a parabola.
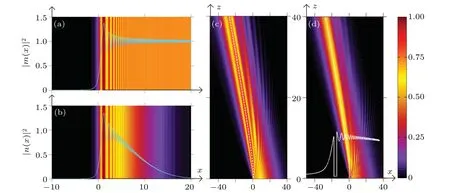
Fig.1. (a)Intensity|m(x)|2,(b)intensity|n(x)|2,for a=0.05. The background images in panels(a)and(b)depict the ideal and attenuated diffraction patterns. (c) Evolution of n(x) with the theoretical accelerating trajectory indicated by the white dashed curve. (d) The setup is similar to that in panel(c),except for the main lobe being initially cut out.
As shown in Fig. 1(d), the beam evolution indicates the“self-healing”property,and the inset panel represents the energy distribution of the beam atz=0. The main lobe of the beam is screened out initially but recovers quickly with an increase in the propagation distance. This is because energy is transferred from the tail to the head of the beam.
2.2. Dynamics of Fresnel finite diffraction beam in nonlocal nonlinear media
Next,we consider the case of a Fresnel diffraction beam propagating in a nonlocal nonlinear medium because the nonlinear medium has significant effects on the evolution of the beam. In a nonlinear medium, the diffracting beam is described by the following dimensionless nonlocal nonlinear Schr¨odinger equation(NNLSE):[33]


We performed numerical simulations of the propagation of a Fresnel diffraction beam with finite energy in a real space and a momentum space, as shown in Figs. 2(a) and 2(b), respectively. In Fig. 1(c), it can be seen that stationary solitons cannot exist in linear media. However, interestingly, the intensity of the finite energy Fresnel diffraction beam shows periodic repetitions, with the distribution exhibiting opposite bending directions in the region of strong nonlocality, as shown in Fig.2(a). Specifically,the propagation dynamics exhibit oscillatory properties,which cause the center of mass to oscillate back and forth in the optical axis for a certain period owing to the nonlocality.[44]The distributions of the intensities of these beams exhibit well-defined Airy-like profiles,with the main lobe and a decaying tail. Additionally, there exists a critical point at which the Airy-like beams no longer exhibit multi-peaked profiles,and instead propagate as asymmetric single-peaked beams. This process is repeated during propagation,leading to an unusual oscillation behavior.Moreover,slightly different phenomena are observed in a real space and a momentum space.As shown in Fig.2(b),when a Fresnel diffracting beam of finite energy evolves from a multi-peaked profile to a single-peaked profile in a real space,it evolves to a decaying tail in a momentum space.
Figures 2(c)and 2(d)show the curves of the peak intensity and the corresponding total powerP=∫|ψ(x,z)|2dxof the beam in a real space and a momentum space as a function of the propagation distance, respectively. It can be seen that the peak intensity of the beam follows a periodic pattern with four sets of maxima over a finite propagation distance,and the peak intensity in a momentum space always lags behind the peak intensity in a real space by half a period. Notably, although the peak intensity decreases gradually with increasing propagation distance, the total power remains approximately constant.[45]
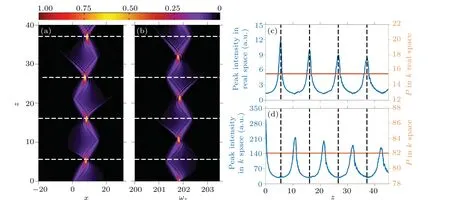
Fig.2. Propagation intensity patterns of the beam described by Eq.(4): (a)in a real space,and(b)in a momentum space. Peak intensity(blue curves),and total power(orange curves)by propagation distance: (c)in a real space,and(d)in a momentum space. Other parameters are w=5 and ρ =5. The unit a.u.is short for arb. units.


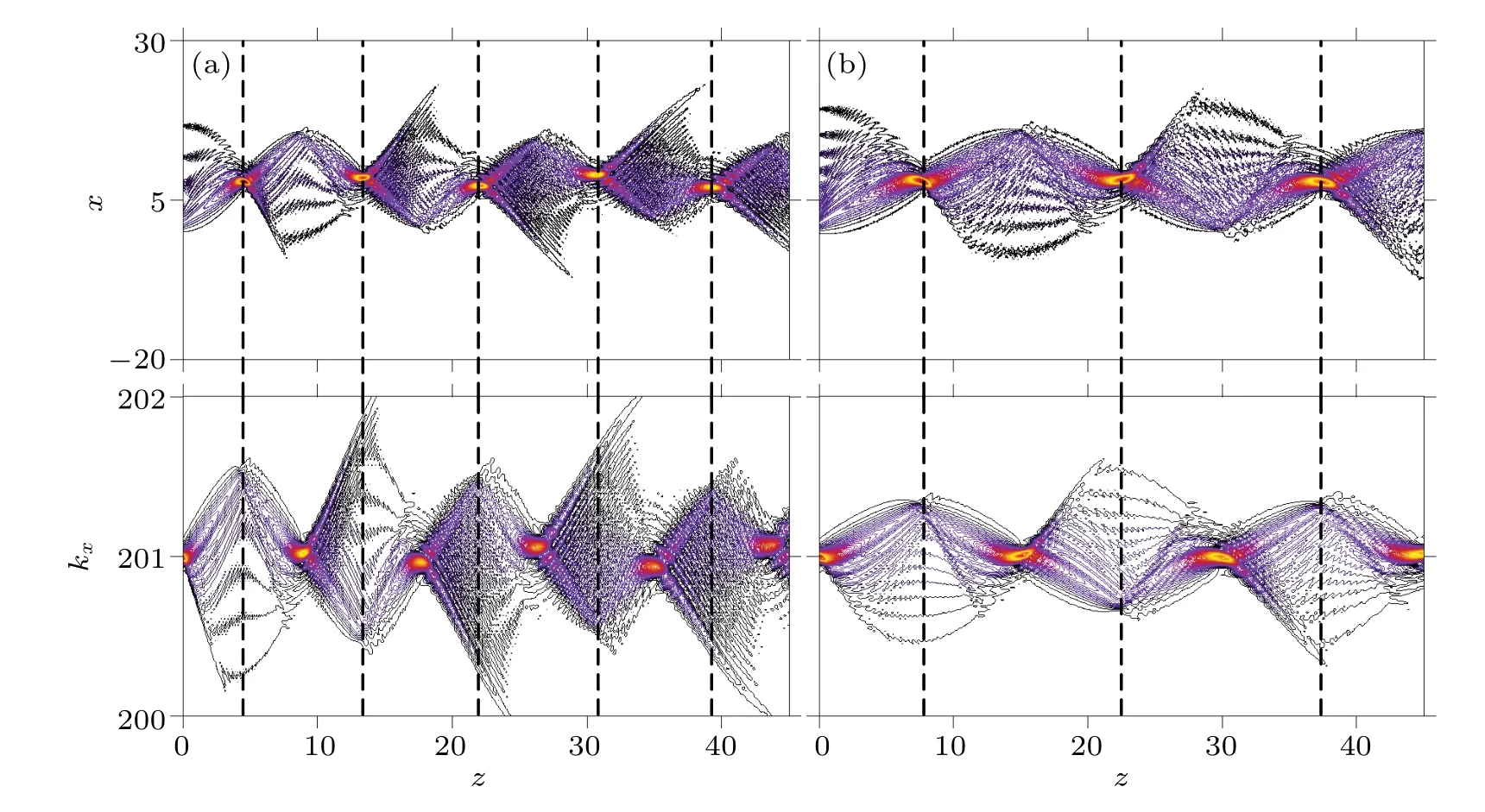
Fig.3. Evolution intensity contour lines patterns of finite-energy Fresnel diffraction beams according to Eq.(4)in real space and momentum space with different degrees of nonlocality. The parameters are the same as those in Fig.2,with(a)ρ =3 and(b)ρ =8.
3. Two-dimensional case
Next,we extend the Fresnel diffracted beam from one to two dimensions and analyze the properties of the diffracted beam in the 2D case. Our analysis shows that the beam is diffracted from a right angle located at the origin of the Cartesian coordinate system (x=0,y=0). The normalized equation describing the amplitude for the Fresnel diffraction pattern can be written as

From Fig.4(a),it is clear that the ideal 2D diffraction pattern based on Eq. (5) is not square-integrable, thereby yielding infinite energy. However, equation (6), which includes a Gaussian aperture function, has finite energy, as presented in Fig.4(b).Furthermore,by utilizing the Lorentz transformation of coordinates,the right-angle corner diffraction can be easily generalized to a 2D acute-or obtuse-angle Fresnel diffraction.In particular, when the angle of the corner is greater thanπ,the diffraction can be regarded as that from the corner of a wedge-shaped angle,and the analytical expression for an ideal diffraction pattern can be written as

Based on this formula and the Lorentz transformation,[47]the 2D Fresnel diffraction pattern from a wedge with an angle 0<θ<πcan be obtained. In Figs. 4(c) and 4(d), we show the infinite and finite diffraction patterns withθ=π/2, respectively.
Concurrently,the Fresnel diffracting beams with finite energy in a 2D nonlocal nonlinear medium exhibit equally interesting properties, including (but not limited to) characteristic periodic reversals and phase transitions in the propagation dynamics. According to the analysis presented in Ref.[48],this periodic behavior can be attributed to the linearity of the problem. The extension from 1D to 2D can be realized naturally,as the 2D case can be considered to be the product of two 1D cases. For the 2D propagation of a finite-energy Fresnel diffraction beam in the nonlocal nonlinear media,equation(4)should be modified as


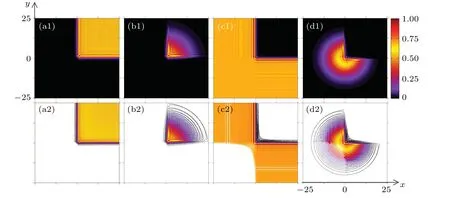
Fig. 4. Panels (a1) and (b1) are Fresnel infinite and finite diffraction patterns at a right-angled corner, respectively. Panels (c1) and (d1) are Fresnel infinite and finite diffraction patterns from a wedge with angle θ =π/2, respectively. The bottom panel shows the intensity contour lines patterns corresponding to the top panel. The decay factor is a=0.05.
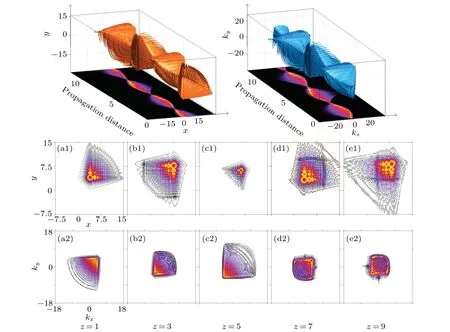
Fig. 5. Propagation of a 2D finite-energy Fresnel diffraction beam in nonlocal nonlinear media. Top panel: Iso-surface plot of the intensity during propagation. Panels (a1)-(e1) and (a2)-(e2) are intensity contour line patterns in a real space and a momentum space, respectively, when the beam propagates from z=1,3,5,7,and 9. The other parameters are w=10 and ρ =5.
As shown in Fig. 5, the three-dimensional (3D) surface plot in the top panel depicts that the beam undergoes twophase oscillations and a periodic inversion. In real space, the spatial intensity distribution of the beam decreases at first and subsequently increases. This process is repeated during propagation,thereby resulting in a quasi-periodic breath-like phenomenon in the evolution. However,in momentum space,the opposite process occurs,with the spatial intensity distribution tending to first increase and then decrease. As described before,in the case of the 2D cross-section,the intensity distribution changes in the real and momentum spaces in the opposite manner.
The oscillation process can be better understood in the projection of the 3D graph,similar to the cases in Figs.2 and 3. To further explore the phase transition,we show the intensity distribution of the beam at specific distances in Figs.5(a)-5(e),where the intensity snapshots are adopted from the same simulation at propagation distancesz=1, 3, 5, 7, and 9, respectively. It can be seen that the Airy-like intensity distribution oscillates between the first and third quadrants. Due to the finite energy,the 2D cross-section of the beam expands or contracts periodically within a limited range as the propagation distance increases.
4. Conclusion
In this study, we have theoretically and numerically demonstrated the propagation dynamics of finite-energy Fresnel diffraction beam in linear and nonlocal nonlinear media.In one dimension, we find that the finite-energy Fresnel diffraction beam accelerates to the left, and self-healing evolution occurs after a small barrier during linear propagation of the beam.In contrast,in the nonlocal nonlinear medium,the propagation dynamics of the 1D finite-energy Fresnel diffraction beam exhibit anomalous oscillation properties, causing the centroid to oscillate back and forth with certain periods across the optical axis, owing to the nonlocality. As the degree of nonlocality increases,the period becomes larger but the intensities of the beams always maintain an Airy-like profile,with the main lobe and a decaying tail. Additionally, we investigate the propagation of Fresnel diffraction from a corner of a different angle when the beam propagates in the 2D nonlinear medium. In particular,the Airy-like intensity profile oscillates between the first and third quadrants, and the process repeats during propagation, resulting in unique oscillations. Overall,our results not only demonstrate a novel accelerating beam but also contribute to the understanding of NNLSE and nonlinear optics.
- Chinese Physics B的其它文章
- Erratum to“Floquet bands and photon-induced topological edge states of graphene nanoribbons”
- Viewing the noise propagation mechanism in a unidirectional transition cascade from the perspective of stability*
- Nonlinear signal transduction network with multistate*
- Optical strong coupling in hybrid metal-graphene metamaterial for terahertz sensing*
- Any-polar resistive switching behavior in Ti-intercalated Pt/Ti/HfO2/Ti/Pt device*
- Magnetic two-dimensional van der Waals materials for spintronic devices*

