Effects of classical random external field on the dynamics of entanglement in a four-qubit system
Edwige Carole Fosso Fridolin Tchangnwa Nya Lionel Tenemeza Kenfack and Martin Tchoffo
1Research Unit of Condensed Matter,Electronic and Signal Processing,Department of Physics,Dschang School of Sciences and Technology,University of Dschang,PO Box: 67 Dschang,Cameroon
2Material Science Research Group,Physics Laboratory,Department of Physics,Post Graduate School,University of Maroua,PO Box: 814 Maroua,Cameroon
3Centre d’Etudes et de Recherches en Agronomie et en Biodiversite,Faculte d’Agronomie et des Sciences Agricoles,Universite de Dschang,Cameroun
Keywords: entanglement,qubit and classical random external field
1. Introduction
Quantum information theory (QIT) as the quantum analog of the classical information theory has attracted more attention so far. Although quantum mechanics and QIT were initially developed separately, it has emerged that they are in fact intimately related.[1]It has been evinced that quantum correlations present between parts of a composite quantum system represents a key resource in the field of QIT.The well-known example of quantum correlations is quantum entanglement.[2-4]Entanglement is a subtle non-local correlation that has no classical analog, which manifests itself in the event of measurement performed on any subsystems of a composite system.[5,6]In fact, measuring one of the subsystems of an entangled system will instantaneously influence the states of the other subsystems no matter how far they are from the subsystem being measured. This phenomenon of entanglement was first introduced in 1935 by Einstein, Podolsky, and Rosen[7]and later by Schr¨odinger.[8]Entanglement has been recognized as an indispensable resource, enabling tasks like quantum cryptography,[9]quantum information processing,[10,11]quantum teleportation,[12]measurement-based quantum computation.[20]Nonetheless,quantum entanglement does not exhaust the realm of quantum correlations. In fact, there exists a second kind of quantum correlations,namely,quantum discord,introduced by Ollivier and Zurek in 2001.[13]So far,quantum discord has proven to be a key resource for certain quantum communication tasks and computational models. Unlike entanglement, quantum discord can capture not only quantum correlations in entangled states but also in the separable states. Besides, under some conditions,QD can be more shielded from decoherence than entanglement.[14-17]Quantum correlations, namely, entanglement, and discord have been astonishingly successful for roughly a century now and beyond its explanatory power,they have enabled us to break new grounds in quantum technology. For instance, quantum correlations allow many tasks in quantum information processing which are classically impossible. Thus,knowledge and exploitation of quantum correlations existing between parts of a composite quantum system will revolutionize the world hundreds of billions of times. Unfortunately, quantum systems are unavoidably influenced by their surrounding environments. The interaction between the environment and the quantum systems of interest may lead to decoherence which is the main obstacle for the development of quantum technologies based on the manipulation of quantum correlations and consequently for the practical implementation of quantum computers.[21,22]In fact,the interaction of a quantum system with the environment makes its quantum correlations which are crucial ingredients for the development of quantum technologies disappear on the short-range time scale.However,it is important to note that in certain situations,decoherence can play a constructive role in affecting the quantum correlations of a system.[18,19]On the other hand, decoherence is very important for crucial issues such as the classicalquantum measurement problem or crossing. Therefore, it is very important to investigate how different kinds of environments affect the evolution of a quantum system to search for possible approaches to understand, control, and even protect either indefinitely or partially the quantum correlations of the emerged system.[24-26]
Emerging from this idea, many investigations have been done recently to understand the behaviors of quantum correlations in the multipartite system interacting with environments described either classically or quantum-mechanically.For instance, in 2012 Lo Francoet al.[24]investigated the revival of quantum correlations without system-environment back-action in a two-qubit system each locally subjected to a classical random external field (CREF) and explained that quantum correlations can revive also for classical independent environments in absence of back-action. They also showed that in such an environment,quantum correlations do not vanish any more when the probabilities of the field phase range from 0.5 to 1(the behavior is symmetric with respect to 0.5).Furthermore,in 2015 the dynamic of quantum correlations of three-qubit states driven by a CREF has been studied by Guoet al.[28]and their results show that tripartite quantum discord may be more robust than entanglement under such a classical environment. They also showed that under this classical field,entanglement displays periodically sudden death and revivals for GHZ-and W-type states and that the survival partial entanglement can be detected employing suitable entanglement witness operators.[28]In 2016, other authors addressed the sudden death and rebirth of entanglement for different dimensional systems driven by CREF.[29]They perceived that entanglement behaviors present decay, sudden death, sudden birth, and long-lived in some period. They also revealed that the systems of larger dimensions are more robust than those of smaller dimensions where entanglement decay smoothly,gradually,and vanish for a very short time.[29]
Therefore, it is clear that many authors have devoted more attention to the dynamics of quantum correlations under CREF.However,much of these works deal only with the case
where each qubit interacts locally with a CREF mode and are also limited to systems of two and three qubits/qutrit only. To the best of our knowledge, the case of a system of more than three qubits together with a situation in which all the qubits present in the system are embedded in one single non-local CREF mode or independent CREF modes with different field phase probabilities has not yet been investigated.
On the other hand, only a few authors investigated the time evolution of quantum correlations in multipartite quantum systems coupled to classical environmental noise.[30-35]More precisely, they focused on the dynamics of entanglement and quantum discord in three-qubit systems, prepared in Greenberger-Horne-Zeilinger (GHZ), W, or mixed GHZW states and subjected to a Gaussian or non-Gaussian noise classical noise. They observed that the entanglement can be indefinitely preserved when the qubits are coupled to a common source of classical noise. They also found that the configuration of the system-environment interaction and the input state of the system may have constructive or destructive impacts on the evolution of quantum correlations. Furthermore,entanglement sudden death (ESD) and entanglement revival(ER) phenomena have been observed and clearly explained.In 2018 the dynamics of entanglement in four-qubit GHZ-and W-type states interacting with a common or with independent classical random telegraph noise has been studied by Kenfacket al.[23]Their results revealed that the entanglement becomes highly protected from degradation when the number of qubits of the system is increased from two to three and then from three to four.
The present investigation aims to study the influence of the types of system-environment interactions together with the number of qubits on the behavior of quantum correlations(in terms of entanglement)in a system of four non-interacting qubits subjected to a classical phase noisy laser characterized by a classical random external field (CREF). We develop a general heuristic analysis when the qubits are initially prepared in the GHZ- and W-type states and then subjected to a classical field for two configurations of qubit-field interaction. In the first configuration, each qubit locally interacts with a CREF mode, the so-called local or independent environments interaction. In the second configuration, all the qubits are embedded in a unique common environment,the socalled non-local or common environment interaction.For each initially prepared state and qubit-field interaction, the evolution of entanglement is investigated for two configurations of the CREF,namely,the case of equal and different field phase probabilities. The amount of entanglement present in our system at any time is detected through suitable entanglement witnesses (EWs)[36]and quantified through genuine multi-qubit negativity.[20,23]
The paper is structured as follows. In Section 2, we introduce the system under consideration and describe its main features such as its Hamiltonian and time-evolution density matrix.Afterwards,we present the explicit definition of entanglement quantifiers and detectors. In Section 3,we investigate the dynamics of entanglement where we present both analytical and numerical results. Finally, the conclusion is given in Section 4.
2. Theoretical method
2.1. Physical model


2.2. Entanglement measures
We presented in this section the essential tools used for the analysis of the dynamics of entanglement. As said earlier,entanglement is detected through suitable EWs and quantified by means of the so-called four-partite negativity.
2.2.1. Entanglement witness
An entanglement witness is an hermitian operator which is able to detect entanglement in a given state. Indeed, the fundamental idea is that the expectation value of the witness operator for the total state under consideration exceeds certain bounds only when the total state is entangled. An expectation value of a witness operator within this bound however does not guarantee that the state is separable. As shown in Ref. [37],four qubits GHZ-type and W-type states in W-B class can be detected by means of the following witness operators,respectively:


Although the presence of entanglement in the system is indicated by negative expectation values of these operators, zero or positive expectative values do not guarantee the absence of entanglement.
2.2.2. Four-qubit negativity
The most useful and practical measure proposed to quantify the global amount of genuine entanglement of an arbitraryN-qubits entangled system in a mixed stateρ ≡ρ1,2,3,4,...,Nis given by the average of the bipartite entanglement measures over all the possible bi-partitions of theN-qubits system.[24]Its mathematical definition can be expressed as

For symmetrical four-partite system as in our case,the bipartite negativity in the different non-equivalent bipartitions of the system coincide. That is,N1|234=N2|341=N3|412=N4|123(fork=1)andN12|34=N13|24=N14|23(fork=2). Hence,the four-qubit negativity expressed by Eq.(8)is reduced to the following expression:
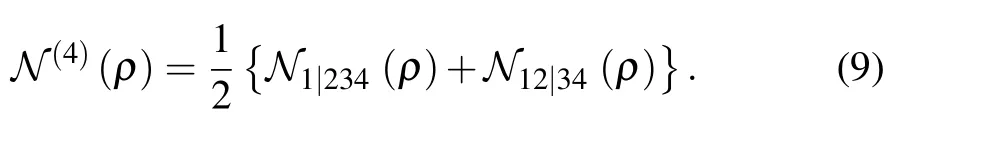
3. Results and discussion
In this section, to evaluate the impacts of the CREF, we address the time evolution of entanglement in the physical model introduced in the previous section. The evolution of entanglement will be investigated for two different configurations of the qubit-field interaction (independent and common environments)and field phase probabilities(different and equal field phase probabilities).
3.1. Independent environments
Here,due to the random nature of the field phase,the state of the system after a given interaction timetcan be written as



3.1.1. Entanglement witnesses
From the time-evolved states of system defined in Eqs. (A1) and (B1), the analytical expressions of the expectation values of the GHZ-type and W-type states witness operators can be written as follows:

In Fig. 1, we plot the evolution of the opposite of the expectation values of GHZ-type (upper panels) and W-type (lower panels)states witness operator as a function of dimensionless timegt,field phase probabilitypand purityr.
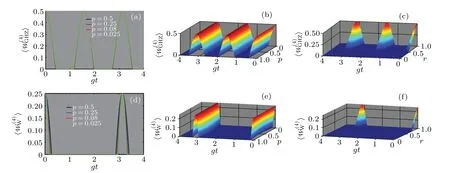
Fig.1. The upper panels display the evolution of the opposite of the expectation value of the GHZ-type states witness operator as a function of gt and field phase probability p both in 2D(a)and 3D(b)for r=1 and purity r(c)for p=1/2. The lower panels display the same information as the upper ones but for the W-type states witness operator.
We observe that the witness operators exhibits periodical oscillations with a periodt=π/2gfor GHZ-type states andt=π/gfor W-type states. This implies that the time interval over which entanglement is not detectable in the system is larger when the system is prepared in a W-type state than when it is prepared in a GHZ-type state.Such a result,therefore,implies that the GHZ-type states may shield entanglement from decoherence more than W-type states. Besides,panels(a)and(d) show that the expectation values of the GHZ and W witness operators vary just slightly with the increase of the field phase probabilityp. In fact, we observe that the expectation value of the witness operators decreases with a decrease ofpwhen p ranges from 0 to 0.5. However, it is important to notice that an opposite behavior occurs when the probabilityprange from 0.5 to 1. In panels(c)and(f),we observe that the amount of residual entanglement detected using the witness operators at any time gt depends on the purity of the initial state and decreases when it is decreasing. Finally,to compare the influence of the number of qubits on the robustness of the system,we focused on the curve generated forp=0.5(equal field phase probabilities)and then we observed that the residual amount of entanglement revealed using the witness operator is higher in the three-qubit system studied in Ref.[28]than in four-qubit system when they are initially prepared in Wtype states. However, the reverse situation is observed when the qubits are prepared in GHZ-type states. It is also observed that at the initial time, the GHZ-type states witness operator detect entanglement only for initial states withr<7/15 for a four-qubit system andr<3/7 for a three-qubit system. On the other hand, the W-type states witness operator detect entanglement only for initial states withr<3/4 for a four-qubit system andr<5/8 for a three-qubit system.
3.1.2. Four-qubit negativity
The evaluation of entanglement in terms of four-qubit negativity has been expressed in Eq. (8). Note that we will focus only on the numerical results since the analytical results are not very enlightening and cannot also be written in compact forms. In fact, due to the high dimension and a large number of parameters in the density matrix, the computation of compact analytical eigenvalues is a complex task even for a computer algebra tool.
In Fig.2,we plot the evolution of the four-partite negativity in the case of GHZ-type(upper panels)and W-type(lower panels) states as a function of dimensionless timegt(panels(a) and (d)), bothgtand field phase probabilityp(panels (b)and(e))and bothgtand purityr(panels(c)and(f)).
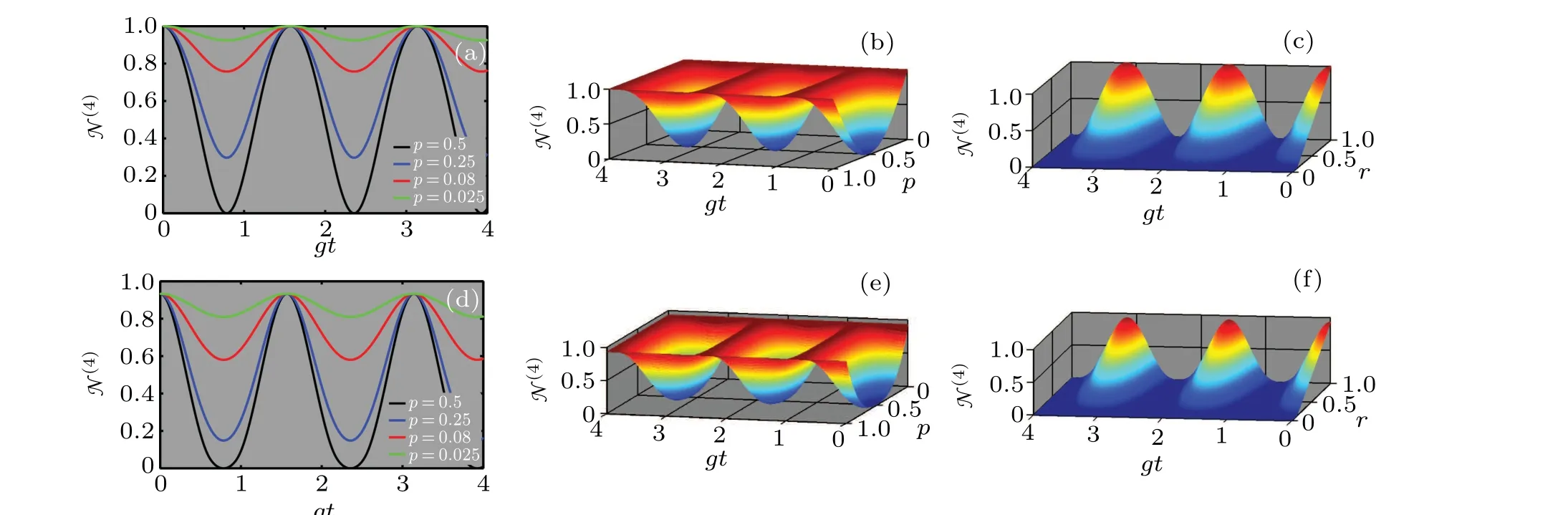
Fig. 2. The upper panels display the evolution of the four-partite negativity N(4) for GHZ-type states as a function of: gt and field phase probability p both in 2D (a) and 3D (b) with r=1; gt and purity r (c) with p=1/2. The lower panels display the same information as the upper ones but for the W-type states.
We remark that this figure presents un-damped oscillating functions of time with the same periodt=π/2gboth for GHZtype(panels(a)and(b))and W-type(panels(d)and(e))states.Other remarkable features that can be observed are the appearance of sudden death and revival phenomena forp=0.5 and freezing dynamics(forpranging from 0 to 0.45),although the four qubits interact with a classical noise.However,because of the classical nature of the noise investigated,these phenomena of entanglement revivals can here be interpreted by referring to the intrinsic features of the qubit’s dynamics namely their non-Markovianity. Also,this figure exhibits in panels(a)and(d)that entanglement decays exponentially with time to a certain saturation value and then revives up to its initial value.It can also be seen that the saturation value of entanglement increases with the decreasing of the probabilityp. Panels(b)and (e) show that the behavior of entanglement for a given probabilitypcchosen in the interval [0,0.5] is symmetric to one obtained with a probability 1?pc. Such a result implies that whatever is the initial phase of the CREF, entanglement always exhibits the same qualitative and quantitative behavior with the increasing ofpcfrom 0 to 0.5 or decreasing of 1?pcfrom 1 to 0.5. Panels (c) and (f) present both for the GHZ-type and W-type states,that the initial amount of entanglement presents in the system as well as the amplitudes of entanglement revivals decreases with the decrease of the purity of the initial state. These observations can be interpreted by noticing that a decrease in purity yields an increase in the degree of mixedness of the initial state.
On the other hand,these results agree with those obtained through entanglement witness operators previously. It is also observed that the GHZ-type states have strong entanglement dynamics under local CREF than the W-type ones. In fact,for the same degree of purity (r=1) and values of the field phase probabilities(p=0.025 for example),it is observed that the saturation values of entanglement or simply the residual amount of entanglement in the system at the end of the evolution is higher for the case of GHZ-type states (12) than for W-type states(13). Such a result appears to be consistent with the one presented in Ref. [23] where the authors investigated the dynamics of quantum correlations in a four-qubit system under random telegraph noise with both common and independent environment coupling.
Finally,to compare how the dynamics of entanglement is affected by the number of qubits in the system,we focus on the case of EFPP and compared the results with those presented in Ref. [28] for a three-qubit system. We observed that when the qubits are prepared in the W-type states,the time takes by entanglement to revive after its death or simply the time during which there is no longer entanglement in the system (the so-called dark period)is approximately the same both for the three-qubit and four-qubit models. On the other hand, when there are instead prepared in GHZ-type states, the dark period in the three-qubit model is larger than in the four-qubit model, implying that entanglement becomes more shielded from degradation when the number of qubits in the system is increased. This result demonstrates the robustness of the fourqubit GHZ-type states against the detrimental effects of the local CREF over the three-qubit model. It agrees with those obtained in Ref.[23]with different models.
3.2. Common environment

From this definition, the statesρ(t) of the system when the qubits are prepared in the GHZ-type and W-type states have been obtained as given in Eqs.(A3)and(B2)of the appendix.
3.2.1. Entanglement witness
From the time evolved state of the system,the expectation value of entanglement witnesses results into
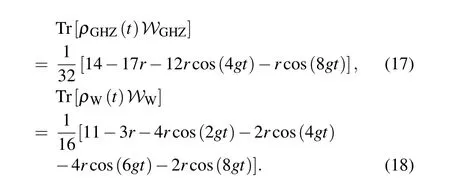

Fig.3. The upper panels display the evolution of the opposite of the expectation values of the GHZ-type state entanglement witness operator as a function of gt with r=1(a)and both gt and r(b). The lower panels display the same information as the upper ones but for W-type state entanglement witness operator.
It is important to note that contrarily to the case of independent environments, these expressions arep-independent.In Fig.3,the evolution of the opposite of the expectation values of GHZ-type (upper panels) and W-type (lower panels)states witness operator is plotted as a function of dimensionless timegt, and bothgtand purityr. It is observed that the dynamics of the opposite of the expectation value of the GHZ-type and W-type states witness operator present periodical oscillations with almost the same period as in the case of independent environments coupling. Similarly, to the case of independent environments, we observe that the amount of entanglement detected through witness operators depends on the purity of the initial state. In fact,the larger the purity,the stronger is the entanglement dynamics. Also, the efficiency of the witness operators in detecting entanglement is almost insensitive to system-environment interaction.
3.2.2. Four-qubit negativity
As for independent environments interaction we will focus only on numerical results since the computation of analytical eigenvalues is a hard task due to the high dimension of the system and large number of parameters in the density matrix.Hence,Fig.4 depicts the evolution of entanglement against dimensionless timegtand field phase probabilityp(panels (b)and(e))and bothgtand purityr(panels(c)and(f)).
It is immediately observed that this figure presents undamped oscillating functions of time with the periodt=π/8gfor GHZ-type states andt=π/2gfor W ones. This implies that the range of time for survival entanglement when the system is prepared in GHZ-type states is longer than when the system is instead prepared in W-type states. Hence,GHZ-type states have strong dynamics under non-local CREF as compared to W-type states. This figure also displays entanglement freezing dynamics and revival phenomena no matter what is the value of field phase probability and no sudden death occurs,implying that entanglement is not completely suppressed by the detrimental impact of the CREF.This of course demonstrates that common environment configuration coupling performs an efficient role in suppressing the detrimental effects induced by the CREF and thereby in delaying the decay rate of entanglement. In fact, the common environment coupling induces an indirect interaction between the qubits which then favors the protection of their entanglement. Hence, common environment configuration offers an alternative and more efficient strategy to completely shield the system from the detrimental effects of decoherence induced by a CREF.Additionally,it is observed in panels(a)and(d)that entanglement falls slightly with time to a certain saturation value and then revive up to its initial value. Similarly to the case of independent environments, it is observed that the saturation value of entanglement increases with the decreasing of the probability p forp ∈[0,1/2] meanwhile the reverse situation occurs forp ∈]1/2,1]. On the other hand,panels(c)and(f)present both in the GHZ- and W-type states that the initial amount of entanglement presents in the system,as well as the amplitude of entanglement revival, also decreases with the decrease of the purity of the initial state. Such a behavior can be ascribed here to the fact that the decrease of the purity results in the reduction of cohering property of quantum states. This figure also reveals that entanglement dynamics under non-local CREF is stronger in the GHZ-type states than in the W-type states, in agreement with what has been observed earlier for the case of independent environments coupling configuration. Overall,we find that the dynamics of entanglement can be efficiently controlled by properly adjusting the input state of the qubits,the field phase probability of the CREF and the qubit-field coupling configuration, namely independent environments or common environment.
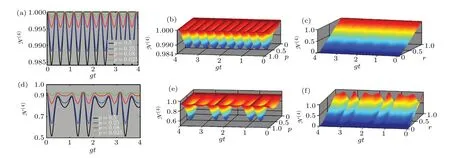
Fig. 4. The upper panels display the evolution of the four-partite negativity N(4) for GHZ-type states as a function of: gt and field phase probability p both in 2D (a) and 3D (b) with r=1; gt and purity r (c) with p=1/2. The lower panels display the same information as the upper ones but for the W-type states.
4. Conclusion
In this paper, we have investigated the dynamics of entanglement in a non-interacting four-qubit system initially prepared in GHZ-and W-type states and then subjected to classical random external field (CREF) in two different qubit-field interactions namely independent environments and common environment. We consider a CREF with a random phase taking two values especially 0 andπwith different probabilities.The dynamics of entanglement have been quantified employing multiqubit negativity and detected using suitable witness operators.
We find that entanglement exhibits un-damped oscillating evolution over time, regardless of the input state, qubit-field coupling configuration, and field phase probabilities considered. We find that the behavior of entanglement for a given probability pc chosen in the interval [0,0.5] is symmetric to one obtained with a probability 1?pc. In other words, we find that no matter is the input state of the qubit and the qubitfield coupling setup, entanglement always exhibits the same qualitative and quantitative behavior with the increasing of pc from 0 to 0.5 or decreasing of 1?pcfrom 1 to 0.5. Especially when the qubits are coupled in independent environments,we find that sudden death and revivals of entanglement occur only forp=0.5 (equal field phase probability) meanwhile freezing dynamics are observed for other values ofp. However,in the case of common environment interaction,entanglement exhibits freezing dynamics even forp=0.5. That is, entanglement is shielded from decoherence no matter what is the value of the field phase probability. In fact, we demonstrate that the coupling of the qubits in a common environment is an alternative and more efficient strategy to completely shield the system from the detrimental impacts of the decoherence process induced by a CREF,independently on the input state and the field phase probabilities considered.On the other hand,we find that GHZ-type states have strong dynamics under CREF as compared to W-type states,independently on the qubit-filed coupling setup. Besides, we find after comparing our results with the case of three qubits system investigated in Ref. [28]that entanglement becomes more shielded from degradation when the number of qubits in the system is increased. Also,we find that the dynamics of entanglement can be efficiently controlled by properly adjusting the input state of the qubits,the field phase probability of the CREF, and the qubit-field coupling configuration. Given that the preservation of entanglement is crucial for development and quantum information processing devices and that the theoretical model proposed in this work allows us to achieve entanglement freezing dynamics,we believe that our study can be relevant for the development of quantum technologies.
Appendix A: Time evolved density matrices of the system: The case of GHZ-type states
A1: Independent environments
The explicit evaluation of the time-evolved density matrix of the system is obtained using Eq. (10) when the qubits are initially prepared in the GHZ-type states of Eq.(12). For this input configuration,we find that the density matrix of the system at a given time takes the following form:
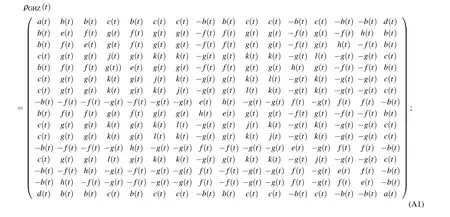
where
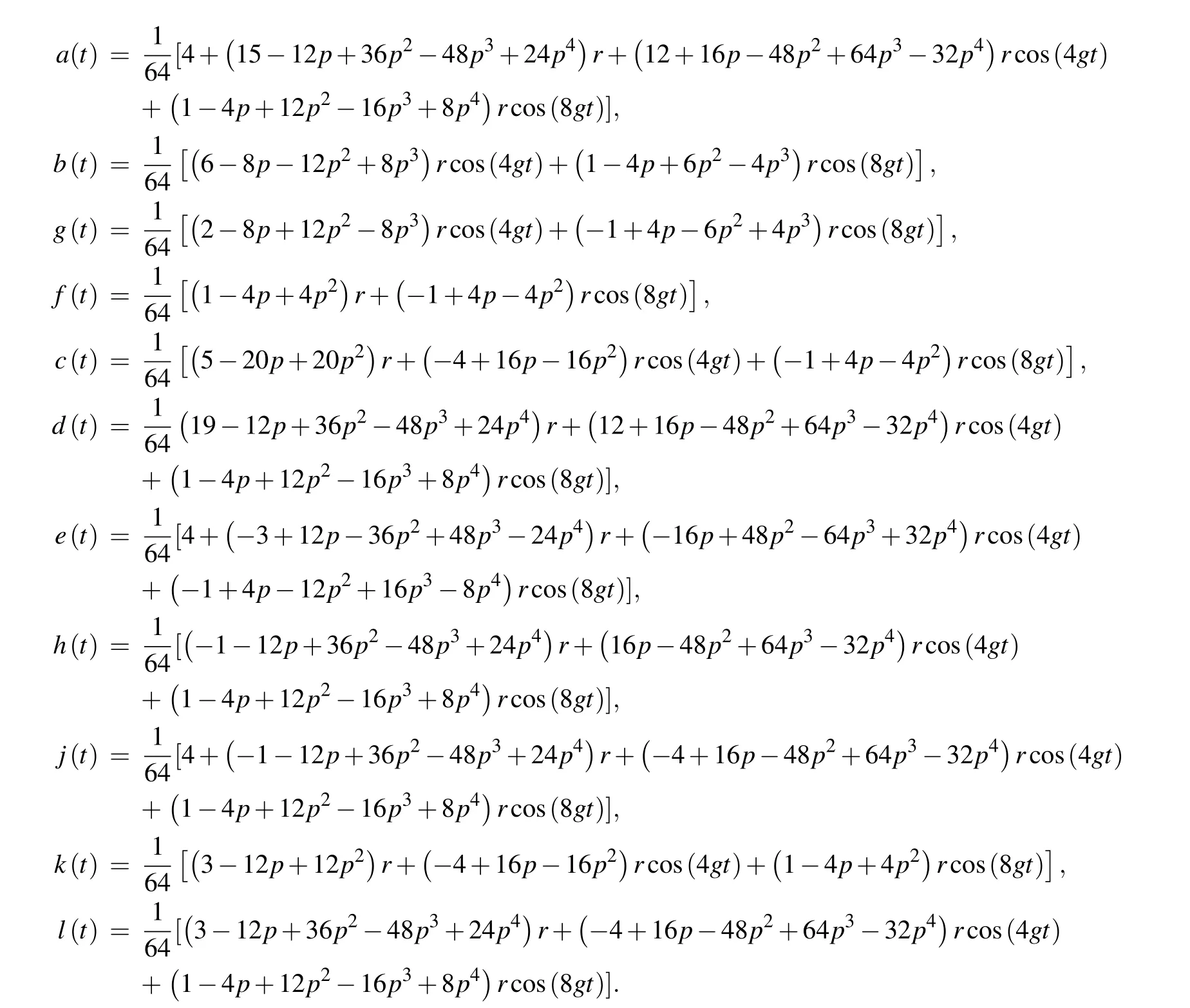
A2: Common environment
On the other hand,when the subsystems are coupled to the CREF in a common environment,the density matrix is obtained using Eq.(16)when the qubits are initially prepared in the GHZ-type states of Eq.(12). For this input configuration,we find that the density matrix of the system at a given time describing the time evolution of the system takes the form
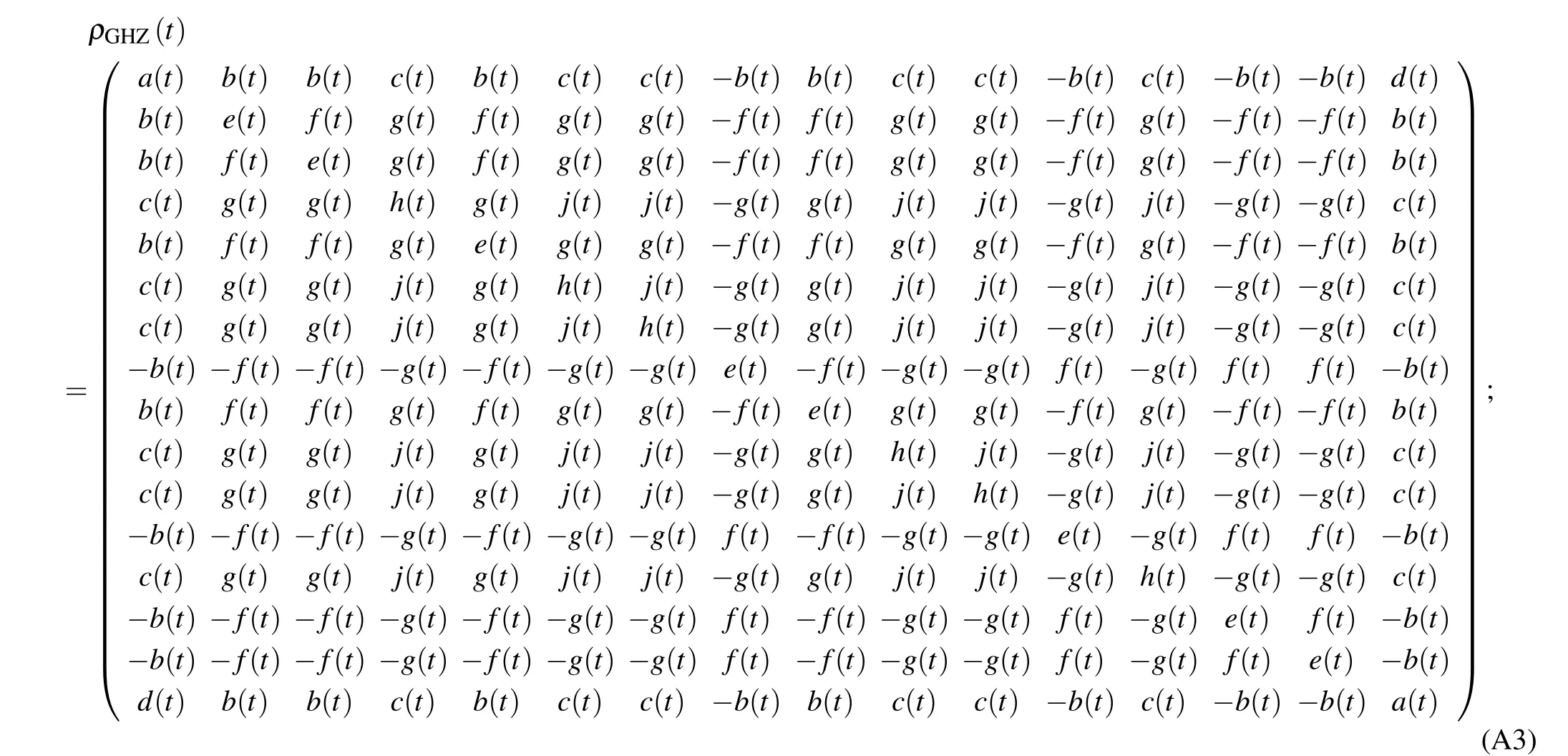
where

Appendix B:Time evolved density matrices of the system: The case of W-type states
B1: Independent environments
The explicit evaluation of the time-evolved density matrix of the system is obtained using Eq. (10) when the qubits are initially prepared in the W-type states of Eq.(13). For this input configuration,we find that the density matrix of the system at a given time takes the following form:


B2: Common environment
On the other hand,when the subsystems are coupled to the CREF in a common environment,the density matrix is obtained using Eq.(16)when the qubits are initially prepared in the W-type states of Eq.(13). For this input configuration,we find that the density matrix of the system at a given time describing the time evolution of the system takes the form

- Chinese Physics B的其它文章
- Erratum to“Floquet bands and photon-induced topological edge states of graphene nanoribbons”
- Viewing the noise propagation mechanism in a unidirectional transition cascade from the perspective of stability*
- Nonlinear signal transduction network with multistate*
- Optical strong coupling in hybrid metal-graphene metamaterial for terahertz sensing*
- Any-polar resistive switching behavior in Ti-intercalated Pt/Ti/HfO2/Ti/Pt device*
- Magnetic two-dimensional van der Waals materials for spintronic devices*

