Connes distance of 2D harmonic oscillators in quantum phase space*
Bing-Sheng Lin(林冰生) and Tai-Hua Heng(衡太驊)
1School of Mathematics,South China University of Technology,Guangzhou 510641,China
2Laboratory of Quantum Science and Engineering,South China University of Technology,Guangzhou 510641,China
3School of Physics and Material Science,Anhui University,Hefei 230601,China
Keywords: Connes distance,noncommutative geometry,harmonic oscillator
1. Introduction
In quantum physics, the physical quantities are represented by some operators in a Hilbert space. Some of the operators are noncommutative with each other. So it is natural to study physical systems by noncommutative geometry. In the 1980’s, Connes formulated the mathematically rigorous framework of noncommutative geometry.[1]Many kinds of noncommutative spaces have been studied by physicists and mathematicians, such as the Moyal plane and fuzzy space.[2-11]The phase space in quantum mechanics is also a Moyal-type noncommutative space, because the position and momentum operators satisfy the noncommutative Heisenberg algebras.
Due to the noncommutativity,there is no traditional point in a noncommutative space. This is different from normal commutative spaces. We only have states in noncommutative spaces. In a noncommutative space, a pure state is the analog of a traditional point in a normal commutative space,and the spectral distance between pure states corresponds to the geodesic distance between points. So there is no normal distance between two points in a noncommutative space,but we can calculate some kinds of distance measures between the states, such as the Connes distance.[12]Many researchers have already studied the Connes distance in some kinds of noncommutative spaces.Bimonteet al.calculated the distances between the points of a lattice on which the usual discretized Dirac operator has been defined.[13]Cagnacheetal.have studied the Connes spectral distance in the Moyal plane.[14]They explicitly computed Connes spectral distance between the pure states which corresponding to eigenfunctions of the quantum harmonic oscillators. Martinettiet al.have studied the metric aspect of the Moyal plane from Connes’noncommutative geometry point of view.[15]They obtained the spectral distance between coherent states of the quantum harmonic oscillator as the Euclidean distance on the plane.They also computed the spectral distance in the so-called double Moyal plane. D’Andreaet al.have studied the Pythagoras’ theorem in noncommutative geometry.[16]They showed that for non-pure states it is replaced by some Pythagoras inequalities. Franco and Wallet also studied metrics and causality on Moyal planes.[17]Scholtz and his collaborators have done many works on the studies of Connes spectral distances in Moyal plane and fuzzy sphere.[18-20]They developed the Hilbert-Schmidt operatorial formulation,and obtained the distances of harmonic oscillator states and also coherent states.Kumaret al.used Dirac eigen-spinor method to compute spectral distances in doubled Moyal plane.[21]Chakrabortyet al.also studied the spectral distance on Lorentzian Moyal plane.[22]
In the present work, we consider the Connes distance of the quantum states (namely the Fock states) of 2D harmonic oscillators. It is known that in noncommutative spaces, for example, the quantum phase space, due to the noncommutativity, there are no simultaneous eigenstates such as|?xi,?pi〉.Therefore there is no traditional coordinate representation in the whole quantum phase space. So in order to describe the states of physical systems in noncommutative spaces,one need some other representations. For example,Fock state representation and coherent state representation.These representations are powerful tools for the studies of physical systems in noncommutative spaces.[5]Fock state representation is one of the simplest and most useful representations in quantum mechanics. The Fock states can be regarded as the discrete points of the abstract background space. So one can obtain some information of geometric structures of the noncommutative spaces and also the physical properties of quantum systems by studying the mathematical structure of Fock states in noncommutative spaces, such as the Connes spectral distance. Actually, some researchers have already studied the Connes distance between the states of one-dimensional (1D) harmonic oscillators.[14,18,20]But we find that the calculations and results of the Connes distance of 2D harmonic oscillators are much more complicated than those of 1D oscillator system.So it is significant to study the explicit formulae of the Connes distance of 2D harmonic oscillator systems. The method used in the present work is also different from those used in the literatures.
This paper is organized as follows. In Section 2, we consider the 4D quantum phase space and construct a corresponding spectral triple. Using the Hilbert-Schmidt operatorial formulation, we construct a boson Fock space and a quantum Hilbert space,and obtain the Dirac operator. In Section 3, we review the definition of Connes spectral distance,and derive some inequalities corresponding to the ball condition. Based on these inequalities, we derive some constraint relations about the optimal elements in Section 4. The Connes distance between two Fock states of 2D harmonic oscillators is calculated in Section 5. Some discussions and conclusions are given in Section 6. Some calculation details of the Dirac operator and the Connes spectral distances are presented in Appendix A and Appendix B.
2. The 4D quantum phase space and spectral triple


Furthermore,one can construct the following quantum Hilbert space:

where tr?(·)denotes the trace overF.
The quantum phase space (4) is also a Moyal-type noncommutative space. In general,a noncommutative space corresponds to a spectral triple (A,H,D) withAan involutive algebra acting on a Hilbert spaceH,andDis the Dirac operator onH.[1]Moyal spaces are non-compact spectral triples.[4]One can construct a spectral triple(A,H,D)for the 4D quantum phase space(4)as follows:

3. Connes spectral distance and ball condition
The Connes spectral distance between two statesωandω'is defined as[12]

The inequality in formula(16)is the so-called ball condition.
Similar to Ref.[18],here we only consider the case where the quantum statesωare normal and bounded so that they are representable by density matricesρ. The action of the stateωon an elemente ∈Acan be written as

Suppose the quantum statesωandω'correspond to the density matricesρandρ',respectively. We have



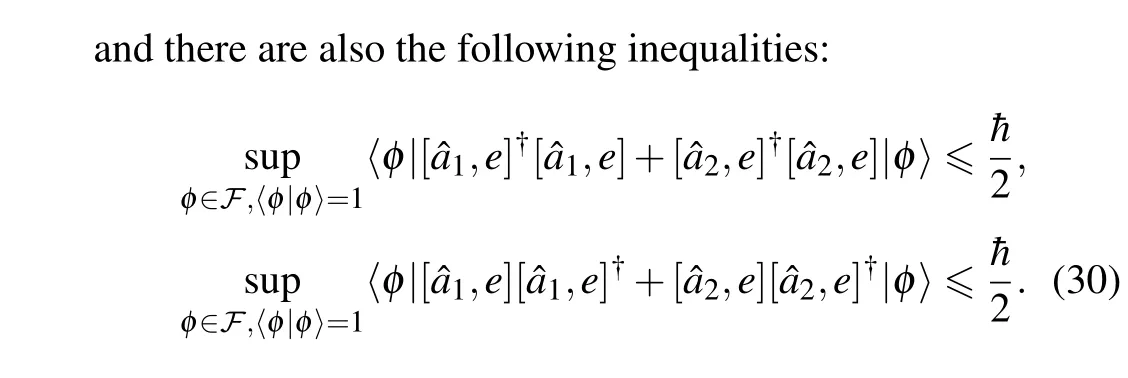
4. Optimal element and constraint relations
Consider the 2D harmonic oscillator states|p,q〉and|m,n〉, and the corresponding density matrices areρp,q=|p,q〉〈p,q| andρm,n=|m,n〉〈m,n|. The Connes distance between these two states is
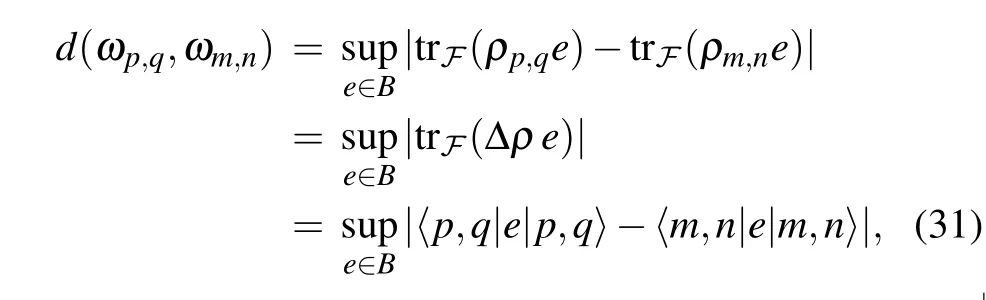


For the elemente[Eq. (32)], using the relations (7), we have
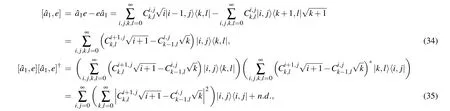
where“n.d.”denotes the sum of terms|k,l〉〈i,j|withk ?=iand/orl ?=j,and these terms can be ignored in the calculations in the following content.



5. Connes distance between harmonic oscillator states
Now let us explicitly calculate the Connes distances between the quantum states of 2D harmonic oscillators. First,let us consider the adjacent states|m+1,n〉and|m,n〉, and the corresponding Connes distance is


Obviously,there isζi;j=?ζj;iandζi;i=0.
In order to attain the supremum of|cm+k,n ?cm,n|,for example,one can choose
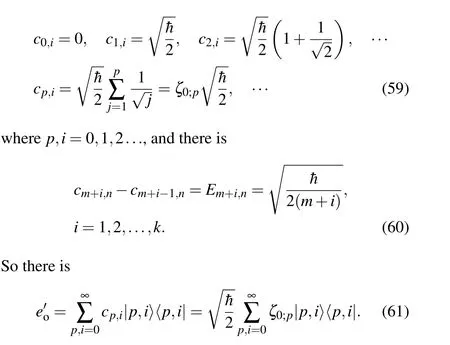

These results coincide with the results of the Connes distance between the quantum states of 1D harmonic oscillators in Refs.[14,18,20]. This means that the Connes spectral distance between the states|m,n〉and|m+k,n〉of 2D harmonic oscillators is the same as that between the states|m〉and|m+k〉of 1D harmonic oscillators.
Similarly,there is

Furthermore, using the above method, one can find that for any integersm,n,k,l≥0,the Connes distance between the states|m,n〉and|k,l〉is(see Appendix B for more details)

So these spectral distances also satisfy the Pythagoras theorem. This also coincides with the result in Ref.[16].
Furthermore, one can also analyse the Connes distance between mixed states. But usually,the calculations and results will be much more cumbersome.
6. Discussion and conclusions
In this paper, we study the Connes distance of quantum states of 2D harmonic oscillators in phase space. By virtue of the Hilbert-Schmidt operatorial formulation, we construct a boson Fock space and a quantum Hilbert space, and obtain the Dirac operator and a spectral triple corresponding to a 4D quantum phase space. From the ball condition, we obtain some constraint relations about the optimal elements. Using these constraint relations, we derive the explicit expressions of the Connes distance between the states of 2D quantum harmonic oscillators.
We find that the Connes distance between two arbitrary Fock states is not just a simple sum of distances of adjacent Fock states. Furthermore,these spectral distances also satisfy the Pythagoras theorem. The calculations and results of the Connes distance of quantum states of 2D harmonic oscillators are much more complicated than those of the states of 1D harmonic oscillators. These results are not just trivial generalizations of the result of 1D case. Our method used in the present work is also different from those used in the literatures. So these results are significant for the study of the Connes distances of physical systems in noncommutative spaces.
Here we only analyse the Connes distance between two pure states. One can also study the distance between two mixed states. Furthermore, one can use our method to study the Connes distance between the quantum states of higherdimensional harmonic oscillators.But usually the calculations and results will be much more complicated.
We are still exploring the intuitive physical meaning of these distances of physical systems. Our methods can be used to study other physical systems in other kinds of noncommutative spaces. We hope that our results can help to study the mathematical structures and physical properties of noncommutative spaces.
Appendix A: Dirac operator for 4D quantum phase space
Similar to Ref. [20], in order to construct the Dirac operator for the 4D quantum phase space, one can consider the following extended noncommutative phase space in which the coordinate operators ?Xi, ?Yi, and ?Pi, ?Qisatisfy the following commutation relations:[24,25]

and the Dirac operator(A3)can be expressed as

Appendix B: Calculations of the distance between|m,n〉and|m+k,n+l〉
First, let us consider the states|m+1,n+1〉and|m,n〉,and the corresponding Connes distance is





It is easy to verify that,these results(B26)and(B27)are also true fork<0 and/orl<0.
- Chinese Physics B的其它文章
- Erratum to“Floquet bands and photon-induced topological edge states of graphene nanoribbons”
- Viewing the noise propagation mechanism in a unidirectional transition cascade from the perspective of stability*
- Nonlinear signal transduction network with multistate*
- Optical strong coupling in hybrid metal-graphene metamaterial for terahertz sensing*
- Any-polar resistive switching behavior in Ti-intercalated Pt/Ti/HfO2/Ti/Pt device*
- Magnetic two-dimensional van der Waals materials for spintronic devices*

