2020年全國Ⅲ卷理科數(shù)學(xué)第23題的探究與推廣
2021-10-22 14:02:22廣東省中山紀(jì)念中學(xué)528454鄧啟龍
中學(xué)數(shù)學(xué)研究(江西) 2021年9期
關(guān)鍵詞:探究
廣東省中山紀(jì)念中學(xué) (528454) 鄧啟龍
高考真題設(shè)a,b,c∈R,a+b+c=0,abc=1.
(1)證明:ab+bc+ca<0;


首先給出第(1)問的三種證明方法.

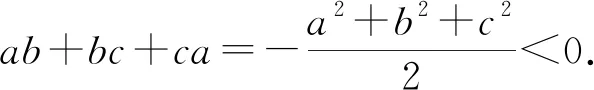
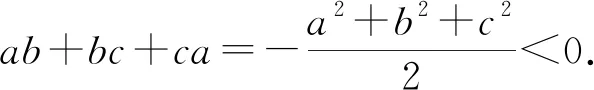

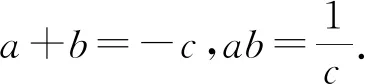
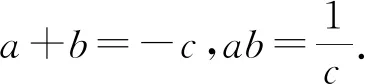


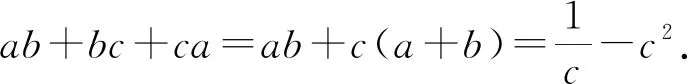
由(a+b+c)2=a2+b2+c2+2(ab+bc+ca)=0得a2+b2+c2=-2(ab+bc+ca),于是得到以下結(jié)論:
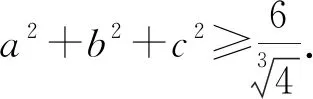
結(jié)論3 設(shè)a,b,c∈R,a+b+c=0,abc=1,則a3+b3+c3=3.
證法一:由a+b+c=0得c=-a-b,所以a3+b3+c3=a3+b3-(a+b)3=a3+b3-(a3+3a2b+3ab2+b3)=-3ab(a+b)=3abc=3.
證法二:由恒等式a3+b3+c3-3abc=(a+b+c)(a2+b2+c2-ab-bc-ca)得a3+b3+c3=3abc=3.





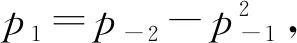
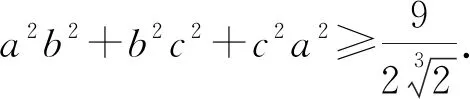
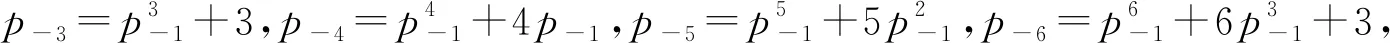



證明:當(dāng)n=1,2,3時,結(jié)論顯然成立.

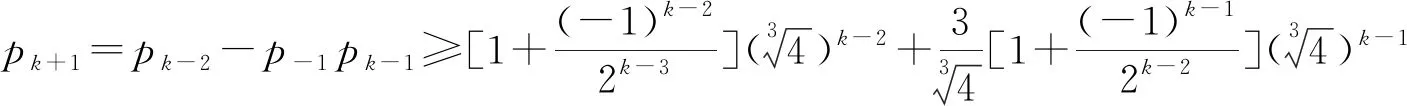
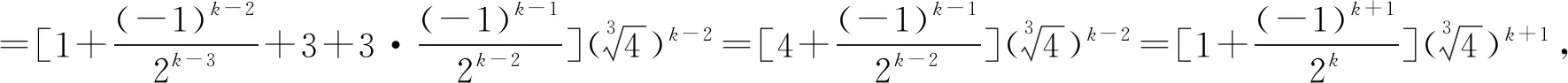
最后,本文提出以下猜想:
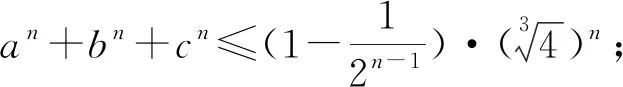
猜你喜歡
中國交通信息化(2023年11期)2023-12-26 07:43:50
中學(xué)生數(shù)理化·高三版(2023年1期)2023-09-04 09:24:31
中學(xué)生數(shù)理化·七年級數(shù)學(xué)人教版(2022年5期)2022-06-05 07:51:48
中等數(shù)學(xué)(2021年11期)2021-02-12 05:11:46
今日農(nóng)業(yè)(2019年14期)2019-09-18 01:21:42
快樂語文(2018年13期)2018-06-11 01:18:16
中等數(shù)學(xué)(2018年11期)2018-02-16 07:47:42
中學(xué)生數(shù)理化·高一版(2017年5期)2017-06-07 07:09:32
中學(xué)數(shù)學(xué)雜志(初中版)(2016年4期)2016-10-08 09:21:22

