Effect of the particle temperature on lift force of nanoparticle in a shear rarefied flow*

Jun-Jie Su(蘇俊杰), Jun Wang(王軍), and Guo-Dong Xia(夏國(guó)棟)

MOE Key Laboratory of Enhanced Heat Transfer and Energy Conservation,Beijing Key Laboratory of Heat Transfer and Energy Conversion,Beijing University of Technology,Beijing 100124,China

Keywords: shear lift force,nanoparticle,temperature effect,gas kinetic theory

1. Introduction

Nanoparticles (NPs) play a crucial role in many industrial processes and natural phenomena in a variety of fields including aerosol technology,[1,2]material synthesis,[3,4]environmental science,[5,6]and biology.[7,8]In these applications,the nanoparticles are usually suspended in a gas. Owing to the gas-particle collisions,the nanoparticles are subjected to various forces. The force perpendiculars to the flow direction due to the flow velocity gradient in a shear flow is termed as shear lift force and was first observed by Poiseuille.[9]

Since the shear lift phenomenon is of considerable importance in practical applications, many previous theoretical and experimental studies have been conducted to investigate the lift force on particles in a shear flow.[10,17]The theoretical challenge is to calculate the momentum transfer from the surrounding gas to the particle during the gas-particle collisions, which strongly depends on the flow regime of the particle. Since the molecular mean free path is in the order of 100 nm for the gas in standard conditions. Thus for nanoparticles with radius in a few nanometers,the flow regime should be in the free molecule regime (Kn=λ/Lc?1, whereλis the mean free path of a gas molecule andLcis the characteristic size of the particle). In the free molecule regime,the gas kinetic theory can be employed to evaluate the forces on the suspended particles.[18,19]For a spherical particle in a weak shear flow of a highly rarefied gas(withKn ?1),the expression for the shear lift force is given by Liu and Bogy[13,14]

whereρis the density of the fluid,Gdenotes the velocity gradient of the shear flow,Ris the radius of the sphere, andVis the relative velocity between the particle and the fluid.In Eq. (1), the calculations are restricted to the case of rigidbody collisions(i.e.,hard collisions)between the gas molecule and the particle. However, it has been verified that the rigidbody collision assumption can be invalid as the particle size approaches to the nanoscale.The gas-nanoparticle intermolecular interactions(for example,van der Waals interactions[20,21]or the ion-induced dipole interactions when the particle is charged[22])should be taken into account.[23-26]Luoet al.[16]theoretically investigated the shear lift of spherical nanoparticles in a shear rarefied gas flow and obtained the analytical expression for the shear lift force

In previous theoretical analyses on the shear lift,it is usually assumed that the particle temperatureTpis equal to the surrounding gas temperatureT, which is reasonable in most cases. However,in some particular cases,the suspended particles can be hotter or colder than the surrounding gas media.Examples include the high-temperature metal nanoparticles prepared by the vacuum evaporation method,[27]the heated magnetic nanoparticles are injected into tumors to kill the cancer cells in clinical applications,[28,29]the cooled nanoparticles in the optical tweezer technology,[30]and lower char surface temperature prolongs the burnout times under O2/CO2conditions.[31]Since there is a gas-particle temperature difference,the thermal energy can be transferred from the particle to the gas(or from the gas to the particle)by thermal convection and radiation.[32]In the free molecule regime, the forces on the particle can be given by the gas-particle momentum transfer in unit time,which is related to the gas-particle scattering scenario.[33]A part of the collisions is specular,while the remaining part is diffuse(first absorbed on the particle surface,and then re-emitted with a Maxwellian velocity distribution at the particle temperature). So, the forces on the particle can be affected by the particle temperature. It has been reported that the gas-particle temperature difference has a significant influence on the drag[34]and photophoresis of the suspended particle in a gas.[35,36]Therefore, it is necessary to analyze the shear lift force by considering the influence of the particle temperature.

The present paper is devoted to the investigation of the particle temperature effect for the shear lift of spherical nanoparticles in a shear flow of rarefied gas. Based on the gas kinetic theory,analytical formulas of the shear lift force are derived under the non-rigid-body collision assumption,wherein the particle temperature effect is considered. In Section 2,the gas molecules-particle collision model is established,and the generalized expressions for the shear lift force are obtained based on the gas kinetic theory, in which the particle could be hotter or colder than the surrounding gas. Further, taking a spherical silver nanoparticle suspended in a diluted helium gas as an example,we present the analytical results of the particle temperature effect on the shear lift in Section 3. Finally,this paper is concluded with a brief summary and discussion in Section 4.

2. Analytical expressions for shear lift forces on the spherical nanoparticles

2.1. Analytical model

The gas molecules-particle collision model is established in Fig. 1. Consider a spherical nanoparticle through into a shear flow with velocity gradientG. The coordinate system{X,Y,Z}is established with the origin is located at the mass center of the nanoparticle, whereZ-axis direction coincides with the direction ofVandVis the velocity vector of particle relative to the gas molecule.i,j, andkare the unit vectors alongX,Y, andZaxes, respectively. The incoming velocity and reflected velocity can be interpreted byg=v-Vandg′=v′-V′, whichv′andV′presented as the reflected velocity of the gas molecule and nanoparticle,respectively.

Fig.1. Collision model between gas molecules and a nanoparticle in a linear shear flow.

Since the mean free path of gas moleculesλis larger than the characteristic length of particleLc(hereLc=R,Ris the nanoparticle radius),the collisions between the impinging and reflected molecules can be neglected,and the presence of particle does not affect the gas molecular velocity distribution.According to the gas kinetic theory, the velocity distribution of the gas molecules in the shear flow with velocity gradient is given by[18]

wheref0is the Maxwell velocity distribution of gas molecules in equilibrium,[37]andΦis the correction term owing to the velocity gradient in the shear flow,

Hereμis the viscosity of gas, andβ=(2RgT)-1/2is the reciprocal of the most probable molecular speed, in whichRg=8.314 J/(mol·K)is the gas constant.V0is the local mass velocity of gas molecules. The superscript ‘°’ indicates that the divergence of the tensor°vvis zero. The scalar product of the two tensors°vv:?V0is defined as the scalar and is equal to the divergence of°vv·?V0.

As mentioned above, the effect of the gas-particle temperature difference should be taken into account in the evaluation of the forces exerted on the nanoparticles suspended in a gas. In some applications,the gas-particle temperature difference can be maintained by a sustained external stimulus which supplies/removes energy to/from the particle.[38,39]For example,the particles can be heated up by the absorption of light[38]or cooled down by the optical tweezer technology.[39]In other cases, the energy source is not sustainable. Then, due to the heat transfer(including thermal convection and radiation)between the particle and surrounding gas, the gas-particle temperature difference decays exponentially with time. The characteristic time for a nanoparticle to adjust its motion to a new condition of forces is in the order of 10-8s-10-7s,[40]while the characteristic time of heat transfer is in the order of 10-3second.[32]Thus,the variation of the particle temperature can be much slower than that of the motion of the particle. In the present paper,to simplify the analytical mode,we assume that the particle temperature is a constant,which differs from the gas media temperature.

2.2. Shear lift force on nanoparticles in the free molecule regime

Following the pioneering work by Luoet al.,[16]equation(4)can be reduced as

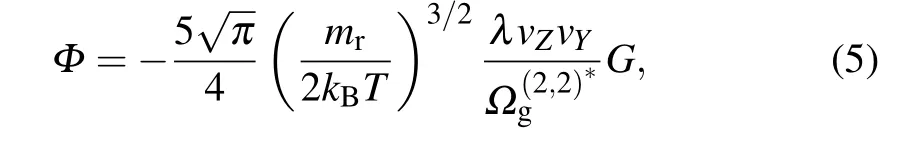
whereG=?V0z/?y,mris the reduced mass of the gas molecule and particle,mr=mgmp/(mg+mp), in whichmpis the mass of the particle (mp?mg), andkB=1.380649×10-23J/K is the Boltzmann constant.vYandvZare the components of velocityvin theYandZaxes,respectively.

According to the momentum transfer between gas molecules and nanoparticle, the force on a nanoparticle can be expressed as

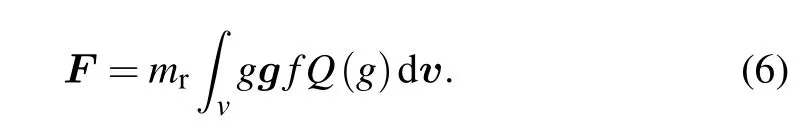
Clearly,equation(6)includes two contributions.The first term is the drag force

which has been proposed in our previous work.[34]The second one is the shear lift force

whereQ(g) is the collision cross-section, which depends on the scattering scenarios of gas molecules upon the collision with the nanoparticle.

The collision cross-section of the specular scattering is given by

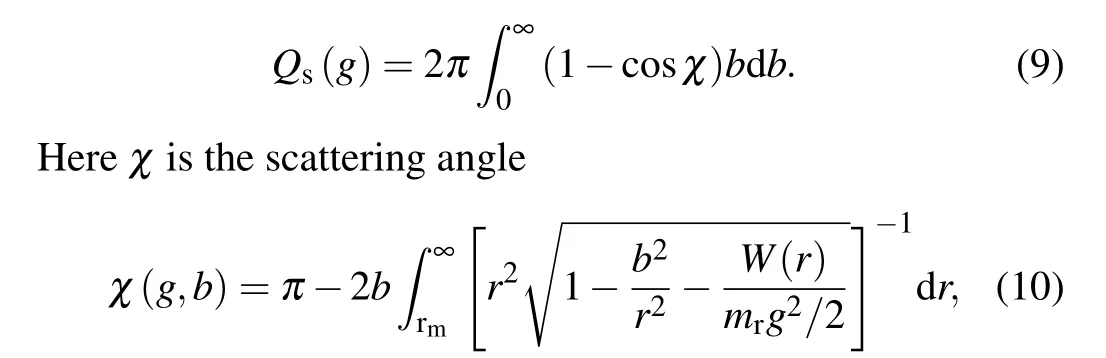
wherebdenotes the impact factor for the gas-particle collisions andW(r) is the gas-particle long-range interaction potential function.

For diffuse scatterings,the velocity distribution of the reflected molecules obeys the Maxwell distribution in equilibrium at particle temperatureTp,

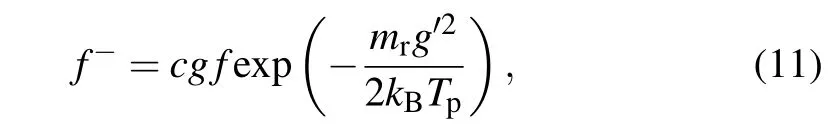
wherecis a constant. According to the conservation of molecules mass before and after the collision, we getc=(mr/kBTp)2/2πandgf=g′g′f-dg′. The collision crosssection for the diffuse scattering can be written as

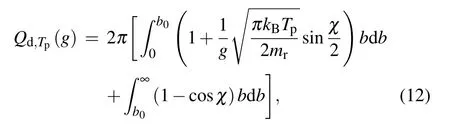
wherebis the critical impact factor corresponding to the orbiting scattering,[41]ris the separation distance,andrmmeans the closest distance that the gas molecules and the particle can approach. For simplicity,equation(14)can be rewritten as

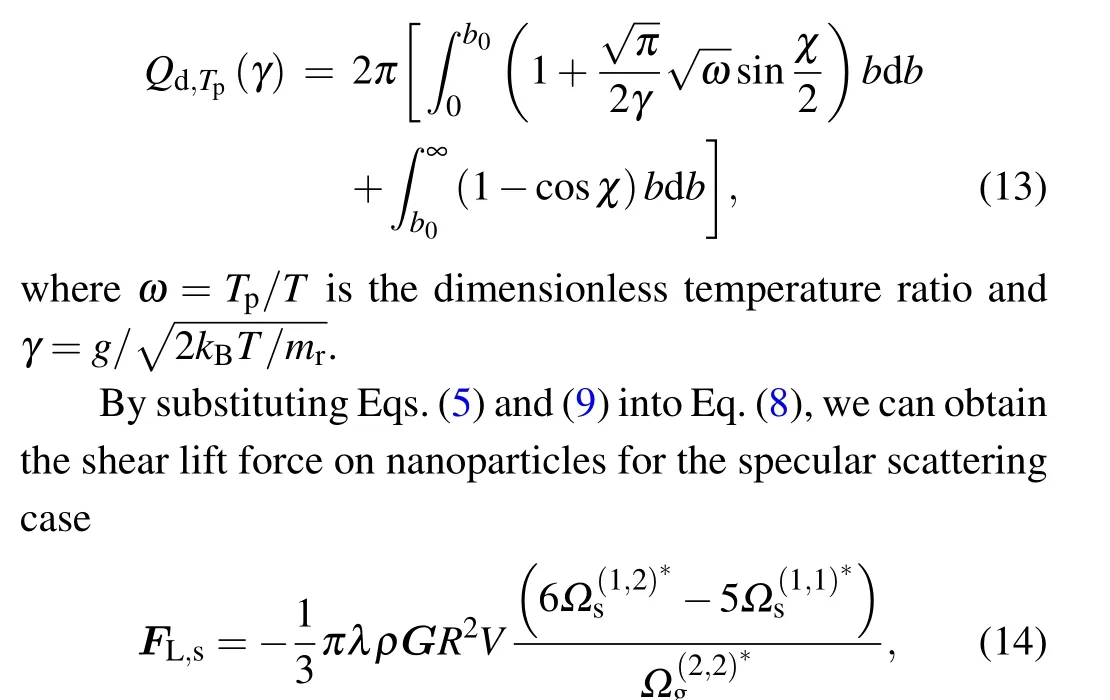
Similarly, by using Eqs (5), (13), and (8), the shear lift force on nanoparticles for the diffuse scattering case can be written as

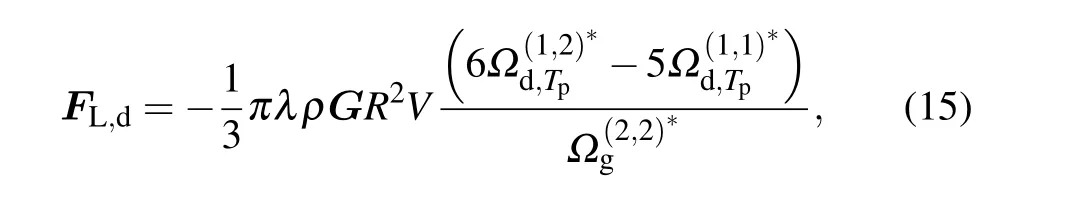
where the reduced collision integral is defined as follows:

Based on Eqs.(14)and(15),it is clear that the particle temperature only takes effect in the case of diffuse scatterings. This is because the incoming gas molecules are first absorbed on the particle surface(associated with momentum transfer from the gas molecules to the particle),and then re-emitted with an equilibrium Maxwell distribution at the particle surface temperature for diffuse scatterings. For specular scatterings, the collision between the gas molecule and the particle is elastic and the reflecting molecules still obey the velocity distribution at the gas temperature.

It should be noted that equations (14) and (15) are expressed in the limiting cases of different scattering kernels.A momentum accommodation coefficientφshould be introduced to represent the proportion of reflected molecules in a diffuse manner.[42]φ=0 andφ=1 correspond to the specular and diffuse limiting cases, respectively. Commonly,φincreases with the particle size.φ=0.9 forR ＞20 μm was obtained from the Millikan’s oil drop experiment.[43,44]Except for the particle size,φalso depends upon many other factors,including surface property,temperature,and gas-particle interactions.[45,46]

By using the momentum accommodation coefficient, a generalized expression for the shear lift force can be given by

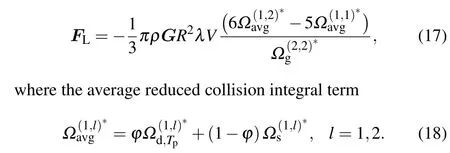
As the particle size increases, the effect of the gasparticle interaction is gradually suppressed and the rigid-body collision assumption is valid. In this case, the reduced collision integrals for specular and diffuse scatterings can be written as

3. Evaluation of the shear lift force on spherical nanoparticles

Based on Eq.(17),the shear lift force on a silver nanoparticle suspends in a shear flow of dilute helium gas is evaluated as an example to analyze the effect of particle temperature on the lift force. Rudyak-Krasnolutski (RK) potential function[47,48]is employed to represent the gas-particle interactions between the polyatomic nanoparticle and gas molecules, which is constructed by the summation of the classical Lennard-Jones (LJ) interactions between the gas molecules and each constituent atom of the particle. The RK potential consists of a repulsive potential termW9(r) in the short-range and an attractive potential termW3(r)in the longrange,

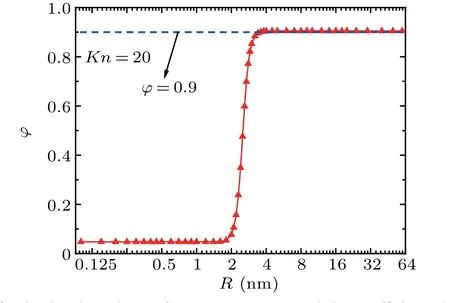
Fig.2. The size-dependence of momentum accommodation coefficient when Kn=20. The blue dotted line denotes φ =0.9, which is corresponding to Millikan’s data.

The size-dependent momentum accommodation coefficient is expressed as follows:[42]

According to the above formula, the variation ofφwith increasing particle sizeRis plotted in Fig.2,whereinKn=20.It can be seen that there exists a transition from specular to diffuse scattering in the range ofR=2 nm-3 nm.φis approximately close to 0 for small particles(R ＜2 nm),and approaches to 0.9 for large particles (R ＞4 nm), which is the classical Millikan’s result for large particles according to the famous oil-drop experiment.

3.1. Effect of the gas-particle interactions on the shear lift force

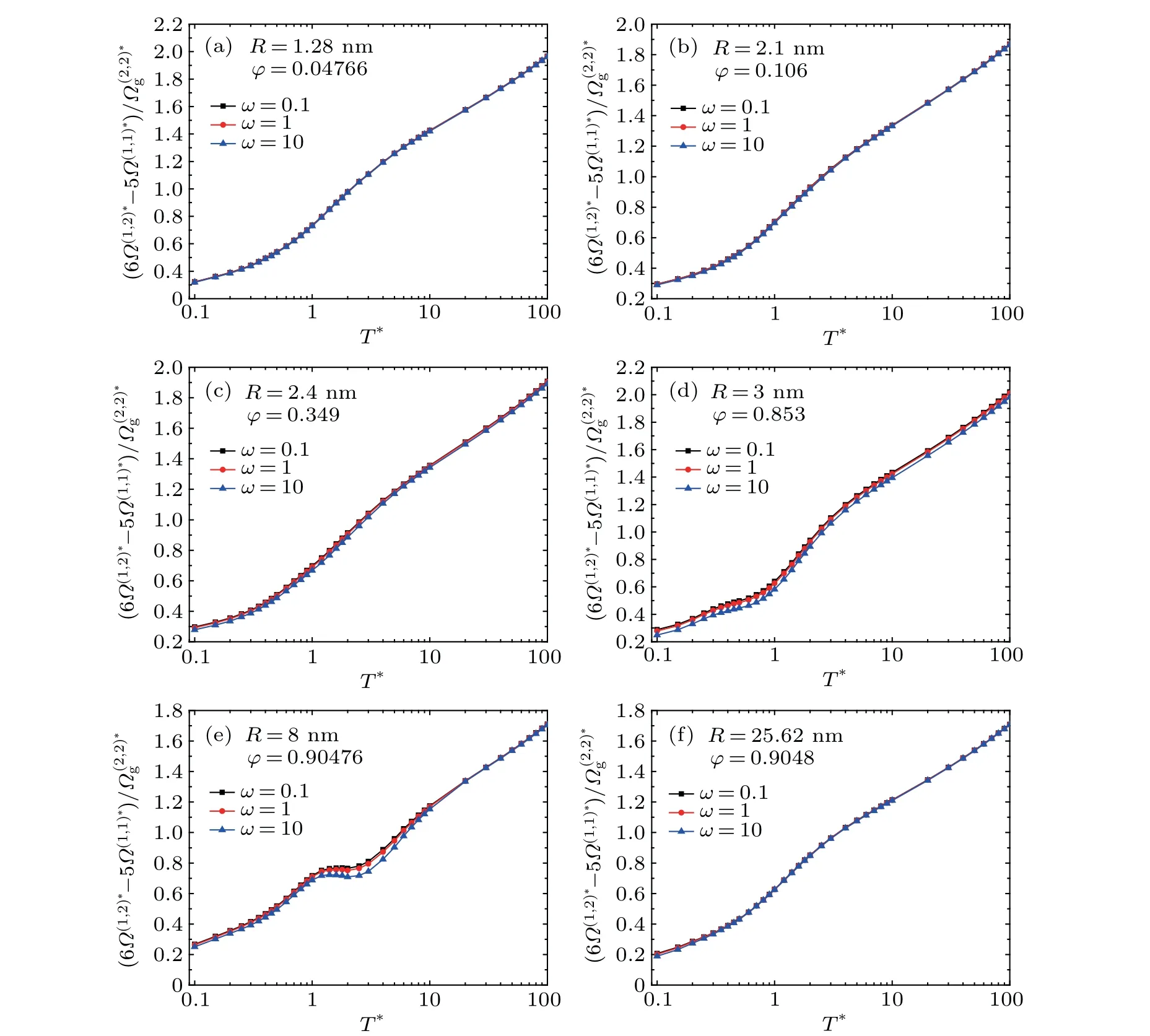
Fig.3. Variation of the average reduced collision integral term *as a function of the tempereture T* for(a)R=1.28 nm,(b)R=2.1 nm,(c)R=2.4 nm,(d)R=3 nm,(e)R=8 nm,and(f)R=25.62 nm.

the gas-particle specular scattering dominates, which is also shown in Fig.2. Therefore,the curves for varying temperature ratioωalmost overlap with each other. For the intermediate particle size(see Figs.3(c)-3(e)),the diffuse scattering begins to contribute to the gas-particle collisions and the particle temperature also takes effect. For large particles (see Fig. 3(f)),the rigid-body collision assumption is valid, and the particle temperature effect can be neglected.

The size-dependence of the relative errorΔRthat is caused by neglecting the gas-particle interactions is shown in Fig. 4. Here,ΔR=(FT/FT,rigid)-1,FTandFT,rigidare respectively given by Eqs.(17)and(1), andσ′=σ/R. Due to the particle size is comparable to the characteristic scale of van der Waals interaction, therefore the gas-particle interactions are significant for small particles(R ＜2 nm),and the relative errorΔRis far beyond the acceptable range.ΔRgradually goes down and fluctuates slightly in the range of 2 nm-20 nm. The fluctuation of theΔRvalue in this range is due to the transition from specular to diffuse scattering. With increasingR,the momentum accommodation coefficient increases and the diffuse scattering gradually dominates the gas-particle collisions. On the other side, according to Eq. (13), the contribution of diffuse scatterings mainly takes effect in the range ofb ＜b0. However, with increasingR, the critical impact factorb0decreases,[41]which reduces the contribution of diffuse scatterings. Therefore, these two effects compete with each other, by which there exists a fluctuation ofΔRvalue. For largeR(R ＞20 nm),ΔRapproximately goes to a constant value which depends on the gas temperature under the rigidbody collision assumption.

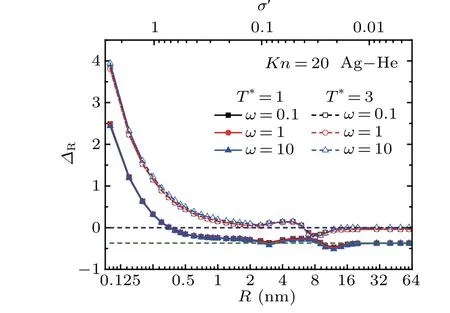
Fig.4. Variation of ΔR as a function of the particle size R for different temperature ratio ω.

Fig.5. Variation of the reduced collision integral term(6Ω(1,2)*-5Ω(1,1)*)/as a function of temperature ratio ω for different particle size R.(a)R=1.28 nm,(b)R=2.1 nm,(c)R=2.4 nm,(d)R=3 nm,(e)R=8 nm,and(f)R=25.62 nm.

3.2. Effect of the particle temperature on shear lift force

Fig.6. Variation of ΔT as a function of the particle size R for different temperature ratio ω.

To evaluate the influence of temperature difference on the shear lift force, figure 6 plots the relative errorΔTas a function of particle sizeRfor varying temperature ratioω, whichΔT=(FT/FT,Tp=T)-1, andFT,Tp=Tmeans the lift force in Eq. (17) in the case ofTp=T. It is reasonable thatΔT=0 forω=1. For other values ofω, the relative errorΔTvaries with the particle size. For small particles, the specular scattering dominates the non-rigid-body collision. According to Eq. (14), the lift force for the specular limiting case is independent of the particle temperatureTp, so|ΔT|＜0.01 forR ＜2 nm. In the particle size range of 2 nm＜R ＜20 nm,the diffuse scattering gradually dominates over the gas-particle collisions with increasingRand the effect of the particle temperature begins to take effect.So,|ΔT|is larger than that of the small particles. Here the wave-like curves are the result of the transition from specular to diffuse scattering. AsRincreases,it should be noted that|ΔT|decreases and approaches 0 again in the range ofR ＞20 nm. It has been illustrated that the gas-particle non-rigid-body collision could be neglected forR ＞20 nm. Therefore,the particle temperature does not influence the lift force in this particle size range andΔTapproaches to 0.

4. Conclusion

In summary,this work presents an analytical investigation on the effect of particle temperature on the shear lift force of nanoparticles. The generalized formula of shear lift force on a nanoparticle has been proposed based on the gas kinetic theory. As an example,the shear lift force on a silver nanoparticle suspended in a shear flow of dilute Helium gas is evaluated to analyze the effect of particle temperature on the shear lift force,which depends on the scattering scenario,particle size,and gas-particle interactions. Because the specular scattering dominates the molecular reflection scenario for small particles(R ＜2 nm) and the rigid-body collision assumption is valid for large particles(R ＞20 nm),the influence of particle temperature on lift force is weak and can be neglected. For the intermediate particle size(2 nm＜R ＜20 nm),the relative error|ΔT|is significant.