The Averaging Principle for Stochastic Fractional Partial Differential Equations with Fractional Noises
JING Yuanyuan,LI Zhi and XU Liping
School of Information and Mathematics,Yangtze University,Jingzhou 434023,China.
Abstract. The purpose of this paper is to establish an averaging principle for stochastic fractional partial differential equation of order α>1 driven by a fractional noise.We prove the existence and uniqueness of the global mild solution for the considered equation by the fixed point principle. The solutions for SPDEs with fractional noises can be approximated by the solution for the averaged stochastic systems in the sense of p-moment under some suitable assumptions.
Key Words: Averaging principle; Stochastic fractional partial differential equation; fractional noises.
1 Introduction
Fractional calculus has attracted many physicists,mathematicians and engineers due to the contributions which have been made to both theory and applications of fractional(partial) differential equations(see,e.g.,[1] and references therein). Mueller [2] and Wu[3] proved the existence of a solution of the stochastic fractional heat equation. Then,Bonaccorsi and Tubaro[4] applied Mittag-Leffler’s function to explore stochastic evolution equations with fractional time derivatives. After that, Cui and Yan [5] studied the existence of mild solutions for a class of fractional neutral stochastic integro-differential equations with infinite delay in Hilbert spaces; In[6], Liu and Yan have established the existence and uniqueness of solutions to a jump-type stochastic fractional partial differential equation with fractional noises by fixed point theorem.
The averaging principle plays a crucial role to obtain the approximation solutions for differential equations dating from mechanics, molecular dynamics, mathematics, material science, and other areas of sciences and engineering. Some rigorous results on the approximation theorem to the solutions of stochastic differential equations can be dated back to Khasminskii[7,8]. Based on this work,recently,Xu et al. [9]have established the averaging principle for the solutions of stochastic partial differential equations driven by L′evy noise under Lipschitz and linear growth conditions. Peculiarly, they have proved that the solutions to the simplified systems converge to that of the corresponding original systems both in the sense of mean square and probability. Similar results were proposed to the multivalued stochastic differential equations by[10]. Not only that,Pei et al. [11]established the averaging principles for a class of stochastic partial differential equations with slow component driven by fractional Brownian motion and a fast one driven by a fast-varying diffusion. In case with Poisson random measure was studied in Pei et al.[12]andα-noise in Bao et al. [13]. An averaging principle for the heat equation driven by a general stochastic measure was studied by Radchenko[14].
On the other hand, there has been some recent interest in studying stochastic partial differential equations driven by a fractional noise. For example, Duncan et al. [15]considered linear stochastic evolution equations in a Hilbert space driven by an additive cylindrical fractional Brownian motion withH∈(,1) and Tindel et al. [16] provided necessary and sufficient conditions for the existence and uniqueness of an evolution solution.Many interesting works on stochastic partial differential equations driven by fBm have been done and we refer to the literatures[17–19].
Based on the above brief discussion and to the author’s best knowledge,the averaging principle for stochastic fractional partial differential equations with fractional noises has not been considered.Therefore,in this paper,we will consider this issue by studying the following stochastic fractional partial differential equation with fractional noises:
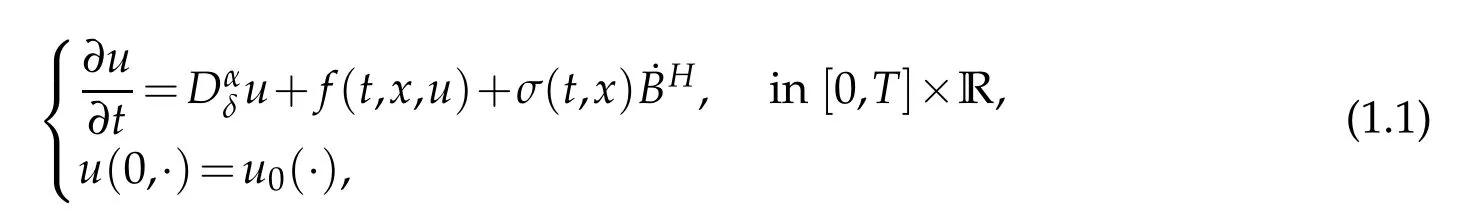
whereDαδis the fractional differential operator with respect to the spatial variable, to be defined in the Appendix which was recently introduced by Debbi [20] and Debbi and Dozzi[21],denotes the fractional noise on[0,T]×R with Hurst indexdefined on a complete probability space (?,F,P) (see Section 2 for precise definitions). In fact,we understand this equation in the Walsh[22] sense,and so we can rewrite Eq. (1.1) as follows:for allt∈[0,T]andx∈R,whereGα(·,?)denotes the Green function associated to Eq.(1.1).

We can notice that the fixed principle and the Picard iteration scheme work in[23–25],which can be used to prove the existence and uniqueness of solutions to Eq. (1.1). The first subject of this paper is to establish the existence and uniqueness of the solution of Eq.(1.2)via the fixed point principle. And then,we will consider the averaging principle for Eq.(1.2)under some appropriate assumptions.
The rest of the paper is organized as follows. In Section 2,we give the definitions of the fractional noises.Section 3 is devoted to proving the existence and uniqueness of the mild solution to Eq. (1.2)in theLp(p≥2)sense under some appropriate conditions. An averaging principle for solutions to stochastic fractional partial differential equation with fractional noises in Section 4.
2 Preliminaries
In this section,we present the definitions of the fractional noises(see Sec.2 in[6]).
Define(?,F,(Ft)t≥0,P)for a complete probability space equipped with the filtration(Ft)t≥0satisfying the usual conditions. Let Bb(R)be a class of bounded Borel sets in R.AndBH([0,t]×A)(t,A)∈[0,T]×Bb(R)is a centered Gaussian family of random variables with the covariance,forH∈(0,1),
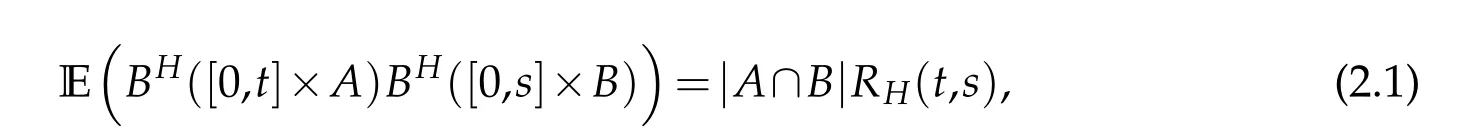
withs,t∈[0,T],A,B∈Bb(R)and covariance kernel.Here|A| denotes the Lebesgue measure of the setA∈Bb(R). We denote by E the set of step functions on[0,T]×R. Let H be the Hilbert space defined as the closure of E with respect to the scalar product,
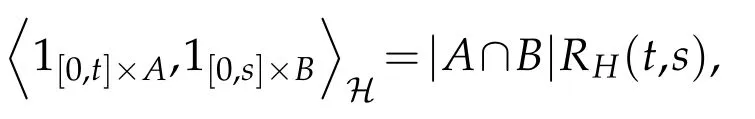
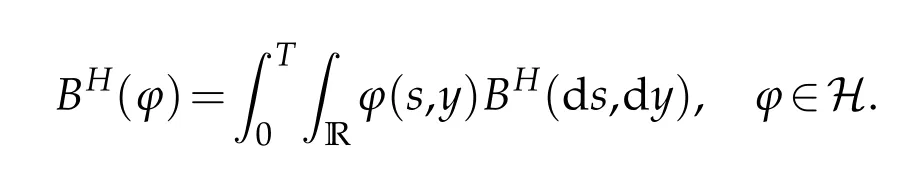
On the other hand,it is well known that the covariance kernelRH(t,s)satisfies
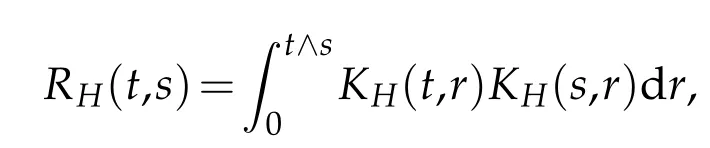
whereKH(t,s)is the square kernel defined,for 0 where, (β(·,·)denotes the Beta function). Particularly,for Definition 2.1.Letbe a linear operator which satisfies Then the operatorK*Hψ gives an isometry fromHto L2([0,T]×R). As a result, defines a space-time white noise. Moreover,one can view BH as In this section,we discuss the existence and uniqueness of the global mild solution to Eq.(1.1). Recall Eq. (1.2) and Definition 2.1, the fractional integral term in Eq. (1.2) can be expressed as with the space-time white noiseW(t,x)for all(t,x)∈[0,T]×R mentioned in Section 2. Theorem 3.1.Letwith, suppose that the following conditions aresatisfied (1) f is uniformly Lipschitzian,i.e. there exists a constant L>0such that for(t,x)∈[0,T]×Rand u,v∈R, (2) f has linear growth onR,i.e. there exists a constant C>0such that|f(t,x,u)|≤C(1+|u|),for(t,x)∈[0,T]×Rand u∈R. Then,for allF0-measurable u0:R×? ?→Rsatisfying,there exists a uniquemild solution u(t,x)(t,x)∈[0,T]×Rto Eq.(1.1)and for allwith α>1, In order to prove the theorem,we need the following two useful Lemmas: Lemma 3.1.([6])Let p∈[1,∞),ρ∈[1,p]and r∈[1,∞)such that Let Gα=Gα(t,x?y)be the Green kernel, π=Gα,or G2α with(t,x,y)∈[0,T]×R×R. Define an operator J by with ν∈L1([0,T];Lρ). Then J:L1([0,T];Lρ)?→L∞([0,T];Lρ)is a bounded linear operator and satisfies the following. =Gα,then there exists a constant C>0such that for all r∈[1,1+α), =>0such that for all Lemma 3.2.([6,26])If H>,then Next, we will mainly prove Theorem 3.1 by the fixed point principle. Let B be the space of allLp(R)-valued Ft-adapted processesu(t,·):[0,T]×R?→R with the norm where Proposition 3.1.Under the assumptions of Theorem3.1,for eachand u∈B,it holdsthatAα(u)∈B. Proof.From(6)of Lemma A.1,Corollary A.2 and the Young inequality,we obtain that which is due to the fact that Now let us consider A2α(u)(t,x). Applying(1)of Lemma 3.1 withand condition(2)of Theorem 3.1,we conclude that sinceu∈B. In what follows, now we turn to(u)(t,x). Noticing that([0,T]×R)?H from Lemma 3.2 whenH>,we deduce that By using the H?lder inequality,it follows that where we have used the fact thatwhen, and under the assumptionSo we have(u)(t,x)∈B forp≥2. Therefore we have proved that the operator Aαdefined by(3.8)is an operator from B to itself. The proof is complete. In what follows,we will prove that the operator Aα:BB is a contraction operator. Proposition 3.2.([6])For,the operatorAα is a contraction onBunder the conditionsof Theorem3.1.That is to say,there exists a constant λ∈(0,1)such that Proof.Assume thatu0andv0are initials of(Ft)t≥0-adapted random fieldsu,v∈B such thatu0=v0.Let us begin by considering A1α(u). Note that,forρ=,by(1)of Lemma 3.1 withand condition(1)of Theorem 3.1,we have Thus where withp≥3. So withλ∈(0,1)by choosingη>0 large enough,then A2αis a contraction on B.Meanwhile,we can quickly conclude from the expression for A3αthat A3αis also a contraction on B. Therefore,it follows from(3.8)that Aα(·)is a contraction on B ifη>0 large enough.Thus the proof of Proposition 3.2 is complete. Motivated by Propositions 3.1 and 3.2 and the fixed point principle on the set{u∈B:u(0)=u0},we conclude that Eq.(1.1)admits a unique solutionu∈B.Thus the conclusion of Theorem 3.1 follows. In this section,we are going to prove the averaging principle of solutions for SPDEs with fractional noises.Consider the Eq. (1.2)in the following form: According to Theorem 3.1, Eq. (4.1)also has a unique mild solutionuε(t,x),t∈[0,T]forε>0. We will examine whether the solution processuε(t,x) can be approximated to the solution process(t,x)of the simplified equation: Based on the assumptions of Theorem 3.1, further, we make the following assumptions throughout this section: Assumption 4.1.σ(s,y):R+×R→R is measurable,bounded,and whereLσis a constant. Assume that there exist the following limit Assumption 4.2.Functionis bounded. Lemma 4.1.Let h(z,y)and h(y)be measurable and functions are bounded. Then where γ is a constant relevant to p,H. Proof.Using the substitutionv=(t?s)/ε,we obtain Then,we can obtain ThenFε(z)is bounded.Denoting|Fε(z)|≤CF,whereCFdoes not depend onε,we have Noticing that ForB2,using the integration by parts and inequality|a?b|≤|a|+|b|, we obtain And then,by(4.3),(4.4)and the inequality(a+b)p≤2p?1(ap+bp),we get where. So when,we can get Thus,we complete the proof of this Lemma. Remark 4.1.From Assumptions 4.1-4.2 and Lemma 4.1,it follows from that Theorem 4.1.Assume that the conditions of Theorem3.1and Assumptions4.1-4.2hold. Then there exist versions of uε andsuch that for γ=pH, Proof.Using the inequality(a+b)p≤2p?1(ap+bp),(4.1)and(4.2),we have ForI1,by inequality(3.11)and Remark 4.2,we deduce that Then forI2,owing to the equalityand H?lder inequality,we have Finally,we get by Gronwall’s inequality,the above inequality can be expressed as That finishes the proof. A Appendix. The Green function([6,23,24]) The fractional differential operatorDδαis an extension of the inverse of the generalized Riesz-Feller potential whenα>2. It is given forα>0 by the following Definition Definition A.1.The fractional differential Dδα? is given by δ≤min{α?[α]2,2+[α]2?α},[α]2is the largest even integer less than or equal to α(even part of α),and for α=0when α∈2N+1,and F(respectively F?1)is the Fourier(respectively Fourier inverse)transform. The operatorDδαis a closed,densely defined operator onL2(R)and it is the infinitesimal generator of a semigroup which is not symmetric and not a contraction. This operator is a generalization of various well-known operators, such as the Laplacian operator(whenα=2), the inverse of the generalized Riesz-Feller potential(whenα>2), the Riemann-Liouville differential operator(whenδ=2+[α]2?αorδ=α?[α]2,see[6,22,23,25]for more details). It is self-adjoint only whenδ=0 and in this case,it coincides with the fractional power of the Laplacian. We refer the readers to Debbi[22]and Debbi and Dozzi[23]for more details about this operator. Let the Green functionGα(t,x)associated with Eq.(1.1)be the fundamental solution of the Cauchy problem whereδ0is the Dirac distribution at the point zero. Using Fourier’s calculus we obtain The functionGα(t,·)has the following properties(see e.g.,[22,23]). Lemma A.1.For α∈(0,∞)N (2)Gα(t,x)is real but in general it is not symmetric relatively to x and it is not everywhere positive. (3)Gα(t,x)satisfies the semigroup property, or the Chapman-Kolmogorov equation, i.e. for0 (4)For0<α≤2,the function Gα(t,·)is the density of a L′evy stable process in time t. (5)For fixed t,Gα(t,·)∈C∞andis bounded and tends to zero when|x|tends to∞for β∈R+. Remark A.1.The proof of this Lemma can be found in[23]. Corollary A.1.Let α∈(1,+∞),then there exists a constant Kα such that Corollary A.2.Let α∈(1,+∞),for n≥1,and T≥0,for γ such that Acknowledgement The authors thank the editors and the reviewers for their useful comments.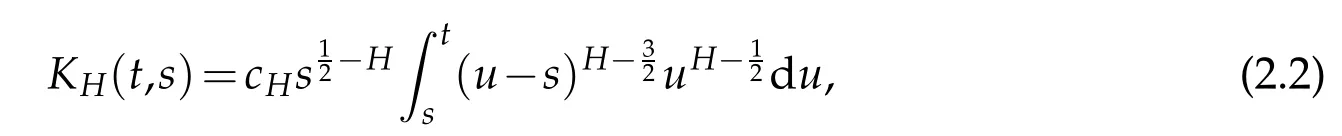
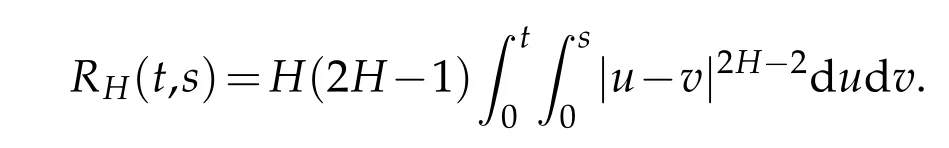
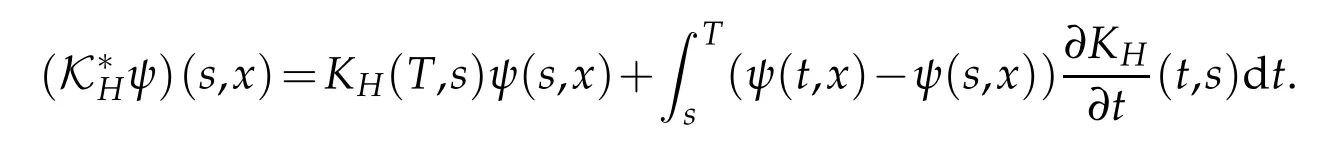
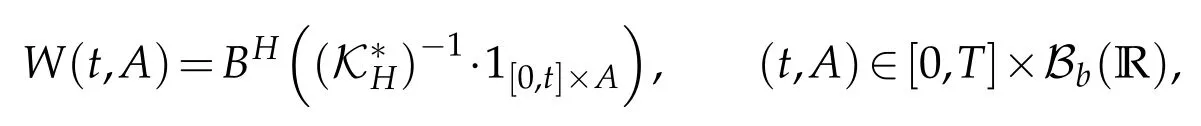
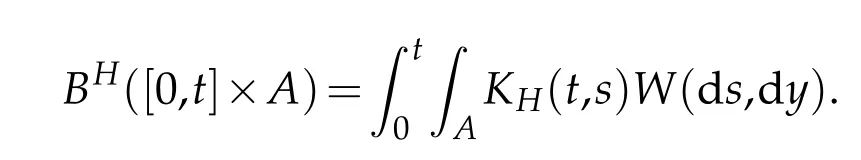
3 Existence and uniqueness
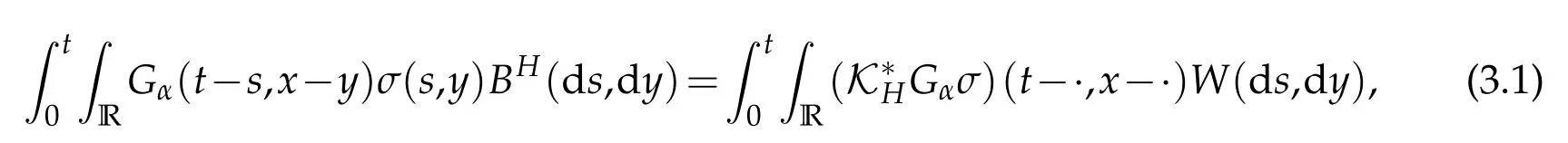
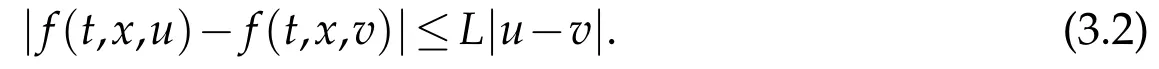
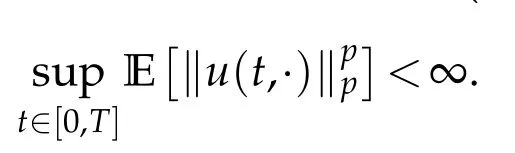
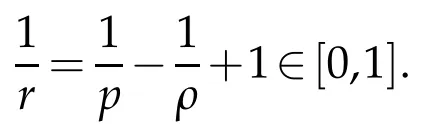
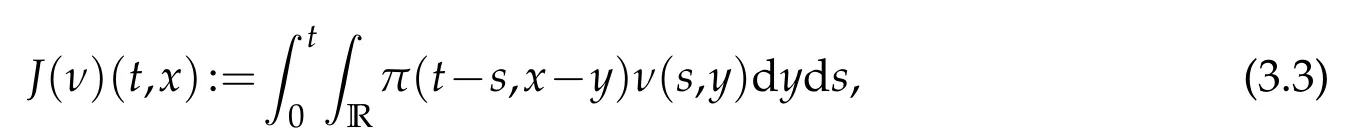
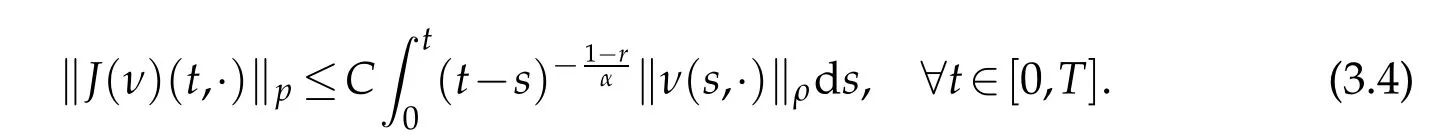
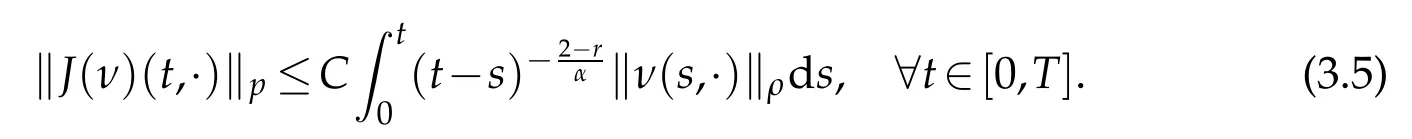

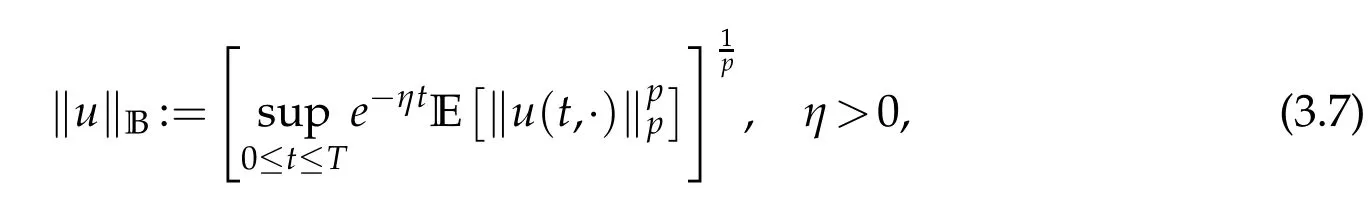

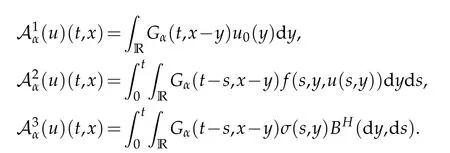
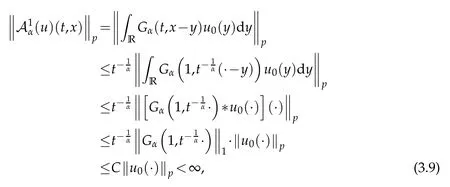

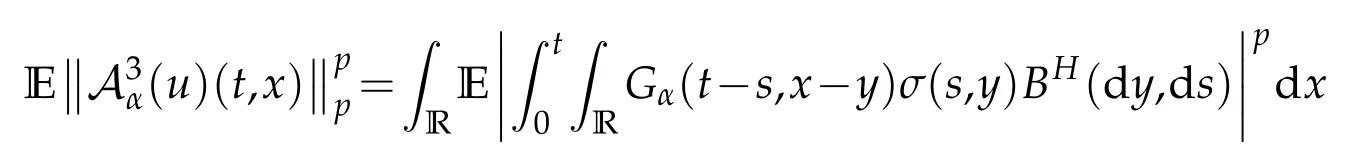
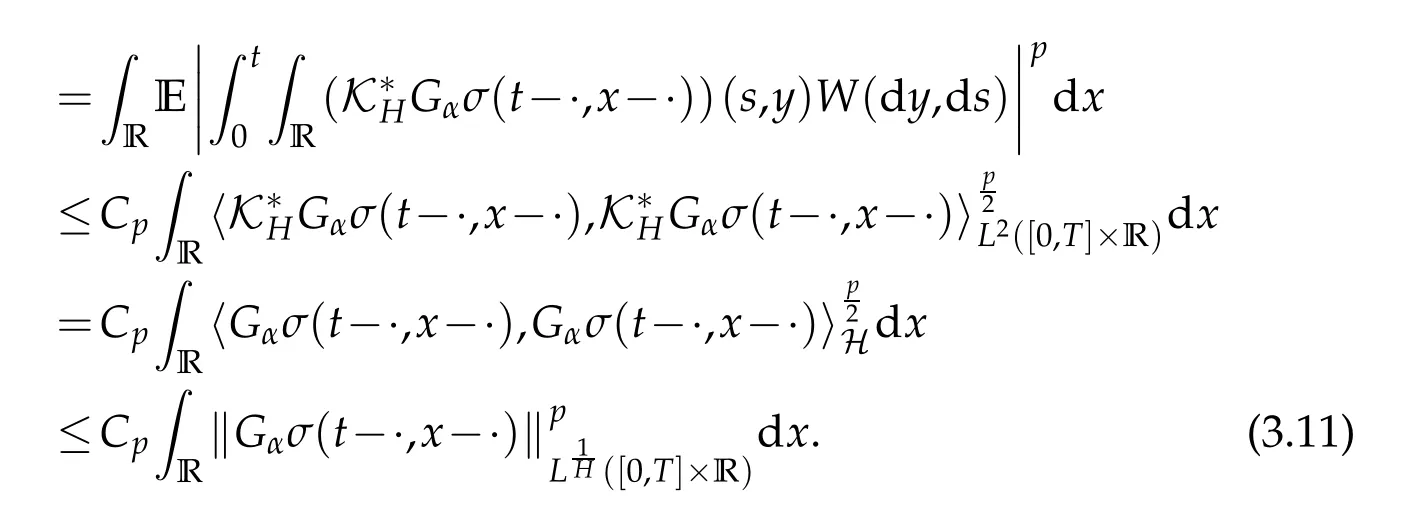

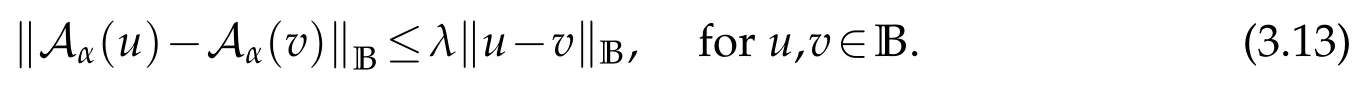
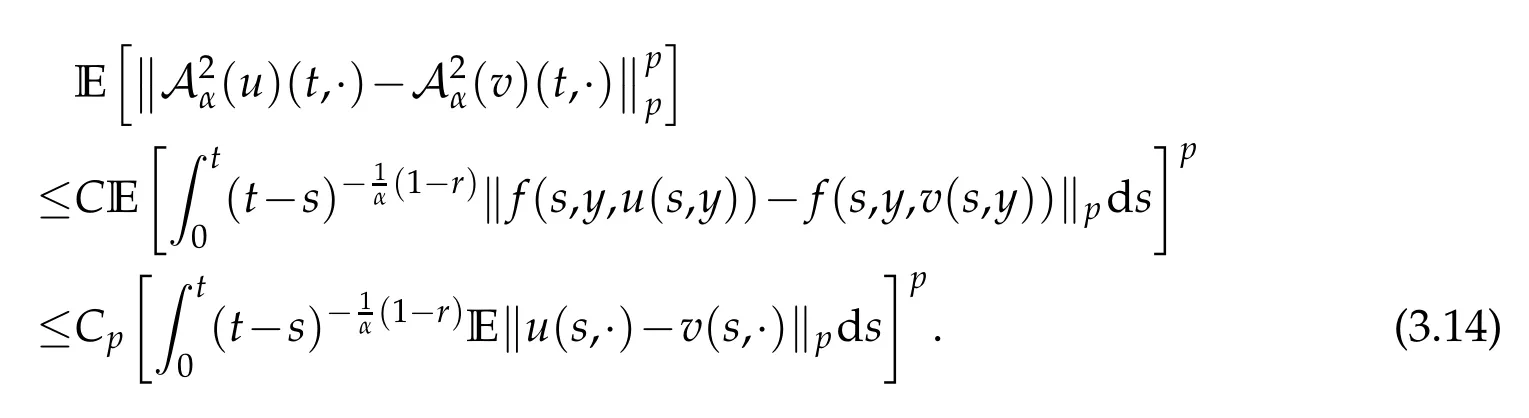
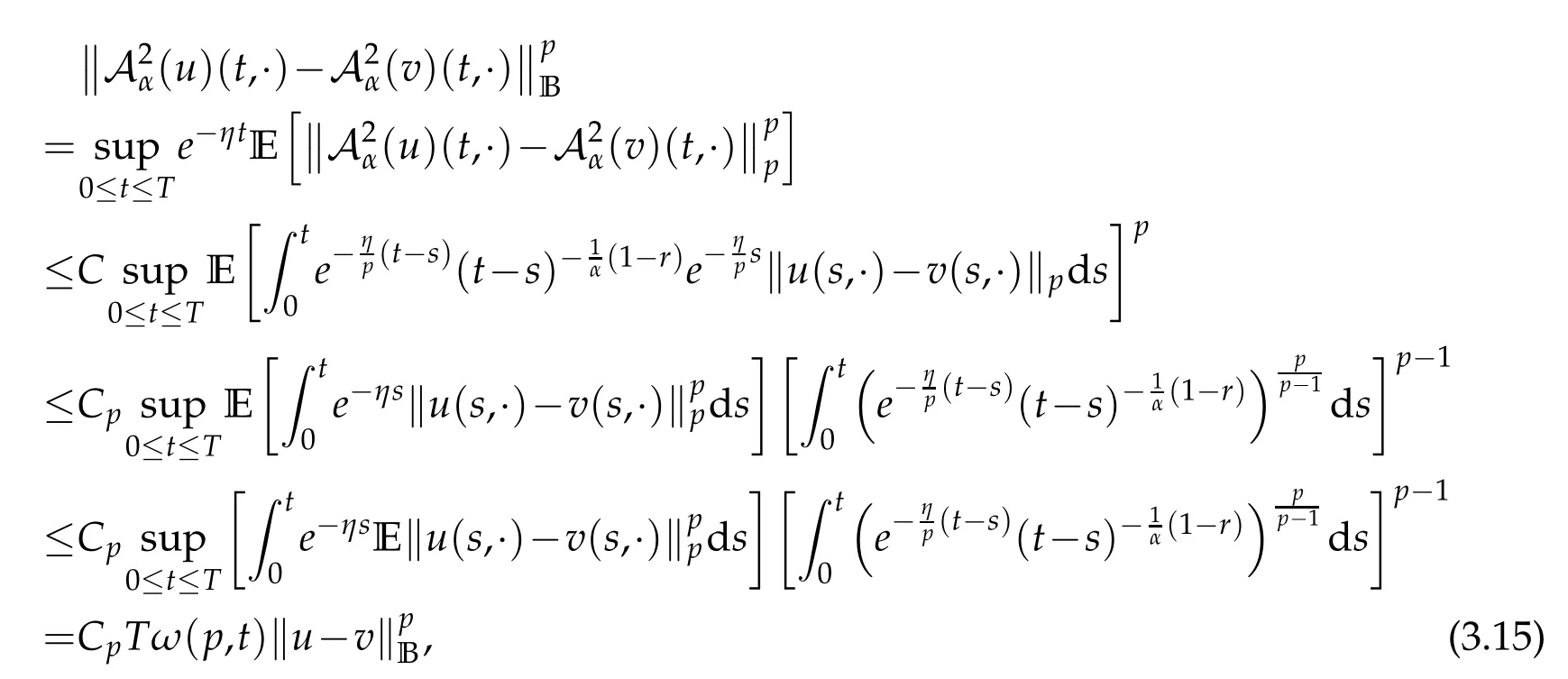
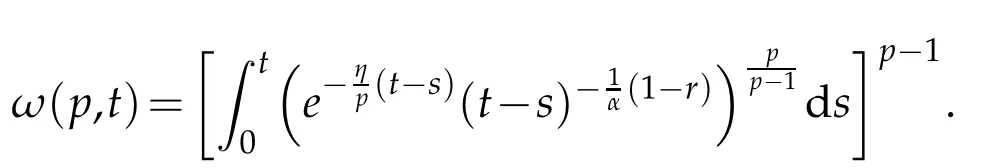
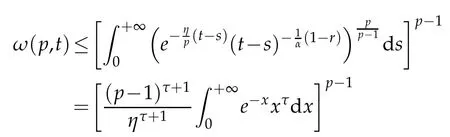
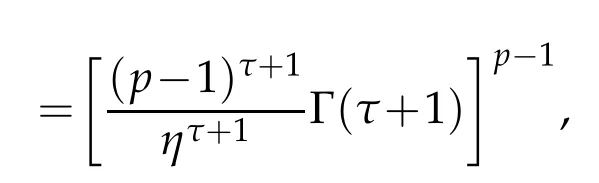
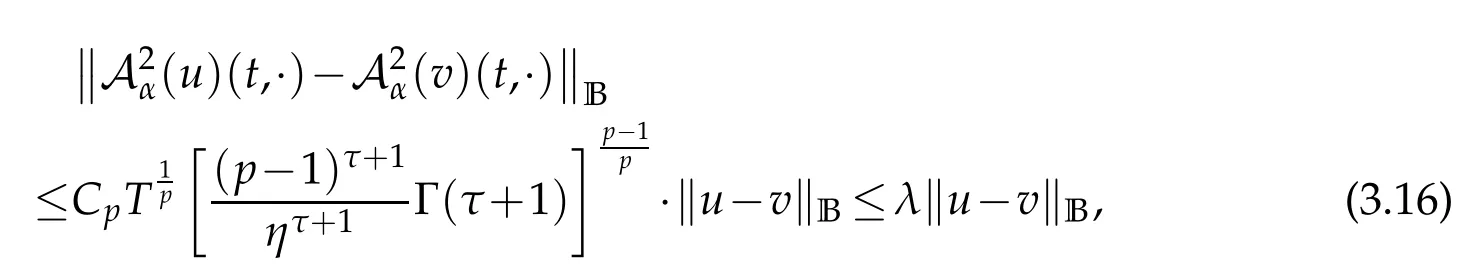
4 The averaging principle
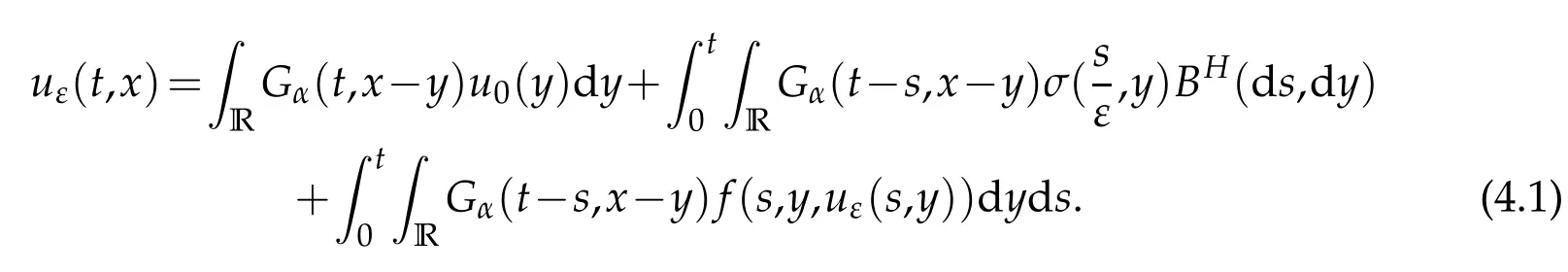
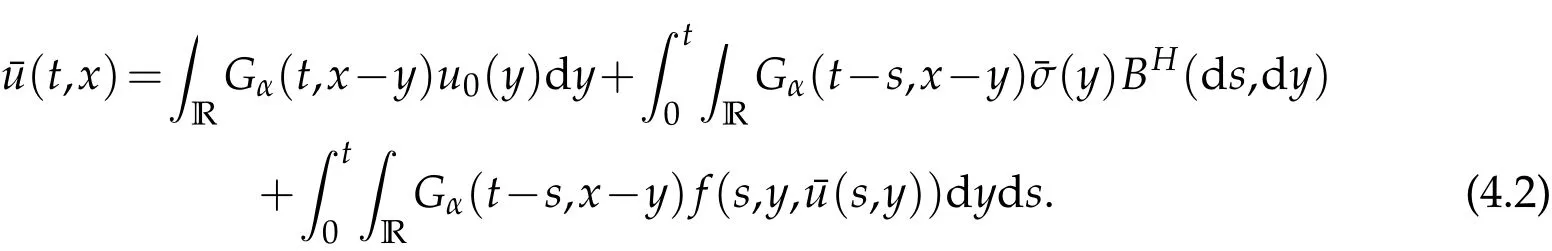
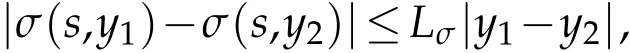
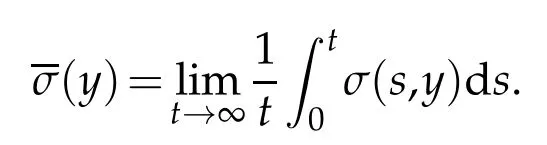
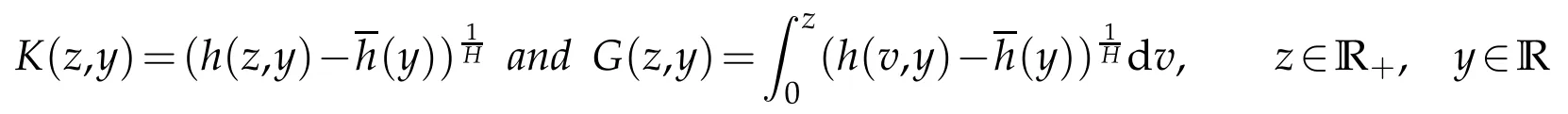
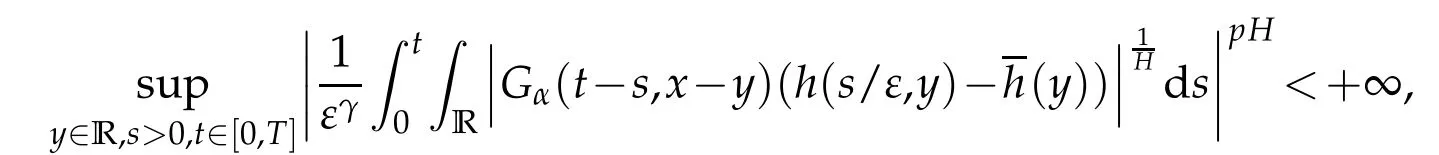
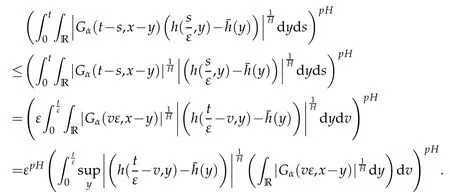
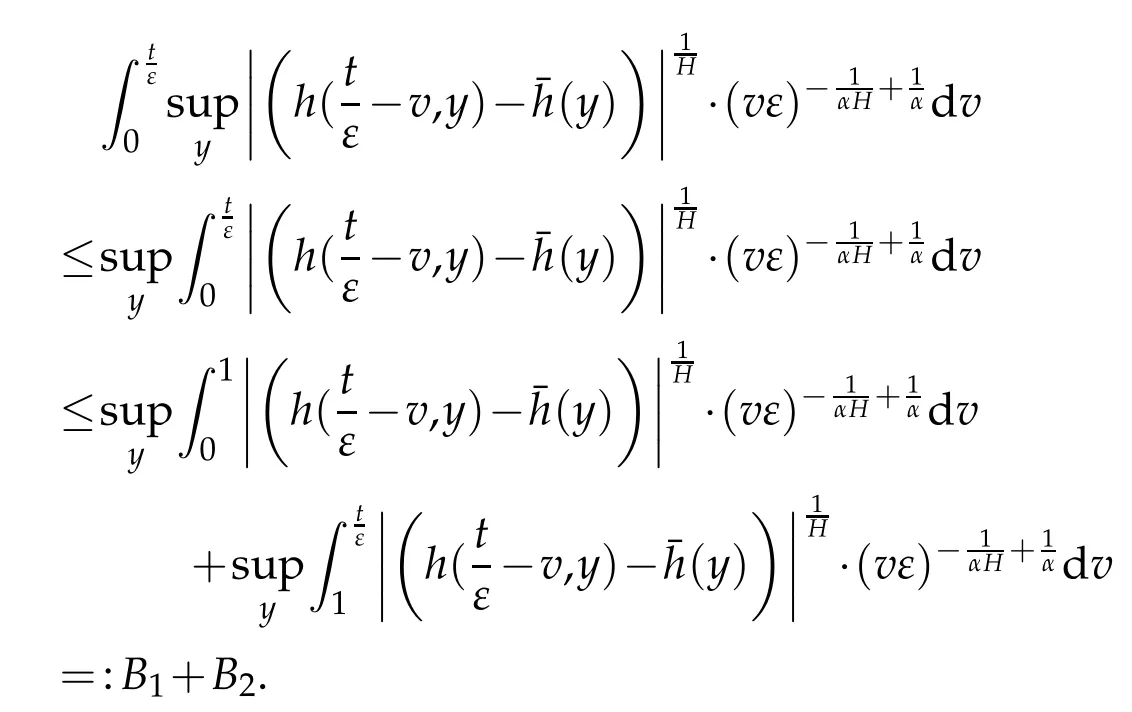

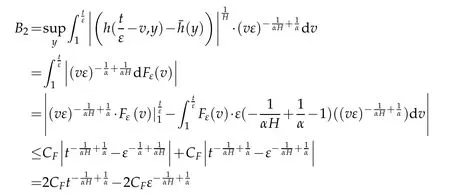

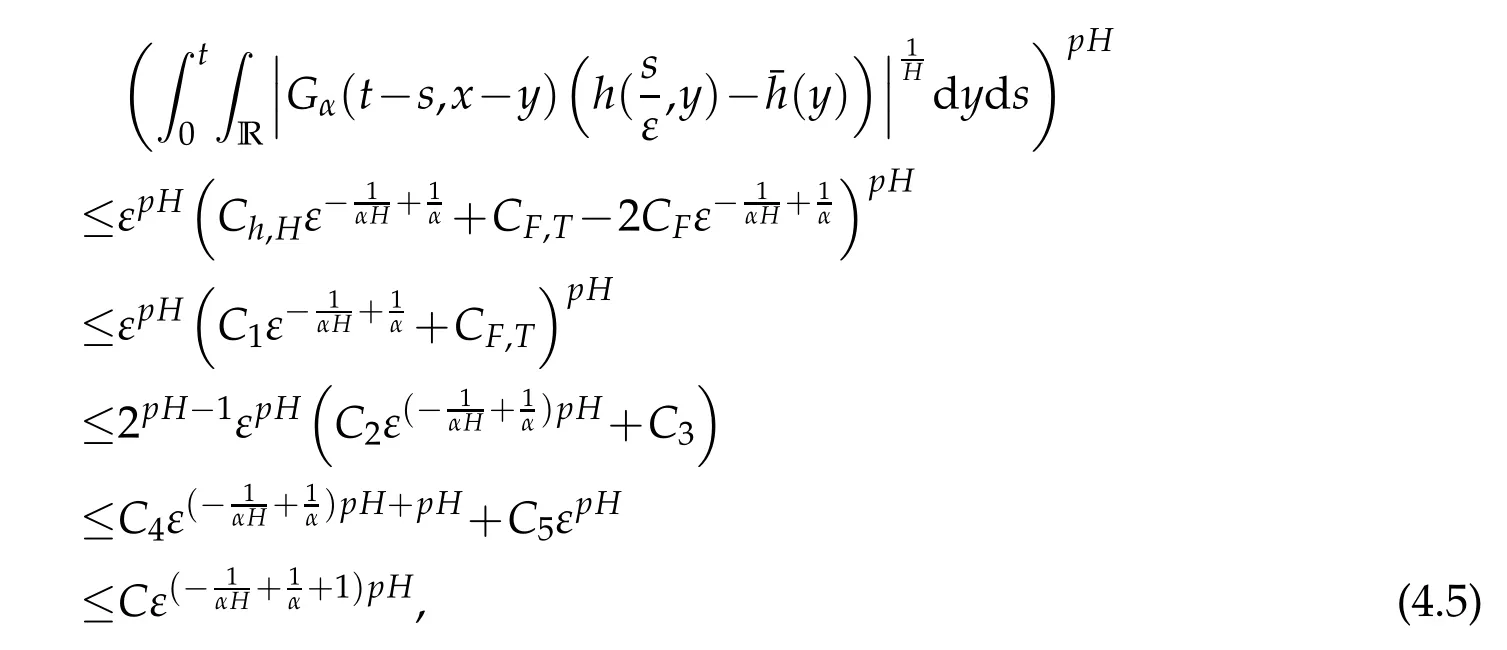
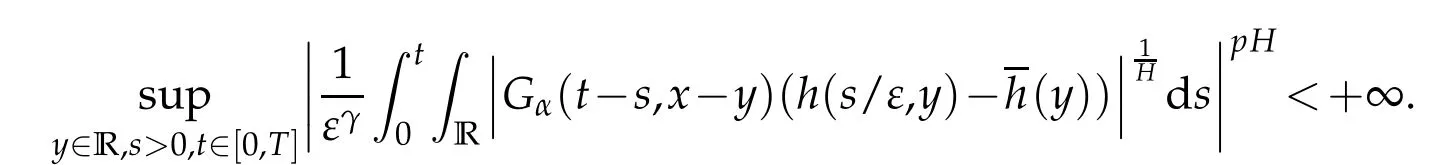
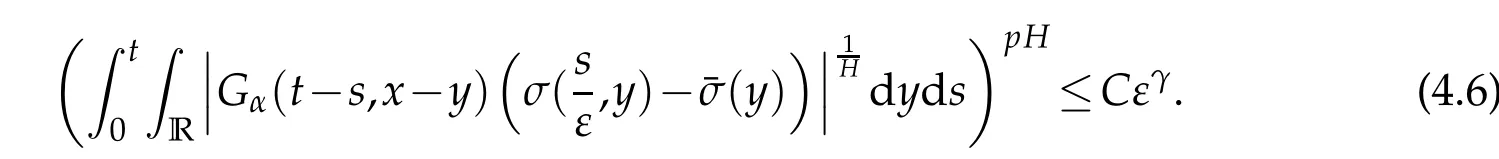
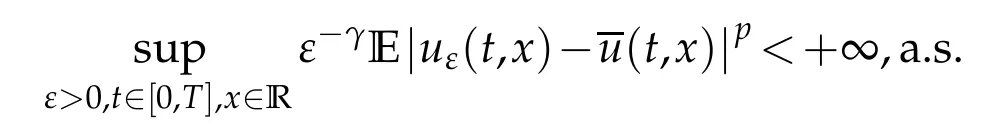
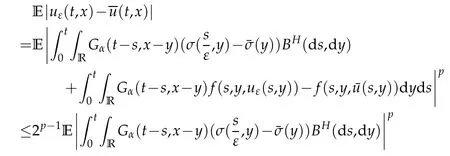
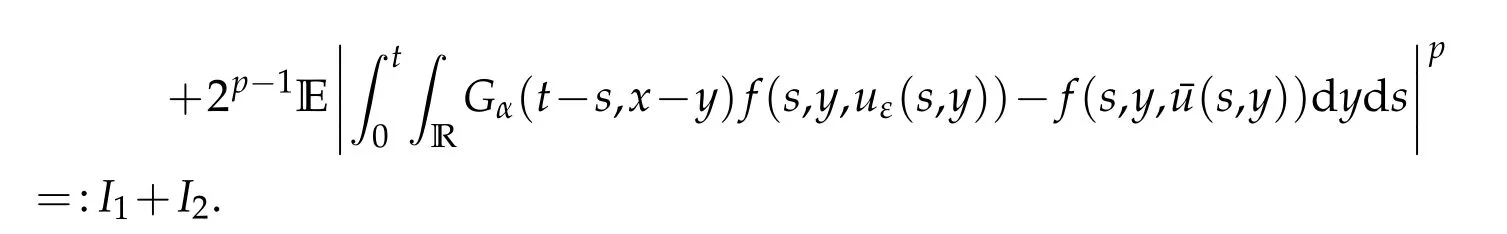
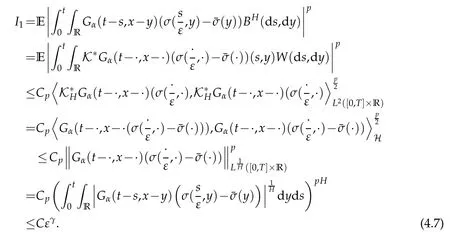
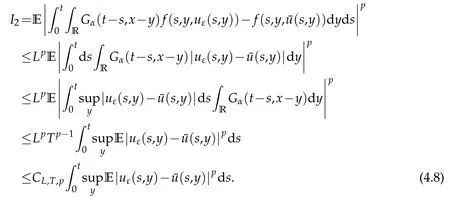
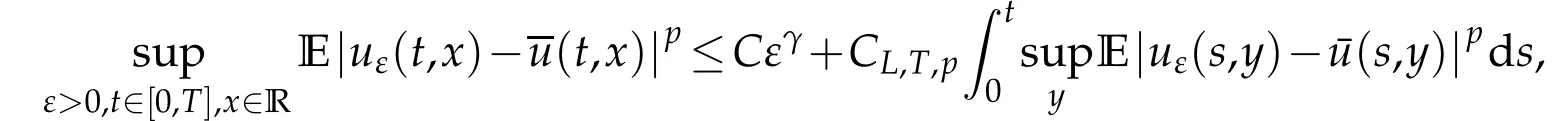
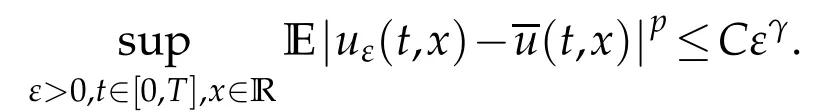
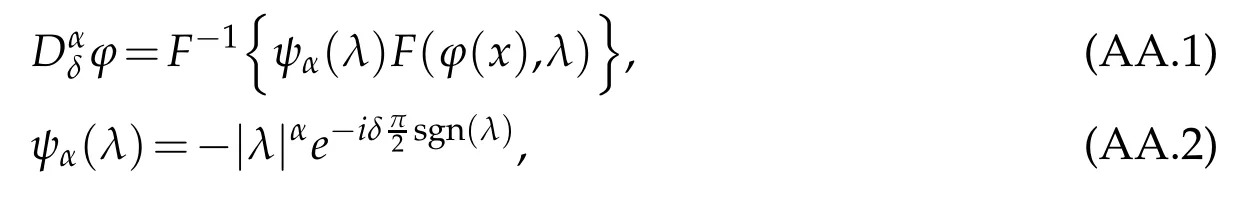
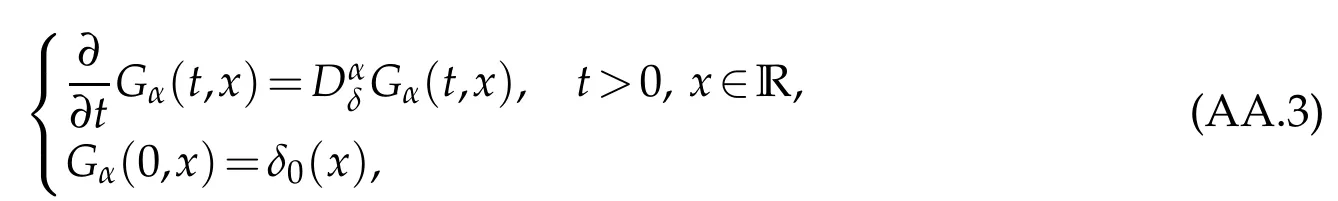
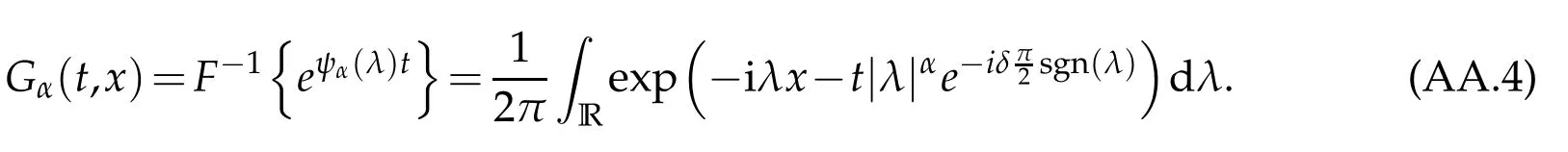
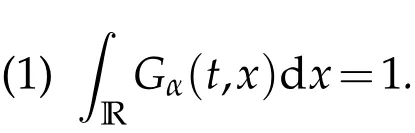
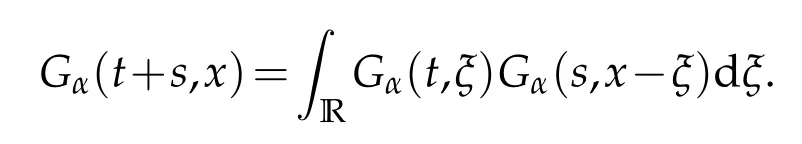
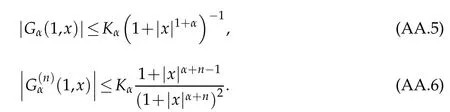
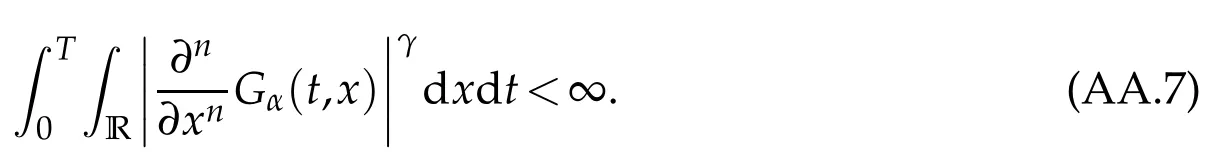
 Journal of Partial Differential Equations2021年1期
Journal of Partial Differential Equations2021年1期
