Global Existence of Smooth Solutions to Three Dimensional Hall-MHD System with Mixed Partial Viscosity
WANG Yuzhu
School of Mathematics and Statistics, North China University of Water Resources and Electric Power,Zhengzhou 450011,China.
Abstract. We investigate the global existence of smooth solutions to the three dimensional generalized Hall-MHD system with mixed partial viscosity in this work. The diffusion of mixed partial viscosity is weaker than that of full viscosity, which cases new difficulty in proving global smooth solutions. Moreover,Hall term heightens the level of nonlinearity of the standard MHD system. Global smooth solutions are established by using energy method and the bootstrapping argument,provided that the initial data is enough small.
Key Words: Hall-MHD system with mixed viscosity;global existence;smooth solutions.
1 Introduction
In this work, we consider smooth solutions to the following Cauchy problem of three dimensional Hall-MHD system with mixed partial viscosity
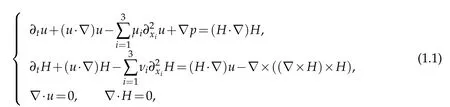
with the initial value
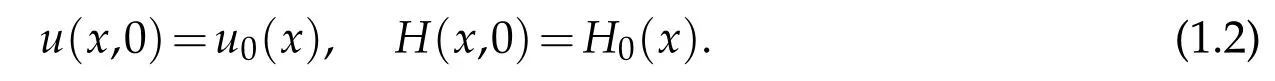
Hereu=u(x,t),H=H(x,t)∈R3,p=p(x,t)∈R are the velocity, magnetic and pressure field,respectively,andμi≥0,νi≥0 represent the kinematic viscosity and diffusivity constants,respectively.
As the incompressible limit of a two-fluid isothermal Euler-Maxwell system for electrons and ions,the Hall-MHD system(1.1)was derived in[1]. It describes the evolution of a system consisting of charged particles that can be approximated as a conducting fluid,in the presence of a magnetic fieldH,withudenoting the fluid velocity,pthe pressure,μithe viscosity,νithe magnetic resistivity andηa constant determined by the ion inertial length.The Hall-MHD system has a wide range of applications in plasma physics and astrophysics, including modelling solar wind turbulence, designing tokamaks as well as studying the origin and dynamics of the terrestrial magnetosphere. Moreover,the Hall-MHD system also serves a vital role in interpreting the magnetic reconnection phenomenon,frequently observed in space plasmas. For more physical backgrounds,we may refer to[2–5]and[6].
The Hall-MHD system were mathematically rigorous derived by Acheritogaray,Degond,Frouvelle and Liu[1]. Existence of global solutions is a challenge open problem in the mathematical fluid mechanics. There are numerous important progresses on the fundamental issue of blow up criterion of smooth solutions or regularity criterion of weak solutions to(1.1),(1.2)(see[7–13]and[14]). Blow up criterion and global small solutions have been established in Chae and Lee [15]. Chae [16] proved that existence of global weak solutions and local classical solutions. Time-decay rate of solution was established in [17]. A stability theorem for global large solutions under a suitable integrable hypothesis in which one of the parcels is linked to the Hall term was proved in[18]. As a byproduct,a class of global strong solutions was also obtained with large velocities and small initial magnetic fields. Global well-posedness of mild solutions in Lei-Lin function spaces (see[19]) was established in [20]. Global well-posedness and analyticity of mild solutions was obtained by Duan [21]. By exploring the nonlinear structure, Zhang [22]constructed a class of large initial data and proved global existence of smooth solutions.Fan et al.[23]established global axisymmetric solutions. Wan and Zhou[24]proved that global existence and large time behavior of strong solutions.Chae and Weng[25]studied singularity formation for the incompressible Hall-MHD system without resistivity. For other some results,we refer to[26].
If ▽×((▽×H)×H) disappear, (1.1) is reduced to the classical MHD system. For our purpose,we emphasize on the global smooth solutions to MHD system and related models with mixed viscosity, see [27–32]. Cao and Wu [27] proved that global regularity for the 2D MHD system with mixed partial dissipation and magnetic diffusion,provided that the initial data belongs toH2. Wang and Wang [29] overcome these difficulties caused by more bad terms and extended the results to the 3D case with mixed partial dissipation and magnetic diffusion. Based on the basic energy estimates only,[32]proved that 2D system always possesses a unique global smooth solution when the initial data are sufficiently smooth. Moreover, they obtain optimal large-time decay rates of both solutions and their higher order derivatives by developing the classic Fourier splitting methods together with the auxiliary decay estimates of the first derivative of solutions and induction technique. We refer to [28] for 2D MHD system with partial hyper-resistivity.
As far as we know,there is few results about global existence of smooth solutions to the Hall-MHD system with mixed partial viscosity. There are the following three main reasons that make it difficult to prove global smooth solutions. Firstly, the diffusion of mixed partial viscosity is weaker than that of full viscosity, which cases new difficulty in dealing with the nonlinear term. Secondly,the Hall term ▽×((▽×H)×H)describes the occurrence of the magnetic reconnection when the magnetic shear is large, which makes the Hall-MHD system different from the usual MHD system. Thirdly, the Hall term ▽×((▽×H)×H)heightens the level of nonlinearity of the standard MHD system from a second-order semilinear to a second-order quasilinear level,significantly making its qualitative analysis more difficult.
Inspired by the recent work[29,30] and [31] for 3D incompressible MHD equations and 3D incompressible magneto-micropolar fluid equations,our objective of this work is to concern the global existence of smooth solutions to the problem(1.1),(1.2)with mixed partial viscosity. The corresponding results are as follows:
Theorem 1.1.Letμi>0(i=1,2),μ3=0and νi>0(i=1,2,3). Assume that u0,H0∈H3and put
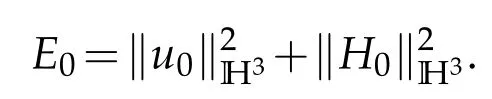
There existence a small constant ?1>0such that if E0≤?1,then the problem(1.1)–(1.2)admits a unique global smooth solution(u,H).Moreover,
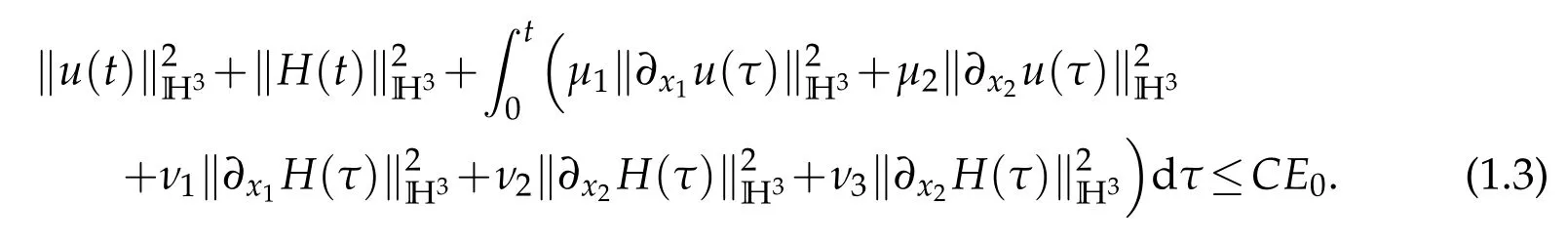
Remark 1.1.When the viscosity and diffusivity coefficients satisfyμi>0(i=1,3),μ2=0 andνi>0(i=1,2,3)orμi>0(i=2,3),μ1=0 andνi>0(i=1,2,3),we also prove that the problem(1.1)–(1.2)admits a unique global smooth solution(u,H).
Notations.We introduce some notations which are used in this paper. For 1 ≤p≤∞,Lp=Lp(R3) denotes the usual Lebesgue space with the norm. The usual Sobolev space of ordermis defined bywith the norm
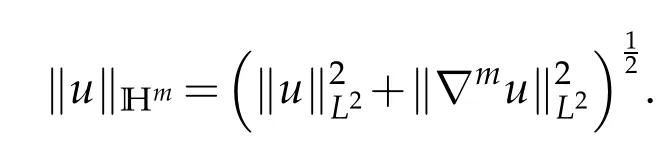
2 Proof of main results
This section is devoted to the proof of main results. We begin with the following lemma which play central role in proving our main results.
Lemma 2.1.([29–31])Assume that f,g,h,?x1f,?x2g,?x3h∈L2,then the following inequality
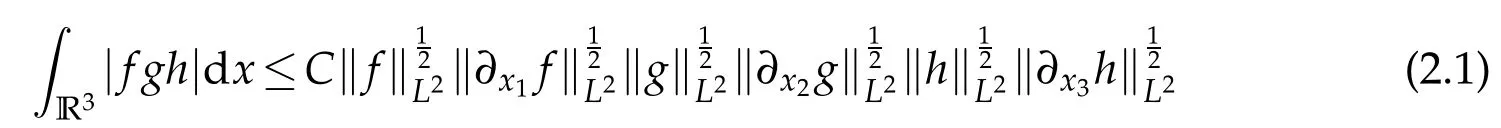
holds.
In what follows,we only give the proof of Theorem 1.1.
Proof.Taking the inner product(1.1)with(u,H)and using integration by parts,we obtain
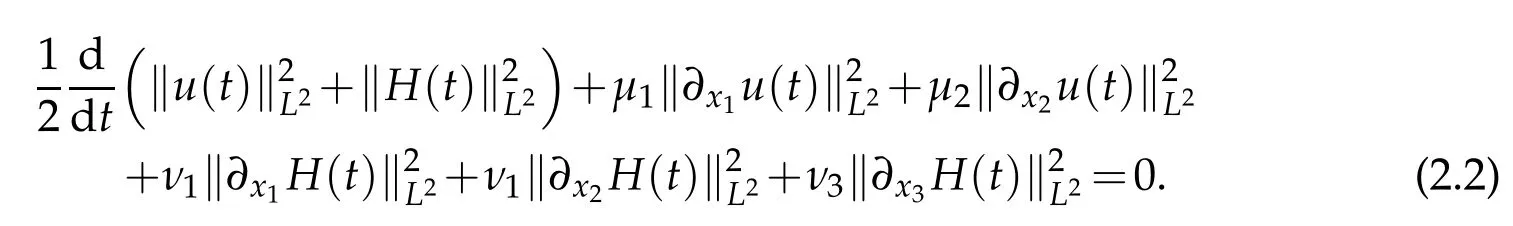
We apply?3xito(1.1)and take the inner product of the resulting equation with(?3xiu,?3xiH),then use integration by parts,make summation ofifrom 1 to 3 and obtain
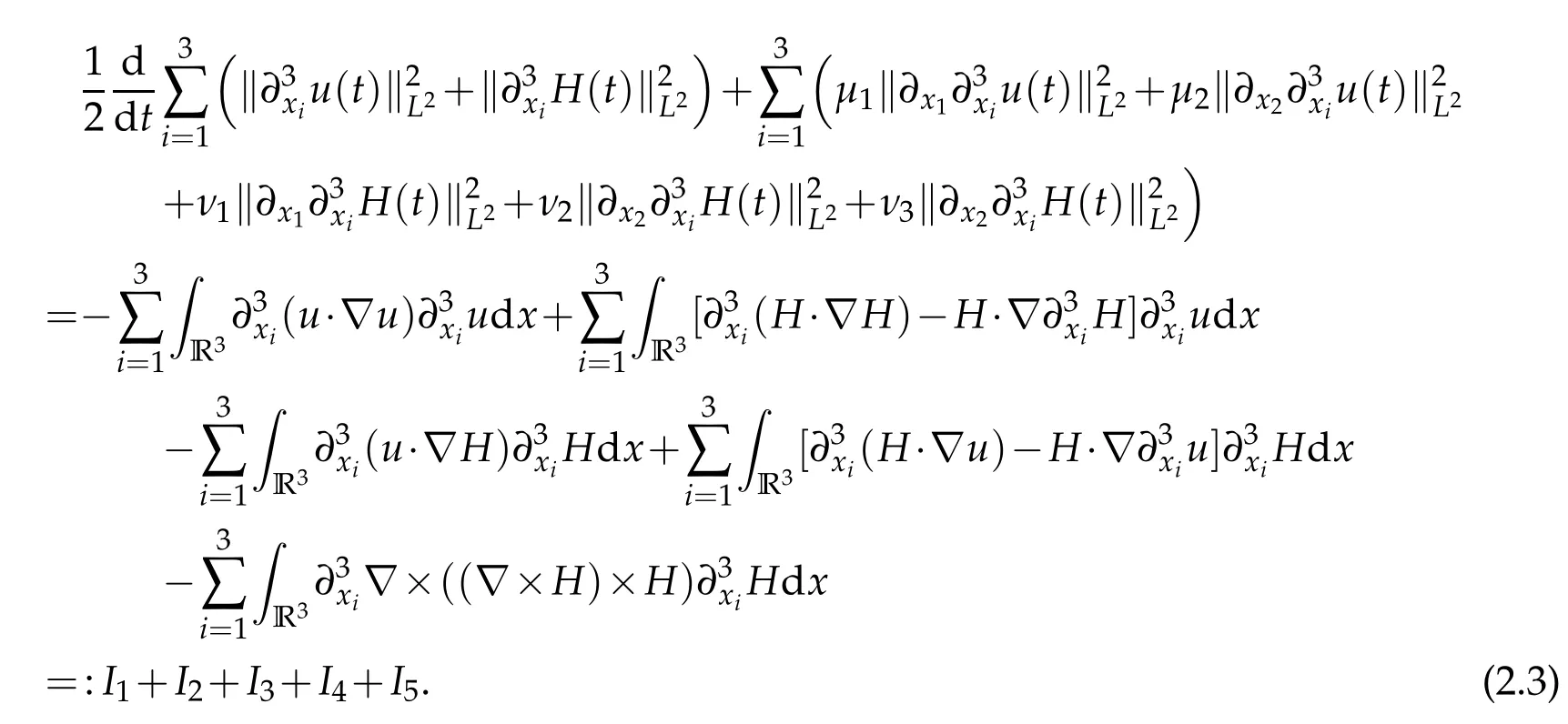
In what follows,we estimateIi(i=1,2,3,4,5). Firstly,I1can be written
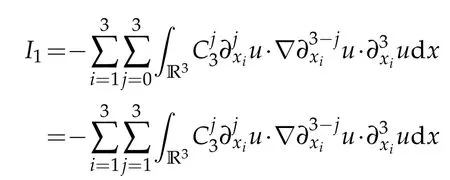
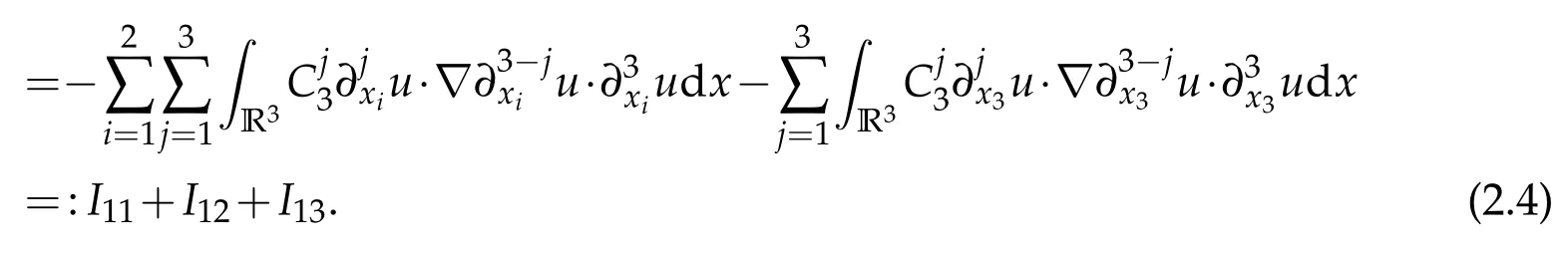
Noting that
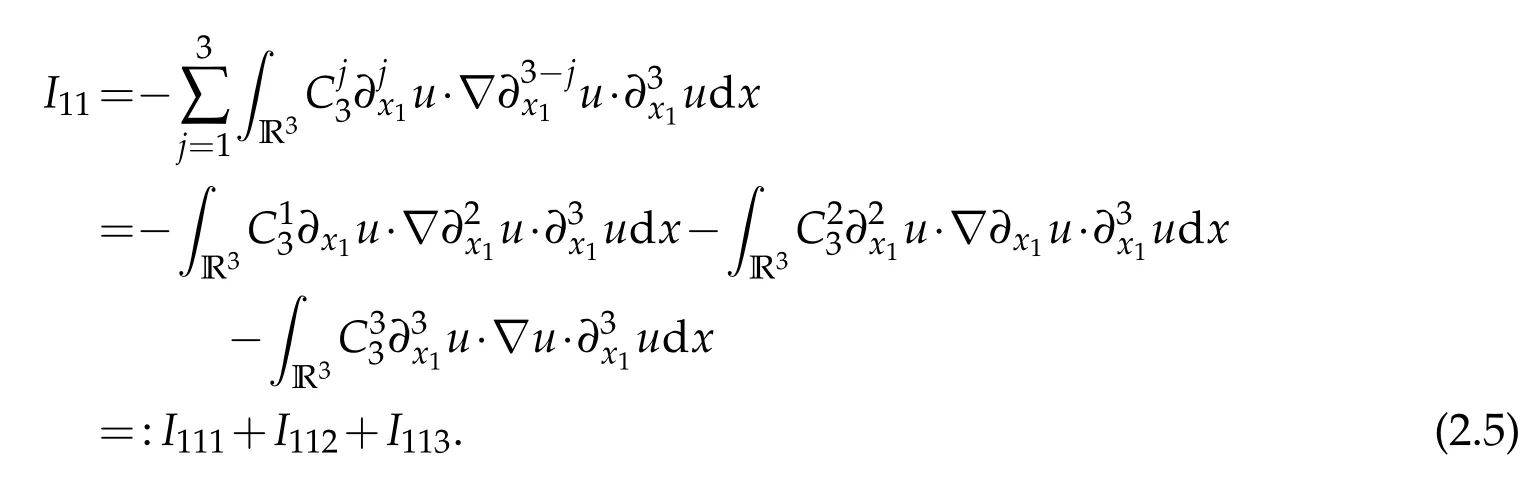
We have from H?lder inequality
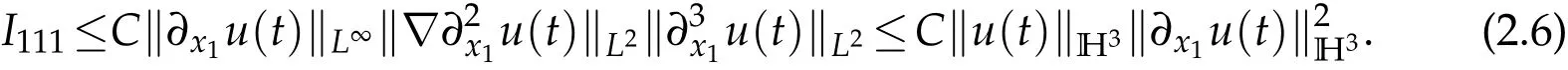
I113can be estimated similarly
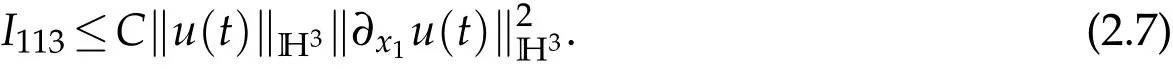
It follows from H?lder inequality and Sobolev embedding theorem that

Using(2.5)-(2.8)gives that
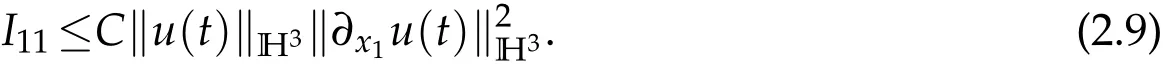
The same produce to lead to(2.9)yields
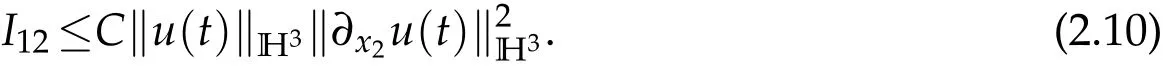
To deal withI13,we writeI13as
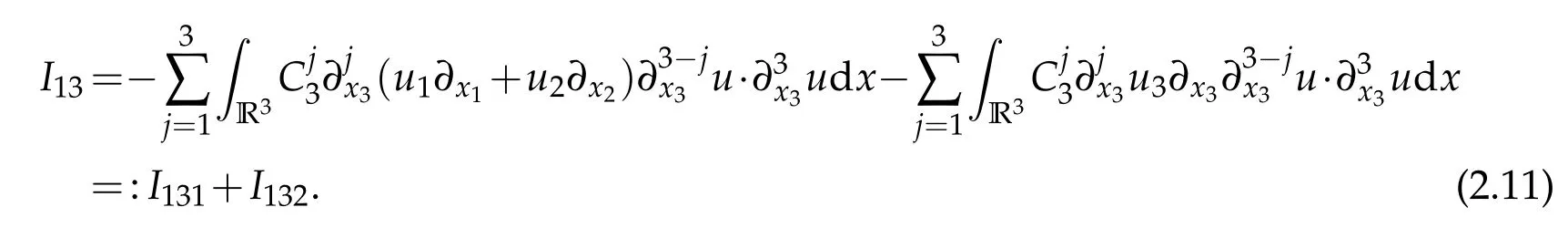
By Lemma 2.1,it holds that
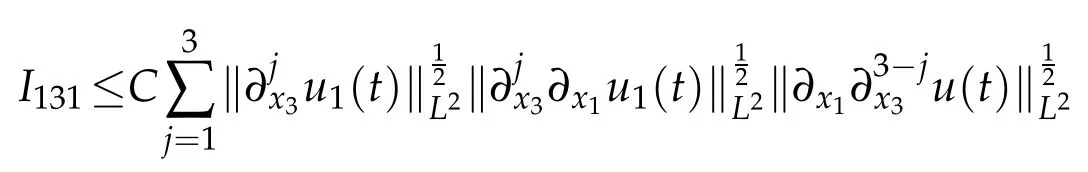
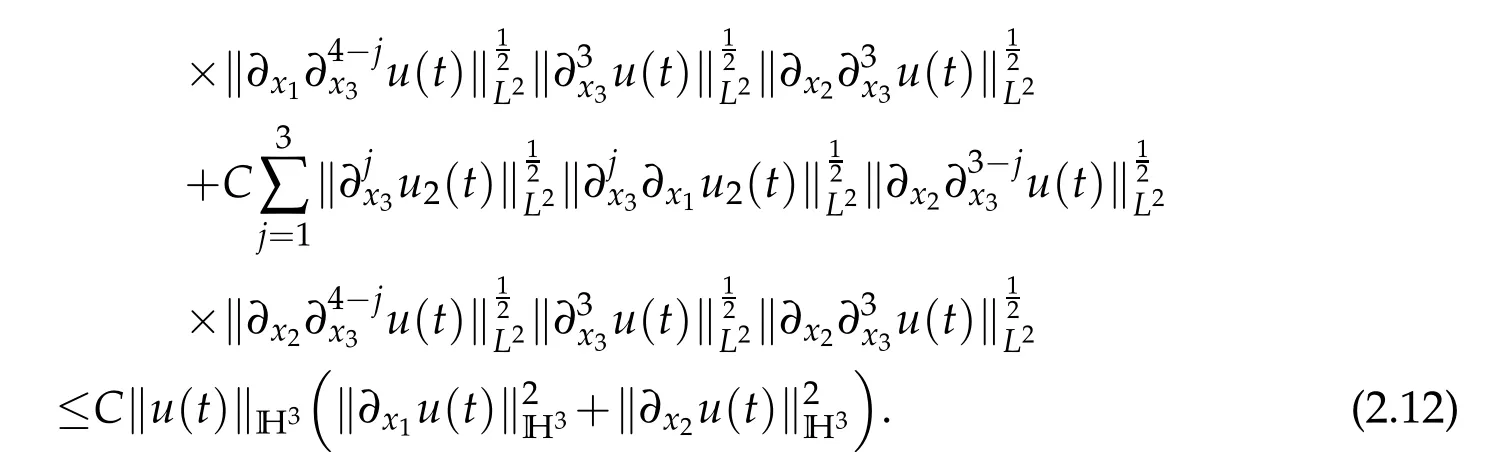
It follows from ▽·u=0 and Lemma 2.1 that
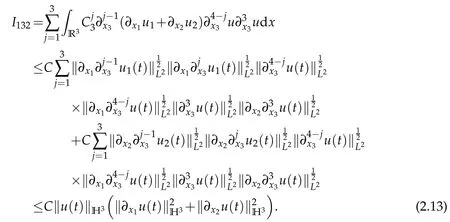
Combining(2.11)–(2.13)yields

We insert(2.9),(2.10)and(2.14)into(2.4)and yields
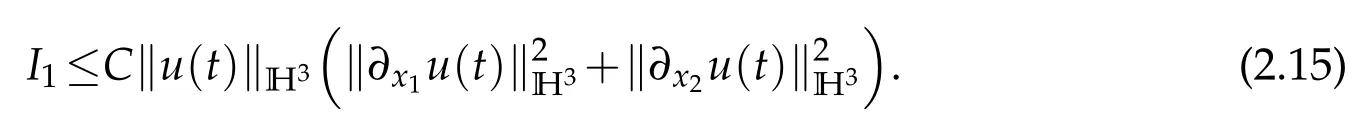
Next,we estimateI2.I2can be written as
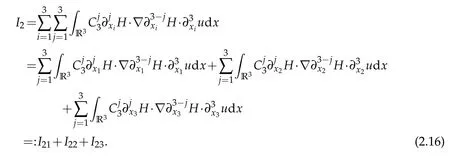
Sobolev embedding theorem and Cauchy inequality entail that
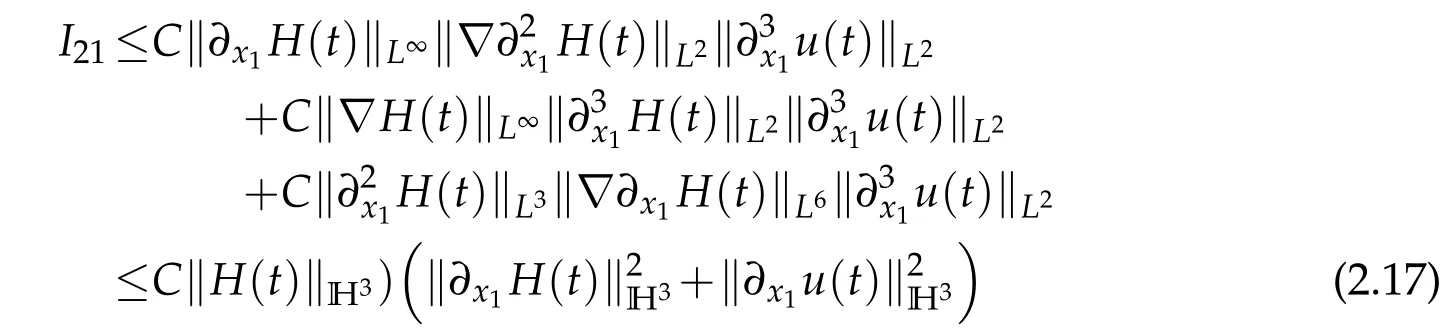
and
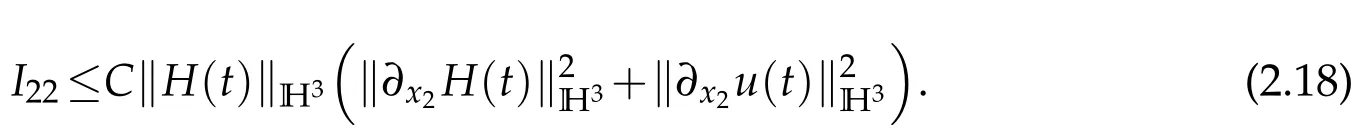
Thanks to Lemma 2.1,we have
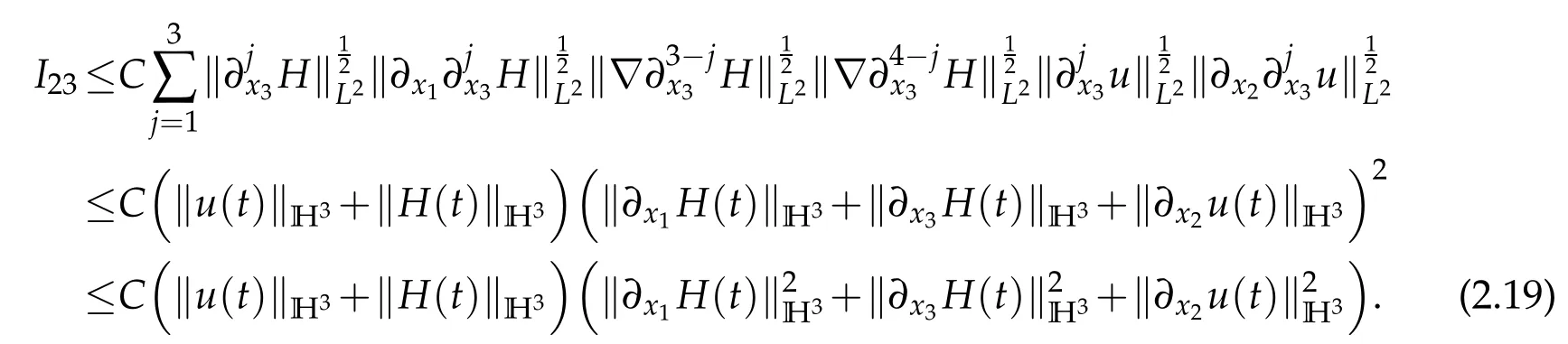
We institute(2.17)–(2.19)into(2.16)and obtain
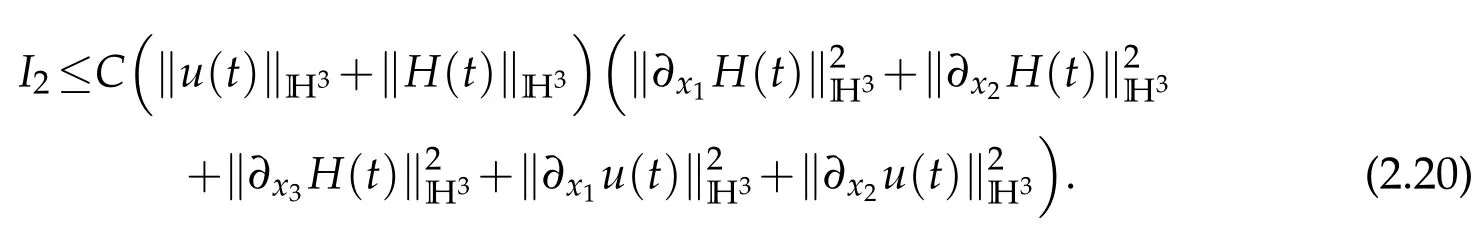
I3can be written as
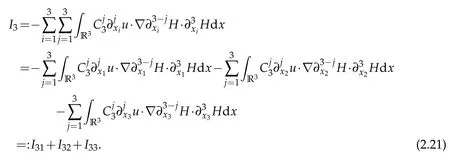
Sobolev embedding theorem and Cauchy inequality entail that
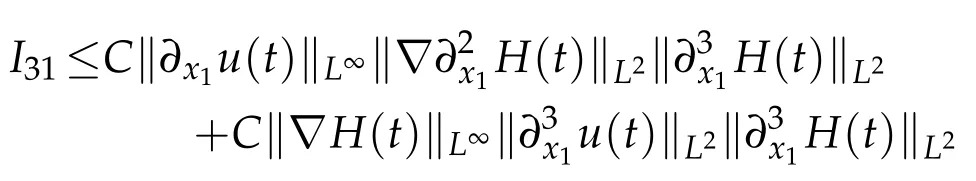
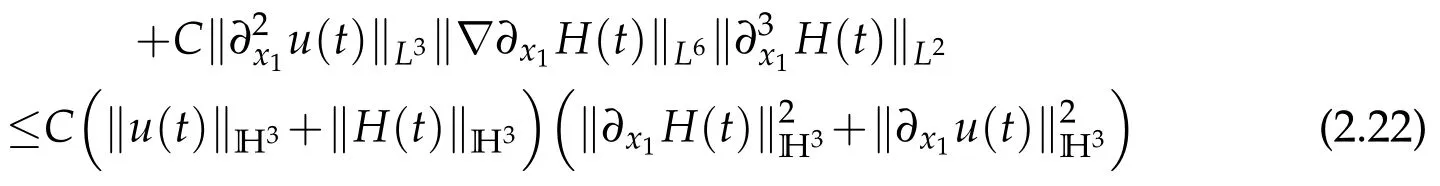
and
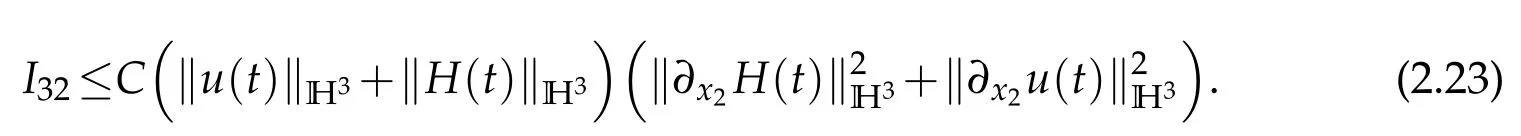
Thanks to Lemma 2.1,we have
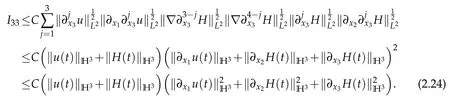
We institute(2.22)–(2.24)into(2.21)and obtain
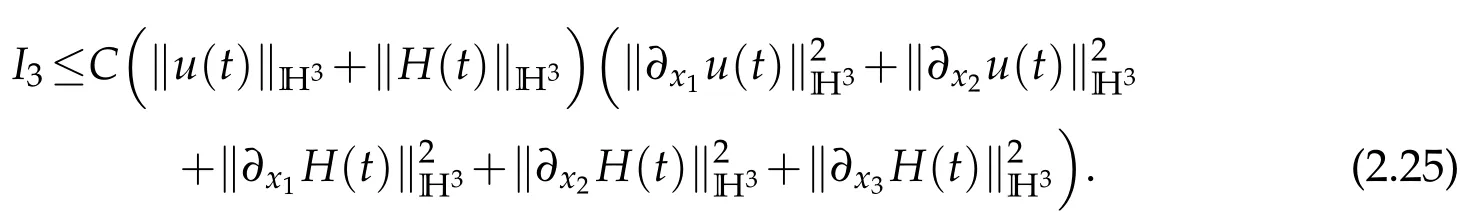
Noting that
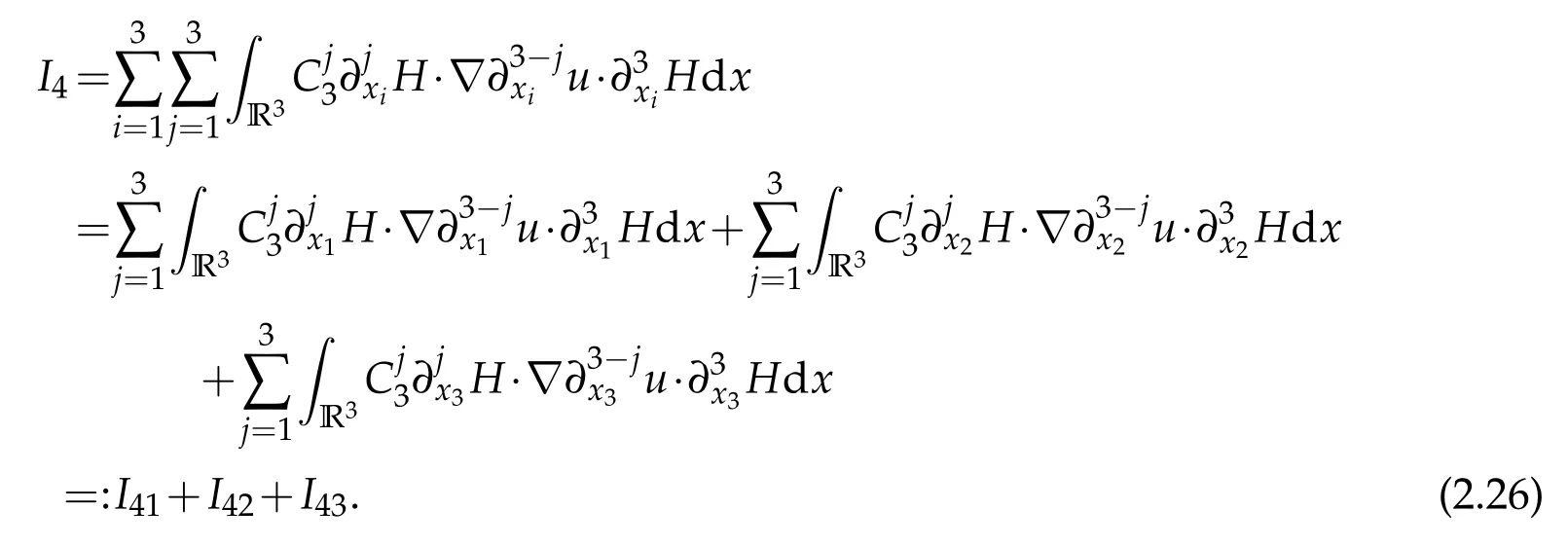
I41can be written as
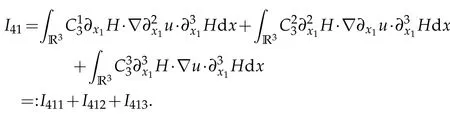
H?lder inequality,Cauchy inequality and Sobolev embedding theorem give
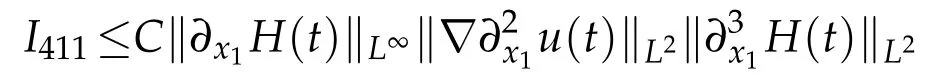
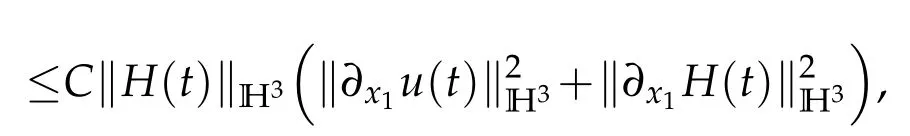
and
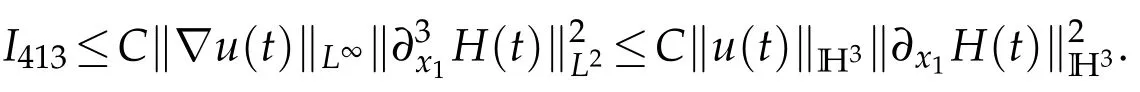
Integration by parts,H?lder inequality and Sobolev embedding theorem entail that
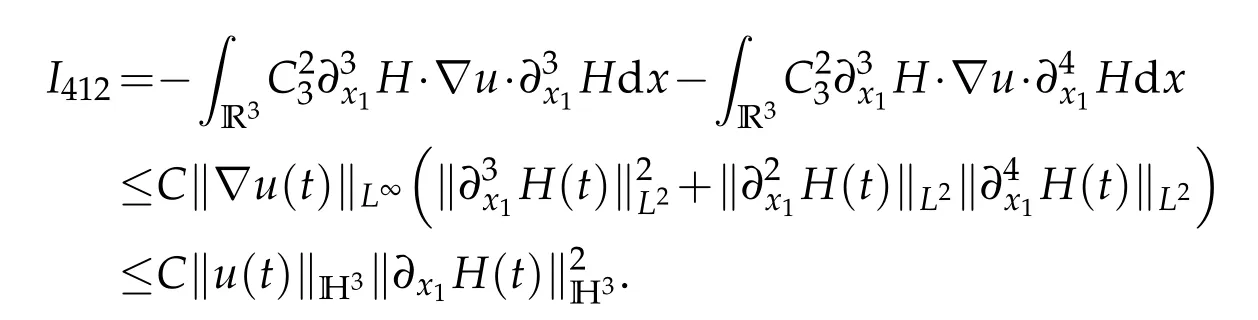
It follows from the above three inequalities that
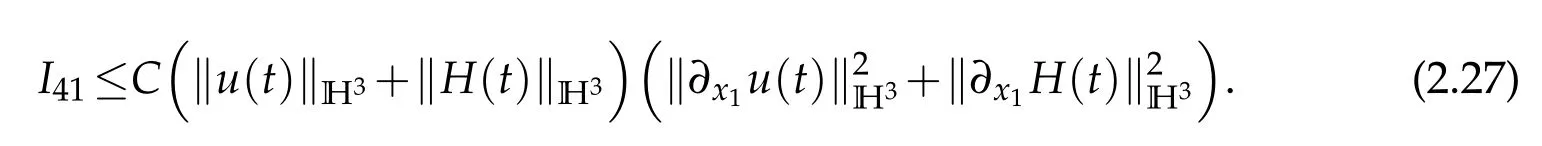
Similarly,it holds that
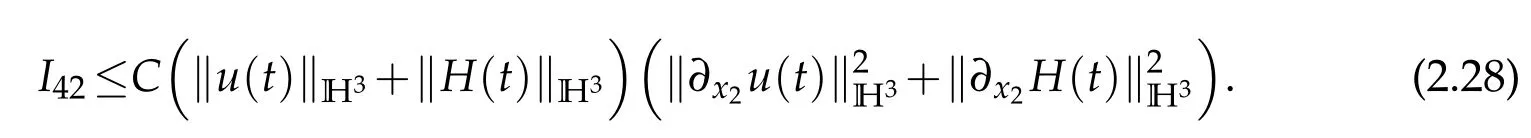
Lemma 2.1 gives
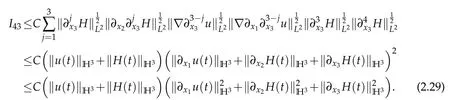
We institute(2.27)–(2.29)into(2.26)and obtain
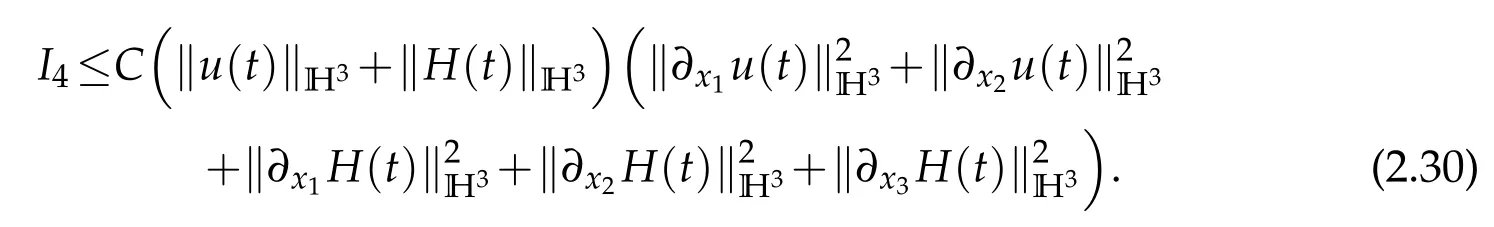
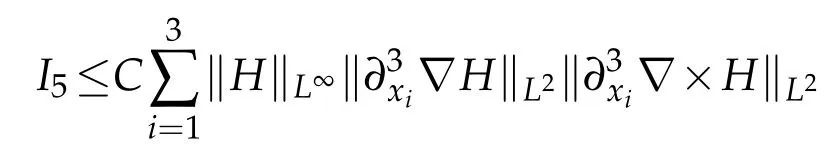
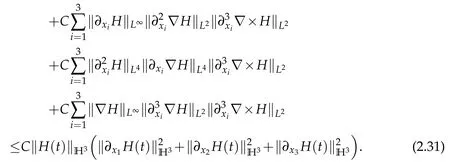
From(2.3),(2.15),(2.20),(2.25),(2.30)and(2.31),we deduce that
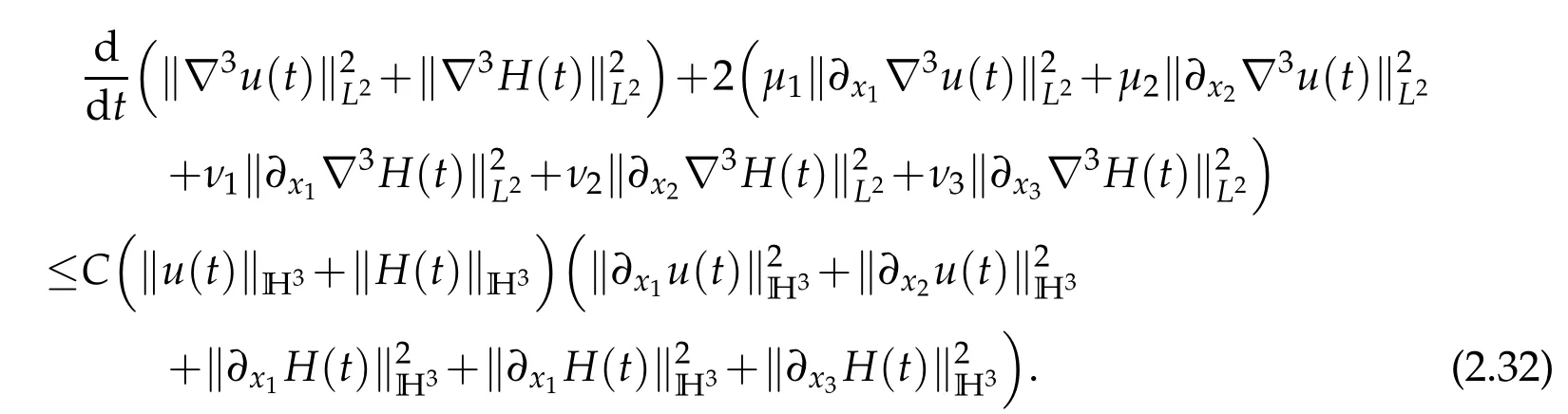
Using(2.2)yields
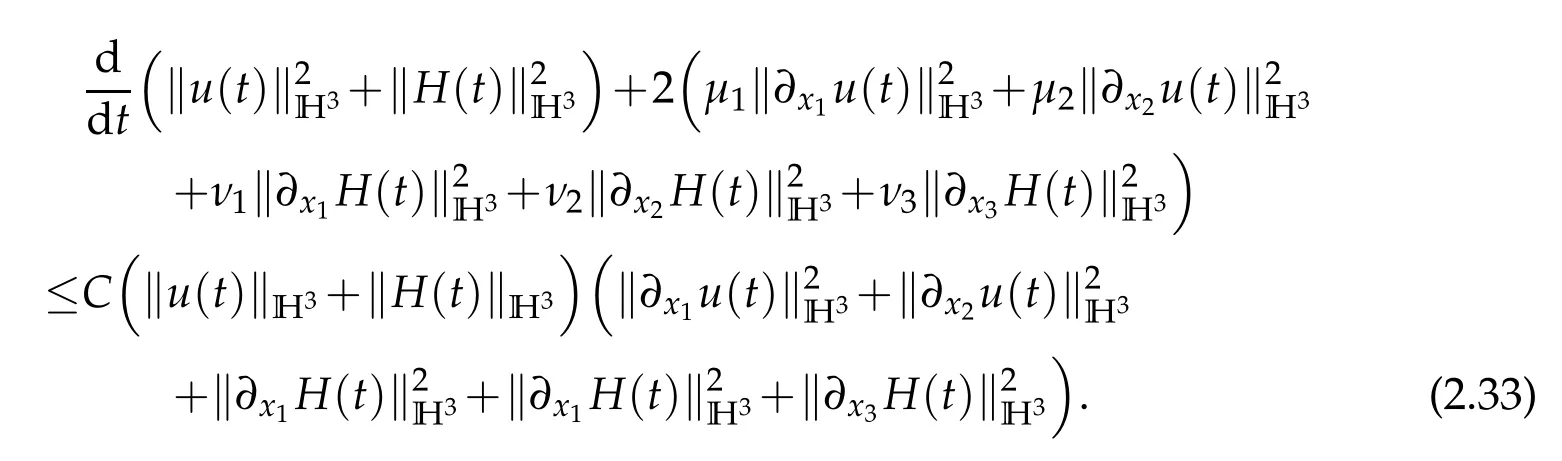
Next we prove global existence of smooth solutions to the problem (1.1), (1.2) by using the bootstrapping argument. Moreover, the inequality (1.3) also holds. Letδ=min{μ1,μ2,ν1,ν2,ν3},we make the ansatz

Then(2.33)and(2.34)imply that
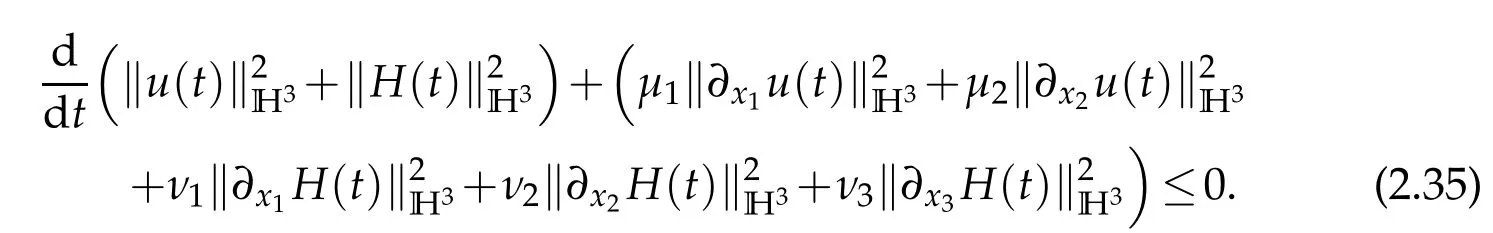
Integrating(2.35)with respect totto yield
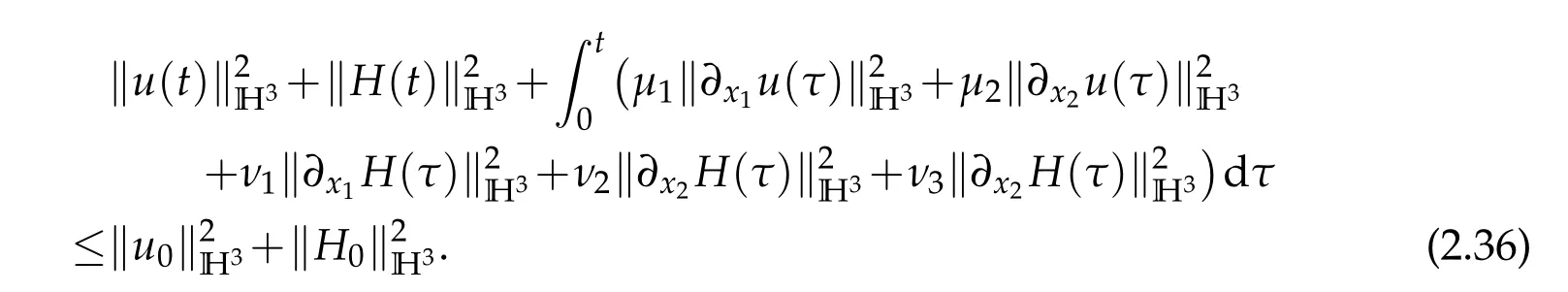
(2.36)entails that
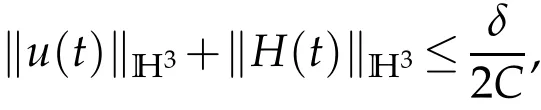
provided that
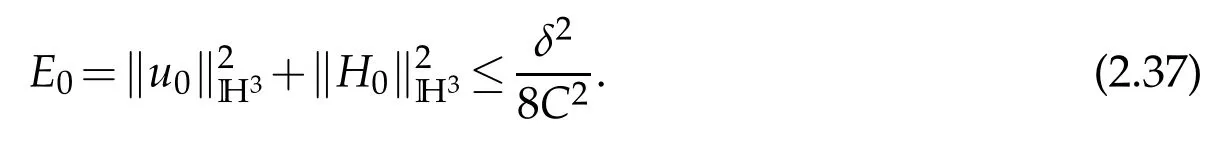
The bootstrapping argument then assesses that(2.36)holds for all time when obeys(2.37).We complete the proof of Theorem 1.1.
3 Appendix
In this section,for the readers’convenience,we give the detail proof of Lemma 2.1. The proof has been given in[27].
Proof.It follows from that the Sobolev embedding theoremH1(R)?→L∞(R)and H?lder’s inequality that

Thus,Lemma 2.1 is proved.
Acknowledgement
The work is partially supported by the NNSF of China (Grant No.11871212) and Basic Research Project of Key Scientific Research Project Plan of Universities in Henan Province(No.20ZX002).
 Journal of Partial Differential Equations2021年1期
Journal of Partial Differential Equations2021年1期
- Journal of Partial Differential Equations的其它文章
- Lower Bound Estimate of Blow Up Time for the Porous Medium Equations under Dirichlet and Neumann Boundary Conditions
- Fixed Point Theorems in Relational Metric Spaces with an Application to Boundary Value Problems
- Finite-Time Blow-Up and Local Existence for Chemotaxis System with a General Memory Term
- The Averaging Principle for Stochastic Fractional Partial Differential Equations with Fractional Noises
- Remarks on Blow-Up Phenomena in p-Laplacian Heat Equation with Inhomogeneous Nonlinearity
- On Free Boundary Problem for the Non-Newtonian Shear Thickening Fluids
